Пирамида

1.

Пирамида.

2.

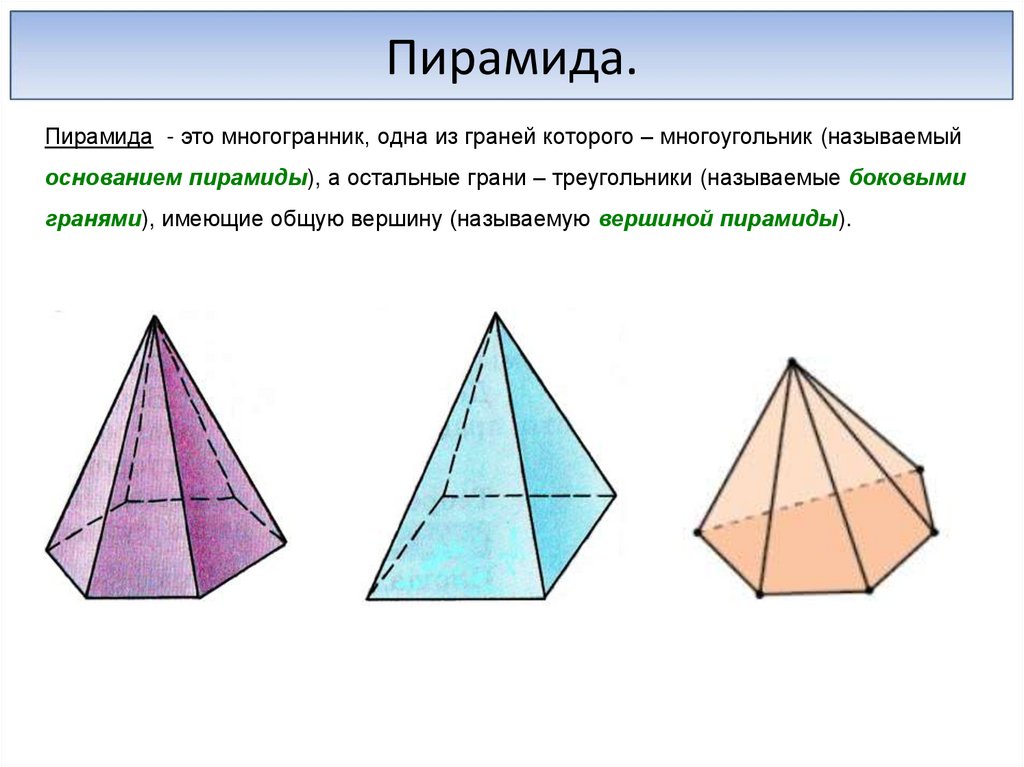
Пирамида.
Пирамида - это многогранник, одна из граней которого – многоугольник (называемый
основанием пирамиды), а остальные грани – треугольники (называемые боковыми
гранями), имеющие общую вершину (называемую вершиной пирамиды).

3.

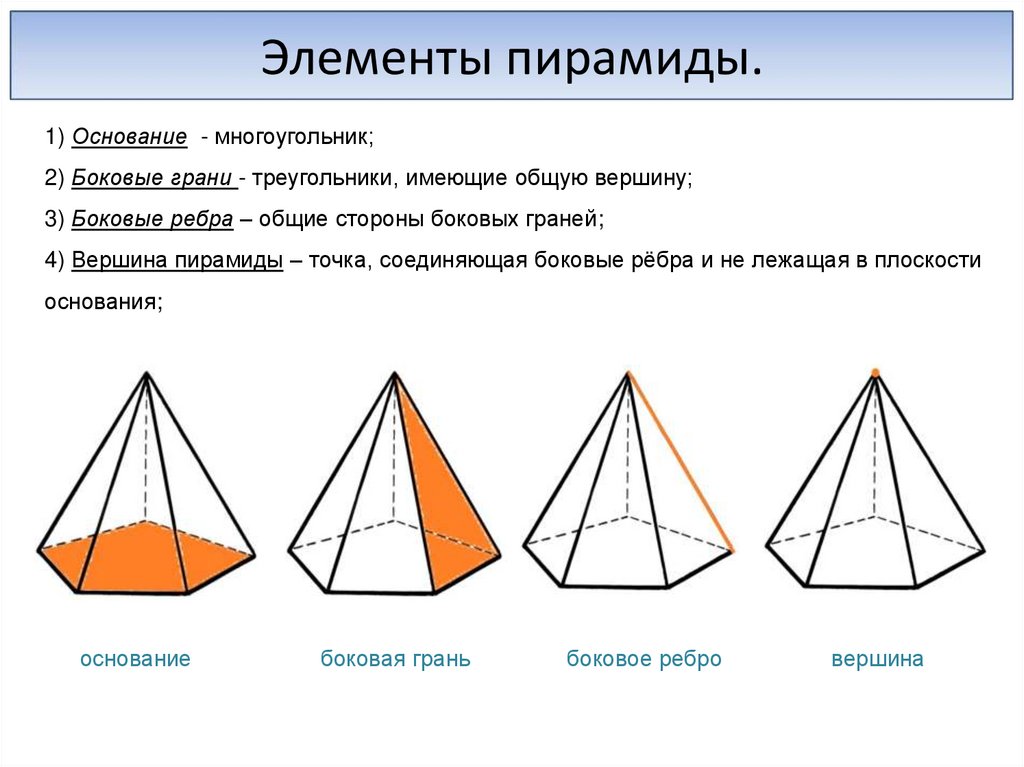
Элементы пирамиды.
1) Основание - многоугольник;
2) Боковые грани - треугольники, имеющие общую вершину;
3) Боковые ребра – общие стороны боковых граней;
4) Вершина пирамиды – точка, соединяющая боковые рёбра и не лежащая в плоскости
основания;
основание
боковая грань
боковое ребро
вершина

4.

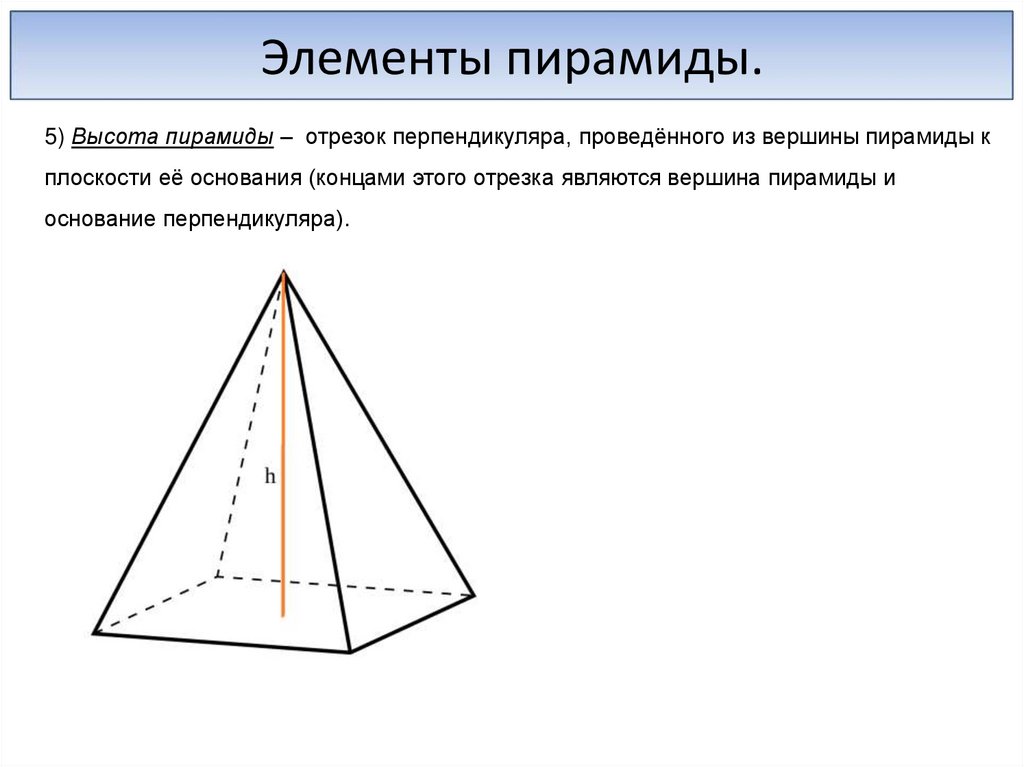
Элементы пирамиды.
5) Высота пирамиды – отрезок перпендикуляра, проведённого из вершины пирамиды к
плоскости её основания (концами этого отрезка являются вершина пирамиды и
основание перпендикуляра).

5.

Название пирамиды.
Название пирамиды формирует многоугольник, расположенный в ее основании. По
числу углов основания пирамиды делят на треугольные, четырехугольные и т. д.

6.

Особые случаи пирамид:
1)
Прямоугольная пирамида – это пирамида, в которой одно из боковых рёбер
перпендикулярно основанию.
В этом случае, это ребро и будет высотой пирамиды.
h

7.

Особые случаи пирамид:
2)
Наклонная пирамида – это пирамида, в которой основание высоты лежит за
пределами основания пирамиды.
h

8.

Особые случаи пирамид:
3)
Правильная пирамида – это пирамида, у которой основанием является
правильный многоугольник, и основание высоты совпадает с центром этого
многоугольника.

9.

Свойства правильной пирамиды:
1) Все боковые ребра правильной пирамиды равны;
2) Все боковые грани правильной пирамиды – это равные равнобедренные
треугольники;
3) Все апофемы правильной пирамиды равны.
Апофема
–
это
высота
боковой
грани
пирамиды, проведенная из вершины пирамиды
(на рисунке – отрезок PH).
Обозначение апофемы – d.
правильной

10.

Свойства пирамиды:
1)
Если все боковые ребра пирамиды равны, то:
около основания пирамиды можно описать окружность,
причём вершина пирамиды проецируется в её центр;
боковые ребра образуют с плоскостью основания
равные углы.
Верно и обратное.

11.

Свойства пирамиды:
2)
Если все грани пирамиды наклонены к плоскости основания под одним углом, то:
в основание пирамиды можно вписать окружность, причём вершина пирамиды
проецируется в её центр.
Верно и обратное.

12.

Поверхность пирамиды.
1) Боковая поверхность пирамиды – это сумма площадей боковых граней пирамиды.
Sб.п. = S1 + S2 + S3 + S4
2) Полная поверхность пирамиды – это сумма площадей всех граней пирамиды.
Sп.п. = Sб.п. + Sосн
Sосн
S1
S2
S3
S4

13.

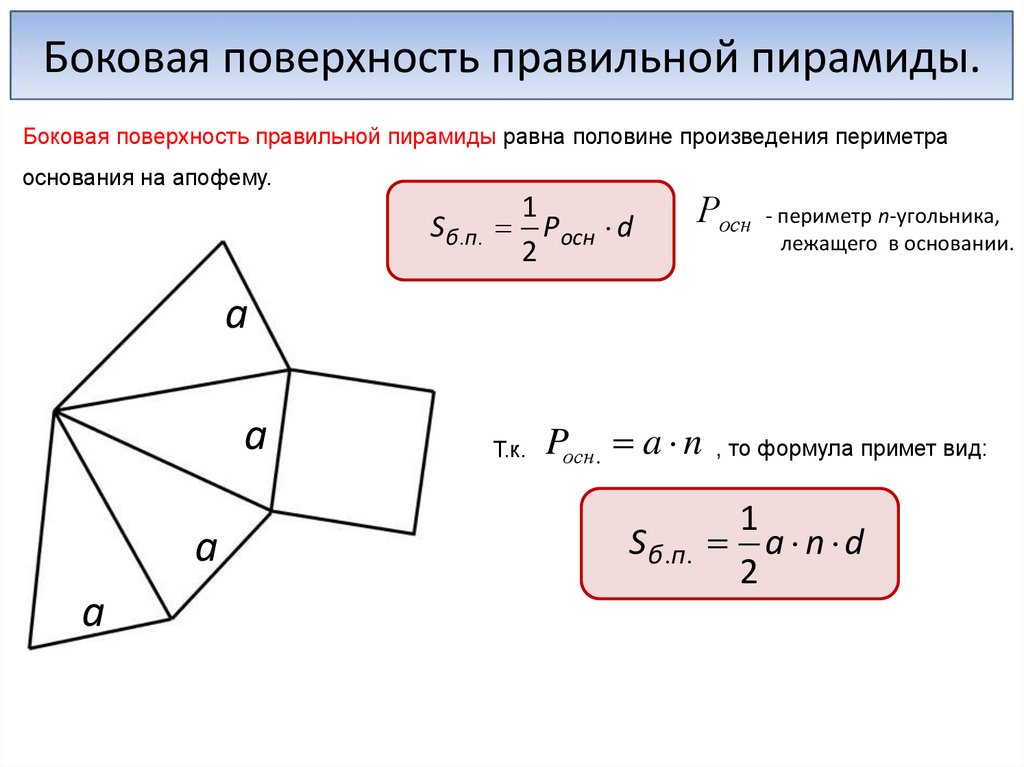
Боковая поверхность правильной пирамиды.
Боковая поверхность правильной пирамиды равна половине произведения периметра
основания на апофему.
1
S б .п . Р осн d
2
Росн - периметр n-угольника,
лежащего в основании.
a
a
a
a
Т.к.
Pосн. a n , то формула примет вид:
1
Sб .п . a n d
2

14.

Объем пирамиды.
Объем пирамиды равен одной трети произведения площади основания на высоту.
1
V S осн h
3

15.

Усеченная пирамида.

16.

Усеченная пирамида.
Усеченная пирамида – это такой многогранник, который образован пирамидой и ее
сечением, параллельным основанию.

17.

Элементы усеченной пирамиды.
1) Основания (нижнее и верхнее) – подобные многоугольники;
2) Боковые грани – трапеции;
3) Боковые ребра – общие стороны боковых граней;
4) Высота усеченной пирамиды – расстояние между основаниями.
основания
боковая грань
боковое ребро
высота

18.

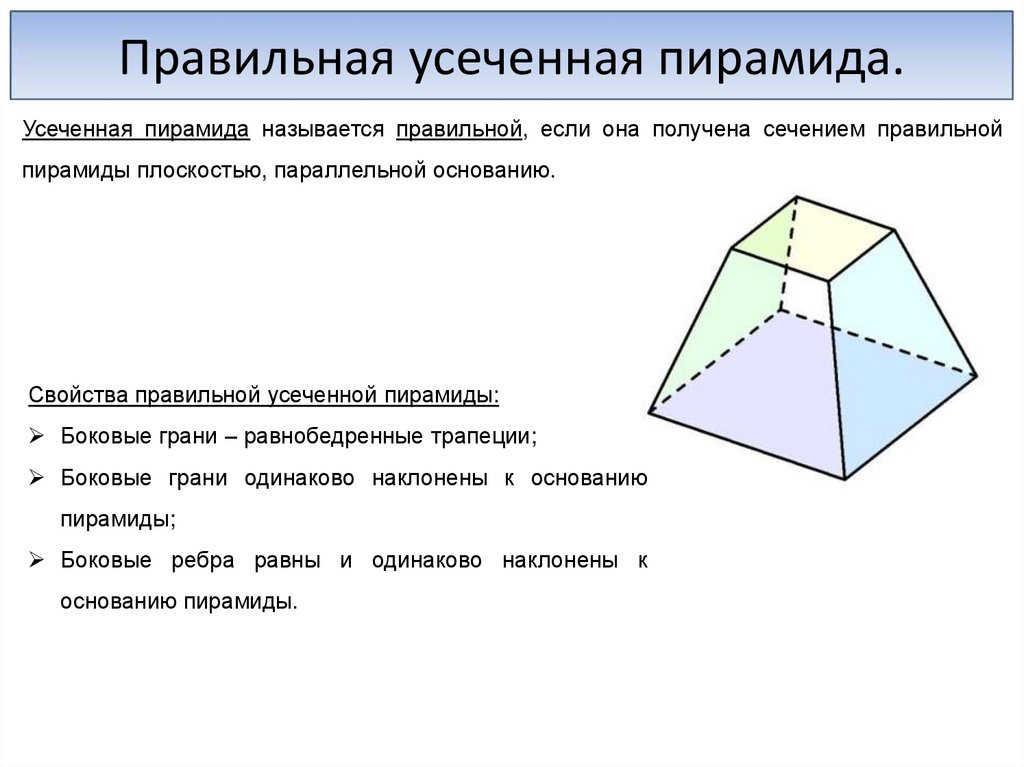
Правильная усеченная пирамида.
Усеченная пирамида называется правильной, если она получена сечением правильной
пирамиды плоскостью, параллельной основанию.
Свойства правильной усеченной пирамиды:
Боковые грани – равнобедренные трапеции;
Боковые грани одинаково наклонены к основанию
пирамиды;
Боковые ребра равны и одинаково наклонены к
основанию пирамиды.

19.

Развертка усеченной пирамиды.
Подумайте, как будет выглядеть развертка правильной треугольной усеченной пирамиды.
На развертке будут изображены следующие плоские фигуры:
Основания –
подобные равносторонние треугольники;
Боковые грани –
три равных равнобедренных трапеции.

20.

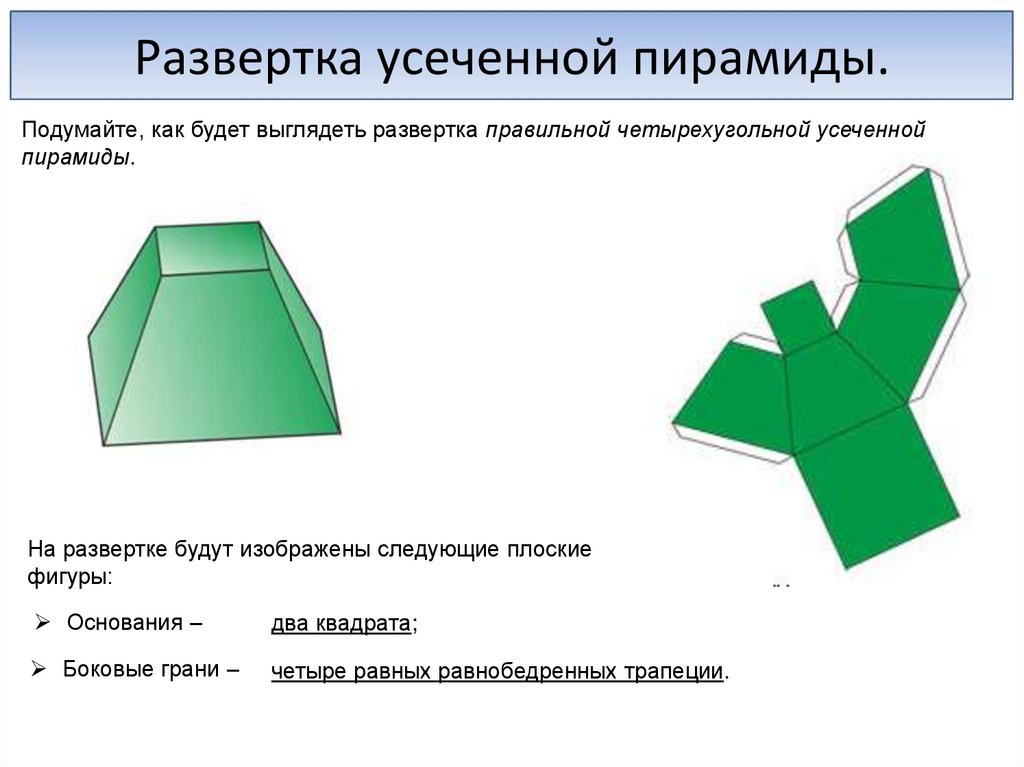
Развертка усеченной пирамиды.
Подумайте, как будет выглядеть развертка правильной четырехугольной усеченной
пирамиды.
На развертке будут изображены следующие плоские
фигуры:
Основания –
два квадрата;
Боковые грани –
четыре равных равнобедренных трапеции.

21.

Поверхность усеченной пирамиды.
1) Боковая поверхность усеченной пирамиды – это сумма площадей боковых граней
усеченной пирамиды.
Sб.п. = S1 + S2 + S3 + S4 + S5
2) Полная поверхность усеченной пирамиды – это сумма площадей всех граней
пирамиды.
Sп.п. = Sб.п. + Sв.осн. + Sн.осн.
S5
Sв.осн.
S4
S3
S1
S2
Sн.осн.

22.

Боковая поверхность правильной усеченной пирамиды.
Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы
периметров оснований на апофему.
1
Sб .п. ( Рв .осн. Рн.осн. ) d
2
Рв .осн. - периметр верхнего основания
Рн.осн. - периметр нижнего основания

23.

Объем усеченной пирамиды.