Усеченная пирамида

1.

2.

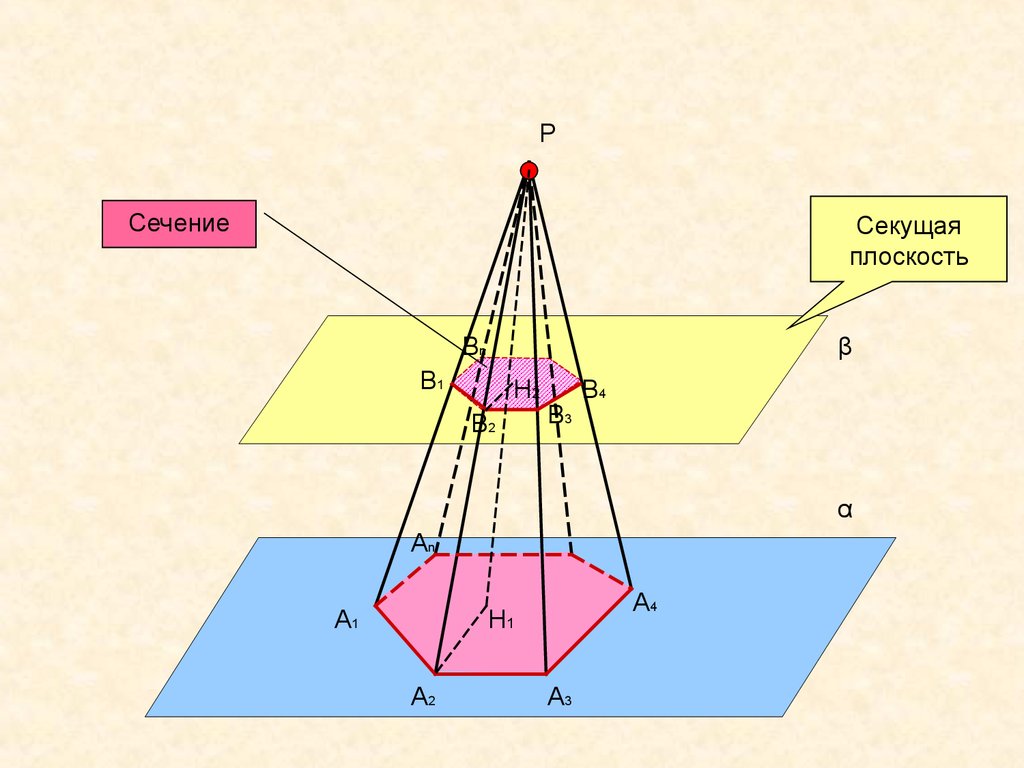
P
Сечение
Секущая
плоскость
Вn
β
В1
Н2
В2
В3
В4
α
An
A1
A4
Н1
A2
A3

3.

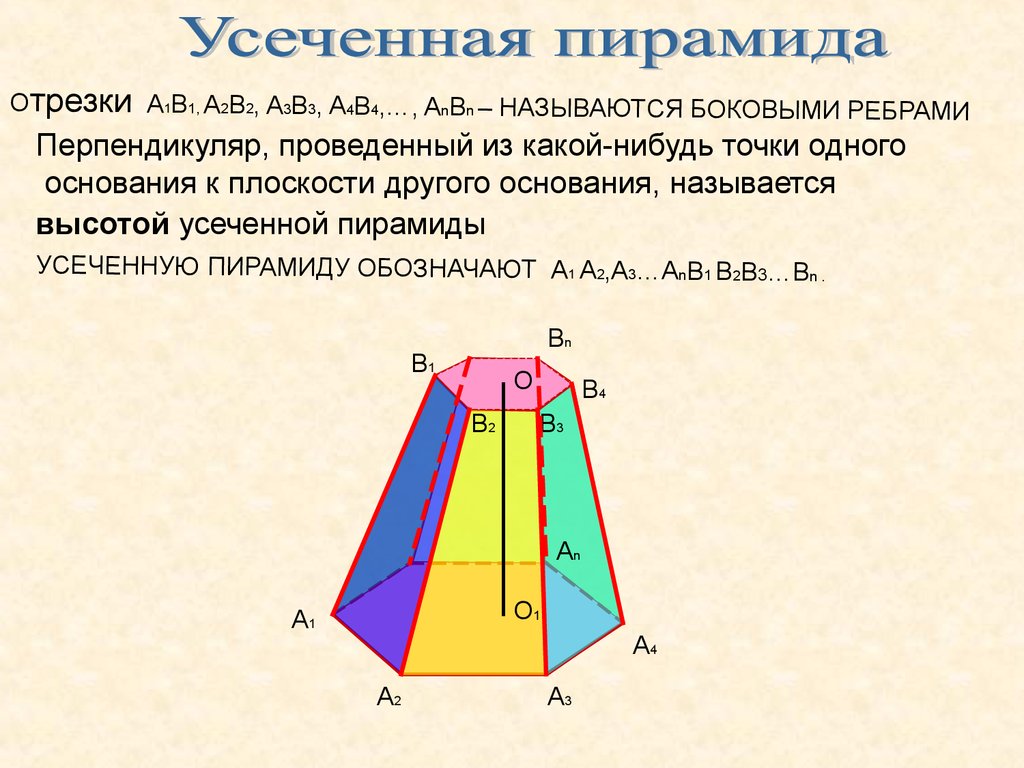
Отрезки A1В1, A2В2, A3В3, A4В4,…, AnВn – НАЗЫВАЮТСЯ БОКОВЫМИ РЕБРАМИ
Перпендикуляр, проведенный из какой-нибудь точки одного
основания к плоскости другого основания, называется
высотой усеченной пирамиды
УСЕЧЕННУЮ ПИРАМИДУ ОБОЗНАЧАЮТ A1 A2,A3…AnВ1 В2В3…Вn .
Вn
В1
О
В2
В4
В3
An
О1
A1
A4
A2
A3

4.

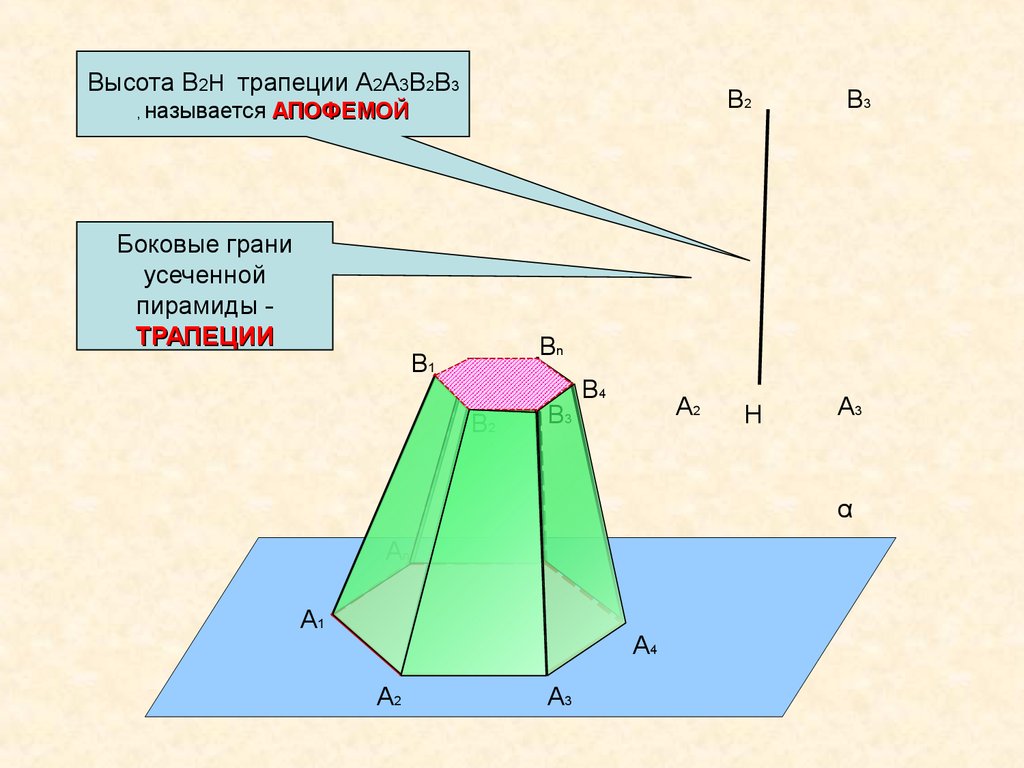
Высота B2H трапеции A2A3B2B3
,
В2
называется АПОФЕМОЙ
Боковые грани
усеченной
пирамиды ТРАПЕЦИИ
В3
Вn
В1
В2
В3
В4
A2
H
A3
α
An
A1
A4
A2
A3

5.

Усеченная пирамида называется правильной, если она
получена сечением правильной пирамиды плоскостью,
параллельной основанию.
Основания правильной усеченной пирамиды — правильные
многоугольники, а боковые грани — равнобедренные
P
трапеции.
Равнобедренная трапеция
Правильный многоугольник
В1
β
Вn
В4
В2
В3
An
α
A1
A4
A2
A3

6.

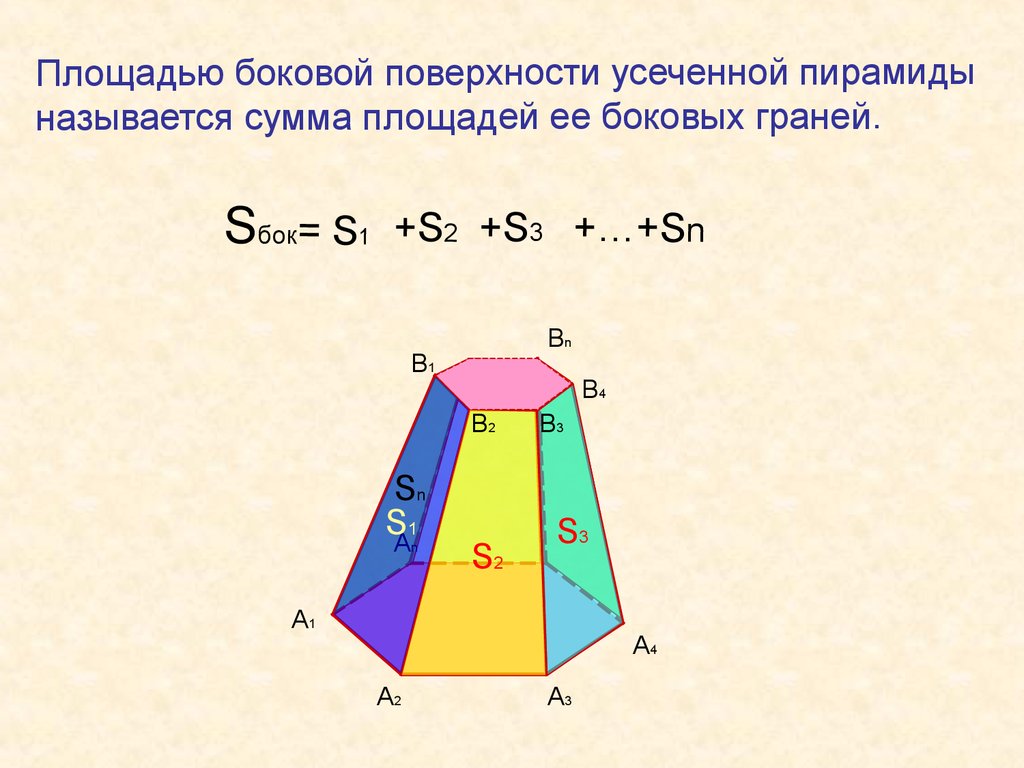
Площадью боковой поверхности усеченной пирамиды
называется сумма площадей ее боковых граней.
Sбок= S1
+S2 +S3 +…+Sn
Вn
В1
В4
В2
Sn
S1
An
S2
В3
S3
A1
A4
A2
A3

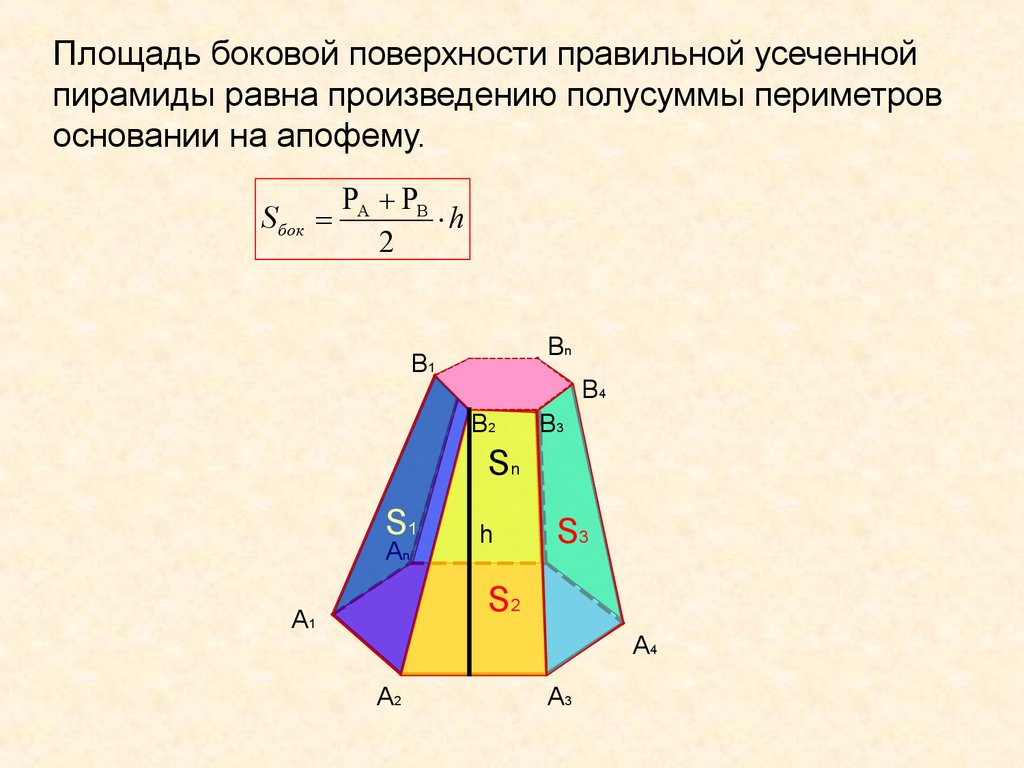
7.

Площадь боковой поверхности правильной усеченной
пирамиды равна произведению полусуммы периметров
основании на апофему.
S бок
PА PВ
h
2
Вn
В1
В4
В2
В3
Sn
S1
An
h
S3
S2
A1
A4
A2
A3

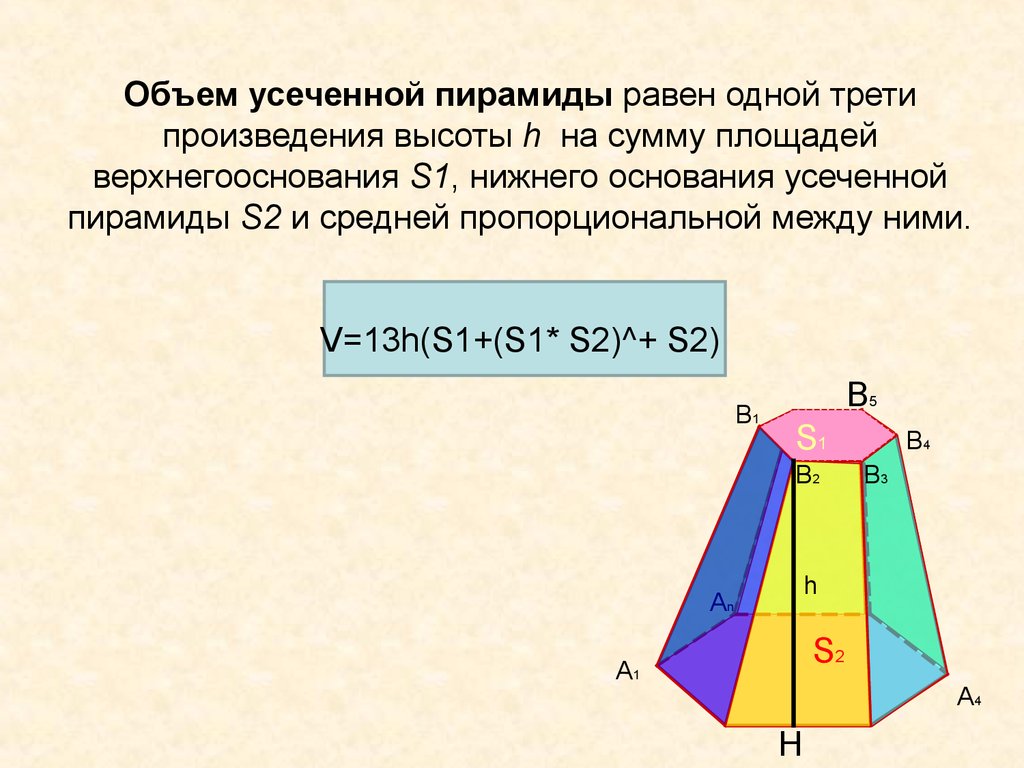
8. Объем усеченной пирамиды равен одной трети произведения высоты h  на сумму площадей верхнегооснования S1, нижнего основания усеченной пи

Объем усеченной пирамиды равен одной трети
произведения высоты h на сумму площадей
верхнегооснования S1, нижнего основания усеченной
пирамиды S2 и средней пропорциональной между ними.
V=13h(S1+(S1* S2)^+ S2)
В1
В5
S1
В2
В4
В3
h
An
S2
A1
A4
H

9. Спасибо за внимание!!!