Презентация6 слайды

1. Инженерная и компьютерная графика

МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Самарский государственный технический университет»
(ФГБОУ ВО «СамГТУ»)
Кафедра «Архитектурно-строительная графика и изобразительное искусство»
Проекции с числовыми отметками
Яшина Наталья Анатольевна – старший преподаватель
кафедры АСГиИИ
САМАРА 2020 г.

2.

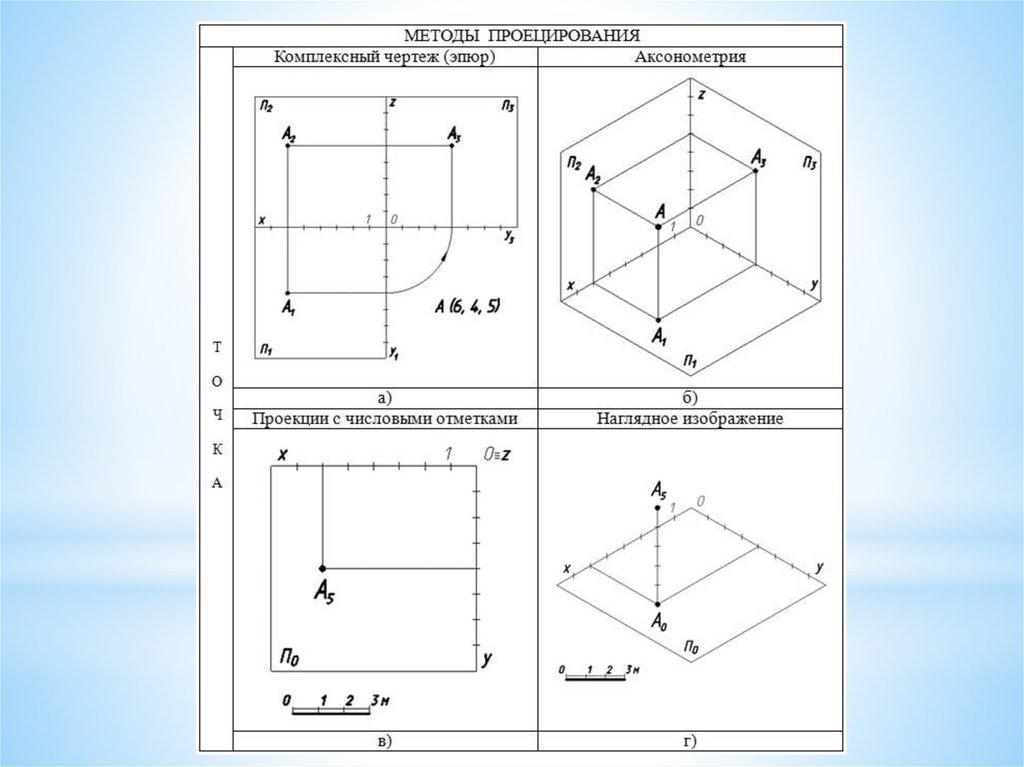
Построения изображений основаны на правилах проецирования.
Наиболее широко используются следующие графические чертежи:
комплексный чертеж,
аксонометрический чертеж,
чертеж в проекциях с числовыми отметками.
Чертеж в проекциях с числовыми отметками
В строительных и горных чертежах очень широко применяют метод
проекций с числовыми отметками. Сущность данного метода заключается в
том, что проецирование ведется ортогонально на одну плоскость проекций
(горизонтальную), называемую плоскостью нулевого уровня. Но одна
проекция не определяет положения предмета в пространстве, поэтому
фронтальную проекцию заменяют числами-отметками, которые пишут справа
от горизонтальных проекций точек, например А5. Отметки показывают высоту
(обычно в метрах) от точек до плоскости нулевого уровня.

3.

4.

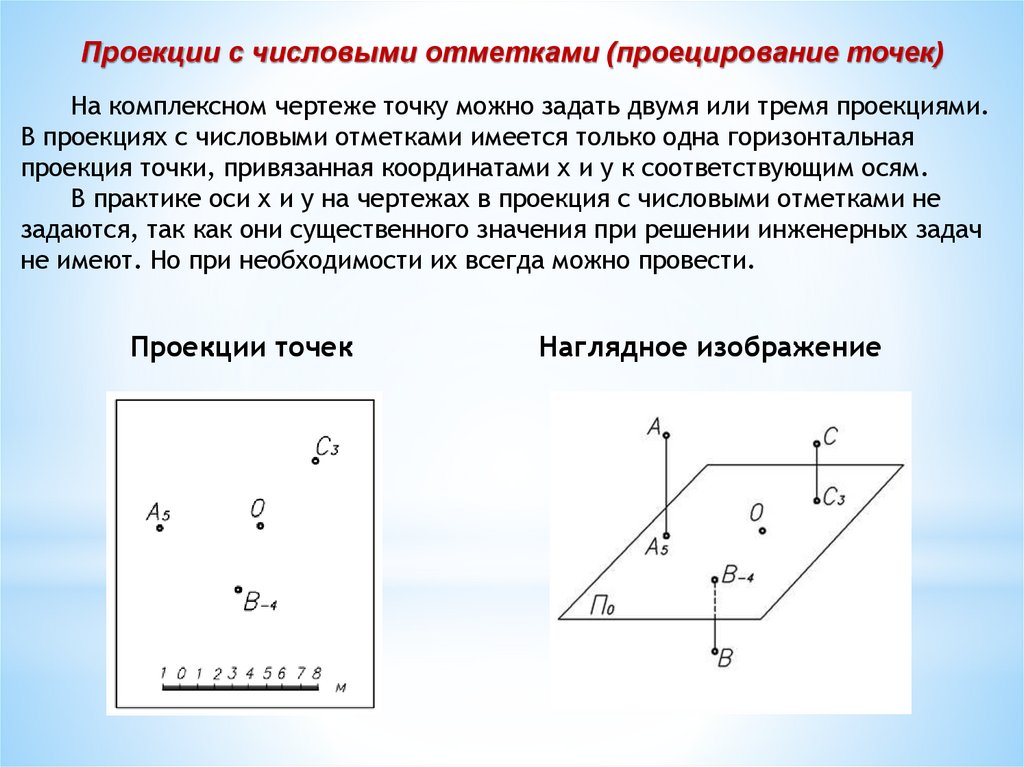
Проекции с числовыми отметками (проецирование точек)
На комплексном чертеже точку можно задать двумя или тремя проекциями.
В проекциях с числовыми отметками имеется только одна горизонтальная
проекция точки, привязанная координатами х и у к соответствующим осям.
В практике оси х и у на чертежах в проекция с числовыми отметками не
задаются, так как они существенного значения при решении инженерных задач
не имеют. Но при необходимости их всегда можно провести.
Проекции точек
Наглядное изображение

5.

Проекцией точки в проекциях с числовыми отметками является точка,
обозначенная либо буквой, рядом с которой ставится отметка этой точки,
либо самой отметкой.
Точки, находящиеся ниже плоскости нулевого уровня, имеют
отрицательные отметки, которые пишутся со знаком минус.
Все чертежи с числовыми отметками сопровождают линейным
масштабом, который указывается проградуированной двойной линией,
сплошной основной и сплошной тонкой:

6.

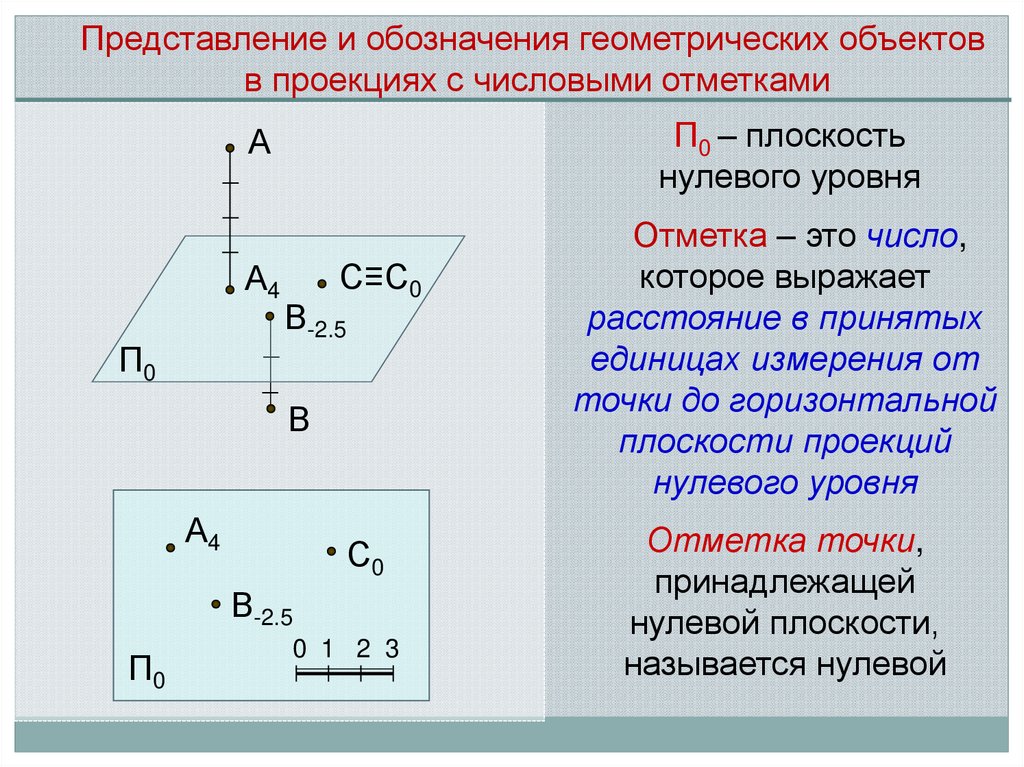
Представление и обозначения геометрических объектов
в проекциях с числовыми отметками
П0 – плоскость
нулевого уровня
А
А4
П0
С≡С0
В-2.5
В
А4
С0
В-2.5
П0
0 1 2 3
Отметка – это число,
которое выражает
расстояние в принятых
единицах измерения от
точки до горизонтальной
плоскости проекций
нулевого уровня
Отметка точки,
принадлежащей
нулевой плоскости,
называется нулевой

7.

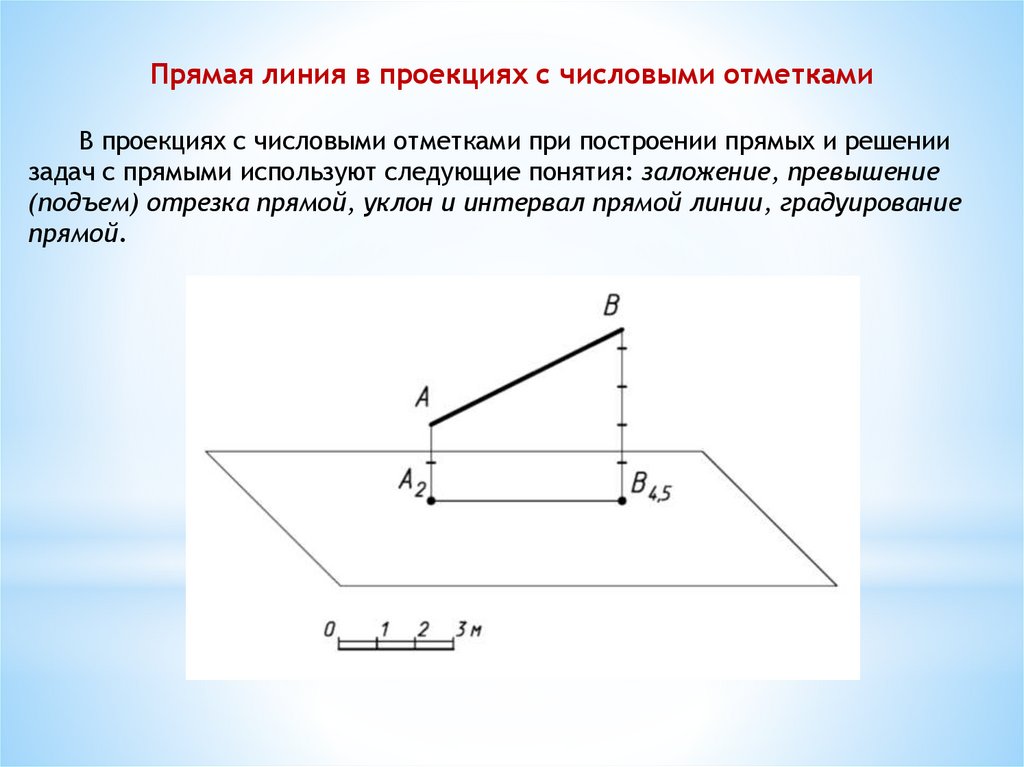
Прямая линия в проекциях с числовыми отметками
В проекциях с числовыми отметками при построении прямых и решении
задач с прямыми используют следующие понятия: заложение, превышение
(подъем) отрезка прямой, уклон и интервал прямой линии, градуирование
прямой.

8.

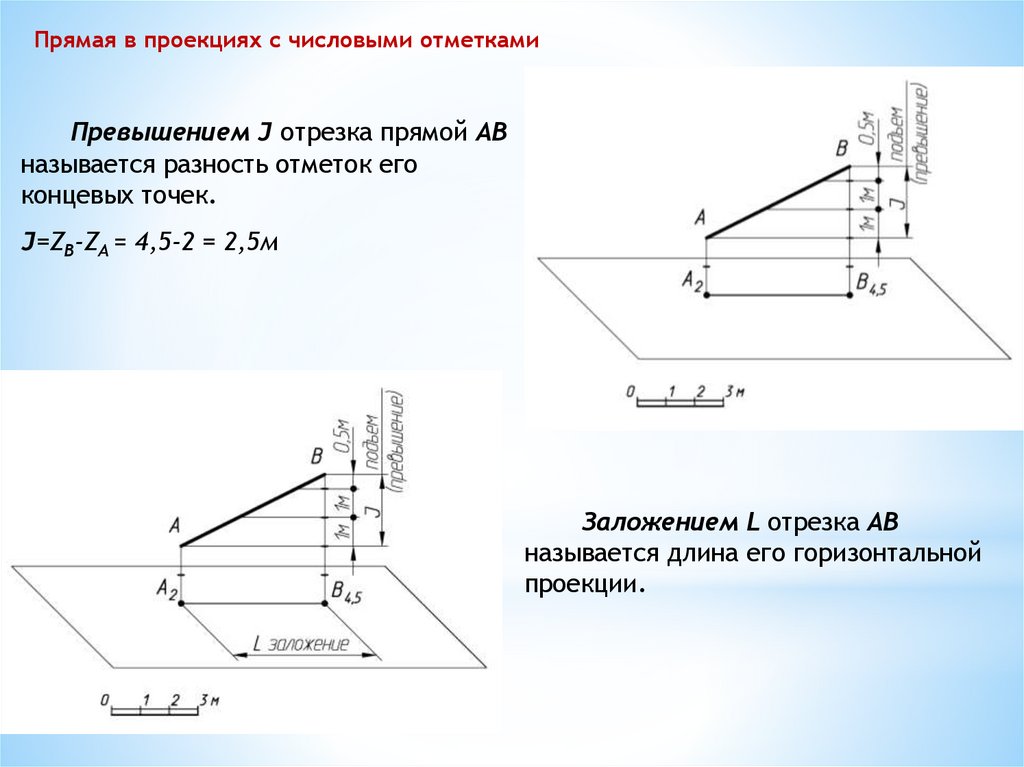
Прямая в проекциях с числовыми отметками
Превышением J отрезка прямой АВ
называется разность отметок его
концевых точек.
J=ZВ-ZА = 4,5-2 = 2,5м
Заложением L отрезка АВ
называется длина его горизонтальной
проекции.

9.

Прямая в проекциях с числовыми отметками
Уклоном прямой i называется
отношение превышения прямой к ее
заложению и определяется тангенсом
угла наклона прямой к плоскости
нулевого уровня П0.
i = J/L= tgφ
Интервалом прямой l
называется часть заложения,
приходящаяся на единицу подъема
(превышения), т.е. на 1 м.
Интервал прямой – это величина,
обратная ее уклону.

10.

Прямые общего и
частного положения

11.

В проекциях с числовыми отметками прямая общего положения
задается:
а) проекциями двух точек отрезка прямой и их отметками;
б) горизонтальной проекцией, отметкой одной из ее точек, стрелкой,
показывающей направление убывание отметок, и уклоном прямой (или углом
наклона прямой к плоскости нулевого уровня);
в) проекцией, одной точкой с числовой отметкой, стрелкой, показывающей
направление убывание отметок, и указанием значения интервала.
а)
б)
в)

12.

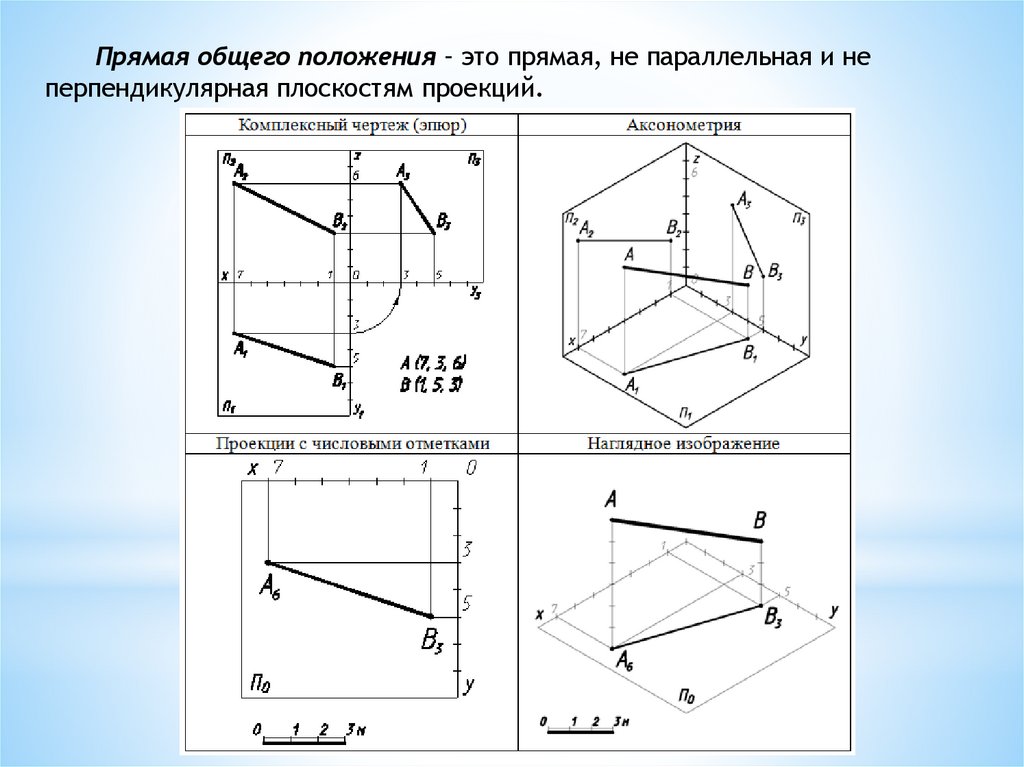
Прямая общего положения – это прямая, не параллельная и не
перпендикулярная плоскостям проекций.

13.

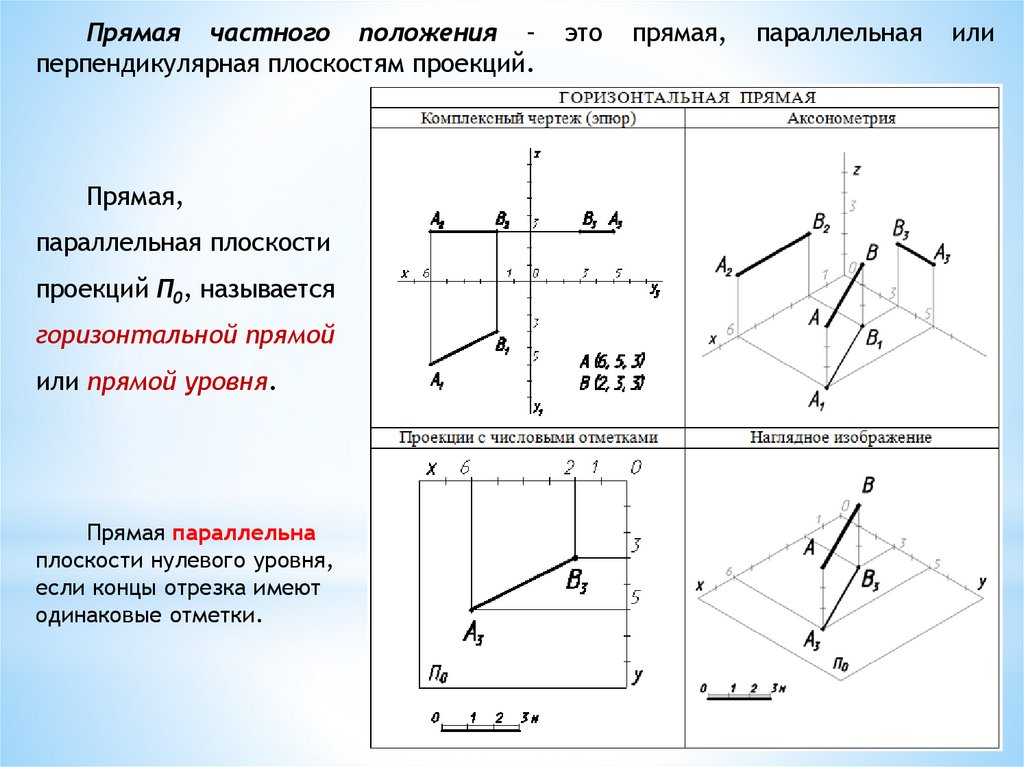
Прямая частного положения –
перпендикулярная плоскостям проекций.
Прямая,
параллельная плоскости
проекций П0, называется
горизонтальной прямой
или прямой уровня.
Прямая параллельна
плоскости нулевого уровня,
если концы отрезка имеют
одинаковые отметки.
это
прямая,
параллельная
или

14.

Все линии уровня имеют одинаковые отметки и проецируются на
плоскость П0 без искажения своей формы, т. е. в натуральную величину.
Поэтому очень удобно в проекциях с числовыми отметками изображать
горизонтали топографических поверхностей.
Если прямая является горизонтальной прямой, то ее числовая отметка
может указываться в разрыве.

15.

Линии в проекциях с числовыми отметками
А
П0
А6
h
N0
В-5
O-7
d
h2
В
O
П0
d-7
А6
O-7
N0
В-5
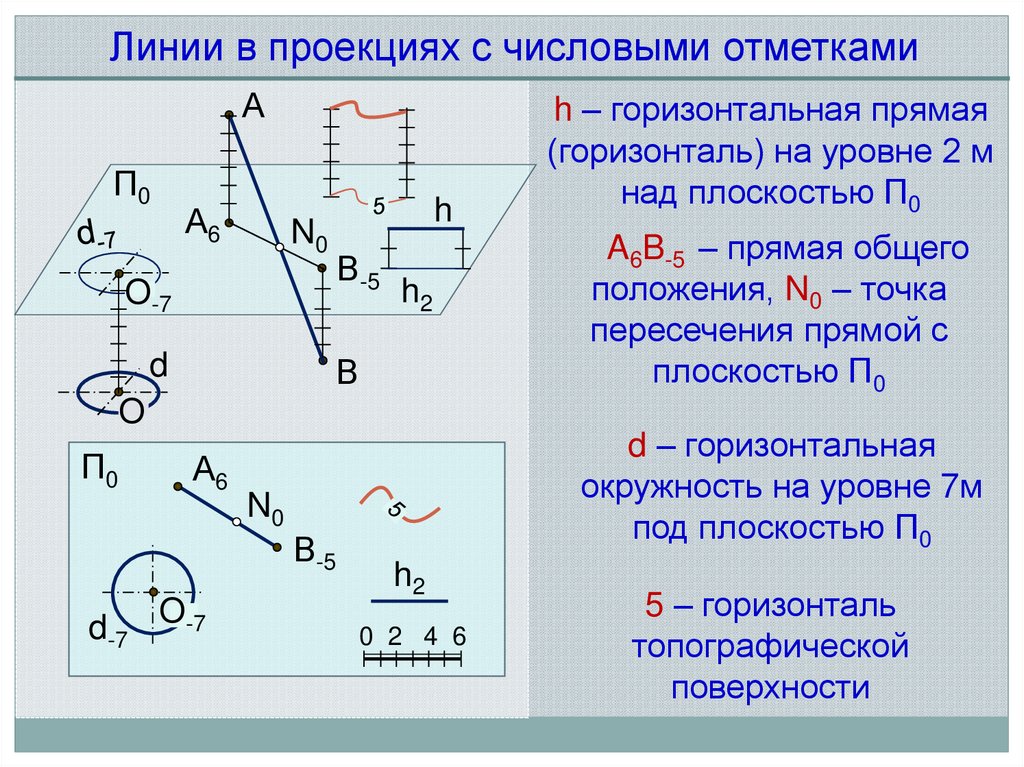
h – горизонтальная прямая
(горизонталь) на уровне 2 м
над плоскостью П0
A6B-5 – прямая общего
положения, N0 – точка
пересечения прямой с
плоскостью П0
d – горизонтальная
окружность на уровне 7м
под плоскостью П0
h2
0 2 4 6
5 – горизонталь
топографической
поверхности

16.

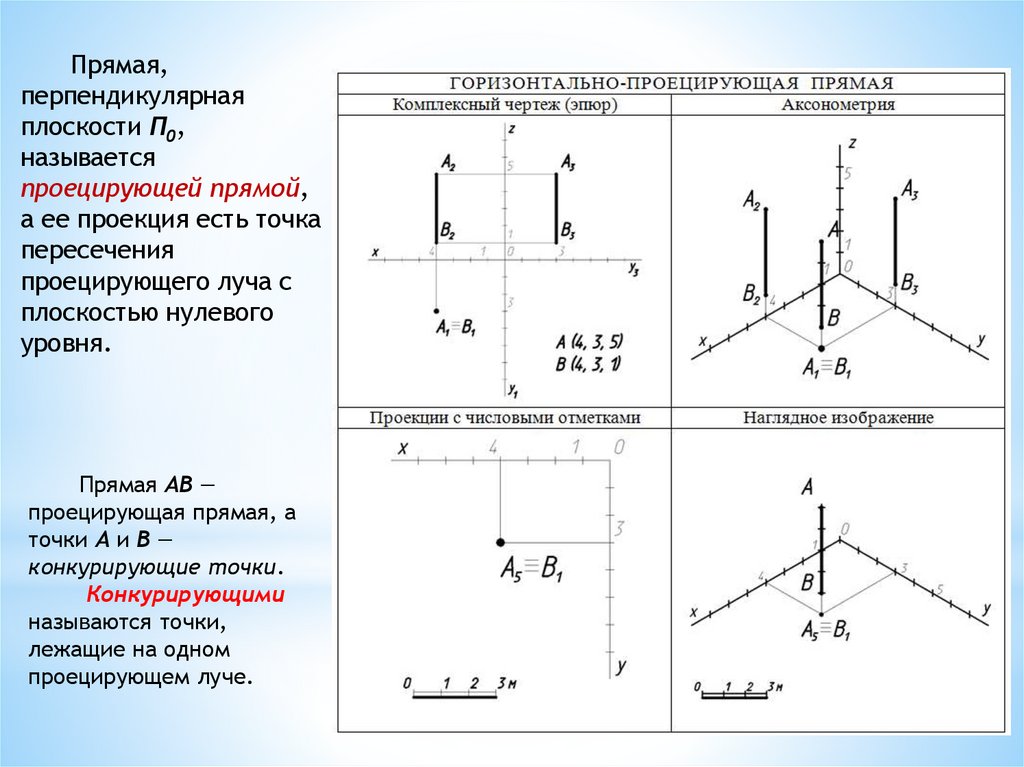
Прямая,
перпендикулярная
плоскости П0,
называется
проецирующей прямой,
а ее проекция есть точка
пересечения
проецирующего луча с
плоскостью нулевого
уровня.
Прямая АВ —
проецирующая прямая, а
точки А и В —
конкурирующие точки.
Конкурирующими
называются точки,
лежащие на одном
проецирующем луче.

17.

Градуирование прямой
Прямая может быть задана точками, имеющими дробные числовые
отметки, а для решения целого ряда задач удобно иметь отметки точек
прямой, выраженные целыми числами. Поэтому применяют градуирование.
Градуированием прямой называется процесс нахождения на
горизонтальной проекции прямой проекций точек с целыми числовыми
отметками, отличающимися друг от друга на единицу длины (подъема).
Градуирование может быть выполнено графически или аналитически.

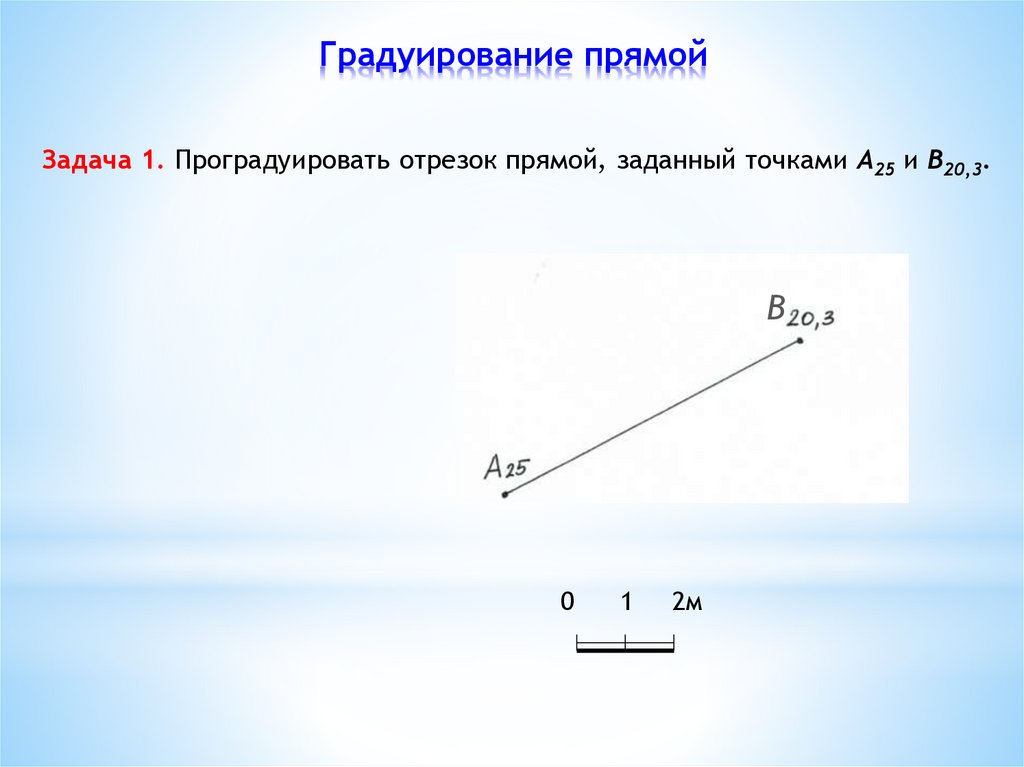
18. Градуирование прямой

Задача 1. Проградуировать отрезок прямой, заданный точками А25 и В20,3.
В
0
1
2м

19.

Решение. Используем теорему Фалéса: если на одной из двух прямых отложить
последовательно несколько равных отрезков и через их концы провести
параллельные прямые, пересекающие вторую прямую, то они отсекут на второй
прямой отрезки, равные между собой.
1. Через точку А25 проведем
произвольную
вспомогательную линию, на
которой нужно отложить
равные отрезки
произвольной длины
(целесообразно откладывать
по 10 мм).
2. Так как разность отметок
точек А и В составляет: 2520,3 = 4,7 единиц, то на
вспомогательном луче
отмечаем 4 равных отрезка
по 10 мм и добавляем 7 мм.
Номеруем от 25 до 20,3.
В
10 мм
25
7 мм (20,3)
24
0
23
22
1
2м
21
20

20.

3. Соединим последнюю точку
полученной пропорции
(20,3), отложенной на
вспомогательной прямой, с
точкой В20,3.
В
21
22
23
24
4. С помощью прямых,
параллельных построенной,
определим на заданной
проекции прямой точки с
целыми числовыми
отметками: 24, 23, 22, 21.
10 мм
25
7 мм (20,3)
24
0
23
22
1
2м
21
20

21.

Задача 2. Проградуировать отрезок прямой, заданный проекцией А12,5 В15,6.
Данный прием градуирования заключается в том, что параллельно проекции
отрезка АВ (А12,5 В15,6) проводят линии с равными расстояниями (как правило, по 10
мм) и обозначают и х как горизонтали с целыми отметками 13, 14, 15, 16.
На перпендикулярах к проекции А12,5 В15,6, которую принимают за линию уровня с
отметкой условно равной, например 12, откладывают от проекции А12,5 вверх значение
0,5 метра (12,5-12=0,5) и от проекции В15,6 – 3,6 метра (15,6-12=3,6). Затем отмечают
точки А0 и В0 и соединяют их прямой линией. Из точек пересечения этой прямой с
горизонталями 13, 14, 15 опускают перпендикуляры на заданную проекцию прямой АВ,
получив необходимые проекции точек с целыми отметками.

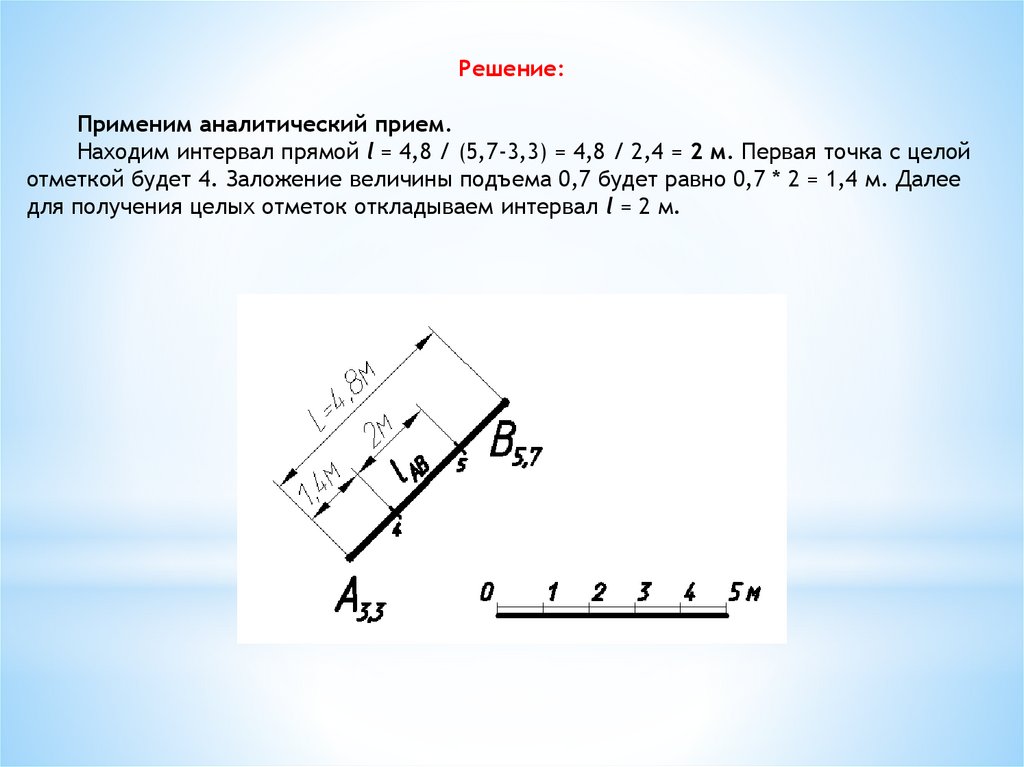
22.

Задача 3. Проградуировать отрезок прямой, заданный проекцией А3,3 В5,7 .
Длина заложения LАВ = 4,8м.

23.

Решение:
Применим аналитический прием.
Находим интервал прямой l = 4,8 / (5,7-3,3) = 4,8 / 2,4 = 2 м. Первая точка с целой
отметкой будет 4. Заложение величины подъема 0,7 будет равно 0,7 * 2 = 1,4 м. Далее
для получения целых отметок откладываем интервал l = 2 м.

24.

Взаимное положение двух прямых
Две прямые в пространстве могут занимать относительно друг друга
различные положения: быть параллельными между собой,
пересекаться или скрещиваться.

25.

Параллельные прямые
Две прямые параллельны, если:
1) их проекции параллельны;
2) интервалы или уклоны прямых равны;
3) отметки возрастают (или убывают) в одном направлении.
Если через точки с одинаковыми
отметками на параллельных прямых
провести горизонтали, то они будут
параллельны между собой.

26.

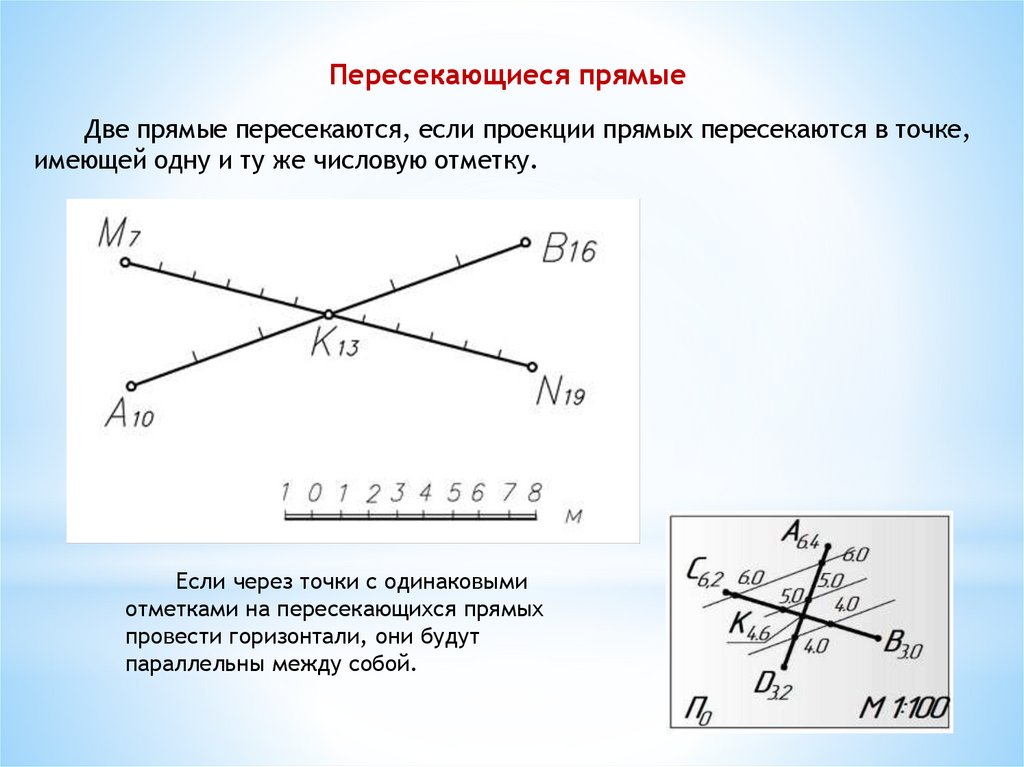
Пересекающиеся прямые
Две прямые пересекаются, если проекции прямых пересекаются в точке,
имеющей одну и ту же числовую отметку.
Если через точки с одинаковыми
отметками на пересекающихся прямых
провести горизонтали, они будут
параллельны между собой.

27.

Скрещивающиеся прямые
Прямые скрещиваются, если их проекции не удовлетворяют условиям
параллельности и пересечения.
Если через точки с одинаковыми отметками на скрещивающихся прямых провести
горизонтали, то они не будут параллельны между собой
На месте пересечения проекций
скрещивающихся прямых лежат конкурирующие
точки.
Точки К и N – конкурирующие точки.

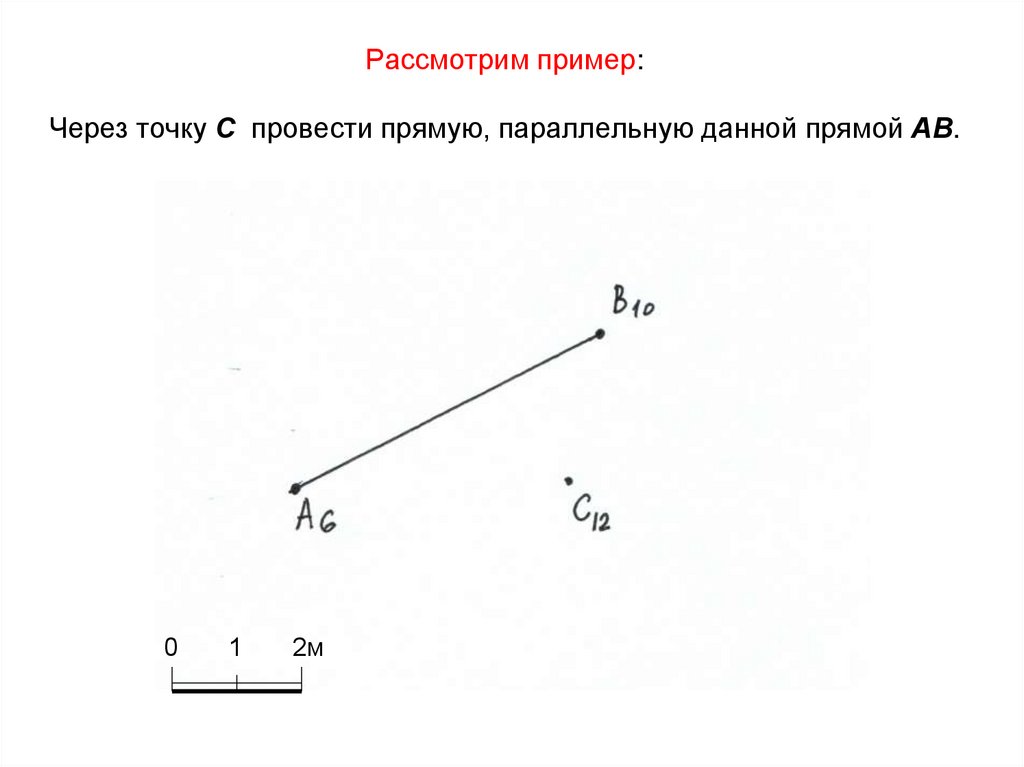
28. Рассмотрим пример: Через точку С провести прямую, параллельную данной прямой АВ.

0
1
2м

29. Решение: 1. Через точку С12 проведем прямую, параллельную заданной проекции А6В10.

0
1
2м

30. 2. С помощью теоремы Фалеса градуируем искомую прямую. Для этого проведем вспомогательную прямую под произвольным углом,

отложим на ней разницу числовых отметок (10-6=4, т.е. четыре
одинаковых единичных отрезка длиной по 10 мм.) и соединим конец
пропорции с конечной отметкой данного отрезка.
10
9
8
7
0
1
2м

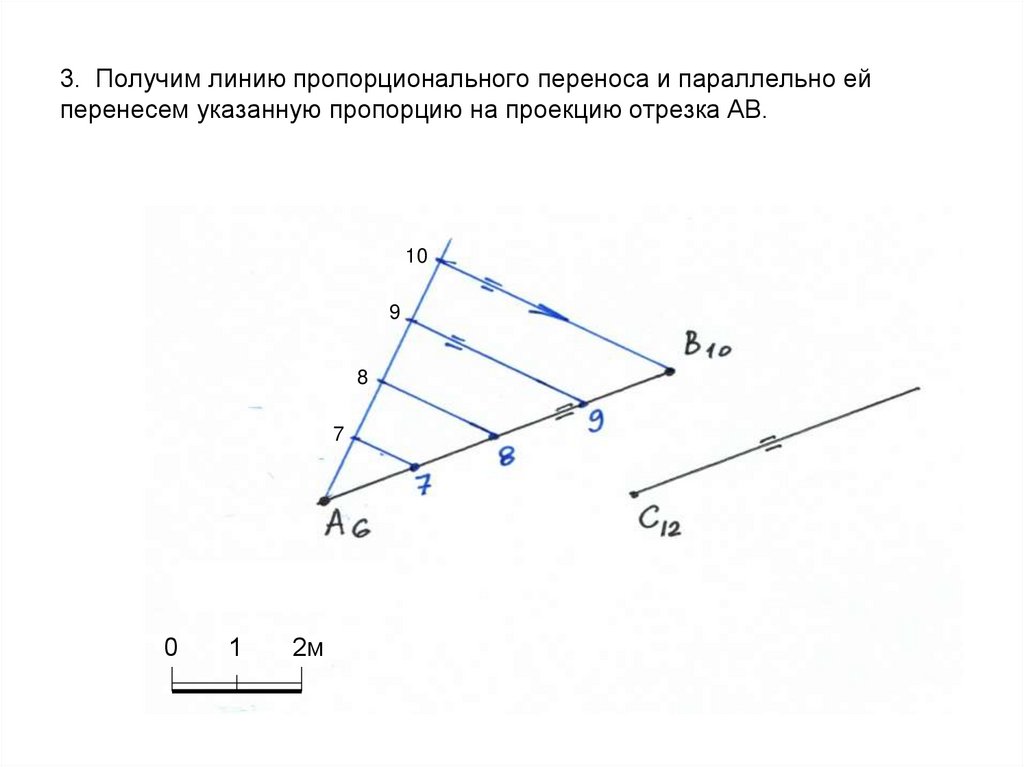
31. 3. Получим линию пропорционального переноса и параллельно ей перенесем указанную пропорцию на проекцию отрезка АВ.

10
9
8
7
0
1
2м

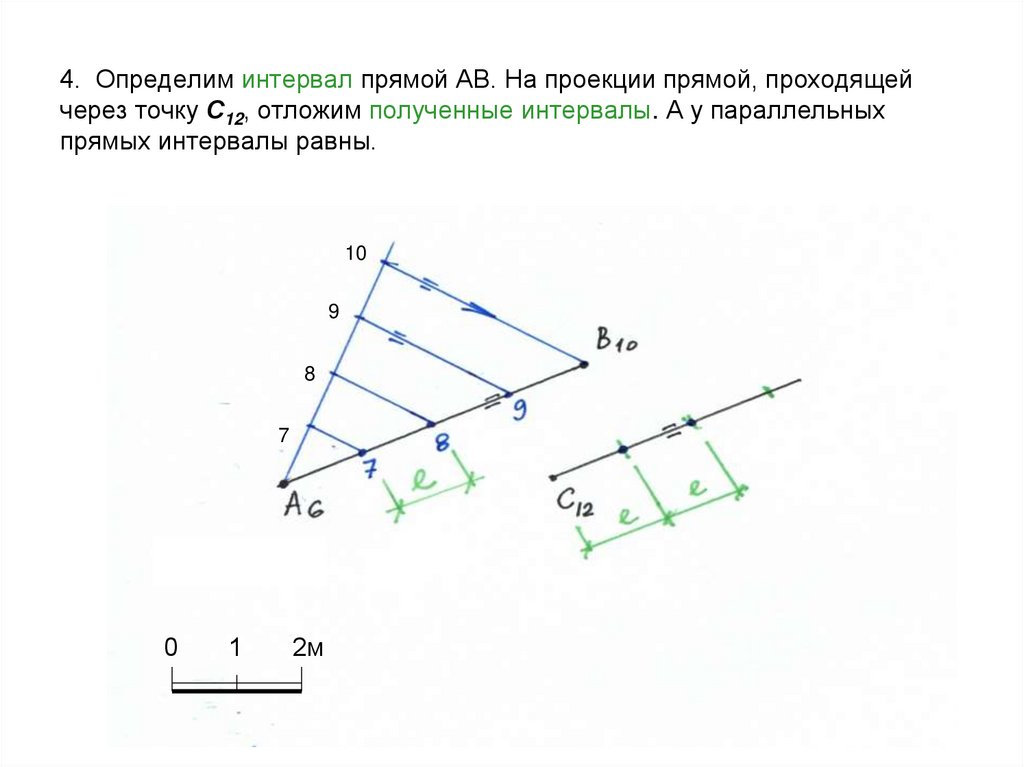
32. 4. Определим интервал прямой АВ. На проекции прямой, проходящей через точку С12, отложим полученные интервалы. А у параллельных

прямых интервалы равны.
10
9
8
7
0
1
2м

33. 4. Числовые отметки возрастают в одном направлении, поэтому проставим отметки на прямой, проходящей через точку С12 в порядке

возрастания: 13,14,15.
10
9
8
7
0
1
2м
Все условия параллельности прямых
выполнены, значит задача решена.