ФР_2оценка_2021

1.

Методы оценки физического развития
детей и подростков
Методы оценки ФР популяции –
генерализирующие методы
Методы оценки ФР индивидуума –
индивидуализирующие методы
Для ИССЛЕДОВАНИЯ ФР нужны ПРИБОРЫ
Для ОЦЕНКИ ФР нужна МАТЕМАТИКА

2.

Паспортный возраст – период,
прожитый ребенком от рождения до
момента обследования, имеющий
четкую возрастную границу (день,
месяц, год).

3.

Определение точного возраста ребенка
на момент обследования
Из даты обследования вычитают дату рождения
ребенка и с учетом возрастной периодизации
определяют паспортный возраст ребенка.
Пример: дата рождения ребенка 17 января 1999 г.,
обследование проводилось 20 мая 2006 г.
20.05.2006
17.01.1999
3 дня 4 месяца 7 лет.
К какой возрастной группе можно отнести
данного ребенка?

4.

Конкретные сроки наблюдения за ребенком с момента
рождения определяются временем (так называемым
возрастным интервалом), за которое в растущем
организме происходят наиболее значимые
количественные и качественные изменения.

5.

На первом году жизни возрастной интервал составляет 1 месяц,
поэтому к детям:
— новорожденным относятся дети до 15 дней;
— 1 мес — от 16 дней до 1 мес. 15 дней;
— 2 мес — от 1 мес. 16 дней до 2 мес. 15 дней и т.д.
После первого года и до 36 мес (3 лет) возрастной интервал
составляет 3 месяца, поэтому к детям:
— 1 года относятся дети от 11 мес.16 дней до 1 г. 1 мес.15 дней;
— 1 г 3 мес. (15 мес.) — от 1 г. 1 мес.16 дней до 1 г. 4 мес.15 дней;
— 1,5 лет (18 мес.) — от 1 г. 4 мес.16 дней до 1 г. 7 мес.15 дней;
— 1 г 9 мес. (21 мес.) — от 1 г. 7 мес.16 дней до 1 г. 10 мес.15 дней;
— 2 лет (24 мес.) — от 1 г. 10 мес.16 дней до 2 лет 1 мес.15 дней и т.д.
После 3 лет и до 7 лет возрастной интервал составляет 6 месяцев,
поэтому к детям:
— 3 лет относятся дети от 2 лет 10 мес. 16 дней до 3 лет 3 мес.;
— 3,5 лет — от 3 лет 3 мес. 1 дня до 3 лет 9 мес.;
— 4 лет — от 3 лет 9 мес. 1 дня до 4 лет 3 мес. и так далее.
Старше 7 лет возрастной интервал равен 1 году, поэтому к детям:
— 7 лет относятся дети от 6 лет 9 мес. 1 дня до 7 лет 6 мес.;
— 8 лет — дети от 7 лет 6 мес. 1 дня до 8 лет 6 мес.;
— 9 лет — дети от 8 лет 6 мес. 1 дня до 9 лет 6 мес. и так далее.

6.

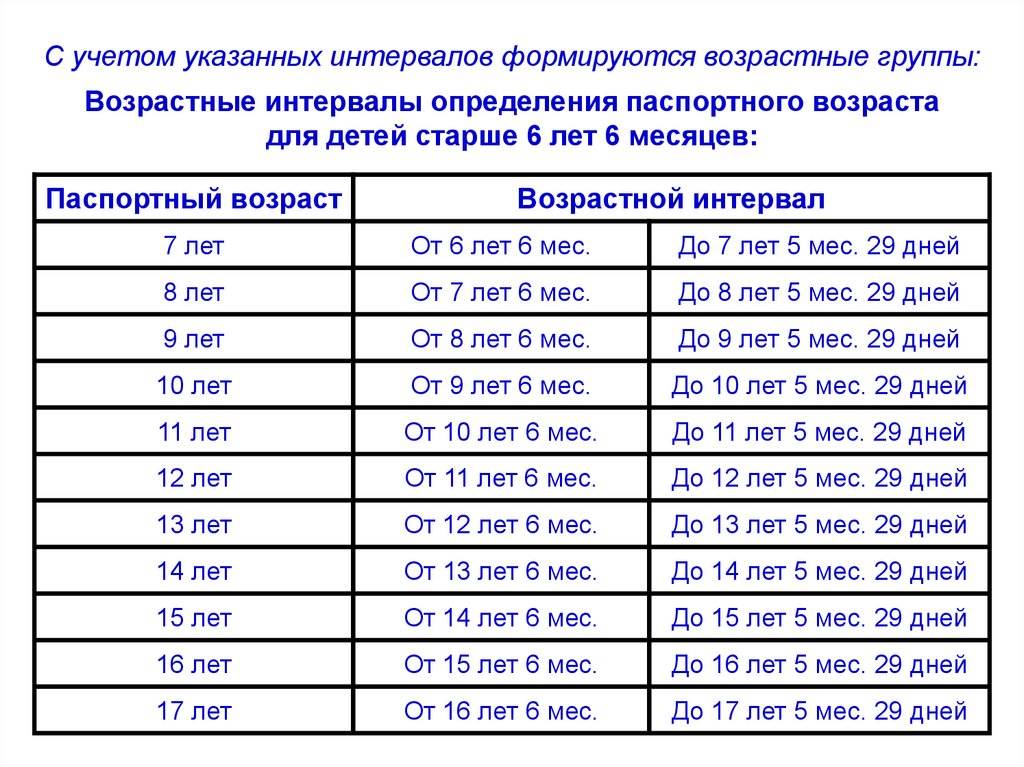
С учетом указанных интервалов формируются возрастные группы:
Возрастные интервалы определения паспортного возраста
для детей старше 6 лет 6 месяцев:
Паспортный возраст
Возрастной интервал
7 лет
От 6 лет 6 мес.
До 7 лет 5 мес. 29 дней
8 лет
От 7 лет 6 мес.
До 8 лет 5 мес. 29 дней
9 лет
От 8 лет 6 мес.
До 9 лет 5 мес. 29 дней
10 лет
От 9 лет 6 мес.
До 10 лет 5 мес. 29 дней
11 лет
От 10 лет 6 мес.
До 11 лет 5 мес. 29 дней
12 лет
От 11 лет 6 мес.
До 12 лет 5 мес. 29 дней
13 лет
От 12 лет 6 мес.
До 13 лет 5 мес. 29 дней
14 лет
От 13 лет 6 мес.
До 14 лет 5 мес. 29 дней
15 лет
От 14 лет 6 мес.
До 15 лет 5 мес. 29 дней
16 лет
От 15 лет 6 мес.
До 16 лет 5 мес. 29 дней
17 лет
От 16 лет 6 мес.
До 17 лет 5 мес. 29 дней

7.

Методы оценки
физического развития

8.

Методы оценки физического развития:
Индивидуализирующий метод – оценка ФР ребенка в
данный момент времени или в динамике с
установлением уровня/соответствия норме/средним
величинам и пропорциональности/гармоничности ФР.
Генерализирующий метод – оценка групп детей с
целью получения региональных возрастно-половых
стандартов и оценочных таблиц, используемых как для
индивидуальной оценки физического развития, так и
для эколого-гигиенического мониторинга территории.
Метод позволяет вести наблюдения за динамическими
сдвигами в физическом развитии детей данного
региона в связи с состоянием здоровья, занятиями
физической культурой, питанием, условиями жизни.

9.

СТАТИСТИЧЕСКИЙ АНАЛИЗ В
ОЦЕНКЕ ФИЗИЧЕСКОГО РАЗВИТИЯ:
СТАТИСТИКА ПАРАМЕТРИЧЕСКАЯ
СТАТИСТИКА НЕПАРАМЕТРИЧЕСКАЯ

10.

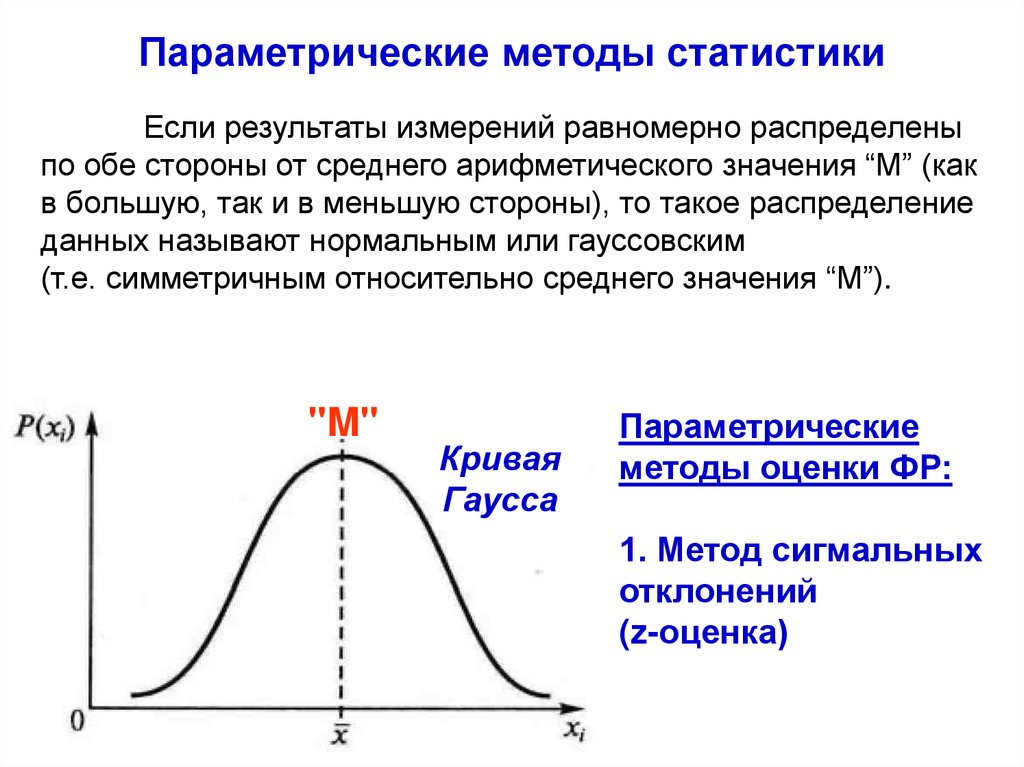
Параметрические методы статистики
Если результаты измерений равномерно распределены
по обе стороны от среднего арифметического значения “M” (как
в большую, так и в меньшую стороны), то такое распределение
данных называют нормальным или гауссовским
(т.е. симметричным относительно среднего значения “M”).
"M"
Кривая
Гаусса
Параметрические
методы оценки ФР:
1. Метод сигмальных
отклонений
(z-оценка)

11.

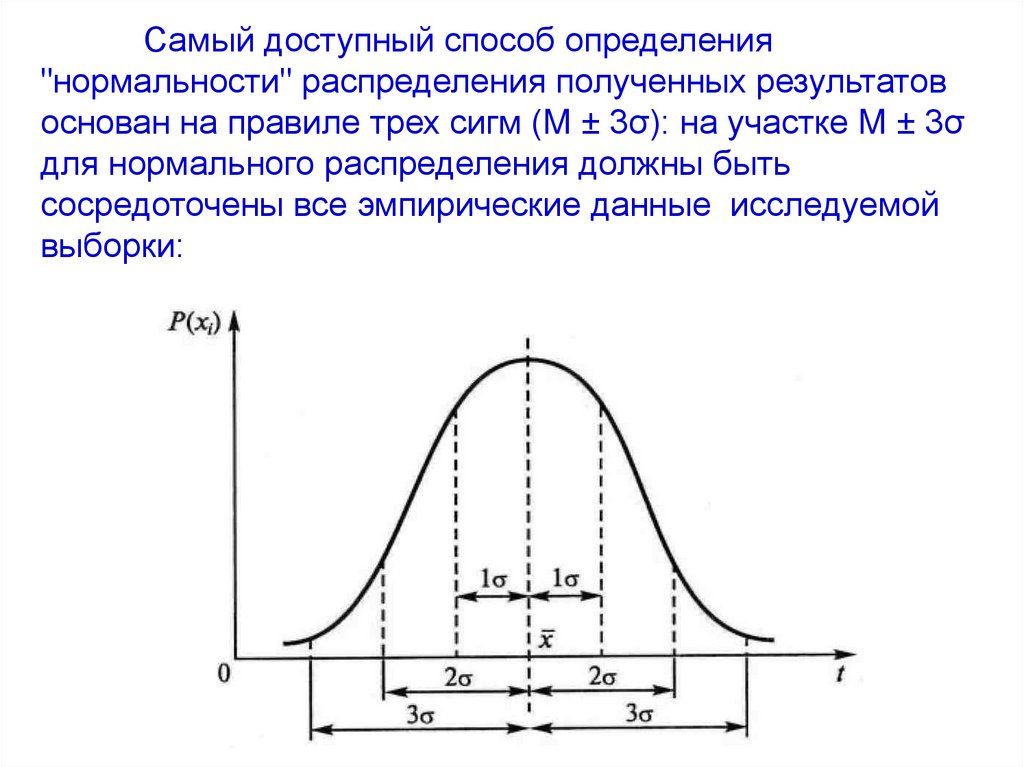
Самый доступный способ определения
"нормальности" распределения полученных результатов
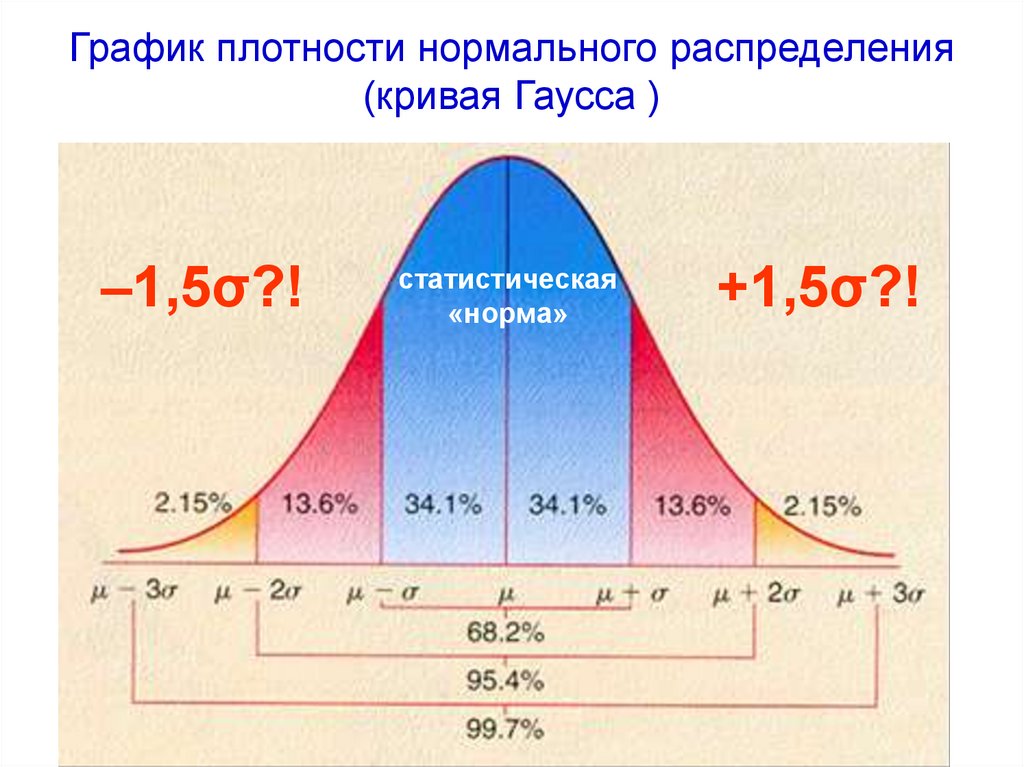
основан на правиле трех сигм (M ± 3σ): на участке M ± 3σ
для нормального распределения должны быть
сосредоточены все эмпирические данные исследуемой
выборки:

12.

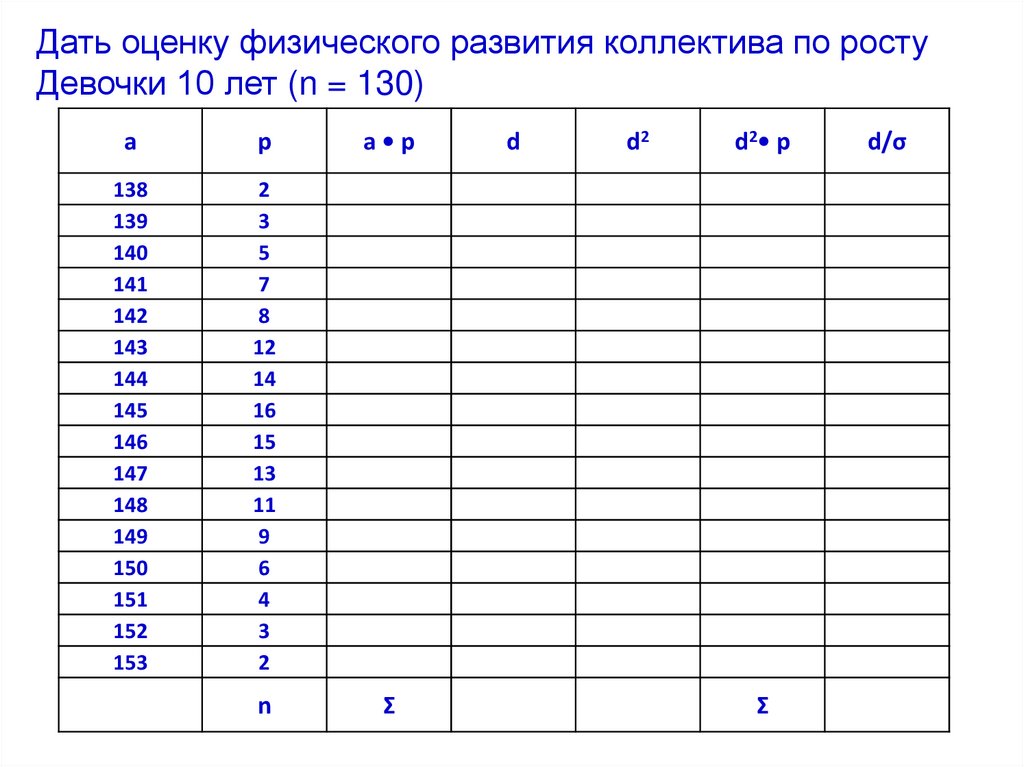
Дать оценку физического развития коллектива
138
2
по росту
139
3
140
5
7
Девочки 10 лет 141
142
8
n = 130
143
12
144
14
145
16
146
15
147
13
148
11
149
9
150
6
151
4
152
3
153
2

13.

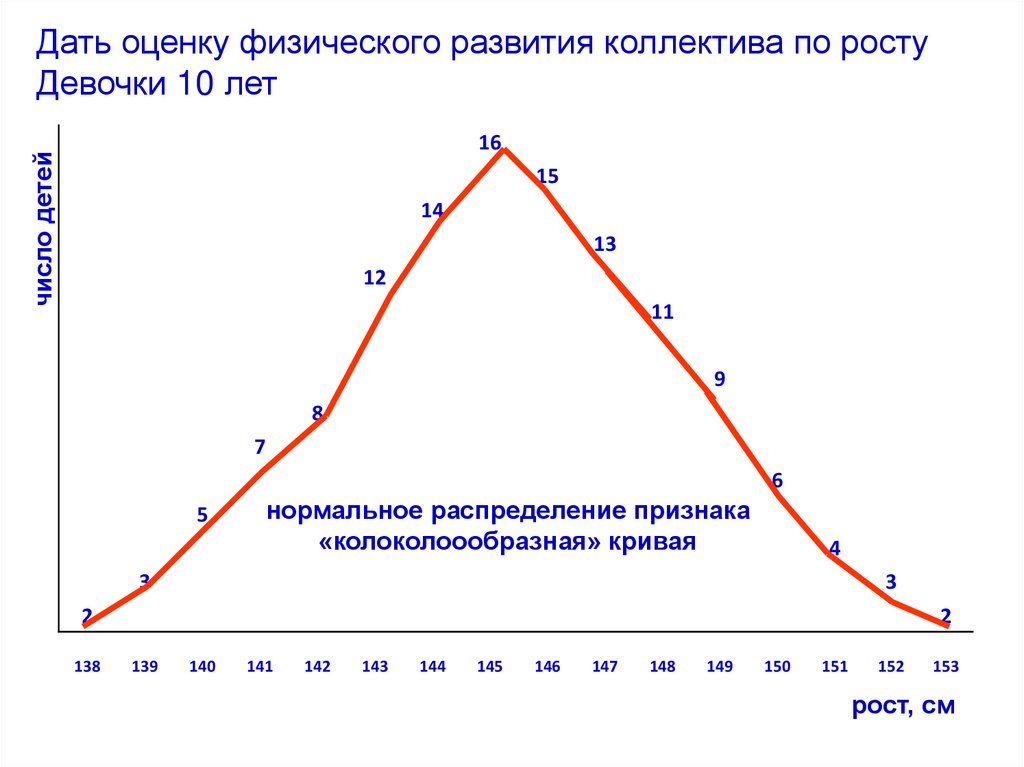
Дать оценку физического развития коллектива по росту
Девочки 10 лет
число детей
16
15
14
13
12
11
9
8
7
6
5
нормальное распределение признака
«колоколоообразная» кривая
4
3
3
2
138
2
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
рост, см

14.

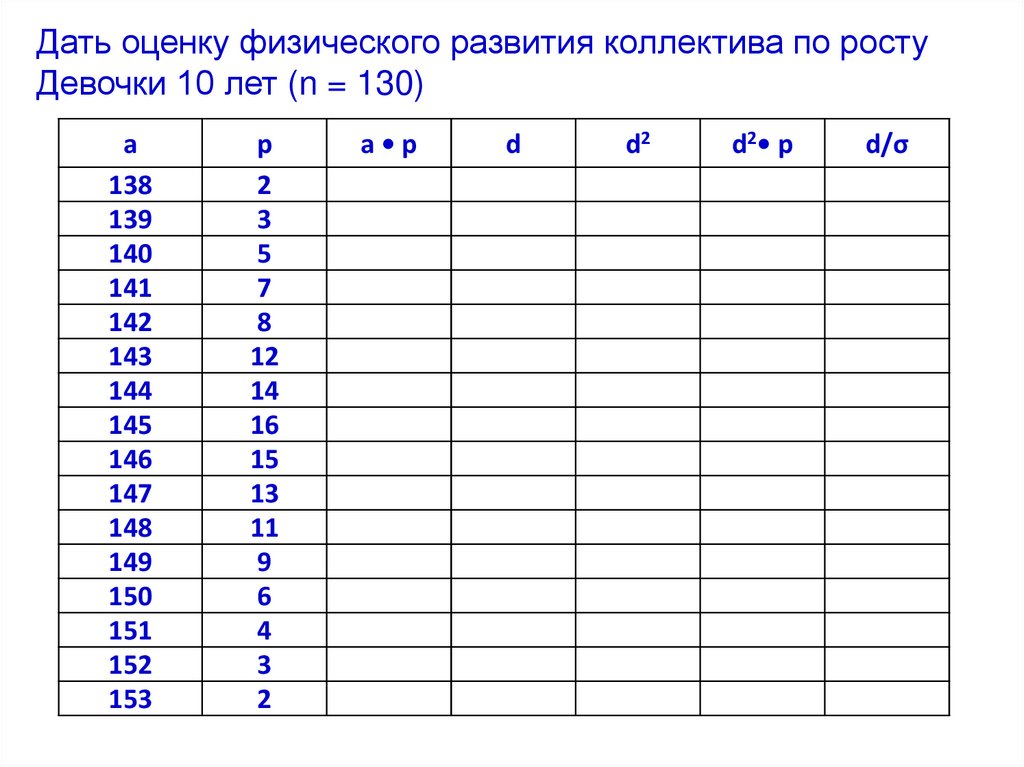
Дать оценку физического развития коллектива по росту
Девочки 10 лет (n = 130)
а
р
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
2
3
5
7
8
12
14
16
15
13
11
9
6
4
3
2
n
а•р
Ʃ
d
d2
d 2• р
Ʃ
d/σ

15.

а – изучаемый признак
р – частота наблюдений данного признака
n – число обследуемых детей
d – индивидуальное отклонение
(дисперсия) для каждого наблюдения
определяется как разность М и а (М–а)
Ʃ – сумма
М – средняя арифметическая
σ – среднее квадратичное отклонение
m – ошибка средней арифметической

16.

Дать оценку физического развития коллектива по росту
Девочки 10 лет (n = 130)
а
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
р
2
3
5
7
8
12
14
16
15
13
11
9
6
4
3
2
а•р
d
d2
d2• р
d/σ

17.

1. рассчитать среднюю арифметическую
Ʃа•р
М=
n
2. дисперсию для каждого наблюдения d = М – a
3. среднее квадратичное отклонение
σ=
Ʃ d2•р
n
4. ошибку средней арифметической
m =±
σ
n

18.

Дать оценку физического развития коллектива по росту
Девочки 10 лет (n = 130)
M±m
σ

19.

График плотности нормального распределения
(кривая Гаусса )
–1,5σ?!
статистическая
«норма»
+1,5σ?!

20.

Параметрическая и непараметрическая
статистика (пример из Википедии)
Предположим, что в одной комнате
оказалось 19 бедняков и один миллионер.
У каждого бедняка есть 5$, а у
миллионера – 1 млн.$.
В сумме получается 1 000 095$.
Среднее арифметическое значение
суммы денег, которая была у всех 20
человек в этой комнате $50 004,75.

21.

Среднее арифметическое множества чисел – сумма
всех чисел, делённая на их количество.
Является одной из наиболее распространённых мер
центральной тенденции в ПАРАМЕТРИЧЕСКОЙ
СТАТИСТИКЕ, связанной с гауссовским
распределением признаков
НО, подавляющее большинство медикобиологических признаков (более 80%) не имеют
нормального распределения и поэтому не могут
обрабатываться методами параметрической
статистики.
В непараметрической статистике выборку
характеризуют Медиана и Мода.

22.

Медиана (от лат. mediana – середина).
Если все элементы выборки различны, то медиана – это
такое число выборки, которое равно половине из
элементов выборки больше него, а другая половина
меньше него. Медиану можно найти, построив
ранжированный ряд и взяв средний элемент.
Например, в выборке 3, 5, 5, 9, 11 её медианой является
число 5 (среднее арифметическое 6,6).
Если в выборке чётное число элементов, медиана может
быть не определена однозначно: для числовых данных
чаще всего используют полусумму двух соседних
значений, то есть медиану набора 1, 3, 5, 7 принимают
равной 4.

23.

Также медиану можно определить для случайных
величин: в этом случае она делит пополам
распределение.
То есть, медианой случайной величины является такое
число, при котором вероятность получить значение
случайной величины справа от него равна вероятности
получить значение слева от него (и они обе равны 1/2).
Можно также сказать, что медиана является 50-м
перцентилем, 0,5-квантилем или вторым квартилем
выборки или распределения.

24.

Мода (Мода = типичность) – значение, которое во
множестве наблюдений встречается наиболее часто.
Иногда в совокупности встречается более чем одна мода
(например: 6, 2, 6, 6, 8, 9, 9, 9, 10; мода – 6 и 9).
В этом случае можно сказать, что совокупность
мультимодальна.
Из структурных средних величин только мода обладает
таким уникальным свойством. Как правило,
мультимодальность указывает на то, что набор данных
не подчиняется нормальному распределению.

25.

Если результаты измерений не
выполняют условия "нормального"
распределения, то необходимо
использовать методы
непараметрической оценки данных.
ПРИМЕРЫ ОПРЕДЕЛЕНИЯ
«НОРМАЛЬНОСТИ»
РАСПРЕДЕЛЕНИЯ:

26.

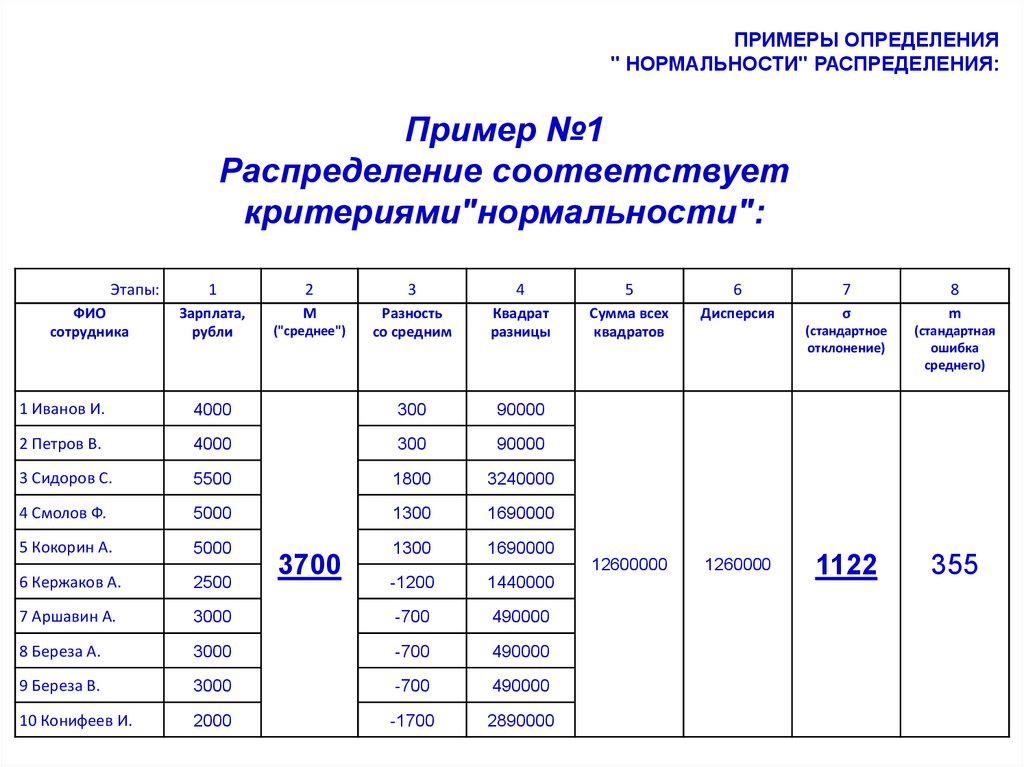
ПРИМЕРЫ ОПРЕДЕЛЕНИЯ
" НОРМАЛЬНОСТИ" РАСПРЕДЕЛЕНИЯ:
Пример №1
Распределение соответствует
критериями"нормальности":
Этапы:
ФИО
сотрудника
1
2
3
4
5
6
Зарплата,
рубли
M
Разность
со средним
Квадрат
разницы
Сумма всех
квадратов
Дисперсия
("среднее")
12600000
1260000
1 Иванов И.
4000
300
90000
2 Петров В.
4000
300
90000
3 Сидоров С.
5500
1800
3240000
4 Смолов Ф.
5000
1300
1690000
5 Кокорин А.
5000
1300
1690000
6 Кержаков А.
2500
-1200
1440000
7 Аршавин А.
3000
-700
490000
8 Береза А.
3000
-700
490000
9 Береза В.
3000
-700
490000
10 Конифеев И.
2000
-1700
2890000
3700
7
8
σ
m
(стандартное
отклонение)
(стандартная
ошибка
среднего)
1122
355

27.

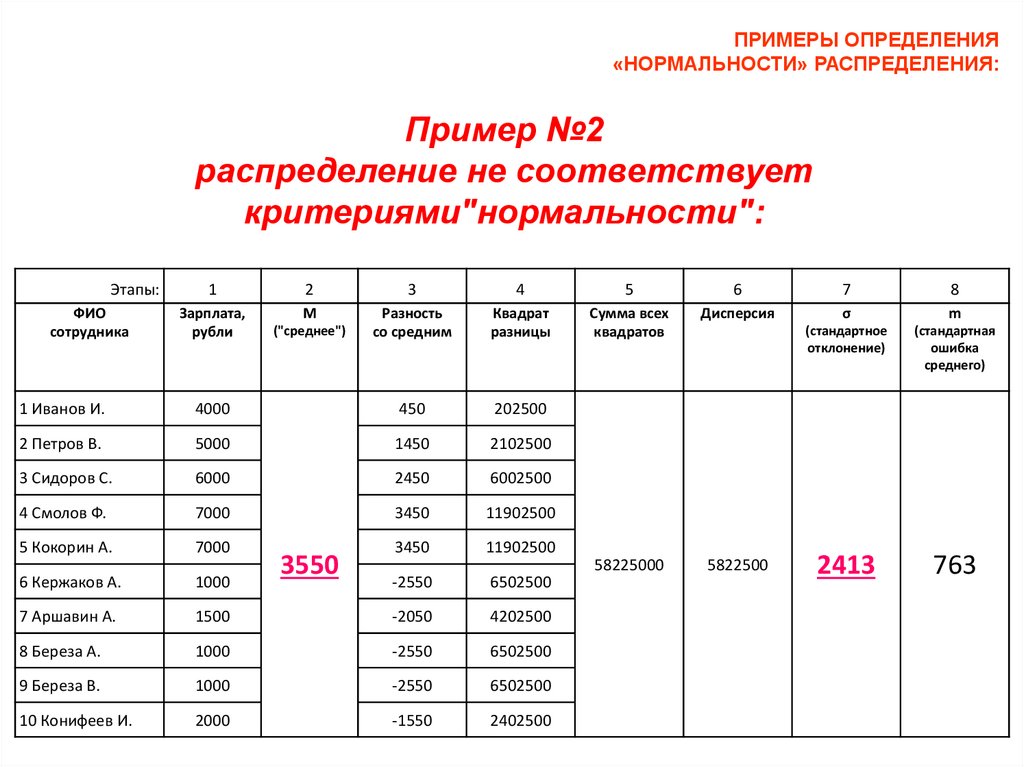
ПРИМЕРЫ ОПРЕДЕЛЕНИЯ
«НОРМАЛЬНОСТИ» РАСПРЕДЕЛЕНИЯ:
Пример №2
распределение не соответствует
критериями"нормальности":
Этапы:
ФИО
сотрудника
1
2
3
4
5
6
Зарплата,
рубли
M
Разность
со средним
Квадрат
разницы
Сумма всех
квадратов
Дисперсия
("среднее")
58225000
5822500
1 Иванов И.
4000
450
202500
2 Петров В.
5000
1450
2102500
3 Сидоров С.
6000
2450
6002500
4 Смолов Ф.
7000
3450
11902500
5 Кокорин А.
7000
3450
11902500
6 Кержаков А.
1000
-2550
6502500
7 Аршавин А.
1500
-2050
4202500
8 Береза А.
1000
-2550
6502500
9 Береза В.
1000
-2550
6502500
10 Конифеев И.
2000
-1550
2402500
3550
7
8
σ
m
(стандартное
отклонение)
(стандартная
ошибка
среднего)
2413
763

28.

Индивидуализирующий метод
оценки физического развития
Параметрическая статистика
I. Метод сигмальных отклонений
Непараметрическая статистика
II. Метод шкал регрессии
III. Центильный метод
IV. Комплексный метод
Метод индексов

29.

I. Метод сигмальных отклонений (Z-оценка)
По трем основным признакам (рост, вес, окружность грудной
клетки) оценить уровень физического развития и пропорциональность
телосложения. (Точно так же можно оценивать любые другие
параметры, в т.ч. данные физиометрии и т.д.).
Сущность метода заключается в том, что показатели физического
развития ребенка: рост, вес, окружность грудной клетки, (каждый в
отдельности) – сравнивают со средними арифметическими стандарта
этих признаков (М) для соответствующей возрастно-половой группы.
Разность (со знаком "+" или "–") между абсолютной величиной
признака и средней арифметической (М) этого признака делят на
величину σ (сигма) – среднее квадратическое отклонение данного
признака, получают сигмальное отклонение.
Таким образом определяют Z-оценку, т.е. на какую долю сигмы (или
на сколько сигм) показатели индивидуума отличаются от стандарта.

30.

I. Метод сигмальных отклонений (Z-оценка)
В зависимости от величины сигмальных отклонений оценку
проводят по нескольким уровням физического развития:
1.Средний уровень – отклонения от средней (М) лежат в
пределах М±σ;
2.Выше среднего – от +1σ до +2σ;
3.Высокий – от +2σ и выше;
4.Ниже среднего – от –1σ до –2σ;
5.Низкий – от –2σ и ниже.
6.Атипичный – ниже –3σ и выше +3σ.

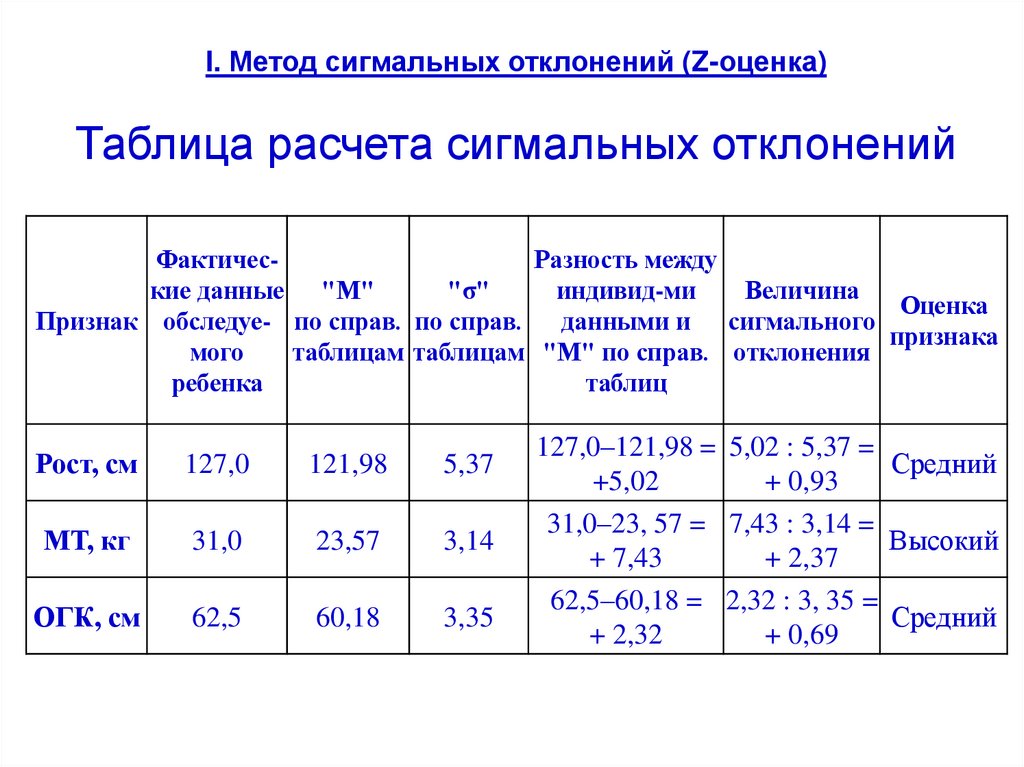
31.

I. Метод сигмальных отклонений (Z-оценка)
Пример: Мальчик 7 лет ростом 127,0 см,
массой тела 31,0 кг, окружностью грудной клетки 62,5 см.
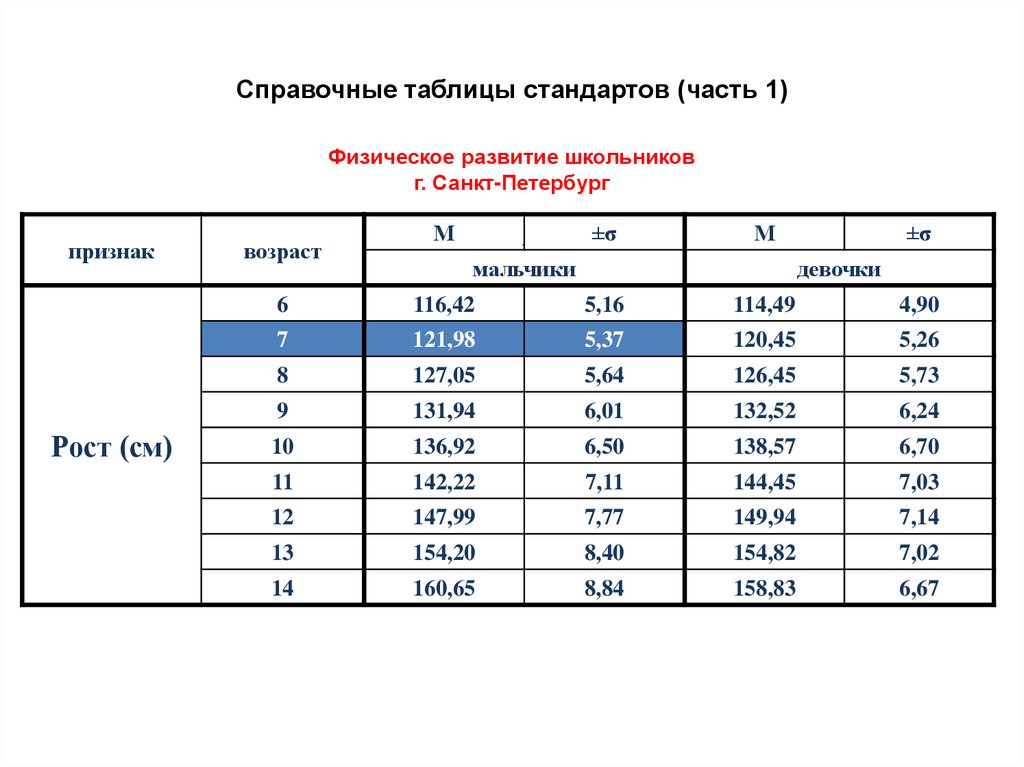
Для определения уровня физического развития
мальчика необходимо использовать справочные таблицы
стандартов (следующие 2 слайда), по которым находят
средние арифметические взвешенные и средние
квадратические отклонения роста, массы, окружности
грудной клетки для мальчиков 7 лет, данные вносят в
таблицу расчета сигмальных отклонений (пример расчета
приведен далее).

32.

Справочные таблицы стандартов (часть 1)
Физическое развитие школьников
г. Санкт-Петербург
признак
Рост (см)
возраст
М
±σ
М
мальчики
±σ
девочки
6
116,42
5,16
114,49
4,90
7
121,98
5,37
120,45
5,26
8
127,05
5,64
126,45
5,73
9
131,94
6,01
132,52
6,24
10
136,92
6,50
138,57
6,70
11
142,22
7,11
144,45
7,03
12
147,99
7,77
149,94
7,14
13
154,20
8,40
154,82
7,02
14
160,65
8,84
158,83
6,67

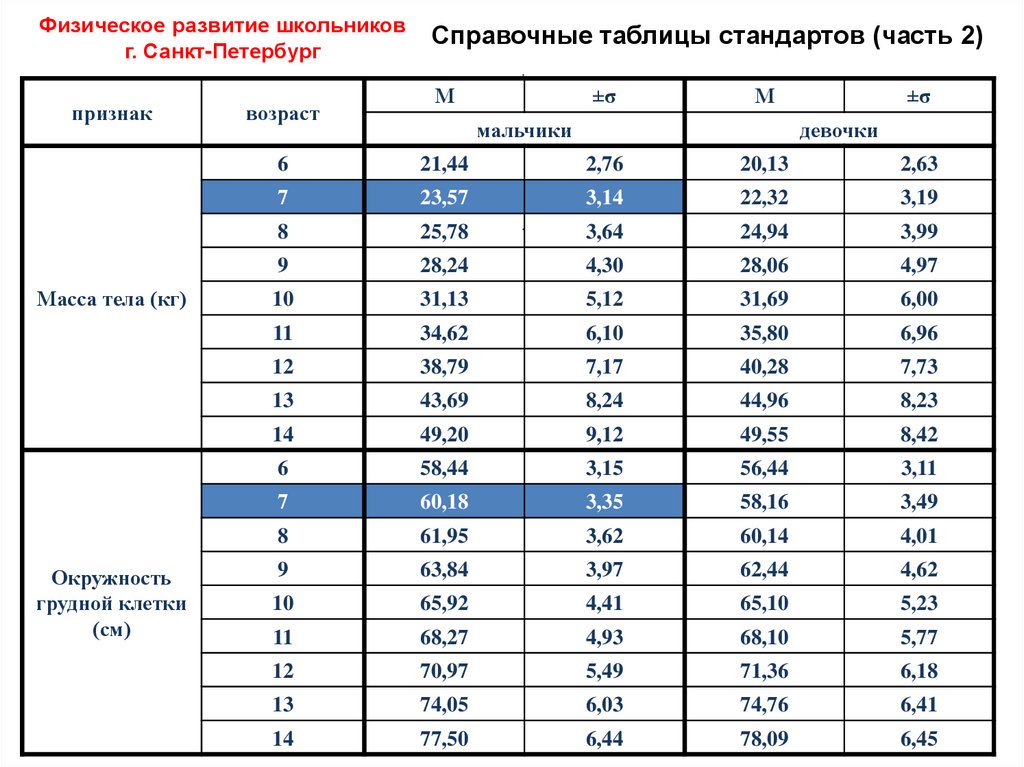
33.

Физическое развитие школьников
г. Санкт-Петербург
признак
Масса тела (кг)
Окружность
грудной клетки
(см)
возраст
Справочные таблицы стандартов (часть 2)
М
±σ
М
мальчики
±σ
девочки
6
21,44
2,76
20,13
2,63
7
23,57
3,14
22,32
3,19
8
25,78
3,64
24,94
3,99
9
28,24
4,30
28,06
4,97
10
31,13
5,12
31,69
6,00
11
34,62
6,10
35,80
6,96
12
38,79
7,17
40,28
7,73
13
43,69
8,24
44,96
8,23
14
49,20
9,12
49,55
8,42
6
58,44
3,15
56,44
3,11
7
60,18
3,35
58,16
3,49
8
61,95
3,62
60,14
4,01
9
63,84
3,97
62,44
4,62
10
65,92
4,41
65,10
5,23
11
68,27
4,93
68,10
5,77
12
70,97
5,49
71,36
6,18
13
74,05
6,03
74,76
6,41
14
77,50
6,44
78,09
6,45

34.

I. Метод сигмальных отклонений (Z-оценка)
Таблица расчета сигмальных отклонений
ФактичесРазность между
кие данные "М"
"σ"
индивид-ми
Величина
Оценка
Признак обследуе- по справ. по справ.
данными и сигмального
признака
мого
таблицам таблицам "М" по справ. отклонения
ребенка
таблиц
Рост, см
127,0
121,98
5,37
МТ, кг
31,0
23,57
3,14
ОГК, см
62,5
60,18
3,35
127,0–121,98 = 5,02 : 5,37 =
Средний
+5,02
+ 0,93
31,0–23, 57 = 7,43 : 3,14 =
Высокий
+ 7,43
+ 2,37
62,5–60,18 = 2,32 : 3, 35 =
Средний
+ 2,32
+ 0,69

35.

I. Метод сигмальных отклонений (Z-оценка)
ФР оцениваем по росту – среднее.
Для оценки пропорциональности телосложения
учитывают сигмальные отклонения всех анализируемых
признаков:
пропорциональным считается телосложение, при
котором сигмальные отклонения для роста, массы и
окружности грудной клетки находятся в одном уровне
сигмальных отклонений или отличаются друг от друга не
более чем на одну сигму;
непропорциональным – если более чем на одну сигму.
В нашем примере: разность между крайними значениями трех
рассчитанных сигмальных отклонений (0,69, 0,93, 2,37) составляет
более 1 сигмы (2,37 – 0,69 = 1,68), следовательно, телосложение
непропорциональное.
ФР среднее, не пропорциональное.

36.

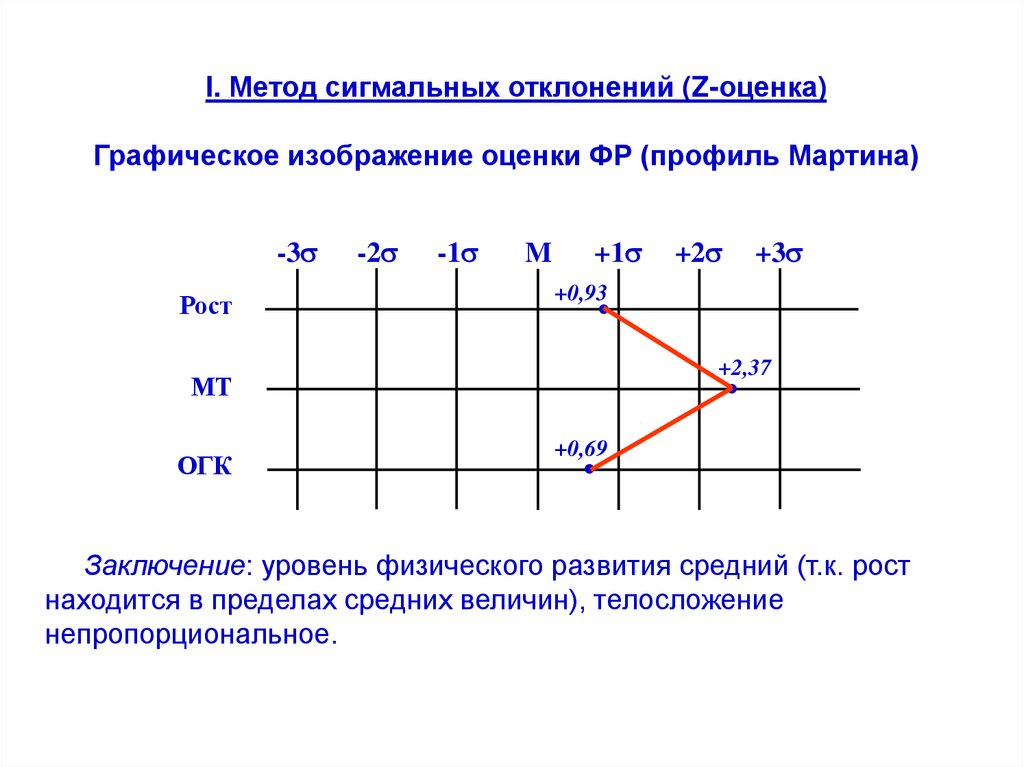
I. Метод сигмальных отклонений (Z-оценка)
Графическое изображение оценки ФР (профиль Мартина)
-3
Рост
-2
-1
M
+1
+3
·
+0,93
·
+2,37
МТ
ОГК
+2
·
+0,69
Заключение: уровень физического развития средний (т.к. рост
находится в пределах средних величин), телосложение
непропорциональное.

37.

Непараметрические методы
Если результаты измерений не выполняют условия
"нормального" распределения, то необходимо
использовать методы непараметрической оценки данных:
Непараметрические методы оценки ФР:
1. Метод шкал регрессии;
2. Центильный метод;
3. Комплексный метод.

38.

II. Метод шкал регрессии
Шкалы регрессии учитывают корреляционную связь между
ростом, массой тела и окружностью грудной клетки для каждой
возрастно-половой группы.
Оценка проводится в несколько действий.
1. Оценивают уровень физического развития по росту ребенка
(средний, выше, ниже среднего, высокий, низкий).
2. Оценивают зависимые параметры – массу тела и окружность
грудной клетки, которые должны соответствовать росту ребенка.
Для этого вычисляют разность между индивидуальным показателем
массы тела ребенка и должной величиной массы тела.
Также оценивают ОГК ребенка, сравнивая с должными величинами
этих показателей.
Величину отличия выражают в сигмальных отклонениях, для чего
полученную разность (с учетом знака) делят на сигму регрессии (σR).
3. По величине сигмального отклонения массы и окружности
грудной клетки устанавливается степень пропорциональности
(гармоничности) телосложения (физического развития).

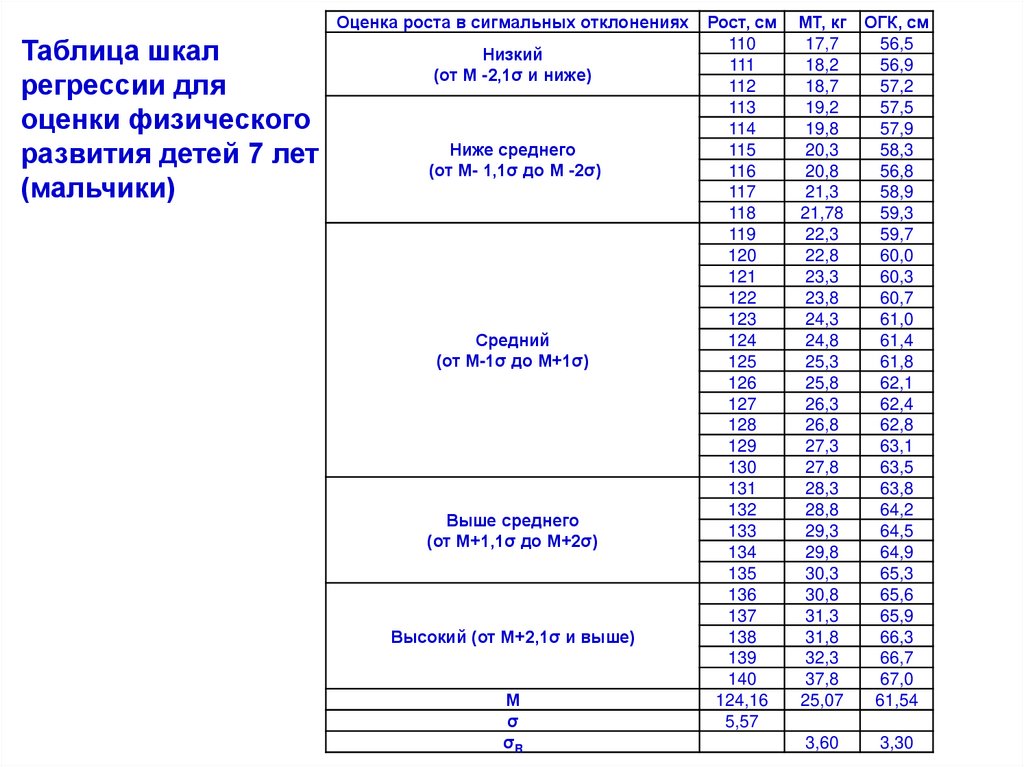
39.

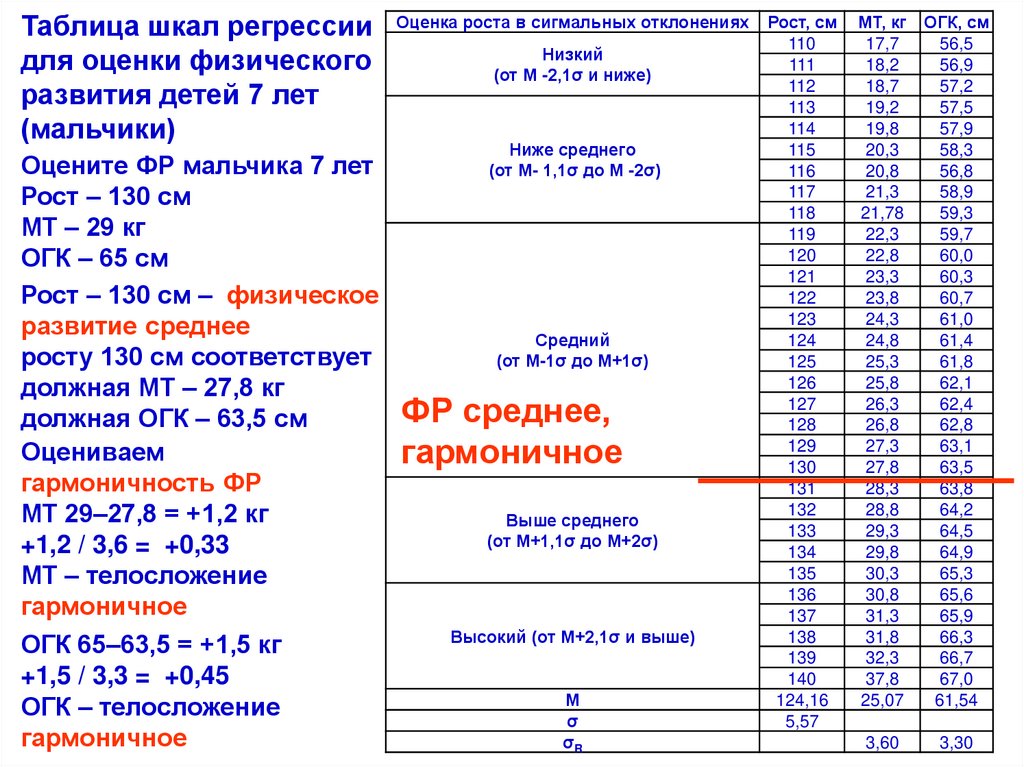
Таблица шкал регрессии
для оценки физического
развития детей 7 лет
(мальчики)
Оцените ФР мальчика 7 лет
Рост – 130 см
МТ – 29 кг
ОГК – 65 см
Рост – 130 см – физическое
развитие среднее
росту 130 см соответствует
должная МТ – 27,8 кг
должная ОГК – 63,5 см
Оцениваем
гармоничность ФР
МТ 29–27,8 = +1,2 кг
+1,2 / 3,6 = +0,33
МТ – телосложение
гармоничное
ОГК 65–63,5 = +1,5 кг
+1,5 / 3,3 = +0,45
ОГК – телосложение
гармоничное
Оценка роста в сигмальных отклонениях
Низкий
(от М -2,1σ и ниже)
Ниже среднего
(от М- 1,1σ до М -2σ)
Средний
(от М-1σ до М+1σ)
ФР среднее,
гармоничное
Выше среднего
(от М+1,1σ до М+2σ)
Высокий (от М+2,1σ и выше)
М
σ
σR
Рост, см
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
124,16
5,57
МТ, кг
17,7
18,2
18,7
19,2
19,8
20,3
20,8
21,3
21,78
22,3
22,8
23,3
23,8
24,3
24,8
25,3
25,8
26,3
26,8
27,3
27,8
28,3
28,8
29,3
29,8
30,3
30,8
31,3
31,8
32,3
37,8
25,07
ОГК, см
56,5
56,9
57,2
57,5
57,9
58,3
56,8
58,9
59,3
59,7
60,0
60,3
60,7
61,0
61,4
61,8
62,1
62,4
62,8
63,1
63,5
63,8
64,2
64,5
64,9
65,3
65,6
65,9
66,3
66,7
67,0
61,54
3,60
3,30

40.

II. Метод шкал регрессии
Среднее, гармоничное физическое развитие –
рост средний, масса тела и окружность грудной клетки
соответствуют росту ребенка или отличаются от должных
величин не более чем на одну сигму (М±σR).
ФР выше (ниже) среднего, гармоничное –
рост выше (или ниже) среднего, масса тела и окружность
грудной клетки соответствуют росту ребенка или
отличаются от должных величин не более чем на одну
сигму (М±σR).
Дисгармоничное физическое развитие – масса тела и
окружность грудной клетки отличаются от должных
величин более ±1,1σR, т.е. либо больше, либо меньше
должных.

41.

II. Метод шкал регрессии
Пример: Мальчик 7 лет, рост 128 см, масса тела 31 кг, окружность
грудной клетки 64 см. Дать оценку физического развития по шкалам
регрессии.
В таблице шкал регрессии для мальчиков 7 лет находим рост 128 см и
определяем уровень физического развития – средний.
Находим должную величину массы тела, соответствующую росту 128 см
– 26,8кг. Масса тела ребенка больше должной на 4,2 кг (31–26,8=+4,2 кг).
Эту разность делим на сигму регрессии массы тела (3,6) и получаем
сигмальное отклонение +1,17 σR. Масса тела мальчика превышает
среднюю более чем на +1,1σR. По массе тела ФР – дисгармоничное.
В следующей графе таблицы находим значение окружности грудной
клетки, соответствующее росту 128 см – 62,8 см.
Фактическая величина окружности грудной клетки мальчика больше
стандартной на 1,2 см (64– 62,8=1,2) или на 0,36 сигмы (+1,2 : 3,3=+0,36
σR). Окружность грудной клетки находится в пределах +1σR.
Заключение: физическое развитие среднее, дисгармоничное
за счет избыточной массы тела

42.

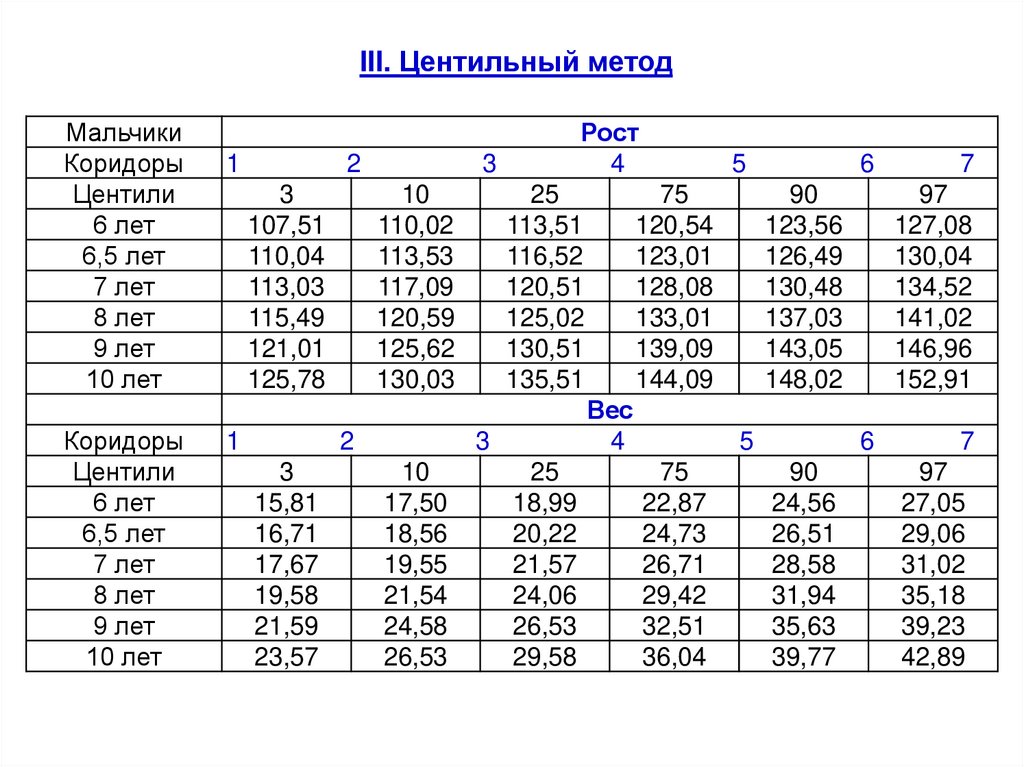
III. Центильный метод
Центильным методом определяют уровень и
гармоничность физического развития.
Центильный метод прост, удобен и используется как экспресс-метод
при массовых обследованиях.
Он основан на процентном распределении частоты встречаемости
величин данного признака в популяции.
Колонки центильных таблиц показывают количественные границы
признака у определенной доли или процента (центиля) здоровых детей
данного возраста и пола. Интервалы между центильными колонками
(зоны, коридоры) отражают тот диапазон разнообразия величин
признака, который свойственен или 3 % (зона до 3-го или от 97-го
центиля), или 7 % (зона от 3-го ло 10-го или от 90-го до 97-го центиля),
или 15 % (зона от 10-го до 25-го или от 75-го до 90-го центиля), или 50
% всех здоровых детей возрастно-половой группы (зона от 25-го до 75го центиля).

43.

III. Центильный метод
Границы центильных групп и номера центильных интервалов (зоны)
представлены в верхних строках каждой таблицы.
Задача врача - найти, в какой центильный интервал (зону) попадает
полученная величина измерения и записать как саму величину, так и
центильный интервал в медицинский документ ребенка. В зависимости
от этого формулируется оценочное суждение:
- зона № 1 (до 3-го центиля) – "очень низкий" уровень,
- зона № 2 (от 3-го до 10-го центиля) – "низкий" уровень,
- зона № 3 (от 10-го до 25-го центиля) - уровень "ниже среднего",
- зона № 4 (от 25-го до 75-го центиля) - "средний" уровень,
- зона № 5 (от 75-го до 90-го центиля) - уровень «выше среднего",
- зона № 6 (от 90-го до 97-го центиля) – "высокий" уровень,
- зона № 7 (от 97-го центиля) – "очень высокий" уровень.

44.

III. Центильный метод
Мальчики
Коридоры
Центили
6 лет
6,5 лет
7 лет
8 лет
9 лет
10 лет
Коридоры
Центили
6 лет
6,5 лет
7 лет
8 лет
9 лет
10 лет
1
2
3
107,51
110,04
113,03
115,49
121,01
125,78
1
3
10
110,02
113,53
117,09
120,59
125,62
130,03
2
3
15,81
16,71
17,67
19,58
21,59
23,57
Рост
4
25
113,51
116,52
120,51
125,02
130,51
135,51
75
120,54
123,01
128,08
133,01
139,09
144,09
Вес
4
3
10
17,50
18,56
19,55
21,54
24,58
26,53
5
25
18,99
20,22
21,57
24,06
26,53
29,58
6
90
123,56
126,49
130,48
137,03
143,05
148,02
5
75
22,87
24,73
26,71
29,42
32,51
36,04
97
127,08
130,04
134,52
141,02
146,96
152,91
6
90
24,56
26,51
28,58
31,94
35,63
39,77
7
7
97
27,05
29,06
31,02
35,18
39,23
42,89

45.

III. Центильный метод
О гармоничности развития судят по результатам
центильных оценок, полученных для длины, массы тела,
окружности грудной клетки.
В случае, если разность номеров центильных
интервалов (зон) между любыми двумя из трех показателей
не превышает 1, то можно говорить о гармоничном
развитии. Если эта разность составляет 2 - развитие
дисгармоничное, 3 и более - резко дисгармоничное.
В случаях, когда все или хотя бы один из оцениваемых
признаков попадают и крайние зоны центильных таблиц (1ю или 7-ю), говорить о гармоничности без дополнительного
анализа зависимых признаков от длины тела некорректно.

46.

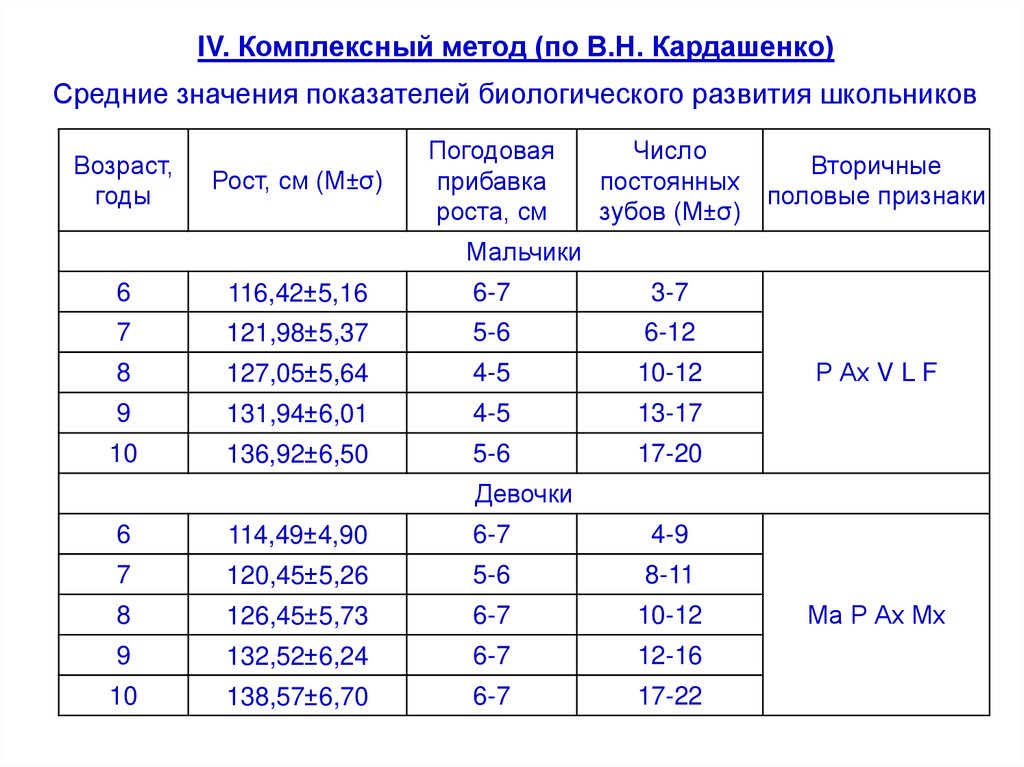
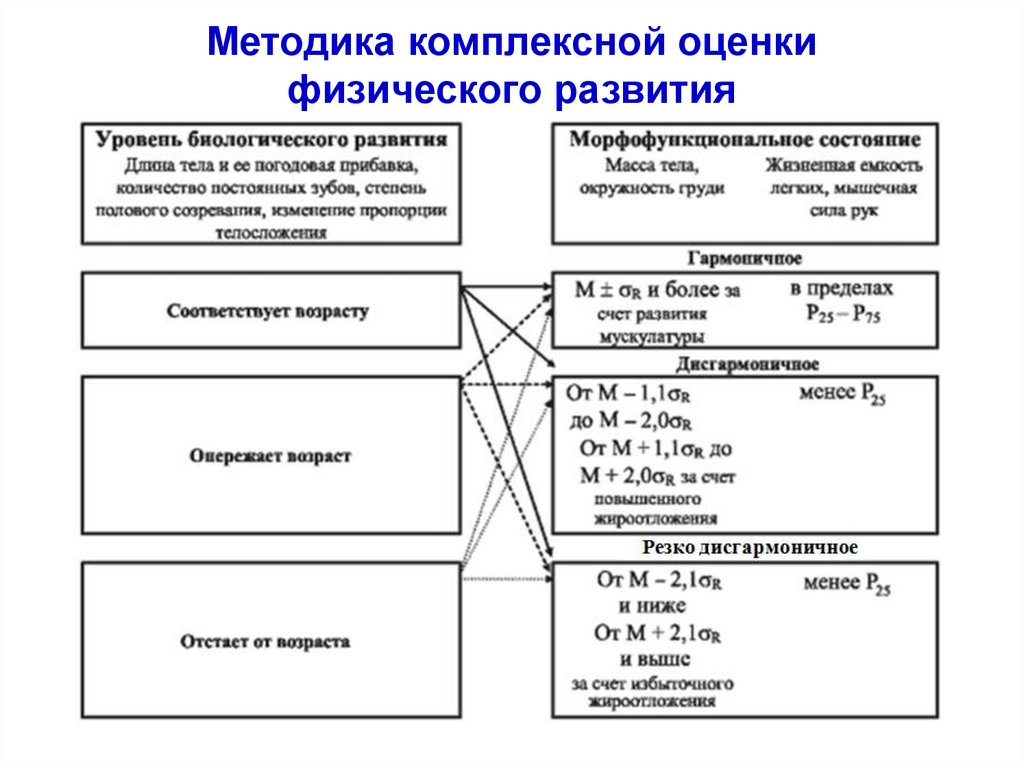
IV. Комплексный метод (по В.Н. Кардашенко)
Оценка ФР проводится по уровню биологического развития
и морфо-функционального состояния.
Проводится в 2 этапа:
1 этап:
оценка уровня биологического развития
(соответствия биологического и паспортного возраста)
по 4 (5) критериям;
2 этап:
оценка морфо-функционального состояния
по степени развития структур организма (по шкалам
регрессии);
по степени развития функциональных показателей
(методом сигмальных отклонений – Z-оценка).

47.

Биологический возраст – это
фактически достигнутый уровень развития
морфологических структур и
функционального состояния организма

48.

Критерии биологического возраста:
1. рост (М±σ) см;
2. погодовые прибавки роста, см;
3. число постоянных зубов;
4. степень развития вторичных половых признаков;
5. оссификация скелета («костный» возраст).
соответствует возрасту
опережает
отстает

49.

IV. Комплексный метод (по В.Н. Кардашенко)
Средние значения показателей биологического развития школьников
Возраст,
годы
Рост, см (М±σ)
Погодовая
прибавка
роста, см
Число
постоянных
зубов (М±σ)
Вторичные
половые признаки
Мальчики
6
116,42±5,16
6-7
3-7
7
121,98±5,37
5-6
6-12
8
127,05±5,64
4-5
10-12
9
131,94±6,01
4-5
13-17
10
136,92±6,50
5-6
17-20
Р Ах V L F
Девочки
6
114,49±4,90
6-7
4-9
7
120,45±5,26
5-6
8-11
8
126,45±5,73
6-7
10-12
9
132,52±6,24
6-7
12-16
10
138,57±6,70
6-7
17-22
Ма Р Ах Мх

50.

IV. Комплексный метод (по В.Н. Кардашенко)
Морфо-функциональное состояние
Структуры оцениваются по массе тела, ОГК в
зависимости от роста (по шкалам регрессии)
Функции – по ЖЕЛ и кистевой динамометрии
(Z-оценка)

51.

Оценка роста в сигмальных отклонениях
Таблица шкал
регрессии для
оценки физического
развития детей 7 лет
(мальчики)
Низкий
(от М -2,1σ и ниже)
Ниже среднего
(от М- 1,1σ до М -2σ)
Средний
(от М-1σ до М+1σ)
Выше среднего
(от М+1,1σ до М+2σ)
Высокий (от М+2,1σ и выше)
М
σ
σR
Рост, см
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
124,16
5,57
МТ, кг
17,7
18,2
18,7
19,2
19,8
20,3
20,8
21,3
21,78
22,3
22,8
23,3
23,8
24,3
24,8
25,3
25,8
26,3
26,8
27,3
27,8
28,3
28,8
29,3
29,8
30,3
30,8
31,3
31,8
32,3
37,8
25,07
ОГК, см
56,5
56,9
57,2
57,5
57,9
58,3
56,8
58,9
59,3
59,7
60,0
60,3
60,7
61,0
61,4
61,8
62,1
62,4
62,8
63,1
63,5
63,8
64,2
64,5
64,9
65,3
65,6
65,9
66,3
66,7
67,0
61,54
3,60
3,30

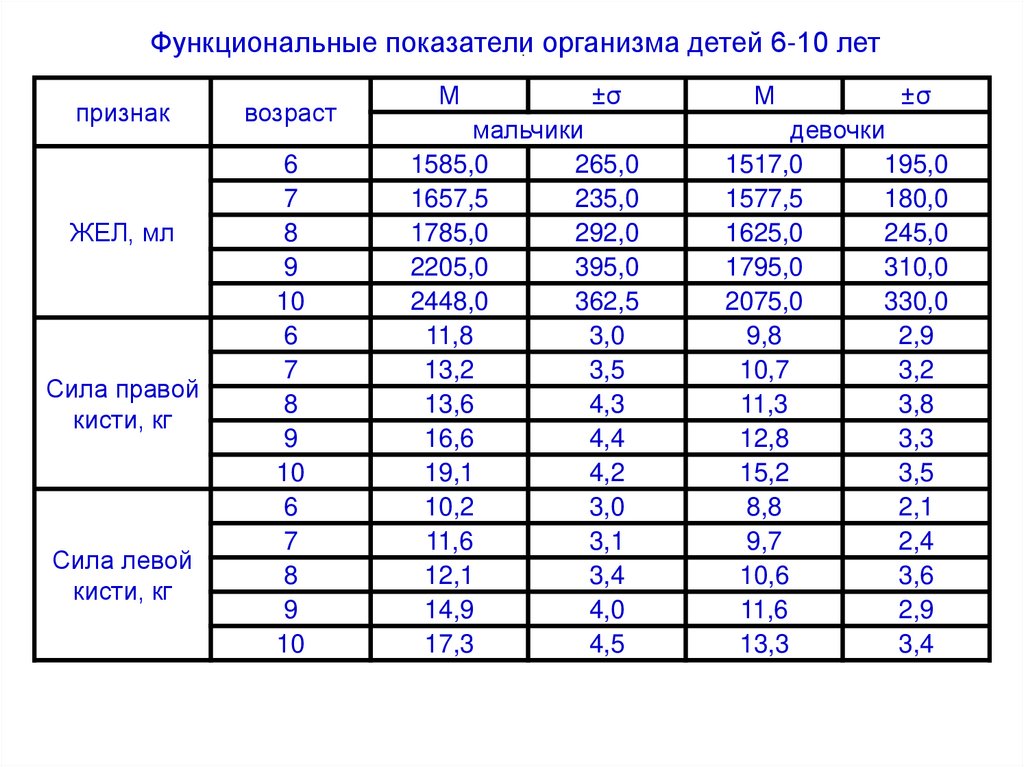
52.

Функциональные показатели организма детей 6-10 лет
признак
ЖЕЛ, мл
Сила правой
кисти, кг
Сила левой
кисти, кг
возраст
6
7
8
9
10
6
7
8
9
10
6
7
8
9
10
М
±σ
мальчики
1585,0
265,0
1657,5
235,0
1785,0
292,0
2205,0
395,0
2448,0
362,5
11,8
3,0
13,2
3,5
13,6
4,3
16,6
4,4
19,1
4,2
10,2
3,0
11,6
3,1
12,1
3,4
14,9
4,0
17,3
4,5
М
±σ
девочки
1517,0
195,0
1577,5
180,0
1625,0
245,0
1795,0
310,0
2075,0
330,0
9,8
2,9
10,7
3,2
11,3
3,8
12,8
3,3
15,2
3,5
8,8
2,1
9,7
2,4
10,6
3,6
11,6
2,9
13,3
3,4

53.

Методика комплексной оценки
физического развития

54.

IV. Комплексный метод (по В.Н. Кардашенко)
Варианты заключений по физическому развитию:
● Биологический возраст соответствует паспортному,
морфо-функциональное состояние гармоничное (рост
средний, МТ и ОГК, оцениваемые в связи с ростом –
пропорциональные (не более чем на ±1,0 σR),
функциональные показатели средние (М±σ) или
превышают.
● Биологический возраст опережает или отстает от
паспортного, морфо-функциональное дисгармоничное
(рост выше (ниже) среднего, МТ, ОГК, функциональные
показатели в пределах ±1,1 – ±2,0 σ.
● Биологический возраст опережает или отстает от
паспортного, морфо-функциональное резко
дисгармоничное (рост высокий (низкий), МТ, ОГК,
функциональные показатели выше (ниже) ±2,1 σ.

55.

IV. Комплексный метод (по В.Н. Кардашенко)
Пример: Мальчик 7 лет, рост 127,0 см, масса тела 31,0
кг, окружность грудной клетки 61,0 см, число постоянных
зубов 9, за последний год длина тела увеличилась на 5
см, ЖЕЛ 1700,0 мл, мышечная сила правой кисти 14,0 кг.
Дать оценку физического развития по комплексной
методике.

56.

IV. Комплексный метод (по В.Н. Кардашенко)
1 этап: Пользуясь таблицей "Средние значения
показателей биологического развития школьников",
определяют биологический возраст мальчика: длина тела
– 127,0 (121,98±5,37) – соответствует; погодовая прибавка
роста 5 см (5–6) – соответствует; число постоянных зубов
– 9 (6–12) – соответствует.
Заключение: биологический возраст обследуемого
ребенка соответствует паспортному возрасту.

57.

IV. Комплексный метод (по В.Н. Кардашенко)
2 этап: оценка морфологического статуса ребенка по
шкалам регрессии : рост ребенка 127,0 – физическое
развитие среднее.
Масса тела мальчика больше должной массы на 0,7 кг
(27,0–26,3=+0,7). Разницу делят на сигму регрессии
массы тела (3,6) и получают сигмальное отклонение: +0,7
/ 3,6 = 0,19 σR. Масса тела находится в пределах ±1,0 σ.
Окружность грудной клетки мальчика меньше должной
на 1,4 см (61,0–62,4= –1,4), что соответствует –0,42 σR
(–1,4 / 3,3= –0,42 σR). Окружность грудной клетки
находится в пределах ±1,0 σ.
Заключение: морфологические параметры ФР ребенка
средние, пропорциональные.

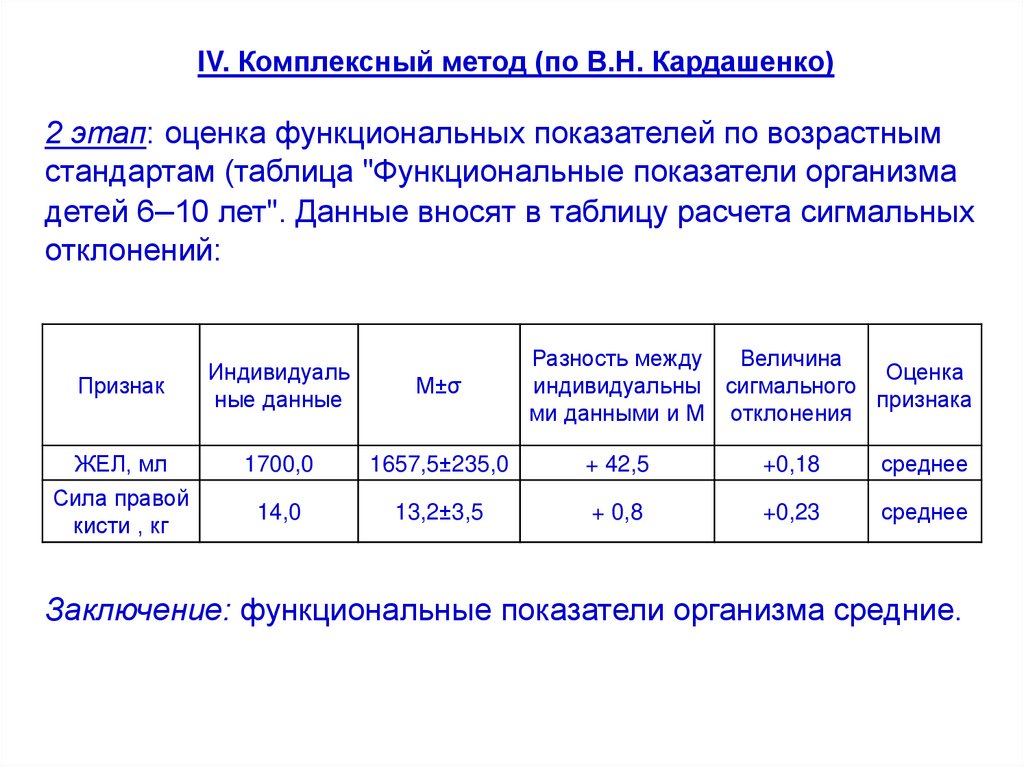
58.

IV. Комплексный метод (по В.Н. Кардашенко)
2 этап: оценка функциональных показателей по возрастным
стандартам (таблица "Функциональные показатели организма
детей 6–10 лет". Данные вносят в таблицу расчета сигмальных
отклонений:
Разность между
Величина
Оценка
индивидуальны сигмального
признака
ми данными и М отклонения
Признак
Индивидуаль
ные данные
М±σ
ЖЕЛ, мл
1700,0
1657,5±235,0
+ 42,5
+0,18
среднее
Сила правой
кисти , кг
14,0
13,2±3,5
+ 0,8
+0,23
среднее
Заключение: функциональные показатели организма средние.

59.

IV. Комплексный метод (по В.Н. Кардашенко)
Общее заключение:
Биологический уровень соответствует возрасту,
морфо-функциональное состояние гармоничное.

60.

IV. Комплексный метод (по В.Н. Кардашенко)
• Ребенку с каким уровнем физического развития
можно рекомендовать обучение в школе с 6 лет?
• Или посещать 5 кружков?
• Или заниматься спортом в школе олимпийского
резерва?
т.е. надо оценить уровень ФР, который
обеспечивает адаптационный потенциал организма
и отсутствие негативных последствий для здоровья
ребенка.

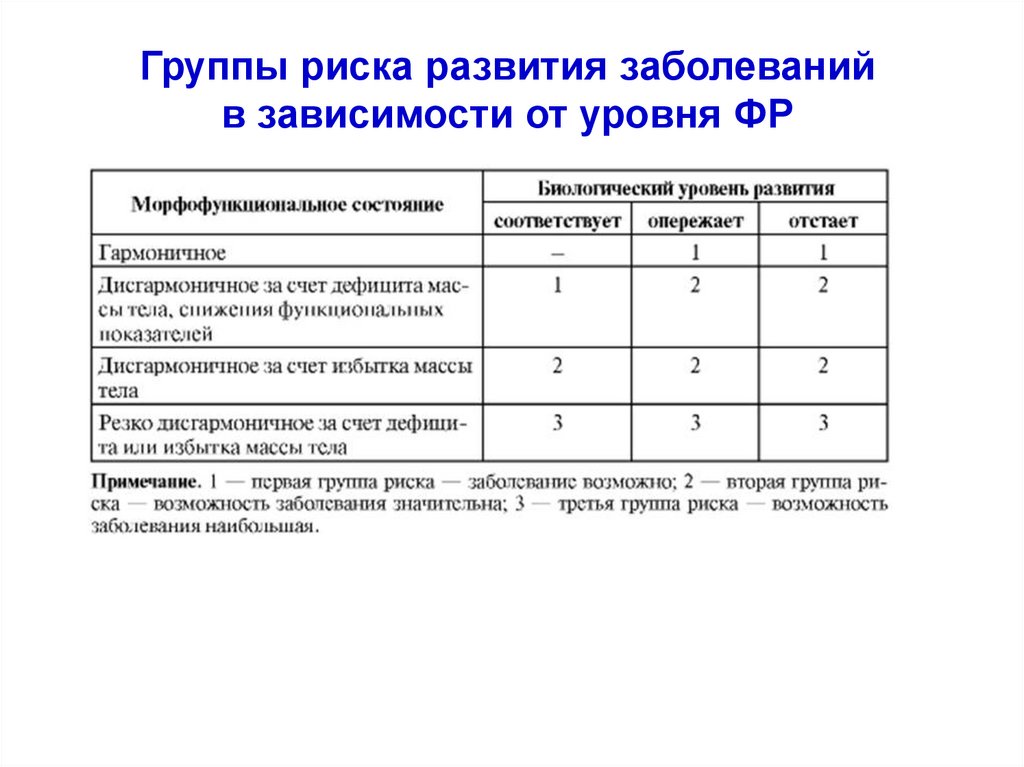
61.

Группы риска развития заболеваний
в зависимости от уровня ФР

62.

V. Метод индексов
Метод основан на расчете индексов – эмпирических числовых
соотношений между отдельными антропометрическими признаками
(двумя, тремя и более), выраженных в эмпирических формулах.
В настоящее время для оценки антропометрических показателей не
используется, а применяется для оперативной оценки состояния
питания или для расчета индексов пропорциональности (показателей
биологической зрелости ребенка).
Для оценки питания наиболее широко используется:
Массо-Ростовой Индекс,
индекс Чулицкой,
Индекс Массы Тела (ИМТ, Кетле II, BMI).
Из наиболее широко используемых индексов пропорциональности следует отметить
следующие: длина ноги/высота верхнего лица, окружность головы/длина тела, высота
верхнего лица/длина тела, длина ноги/длина тела. Оценка производится путем
сравнения рассчитанного индекса для данного ребенка со среднестатистическим
центильным распределением индекса с учетом возраста и пола.

63.

Бельгийский математик,
астроном, метеоролог,
социолог.
Один из родоначальников
статистики.
Адольф Кетле
Lambert-Adolph-Jacques Quetelet
1796–1874

64.

V. Метод индексов
Для оценки соответствия массы длине тела
(весо-ростового соотношения) используют индекс Кетле:
Масса тела (кг )
Индекс Кетле
2
[ Рост ( м)]
Пример: Мальчик 9 лет имеет рост 135 см, массу 31,0 кг.
Рост = 135 см, т. е. 1,35 м
Рост2 = 1,35 • 1,35 = 1,8 м2
31 кг
2
Индекс Кетле
17
,
22
кг
/
м
2
1,8 м

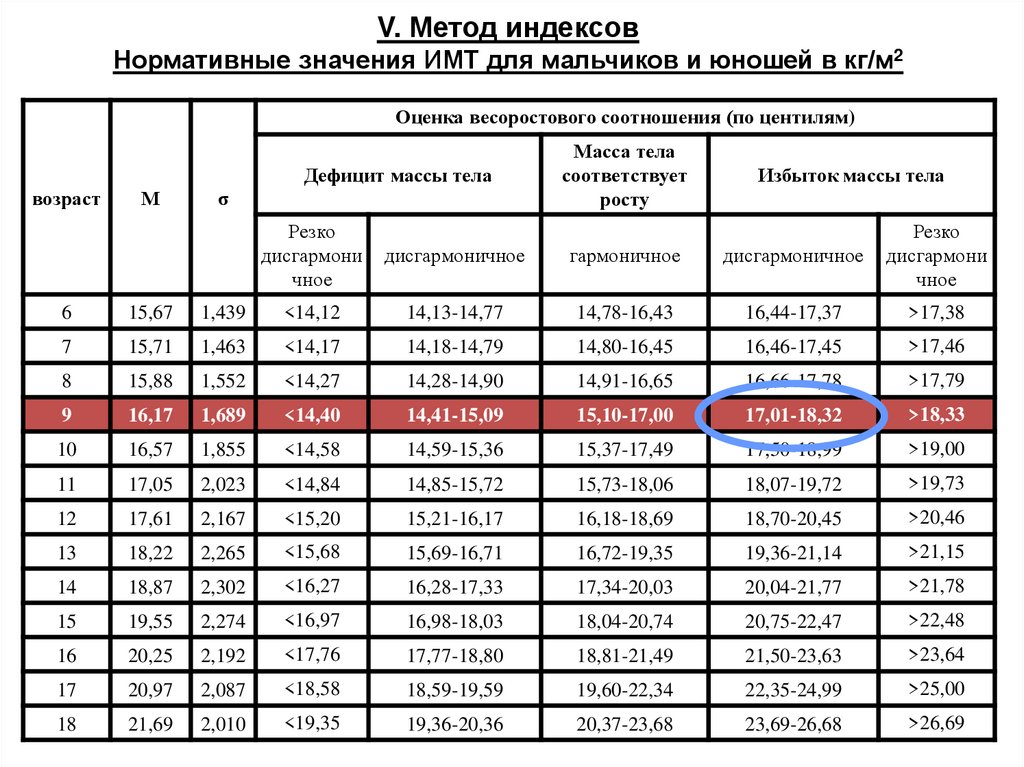
65.

V. Метод индексов
Нормативные значения ИМТ для мальчиков и юношей в кг/м2
Оценка весоростового соотношения (по центилям)
Дефицит массы тела
возраст
М
σ
Масса тела
соответствует
росту
Избыток массы тела
Резко
дисгармони
чное
дисгармоничное
гармоничное
дисгармоничное
Резко
дисгармони
чное
6
15,67
1,439
<14,12
14,13-14,77
14,78-16,43
16,44-17,37
>17,38
7
15,71
1,463
<14,17
14,18-14,79
14,80-16,45
16,46-17,45
>17,46
8
15,88
1,552
<14,27
14,28-14,90
14,91-16,65
16,66-17,78
>17,79
9
16,17
1,689
<14,40
14,41-15,09
15,10-17,00
17,01-18,32
>18,33
10
16,57
1,855
<14,58
14,59-15,36
15,37-17,49
17,50-18,99
>19,00
11
17,05
2,023
<14,84
14,85-15,72
15,73-18,06
18,07-19,72
>19,73
12
17,61
2,167
<15,20
15,21-16,17
16,18-18,69
18,70-20,45
>20,46
13
18,22
2,265
<15,68
15,69-16,71
16,72-19,35
19,36-21,14
>21,15
14
18,87
2,302
<16,27
16,28-17,33
17,34-20,03
20,04-21,77
>21,78
15
19,55
2,274
<16,97
16,98-18,03
18,04-20,74
20,75-22,47
>22,48
16
20,25
2,192
<17,76
17,77-18,80
18,81-21,49
21,50-23,63
>23,64
17
20,97
2,087
<18,58
18,59-19,59
19,60-22,34
22,35-24,99
>25,00
18
21,69
2,010
<19,35
19,36-20,36
20,37-23,68
23,69-26,68
>26,69

66.

V. Метод индексов
Для оценки соответствия массы длине тела
(весо-ростового соотношения) используют индекс Кетле:
Масса тела (кг )
Индекс Кетле
2
[ Рост ( м)]
Пример: Мальчик 9 лет имеет рост 135 см, массу 31,0 кг.
Рост = 135 см, т. е. 1,35 м
Рост2 = 1,35 • 1,35 = 1,8 м2
31 кг
2
Индекс Кетле
17
,
22
кг
/
м
2
1,8 м
Таким образом, у данного ребенка наблюдается
дисгармоничное развитие за счет избыточной массы тела.

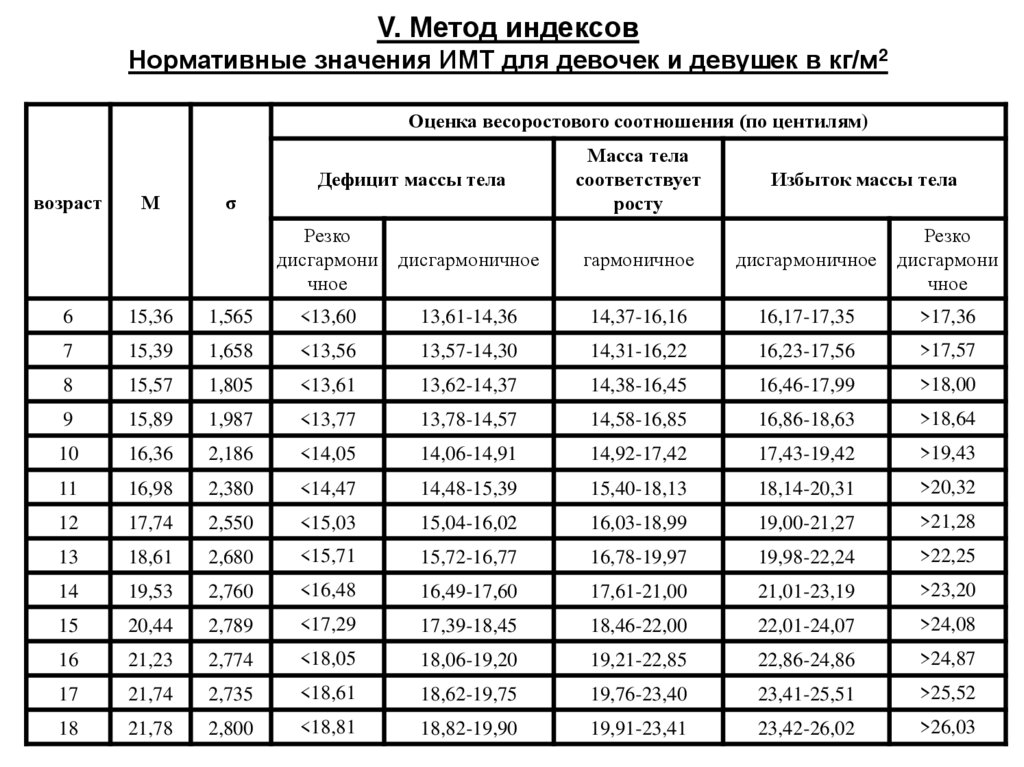
67.

V. Метод индексов
Нормативные значения ИМТ для девочек и девушек в кг/м2
Оценка весоростового соотношения (по центилям)
Дефицит массы тела
возраст
М
σ
Масса тела
соответствует
росту
Избыток массы тела
Резко
дисгармони
чное
дисгармоничное
гармоничное
дисгармоничное
Резко
дисгармони
чное
6
15,36
1,565
<13,60
13,61-14,36
14,37-16,16
16,17-17,35
>17,36
7
15,39
1,658
<13,56
13,57-14,30
14,31-16,22
16,23-17,56
>17,57
8
15,57
1,805
<13,61
13,62-14,37
14,38-16,45
16,46-17,99
>18,00
9
15,89
1,987
<13,77
13,78-14,57
14,58-16,85
16,86-18,63
>18,64
10
16,36
2,186
<14,05
14,06-14,91
14,92-17,42
17,43-19,42
>19,43
11
16,98
2,380
<14,47
14,48-15,39
15,40-18,13
18,14-20,31
>20,32
12
17,74
2,550
<15,03
15,04-16,02
16,03-18,99
19,00-21,27
>21,28
13
18,61
2,680
<15,71
15,72-16,77
16,78-19,97
19,98-22,24
>22,25
14
19,53
2,760
<16,48
16,49-17,60
17,61-21,00
21,01-23,19
>23,20
15
20,44
2,789
<17,29
17,39-18,45
18,46-22,00
22,01-24,07
>24,08
16
21,23
2,774
<18,05
18,06-19,20
19,21-22,85
22,86-24,86
>24,87
17
21,74
2,735
<18,61
18,62-19,75
19,76-23,40
23,41-25,51
>25,52
18
21,78
2,800
<18,81
18,82-19,90
19,91-23,41
23,42-26,02
>26,03

68.

Надежность методов оценки
физического развития
детей и подростков

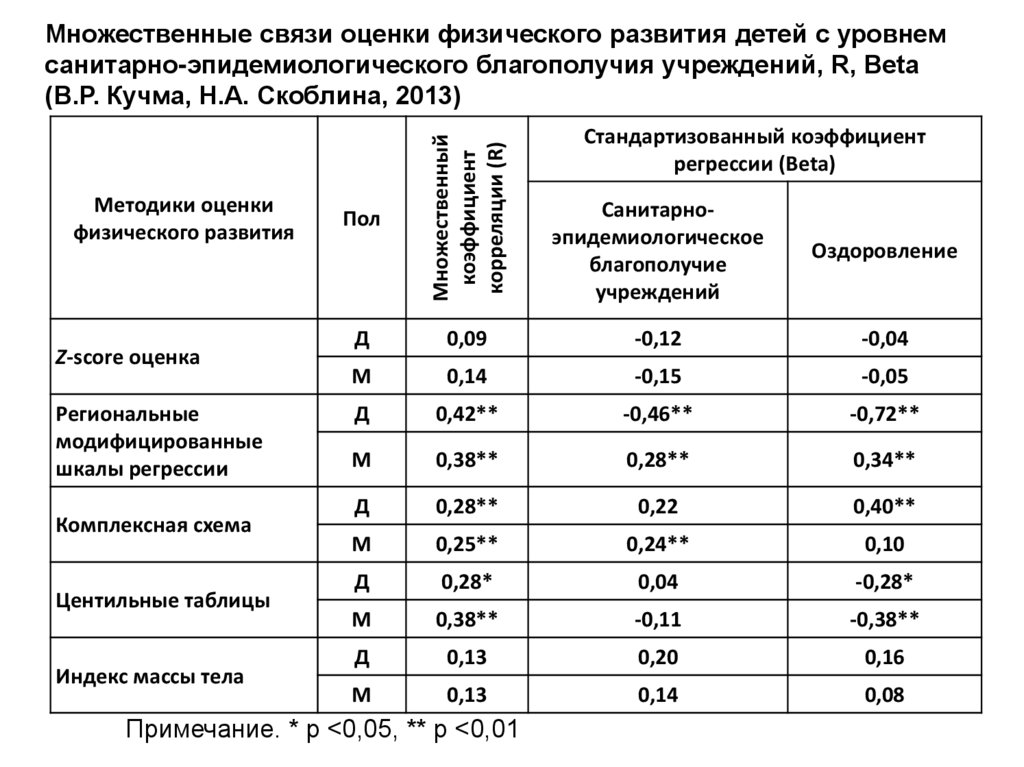
69.

Множественные связи оценки физического развития детей с уровнем
санитарно-эпидемиологического благополучия учреждений, R, Beta
(В.Р. Кучма, Н.А. Скоблина, 2013)
Z-score оценка
Региональные
модифицированные
шкалы регрессии
Комплексная схема
Центильные таблицы
Индекс массы тела
Множественный
коэффициент
корреляции (R)
Методики оценки
физического развития
Стандартизованный коэффициент
регрессии (Beta)
Санитарноэпидемиологическое
благополучие
учреждений
Д
0,09
-0,12
-0,04
М
0,14
-0,15
-0,05
Д
0,42**
-0,46**
-0,72**
М
0,38**
0,28**
0,34**
Д
0,28**
0,22
0,40**
М
0,25**
0,24**
0,10
Д
0,28*
0,04
-0,28*
М
0,38**
-0,11
-0,38**
Д
0,13
0,20
0,16
М
0,13
0,14
0,08
Пол
Примечание. * р <0,05, ** р <0,01
Оздоровление

70.

Оценка физического развития коллективов
(генерализирующий метод)
1. Определение различий по
арифметическим взвешенным
основных признаков в
однородных статистических
совокупностях с определением
достоверности их различий по
критерию Стьюдента.
2. Суммирование
индивидуальных оценок и
вычисление процентного
распределения детей по
отдельным уровням
физического развития.

71.

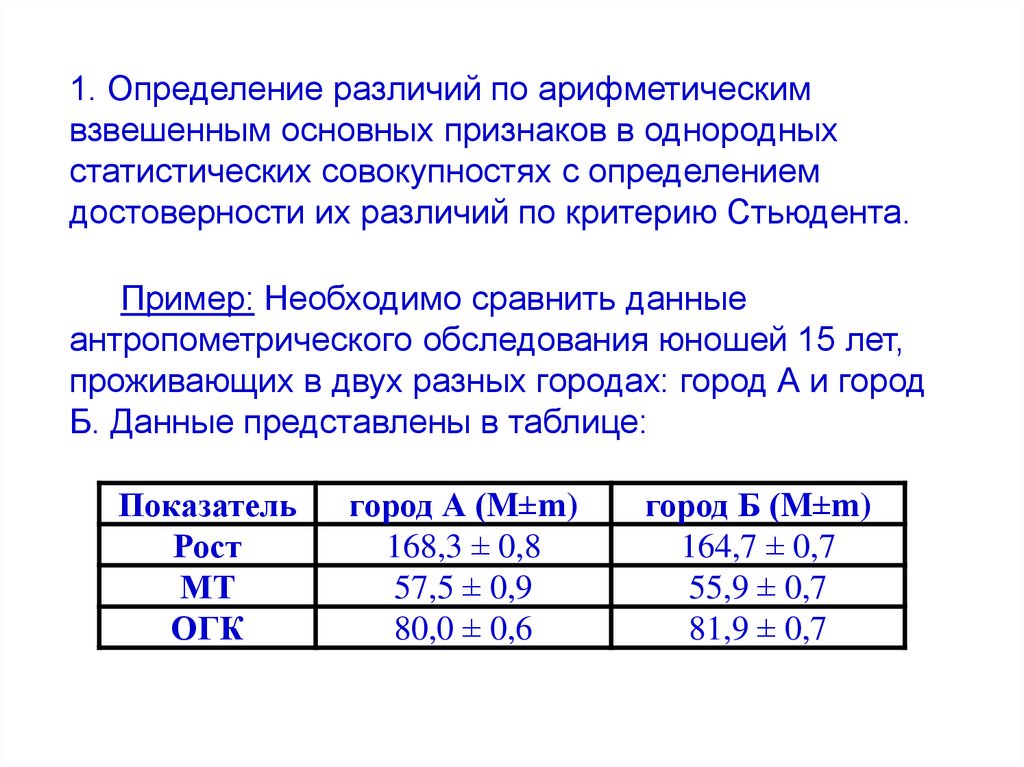
1. Определение различий по арифметическим
взвешенным основных признаков в однородных
статистических совокупностях с определением
достоверности их различий по критерию Стьюдента.
Пример: Необходимо сравнить данные
антропометрического обследования юношей 15 лет,
проживающих в двух разных городах: город А и город
Б. Данные представлены в таблице:
Показатель
Рост
МТ
ОГК
город А (M±m)
168,3 ± 0,8
57,5 ± 0,9
80,0 ± 0,6
город Б (M±m)
164,7 ± 0,7
55,9 ± 0,7
81,9 ± 0,7

72.

Показатель
Рост
МТ
ОГК
город А (M±m)
168,3 ± 0,8
57,5 ± 0,9
80,0 ± 0,6
город Б (M±m)
164,7 ± 0,7
55,9 ± 0,7
81,9 ± 0,7
При сравнении показателей роста и массы тела выявлены более
высокие их величины у юношей города А, в то время как показатели
окружности грудной клетки выше у юношей города Б.
Определим достоверность этих различий, для чего рассчитаем для
каждой пары показателей критерий t Стьюдента:
t
M1 M 2
m1 m2
2
2
где M1 и M2 – средние арифметические признаков,
m1 и m2 – ошибки средних арифметических.

73.

168,3 164,7
3,6
t ДТ
3,39 ( p 0,01);
0,82 0,7 2 1,06
57,5 55,9
1,6
t МТ
1,4 ( p 0,05);
0,9 2 0,7 2 1,14
81,9 80,0
1,9
t ОГК
2,06 ( p 0,05).
2
2
0,92
0,6 0,7
Полученный критерий t оценивается следующим образом:
t ≥ 3 – различия средних величин достоверны с вероятностью
безошибочного прогноза, равной 99% и более (р < 0,01);
3 > t > 2 – различия средних величин достоверны с
вероятностью безошибочного прогноза, равной 95% и более (р < 0,05);
t < 2 – различия их не достоверны.
Таким образом, выявлены достоверные различия в росте и окружности
грудной клетки юношей 15 лет гор. А. и гор. Б.

74.

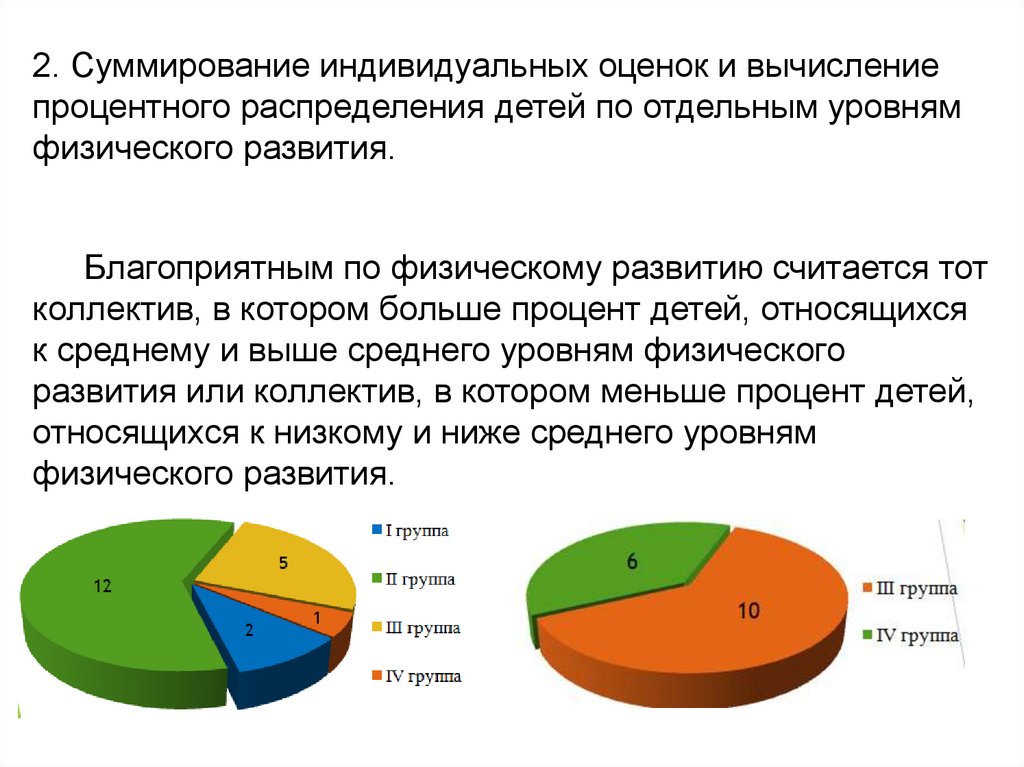
2. Суммирование индивидуальных оценок и вычисление
процентного распределения детей по отдельным уровням
физического развития.
Благоприятным по физическому развитию считается тот
коллектив, в котором больше процент детей, относящихся
к среднему и выше среднего уровням физического
развития или коллектив, в котором меньше процент детей,
относящихся к низкому и ниже среднего уровням
физического развития.