ОЭ 3.6 Переходные процессы

1.

ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
Раздел 3
Электрические цепи переменного тока
Тема 3.6
Переходные процессы в цепях переменного тока

2.

Основные понятия
Переходный процесс – электромагнитный процесс, возникающий в
электрической цепи при переходе от одного установившегося
(принужденного) режима к другому.
Установившийся режим – режим работы электрической цепи, при
котором электрические параметры остаются неизменными.
Переходный процесс вызывается коммутацией в цепи.
Коммутация – процесс замыкания или размыкания рубильников или
выключателей.

3.

Основные понятия
Первый закон коммутации
Ток в катушке индуктивности не может изменяться скачком, или ток в
момент после коммутации имеет точно такое же значение, какое имел
до.
ЭДС самоиндукции определяется
формулой:
При изменении тока в индуктивности скачком, ЭДС самоиндукции
стремится к бесконечности
, что противоречит закону
самоиндукции.
Второй закон коммутации
Напряжение на емкости не может изменяться скачком, или напряжение в
момент после коммутации остается таким же, что и до коммутации.

4.

Основные понятия
Переходный процесс состоит из нескольких процессов:
установившийся (после коммутации);
свободный (переход от прежнего режима к установившемуся).
Ток и напряжение в цепи в течение переходного процесса определяется:
В результате переходного процесса происходят изменения тока,
напряжения, фазы, частоты и т.д.

5.

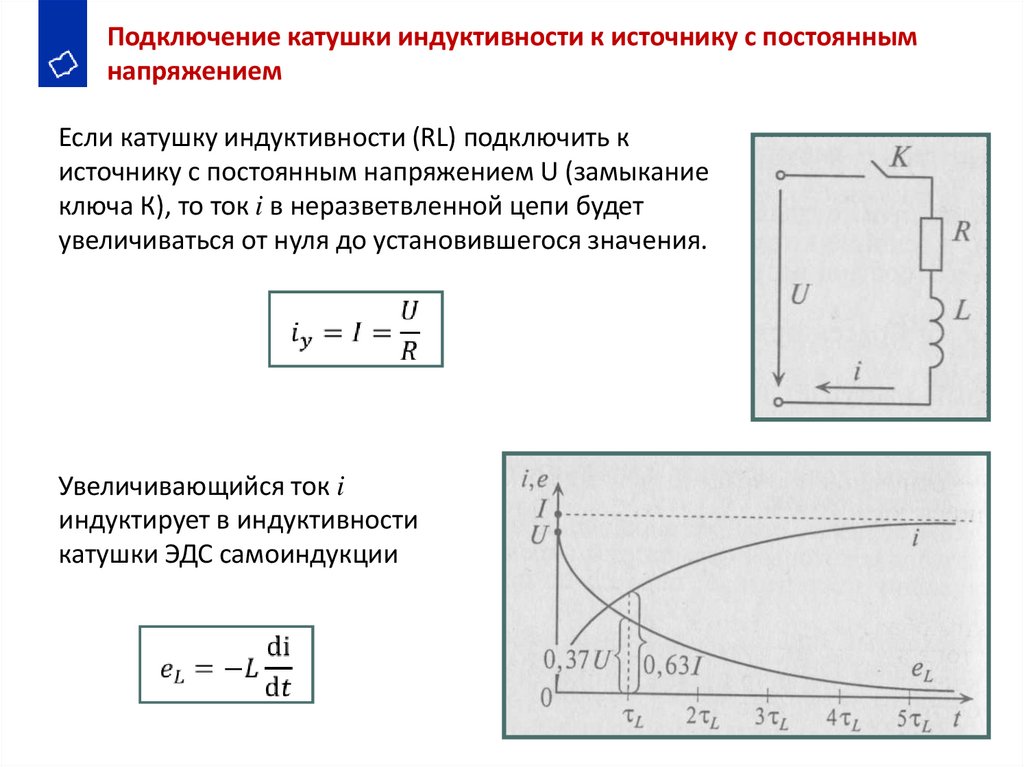
Подключение катушки индуктивности к источнику с постоянным
напряжением
Если катушку индуктивности (RL) подключить к
источнику с постоянным напряжением U (замыкание
ключа К), то ток i в неразветвленной цепи будет
увеличиваться от нуля до установившегося значения.
Увеличивающийся ток i
индуктирует в индуктивности
катушки ЭДС самоиндукции

6.

Подключение катушки индуктивности к источнику с постоянным
напряжением
Для любого момента времени переходного процесса по второму закону
Кирхгофа можно записать двумя способами:
Установившийся ток в конце переходного
процесса находится следующим уравнением:
Постоянная времени RL-цепи обозначается буквой
τ и определяет скорость переходного процесса или
его длительность.
Ток свободного процесса:

7.

Подключение катушки индуктивности к источнику с постоянным
напряжением
Уравнение, для определения величины тока в цепи с индуктивностью L:
Переходный процесс считается законченным, когда ток увеличивается
до значения i = 99 % установившегося тока I.
Что соответствует времени переходного процесса
ЭДС самоиндукции в цепи, вызванная свободным током
определяется выражением:
Таким образом, ЭДС самоиндукции в RL-цепи, подключенной к источнику
с постоянным напряжением будет уменьшаться.

8.

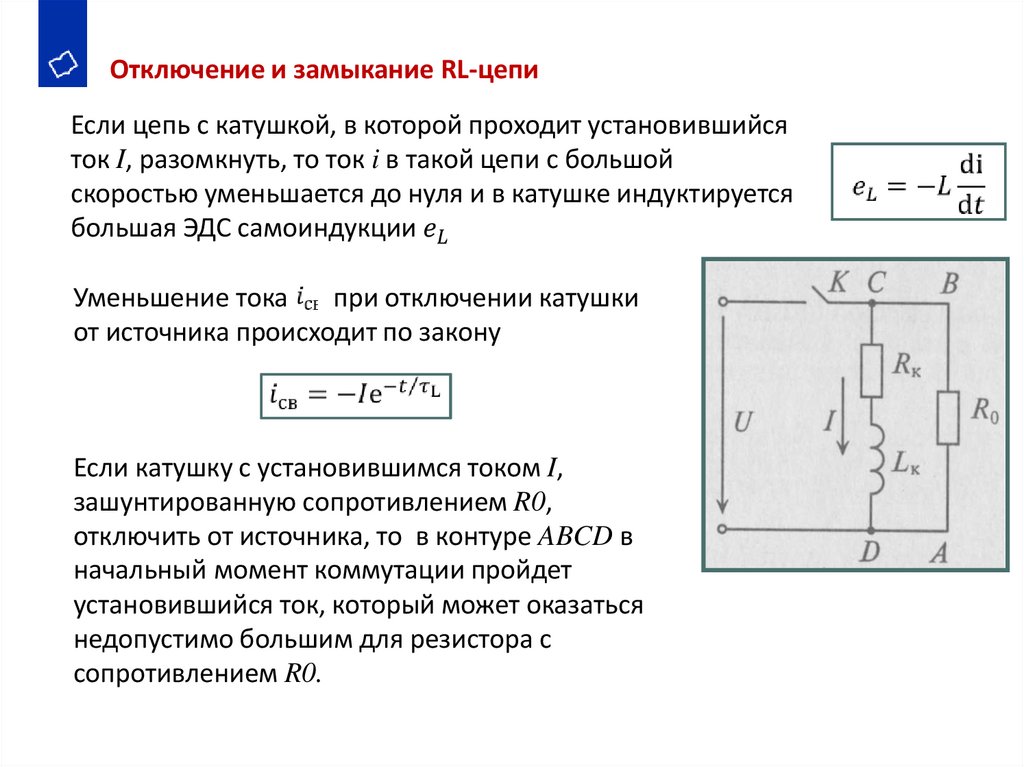
Отключение и замыкание RL-цепи
Если цепь с катушкой, в которой проходит установившийся
ток I, разомкнуть, то ток i в такой цепи с большой
скоростью уменьшается до нуля и в катушке индуктируется
большая ЭДС самоиндукции
Уменьшение тока
при отключении катушки
от источника происходит по закону
Если катушку с установившимся током I,
зашунтированную сопротивлением R0,
отключить от источника, то в контуре ABCD в
начальный момент коммутации пройдет
установившийся ток, который может оказаться
недопустимо большим для резистора с
сопротивлением R0.

9.

Отключение и замыкание RL-цепи
Для определения активного сопротивления катушки Rк и полного ее
сопротивления Zк включают амперметр и вольтметр, который включается
вместо резистора с сопротивлением R0 в контур.
Вольтметр может не быть рассчитан
на установившийся ток, проходящий
через него при размыкании ключа, в
результате чего может сгореть.
Для избежания данной ситуации
необходимо сначала отключить
вольтметр, только после чего можно
размыкать ключ.

10.

Зарядка, разрядка и саморазрядка конденсатора
Если конденсатор с сопротивлением (утечки) R и емкостью C подключить к
источнику с постоянным напряжением U (замыканием ключа K), то в цепи
появится ток зарядки конденсатора:
- напряжение на конденсаторе в любой
момент времени переходного процесса.
По второму закону Кирхгофа
для цепи зарядки
конденсатора можно записать
следующие уравнения:

11.

Зарядка, разрядка и саморазрядка конденсатора
Из предыдущего уравнения
можно получить выражение для
установившегося напряжения на
конденсаторе:
Следовательно, напряжение на заряжающемся конденсаторе в любой
момент переходного процесса определяется выражением:
Теоретически, зарядка конденсатора длится бесконечно долго, а
конденсатор считается заряженным, когда напряжение на нем достигает
99% напряжения источника U.
Таким образом, в RC-цепи, чем больше постоянная времени
, тем
больше времени тратится на зарядку конденсатора, т.е. постоянная
времени
характеризует длительность зарядки и разрядки конденсатора.

12.

Зарядка, разрядка и саморазрядка конденсатора
Ток i при зарядке конденсатора
уменьшается по закону:
где
– максимальный ток, который имеет место в начальный момент
t=0 зарядки конденсатора (момент коммутации).
Если конденсатор емкостью C, заряженный предварительно до напряжения
U, разряжать через резистор с сопротивлением R, то напряжение
на
конденсаторе и ток в цепи разрядки будут уменьшаться по закону
Где U – напряжение на конденсаторе до начала разрядки, а I=U/R –
максимальный ток в момент разрядки,
– постоянная времени в
цепи разрядки конденсатора.

13.

Зарядка, разрядка и саморазрядка конденсатора
За время
напряжение и ток уменьшатся до 37%
своих максимальных значений.
Если конденсатор емкостью C, заряженный до напряжения U, отсоединить
от источника, то он будет разряжаться через свой диэлектрик. Напряжение
на нем будет уменьшаться по закону
. Процесс разрядки
конденсатора через свой диэлектрик называется саморазрядом.
Постоянная времени саморазряда зависит от физических свойств
диэлектрика
где – удельное сопротивление диэлектрика;
– электрическая
постоянная;
– диэлектрическая проницаемость диэлектрика
(относительная).

14.

ПТИ, кафедра радиосистем, 2024