философия

1.

Обзор книг Льюиса
Кэрролла как сложных
логико-математических
трактатов
Произведения Кэрролла — многослойные
логико-математические конструкции под
маской детских сказок.

2.

Жизнь и творческий путь
Льюиса Кэрролла
Чарльз Латвидж Доджсон, профессор математики
Оксфорда XIX века, впитал элементы
формальной логики и алгебры, что определило
уникальность его литературных произведений.
2

3.

Математические мотивы в «Алисе в стране чудес»
В произведении отражены
задачи с изменением размеров,
символизирующие
преобразования и вариации
параметров в дискретной
математике.
Образы и ситуации
иллюстрируют парадоксы
бесконечности, раскрывая
сложные концепции теории
множеств и бесконечных
множеств.
Персонажи и сцены моделируют
свойства математических структур
и логических схем через
аллегории и метафоры в сюжете.
3

4.

Логические парадоксы и игры слов в произведениях Кэрролла
Игра с отрицанием: парадокс
«обманутого лжеца»
Этот классический парадокс, который
запутывает логическое мышление,
представлен в диалогах, где
высказывания одновременно
истинны и ложны, создавая
двусмысленность.
Мад Хеттер и временная петля
Образ Мад Хеттера иллюстрирует
цикличность времени и бесконечные
повторения, демонстрируя парадоксы
бесконечности, которые связываются
с логическими временными
конструкциями.
Языковые игры и
двусмысленность
Тексты насыщены каламбурами и
многозначными фразами, которые
раскрывают скрытые логические
противоречия, стимулируя
аналитическое восприятие речи.
4

5.

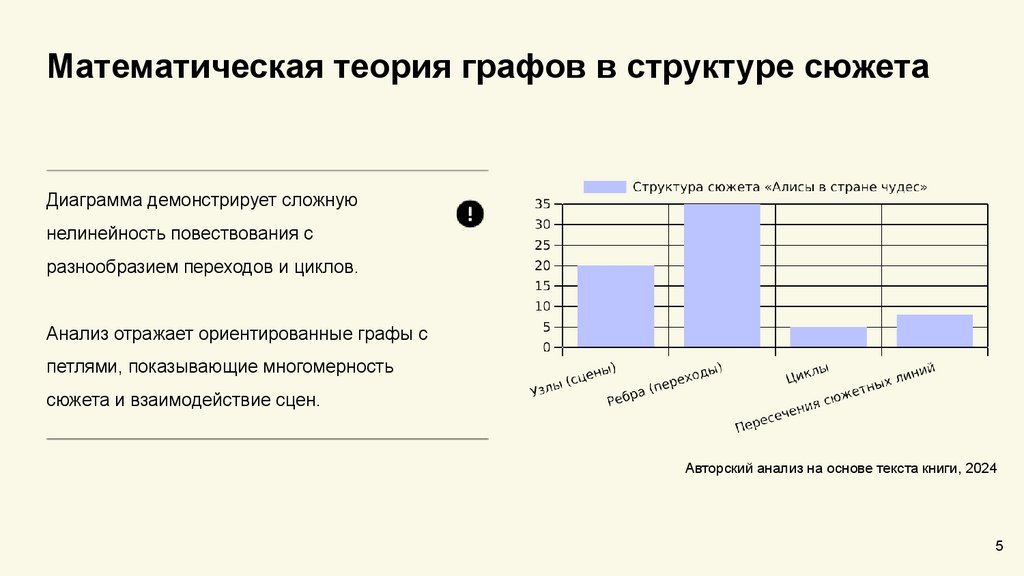
Математическая теория графов в структуре сюжета
Диаграмма демонстрирует сложную
нелинейность повествования с
разнообразием переходов и циклов.
Анализ отражает ориентированные графы с
петлями, показывающие многомерность
сюжета и взаимодействие сцен.
Авторский анализ на основе текста книги, 2024
5

6.

Персонажи и логико-математические концепции
Таблица сопоставляет персонажей с соответствующими
логическими и математическими идеями в
произведениях Кэрролла.
Персонажи служат метафорической визуализацией
абстрактных математических и логических понятий,
облегчая их восприятие.
Собственный аналитический разбор
6

7.

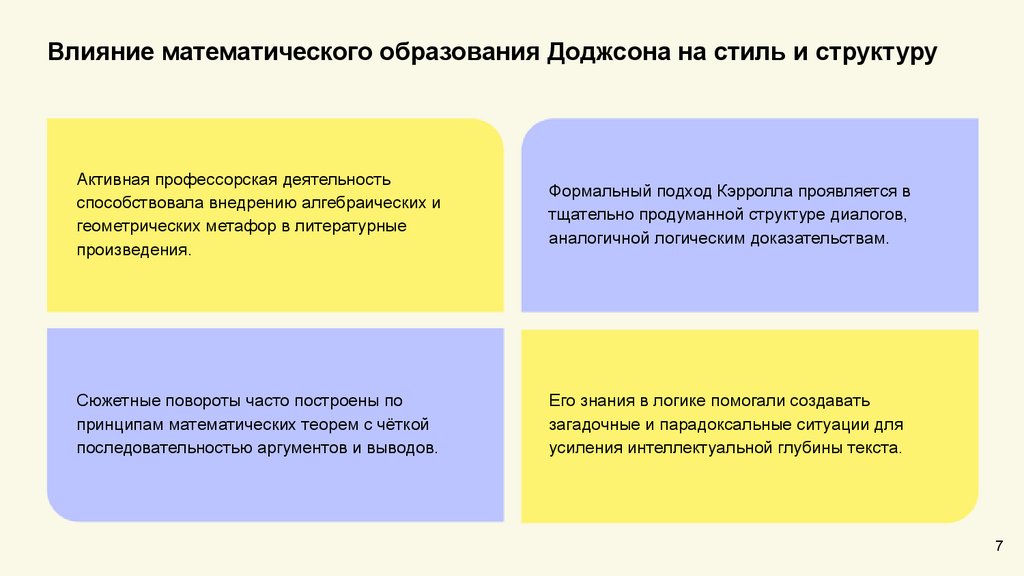
Влияние математического образования Доджсона на стиль и структуру
Активная профессорская деятельность
способствовала внедрению алгебраических и
геометрических метафор в литературные
произведения.
Формальный подход Кэрролла проявляется в
тщательно продуманной структуре диалогов,
аналогичной логическим доказательствам.
Сюжетные повороты часто построены по
принципам математических теорем с чёткой
последовательностью аргументов и выводов.
Его знания в логике помогали создавать
загадочные и парадоксальные ситуации для
усиления интеллектуальной глубины текста.
7

8.

Символизм и аллюзии на математику в творчестве Кэрролла
Геометрические и топологические метафоры
Образы лестниц и зеркал символизируют изменения
пространства и симметрию, раскрывая идеи геометрии и
топологии в повествовании.
Пространственные трансформации и их значение
Искажения пространства и переходы между мирами
иллюстрируют математические преобразования, усиливая
связь сюжета с абстрактными концепциями.
8

9.

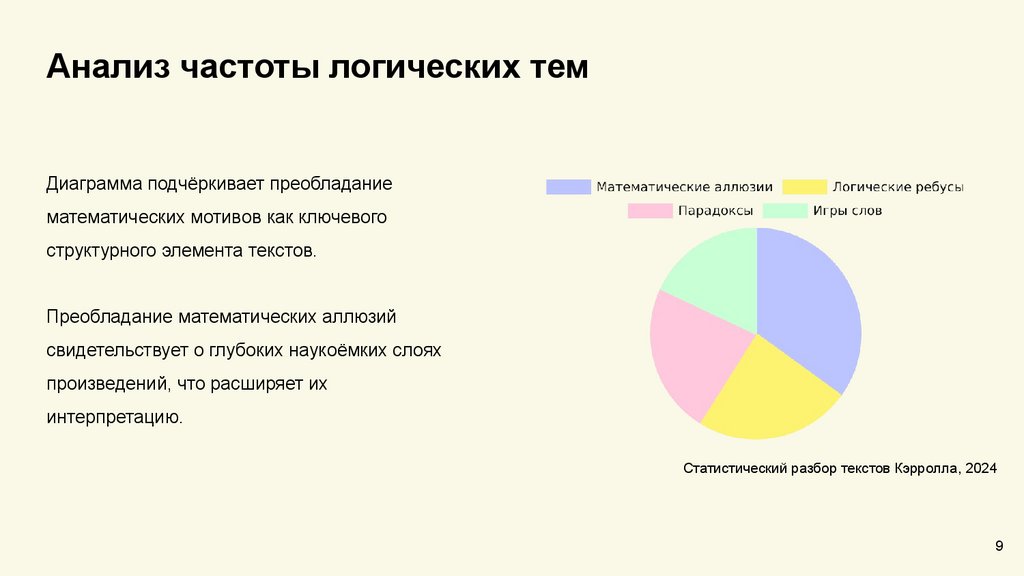
Анализ частоты логических тем
Диаграмма подчёркивает преобладание
математических мотивов как ключевого
структурного элемента текстов.
Преобладание математических аллюзий
свидетельствует о глубоких наукоёмких слоях
произведений, что расширяет их
интерпретацию.
Статистический разбор текстов Кэрролла, 2024
9

10.

Заключение: роль трудов Льюиса Кэрролла в
литературе и науке
Произведения Кэрролла гармонично объединяют художественное воображение и
строгую математику, стимулируя междисциплинарные исследования и творческое
мышление.