Асонов Д. 23ПМ2

1.

2.

Цель: Разработка математической модели равномерного
движения материальной точки по заданной траектории с
использованием численных методов.
Задачи:
1. Приближение дискретных данных методами интерполяции.
2. Численное дифференцирование для вычисления скорости.
3. Численное интегрирование для расчёта площади под
кривой.
4. Построение динамической модели движения с
визуализацией.

3.

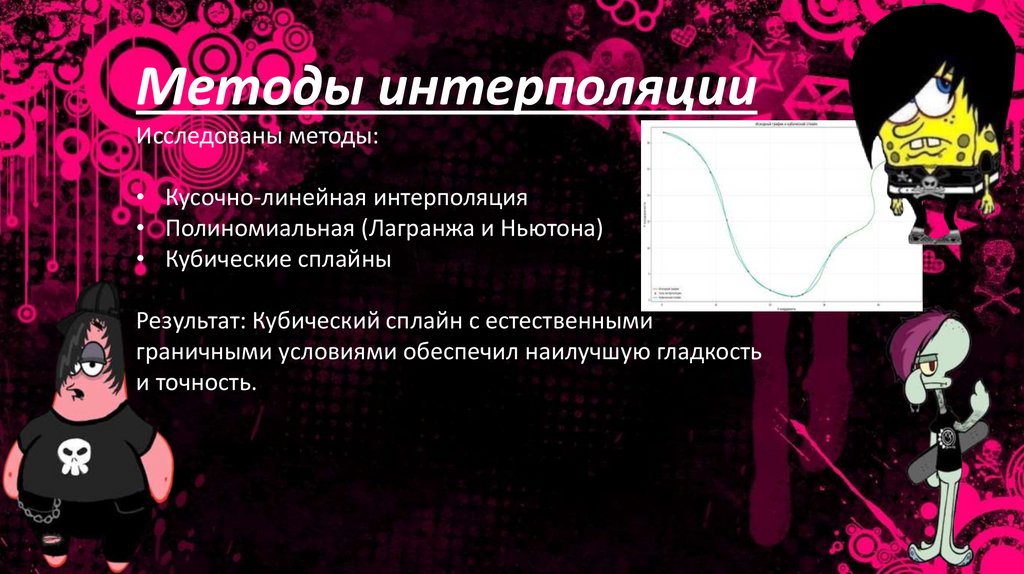
Методы интерполяции
Исследованы методы:
• Кусочно-линейная интерполяция
• Полиномиальная (Лагранжа и Ньютона)
• Кубические сплайны
Результат: Кубический сплайн с естественными
граничными условиями обеспечил наилучшую гладкость
и точность.

4.

Дифференцирование:
Реализованы методы левых, правых и центральных
разностей.
Центральные разности дали наивысшую точность
(погрешность O(h^2)).
Интегрирование:
Применены методы прямоугольников, трапеций и
Симпсона.
Метод Симпсона показал наименьшую погрешность.

5.

• Траектория задана кубическим сплайном.
• Движение смоделировано с учётом закона
сохранения энергии и гравитации.
• Реализована анимация с отображением вектора
скорости.
• Построены графики зависимости скорости от
времени и пройденного пути.

6. Результаты и выводы

Результаты:
• Создан программный комплекс на Python с
использованием NumPy и Matplotlib.
• Получена гладкая траектория, рассчитаны скорость и
интегральные характеристики.
• Визуализировано движение точки с упругими
отражениями.
Выводы:
• Численные методы эффективны для моделирования
динамических систем.
• Кубические сплайны оптимальны для аппроксимации
траекторий.
• Модель может быть расширена для задач с
переменными силами.

7. Спасибо за внимание!