TEAM6

1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ

М АТ Е М АТ И Ч Е С К И Е
М ОД ЕЛ И
Подготовила команда 6 :
Шершунов Демьян
Савостин Олег
Елисейкина Надежда
Мурашов Дмитрий
Евсеев Максим
Каримов Тимур
МОСКВА
2025

2. В чем заключалась наша задача

В ЧЕМ ЗАКЛЮЧАЛАСЬ НАША ЗАДАЧА
Перед нами были поставлены следующие четыре задач, которые надо было решить
математическими методами:
1
Задача на анализ
размерностей
периодических
колебаниях звезды.
3
Задача на нахождение
температурного поля
на глубинах водного
резервуара.
2
4
"Подгон" модели к
имеющимся
данным о рыбах.
Задача на определение
оптимального
ассортимента
производства.

3. ЗАДАЧА №

З А Д АЧ А № 1
Считается, что некоторые звезды, свет и радиальные
скорости которых совершают периодические колебания,
пульсируют. Гипотетически известно, что период t
пульсаций зависит от радиуса звезды r, ее массы m и
гравитационной постоянной g. Используя анализ
размерностей, найти выражение для t через
перечисленные величины.

4.

1
РЕШЕНИЕ
Нам известно, что t зависит от радиуса звезды r, массы m и гравитационной
постоянной G. Перед нами стоит задача найти t = f(r, m, G). Выпишем
размерности этих переменных:
Переменная
Размерность
t
T
r
L
m
M
G
L3M-1T-2
По П-Теореме эта задача может быть записана в однородном по
размерности виде F(Π) = 0, где Π является безразмерным
произведением.
Ищем размерность
П = tarbmcGd =TaLbMcL3dM-dT-2d = Ta-2dMc-dLb+3d
Это произведение является безразмерным, только когда степени равны
нулю.
Справочник
Формула гравитационной
постоянной
Размерности
L - Длина
M - Масса
T - Время

5.

1
Для простоты, будем считать что зависимая переменная t входит в
произведение со степенью 1. Получаем следующую систему уравнений:
{
T: 1-2d = 0
M: c-d = 0
L: b+3d = 0
Откуда получаем:
{
D=½
C=½
B = -3/2
Вставляем в исходное уравнение и получаем: t1r -3/2m1/2G1/2
Так как у нас только одно безразмерное произведение F(П)= 0 , то П = С , где С - некоторая
безразмерная константа. Получаем:
tr-3/2m1/2G1/2 = П
Ответ:
tr-3/2m1/2G1/2 = C
t = C(r3/2m-1/2G-1/2)

6. ЗАДАЧА №

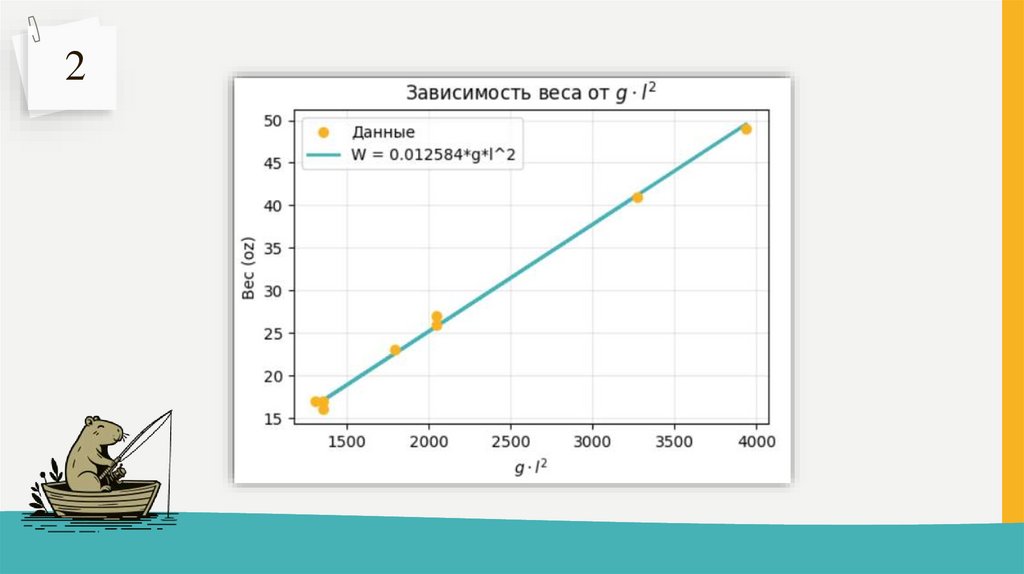
2
В приведенном наборе данных W обозначает
вес рыбы (окуня), l – длину рыбы а g – обхват
рыбы. «Подгоните» модель W = kgl2 к
имеющимся данным с помощью критерия
наименьших квадратов.

7.

2
РЕШЕНИЕ
1. Математическая постановка задачи
У нас есть модель: W = kgl2
Перепишем её как: W = kX, где X = gl2
Это линейная модель относительно коэффициента (нет свободного члена).
2. Метод наименьших квадратов для такой модели
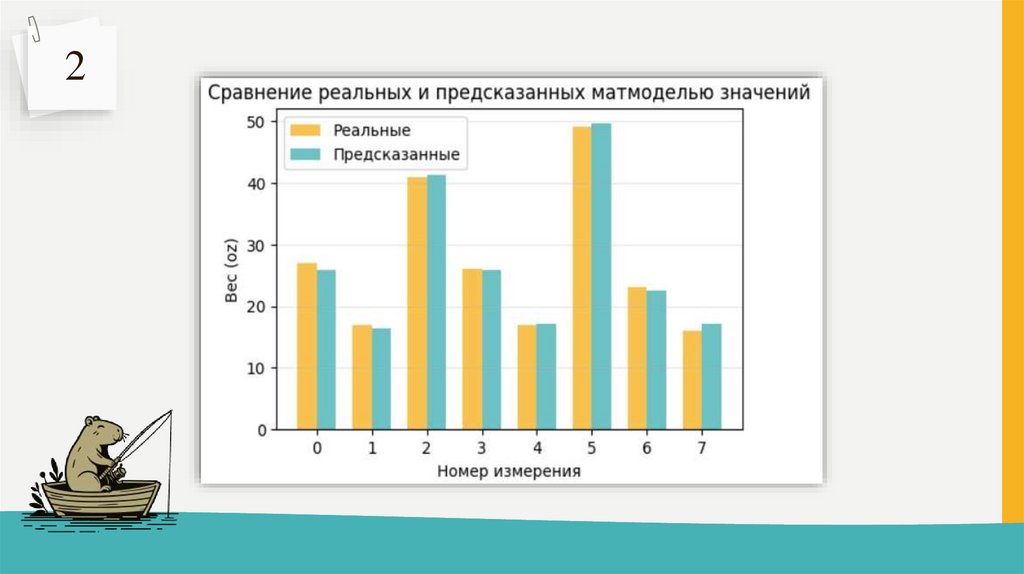
Мы хотим найти такое , чтобы минимизировать сумму квадратов ошибок:
n = 8 (количество измерений)
Wi - реальный вес i-й рыбы
Xi = gili2
kXi - предсказанный вес

8.

2
3. Аналитическое решение.
Берём производную и приравниваем к нулю:
Отсюда получаем формулу для k:

9.

2

10.

2

11. ЗАДАЧА №

3
Рассмотрим очень глубокий резервуар с жидкостью (почти
как Марианская впадина), и пусть боковая поверхность
резервуара теплоизолирована. Пусть начальная
температура жидкости равна −24◦С, и пусть температура
воздуха над жидкостью равна 0 ◦С (начало отсчета
температур). Найти температурное поле в жидкости на
различных глубинах и в различные моменты времени.
1. Решить задачу с помощью преобразования Лапласа и
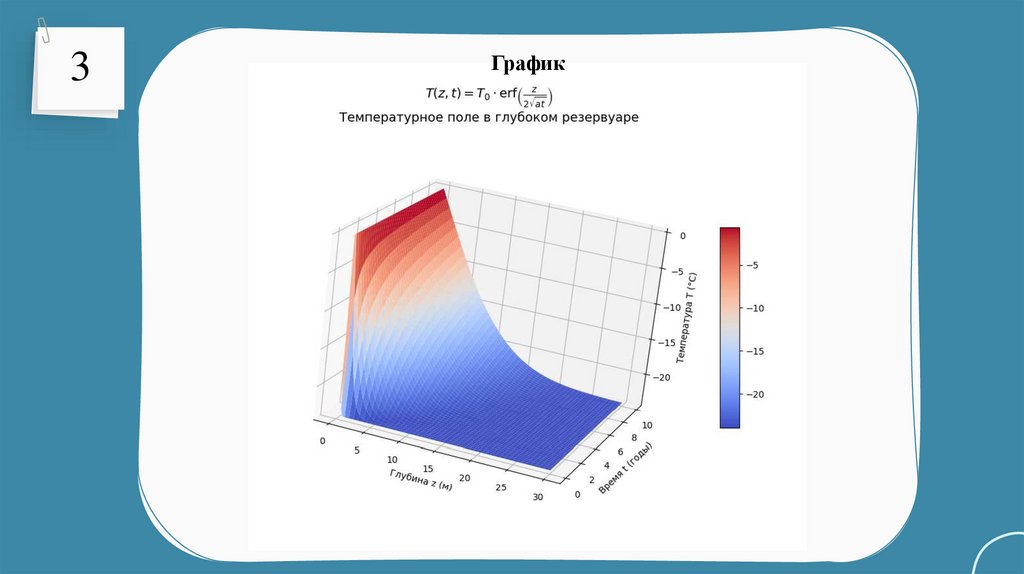
построить 3D-график полученного решения.
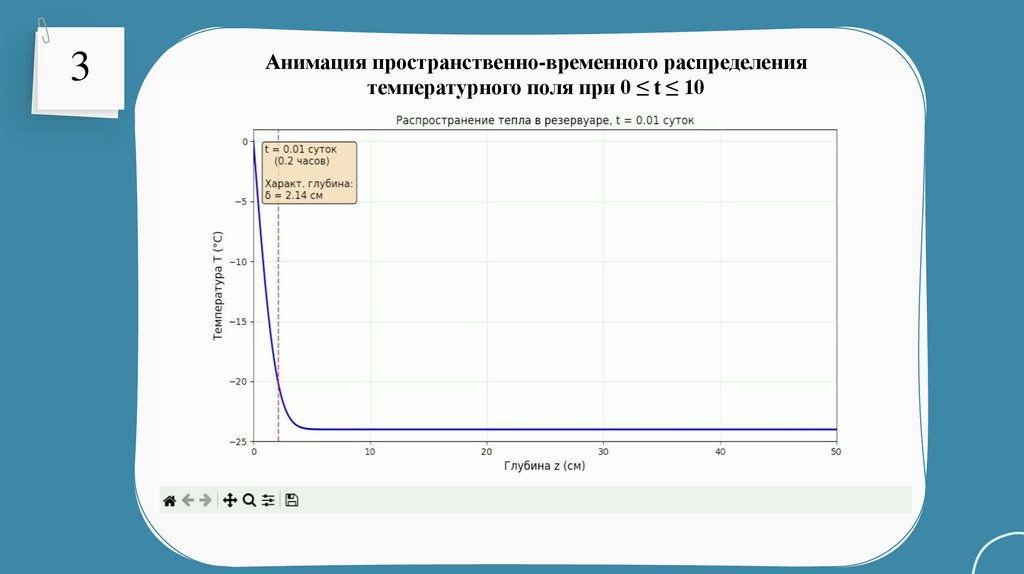
2. Построить анимацию пространственно-временного
распределения температурного поля при 0 ≤ t ≤ 10

12.

3
РЕШЕНИЕ
Начальное условие
Граничные условия

13.

3
Для левой части
Для правой части
Получаем ОДУ
или

14.

3
Получим полное решение:
Из граничного условия Т(0,t) = 0
Обратное преобразование Лапласа
Используем табличную формулу:
Подставляем z = 0
Где erfc(x) - дополнительная функция ошибок.
Применяем линейность:
Итого:
Так как erfc(x) = 1 – erf(x), то:

15.

3
Итоговое решение:
To = -24 Co
Однако мы имеем физическую задачу, так что проанализируем физический смысл:
Функция erf(x) растёт от 0 до 1 при x: 0-> inf и характерна глубина прогрева:
Примеры ( при а = 1.33х10-7 м2/с):

16.

3
График

17.

3
Анимация пространственно-временного распределения
температурного поля при 0 ≤ t ≤ 10

18.

ЗАДАЧА № 4
Химический завод специализируется на выпуске
двух видов сельскохозяйственных удобрений:
«Агро-стандарт» и «Агро-премиум».
Маржинальная прибыль от продажи одной тонны
удобрения «Агро-стандарт» составляет 8000
рублей, а одной тонны «Агро-премиума» — 12000
рублей.
Определить оптимальный ассортимент
производства удобрений, который максимизирует
общую прибыль при заданных ограничениях на
сырьевые ресурсы.
Ограничения
производственного процесса:
• Азот: На 1 тонну «Агростандарт» требуется 50 кг азота,
на 1 тонну «Агро-премиум» — 80
кг азота.
• Фосфор: На 1 тонну «Агростандарт» требуется 30 кг
фосфора, на 1 тонну «Агропремиум» — 40 кг фосфора.
• Калий: На 1 тонну «Агростандарт» требуется 20 кг калия,
на 1 тонну «Агро-премиум» — 25
кг калия. Ежедневно доступно:
• Азот: не более 2000 кг;
• Фосфор: не более 1200 кг;
• Калий: не более 800 кг.

19.

4
РЕШЕНИЕ
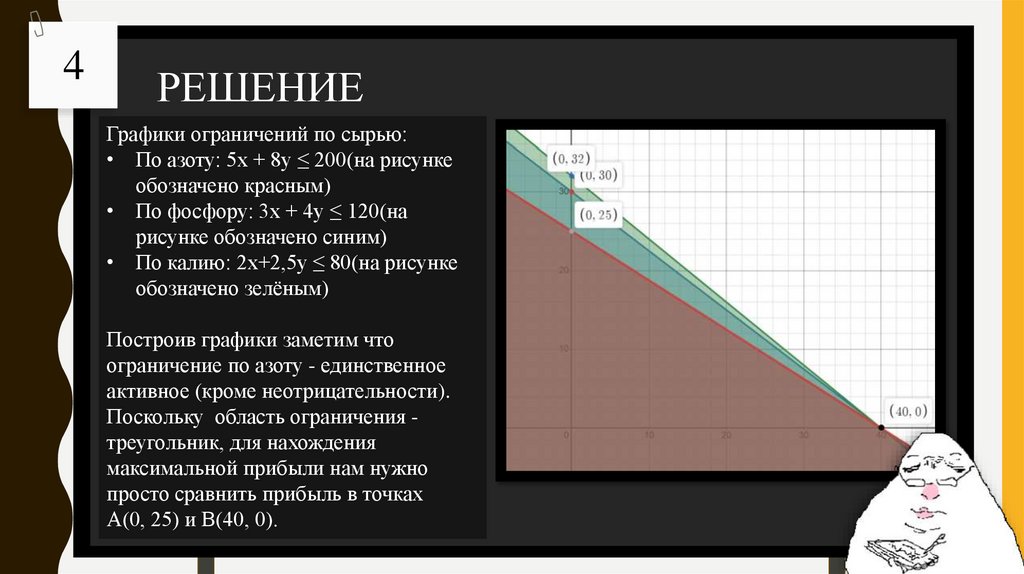
Графики ограничений по сырью:
• По азоту: 5x + 8y ≤ 200(на рисунке
обозначено красным)
• По фосфору: 3x + 4y ≤ 120(на
рисунке обозначено синим)
• По калию: 2x+2,5y ≤ 80(на рисунке
обозначено зелёным)
Построив графики заметим что
ограничение по азоту - единственное
активное (кроме неотрицательности).
Поскольку область ограничения треугольник, для нахождения
максимальной прибыли нам нужно
просто сравнить прибыль в точках
A(0, 25) и B(40, 0).

20.

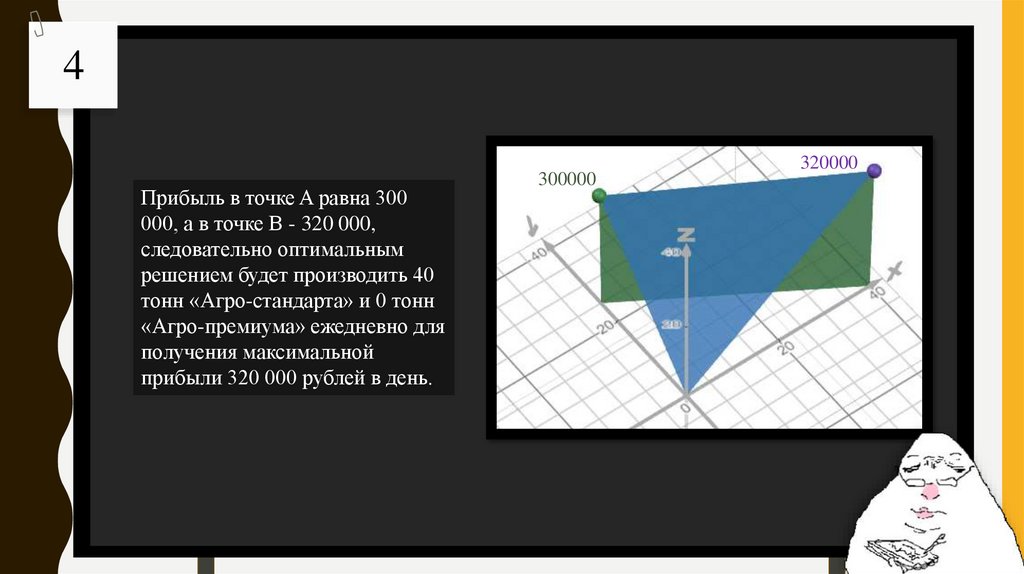
4
Прибыль в точке A равна 300
000, а в точке B - 320 000,
следовательно оптимальным
решением будет производить 40
тонн «Агро-стандарта» и 0 тонн
«Агро-премиума» ежедневно для
получения максимальной
прибыли 320 000 рублей в день.
300000
320000

21.

Благодарим за внимание!
Ждём ваших вопросов!