Интерференция света

1. Интерференция света

2. Электромагнитная теория света

Электромагнитная волна – это переменное
распространяющееся в пространстве
электромагнитное поле, которое характеризуется
векторами напряженностей Е и Н электрического и
магнитного полей.
Электромагнитные волны поперечны, т.е. вектора
Е и Н перпендикулярны друг другу и направлению
распространения волны.

3.

Если электромагнитная волна распространяется в
направлении х, то волновые уравнения имеют вид:
Е
1 Е
Н
1 H
2 2 ,
2
.
2
2
2
х
υ t
х
υ t
v – фазовая скорость волны
2
2
2
2
Решения данных дифференциальных уравнений
Е = Е0sin (ωt-kx+φ); H = H0sin (ωt-kx+φ)
k = ω/υ – волновое число
φ – начальная фаза колебания
Мгновенные значения Е и Н в любой точке пространства
связаны соотношением:
0 Е 0 Н

4.

Электромагнитная волна называется
монохроматической, если в ней происходят
колебания только одной частоты.
Энергия, переносимая волнами за единицу времени
через единичную площадку, перпендикулярную
фазовой скорости волны, называется
плотностью потока энергии S
электромагнитной волны:
S = [EH].
Вектор S называется вектором Умова-Пойнтинга.
Он совпадает по направлению со скоростью волны.
Среднее значение плотности потока энергии S
называют интенсивностью излучения I
(I=<S>).

5.

Экспериментально доказано, что физиологическое,
фотохимическое и другие действия света вызываются
колебаниями электрического вектора Е, поэтому он
получил название светового вектора.
Волновой процесс - процесс распространения волны в
некоторой среде.
Волновой фронт - геометрическое место точек, до которых
доходит волновое возмущение к данному моменту времени.
Волновая поверхность - геометрическое место точек,
колеблющихся в одинаковой фазе. Волновых поверхностей
можно провести бесконечное множество, а волновой фронт для
данного момента времени только один.
Если волновой фронт имеет форму сферы, то волна называется
сферической (например, световая волна, распространяющаяся
от точечного источника), если он представляет собой плоскость,
то волна называется плоской.

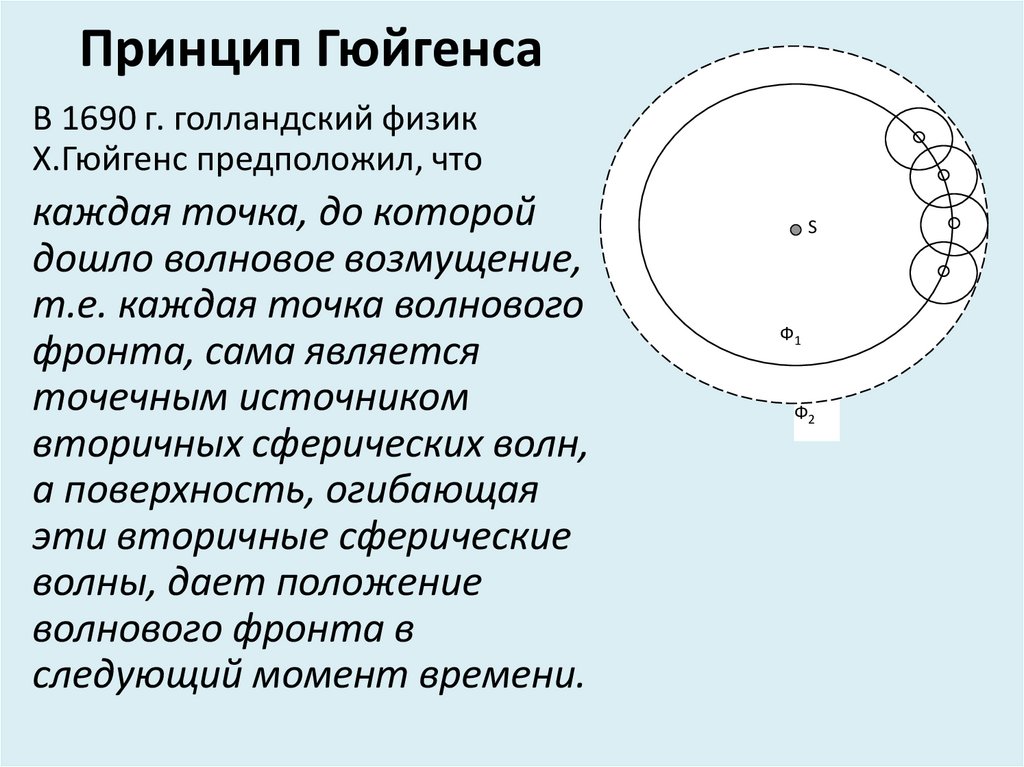
6. Принцип Гюйгенса

В 1690 г. голландский физик
Х.Гюйгенс предположил, что
каждая точка, до которой
дошло волновое возмущение,
т.е. каждая точка волнового
фронта, сама является
точечным источником
вторичных сферических волн,
а поверхность, огибающая
эти вторичные сферические
волны, дает положение
волнового фронта в
следующий момент времени.
S
Ф1
Ф2

7. Интерференция световых волн

Если монохроматические световые волны имеют
постоянную во времени разность фаз и
колебания их световых векторов происходят в
одной плоскости, то они называются
когерентными (согласованными).
Такие согласованные когерентные волны при
наложении их друг на друга могут создать в
пространстве картину, заключающуюся в чередовании
светлых и темных областей.
Явление перераспределения интенсивности
световой волны в пространстве при наложении
двух или нескольких когерентных волн
называется интерференцией света.

8.

Любое светящееся тело состоит из огромного
количества светящихся атомов, каждый из которых
излучает лишь очень короткое время τ = 10 – 8 с и затем
«потухает». За это время атом испускает кусок волны
приблизительно 3 м, называемый волновым цугом.
Затем возбуждение атома повторяется, но излучаемый
волновой цуг будет иметь другую начальную фазу,
которая задается случайным образом. Следовательно,
цуги одного атома, а тем более цуги разных атомов,
принадлежащих одному источнику, будут
некогерентными. По этой причине в результате
наложения световых волн от двух независимых
источников (например, двух электрических ламп
накаливания) явление интерференции никогда не
наблюдается.

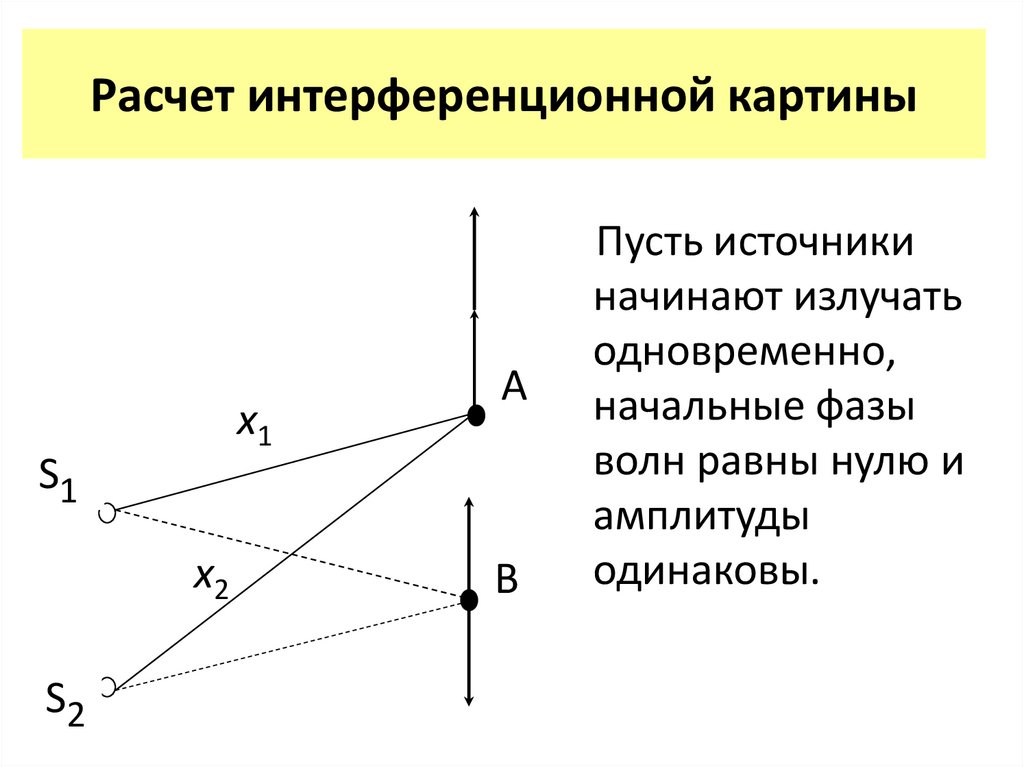
9. Расчет интерференционной картины

x1
А
S1
x2
S2
В
Пусть источники
начинают излучать
одновременно,
начальные фазы
волн равны нулю и
амплитуды
одинаковы.

10.

x1
Е1 Е0sin(ω t kx1) E0sin (t - ) ,
c
2π 2πν ω
поскольку k
;
λ
c
c
x2
E2 E0sin(ω t - kx2 ) E 0sin ω ( t ) .
c
Результирующая величина Е в точке А :
Уравнения волн:
x2 x1
x1 x2
Е Е1 Е2 2Е0 cos ω
sin ω(t )
2c
2c
x2 x1 не зависит от времени и является
2Е0 cos ω
2c амплитудой суммарного
колебания в точке А.

11.

x2 x1
2 Е0cos ω
0
2c
если
x2 x1
cos ω
0,
2c
т.е.
x2 x1
ω
(2m 1)
2c
2
При этом происходит взаимное «гашение» волн и мы
наблюдаем ослабление интенсивности суммарной
волны, то есть интерференционный минимум.

12.

x2 x1 2 π c ( x2 x1 ) π
π
ω
( x2 x1 ) (2m 1) ,
2c
λ
2c
λ
2
λ
откуда x 2 x1 (2m 1)
2
где m = 0, 1, 2…. - любое целое число, которое
называется порядком интерференции, запись
означает нечетное число, х1 и х2 –
геометрические пути световых волн от
источников света S1 и S2 соответственно, до
произвольной точки А.
Разность х2 - х1 = Δ называется
геометрической разностью хода волн.

13.

Если свет распространяется в среде с
показателем преломления n, необходимо
рассматривать оптический путь волн l = xn.
Если световые волны проходят в разных средах,
их оптические пути будут l1=x1n1 и l2=x2n2 и
оптическая разность хода Δ = l2 - l1.
Условие интерференционного минимума:
λ
Δ min (2m 1)
2

14.

x2 x1
Если cos ω
1,
2c
что возможно при равенстве аргумента нулю или
четному числу π/2, амплитуда светового вектора для
данной точки будет в любой момент времени равна
2Е0:
2 π c ( x2 x1 )
π
λ
2m , откуда x2 x1 2m mλ
λ
2c
2
2
Условие интерференционного максимума:
λ
Δ max 2m m
2

15.

Если между световыми волнами существует разность
хода, то они также обладают разностью фаз:
δ (ω t kx1 ) (ω t kx2 ) k ( x2 x1 ) kΔ
Если вместо Δ подставить значения Δmax и Δ min, то мы
получим условия максимума и минимума
интерференции для разности фаз:
δ max = ±2πm
и
δ min = ±(2m+1)π, ( m = 0,1,2…).

16.

Если амплитудные значения светового вектора не
равны друг другу, т.е. Е01 ≠ Е02, то квадрат
результирующей амплитуды определяется по
формуле:
Е2 = Е012 + Е022 + 2Е01Е02cos (φ2 – φ1),
где (φ2 – φ1) – разность фаз колебаний. Поскольку
интенсивность света I пропорциональна квадрату
амплитудного значения Е, то
I I1 I 2 2 I1 I 2 cos( 2 - 1 )
В точках пространства, где cos (φ2 – φ1) > 0, результирующая
интенсивность I > I1 + I2. Если cos (φ2 – φ1) < 0, то I < I1 + I2.
Таким образом, мы наблюдаем перераспределение
интенсивности и интерференционную картину.

17. Методы наблюдения интерференции

Когерентных источников света в природе не
существует. Однако когерентные световые
волны можно получить, если свет, идущий от
одного источника, разделить на две (или
более) части и затем заставить их
встретиться. В силу общности своего
происхождения полученные лучи должны быть
когерентными и при наложении
интерферировать. Такое разделение может
быть осуществлено с помощью экранов и щелей
(метод Юнга), зеркал (зеркала Френеля) и
преломляющих тел (бипризма Френеля).

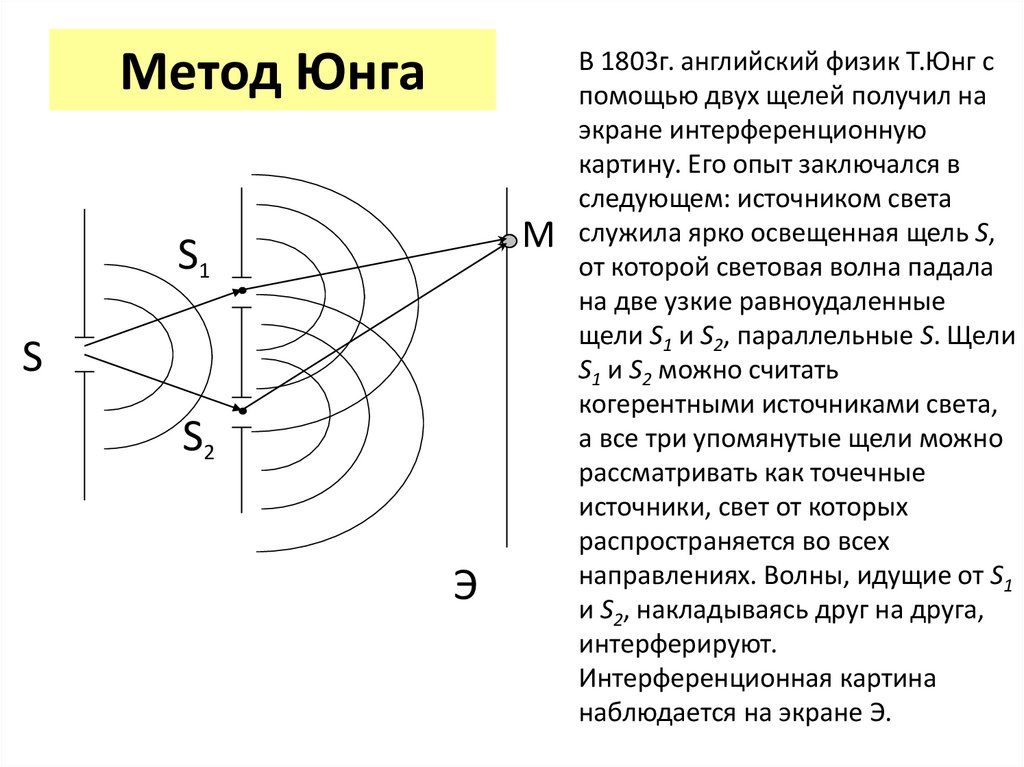
18. Метод Юнга

М
S1
S
S2
Э
В 1803г. английский физик Т.Юнг с
помощью двух щелей получил на
экране интерференционную
картину. Его опыт заключался в
следующем: источником света
служила ярко освещенная щель S,
от которой световая волна падала
на две узкие равноудаленные
щели S1 и S2, параллельные S. Щели
S1 и S2 можно считать
когерентными источниками света,
а все три упомянутые щели можно
рассматривать как точечные
источники, свет от которых
распространяется во всех
направлениях. Волны, идущие от S1
и S2, накладываясь друг на друга,
интерферируют.
Интерференционная картина
наблюдается на экране Э.

19.

М
S1
d
S2
l1
m =1
x
l2
0
m=0
l
Э
m = -1
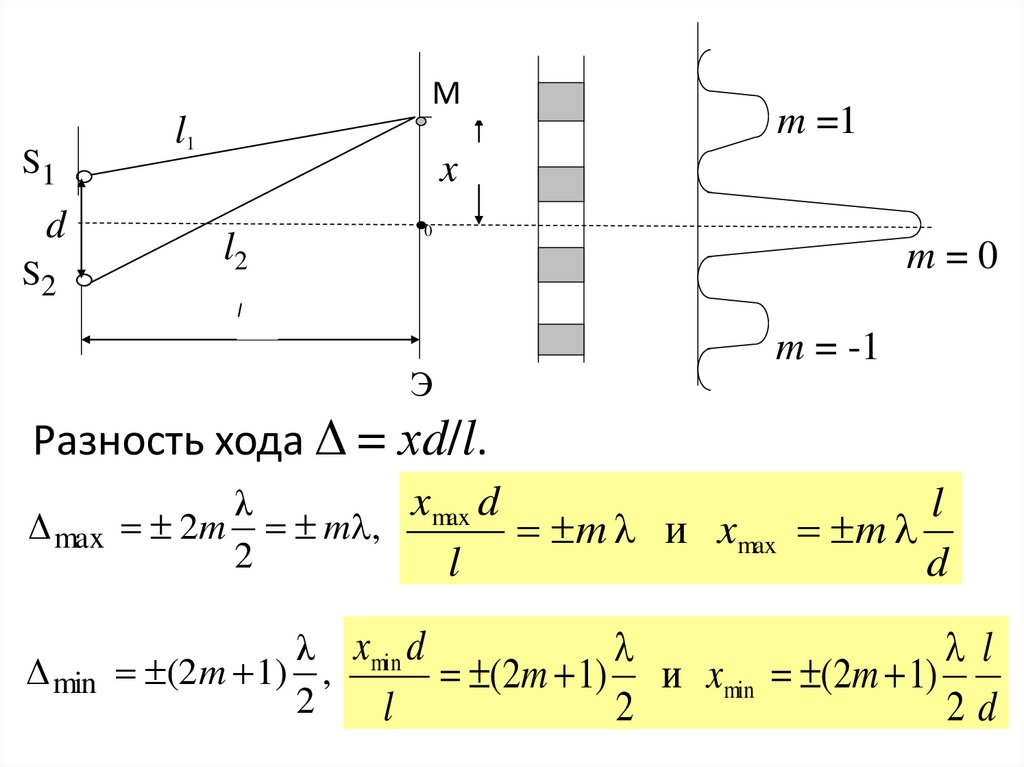
Разность хода Δ = хd/l.
xmax d
λ
l
Δ max 2m m ,
m λ и xmax m
2
l
d
λ xmin d
l
Δ min (2m 1) ,
(2m 1) и xmin (2m 1)
2
l
2
2d

20.

Шириной интерференционной полосы Δх
называется расстояние между соседними
максимумами или минимумами
l
l
l
Δх х m 1 x m (m 1) λ m λ
d
d
d
Величина Δх постоянна при заданных d, l и λ и не зависит от
порядка интерференции m. Таким образом, при освещении щелей
монохроматическим светом на экране наблюдается чередование
светлых и темных полос одинаковой ширины.
При освещении щелей белым светом интерференционные
максимумы становятся радужными, т.к. белый свет содержит в
себе все цвета спектра. Максимумы коротких длин волн
(фиолетовых) будут располагаться ближе к центру экрана, в
середине экрана максимумы всех волн совпадут из-за отсутствия
разности хода и получится белая полоса.

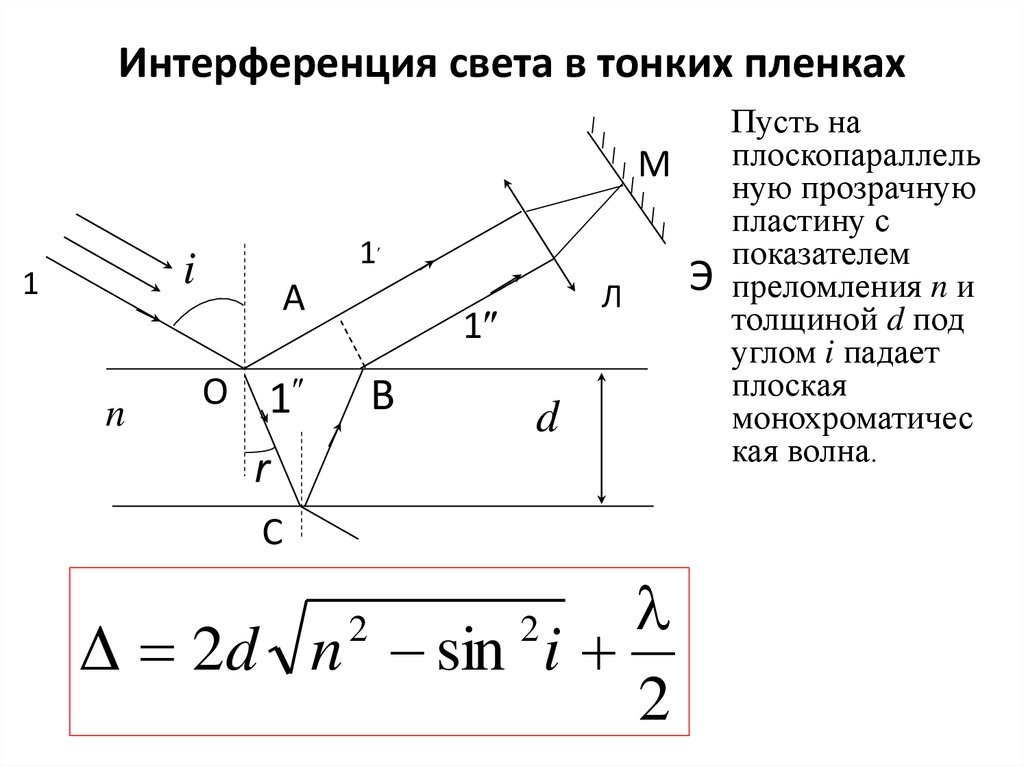
21. Интерференция света в тонких пленках

1
i
1
n
A
O
1
1
B
d
r
Пусть на
М плоскопараллель
ную прозрачную
пластину с
показателем
Э преломления n и
Л
толщиной d под
углом i падает
плоская
монохроматичес
кая волна.
C
Δ 2d n sin i
2
2
2

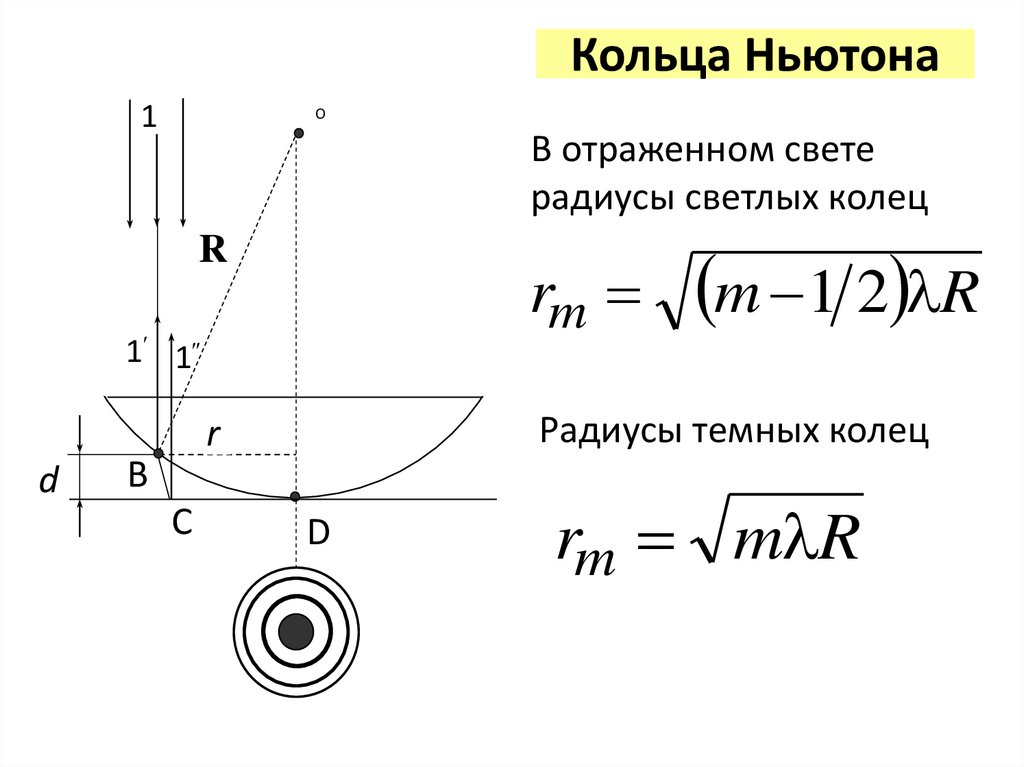
22. Кольца Ньютона

1
О
В отраженном свете
радиусы светлых колец
R
rm
1 1
Радиусы темных колец
r
d
B
C
m 1 2 R
D
rm m R

23. Применение интерференции

1. Измерение длин с очень большой точностью; это позволило
дать легко воспроизводимое и достаточно точное определение
единицы длины - метра, в зависимости от длины волны оранжевой
линии криптона. Интерференционные компараторы позволяют
сравнивать размеры до 1 метра с точностью до 0,05 мкм; меньшие
размеры могут быть измерены с еще большей точностью. Такая
высокая точность обусловлена тем, что изменение разности хода
на десятую долю длины волны заметно смещает
интерференционные полосы.
2. На явлении интерференции основано действие большого
количества оптических приборов под общим названием
интерферометры, которые используются для различных
измерений. В оптикомеханической промышленности
интерферометры используются для контроля качества оптических
систем и контроля поверхности отдельных оптических деталей. В
металлообрабатывающей промышленности – для контроля
чистоты обработки металлических поверхностей. Изучение и
контроль полировки зеркальных поверхностей (для этого
применяется так называемый интерферометр Линника)
проводится с точностью до сотых долей длины волны.

24.

3. С использованием явления интерференции
проводится определение ряда важнейших величин,
характеризующих вещества: коэффициента
расширения твердых тел (дилатометры), показателя
преломления газообразных, жидких и твердых тел
(рефрактометры) и т.п. Интерференционные
дилатометры позволяют зафиксировать удлинение
образца на 0,02 мкм.
4. Широко распространены интерференционные
спектроскопы, применяемые для исследования
спектрального состава излучения различных веществ.
5. Посредством интерференции поляризованных лучей
проводиться определение величин внутренних
напряжений в различных деталях (метод
фотоупругости).

25. Лекция окончена. Спасибо за внимание!