Похожие презентации:
Уравнения Максвелла
1. Уравнения Максвелла
2.
3.
Единая теория электрических и магнитныхявлений была создана Максвеллом в 1860 г.
В классическом учении об электромагнетизме
уравнения Максвелла играют такую же роль, как
законы Ньютона в классической механике.
Рассмотрим факты, которые нам известны об
электрическом и магнитном полях. Сформулируем их
в виде утверждений.
4. Утверждение 1
Электростатическое поле создаетсянеподвижными зарядами. Силовые линии
электростатического поля начинаются и
заканчиваются на зарядах.
Математической формулировкой этого утверждения
является теорема Остроградского-Гаусса для
электрического поля:
1
E
d
S
dV
S
0 V
(1)
Закон Кулона также содержится в этом уравнении.
5.
Теорема Остроградского-Гаусса дляэлектрического поля:
в вакууме поток вектора
напряженности
электростатического поля через
замкнутую поверхность
произвольной формы численно равен
алгебраической сумме электрических
зарядов, охватываемых этой
поверхностью, деленной на
электрическую постоянную ε0.
6. Утверждение 2
Магнитные заряды отсутствуют вприроде
Математической формулировкой этого утверждения
является теорема Остроградского-Гаусса для
магнитного поля:
поток вектора магнитной индукции через
замкнутую поверхность произвольной формы
численно равен нулю.
B
d
S
0
S
(2)
7. Утверждение 3
Электростатическое полепотенциально: в нем нет замкнутых
силовых линий.
Математически это выражается как равенство нулю
циркуляции вектора напряженности
электростатического поля по произвольному
замкнутому контуру (теорема о циркуляции вектора
напряженности электростатического поля) :
E
d
l
0
L
(3)
8. Утверждение 4
Вихревое магнитное поле создаетсятоками.
Математическим выражением этого утверждения
является теорема о циркуляции вектора магнитной
индукции:
(4)
B
d
l
j
d
S
0
L
S
Уравнение (4) содержит в себе закон БиоСавара-Лапласа.
9.
Теорема о циркуляции векторамагнитной индукции:
в вакууме циркуляция вектора
индукции магнитного поля по
произвольному замкнутому контуру
численно равна алгебраической сумме
токов, охватываемых этим
контуром, умноженной на магнитную
постоянную µ0:
10.
Эти четыре уравнения надо дополнитьвыражением для силы Лоренца,
действующей на движущиеся заряды со
стороны электромагнитных полей:
F Л q E q v ,B (5)
В выписанных уравнениях еще не отражено
явление электромагнитной индукции.
11. Вихревое электрическое поле
В трактовке Фарадея электромагнитнаяиндукция сводится к возбуждению токов в
замкнутом проводнике под действием
магнитного поля. Максвелл показал, что
сущность электромагнитной индукции
заключается в создании электрического поля
изменяющимся во времени магнитным
полем.
Индукционный ток при этом – вторичный
эффект, возникающий при наличии
проводящей среды.
12.
Если магнитный поток через замкнутый проводящийвиток L меняется, то в витке возникает ЭДС индукции.
Это значит, что заряды, находящиеся в проводнике,
будут испытывать действие силы, связанной с этой
ЭДС. Но, сила, действующая на заряды, означает
появление какого-то электрического поля.
Циркуляция этого поля по периметру витка и есть по
определению ЭДС индукции:
Отличие циркуляции от
нуля означает, что данное
(6)
E
d
l
i
электрическое поле не
L
является потенциальным,
а имеет вихревой
характер, подобно
магнитному полю.
13.
Проводящий виток при изменении магнитногопотока играет роль детектора для регистрации
появления вихревого электрического поля по
возникающему в нем индукционному току.
Перепишем закон Фарадея в виде:
d
B (7)
i
B dS
dS
dt
t S
t
S
Объединяем (6) и (7), получим модифицированное
утверждение 3.
14. Утверждение 3 м
Изменяющееся магнитное полеприводит к возникновению вихревого
электрического поля.
B
E
d
l
d
S
L
S t
(8)
15.
Отличие вихревого электрического поля отэлектростатического поля:
1) Силовые линии вихревого электрического поля
замкнуты и охватывают силовые линии
создающего его магнитного поля.
2) Электростатическое поле создается
неподвижными зарядами, а вихревое
электрическое поле – переменным магнитным
полем.
3) Электростатическое поле - потенциальное,
работа его сил по перемещению заряда по любой
замкнутой траектории равна нулю, а для
вихревого поля – эта работа отлична от нуля.
4) Поток вихревого поля через замкнутую
поверхность равен нулю. Это поле не дает вклада
в левую часть уравнения (1).
16. Ток смещения
Утверждение 4 тоже нуждается вмодификации. Возникает вопрос о
нарушении симметрии между
электрическими и магнитными явлениями.
Электрическое (вихревое) поле можно
породить без зарядов, просто изменением
магнитного поля. А можно ли сделать
наоборот? Создать магнитное поле не
токами, а изменяющимся электрическим
полем?
17.
Рассмотрим плоский конденсатор, подключенный кисточнику переменного тока. Как известно, переменный
ток проходит по такой цепи. В соединительных проводах
и в источнике он представлен током проводимости. Но в
конденсаторе электроны не могут проникать через
диэлектрик с одной обкладки на другую. При
прохождении переменного тока по цепи в конденсаторе
происходят два физических явления:
1) между обкладками существует переменное
электрическое поле, создаваемое
переменными зарядами на обкладках;
2) действием этого поля создается
переменная поляризация диэлектрика в
конденсаторе.
18.
Как показывает опыт, между обкладками вконденсаторе создается переменное магнитное поле
подобно тому, как оно имеет место вокруг
соединительных проводов. Следовательно,
переменное электрическое поле и переменная
поляризация среды создают магнитное поле
так же, как обычные токи проводимости, и их
рассматривают как особый вид тока,
получивший название тока смещения.
Создание магнитного поля переменной поляризацией диэлектрика
объясняется тем, что при этом происходит колебательное движение
зарядов, входящих в атомы или молекулы вещества. Как и всякое
движение электрических зарядов, оно создает магнитное поле.
Но магнитное поле будет создаваться и в вакууме под действием только
переменного электрического поля.
19.
Плотность тока смещения определяетсяскоростью изменения вектора
электрического смещения во времени:
D
jсм
t
D 0E P
Для однородных диэлектриков: D 0 E
E
jсм 0
t
20.
Если ввести понятие полного тока, которыйвключает в себя ток проводимости и ток
смещения, то для его плотности имеем:
E
jполн j jсм j 0
t
Именно полный ток должен стоять в правой части
уравнения (4). Таким образом имеем
модифицированное утверждение 4.
21. Утверждение 4 м
Вихревое магнитное поле создаетсяполным током, т.е. токами
проводимости и током смещения,
вызванным изменяющимся
электрическим полем.
E
B dl 0 j dS 0 0 t dS (9)
L
S
S
22. Система уравнений Максвелла в интегральной форме
Четыре уравнения, соответствующие нашиммодифицированным утверждениям,
называются уравнениями Максвелла.
Уравнения Максвелла являются основными
законами классической электродинамики.
Они постулируются на основе обобщения
экспериментальных данных.
23.
1E
d
S
dV
S
0 V
1 уравнение Максвелла
(теорема Гаусса для электрических полей)
выражает закон создания
электрических полей электрическими
зарядами и отражает наличие в природе
свободных электрических зарядов.
24.
Bd
S
0
S
2 уравнение Максвелла
представляет собой теорему Гаусса для
магнитного поля.
Оно отражает отсутствие в природе
магнитных зарядов.
25.
BE
d
l
d
S
L
S t
3 уравнение Максвелла
выражает закон создания
электрических полей изменяющимися
во времени магнитными полями.
26.
EB dl 0 j dS 0 0 t dS
L
S
S
4 уравнение Максвелла
выражает закон создания магнитных
полей электрическими токами и
изменяющимися во времени
электрическими полями
27.
Чтобы получить уравнения Максвелла всреде, надо произвести стандартную замену:
ε→ε0ε, µ→µ0µ, где ε0 и µ0 – электрическая и
магнитная постоянные, ε и µ - диэлектрическая и
магнитная проницаемости вещества.
Материальные уравнения характеризуют
электромагнитные свойства вещества и для
изотропных линейных сред имеют вид:
D 0 E
B 0 H
j Е
– удельная
проводимость
вещества.
28. Система уравнений Максвелла в дифференциальной форме
Используя известные из векторного анализа теоремыСтокса и Остроградского-Гаусса, можно представить
систему уравнений Максвелла в дифференциальной
форме, характеризующую электромагнитное поле в
каждой точке пространства:
div E
0
divB 0
B
rotE
t
E
rotB 0 j 0
t
29.
«Дивиргенция» – по латыни означает«расхождение». Эта операция описывает
конфигурацию силовых линий типа «ежа»,
расходящихся из точек, где имеются
электрические заряды.
«Ротор» – операция, описывающая
вихревые поля с замкнутыми силовыми
линиями вокруг их источников – токов или
полей, меняющихся во времени.
30. Свойства уравнений Максвелла:
1.Система четырех структурных и трехматериальных уравнений Максвелла
представляют собой замкнутую систему
уравнений, из которой можно рассчитать
электромагнитные поля, создаваемые любыми
распределениями зарядов и токов.
2.Уравнения Максвелла отражают неразрывное
существование переменных электрических и
магнитных полей: эти поля непрерывно друг друга
создают, связаны друг с другом и образуют
единое электромагнитное поле.
3.Уравнения Максвелла линейные, поэтому
электромагнитное поле удовлетворяет принципу
суперпозиции.
31.
4. Уравнения Максвелла не симметричныотносительно электрического и магнитного
полей. Это связано с существованием в
природе электрических зарядов и отсутствием
магнитных зарядов.
5. Уравнения Максвелла инвариантны
относительно преобразований Лоренца и не
инвариантны относительно преобразований
Галилея.
Теория Максвелла не только объяснила
известные к тому времени экспериментальные
факты, но и предсказала новые явления.
32.
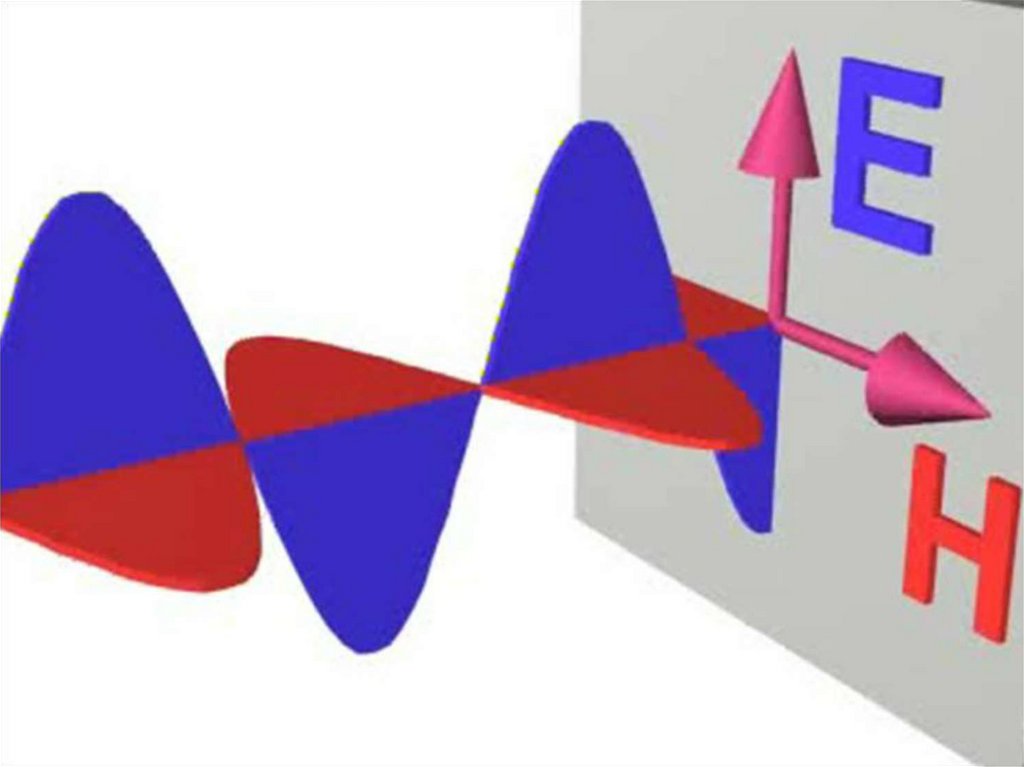
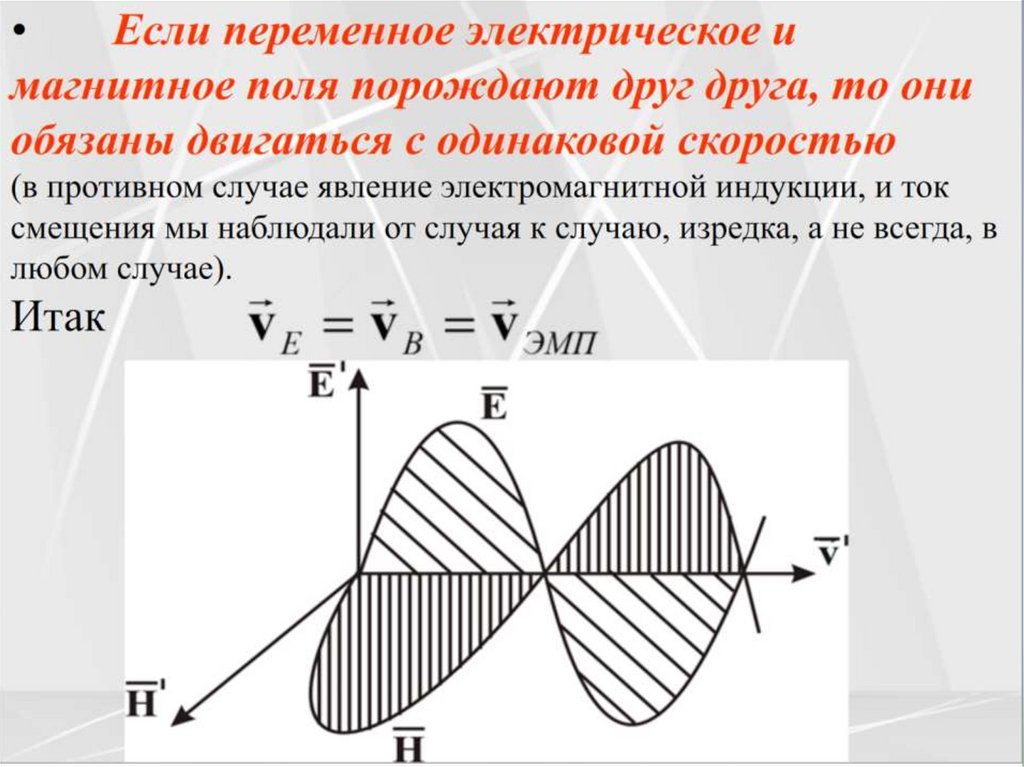
Из уравнений Максвелла следуетсуществование электромагнитных волн –
переменного электромагнитного поля,
распространяющегося в пространстве с
конечной скоростью.
При этом для существования
электромагнитных волн не обязательно
необходимо вещество, они могут
распространяться и в вакууме.
Скорость распространения электромагнитных
волн в вакууме совпадает со скоростью света в
вакууме.
33.
Вывод о существовании электромагнитныхволн и теоретическое исследование их свойств
позволили Максвеллу создать
электромагнитную теорию света, согласно
которой свет представляет собой
электромагнитные волны.
В дальнейшем электромагнитные волны были
получены экспериментально, тем самым была
подтверждена электромагнитная теория света,
а вместе с ней и теория Максвелла.
34. Принцип относительности в электродинамике
Принцип относительности —фундаментальный физический принцип,
согласно которому все физические явления при
одинаковых условиях в инерциальных
системах отсчёта (ИСО) протекают одинаково.
Поэтому законы физики одинаковы во всех
инерциальных системах отсчёта.
35.
Из принципа относительности следует, что отдельноерассмотрение электрического и магнитного полей имеет
относительный смысл. Так, система неподвижных в некоторой
ИСО зарядов будет создавать только стационарное
электрическое поле, и магнитное поле в этой ИСО не будет
наблюдаться. Но в другой ИСО, движущейся относительно
первой, эта система будет системой движущихся зарядов, и
они помимо электрического поля будут создавать постоянное
магнитное поле. Аналогично, неподвижный относительно
одной ИСО проводник с постоянным током, создает в
окружающем пространстве в этой ИСО постоянное магнитное
поле. Вихревое электрическое поле в этой ИСО наблюдаться не
будет. В другой ИСО, относительно которой он движется,
проводник с током будет возбуждать переменное магнитное
поле, которое в свою очередь будет возбуждать вихревое
электрическое поле. Таким образом, поле, которое
относительно некоторой системы отсчета оказывается
«чисто» электрическим или «чисто» магнитным,
относительно других систем отсчета будет представлять
собой совокупность электрического и магнитного полей,
образующих единое электромагнитное поле.













































 Физика
Физика








