Уравнения Максвелла

1.

УРАВНЕНИЯ МАКСВЕЛЛА

2.

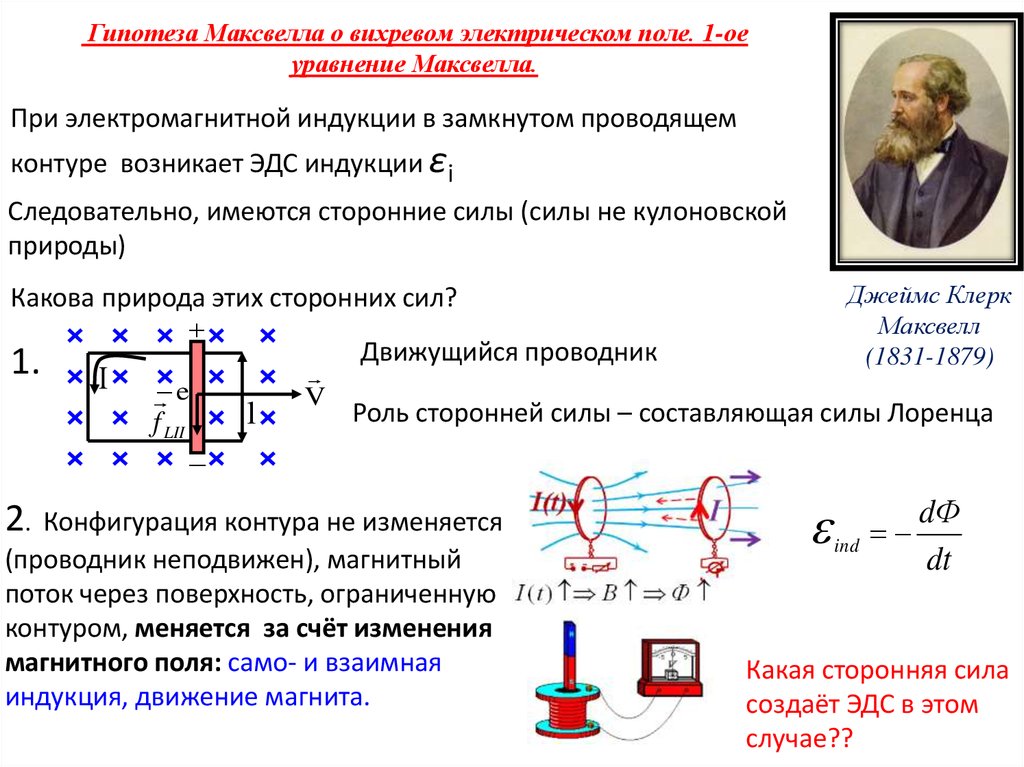
Гипотеза Максвелла о вихревом электрическом поле. 1-ое
уравнение Максвелла.
При электромагнитной индукции в замкнутом проводящем
контуре возникает ЭДС индукции εi
Следовательно, имеются сторонние силы (силы не кулоновской
природы)
Джеймс Клерк
Максвелл
(1831-1879)
Какова природа этих сторонних сил?
1.
I
e
f LII
l
V
Движущийся проводник
Роль сторонней силы – составляющая силы Лоренца
2. Конфигурация контура не изменяется
(проводник неподвижен), магнитный
поток через поверхность, ограниченную
контуром, меняется за счёт изменения
магнитного поля: само- и взаимная
индукция, движение магнита.
ind
dФ
dt
Какая сторонняя сила
создаёт ЭДС в этом
случае??

3.

Гипотеза Максвелла о вихревом электрическом поле. 1-ое
уравнение Максвелла.
2. Магнитный поток через поверхность,
Какая сторонняя сила
создаёт ЭДС в этом
ограниченную контуром, меняется за
счёт изменения магнитного поля.
случае
εi??
Максвелл:
изменяющееся во времени магнитное поле приводит к возникновению вихревого (не
потенциального) электрического поля, существование которого не зависит от наличия
проводников
напряженность вихревого электрического поля E * в точке :
по аналогии с определением напряженности
электростатического поля
F*
– сила, действующая со стороны вихревого электрического поля на
точечный заряд q, помещенный в данную точку.
В проводнике, помещенном в вихревое электрическое поле, возникает индукционный ток движение свободных носителей заряда под действием сил вихревого электрического поля.
F*
i
- сторонняя сила
Aстор
q
1
Fl*dl
ql
i El*dl
l

4.

Гипотеза Максвелла о вихревом электрическом поле. 1-ое
уравнение Максвелла.
i El*dl
Bn f (t , x, y, z )
l
d
i
dt
Bn dS
d
l E dl dt Bn dS
S
*
l
Bn
l E dl t dS
S
*
l
S
Максвелл: контур ℓ – не обязательно проводящий!
Это может быть воображаемый, мысленный контур.
Переменное магнитное поле приводит к появлению вихревого электрического
поля независимо от того, в какой среде это происходит.
Например, если магнитное поле меняется в вакууме, то вихревое электрическое
поле существует в вакууме (как и кулоновское)

5.

Гипотеза Максвелла о вихревом электрическом поле. 1-ое уравнение Максвелла.
Особенности вихревого электрического поля
ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
Bn
E
dl
l
S t dS ≠
*
l
ПОТЕНЦИАЛЬНОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
кул
E
l dl
0
l
Поле характеризуется потенциалом
Нельзя ввести потенциал
Источником вихрев. электр. поля
не являются электр. заряды
ВСЕГДА:
*
E
n dS
=0
S
Силовые линии вихревого
электр. поля замкнуты (не
имеют начала и конца)
=0
Теорема
Гаусса
Источником потенц. электр. поля
являются электр. заряды
E
кул
n
S
dS
1
dV ≠ 0
0 V
Силовые линии потенц. электр.
поля начинаются и заканчиваются
на электрических зарядах

6.

1-ое уравнение Максвелла
+
кул
E
l dl 0
l
Bn
l E dl t dS
S
*
l
Bn
l El dl S t dS
El E
кул
l
E
кул
n
dS
S
+
*
E
n dS 0
S
E
*
l
1
проекция напряженности результирующего электрического
поля на направление элементарного перемещения вдоль
замкнутого контура
dV
0 V
1-ое уравнение Максвелла
1
E dS dV
n
S
0 V
D dS dV
n
S
3-е уравнение Максвелла
V

7.

2-е ур-е Максвелла

8.

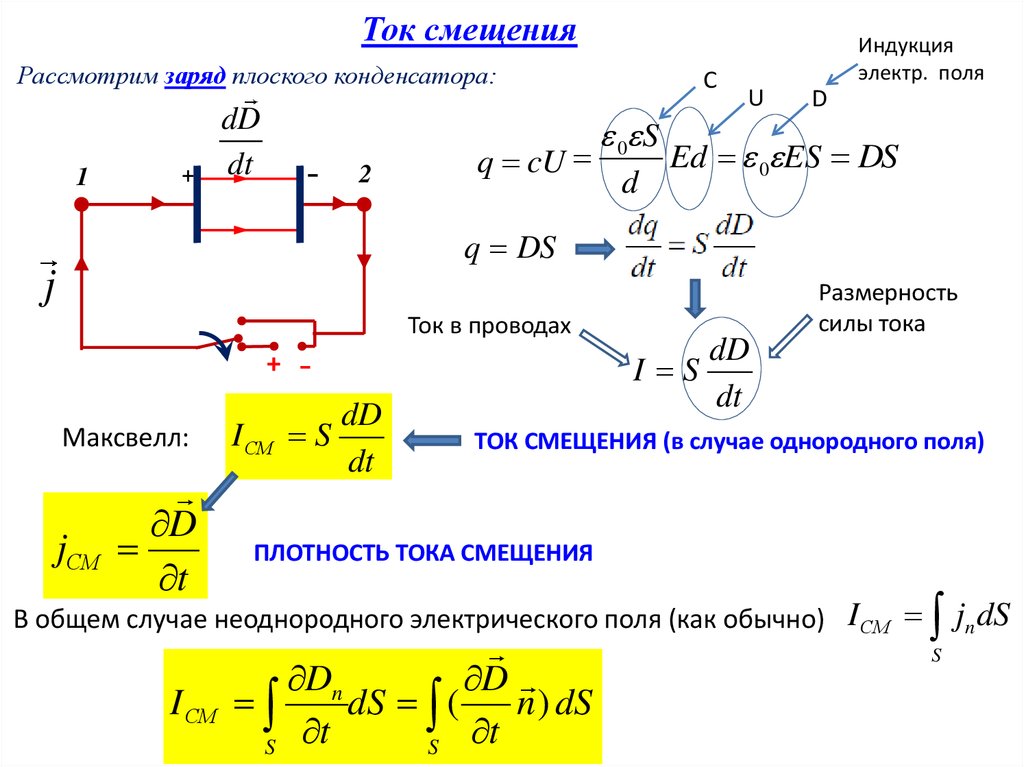
Ток смещения
Рассмотрим заряд плоского конденсатора:
1
+
dD
dt
-
2
q cU
С
0 S
d
Индукция
электр. поля
U
D
Ed 0 ES DS
q DS
j
Ток в проводах
+
Максвелл:
jСМ
D
t
I СМ
I S
dD
S
dt
dD
dt
Размерность
силы тока
ТОК СМЕЩЕНИЯ (в случае однородного поля)
ПЛОТНОСТЬ ТОКА СМЕЩЕНИЯ
В общем случае неоднородного электрического поля (как обычно) I СМ
I СМ
Dn
D
dS (
n ) dS
t
t
S
S
j dS
n
S

9.

Плотность тока смещения
Покажем: направления токов проводимости и смещения совпадают
Рассмотрим заряд плоского
конденсатора:
1
+
dD
dt
-
Рассмотрим разаряд плоского конденсатора:
+
dD
dt
-
2
j
j
+
+
-
D
D
dD
dt
j
На участке 1-2 j и jСМ совпадают
dD
0
dt
по направлению
-
dD
0
dt
dD
dt
j
На участке 1-2 j и jСМ совпадают
по направлению

10.

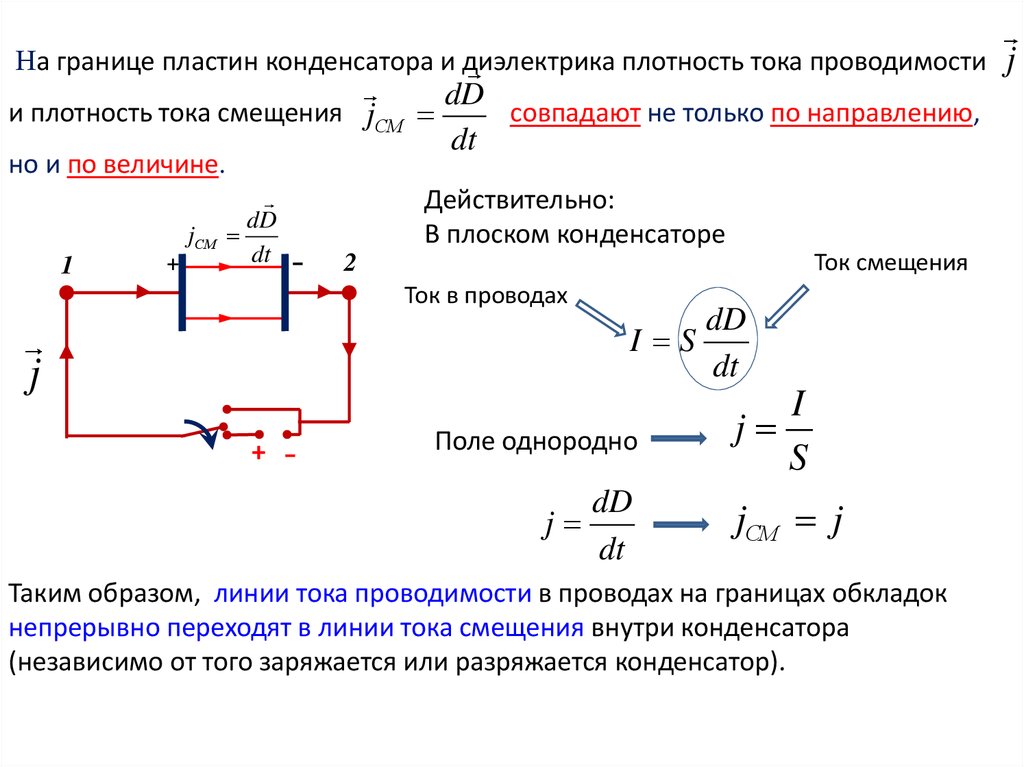
На границе пластин конденсатора и диэлектрика
плотность тока проводимости
dD
и плотность тока смещения jСМ
совпадают не только по направлению,
dt
но и по величине.
jСМ
1
+
dD
dt
-
Действительно:
В плоском конденсаторе
Ток смещения
2
Ток в проводах
I S
j
+
-
Поле однородно
j
dD
dt
dD
dt
I
j
S
jСМ j
Таким образом, линии тока проводимости в проводах на границах обкладок
непрерывно переходят в линии тока смещения внутри конденсатора
(независимо от того заряжается или разряжается конденсатор).
j

11.

Гипотеза Максвелла
Ток смещения создает в пространстве
его окружающем магнитное поле такое
же,
как
и
магнитное
поле
эквивалентного тока проводимости.

12.

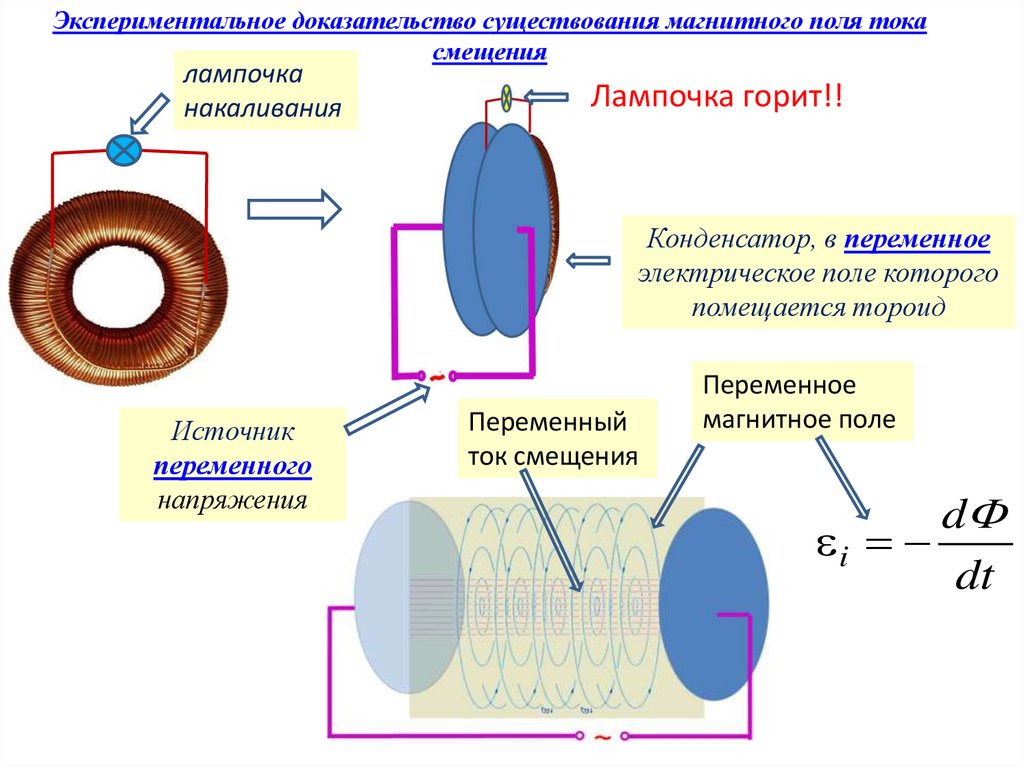
Экспериментальное доказательство существования магнитного поля тока
смещения
лампочка
накаливания
Лампочка горит!!
Конденсатор, в переменное
электрическое поле которого
помещается тороид
Источник
переменного
напряжения
Переменный
ток смещения
Переменное
магнитное поле
d
i
dt

13.

Теорема о циркуляции вектора
магнитной индукции:
Постоянный ток
Bdl 0 I i
i
l
Bdl 0 jn dS
l
Циркуляция
вектора
магнитной
индукции по произвольному замкнутому
контуру равна алгебраической сумме
токов (полному току), охватываемых
этим контуром, умноженной на …….
S
Равноценны в отношении
создания магнитного поля
МАКСВЕЛЛ: полный ток
Плотность полного тока
I полн I I СМ
D
jполн j jСМ j
t
Плотность тока
проводимости
Плотность тока
смещения
Из всех свойств, присущих
току
присуще лишь одно – создавать в
окружающем пространстве магнитное поле

14.

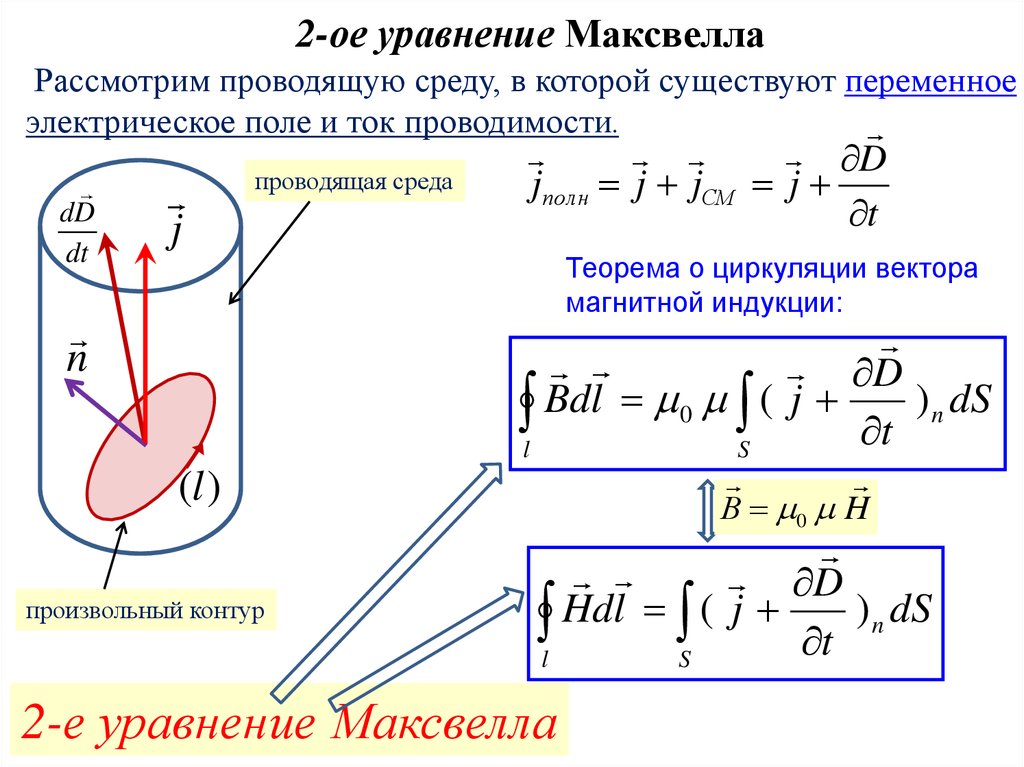
2-ое уравнение Максвелла
Рассмотрим проводящую среду, в которой существуют переменное
электрическое поле и ток проводимости.
проводящая среда
dD
dt
j
D
jполн j jСМ j
t
Теорема о циркуляции вектора
магнитной индукции:
D
l Bdl 0 S ( j t ) n dS
n
(l )
произвольный контур
В 0 H
D
l Hdl S ( j t ) n dS
2-е уравнение Максвелла

15.

2-ое уравнение Максвелла
2-ое уравнение Максвелла справедливо для любой среды, в
том числе для диэлектрика, вакуума или неоднородной
среды, включающей в себя проводники и диэлектрики.
dD
dt
Например, в случае вакуума (воздуха)
n
(l )
произвольный контур
D
l Bdl 0 S ( t ) n dS
D
l Hdl S ( t ) n dS

16.

Система уравнений Максвелла в интегральной форме
Дополнив основные факты из области электромагнетизма установлением
магнитных действий токов смещения, Максвелл написал систему
фундаментальных уравнений электродинамики.
1.
B
E dl ( t ) dS
l
n
l
S
циркуляция вектора напряженности электрического поля
по произвольному контуру, равна «минус» скорости
изменения магнитного потока через поверхность,
ограниченную этим контуром (закон ЭМИ Фарадея).
D
) n dS
2. H l dl ( j
t
l
S
3.
D dS dV
n
S
4.
V
B dS 0
n
S
циркуляция вектора напряжённости магнитного
поля по произвольному контуру равна
алгебраической сумме токов проводимости и
токов смещения, охватываемых этим контуром
(теорема о циркуляции для м.п. +.ток смещения)
поток вектора электрической индукции через
произвольную замкнутую поверхность равен
алгебраической сумме свободных зарядов,
находящихся внутри этой поверхности (теорема
Гаусса – закон Кулона)).
Поток вектора магнитной индукции через
произвольную замкнутую поверхность равен нулю
(отсутствие магнитных зарядов)

17.

Система уравнений Максвелла в интегральной форме
B
E
dl
1. l (
) n dS
Уравнения Максвелла - это основные
t
l
S
D
) n dS
2. H l dl ( j
t
l
S
3.
D dS dV
n
S
4.
аксиомы электродинамики полученные
путём обобщения опытных фактов (их
нельзя вывести).
V
B dS 0
n
S
Из уравнений Максвелла следует возможность существования электромагнитных
волн.

18.

Система уравнений Максвелла в интегральной форме
B
4 уравнения Максвелла не составляют
E
dl
1. l (
) n dS
полной
системы
уравнений
t
l
S
D
) n dS
2. H l dl ( j
t
l
S
3.
D dS dV
n
S
4.
V
B dS 0
n
электромагнитного поля.
Уравнения Максвелла не содержат
данных о свойствах среды.
Уравнения
Максвелла
следует
дополнить
соотношениями,
характеризующими свойства среды –
«материальными уравнениями»
S
D 0 E
B 0 H
j E
Если электромагнитное поле
не слишком сильное,
не меняется слишком быстро в о времени и
резко в пространстве,
отсутствуют ферромагнетики и
сегнетоэлектрики,
материальные уравнения

19.

Сивухин

20.

Уравнения Максвелла в
дифференциальной форме

21.

Математическое введение к ур-ниям
Максвелла в дифференциальной форме
Теоремы Стокса и Остроградского-Гаусса
Al dl (rotA) n dS
Т. Стокса
(l )
Т. Остроградского Гаусса
где
S
A n dS div A dV
(S)
(a )
(b)
S – поверхность
ограниченная контуром l
V – объём внутри
замкнутой поверхности S
V
A x A y A z
div A
x
y
dz
Дивергенция векторного
(c)
поля, скаляр
A z A y
(rotA ) x
y
z
A x A z
(rotA ) y
z
x
A y A x
(rotA ) z
x
y
Ротор векторного поля,
(d ) вектор

22.

Пример перехода к дифф. форме.
Теор. Гаусса (3-е ур-е М.)
D dS dV
n
S
V
=
Т. О.– Г.
div D dV
V
div D dV dV
V
div D
V
Физ. смысл дивергенции вектора
ρ = 0, поток через замкн. поверхность =0, нет
источников
и стоков, поток не расходится. При этом
дивергенция характеристика
div D 0
расходимости потока
Закон Фарадея (1-е ур-е Максвелла)
dB
(l ) El dl S dt dS
n
=
Т. Стокса
(rotE ) n dS
(S )
dB
( S )(rotE ) n dS S dt dS
n
B
rotE
t

23.

Уравнения Максвелла
B
rotE
t
B
E dl ( t ) dS
1.
l
n
D
) n dS
2. H l dl ( j
t
l
S
l
3.
S
div D
D dS dV
n
S
4.
D
rotH jпр
t
V
divB 0
B dS 0
n
S
Интегральная форма
Дифференциальная форма
Материальные уравнения
D 0 E
B 0 H
j E