Похожие презентации:
Лекция 7 от 27.11.22
1.
2. Физика колебаний
ФИЗИКАКОЛЕБАНИЙ
21.12.2025
2
3.
21.12.20253
4.
КОЛЕБАНИЯКолебания – это физические процессы, обладающие
той или иной степенью повторяемости во времени.
Колебательные процессы весьма часто встречаются в
окружающей нас природе и технике.
Колебания могут иметь различную физическую
природу, но иметь общие закономерности и описываться
однотипными математическими методами.
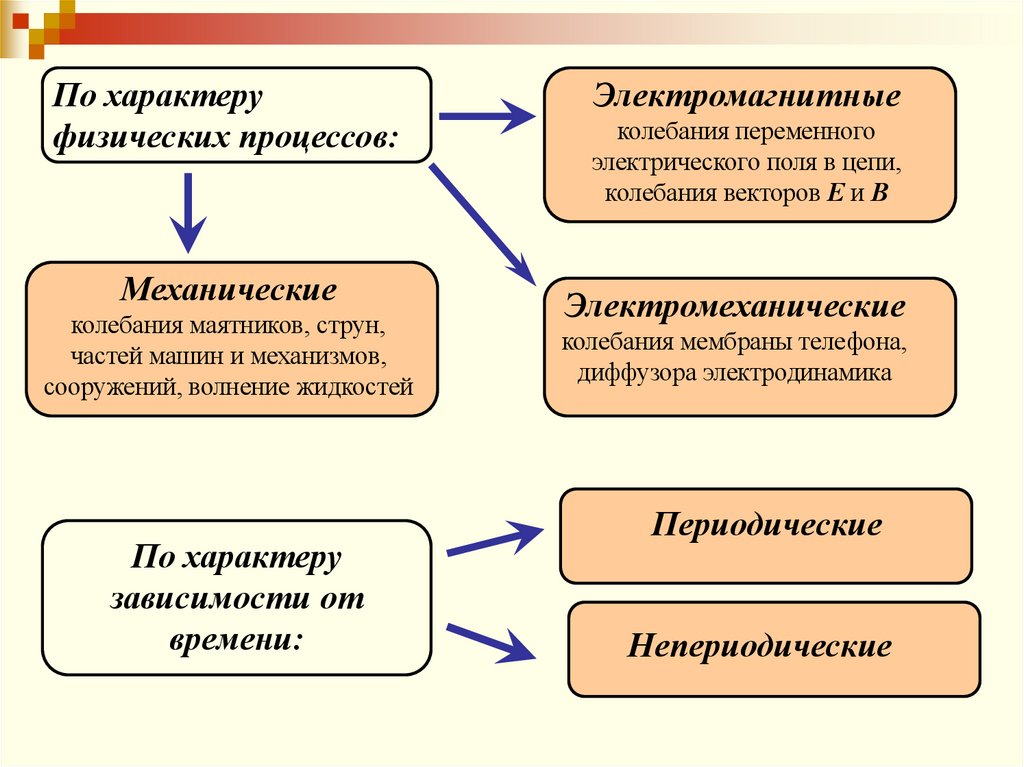
Колебания различают:
•по характеру физических процессов
•по характеру зависимости от времени
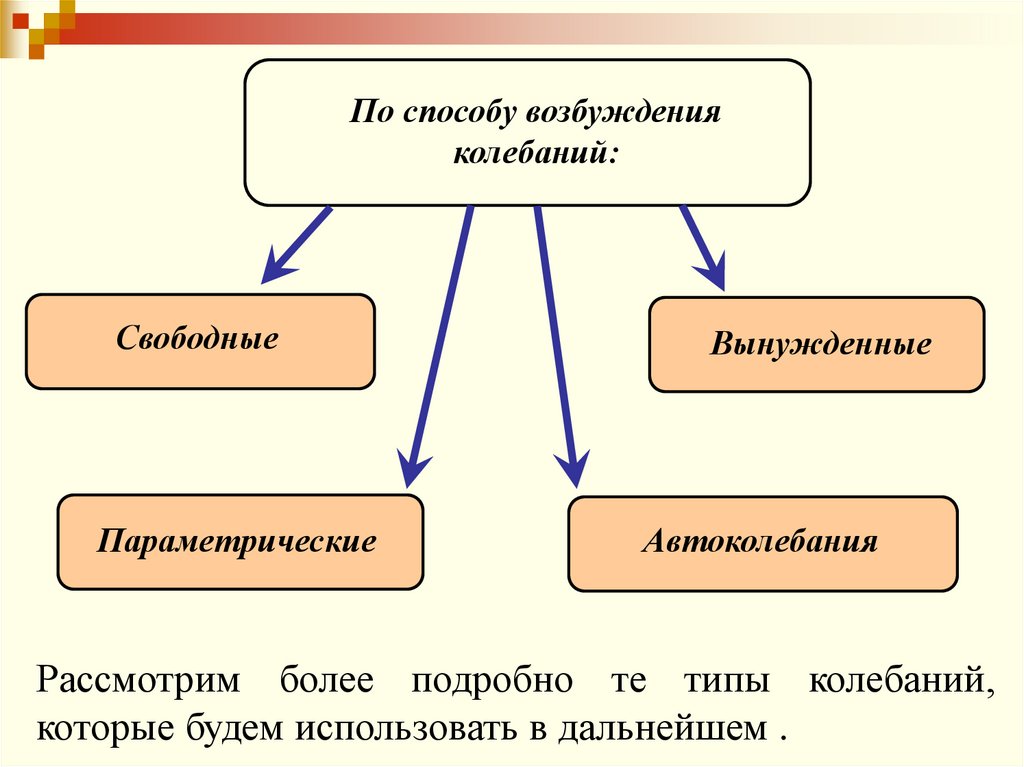
•по
способу возбуждения колебаний
21.12.2025
4
5.
По характеруфизических процессов:
Механические
колебания маятников, струн,
частей машин и механизмов,
сооружений, волнение жидкостей
По характеру
зависимости от
времени:
Электромагнитные
колебания переменного
электрического поля в цепи,
колебания векторов Е и В
Электромеханические
колебания мембраны телефона,
диффузора электродинамика
Периодические
Непериодические
6.
По способу возбужденияколебаний:
Свободные
Параметрические
Вынужденные
Автоколебания
Рассмотрим более подробно те типы колебаний,
которые будем использовать в дальнейшем .
7.
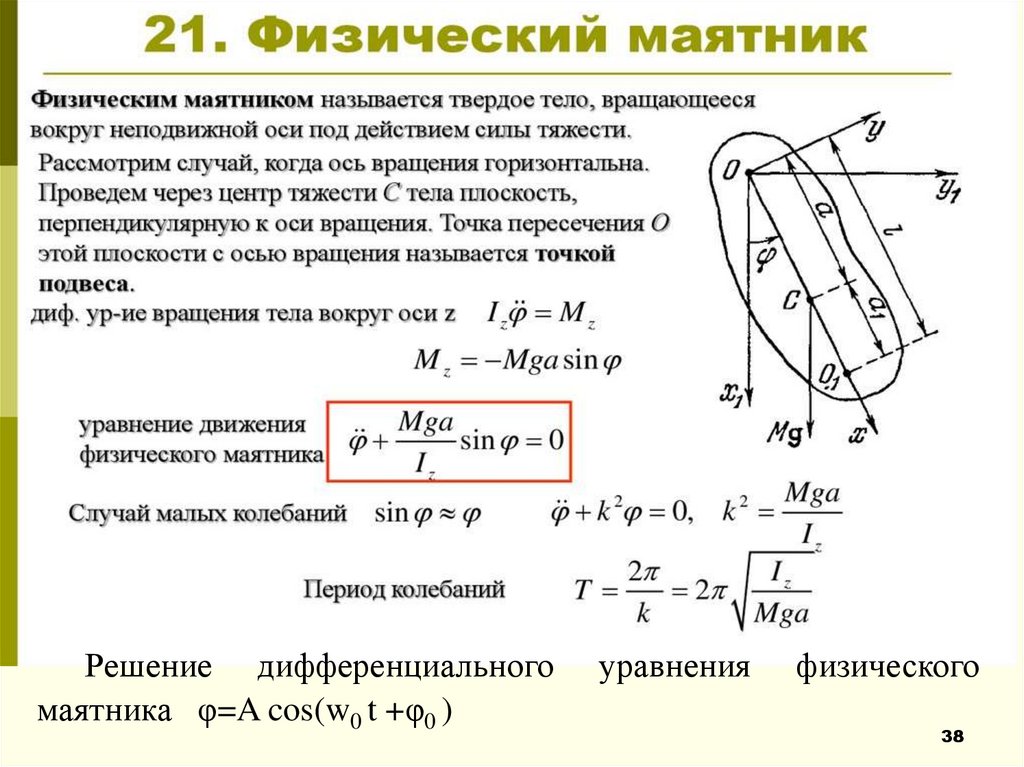
Механическиеколебания
совершают
механизмы, работающие циклически, они
возникают при биении сердца, колебании атомов.
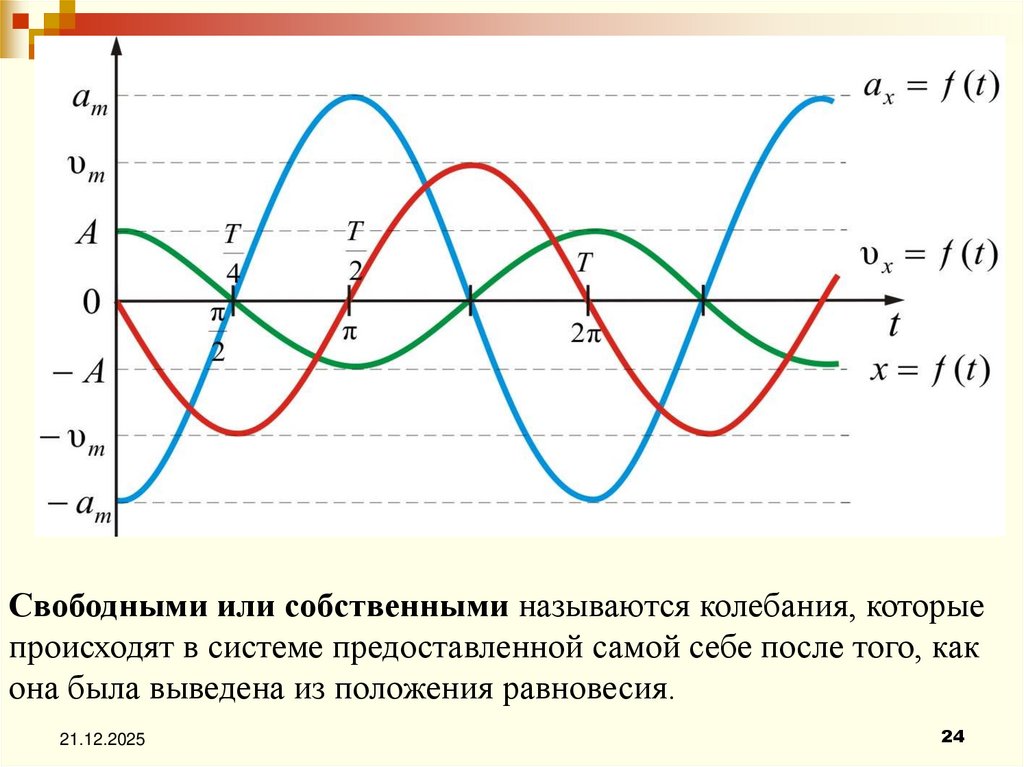
Свободные(или собственные) колебания
—
возникают в системе не подверженной действию
переменных внешних сил, после того, как
система выведена из состояния равновесия.
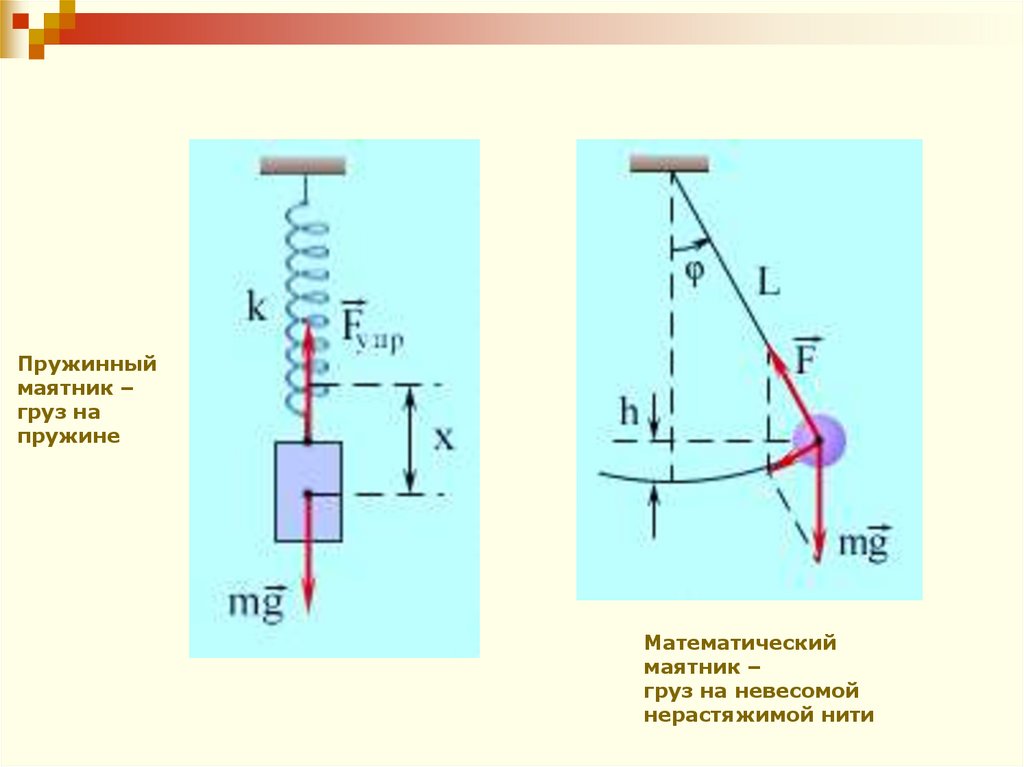
Простейшими примерами свободных колебаний
являются колебания груза, прикреплённого к
пружине, или груза, подвешенного на нити.
21.12.2025
7
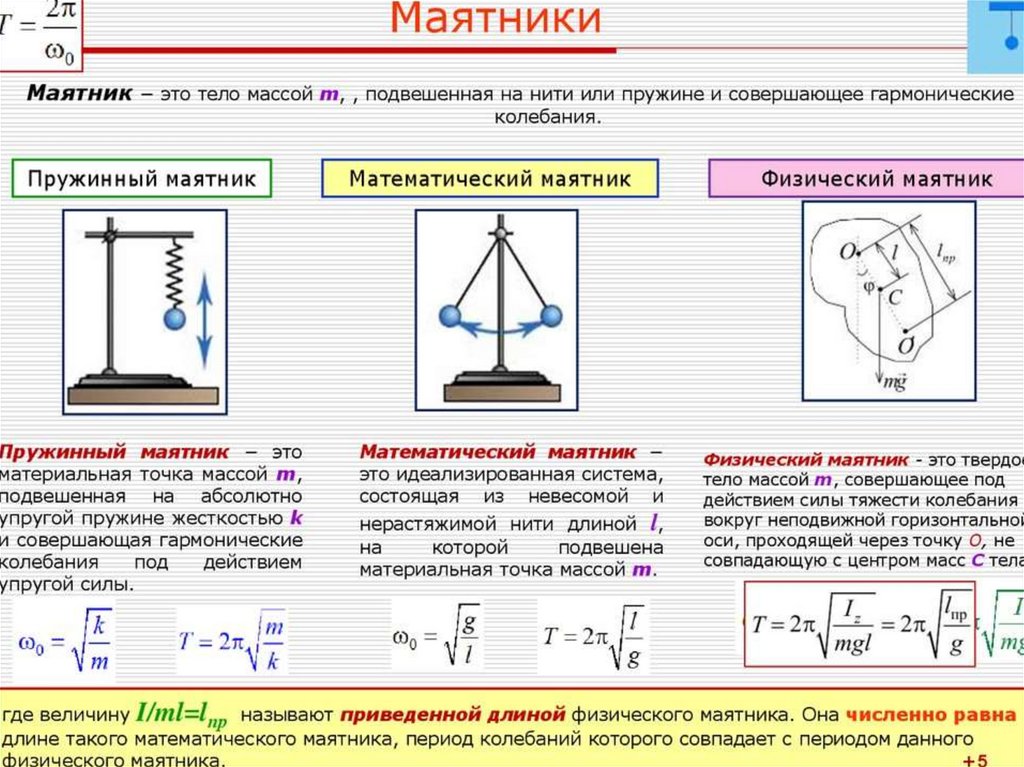
8.
Пружинныймаятник –
груз на
пружине
Математический
маятник –
груз на невесомой
нерастяжимой нити
9. Условия возникновения свободных колебаний 1. Колебательная система должна иметь поло- жение устойчивого равновесия. 2. При
Условия возникновениясвободных колебаний
1. Колебательная система должна иметь положение устойчивого равновесия.
2. При выведении системы из положения равновесия должна возникать равнодействующая сила, возвращающая систему в исходное
положение.
3. Силы трения (сопротивления) очень малы.
10.
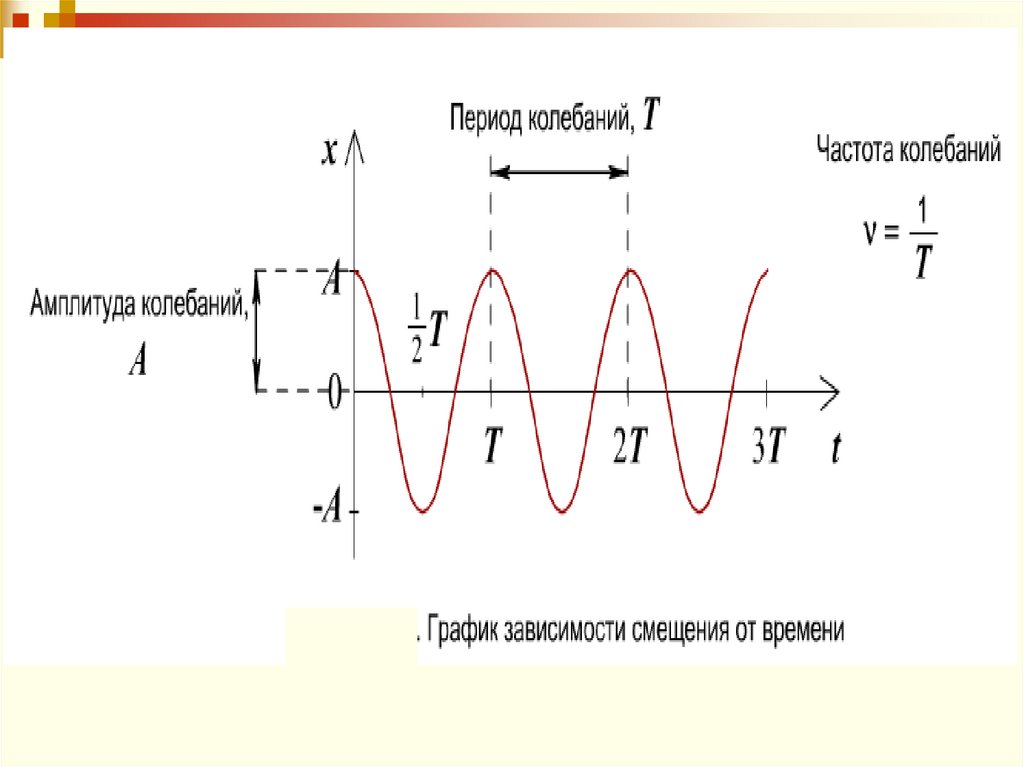
Колебания периодические возникают - еслизначения физических величин, изменяющихся
в процессе колебаний, повторяются через
равные промежутки времени, называемые
периодом.
Гармонические колебания – колебания, при
которых колеблющаяся величина изменяется со
временем по закону синуса
или косинуса
21.12.2025
10
11.
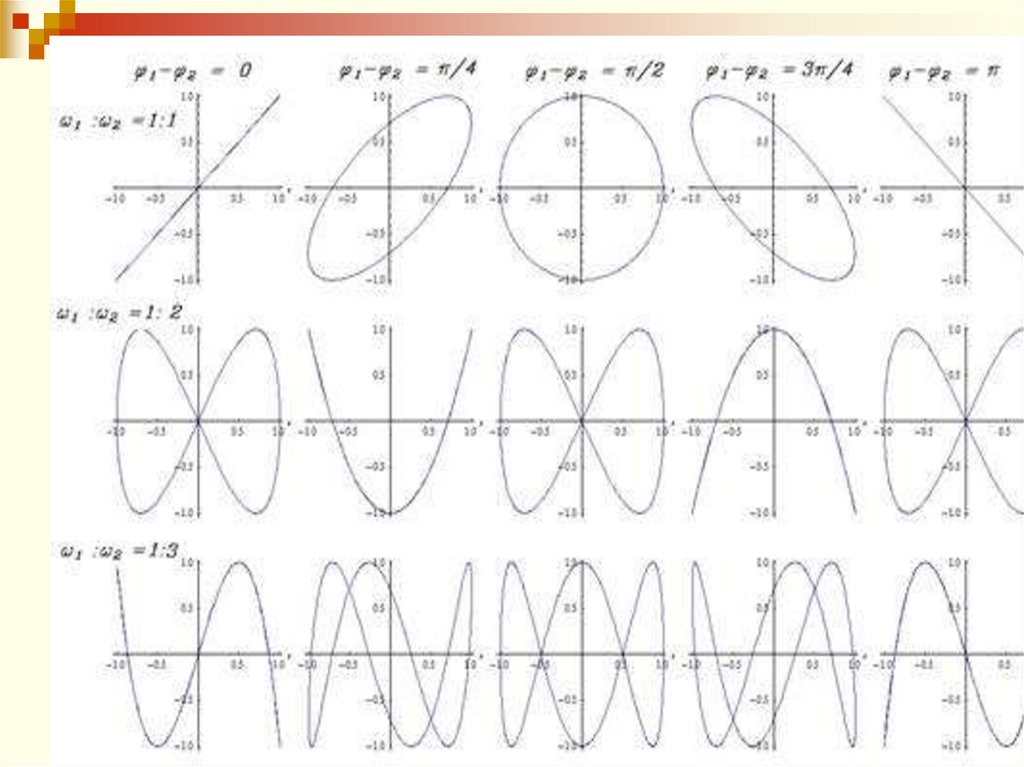
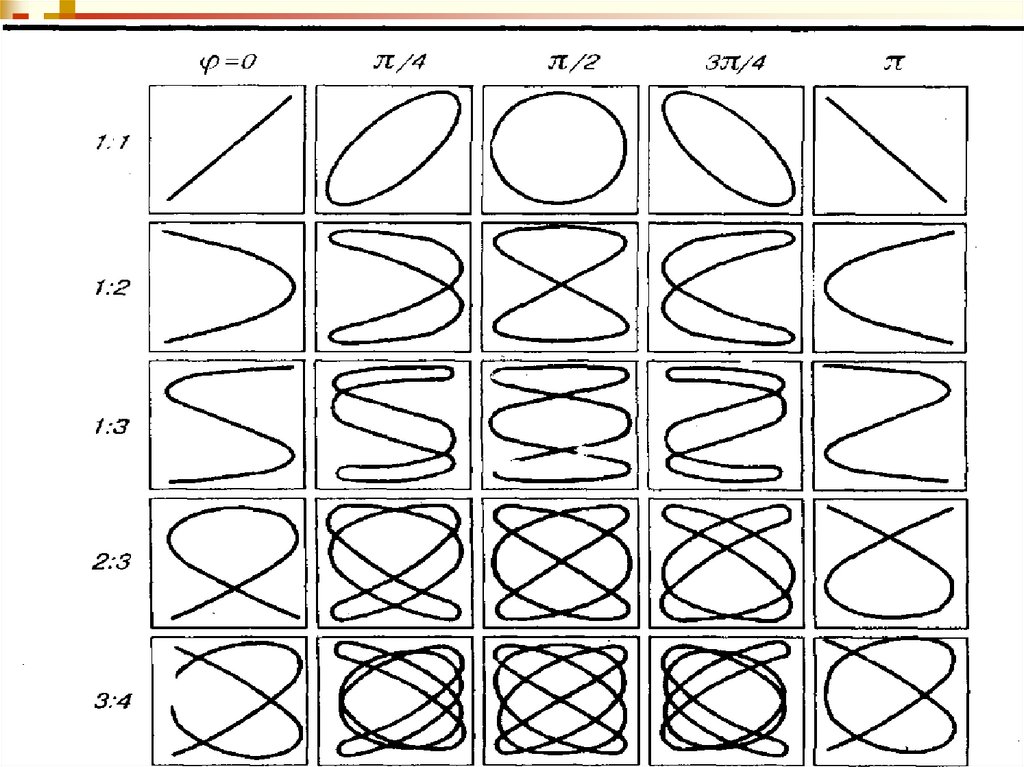
Фурье установил, что любое периодическое негармоническое колебание может быть представлено каксумма гармонических колебаний.
Теорема Фурье - любое сложное периодическое
колебание S = f(t) можно представить в виде суммы
простых гармонических колебаний с циклическими
частотами, кратными основной циклической частоте ω0 =
2π ∕ Т, где Т – период колебаний:
A0
S f t A1cos 0t 1 A2 cos 2 0t 2 ... An cos n 0t n
2
A0
An cos n 0t n ,
2 n 1
Такое представление периодической функции f(t)
называется разложением функции в ряд Фурье или
гармоническим анализом сложного периодического
11
12.
Члены ряда Фурье, соответствующие гармоническимколебаниям с циклическими частотами ω0, 2ω0, 3ω0 …
называются первой (основной), второй, третьей и т.д.
гармониками сложного периодического колебания S = f(t).
Совокупность этих гармоник образуют спектр колебаний
S = f(t).
В простейших случаях спектр может состоять из
небольшого числа гармоник.
Часто под спектром колебаний понимают спектр
(совокупность) его частот.
21.12.2025
12
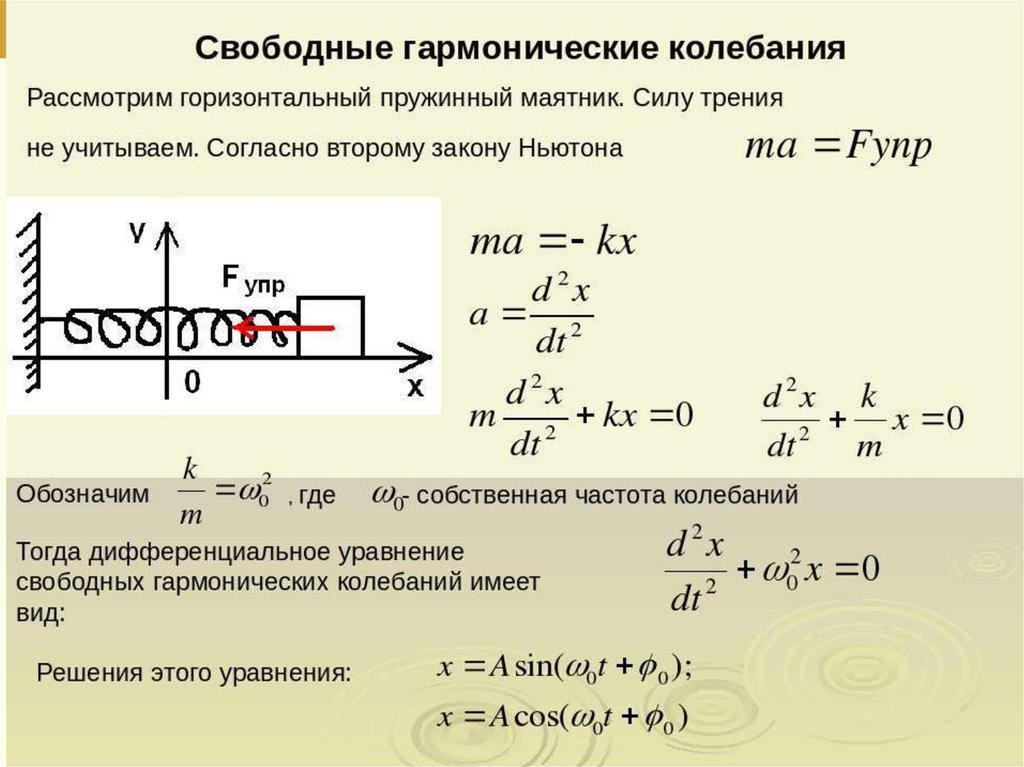
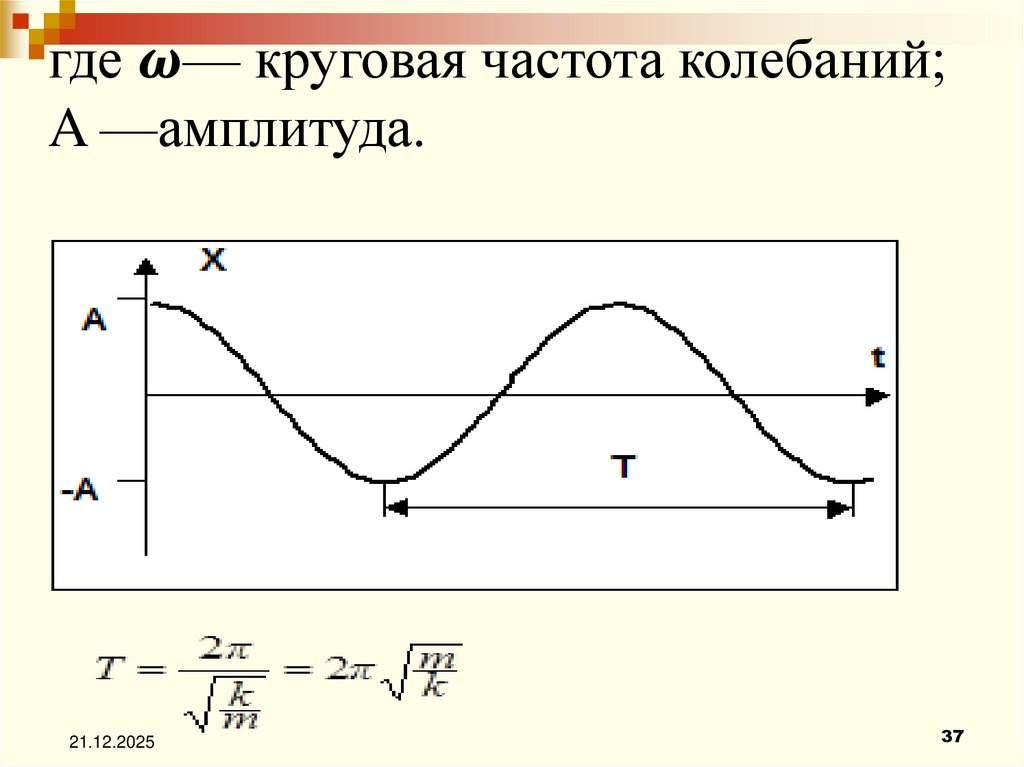
13. Механические гармонические колебания
Рассмотрим прямолинейные гармонические колебанияматериальной точки вдоль оси х около положения
равновесия, совпадающего с началом координат х = 0.
Зависимость координаты х от времени t задается
уравнениями
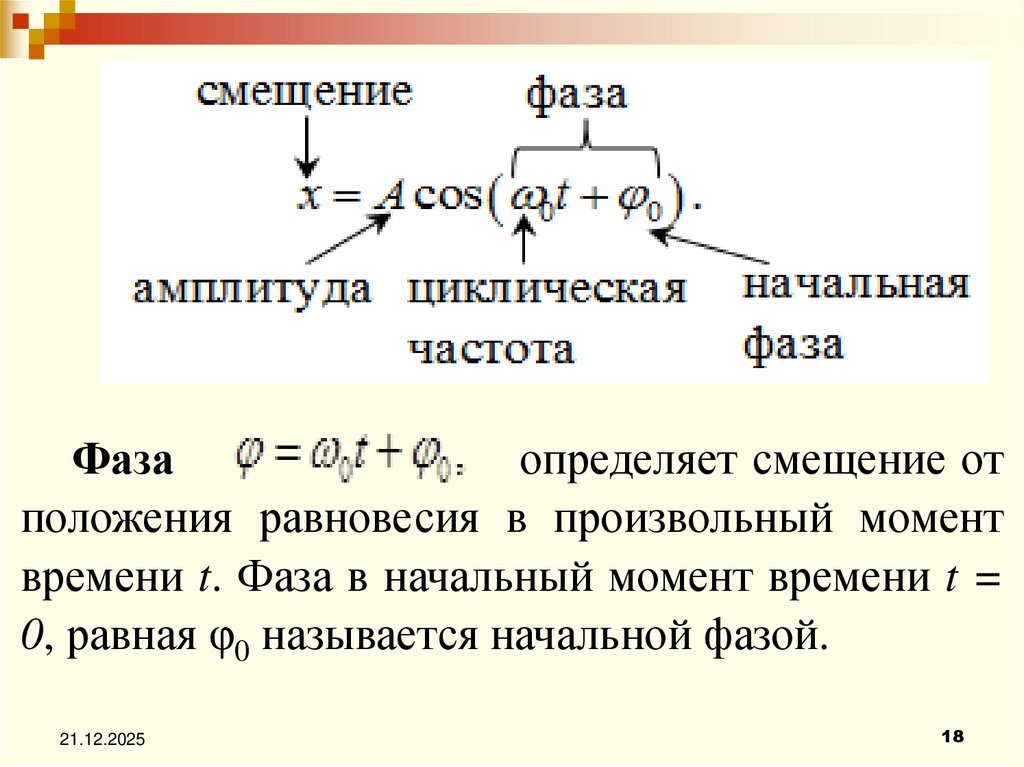
x A cos( t )
0
А – максимальное значение колеблющейся величины, называется
амплитудой колебаний, ω – круговая (циклическая) частота,
t – фаза колебаний в момент времени t.
0
Система,
совершающая
колебательной системой.
колебания,
называется
14.
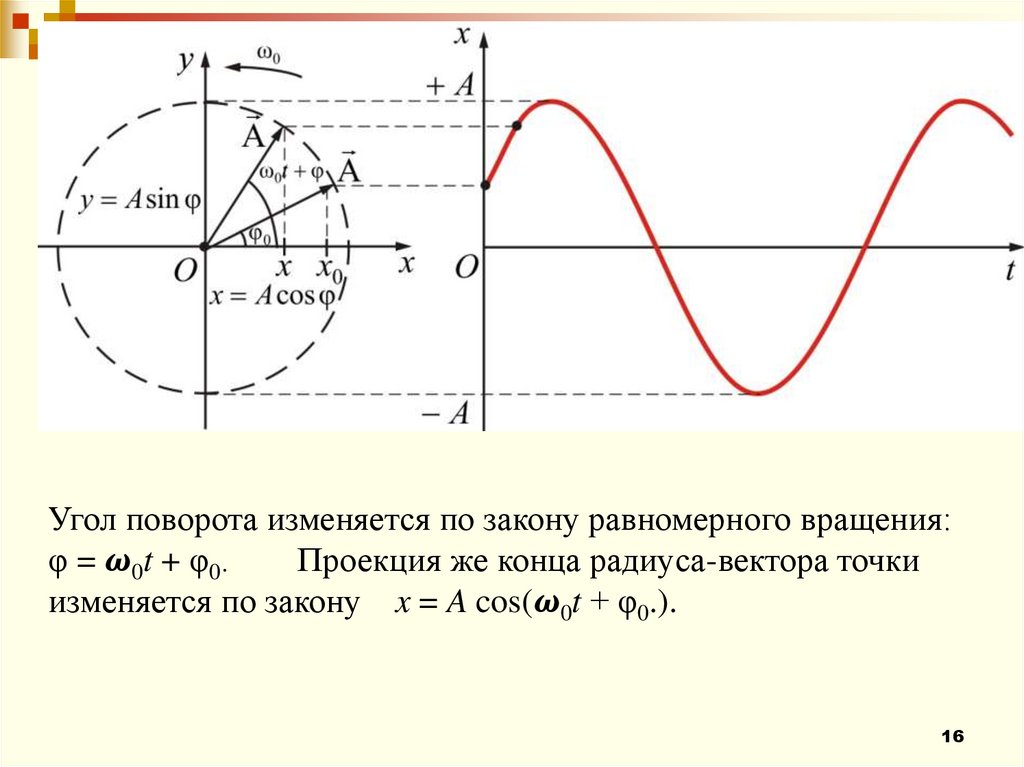
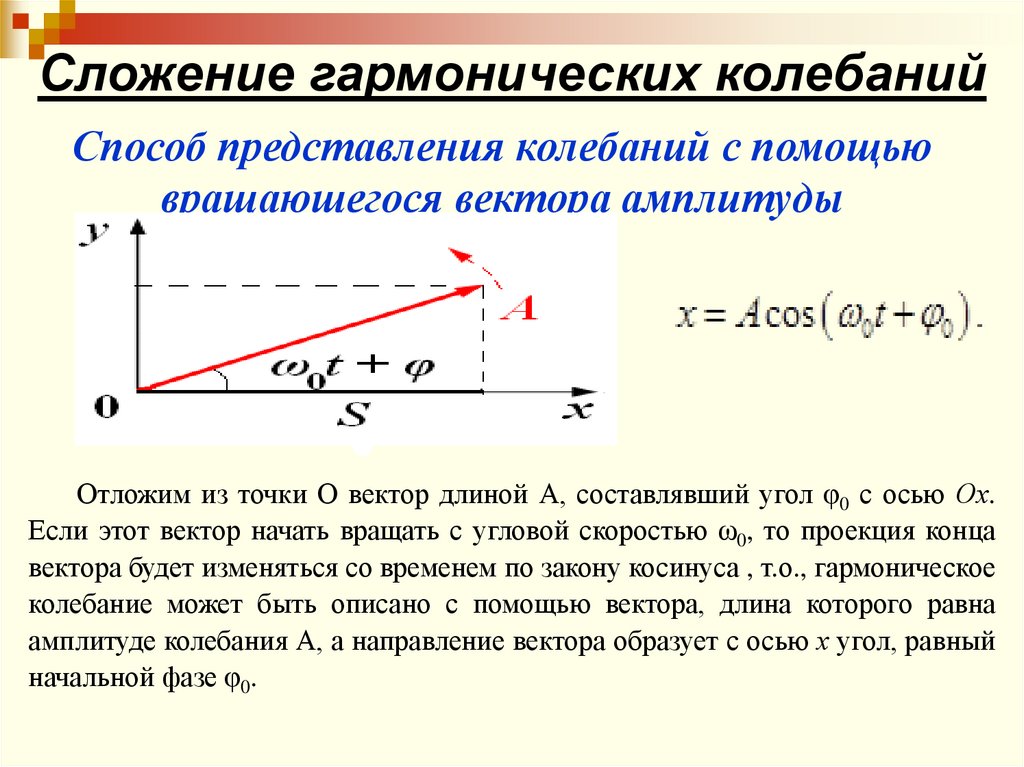
Простейшей моделью гармоническогоколебания является колебание
проекции x конца радиуса-вектора r
точки, движущейся по окружности
радиусом A с постоянной угловой
скоростью ω0. Такое представление
гармонических колебаний называют
векторной диаграммой.
21.12.2025
14
15.
21.12.202515
16.
Угол поворота изменяется по закону равномерного вращения:φ =



























































 Физика
Физика








