Похожие презентации:
Механические колебания
1. Лекция 6. Механические колебания
2.
1.Гармонические колебания и их характеристики.2.Метод вращающегося вектора амплитуды.
3.Гармонический осциллятор. Пружинный,
физический и математический маятники.
4.Превращение энергии при свободных механических колебаниях.
5.Затухающие колебания
6.Вынужденные колебания. Резонанс.
7.Сложение гармонических колебаний одного
направления и частоты.
3.
Гармонические колебания и их характеристикиНаряду с поступательным и вращательным движениями тел в механике значительный интерес представляет и колебательное движение.
Механическими колебаниями называются повторяющиеся во времени изменения физической величины, описывающей механическое движение тела
(координата, угол отклонения, скорость, ускорение,
сила, кинетическая и потенциальная энергия и т. п.).
Колебания называются периодическими, если
значения физических величин, изменяющихся
4.
в процессе колебаний, повторяются через равные промежутки времени, которые называются периодом колебания.Простейшим типом периодических колебаний являются гармонические колебания, при которых колеблющаяся величина изменяется со временем по закону
синуса или косинуса:
x A cos ω0t φ ,
где x – координата колеблющейся около положения
равновесия вдоль оси Ох точки,
A – амплитуда колебаний – максимальное смещение
(xm) колеблющейся величины от положения равновесия,
ω0 – циклическая частота колебаний,
t – время, φ – начальная фаза колебаний.
5.
Периодически изменяющийся аргумент косинусаω0t φ называется фазой колебания.
За один период фаза колебания получает приращение равное 2π , т. е.
ω0 (t T ) φ= ω0t φ 2π,
откуда
2π
T
.
ω0
1
Величина, обратная периоду колебаний ν =
T
называется частотой колебаний.
Частота колебаний измеряется в герцах (Гц) и равна
числу колебаний за 1с.
6.
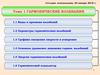
Частота колебаний связана с циклической частотойсоотношением:
ω0 2πν.
На этом рисунке изображены положения тела через одинаковые промежутки времени при гармонических колебаниях.
Такую картину можно получить экспериментально при
освещении колеблющегося
тела короткими периодическими вспышками света (стробоскопическое освещение).
7.
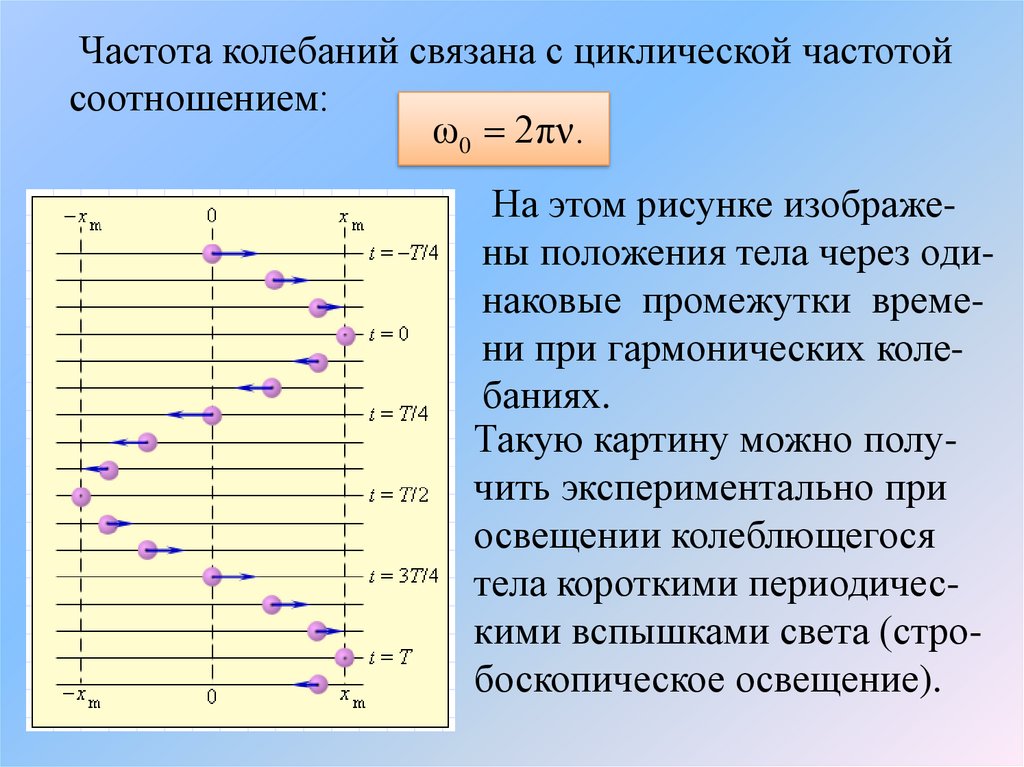
Стрелки изображают векторы скорости тела в различные моменты времени.На этих рисунках показаны
изменения, которые происходят на графике гармонического процесса x(t),
если изменяются (красные
кривые): амплитуда xm колебаний (рис.1), период T
(рис. 2), начальная фаза φ0
(рис. 3).
8.
Колебания называются свободными (или собственными), если они продолжаются неограниченно долгоза счёт первоначально сообщённой кинетической или
потенциальной энергии.
Совокупность тел, участвующих в колебательном
процессе, называют колебательной системой.
Найдём скорость и ускорение колеблющейся вдоль
оси Ох точки, как первую и вторую производные от
смещения по времени:
dx
π
v x x Aω0 sin ω0t φ Aω0 cos ω0t φ ;
dt
2
dv x
ax
x Aω02 cos ω0t φ Aω02 cos ω0t φ+π .
dt
9.
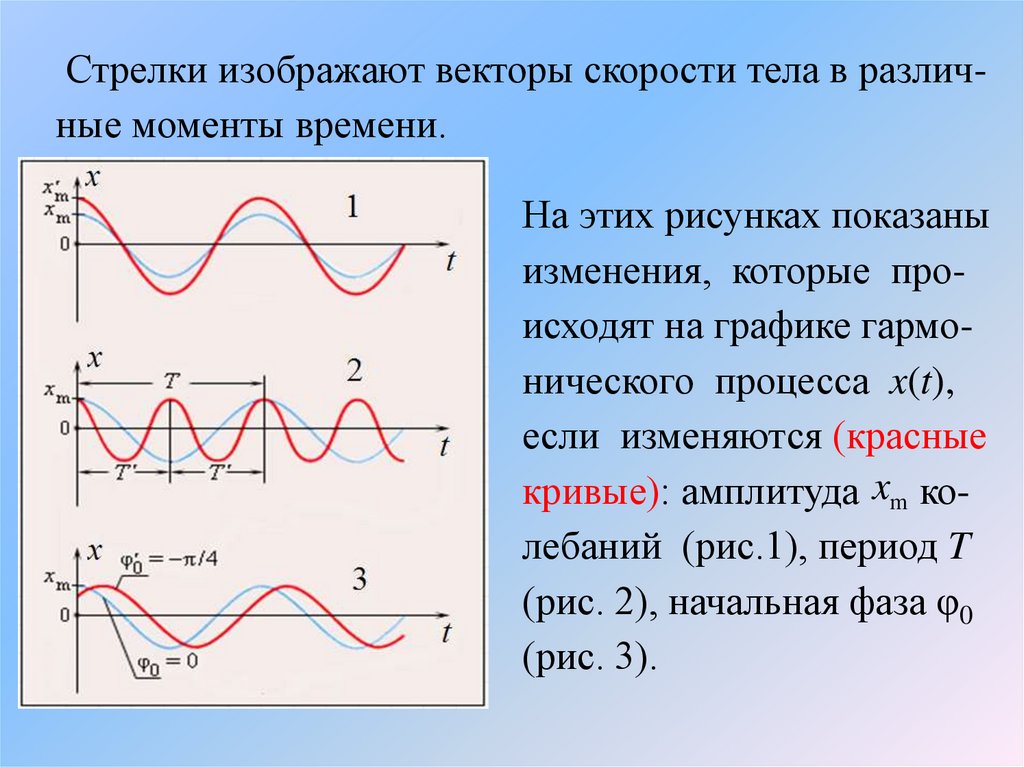
На этом рисунке показаны графики смещения (1), скорости (2 ) ии ускорения (3) колеблющейся точки от времени при гармонических колебаниях.
Видно, что фаза скорости отличается от фазы смещения на π/2 , а
фаза ускорения на π.
10.
Запишем выражение для ускорения в виде:ax Aω02 cos ω0t φ ax ω02 x 0.
Или
x ω02 x 0.
Это уравнение называется дифференциальное уравнение гармонических колебаний.
11.
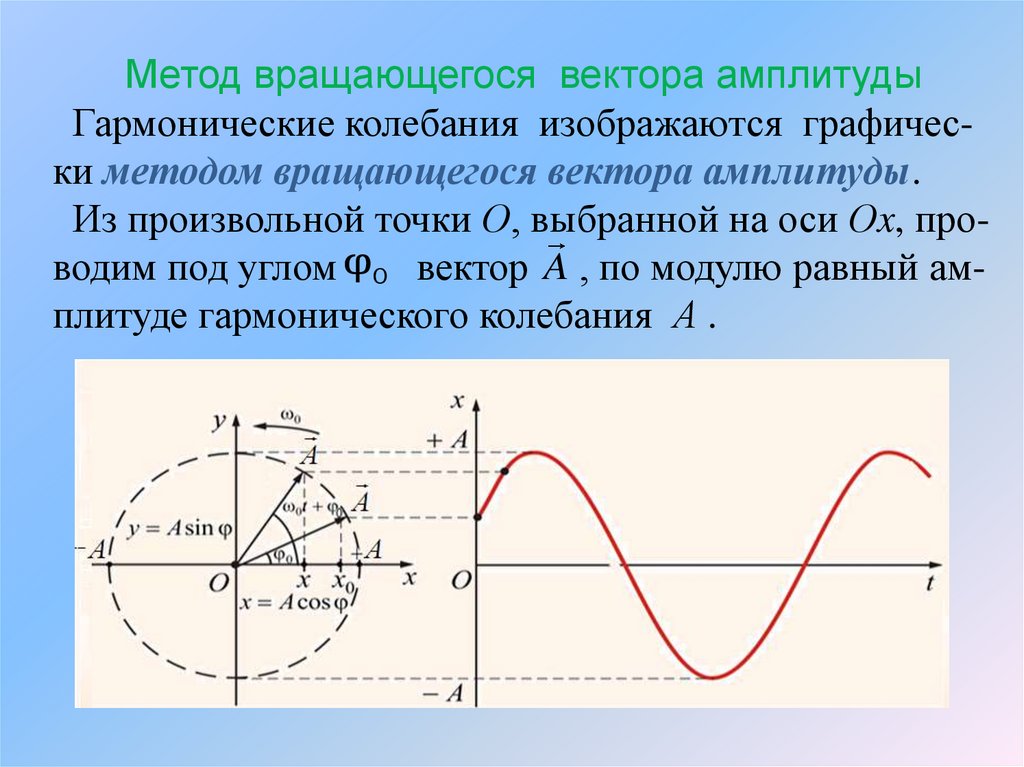
Метод вращающегося вектора амплитудыГармонические колебания изображаются графически методом вращающегося вектора амплитуды.
Из произвольной точки О, выбранной на оси Оx, проводим под углом φ0 вектор A , по модулю равный амплитуде гармонического колебания А .
12.
Приводим его во вращение с угловой скоростью ω0вокруг точки О в плоскости координатных осей x, y.
По мере того, как вектор A будет вращаться по окруности, проекция конца вектора на ось Ox будет совершать линейные гармонические колебания с циклической частотой ω0 : x A cos ω0t φ 0 .
13.
Гармонический осциллятор.Пружинный, математический и физический
маятники
Свободные колебания совершаются под действием
внутренних сил системы после того, как система была
выведена из положения равновесия.
Для того чтобы свободные колебания совершались по
гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную
смещению: F t max t m ω02 x t .
14.
В этом соотношении ω0 – циклическая частота гармонических колебаний.Таким свойством обладает упругая сила в пределах
применимости закона Гука: Fупр kx.
Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими.
Тело, совершающее колебания под действием квазиупругих сил, называют гармоническим осциллятором, а уравнение вида
x ω02 x 0 – уравнением гармонического осциллятора .
15.
Груз массы m, прикреплённый к горизонтальной пружине жёсткости k, второйконец которой закреплён
неподвижно, составляют
колебательную систему, способную совершать свободные гармонические колебания (пружинный маятник).
Циклическая частота ω0 свободных колебаний груза
на пружине находится из второго закона Ньютона:
k
max Fупр mx kx x x 0.
m
Следовательно, колебания пружинного маятника
описываются уравнением гармонического осциллятора.
16.
kОткуда ω0
и
m
2π
m
T
2π
.
ω0
k
Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо
мала по сравнению с массой тела.
В положении равновесия, когда маятник висит по
отвесу, сила тяжести mg уравновешивается силой
натяжения нити Т .
17.
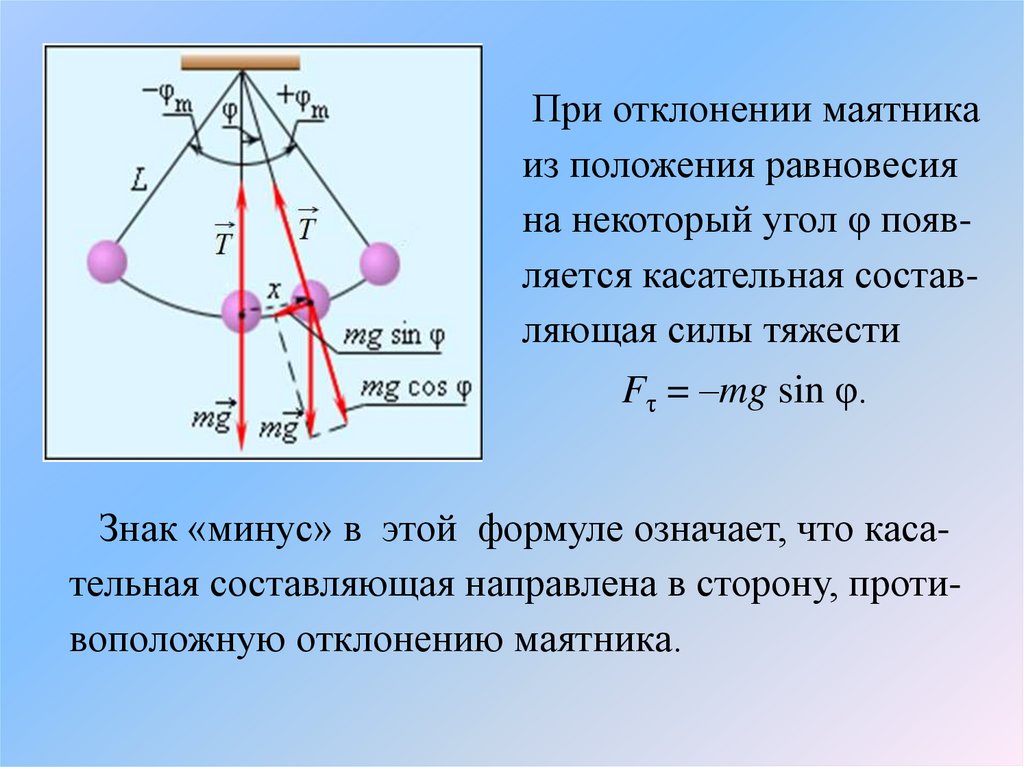
При отклонении маятникаиз положения равновесия
на некоторый угол φ появляется касательная составляющая силы тяжести
Fτ = –mg sin φ.
Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.
18.
Эта составляющая создаст вращающий моментM l mg sin φ l mg φ.
В соответствии с основным законом динамики вращательного движения этот момент сил должен быть
равен
l mg φ = I φ,
где I – момент инерции тела относительно оси подвеса, φ – угловое ускорение тела.
Или
l mg
φ 0
I φ + l mg φ = 0 φ +
I
lmg
φ+ 2 φ = 0 φ+ g φ=0.
ml
l
19.
Таким образом, колебания математического маятникаописываются уравнением гармонического осцилля-
тора.
Следовательно, ω0
g
l
и
l
T 2π
.
g
Любое тело, насаженное на горизонтальную ось
вращения и способное совершать в поле тяготения
свободные колебания называется физическим маятником.
Он отличается от математического маятника только
распределением масс.
20.
В положении устойчивого равновесия центр масс Cфизического маятника находится ниже оси вращения
О на вертикали, проходящей через ось.
При отклонении маятника на угол φ возникает
момент силы тяжести,
стремящийся возвратить
маятник в положение равновесия:
M mg sin φ d ,
где d – расстояние между осью вращения и центром
масс C.
21.
Знак «минус» в этой формуле означает, что моментсил стремится повернуть маятник в направлении,
противоположном его отклонению из положения
равновесия.
Как и в случае математического маятника, возвращающий момент M пропорционален sin φ.
Это означает, что только при малых углах φ, когда
sin φ ≈ φ, физический маятник способен совершать
свободные гармонические колебания.
В случае малых колебаний M mgd φ,
22.
и основной закон динамики для вращательногодвижения физического маятника принимает вид:
mgd
Iφ mgd φ = 0, φ
φ = 0.
I
Таким образом, колебания физического маятника
также описываются уравнением гармонического осциллятора.
mgd
mgd
2
ω0 ω0 =
.
Следовательно,
I
I
Период колебания физического маятника отсюда:
I
T 2π
.
mgd
23.
Сравнивая формулыl
T 2π
g
I
T 2π
mgd
заключаем, что математический маятник с длиной
I , которая называется приведённая длина
lпр
md
физического маятника, будет колебаться
с тем же периодом, что и физический.
Центр качания – точка на продолжении прямой ОС и
отстоящая от точки подвеса на расстоянии l пр .
Точка подвеса и центр качания обладают свойством
взаимозаменяемости:
24.
если физический маятник подвесить за центр качания, то его период не изменится и прежняя точка подвеса сделается новым центром качания.25.
26.
Превращение энергии при свободныхмеханических колебаниях
При свободных механических колебаниях кинетическая и потенциальная энергии тела изменяются
периодически.
При максимальном отклонении тела от положения
равновесия его скорость, а, следовательно, и кинетическая энергия обращаются в нуль.
В этом положении потенциальная энергия колеблющегося тела достигает максимального значения.
27.
Для груза на горизонтально расположенной пружинепотенциальная энергия – это энергия упругих деформаций пружины. Для математического маятника –
это энергия в поле тяготения Земли.
Когда тело при своем движении проходит через положение равновесия, его скорость максимальна.
В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией.
Увеличение кинетической энергии происходит за
счет уменьшения потенциальной энергии.
28.
Таким образом, при гармонических колебанияхпроисходит периодическое превращение кинетической энергии в потенциальную и наоборот.
Кинетическую энергию колеблющегося тела вычислим по формуле:
2
2 2
v
m
m ω0 A
Ek
sin 2 ω0t φ
2
2
m A2ω02
1 cos 2 ω0t φ .
4
29.
Потенциальная энергия материальной точки, совершающей гармонические колебания по действием упругой силы F mω02 x,2 2
m
ω
x
2
mω x
0A
cos
ω 0t φ
Ep F dx
0
2
2
2
0
2
m A2ω02
1 cos 2 ω0t φ .
4
Из этих формул следует, что кинетическая и потенциальная энергии колеблются с удвоенной частотой.
2
2
sin
ω
t
φ
cos
0
ω0t φ 1,
Так как
30.
то полная энергия колеблющейся точкиm ω02 A2
Eп Ek Ep
2
остаётся при свободных гармонических колебаниях
величиной постоянной.
п
31.
Затухающие колебанияВ реальных условиях любая колебательная система
находится под воздействием сил трения (сопротивления).
При этом часть механической энергии превращается
во внутреннюю энергию теплового движения атомов
и молекул, и колебания становятся затухающими.
Затухающие колебания описываются дифференциальным уравнением вида:
x 2δx ω02 x 0.
где δ – коэффициент затухания.
32.
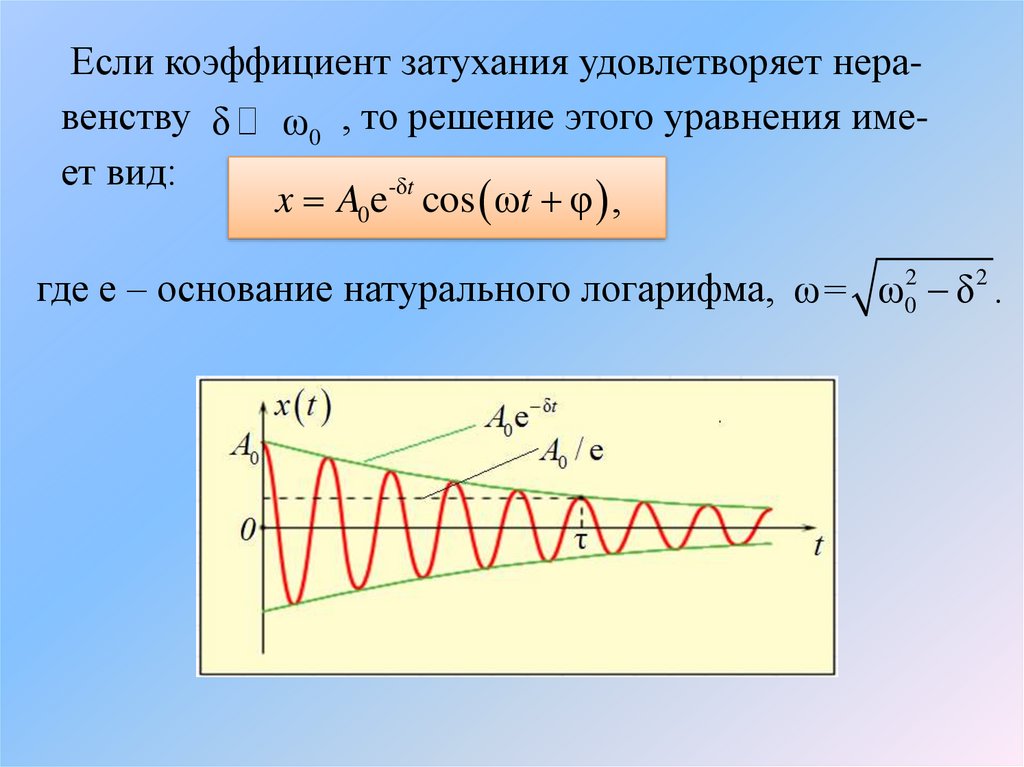
Если коэффициент затухания удовлетворяет неравенству δ ω0 , то решение этого уравнения имеет вид:x A0e-δt cos ωt φ ,
где е – основание натурального логарифма, ω= ω02 δ 2 .
33.
Промежуток времени τ, в течении которого амплитуда колебаний уменьшается в е раз, называется временем релаксации.Период затухающих колебаний
2π
2π
T
.
ω
ω02 δ 2
A t
δT
e
Отношение
A t T
называется декрементом затухания, а его натуральный логарифм
34.
θ = ln eδT
T
1
δT
,
Ne
где N e – число колебаний, совершаемых за время релаксации, – логарифмическим декрементом затухания.
Для пружинного маятника массой m, колеблющегося под действием упругой силы F kx , сила сопротивления (трения) пропорциональна скорости:
Fc rx, где r – коэффициент сопротивления.
С учётом этих сил уравнение движения пружинного
mx kx rx.
маятника примет вид:
35.
2Если в это уравнение подставить величины k mω0 ,
r 2δm то получим уравнение x 2δx ω02 x 0,
решением которого будет уравнение
x A0e-δt cos ωt φ .
Важной характеристикой колебательной системы,
совершающей затухающие колебания, является добротность Q.
Этот параметр определяется как число полных колебаний N e , совершаемых системой за время релаксации, умноженное на π :
Q πN e .
36.
Чем медленнее происходит затухание свободныхколебаний, тем выше добротность колебательной
системы.
Добротности механических колебательных систем
могут быть очень высокими – порядка нескольких
сотен и даже тысяч.
Понятие добротности имеет глубокий энергетический смысл.
Можно определить добротность Q колебательной
системы следующим энергетическим соотношением:
37.
Полный запас энергии КСQ 2π
Потеря энергии за 1 период
Таким образом, добротность характеризует относительную убыль энергии колебательной системы изза наличия трения на интервале времени, равном одному периоду колебаний.
38.
39.
40.
Вынужденные колебания. РезонансРассмотрим систему, на которую кроме упругой
силы (– kx) и сил сопротивления (– rυ) действует
добавочная периодическая сила F – вынуждающая
сила:
mx kx rx F cos ωt.
Или
0
x 2δx ω02 x F0 cosωt.
Уравнение установившихся вынужденных колебаний имеет вид
x A sin ωt φ ,
41.
гдеF0
A
m
ω
2
0
ω
2 2
,
4δ ω
2
2
2δω
φ = arctg 2
.
2
ω0 ω
Проанализируем зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы и
коэффициента затухания.
1.
ω = 0 – частота вынуждающей силы равна нуF0
лю. Тогда Aст
– статическая амплитуда
2
mω0
(смещение) в отсутствии колебаний;
42.
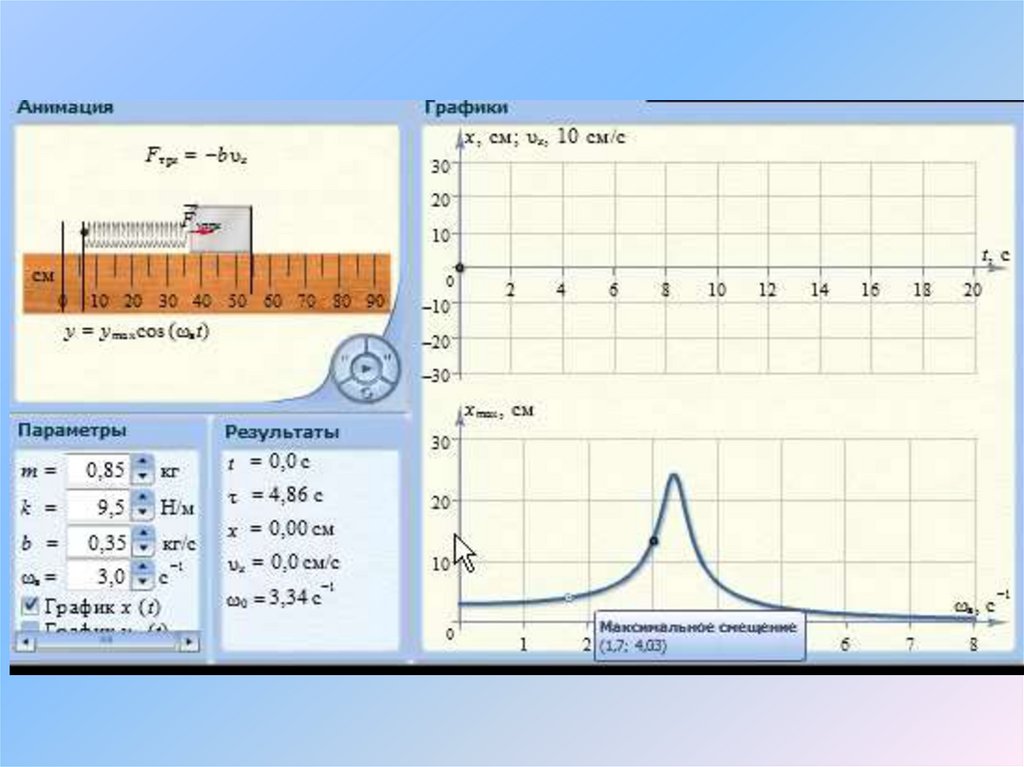
2. δ = 0 – (затухания нет). С увеличением ω (нопри ω< ω0 ) амплитуда растёт и при ω= ω0 происходит резкое увеличение амплитуды вынужденных колебаний ( A ). Это явление называется резонансом.
При дальнейшем увеличении частоты вынуждающей силы ( ω> ω0 ) амплитуда уменьшается и
при ω A 0.
43.
3.В реальных условиях амплитуда устаδ 0
новившихся вынужденных колебаний определяется условием: работа внешней силы в течение
периода колебаний должна равняться потерям
механической энергии за то же время из-за трения.
Чем меньше трение (т. е. чем выше добротность
Q колебательной системы), тем больше амплитуда вынужденных колебаний при резонансе.
Ap
F0
2mδ ω02 δ 2
.
44.
На рисунке приведены резонансные кривые приразличных значениях коэффициента затухания:
δ1= 0; δ4 > δ3 > δ2 .
45.
У колебательных систем с невысокой добротностьюQ 10 резонансная частота с увеличением коэффициента затухания смещается в сторону низких частот:
2
2
ω ω 2δ .
p
0
Явление резкого увеличения поглощения энергии
колебательной системой при резонансе называется
резонансным поглощением энергии.
Явление резонанса играет большую роль в природе,
науке и технике. Большинство сооружений и машин,
обладая определённой упругостью, способны совершать малые свободные колебания.
46.
Поэтому внешние периодические воздействия могутвызвать их резонанс, что может привести к механическим разрушениям и поломкам.
Предотвратить вредное воздействие резонанса можно путём уменьшения добротности систем, подверженных механическим колебаниям.
Полезное применение резонанса: акустика (усиление
звучания музыкальных инструментов; радиотехника и
электротехника (выделение полезного сигнала, измерение частоты колебаний различных систем); резонансное поглощение энергии гамма-квантов (эффект Мёссбауэра, ЭПР, ЯМР) и т.д.
47.
48.
Сложение гармонических колебаний одногонаправления и одинаковой частоты
Пусть точка одновременно участвует в двух гармонических колебаниях одинакового периода, направленных вдоль одной прямой.
x1 A1 cos ω0t φ1 ,
x2 A2 cos ω0t φ 2 .
Найдём уравнение результирующего колебания, воспользовавшись методом вращающегося вектора амплитуды.
49.
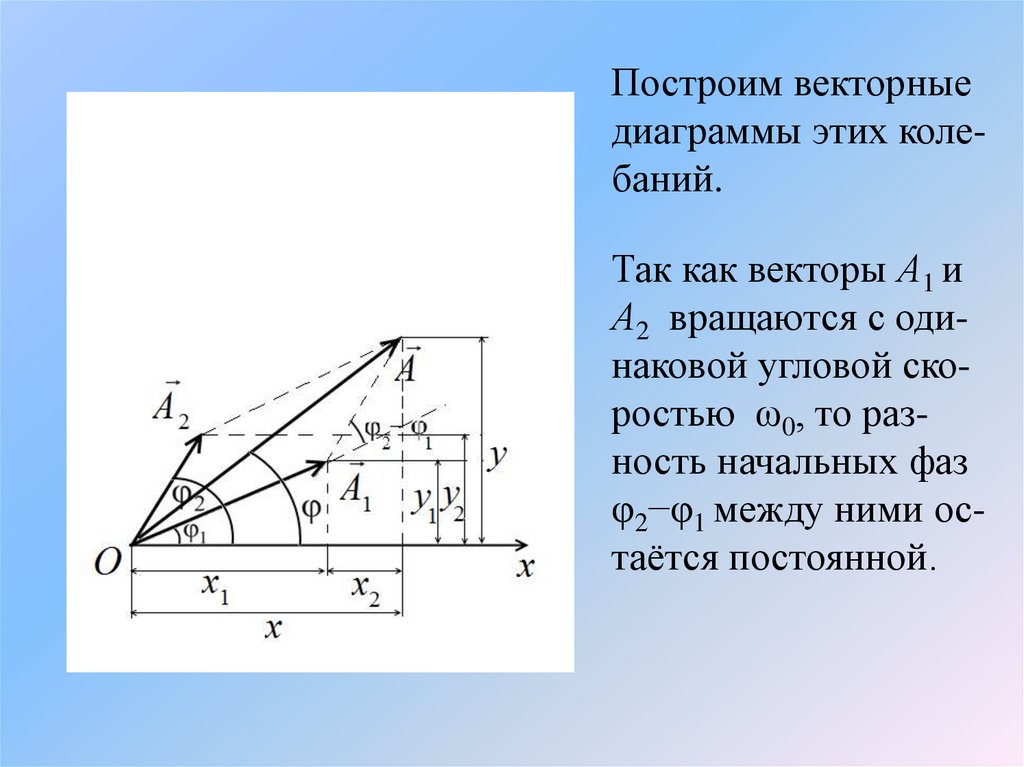
Построим векторныедиаграммы этих колебаний.
Так как векторы А1 и
А2 вращаются с одинаковой угловой скоростью ω0, то разность начальных фаз
φ2−φ1 между ними остаётся постоянной.
50.
Очевидно, что уравнение результирующегоколебания будет
x x1 x2 A cos ω0t φ ,
где
A2 A12 A22 2 A1 A2 cos φ 2 φ1 ,
A1 sin φ1 A2 sin φ 2
tg φ
A1 cos φ1 A2 cosφ 2
51.
Проанализируем выражение для результирующейамплитуды:
Если:
φ 2 φ1 2mπ
m 0, 1, 3,...
Тогда A A1 A2 , т. е. результирующая амплитуда равна сумме слагаемых амплитуд.
Если:
φ 2 φ1 2m 1 π
m 0, 1, 3,...
Тогда A A1 A2 , т. е. результирующая амплитуда равна разности слагаемых амплитуд.










































 Физика
Физика