Распределение Максвелла с заметками

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра строительной физики и химии
Физика
Тема 7
Распределение молекул по
скоростям
Кирк Яна Геннадьевна
к.п.н., доцент, доцент

2.

2
План лекции
1. Функция распределения молекул по скоростям.
2. Распределение Максвелла.
3. Характерные скорости молекул.
4. Эксперимент по проверке распределения Максвелла.
5. Распределение молекул по координатам.
6. Распределение Максвелла — Больцмана.

3.

1. Функция распределения молекул по скоростям.
3
С макроскопической точки зрения в состоянии равновесия в газе устанавливаются постоянная температура
и постоянное давление.
Молекулы газа в равновесии движутся беспорядочно, сталкиваются между собой и со стенками сосуда,
беспрерывно меняют свою скорость.
Но, среднее значение квадрата скорости, как это следует из формулы молекулярно-кинетической теории
идеальных газов, остается постоянным и равным
Определить распределение молекул по скоростям — это означает рассчитать, сколько молекул или
какая доля молекул из общего числа N обладают скоростями, лежащими в интервале от v до v + dv.
Или, какова вероятность следующего события: вектор скорости
имеет проекции на оси
некоторой декартовой системы координат в пространстве скоростей одновременно принадлежащих
следующим интервалам

4.

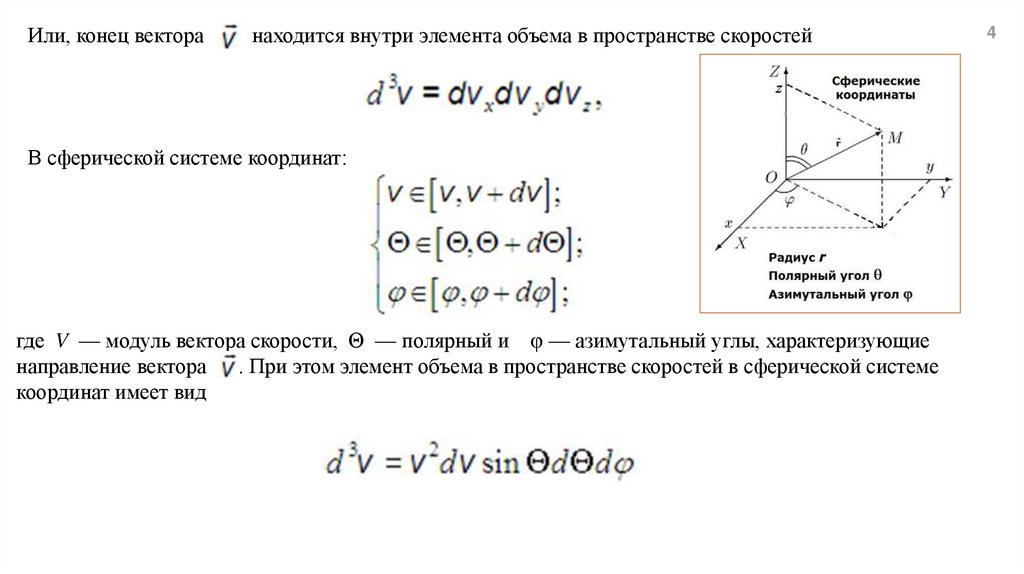
Или, конец вектора
находится внутри элемента объема в пространстве скоростей
В сферической системе координат:
где V — модуль вектора скорости, Θ — полярный и φ — азимутальный углы, характеризующие
направление вектора . При этом элемент объема в пространстве скоростей в сферической системе
координат имеет вид
4

5.

5
Обозначим ∆N — число молекул, имеющих вектор скорости в интервале от
до
, тогда это
число зависит от:
общего числа молекул N в системе;
величины объема в пространстве скоростей
(интервала
);
значения самого вектора скорости
(так как при одинаковых по величине элементах объема,
но при разных его положениях в пространстве скоростей, в общем случае, число частиц будет
различным).
Таким образом,
В состоянии термодинамического равновесия распределение молекул по направлениям движения
изотропное. Т.е. функция ∆N зависит только от модуля вектора скорости и не зависит от его направления.
Следовательно:

6.

При достаточно малых величинах объема
, число молекул в нём (число молекул с вектором
скорости, принадлежащем этому объёму) будет пропорционально его величине, то есть
где
- это концентрация частиц в пространстве скоростей, а при стремлении объема в
пространстве скоростей
к нулю,
Но, чем больше частиц в системе, тем «при прочих равных условиях» будет больше частиц и в объеме
и их концентрация
.
Поэтому, от концентрации частиц можно перейти к удельной величине не зависящей от полного числа
частиц в системе
- это относительное количество (долю) молекул, имеющих скорость в единичном объеме в пространстве
скоростей вблизи скорости с модулем
. Эта функция F(V) называется функцией
распределения молекул для вектора скорости.
6

7.

Зная вид функции F(V), можно найти количество молекул dN из общего числа молекул N, проекции
вектора скорости которых одновременно принадлежат интервалам
Это число равно
или, при использовании сферических координат в пространстве скоростей,
Причем, это распределение вероятностей для вектора скорости, то есть сразу для трех величин:
либо для
либо для
, в зависимости от используемой в пространстве
скоростей системы координат…
7

8.

8
Т.е. условие нормировки функции распределения
В декартовой системе:
В сферических координатах

9.

2. Распределение Максвелла.
9
Поскольку все направления движения молекул в пространстве равноправны, распределение
скоростей должно быть изотропным и функция распределения n(v) не может зависеть от направления
скорости. Это означает, что n(v) не может быть произвольной функцией от компонент
скорости vх, vy, vz, а должна зависеть лишь от абсолютной величины скорости
В зависимости от выбранной системы координат вероятность
В декартовой системе
В сферической системе
имеет различный вид.

10.

Число столкновений молекул, движущихся со скоростями v1 и v2 в единицу времени в единице
объема ⁓ n(v1)·n(v2).
Число соударений молекул, движущихся со скоростями v3 и v4 в единицу времени в объеме
пропорционально количеству молекул со скоростями вблизи v3 и v4, то есть n(v3)·n(v4).
Взяв логарифм, получим
Продифференцируем по аргументу v1:
Аналогично
10

11.

Учитывая полученное выражение для v4 , находим
Подставляя в правые части предыдущих соотношений, приходим к равенству
где А — постоянная интегрирования.
11

12.

Постоянная А определяется из условия нормировки
а параметр α должен быть связан с абсолютной температурой T соотношением
Объединяя последние выражения получим искомое распределение молекул по скоростям.
12

13.

Учитывая, что n(v) зависит только от модуля скорости, а их направления равновероятны, можно
ввести функцию распределения f(v) молекул по абсолютной величине скорости. Для этого надо
проинтегрировать выражение
13
по углам, что дает
Отсюда следует выражение для функции распределения Максвелла для модуля вектора
скорости f(v):
Величина f(v)dv есть вероятность найти частицу с модулем скорости, лежащим в интервале
от v до v + dv. Условие нормировки распределения f(v) принимает теперь вид

14.

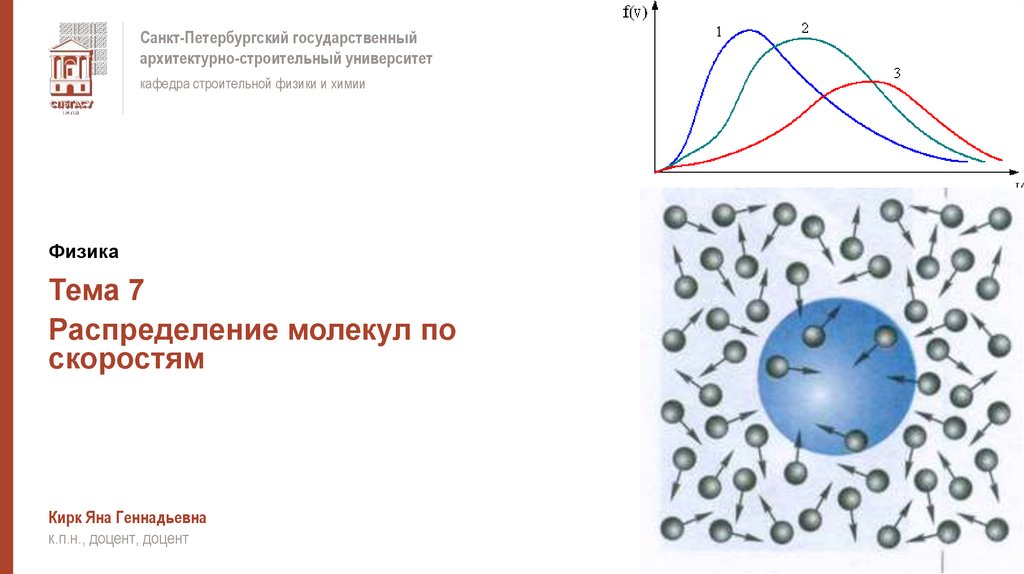
3. Характерные скорости молекул
Распределения f(v) молекул кислорода O2 по абсолютным величинам скоростей при температурах
Т1 = 300 К и Т2 = 1 300 К.
…Наиболее вероятная скорость vВЕР — это скорость, отвечающая
максимальному значению функции распределения.
Ее можно найти, решая уравнение
откуда следует, что
14

15.

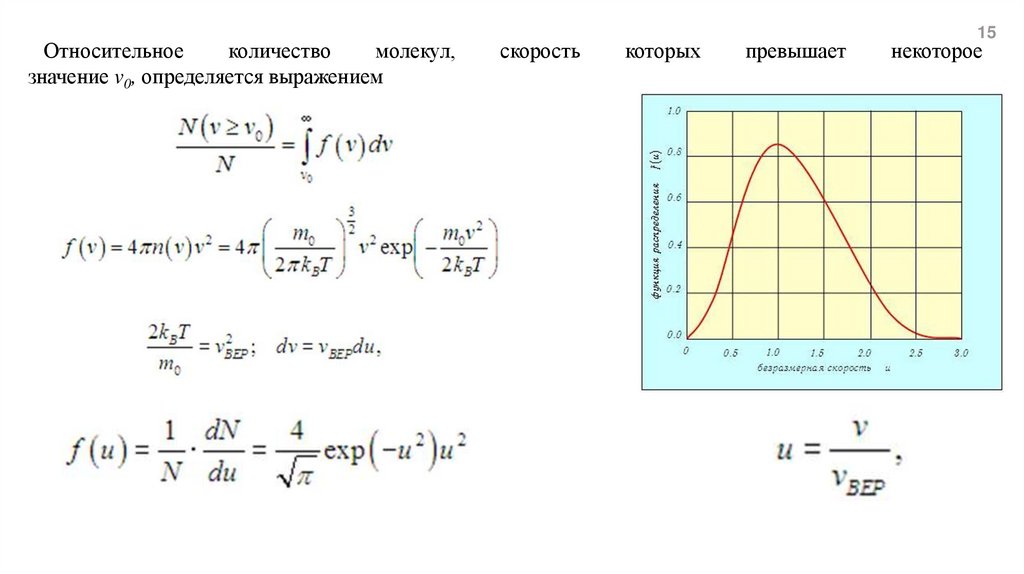
Относительное
количество
молекул,
значение v0, определяется выражением
скорость
которых
превышает
15
некоторое

16.

Средняя арифметическая скорость <v> — это отношение суммы абсолютных величин скоростей всех
молекул в системе к числу этих молекул.
Разобьем интервал всех возможных значений скорости от 0 до бесконечности на малые интервалы ∆vi.
Каждому интервалу соответствует количество молекул
Так как интервалы ∆ vi, малы, то можно приближенно считать скорости молекул данного интервала
одинаковыми и равными vi. Сумма значений скоростей молекул интервала
Сумма значений скоростей всех молекул
Разделив эту сумму на число молекул, получим выражение для средней арифметической скорости
Переходя от суммы к интегралу, получаем
Вычисляя интеграл, получаем среднюю арифметическую скорость молекул
16

17.

Среднеквадратичная скорость — это корень квадратный из среднего значения квадрата скорости17
молекул
В частности, при L(v) = v отсюда находится <v>.
Среднее значение квадрата скорости равно отношению суммы квадратов скоростей всех молекул
системы к общему числу молекул. Таким образом,

18.

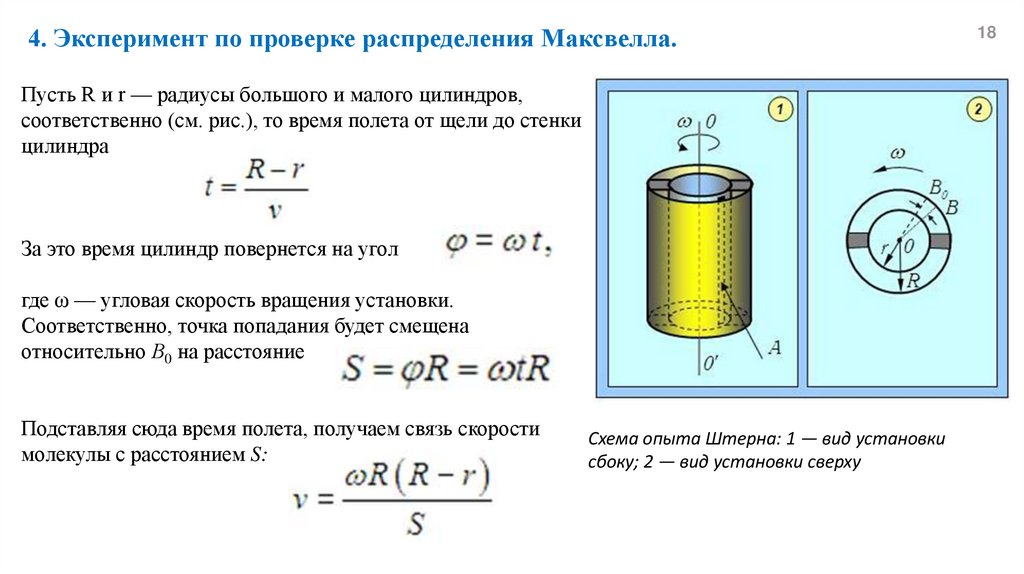
4. Эксперимент по проверке распределения Максвелла.
Пусть R и r — радиусы большого и малого цилиндров,
соответственно (см. рис.), то время полета от щели до стенки
цилиндра
За это время цилиндр повернется на угол
где ω — угловая скорость вращения установки.
Соответственно, точка попадания будет смещена
относительно В0 на расстояние
Подставляя сюда время полета, получаем связь скорости
молекулы с расстоянием S:
Схема опыта Штерна: 1 — вид установки
сбоку; 2 — вид установки сверху
18

19.

Подставляя, в свою очередь, полученное выражение в распределение Максвелла и учитывая, что
находим распределение молекул по расстояниям S:
(мы опускаем выражение для нормировочной постоянной С).
Опыты Штерна подтвердили справедливость закона, установленного Максвеллом.
19

20.

5. Распределение молекул по координатам
20
Барометрическая формула - закон, по которому изменяется
давление атмосферы (или плотность воздуха) по мере удаления от
поверхности Земли.
Пусть на высоте h давление р, тогда на высоте h + dh давление р +
dp (рис.). При этом, если dh > 0, то давление уменьшается, dp < 0,
так как уменьшается вес вышележащих слоев атмосферы.
Выделенный слой газа, высотой dh и массой m, находится в
равновесии. Следовательно, сумма действующих на него сил равна
нулю:
В проекции на вертикальную ось получаем
где ρ — плотность газа на высоте h.
Вертикальный воздушный цилиндр

21.

Раскрывая скобки и приводя подобные члены,
переходим к уравнению
21
Воспользуемся уравнением Клапейрона —
Менделеева для выделенной массы газа m и выразим
плотность через давление:
Объединяя данные выражения, окончательно
получаем
Это уравнение можно проинтегрировать в случае
изотермической атмосферы (Т = const):
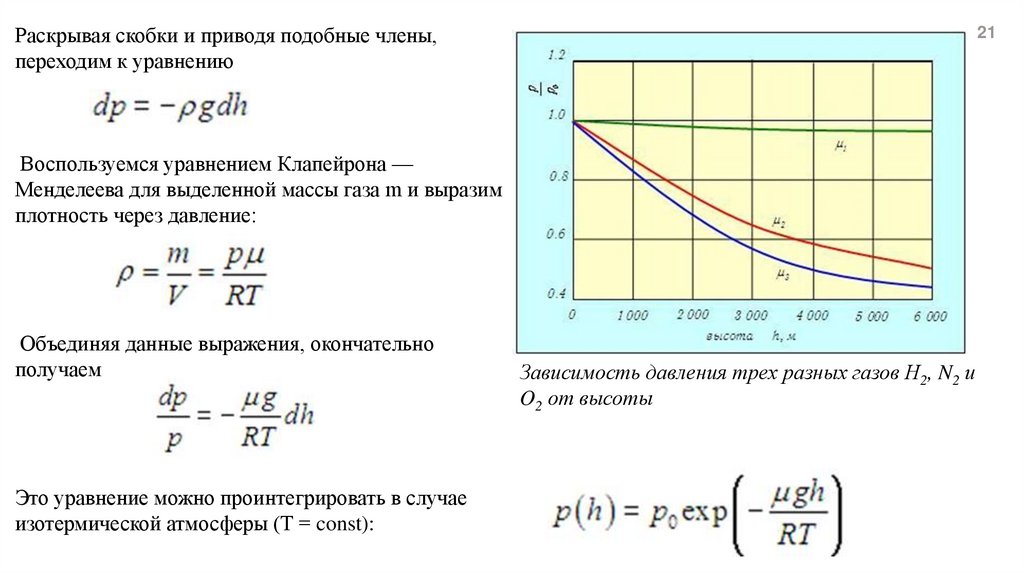
Зависимость давления трех разных газов Н2, N2 и
O2 от высоты

22.

Используя уравнение идеального газа в форме
из барометрической формулы легко получить закон изменения с высотой числа n молекул в единице
объема:
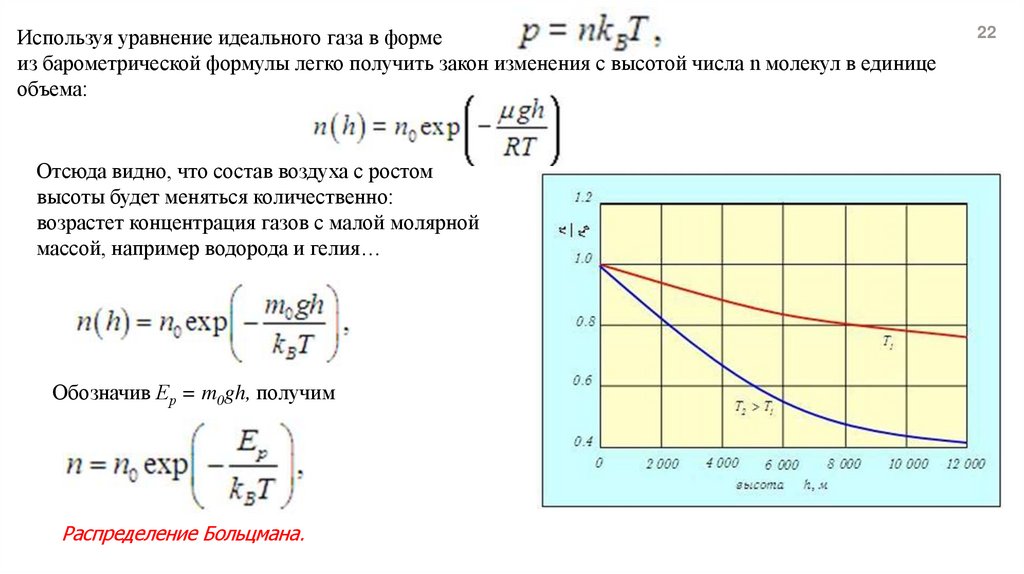
Отсюда видно, что состав воздуха с ростом
высоты будет меняться количественно:
возрастет концентрация газов с малой молярной
массой, например водорода и гелия…
Обозначив Ер = m0gh, получим
Распределение Больцмана.
22

23.

6. Распределение Максвелла — Больцмана
23
Рассмотрим бесконечно малый объем dV газа, расположенный в точке с радиусом-вектором
в большой
системе, представляющей идеальный газ при постоянной температуре и во внешних силовых полях. Число
молекул в выделенном объеме есть n(
) d3r. Для числа молекул dN, имеющих скорости от v до v + dv и
находящихся в объеме d3r, в результате объединения зависимостей, получаем следующую формулу:
где n0 — концентрация молекул в точке, где Еp = 0.
Тогда
поскольку выражение
представляет собой полную энергию частицы во внешнем потенциальном силовом поле, мы приходим к
обобщенному распределению Максвелла — Больцмана по энергиям молекул:
где N — полное число частиц в системе, a dN — число частиц с координатами между r и r + dr и
(одновременно) со скоростями между v и v + dv.

24.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра строительной физики и химии
Авторы:
Кирк Яна Геннадьевна
sfh@spbgasu.ru