Статистическая физика. Термодинамика

1. Раздел II Статистическая физика Термодинамика  

Раздел II
Статистическая физика
Термодинамика
1

2. Молекулярно-кинетическая теория Статистическая физика

ВоГУ
Лекция 6
Молекулярно-кинетическая теория
Статистическая физика
Кузина Л.А.,
к.ф.-м.н., доцент
2015 г.
2

3. План

3

4.

Молекулярная физика изучает строение и свойства вещества
Молекулярно-кинетическая теория (МКТ) исходит из
молекулярно-кинетических представлений:
1) все вещества состоят из молекул (атомов);
2) молекулы (атомы) находятся в непрерывном движении;
3) молекулы взаимодействуют между собой.
Экспериментальные доказательства
молекулярно-кинетических представлений:
1) Броуновское движение
2) диффузия

5.

Методы исследований:
1) статистический
метод основан на том, что свойства
макросистем, состоящих из большого
числа микрочастиц, определяются
усреднёнными значениями
характеристик этих микрочастиц
(например, скоростей, энергий)
2) термодинамический
Термодинамика изучает общие свойства
макросистем, находящихся в состоянии
термодинамического равновесия, и процессы
перехода между состояниями.
В основе термодинамики лежат 3 закона (начала)
термодинамики, основанных на опыте.

6.

Основные понятия (определения)
Система – это любая мысленно выделенная совокупность тел
Окружающая среда
– это всё, что не входит в систему
Параметры
(термодинамические переменные) – переменные,
определеляющие состояние системы в
термодинамике – температура, давление, объём
Экстенсивные
зависят от количества вещества (V, m,
Интенсивные
не зависят от количества вещества (T, p)
Уравнение состояния – уравнение вида: f(p,V,T)=0,
связывающее параметры системы
m
)

7.

Молекулярно-кинетическая теория идеального газа.
Уравнение состояния
Газ идеальный, если
1) Собственным объёмом молекул можно пренебречь по
сравнению с объёмом сосуда.
2) Взаимодействием молекул между собой можно
пренебречь.
3) Столкновения молекул между собой и со стенками сосуда
– абсолютно упругие.
При нормальных условиях ( T=273 К, p= 105 Па)
газ можно считать идеальным

8.

Законы идеального газа, найденные опытным путём:
1) Закон Бойля-Мариотта (T=const)
изотермический процесс
pV const
2) Закон Гей-Люссака (p=const)
изобарический процесс
V
const
T
3) Закон Шарля (V=const)
изохорический процесс p
T
const

9.

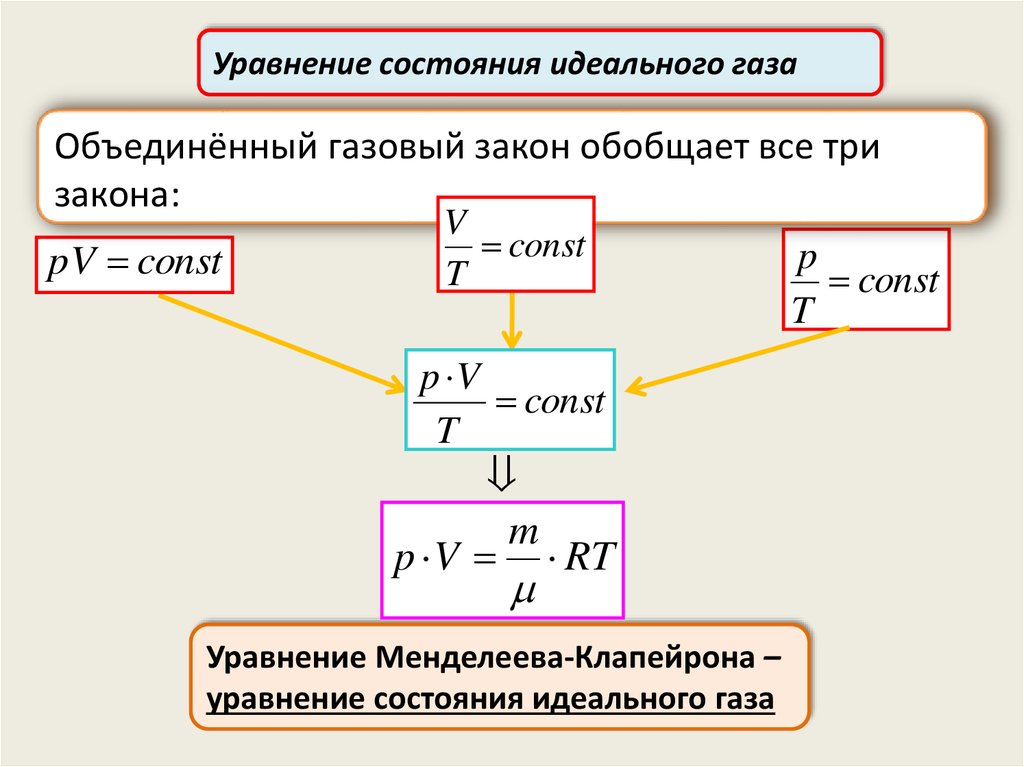
Уравнение состояния идеального газа
Объединённый газовый закон обобщает все три
закона:
pV const
V
const
T
p V
const
T
p V
m
RT
Уравнение Менделеева-Клапейрона –
уравнение состояния идеального газа
p
const
T

10.

Уравнение состояния идеального газа
Закон Авогадро: В одном моле любого вещества содержится
одинаковое число молекул (атомов), равное числу Авогадро NА
m RT m0 N RT N R
p
T n k T
V
m0 N А V
V NА
m m0 N масса
m0 N А молярная масса
p V
m
RT
p n k T
R
k
постоянная
NА
Больцмана
N
n
V
концентрация

11.

Давление смеси газов
Парциальное давление – это давление, которое оказывал
бы данный газ в отсутствие других газов при тех же условиях
Закон Дальтона: давление смеси газов равно сумме
парциальных давлений всех входящих в смесь газов:
p pi
Доказательство:
i
p n k T ni kT ni kT pi
i
i
i
Закон Паскаля: давление в любой точке покоящегося газа
одинаково по всем направлениям и одинаково передаётся
по всему объёму

12.

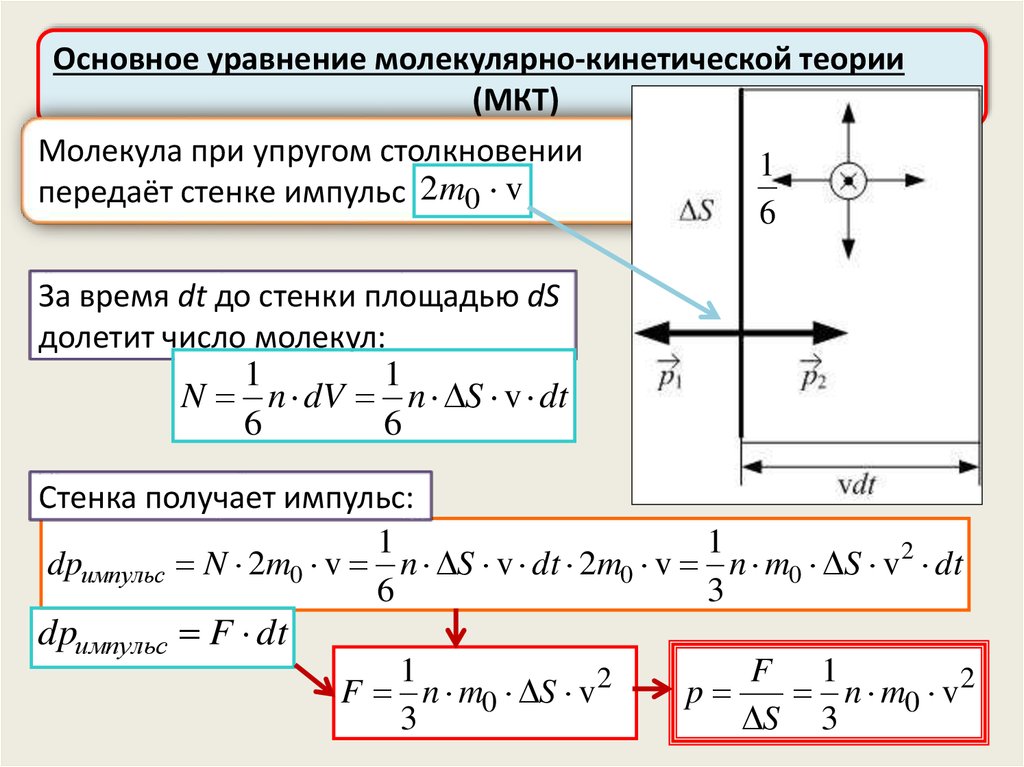
Основное уравнение молекулярно-кинетической теории
(МКТ)
Давление газа на стенку – результат передачи стенке импульса
молекулами при упругих соударениях со стенкой
Предположения:
1) все молекулы имеют
одинаковые скорости v
2) молекулы могут двигаться
только в трёх взаимно
перпендикулярных
направлениях – либо
параллельно стенке, либо
перпендикулярно ей
1
6

13.

Основное уравнение молекулярно-кинетической теории
(МКТ)
Молекула при упругом столкновении
1
передаёт стенке импульс 2m0 v
6
За время dt до стенки площадью dS
долетит число молекул:
1
1
N n dV n S v dt
6
6
Стенка получает импульс:
1
1
dpимпульс N 2m0 v n S v dt 2m0 v n m0 S v2 dt
6
3
dpимпульс F dt
1
F n m0 S v2
3
F 1
p
n m0 v 2
S 3

14.

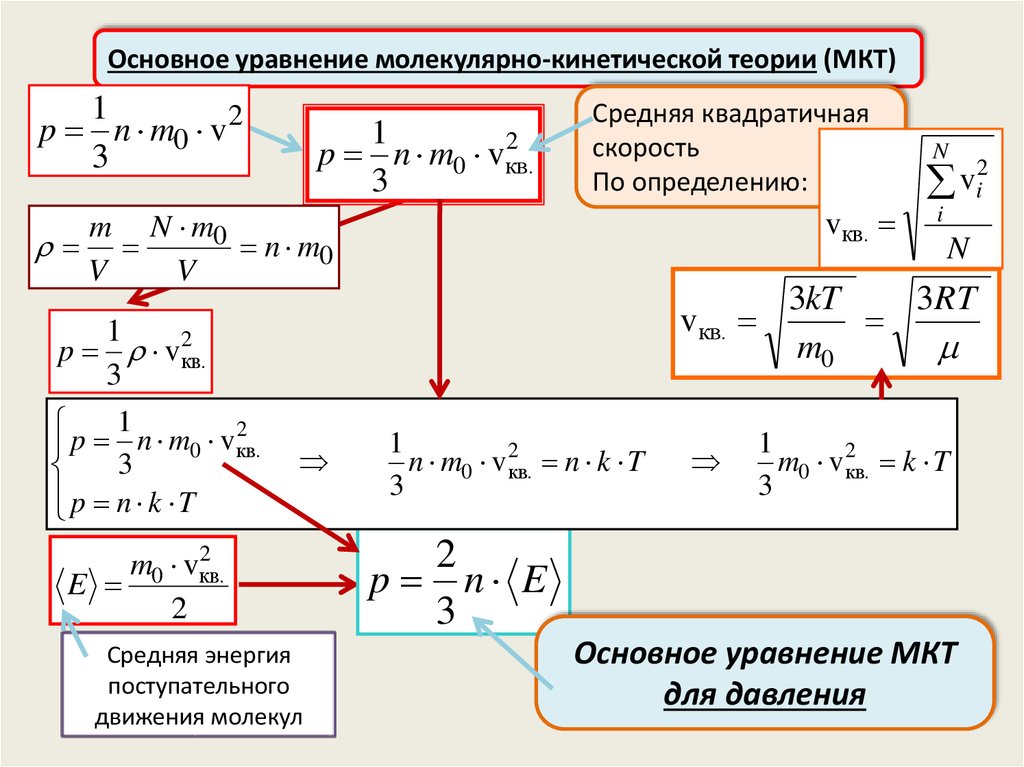
Основное уравнение молекулярно-кинетической теории (МКТ)
1
p n m0 v 2
3
1
2
p n m0 vкв.
3
Средняя квадратичная
скорость
По определению:
vкв.
m N m0
n m0
V
V
1
2
p vкв.
3
1
2
p n m0 v кв.
3
p n k T
2
m0 vкв.
E
2
Средняя энергия
поступательного
движения молекул
N
2
v
i
i
N
3kT
3RT
vкв.
m0
1
2
n m0 v кв.
n k T
3
1
2
m0 vкв.
k T
3
2
p n E
3
Основное уравнение МКТ
для давления

15.

Основное уравнение молекулярно-кинетической теории (МКТ)
2
p
n E
3
p n k T
2
n E n k T
3
2
E k T
3
3
E k T
2
Основное уравнение МКТ для температуры
Отсюда
смысл абсолютной температуры: при абсолютном
нуле (T=0 К) прекращается тепловое движение молекул, →
абсолютный нуль недостижим. Этим соотношением можно
ввести понятие (определение) абсолютной температуры T

16.

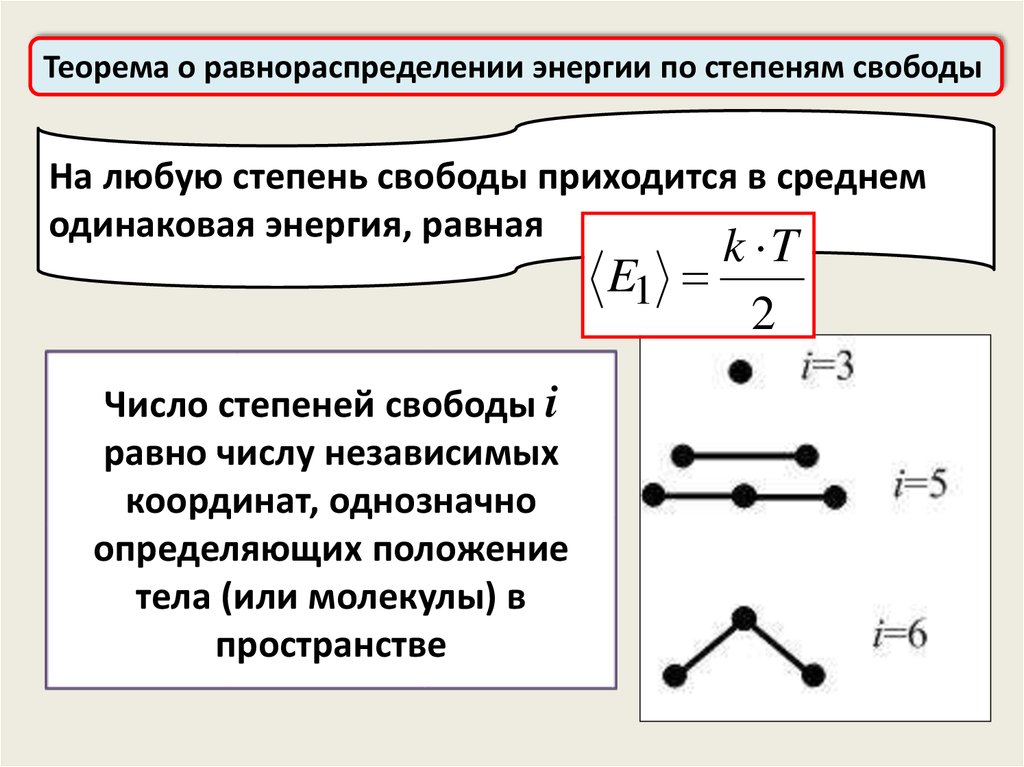
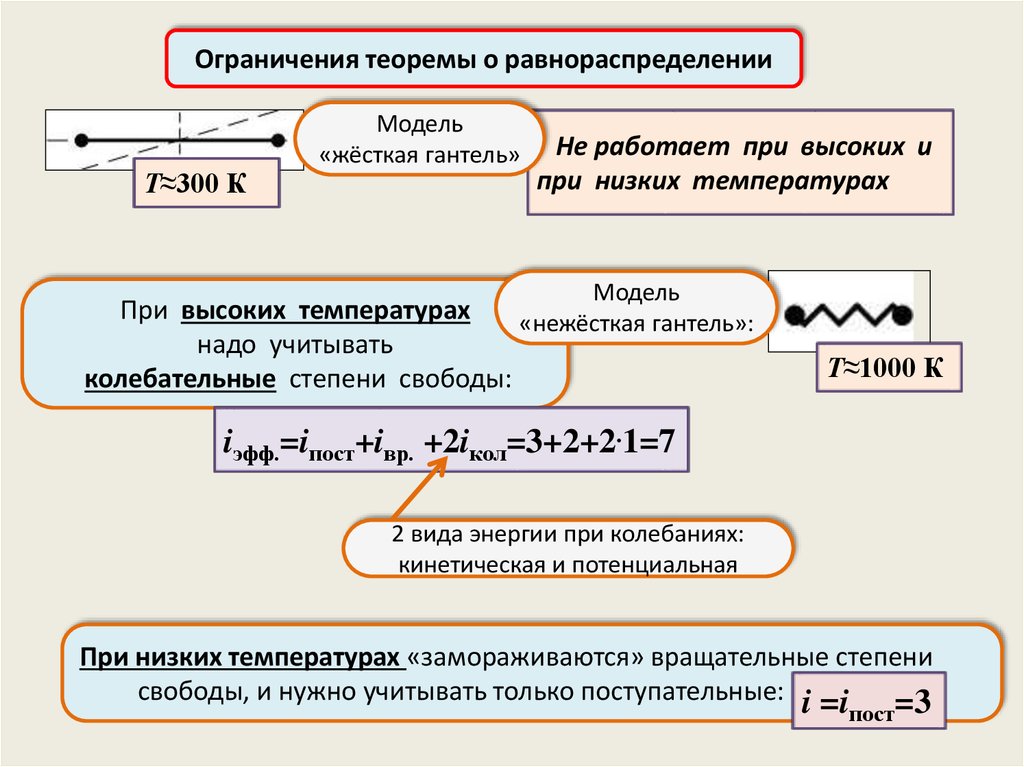
Теорема о равнораспределении энергии по степеням свободы
На любую степень свободы приходится в среднем
одинаковая энергия, равная
k T
E1
2
Число степеней свободы i
равно числу независимых
координат, однозначно
определяющих положение
тела (или молекулы) в
пространстве

17.

Число степеней свободы
Одноатомные:
i =iпост=3 (3 координаты - x, y, z)
Двухатомные:
i=iпост+iвр.=3+2=5
(3 координаты центра масс и
2 угловых;
одна из осей неактивна)
Модель
«жёсткая гантель»
Многоатомные нелинейные и абсолютно
твёрдое тело:
i=iпост+iвр.=3+3=6
(3 координаты центра масс и 3 угловых)
iэфф.=iпост+iвр. +2iкол=3+2+2.1=7
2 вида энергии при колебаниях:
кинетическая и потенциальная

18.

Ограничения теоремы о равнораспределении
Т≈300 К
Модель
«жёсткая гантель»
При высоких температурах
надо учитывать
колебательные степени свободы:
Не работает при высоких и
при низких температурах
Модель
«нежёсткая гантель»:
Т≈1000 К
iэфф.=iпост+iвр. +2iкол=3+2+2.1=7
2 вида энергии при колебаниях:
кинетическая и потенциальная
При низких температурах «замораживаются» вращательные степени
свободы, и нужно учитывать только поступательные: i =i
=3
пост

19.

Внутренняя энергия идеального газа
На одну степень свободы:
k T
E1
2
Средняя энергия молекулы с i степенями свободы:
Eмол.
i
k T
2
Суммарная энергия N молекул идеального газа:
N i k T N А k i T i N А k T
i
U N E1
RT
2
2
2
2
Внутренняя энергия идеального газа – суммарная кинетическая энергия всех
молекул; потенциальная энергия взаимодействия молекул не учитывается
Внутренняя энергия U – суммарная кинетическая и потенциальная
энергия всех частиц: электронов в атомах, нуклонов в ядрах атомов и т.д.
Внутренняя энергия не включает энергию движения тела как
целого (движения центра масс и вращения тела как целого) и
потенциальную энергию тела во внешних полях

20.

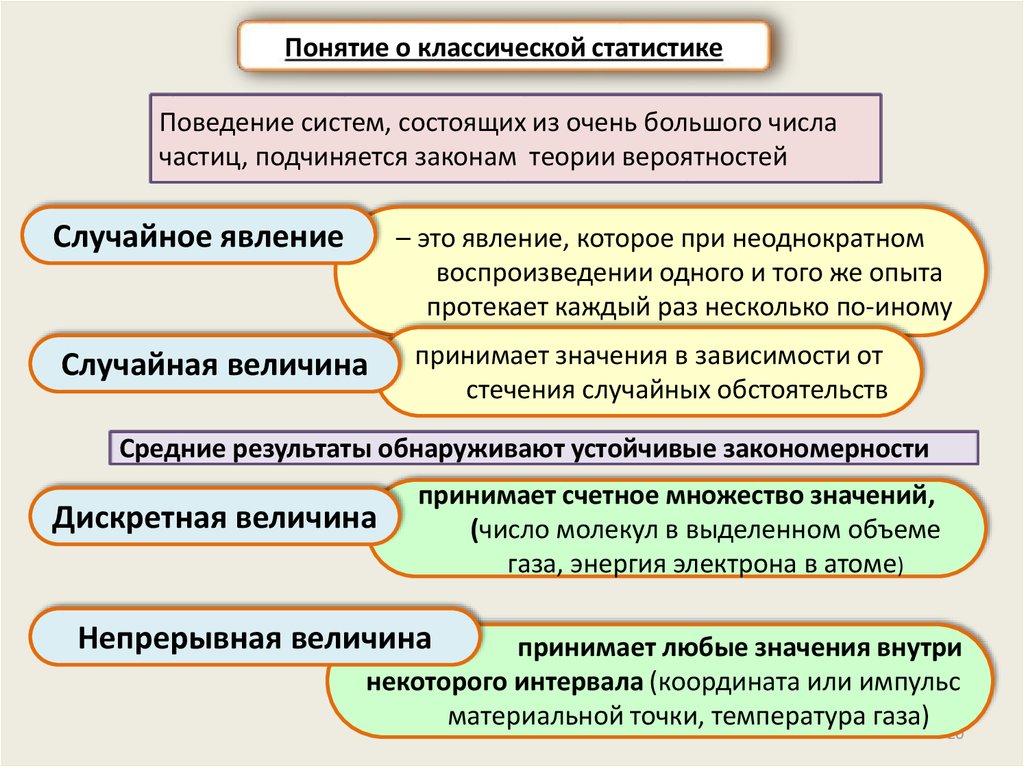
Понятие о классической статистике
Поведение систем, состоящих из очень большого числа
частиц, подчиняется законам теории вероятностей
Случайное явление
– это явление, которое при неоднократном
воспроизведении одного и того же опыта
протекает каждый раз несколько по-иному
Случайная величина
принимает значения в зависимости от
стечения случайных обстоятельств
Средние результаты обнаруживают устойчивые закономерности
Дискретная величина
принимает счетное множество значений,
(число молекул в выделенном объеме
газа, энергия электрона в атоме)
Непрерывная величина
принимает любые значения внутри
некоторого интервала (координата или импульс
материальной точки, температура газа)
20

21.

Пусть имеется макросистема, то есть система,
состоящая из большого числа микрочастиц
Пусть случайная дискретная величина х может
принимать значения х1, х2, х3, ….
Произведем N измерений величины х, приводя систему
каждый раз перед измерением в одно и то же состояние
Или: вместо того, чтобы производить N измерений над одной системой,
можно взять N одинаковых систем и измерять величину х один раз
в каждой системе
Статистический ансамбль
(статансамбль)
– это набор одинаковых
систем, находящихся в
одинаковом состоянии
21

22.

Вероятность
значение х1 – в N1 измерениях
х2 – в N2
При измерениях получаем:
х3 – в N3
……..
Полное число измерений:
N
i
N
i
Частота появления i-того результата:
Ni
N
Ni
Вероятность – это предел частоты: pi lim N
Условие
нормировки:
pi 1
i
N

23.

Среднее арифметическое значение
N i xi
дискретной случайной величины x i
x pi xi
i
0≤р≤1
р=0 для невозможного события
р=1 для достоверного события
N
pi lim
Ni
N
N
Два события несовместны
если их одновременное осуществление
невозможно (например, выпадение 1 и 3 при
однократном бросании игральной кости).
Два события независимы
если наступление одного из них не
влияет на вероятность наступления второго
23

24.

.
Закон сложения вероятностей
Вероятность появления одного (безразлично какого) события из
нескольких несовместных событий равна сумме их вероятностей:
р(хi или хj)= р(хi)+ р(хj)
Пример: при бросании игральной
кости вероятность выпадения
чётного числа
1 1 1 1
p(2 или 4 или 6)
6 6 6 2
Закон умножения вероятностей
Вероятность совместного появления независимых
событий равна произведению их вероятностей:
р(хi и хj)= р(хi) р(хj)
Пример: при бросании двух игральных костей
вероятность получить 12 очков
1 1 1
p(6 и 6)
6 6 36

25.

.
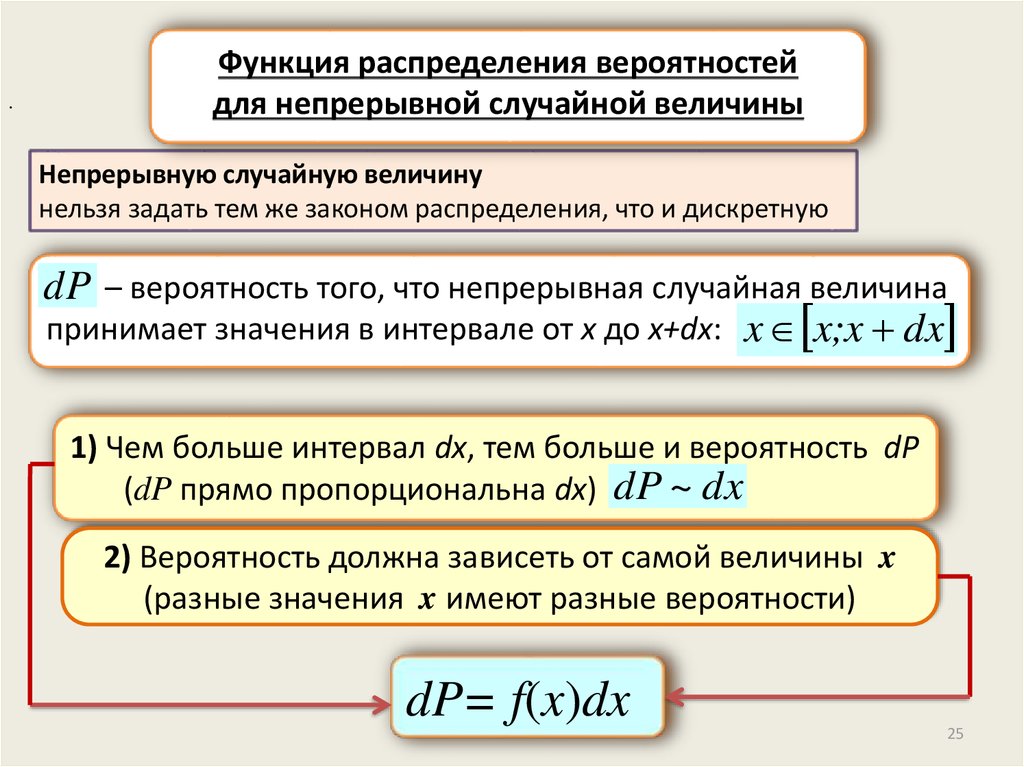
Функция распределения вероятностей
для непрерывной случайной величины
Непрерывную случайную величину
нельзя задать тем же законом распределения, что и дискретную
dP – вероятность того, что непрерывная случайная величина
принимает значения в интервале от x до x+dx: x x;x dx
1) Чем больше интервал dx, тем больше и вероятность dP
(dP прямо пропорциональна dx) dP ~ dx
2) Вероятность должна зависеть от самой величины x
(разные значения x имеют разные вероятности)
dP= f(x)dx
25

26.

dP= f(x)dx
– вероятность того, что величина
x x;x dx
.
dP
f ( x)
dx
– функция распределения вероятностей
b
Вероятность того,
Pa,b f ( x)dx что величина принимает
a
какое-либо значение в
интервале от a до b:
x a;b
f ( x)dx 1
по области
определения
функции
Условие нормировки:
Площадь под графиком функции равна 126

27.

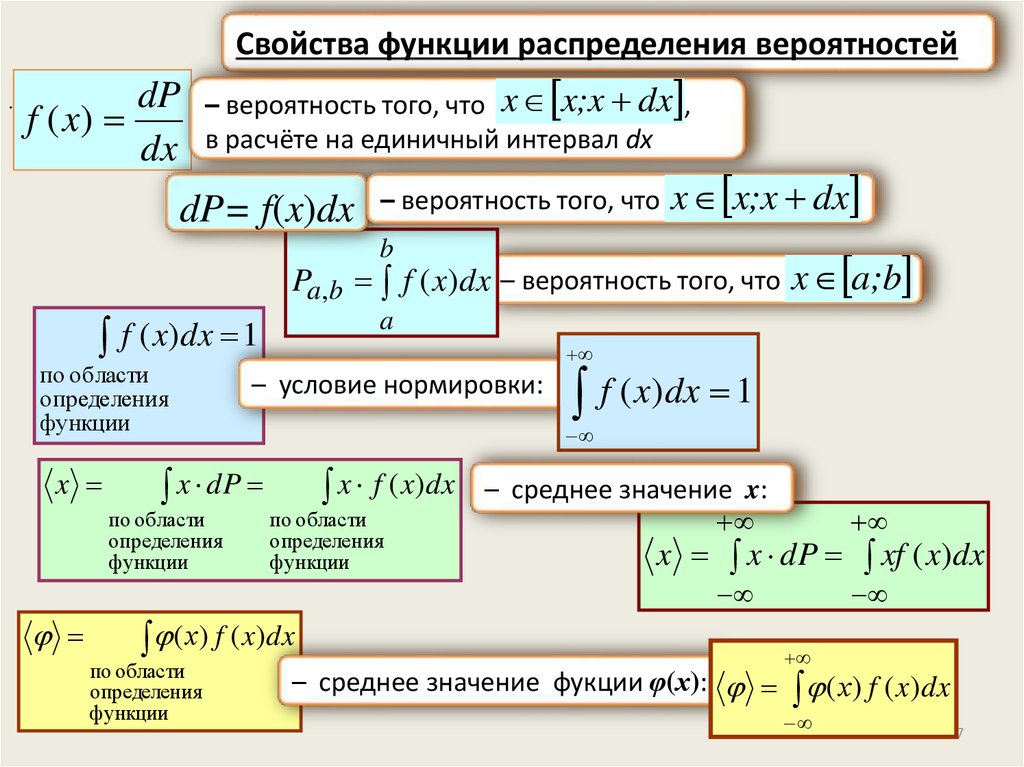
Свойства функции распределения вероятностей
.
dP
f ( x)
dx
– вероятность того, что x x;x dx ,
в расчёте на единичный интервал dx
dP= f(x)dx
– вероятность того, что
x x;x dx
b
Pa,b f ( x)dx – вероятность того, что x a;b
по области
определения
функции
x
a
f ( x)dx 1
– условие нормировки:
x dP
по области
определени я
функции
f ( x)dx 1
x f ( x)dx
по области
определени я
функции
– среднее значение x:
x x dP xf ( x)dx
( х) f ( x)dx
по области
определени я
функции
– среднее значение фукции φ(х): ( х) f ( x)dx
27

28.

Распределение Максвелла. Постановка задачи
.
Рассмотривается газ, находящийся в состоянии равновесия
Все направления скорости равновероятны, а сами скорости – различны
N – число молекул газа (велико, но конечно)
ΔN – число молекул со скоростями v v; v v
N – доля молекул со скоростями v v; v v ;
Pv
N вероятность, что скорость
1) чем больше интервал Δv, тем больше ΔN
2) ΔN зависит от самой скорости v, так как
значения скорости не являются
равновероятными
3) чем больше полное число молекул N, тем
больше ΔN
N f v N v
N
f ( v) v
N
28

29.

Смысл функции распределения
.
N
f ( v) v
N
В пределе
dN
dPv
f ( v) dv
N
dN
f ( v)
N dv
Функция распределения f(v) численно равна доле
молекул (вероятности) того, что молекула
имеет скорость в промежутке v v; v v ,
в расчёте на единичный интервал скоростей
29

30.

Распределение по компонентам (проекциям) скоростей
.
dN v x
dPv x
– число молекул, проекции скорости которых на ось ОХ лежат в
интервале от vх до vх+dvх
dN v x
N
– доля молекул, проекции скорости
x ( v x ) dv x которых на ось ОХ лежат в интервале
от vх до vх+dvх (или вероятность) –
пропорциональна величине
интервала dvх и зависит от vх
Коэффициент пропорциональности х есть функция
распределения по компонентам скоростей
1
m v2
2
m
0
Максвелл показал, что v
0 x
exp
x x
2kT
2 kT
30

31.

1
2
2
m
m
v
0
0 x
x v x
exp
2kT
2 kT
.
Нормировка:
x v x dv x 1
Все направления
скорости
равновероятны
m v2
m0 2
0 y
y vy
exp
2kT
2
kT
1
1
m v2
m0 2
z v z
exp 0 z
2kT
2 kT
31

32.

Распределение по модулю скорости
.
По закону умножения вероятностей:
dPv x , v y , v z dPv x dPv y dPv z – вероятность того, что
dPv x x ( v x ) dv x
молекула одновременно имеет
компоненты скорости, лежащие в
интервалах: v x v x ; v x dv x
v y v y ; v y dv y
1
2
2
m
m
v
0
x v x
exp 0 x
2kT
2 kT
m0
dPv x , v y , v z
2 kT
3
2
v z v z ; v z dv z
m v2 v2 v2
0 x
y
z
exp
dv x dv y dv z
2kT
32

33.

Распределение по модулю скорости
.
2
2
2
m
v
v
v
0 x
y
z
m0 2
dPv x , v y , v z
dv x dv y dv z
exp
2kT
2 kT
3
v2x v2y v2z v2
3
m v2
m0 2
dPv x , v y , v z
exp 0 dv x dv y dv z
2kT
2 kT
33

34.

Распределение по модулю скорости
.
Рассматривается пространство скоростей:
каждой молекуле в нём соответствует точка
v2x v2y v2z v2
Вероятность
пропорциональна плотности
точек в v-пространстве
и элементу объёма dV
3
m v2
m0 2
dPv x , v y , v z
exp 0 dv x dv y dv z
2kT
2 kT
3
m v2
m0 2
2
dPv
exp 0 4 v dv – вероятность
2 kT
2kT
2
– объём сферического слоя
dV 4 v dv
v v; v v
34

35.

Распределение по модулю скорости
.
3
2
2
m
m
v
0 exp 0 4 v 2 dv
dPv
2kT
2 kT
dPv f ( v) dv
3
2
m
v
m0 2
2
f v
4 v exp 0 – это функция
2kT
2 kT
распределения по
скоростям Максвелла
35

36.

Распределение по модулю скорости
.
3
2
2
m
m
v
0 4 v 2 exp 0
f v
2kT
2 kT
График функции:
dPv f ( v) dv
T1
Нормировка:
f ( v) dv 1
0
T2>T1
Площадь под графиком равна 1 и не
изменится при изменении температуры
Наиболее вероятная скорость
36

37.

Наиболее вероятная скорость
.
соответствует максимуму функции:
df
0
dv
3
m v2
m0 2
2
f v
4 v exp 0
2kT
2 kT
3
2
2
m0 v
d m0
2
4
v
exp
0
2kT
dv 2 kT
m0 v 2
v 2 e 2kT 0
37

38.

Наиболее вероятная скорость
.
m0 v 2
2
2
m0 v m0 v
v 2 e 2kT 0 v 2 e 2kT e 2kT v 2 0
m0 v 2
m0 v 2
2 kT
2 kT m 2v 2
0
2v e
e
v 0
m0 v 2
2v
v 0
kT
2kT
m0 2
2
v
kT
2kT
vвер.
m0
38

39.

Характерные скорости молекул
.
Наиболее вероятная
2kT
2 RT
vвер.
m0
Средняя арифметическая
N
v v f v d v
vi
v i 1
v i2
v 2 i 1
0
N
N
8kT
8RT
v
m0
Средняя квадратичная
N
v
2
vкв.
3kT
v f v d v
m0
0
2
v2
vкв.
3kT
3RT
m0
39

40.

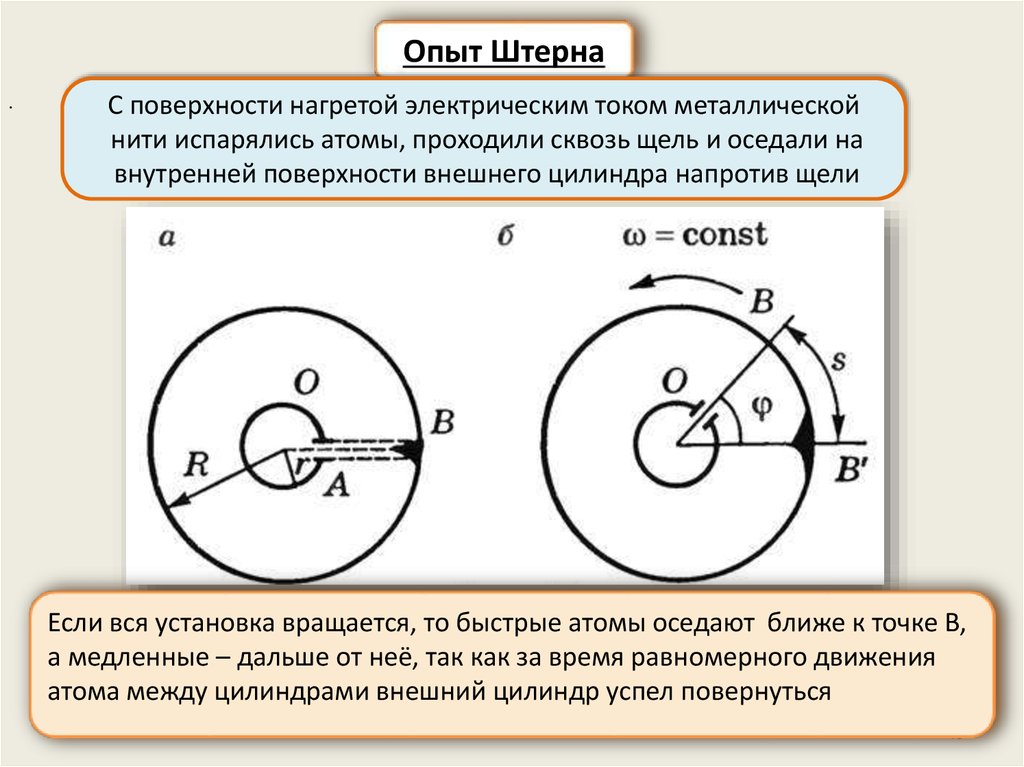
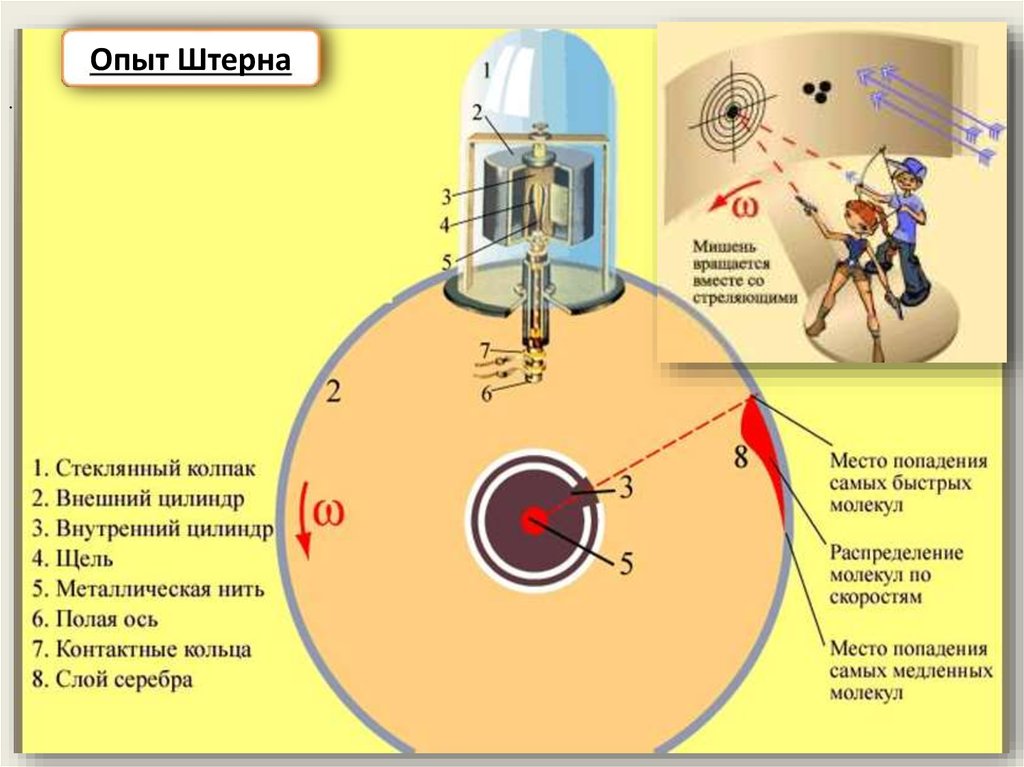
Опыт Штерна
.
С поверхности нагретой электрическим током металлической
нити испарялись атомы, проходили сквозь щель и оседали на
внутренней поверхности внешнего цилиндра напротив щели
Если вся установка вращается, то быстрые атомы оседают ближе к точке В,
а медленные – дальше от неё, так как за время равномерного движения
атома между цилиндрами внешний цилиндр успел повернуться
40

41.

Опыт Штерна
.
41

42.

Распределение по энергиям
.
dN – число молекул с энергиями E∈[E ;E+dE]
dNE
dPE
f(E) dE
N
m0 v 2
E
2
dv
dE
– доля молекул с такими энергиями
(вероятность, что E∈[E ;E+dE] )
dN E dN v
1
2 1 2
E
m0 2
f E dE f v dv
dv
f E f v
dE
1
2 Em0
f E f v
m0 v 2
3
2
2 2kT
4 v e
dv m0
dE 2 kT
f E kT 2
3
2
1
2 Em0
E
E e kT
42

43.

Газ в поле тяготения. Барометрическая формула
.
Молекулы воздуха в атмосфере Земли распределены неравномерно.
В результате действия двух конкурирующих факторов:
1) теплового движения
(в результате теплового движения газ стремится
занять весь предоставленный объём)
2) притяжения Земли
устанавливается стационарное распределение молекул
по высоте
Давление газа с высотой уменьшается по некоторому закону.
Задача: найти этот закон p=f(h)
Предположения:
1) газ – идеальный (подчиняется уравнению
Менделеева-Клапейрона);
2) температура постоянна: T=const
3) поле тяготения однородно: g=const
43

44.

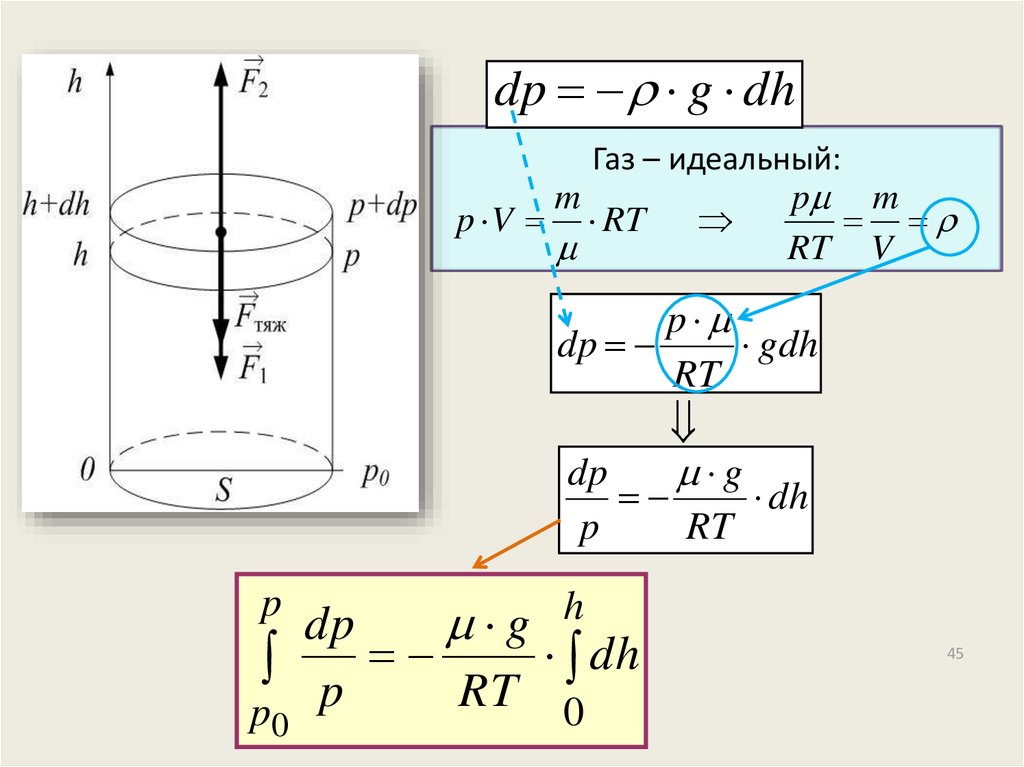
Газ в поле тяготения. Барометрическая формула
.
Рассмативается вертикальный столб газа,находящийся в равновесии
Сила давления снизу:
F2 pS
Сила давления сверху:
Сила тяжести:
F1 p dp S
Fтяж dm g
Fтяж dV g S dh g
F2 F1 mg 0
pS p dp S S dh g 0
dp dh g 0
dp g dh
44

45.

dp g dh
Газ – идеальный:
m
p m
p V RT
RT V
p
dp
gdh
RT
dp
g
dh
p
RT
p
h
g
dp
p RT dh
p0
0
45

46.

p
.
dp
g h
p RT dh
p
0
ln p ln p0
0
p
g
ln
h
p0
RT
g
RT
h
g
h
p
e RT
p0
m0 N m0
R k NА
k
p p0 e
g h
RT
m0 g h
m0 g h
kT
p p0 e
p0 exp
kT
46

47.

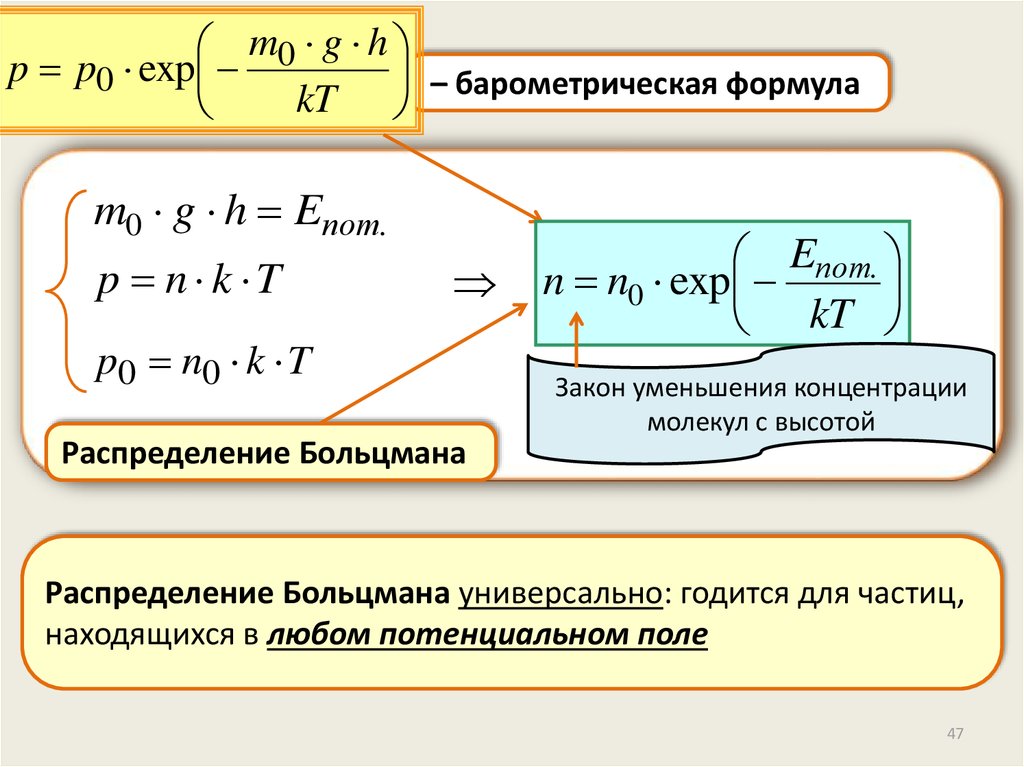
m0 g h
p p0 exp
– барометрическая формула
.
kT
m0 g h Eпот.
p n k T
p0 n0 k T
Eпот.
n n0 exp
kT
Закон уменьшения концентрации
молекул с высотой
Распределение Больцмана
Распределение Больцмана универсально: годится для частиц,
находящихся в любом потенциальном поле
47

48.

Распределение Больцмана
.
Eпот.
n n0 exp
kT
E пот.
n2
kT
e
n1
Смысл распределения Больцмана:
E по т.
e kT
Величина
показывает, во сколько раз отличаются
концентрации частиц в двух точках
потенциального поля, если их
потенциальные энергии отличаются на
E по т. E 2 E1
Знак «минус» означает, что концентрация больше в
тех точках, где потенциальная энергия меньше:
более вероятно состояние с меньшей потенциальной
энергией
48

49.

– это распределение частиц
по координатам, потому что
потенциальная энергия
зависит от координат
E
f
r
частицы:
п о т.
Распределение Больцмана
Eпот.
n n0 exp
kT
Вероятность
найти частицу в объёме dV вблизи точки
r ( x, y , z ) пропорциональна объёму и концентрации:
dPx, y, z
dN x, y, z
N
dPx, y , z ~ n dV
n( x, y, z ) dV
N
Eпот.
kT
e
dV
49

50.

Распределение Максвелла-Больцмана
dPx, y , z ~ n dV
Eпот.
kT
e
– вероятность того, что
dx dy dz
x x; x dx
y y; y dy
z z; z dz
dPv
x
,v y ,v z
Eкин.
kT
~ e
dv x dv y dv z
– вероятность того, что
v x v x ; v x dv x
v y v y ; v y dv y
v z v z ; v z dv z
Можно объединить распределения по скоростям и по координатам
По закону умножения вероятностей:
dN x, y , z , v
N
x
,v y ,v z
dPx, y , z , v
x
,v y ,v z
E - полная
Eкин Eпот.
kT
A e
dv x dv y dv z dxdydz
50

51.

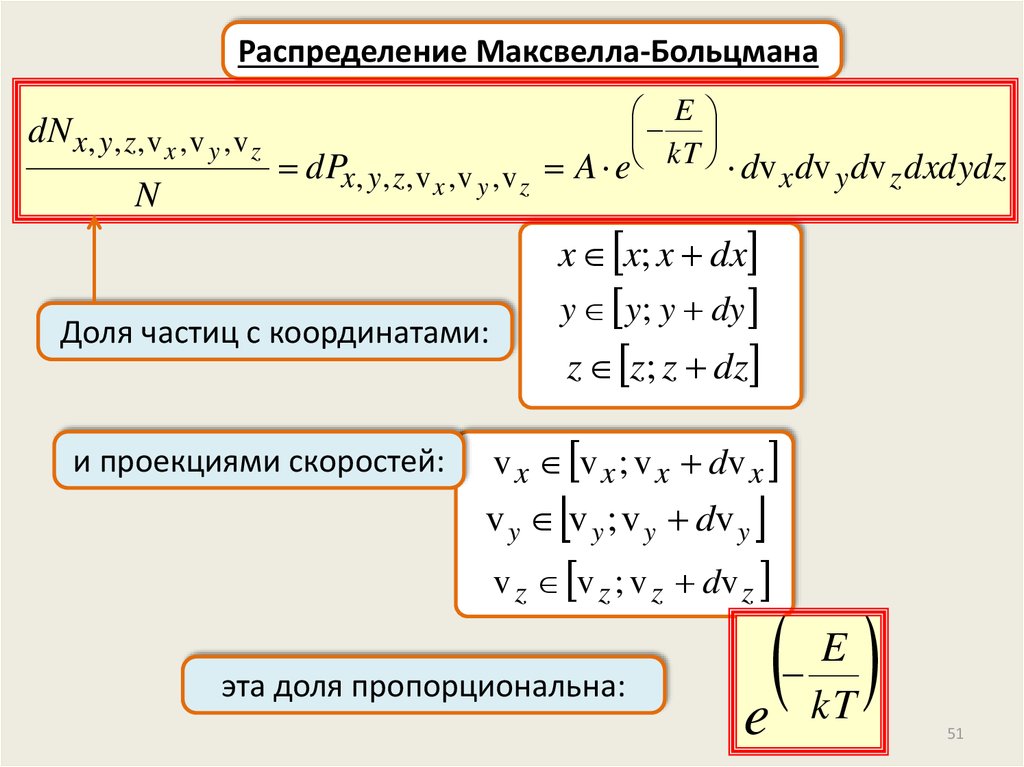
Распределение Максвелла-Больцмана
E
dN x, y, z , v x , v y , v z
dPx, y, z , v x , v y , v z A e kT dv x dv y dv z dxdydz
N
x x; x dx
Доля частиц с координатами:
и проекциями скоростей:
y y; y dy
z z; z dz
v x v x ; v x dv x
v y v y ; v y dv y
v z v z ; v z dv z
эта доля пропорциональна:
e
E
kT
51