Похожие презентации:
L10-11_Combined_Motion_2025_11_10-17
1.
Общая Физика. МеханикаЛекция 10
Механика твердого тела
Вращательное и комбинированное
движение
Лектор:
Профессор НИЯУ МИФИ
Ольчак Андрей Станиславович(
2.
Твердое тело. Формы движенияТвердое тело = протяженное тело, расстояние между любой парой
точек которого в процессе движения остается неизменными.
При поступательном движении твердого тела любая прямая,
соединяющая любую пару точек, принадлежащих телу, при движении
остается
φ параллельной самой себе. Для описания поступательного
движения достаточно следить за координатами одной (любой) точки,
принадлежащей телу (например, за его центром масс).
При вращении твердого тела вокруг фиксированной оси все его точки
движутся по окружностям с центрами на оси вращения. Достаточно
следить за одной координатой любой точки - углом поворота φ ее радиуса
вращения по отношению к некоторой опорной оси
Комбинированное движение: сочетание поступательного и
вращательного. Для его полного описания нужны три координаты
центра масс и, если учесть возможность изменения направления оси
вращени, от одной до трех угловых координат.
..
3.
Связь угловой и линейной скоростиУгловая скорость вращения ω = dφ/dt [с-1 ] вектор, направленный вдоль оси вращения по
правилу правого винта.
Связь угловой скорости вращения ω и линейной
скорости движения v точки, положение которой
задается радиус-вектором r:
v = [ω,r]; v = Rω
R – расстояние от точки до оси вращения (радиус
вращения)
При вращательном движении, линейная скорость точки
направлена по касательной к траектории движения (окружности).
Угловое ускорение: β = dω/dt
[рад/с2] = [с-2 ]
4.
Момент импульса и момент инерции вращающейся точкиМомент импульса точки отн. оси ОZ:
Mz = [R, p] = m[R[ω, R] = mω(R,R) – mR(R,ω) =
= mR2ω ; M || ω || 0Z ; ωz= dφ/dt
Mz = mR2ωz = Izωz ; Iz = mR2 – момент
инерции мат. точки массы m, для вращения
относительно оси 0Z . R – радиус вращения
5.
Момент инерции твердого телаосиМомент импульса каждой элементарной массы dmi относительно оси OZ
dMi = Ri dmi Riωz = ωzdmiRi2
Момент импульса всего тела
относительно оси OZ :
Mz = ωzΣdmiRi2 = ωzIz ,
Iz - момент инерции вращения
твердого тела относительно оси OZ
Переходя от суммы к интегрированию, вычисляем момент инерции
как интеграл по всему объему тела от плотности массы , которая в
разных точках может быть разной.:
Iz = Σ mi Ri2 = ∫ρ(r)r2dV
6.
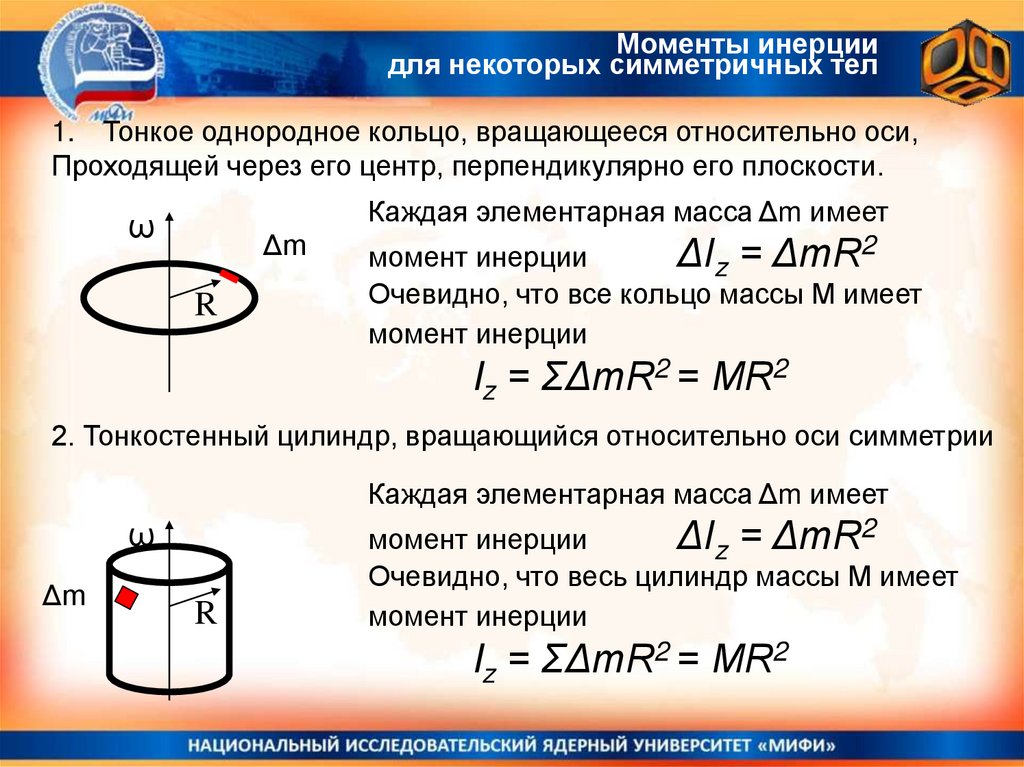
Моменты инерциидля некоторых симметричных тел
1. Тонкое однородное кольцо, вращающееся относительно оси,
Проходящей через его центр, перпендикулярно его плоскости.
Каждая элементарная масса Δm имеет
ω
Δm
R
момент инерции
ΔIz = ΔmR2
Очевидно, что все кольцо массы М имеет
момент инерции
Iz = ΣΔmR2 = МR2
2. Тонкостенный цилиндр, вращающийся относительно оси симметрии
Каждая элементарная масса Δm имеет
ω
Δm
R
момент инерции
ΔIz = ΔmR2
Очевидно, что весь цилиндр массы М имеет
момент инерции
Iz = ΣΔmR2 = МR2
7.
Моменты инерциидля некоторых симметричных тел
1. Материальная точка, вращающаяся
вокруг оси на расстоянии R от нее:
Iz = MR2
2. Кольцо и тонкостенный цилиндр, радиуса R,
вращающиеся вокруг оси симметрии
Iz = MR2
3. Однородный цилиндр радиуса R,
вращающийся вокруг оси симметрии
Iz = MR2/2
4. Тонкостенная сфера радиуса R,
вращающаяся вокруг оси симметрии
Iz = 2MR2/3
5. Однородный шар радиуса R,
вращающийся вокруг оси симметрии
Iz = 2MR2/5
6. Однородный тонкий стержень длины L,
вращающийся вокруг оси перпендикулярной ему
и проходящей через центр масс стержня
Iz = MR2/12
8.
Теоремаmi
Rci
C
Ri
o
a
Штайнера
Пусть нам известен момент инерции тела массы М
относительно оси, проходящей через центр масс С.
Найдем его момент инерции относительно
параллельной оси, проходящей через точку О,
отстоящую от С на расстояние а.
IО = ΣmiRi2 = Σmi(Rci + a)2 = ΣmiRci2 + 2aΣmiRci +(Σmi)a2
ΣmiRci2 = IС ; 2aΣmiRci = 0 ; (Σmi)a2 = Ма2
IО = IС + Ма2
Момент инерции тела относительно произвольной оси равен его моменту
инерции относительно параллельной оси, проходящей через центр масс,
плюс произведение массы тела на квадрат расстояния между осями.
9.
Уравнение для момента импульсаСкорость изменения полного момента
импульса
системы
равна
результирующему моменту внешних сил.
dM сист
Ni
dt
i
Для твердого тела, вращающегося вокруг закрепленной оси OZ , его
момент импульса в проекции на ось вращения удобно выразить через
момент инерции относительно этой оси:
d(ωzIz)/dt = Izβz = ΣNiz
βz - угловое ускорение вращающегося тела в проекции на ось вращения
ΣNiz - сумма проекций моментов внешних сил на ось OZ.
Это уравнение движения для твердого тела, вращающегося
вокруг неподвижной оси = аналог второго закона Ньютона для
вращательного движения.
10.
Кинетическая энергия твердого телапри вращении вокруг неподвижной оси
Кинетическая энергия твердого тела:
T = Σmivi 2/2
Линейная скорость i-ой точки:
vi = [ω,ri] ; vi = ωRi
T = Σdmivi 2/2 = ω2ΣdmiRi 2/2
ΣdmiRi 2 = Iz
=> T = Iz ω2/2
11.
Работа внешних сил при вращениитвердого тела вокруг неподвижной оси
Fi- суммарная сила, действующая на точку mi
dAi = (Fi dri) - элементарная работа сил при перемещении точки mi на dri
В полярных координатах (поворот на малый угол dφ вокруг оси 0Z):
dAi = (Fi dri) = (Fi [dφ,ri ]) = (dφ [ri , Fi,]) = (dφ, Ni) = NZ i dφ
NZ i – суммарный момент сил, действующий на точку. mi, в проекции на 0Z
Твердое тело = множество мат. точек. Суммируем по всем точкам, :
dА = NZ внешdφ, = (dφ, Nвнеш)
NZ внеш - суммарный момент внешних сил, действующих на все точки
твердого тела, в проекции на ось 0Z
При повороте на конечный угол: A = ⌠NZ внешdφ
12.
13.
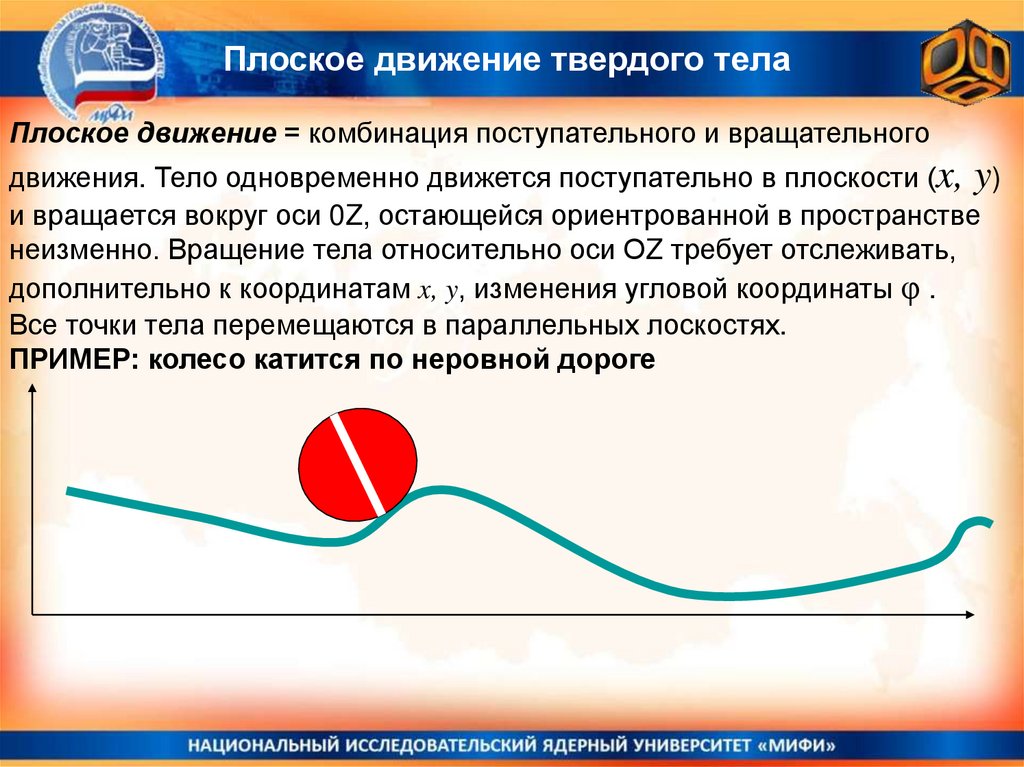
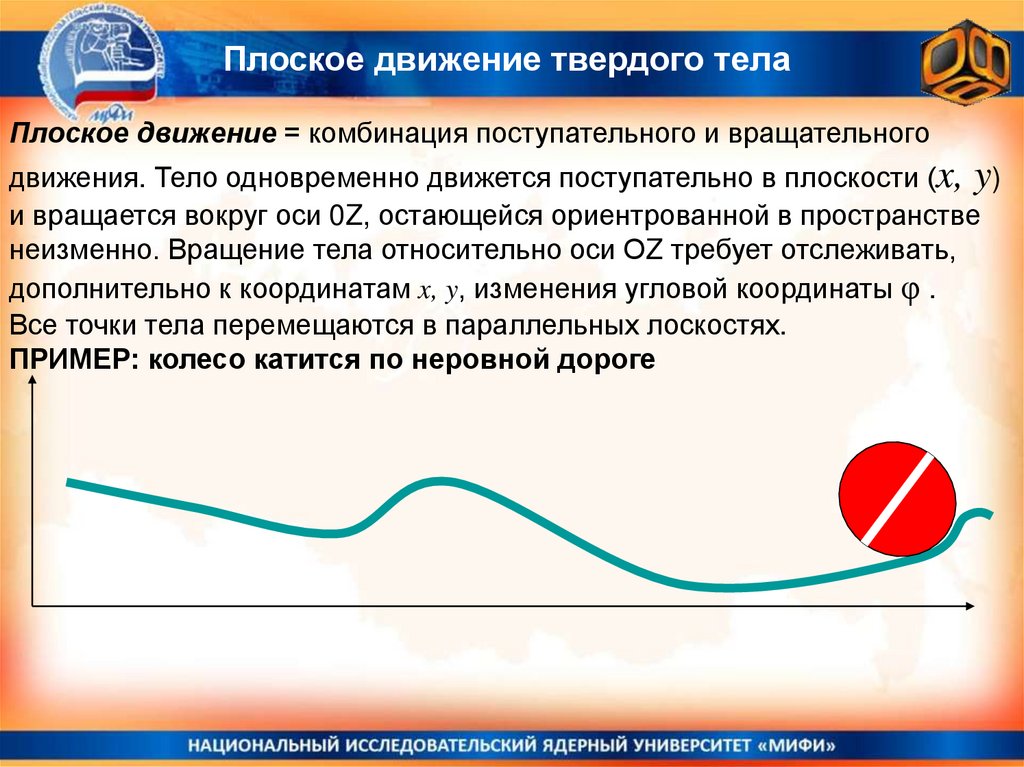
Плоское движение твердого телаПлоское движение = комбинация поступательного и вращательного
движения. Тело одновременно движется поступательно в плоскости (x, y)
и вращается вокруг оси 0Z, остающейся ориентрованной в пространстве
неизменно. Вращение тела относительно оси ОZ требует отслеживать,
дополнительно к координатам x, y, изменения угловой координаты φ .
Все точки тела перемещаются в параллельных лоскостях.
ПРИМЕР: колесо катится по неровной дороге
14.
Плоское движение твердого телаПлоское движение = комбинация поступательного и вращательного
движения. Тело одновременно движется поступательно в плоскости (x, y)
и вращается вокруг оси 0Z, остающейся ориентрованной в пространстве
неизменно. Вращение тела относительно оси ОZ требует отслеживать,
дополнительно к координатам x, y, изменения угловой координаты φ .
Все точки тела перемещаются в параллельных лоскостях.
ПРИМЕР: колесо катится по неровной дороге
15.
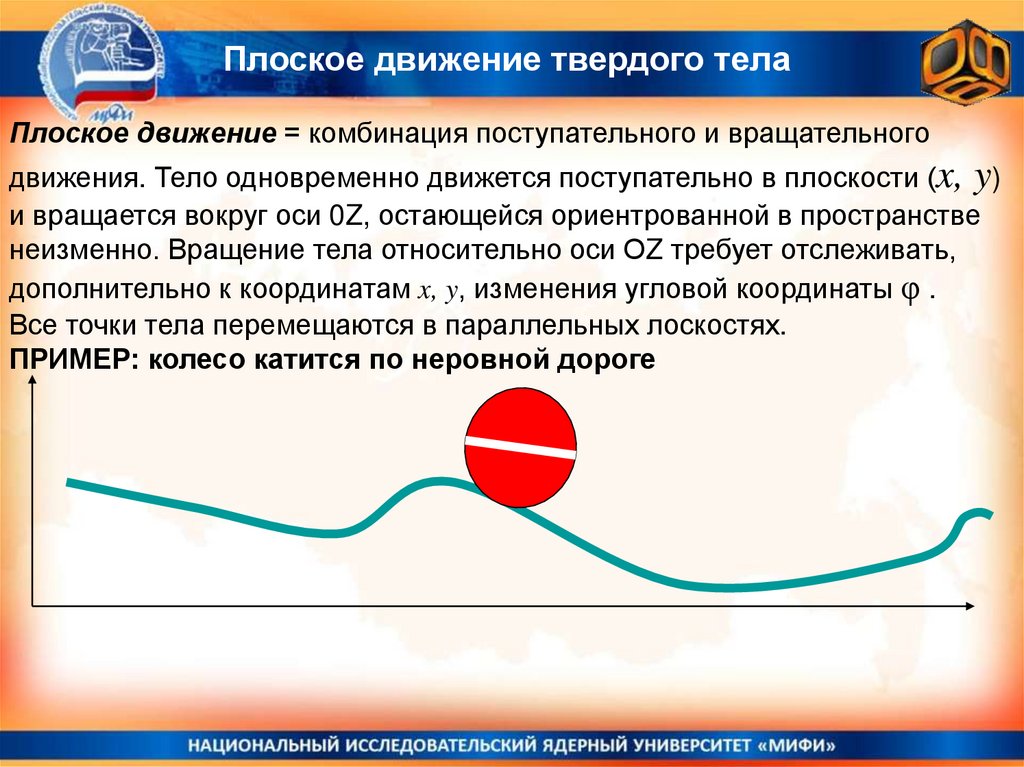
Плоское движение твердого телаПлоское движение = комбинация поступательного и вращательного
движения. Тело одновременно движется поступательно в плоскости (x, y)
и вращается вокруг оси 0Z, остающейся ориентрованной в пространстве
неизменно. Вращение тела относительно оси ОZ требует отслеживать,
дополнительно к координатам x, y, изменения угловой координаты φ .
Все точки тела перемещаются в параллельных лоскостях.
ПРИМЕР: колесо катится по неровной дороге
16.
Плоское движение твердого телаПлоское движение = комбинация поступательного и вращательного
движения. Тело одновременно движется поступательно в плоскости (x, y)
и вращается вокруг оси 0Z, остающейся ориентрованной в пространстве
неизменно. Вращение тела относительно оси ОZ требует отслеживать,
дополнительно к координатам x, y, изменения угловой координаты φ .
Все точки тела перемещаются в параллельных лоскостях.
ПРИМЕР: колесо катится по неровной дороге
17.
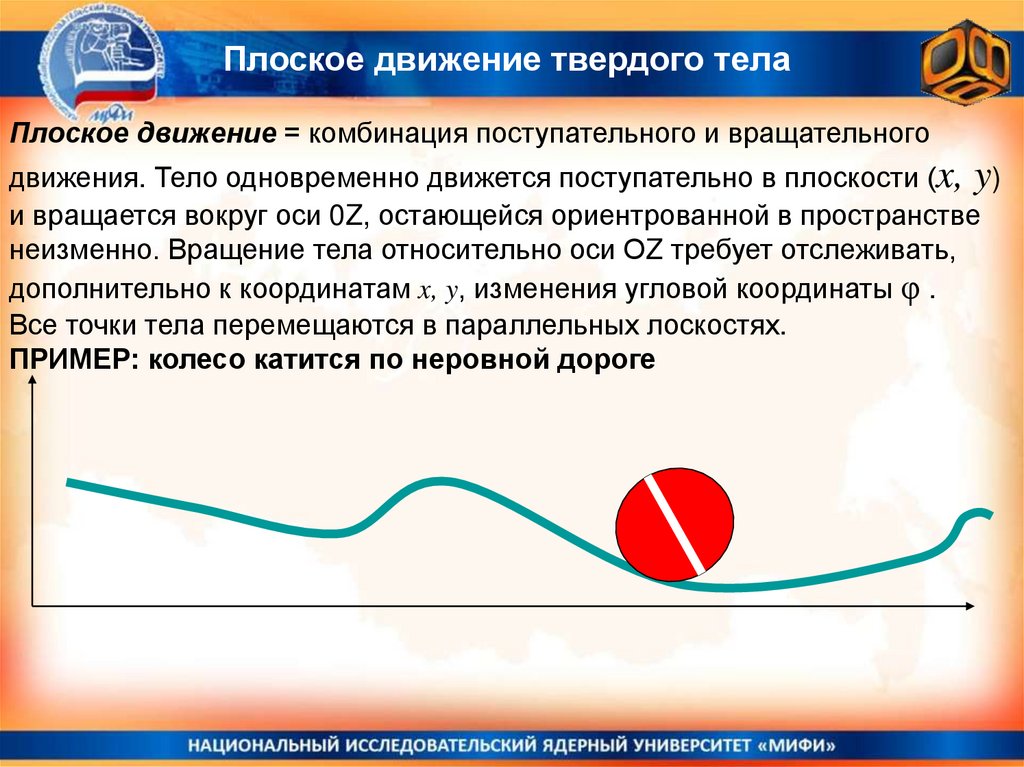
Плоское движение твердого телаПлоское движение = комбинация поступательного и вращательного
движения. Тело одновременно движется поступательно в плоскости (x, y)
и вращается вокруг оси 0Z, остающейся ориентрованной в пространстве
неизменно. Вращение тела относительно оси ОZ требует отслеживать,
дополнительно к координатам x, y, изменения угловой координаты φ .
Все точки тела перемещаются в параллельных лоскостях.
ПРИМЕР: колесо катится по неровной дороге
18.
Плоское движение твердого телаПлоское движение = комбинация поступательного и вращательного
движения. Тело одновременно движется поступательно в плоскости (x, y)
и вращается вокруг оси 0Z, остающейся ориентрованной в пространстве
неизменно. Вращение тела относительно оси ОZ требует отслеживать,
дополнительно к координатам x, y, изменения угловой координаты φ .
Все точки тела перемещаются в параллельных лоскостях.
ПРИМЕР: колесо катится по неровной дороге
19.
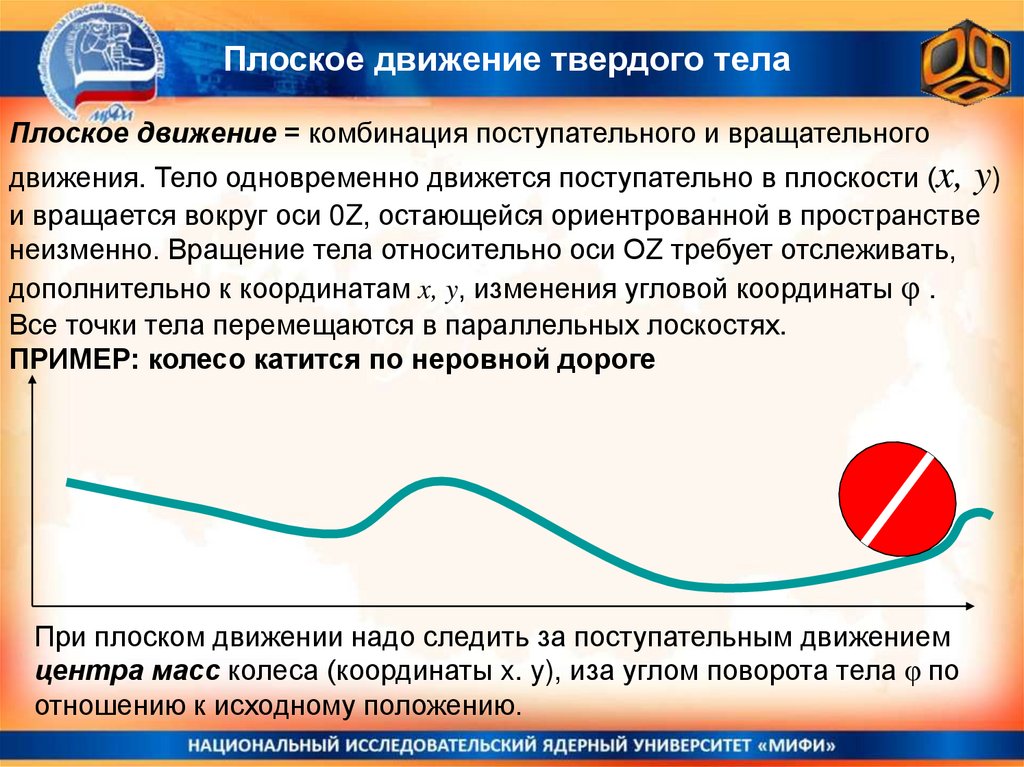
Плоское движение твердого телаПлоское движение = комбинация поступательного и вращательного
движения. Тело одновременно движется поступательно в плоскости (x, y)
и вращается вокруг оси 0Z, остающейся ориентрованной в пространстве
неизменно. Вращение тела относительно оси ОZ требует отслеживать,
дополнительно к координатам x, y, изменения угловой координаты φ .
Все точки тела перемещаются в параллельных лоскостях.
ПРИМЕР: колесо катится по неровной дороге
При плоcком движении надо следить за поступательным движением
центра масс колеса (координаты x. y), иза углом поворота тела φ по
отношению к исходному положению.
20.
Плоское движение твердого телаПри плоском движении скорость любой точки тела складывается из 2-х
компонент:
v = vc + [ω, r]
vc – скорость поступательного движения центра масс тела.
r - радиус-вектор точки относительно центра масс тела (или любой
точки на оси вращения, проходящей через центр масс тела)
Кинетическая энергия плоского движения твердого тела:
T = Izω2/2 + mvc2/2
.Кин. энергия вращения = энергия в СЦМ (теорема Кёнига)
Плоское движение описывают двумя уравнениями движения::
1. Уравнение движения центра масс: mwc = mdvc/dt = ΣFBH
2. Уравнение моментов для вращения вокруг оси 0Z, проходящей через
центр масс: dM/dt = ΣNBH или dMZ/dt = IZ dω/dt = ΣNBH Z
21.
Плоское движение твердого тела. ПРИМЕРыПРИМЕР 1: Скатывание БЕЗ проскальзывания
mdvc/dt = ΣF => mwc= mg sin(a) – FTP
Izdωz/dt = Izβz = ΣNz= RFTP
wc = Rβz => mR2wc= mgR2sin(a) – Izwc
wc = mgR2sin(a) /(Iz+mR2)
Заметим:
FTP = mg sin(a) – mwc = mg sin(a)Iz /(Iz+mR2) < kmg cos(a)
=> k> tg(a) Iz /(Iz+mR2)
…а если k< tg(a) Iz /(Iz+mR2) ???
22.
Плоское движение твердого тела. ПРИМЕРыПРИМЕР 2: Скатывание с проскальзыванием
mdv/dt = ΣF =>
mw = mg sin(a)+kmg cos(a)
Izdωz/dt = - Rkmg cos(a)
причем k< tg(a)Iz/(Iz+mR2)
w = g(sin(a) + k cos(a)) > g(sin(a) ,
но w < g(sin(a) (1+ Iz/(Iz+mR2))
23.
Курс общей физики НИЯУ МИФИСпасибо за внимание!
Далее:
Свободное движение твердого тела.
.
24.
Общая Физика. МеханикаЛекция 11
Механика твердого тела
Вращательное, свободное и
комбинированное движение
Лектор:
Профессор НИЯУ МИФИ
Ольчак Андрей Станиславович(
25.
Свободное движение твердого телаКомбинация поступательного и вращательного движения без всяких
ограничений. Возможно поступательное движение в трех пространственных направлениях, сочетаемое с вращением вокруг любой оси, причем
ось вращения в процессе движения может менять направление.
При любом, самом сложном движении скорость любой точки тела,
наблюдаемую из «лабораторной» системы отсчета, можно представить
как сумму двух компонент:
• поступательной (вместе с центром масс), и
• вращательной (вокруг центра масс)
v = vC + [ω, r]
здесь r - радиус-вектор точки относительно центра масс тела, а
ω – угловая скорость его вращения
26.
Свободное движение твердого телаПри свободном движении твердого тела связь векторов угловой
скорости и момента импульса усложняется
Mi= Iijωj
Iij =
Ixx
Iyх
Izx
Ixy
Iyy
Izy
Ixz
Iyz
Izz
тензор (матрица)
моментов инерции
Mx= Ixх ωx + Ixy ωy + Ixz ωz
My= Iyх ωx + Iyy ωy + Iyz ωz
Mz= Izх ωx + Izy ωy + Izz ωz
27.
Свободное движение твердого телаЕсли тело имеет оси симметрии, и если направить оси координат x, y,
z вдоль осей симметрии, тензор инерции может стать диагональным
Ixx
0
0x
0
Iyy
0
0
0
Izz
Mx= Ixх ωx
My= Iyy ωy
Mz= Izz ωz
Mi= Iiiωi
Для “самых симметричных” тел (сфера, шар) Ixx = Iyy = Izz = I; M= Iω
Свободно движущееся тело вращается вокруг оси, проходящей через
центр масс тела.
Оси вращение несимметричных тел, как правило, не устойчивы. При
наличии внешних сил (даже слабых) ось вращения может менять
направление, а при вращении тела вокруг закрепленной оси на оси могут
возникать заметные нагрузки. Если убрать закрепление - тело может
начать «кувыркаться».
У симметричных тел могут быть т.н. главные оси симметрии, вращение
вокруг которых может быть устойчиво.
28.
Движение с произвольной осью вращенияУ симметричных тел могут быть т.н. главные оси
симметрии, вращение вокруг которых может быть
устойчиво. «Самые главные» оси те, вращение вокруг
которых всегда устойчиво. Такое вращение может
продолжаться и после снятия закрепления.
Пример: быстрое вращение стержня на подвесе
остается устойчивым еще некоторое время, если снять
нить с подвеса. По мере замедления вращения
устойчивость его теряется.
Смотрите «ФИЗИКУ в ОПЫТАХ» на openedu.ru!
Это необходимо для получения «зачета» и допуска к
экзамену. Но ГЛАВНОЕ: Вы станете лучше понимать
физику!
Особенно это касается механики вращательного
движения!^
29. ГИРОСКОПЫ
Гироскоп- массивное симметричное твердое тело, вращающееся с большой угловойскоростью вокруг оси симметрии, причем ось симметрии гироскопа может
поворачиваться в пространстве
Ось гироскопа – ось симметрии гироскопа – ось Х, является одной из главных
осей инерции гироскопа. Две другие главные оси инерции (оси Y и Z ),
проведенные через точку О, лежат в плоскости, перпендикулярной оси Х.
Точка опоры гироскопа – неподвижная точка на оси гироскопа –точка О.
Момент инерции гироскопа - главный момент инерции относительно оси Х:
dM
N
dt
M I I ex
M I const.
30.
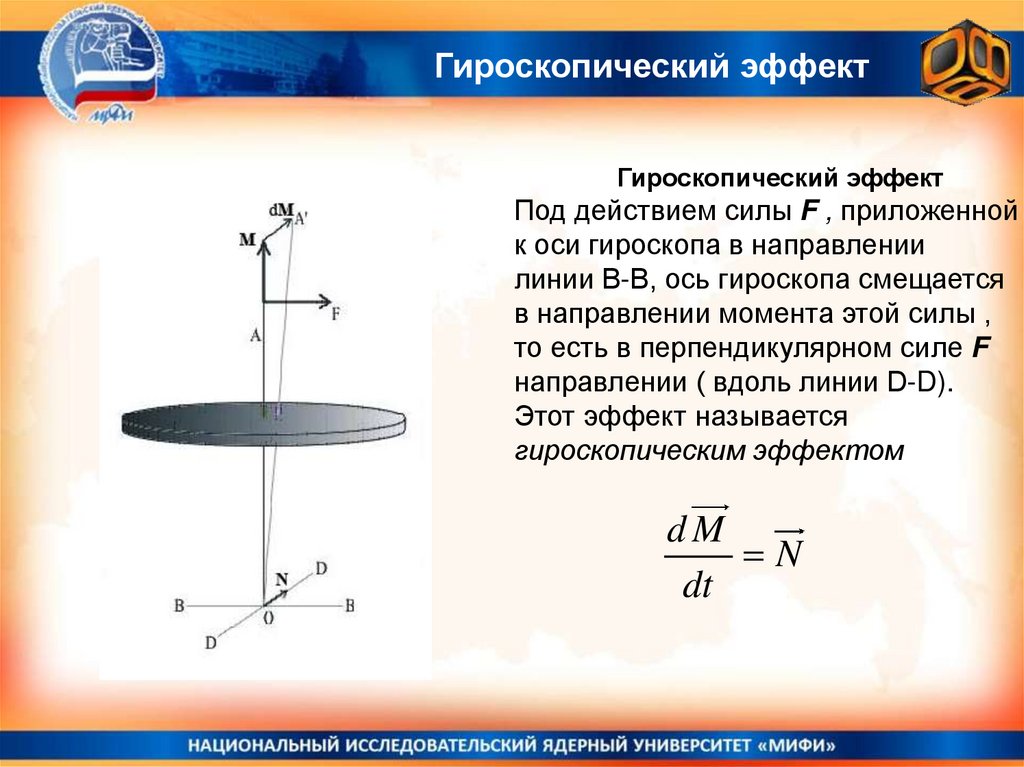
Гироскопический эффектГироскопический эффект
Под действием силы F , приложенной
к оси гироскопа в направлении
линии В-В, ось гироскопа смещается
в направлении момента этой силы ,
то есть в перпендикулярном силе F
направлении ( вдоль линии D-D).
Этот эффект называется
гироскопическим эффектом
dM
N
dt
31.
Прецессия гироскопаПрецессия гироскопа –
вращение оси гироскопа под действием
приложенных к оси внешних сил (силы
тяжести Р, например).
Угловая скорость прецессии ω<<Ω
dM
, M N
dt
PX c
I
ЧТО НАДО ЗНАТЬ из теории движения гороскопа:
• Угловая скорость прецессии ω обратно пропорциональна угловой
скорости вращения гироскопа ω ~ 1/Ω
• Вектор ω направлен против вектора внешней силы;
• Приближенная теория справедлива, когда ω<<Ω .
• При ω ~ Ω наблюдаются колебания оси гироскопа – нутация
• По мере уменьшения Ω, вращение гироскопа теряет устойчивость
32.
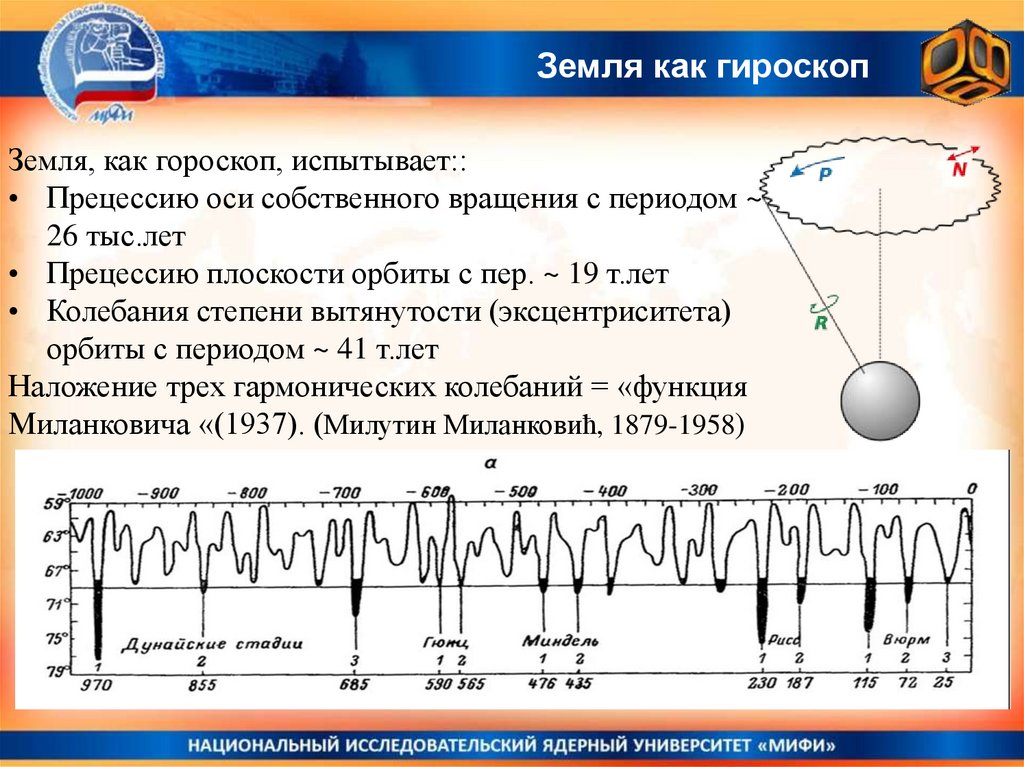
Земля как гироскопЗемля, как гороскоп, испытывает::
• Прецессию оси собственного вращения с периодом ~
26 тыс.лет
• Прецессию плоскости орбиты с пер. ~ 19 т.лет
• Колебания степени вытянутости (эксцентриситета)
орбиты с периодом ~ 41 т.лет
Наложение трех гармонических колебаний = «функция
Миланковича «(1937). (Милутин Миланковиħ, 1879-1958)
33.
Курс общей физики НИЯУ МИФИСпасибо за внимание!
Далее:
Условия равновесия твердого тела.
Движение вблизи положения
равновесия..

























 Физика
Физика








