Динамика вращательного движения

1.

Курс общей физики
Механика
Лекция №3
Динамика вращательного движения
к.ф.-м.н., доцент ШЕН
Стеблий Максим Евгеньевич
г. Владивосток
2017

2.

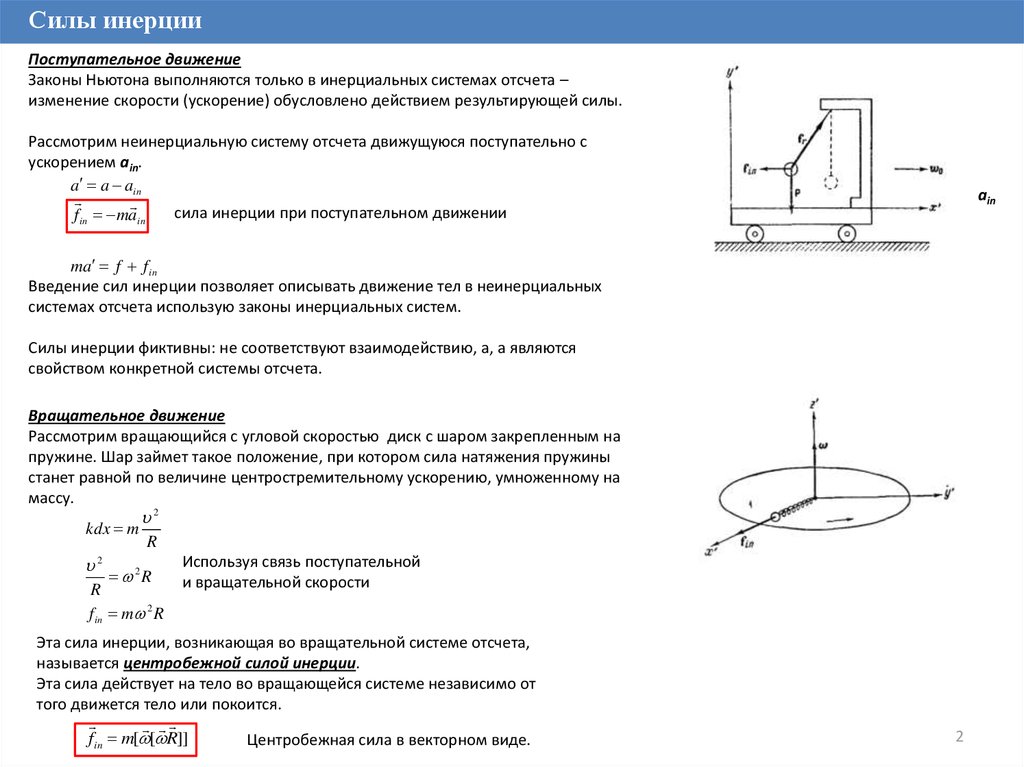
Силы инерции
Поступательное движение
Законы Ньютона выполняются только в инерциальных системах отсчета –
изменение скорости (ускорение) обусловлено действием результирующей силы.
Рассмотрим неинерциальную систему отсчета движущуюся поступательно с
ускорением ain.
a a ain
сила инерции при поступательном движении
f in main
ain
ma f f in
Введение сил инерции позволяет описывать движение тел в неинерциальных
системах отсчета использую законы инерциальных систем.
Силы инерции фиктивны: не соответствуют взаимодействию, а, а являются
свойством конкретной системы отсчета.
Вращательное движение
Рассмотрим вращающийся с угловой скоростью диск с шаром закрепленным на
пружине. Шар займет такое положение, при котором сила натяжения пружины
станет равной по величине центростремительному ускорению, умноженному на
массу.
2
kdx m
R
2
Используя связь поступательной
2R
и вращательной скорости
R
f in m 2 R
Эта сила инерции, возникающая во вращательной системе отсчета,
называется центробежной силой инерции.
Эта сила действует на тело во вращающейся системе независимо от
того движется тело или покоится.
fin m[ [ R]]
Центробежная сила в векторном виде.
2

3.

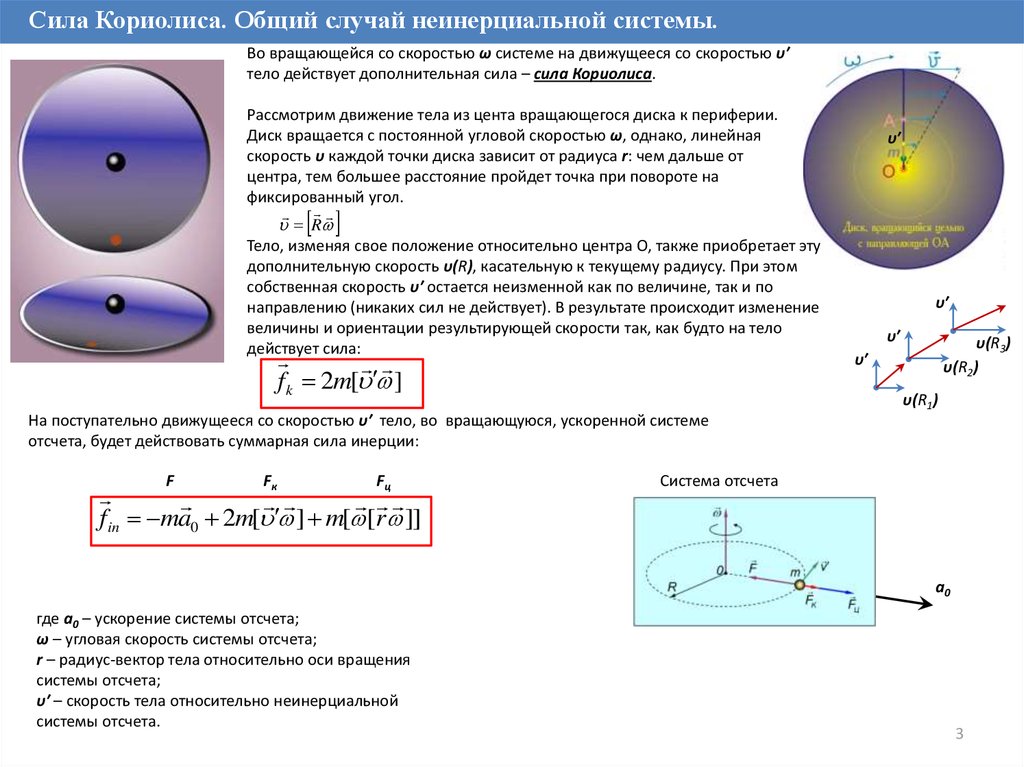
Сила Кориолиса. Общий случай неинерциальной системы.
Во вращающейся со скоростью ω системе на движущееся со скоростью υ′
тело действует дополнительная сила – сила Кориолиса.
Рассмотрим движение тела из цента вращающегося диска к периферии.
Диск вращается с постоянной угловой скоростью ω, однако, линейная
скорость υ каждой точки диска зависит от радиуса r: чем дальше от
центра, тем большее расстояние пройдет точка при повороте на
фиксированный угол.
R
Тело, изменяя свое положение относительно центра O, также приобретает эту
дополнительную скорость υ(R), касательную к текущему радиусу. При этом
собственная скорость υ′ остается неизменной как по величине, так и по
направлению (никаких сил не действует). В результате происходит изменение
величины и ориентации результирующей скорости так, как будто на тело
действует сила:
υ′
f k 2m[ ]
υ′
υ′
υ(R3)
υ(R2)
υ′
υ(R1)
На поступательно движущееся со скоростью υ′ тело, во вращающуюся, ускоренной системе
отсчета, будет действовать суммарная сила инерции:
F
Fк
Fц
fin ma0 2m[ ] m[ [r ]]
Система отсчета
a0
где a0 – ускорение системы отсчета;
ω – угловая скорость системы отсчета;
r – радиус-вектор тела относительно оси вращения
системы отсчета;
υ′ – скорость тела относительно неинерциальной
системы отсчета.
3

4.

Центр инерции
При поступательном движении все точки тела получают за один и тот же промежуток
времени равное по величине и направлению перемещения, в следствие чего скорость и
ускорение всех точек в каждый момент времени оказываются одинаковыми.
При вращательном движении все точки твердого тела движутся по окружностям, центры
которых лежат на одной и той же прямой, называемой осью вращения.
В предыдущих разделах «Кинематика» и «Динамика» рассматривалось движение
материальной точки. При этом как при поступательном, так и при вращательном
движении вся масса m была сконцентрирована в одной точке с радиус-вектором r.
Рассматривая твердое тело вводится понятие центра инерции (центр масс). Для определения его
положения необходимо разбить тело на элементарные объемы с массой mi и радиус-вектором ri.
Центром инерции называется точка, определимая следующим образом
m1r1 m1r1 ... mN rN mi ri mi ri
rc
m1 m1 ... mN
m
m
i
c r c
m r m
m
m
ac c r c
mac Fi
i i
Δmi
i i
Δm1
i
r1
r2
Δm2
Центр инерции твердого тела движется так, как двигалась бы материальная точка с массой,
равной массе тела, под действием всех приложенный к телу сил.
Движение твёрдого тела можно рассматривать как суперпозицию движения центра масс
и вращательного движения тела вокруг его центра масс.
Тогда для описания этого движения применимы все законы Ньютона. Во многих случаях можно
вообще не учитывать размеры и форму тела и рассматривать только движение его центра масс.
4

5.

Описание плоского движения
Любое движение твердого тела можно представить как наложение поступательного и
вращательного движения. Рассмотрим на примере плоского движения – качения
цилиндра.
За промежуток времени dt каждая точка цилиндра совершит перемещение связанное с
поступательным и вращательным движением:
ds dsпост dsвращ
Дифференцируя по времени можно найти скорости обусловленные этими движениями:
ds dsпост dsвращ
0
dt
dt
dt
Используя связь между поступательной скоростью и угловой скоростью:
[ r ]
0 [ r ]
Скорость каждой точки твердого тела участвующего в поступательном и вращательной
движении описывается скоростью υ0 движения оси вращения O и угловой скоростью ω
вращения тела вокруг этой оси.
dsвращ
dsпост
υ0
В теле, одновременно участвующем в поступательном и вращательном движении,
существует точка с нулевой мгновенной скоростью – мгновенный центр вращения,
через который проходит мгновенная ось вращения. В случае катящегося цилиндра он
совпадает с точкой касания с поверхностью.
В общем случае, сложное движение можно описывать как ряд последовательных
элементарных вращений вокруг мгновенной оси и ее перемещений.
5

6.

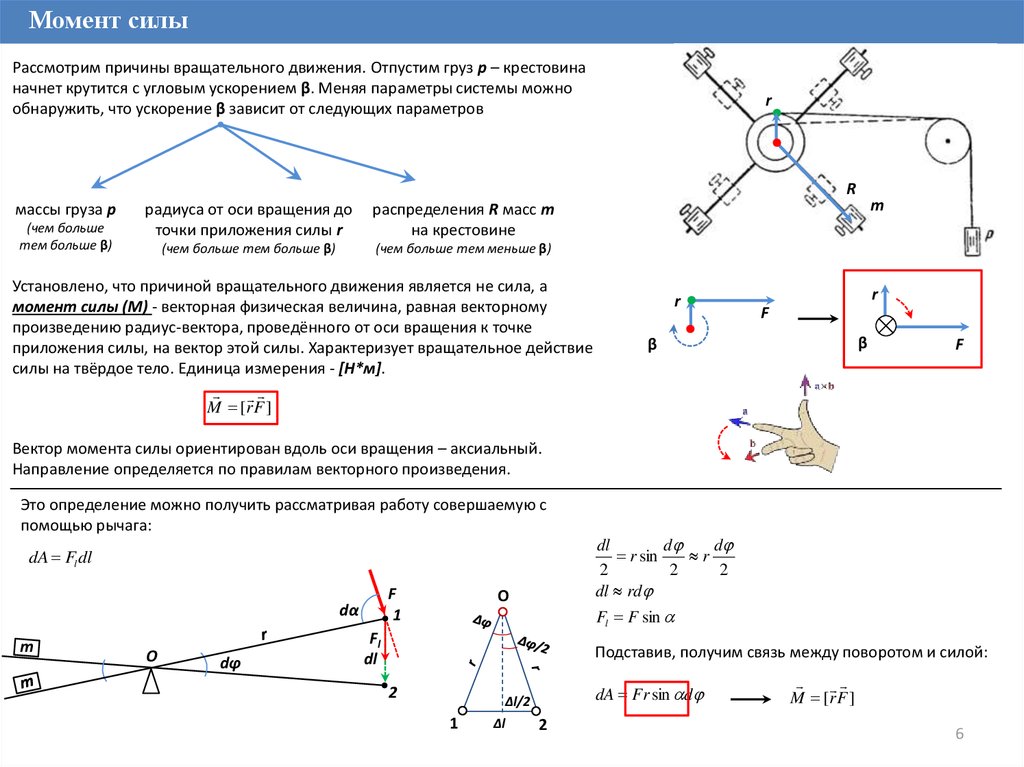
Момент силы
Рассмотрим причины вращательного движения. Отпустим груз p – крестовина
начнет крутится с угловым ускорением β. Меняя параметры системы можно
обнаружить, что ускорение β зависит от следующих параметров
r
R
массы груза p
(чем больше
тем больше β)
радиуса от оси вращения до
точки приложения силы r
распределения R масс m
на крестовине
(чем больше тем больше β)
(чем больше тем меньше β)
Установлено, что причиной вращательного движения является не сила, а
момент силы (M) - векторная физическая величина, равная векторному
произведению радиус-вектора, проведённого от оси вращения к точке
приложения силы, на вектор этой силы. Характеризует вращательное действие
силы на твёрдое тело. Единица измерения - [Н*м].
M [r F ]
r
m
r
F
β
β
F
Вектор момента силы ориентирован вдоль оси вращения – аксиальный.
Направление определяется по правилам векторного произведения.
Это определение можно получить рассматривая работу совершаемую с
помощью рычага:
dA Fl dl
F
1
dα
m
O
dϕ
O
dl
d
d
r sin
r
2
2
2
dl rd
Fl F sin
Fl
dl
Подставив, получим связь между поворотом и силой:
2
dA Fr sin d
Δl/2
1
Δl
2
M [r F ]
6

7.

Момент импульса
По аналогии с понятием момента силы вводится понятие момента импульса.
Момент импульса (L) - векторная физическая величина, равная векторному произведению
радиус-вектора, проведённого от оси вращения к вращающейся точке, на импульс этой точки –
относительная величина. Характеризует количество вращательного движения. Единица измерения [м2кг/c].
L [r p] m[r ]
Найдем причину изменения момента импульса. Продифференцируем по времени:
dL d
dr
dp
[r p] [ p] [ r ]
dt dt
dt
dt
dL
[r F ]
dt
dL
M
dt
dp
F
dt
Важным следствием этой взаимосвязи является то, что в замкнутой системе, в
отсутствие сил (и моментов сил), величина суммарного момента импульса
сохраняется.
Закон сохранения момента импульса – момент импульса замкнутой системы
остается постоянным.
Свяжем момент импульса с угловой скоростью вращения:
L [r p] m[r ] [ r ]
Момент инерции - скалярная физическая величина, мера инертности
во вращательном движении вокруг оси, подобно тому, как масса тела
L m[r [ r ]] (mr 2 )
является мерой его инертности в поступательном движении.
Момент инерции точки:
Характеризуется распределением масс в теле. Единица измерения - [м2кг].
I mr 2
Момент инерции тела:
I mi ri
2
Тогда момент импульса можно записать в виде:
Изменение момента импульса:
Основное уравнение динамики вращательного движения:
L I
dL d
I I
dt
dt
M I
7

8.

Момент инерции
L
Момент инерции (I) — скалярная величина, характеризующая распределение масс в теле
и являющаяся, наряду с массой, мерой инертности тела при непоступательном движении.
Единица измерения - [кг*м2].
Момент инерции материальной точки определяется:
, где r- расстояние от точки до оси вращения.
I mr
p
r
m
2
• Момент инерции – относительная величина, зависит от выбора оси.
• Момент инерции – аддитивная величина, момент инерции тела определяется
как сумма моментов инерции всех i «точек» его образующих.
I mi ri
2
Для тела с однородно распределенной массой момент инерции можно выразить через плотность:
m
Элементарную массу можно выразить в виде:
V
m dm
mi i Vi
В результате предельного перехода:
- в неоднородном случае.
i lim
V 0 V
dV
I i ri 2 Vi
I r 2 dm r 2 dV
I ri 2 Vi
Рассмотрим расчет момента инерции на примере однородного диска:
Ввиду симметрии задачи в качестве элементарных объемов выберем
кольца шириной dr. Найдем объем такого кольца:
dV bds
S2
S1
ds (r dr ) 2 r 2
Можно пренебречь ввиду большего порядка малости.
ds r 2 2 rdr dr 2 r 2
ds 2 rdr
dV b2 rdr - объем кольцевого слоя.
Подставив в общую формулу
R
I r 2 dV r 2b2 rdr
0
R
m
SV
4
R
R2
2
I 2 b r dr 2 b
R b
4
2
0
3
Момент инерции однородного диска
I
mR2
2
8

9.

Момент инерции
Рассмотрим расчет момента инерции на примере однородной сферы:
Разобьем сферу радиусом R на диски толщиной dz, перпендикулярно оси вращения.
Найдем радиус такого диска, расположенного на высоте z от центра сферы:
r R2 z2
Так как момент инерции диска
I
1 2
r dm
2
dm dV r 2 dz
mR2
2
dI
R
R
R
R
0
0
I dI 2 dI R 4 2 R 2 z 2 z 4 dz
R
2
1
I R 4 z R 2 z 3 z 5
3
5 0
объем шара
2
1 2
1
1
2
1 8
4
2
r r 2 dz r 4 dz R 2 z 2 dz
I R 5 R 5 R 5 R 5 R 3 R 2
2
2
2
3
5 15
3
5
1
4
2 2
4
Момент инерции однородного шара
dI R 2 R z z dz
2
2
I mR 2
5
dI
Гораздо более сложной является задача расчета величины момента инерции относительно
осей не проходящих через центры симметрии тел.
mR2
I
Например, момент инерции диска относительно его оси OO:
2
Однако прямой расчет этой величины относительно оси O′O′ слишком сложен.
Теорема Гюйгенса – Штейнера
- момент инерции I относительно произвольной оси равен сумме момента
инерции I0 относительно оси, параллельной данной и проходящей через центр
масс тела, и произведения массы тела m на квадрат расстояния между осями a.
a
I I 0 ma 2
Используя теорему Штейнера момент инерции диска относительно оси :
I
mR2
ma 2
2
9

10.

Кинетическая энергия твердого тела
Если тело участвует только во вращательном движении:
Δmi
Если тело вращается вокруг неподвижной оси с угловой скоростью ω, то линейную
скорость υi элементарной массы тела mi, находящегося на расстоянии ri от оси
вращения, можно выразить как:
ri
i ri
ω
Следовательно, кинетическая энергия этой i–й массы:
mi i
1
2
mi ri 2
2
2
Кинетическая энергия тела слагается из кинетической энергии его частей:
2
Ti
1
2
T Ti 2 mi ri
2
I
T
I 2
2
- кинетическая энергия вращательного движения.
Если тело участвует и в поступательном и во вращательном движении:
Сложное движение может быть представлено как наложение поступательного и
вращательного движения. Скорость i-й точки участвующей в таком движении
определяется:
i 0 [ ri ]
Кинетическая энергия i-й массы определяется в общем виде:
2
mi i 1
Ti
mi 0 [ ri ]
2
2
1
Ti mi 02 2 0 [ ri ] [ ri ]2
2
Учтем, что вектора ri и ω ортогональны и просуммируем по всем массам:
1
1
2
центр масс
T mi 02 0 [ mi ri ] 2 mi ri
2
2
mi ri
rc
масса тела
m
m
1
1
2
T 02 mi 0 mi ri 2 mi ri
2
m
2
Момент
инерции
Δmi
ri
υ0
ω
После всех замен получим:
T
m 02
I 2
0 m[ rc ]
2
2
Если центр масс совпадает с осью вращения,
то кинетическая энергия плоского движения:
m c2 I c 2
T
2
2
10

11.

Работа при вращении твердого тела
Рассмотрим, какую работу совершает внешняя сила при
вращении тела вокруг неподвижной оси.
За время dt i–я масса проходит путь dsi, который можно связать с
углом поворота dϕ:
dsi ri d
Тогда работа, рассматривая проекцию силы на траекторию dsi :
dAi f dsi f ri d
dAi M i d
Суммируя работу над всеми точками
dA M i d
A Md
dA Md
Где M – результирующий момент сил относительно оси вращения.
11

12.

Описание поступательного и вращательного движения
Поступательное
Координата
r
[м]
Мера инертности
m
[кг ]
Скорость
Ускорение
Момент количества
движения
Причина изменения
движения
Основное уравнение
динамики
Кинетическая
энергия
[Дж]
Работа
[Дж]
dr
dt
d
a
dt
p m
F
[ м / с]
[ м / с2 ]
[кг м / с 2 ]
[Н ]
Вращательное
[ рад]
I mi ri
2
d
n
dt
d
dt
L [r p] I
M [r F ]
[кг м 2 ]
m
F
[ рад / с]
[ рад / с 2 ]
[кг м 2 / с]
ω M
F
[ Н м]
r
dp
ma
Fi
dt
T
m c2
2
dA Fl dl
dL
I
Mi
dt
T
a
m
I c 2
2
dA M d
12