1c977786c53bfc420bf9a758a15926a3

1. Механика твердого тела

1. Разложение движения на вращательное и поступательное.
2. Центр инерции
3. Моменты силы и инерции
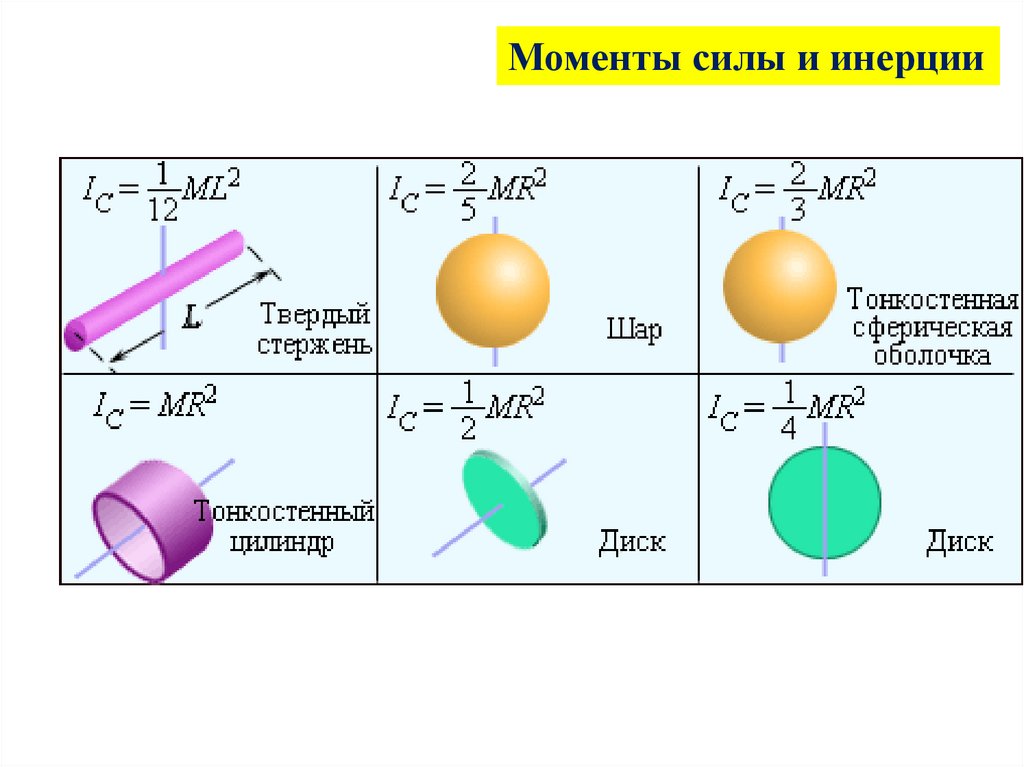
4. Таблица моментов инерции
5. Кинетическая энергия при вращательном движении
6. Теорема Штейнера
7. Основное уравнение вращательного движения.
8. Момент импульса
9. Свободные оси. Главные оси инерции
10. Гироскоп
11. Аналоги законов

2.

Разложение движения на вращательное и поступательное
Абсолютно твердое тело – система материальных
точек, взаимное расположение которых не меняется
во время движения.
Сумма внутренних сил по 3 з-ну Ньютона
равна 0. Движение только из-за внешних сил.
Движение твердого тела можно представить в виде двух
движений:
1. поступательного
2. вращательного.
При поступательном движении все точки тела имеют одну
и ту же скорость и описывают траектории одинаковой формы,
только смещенные друг относительно друга.
При вращении различные точки тела описывают
окружности в плоскости перпендикулярной оси вращения.

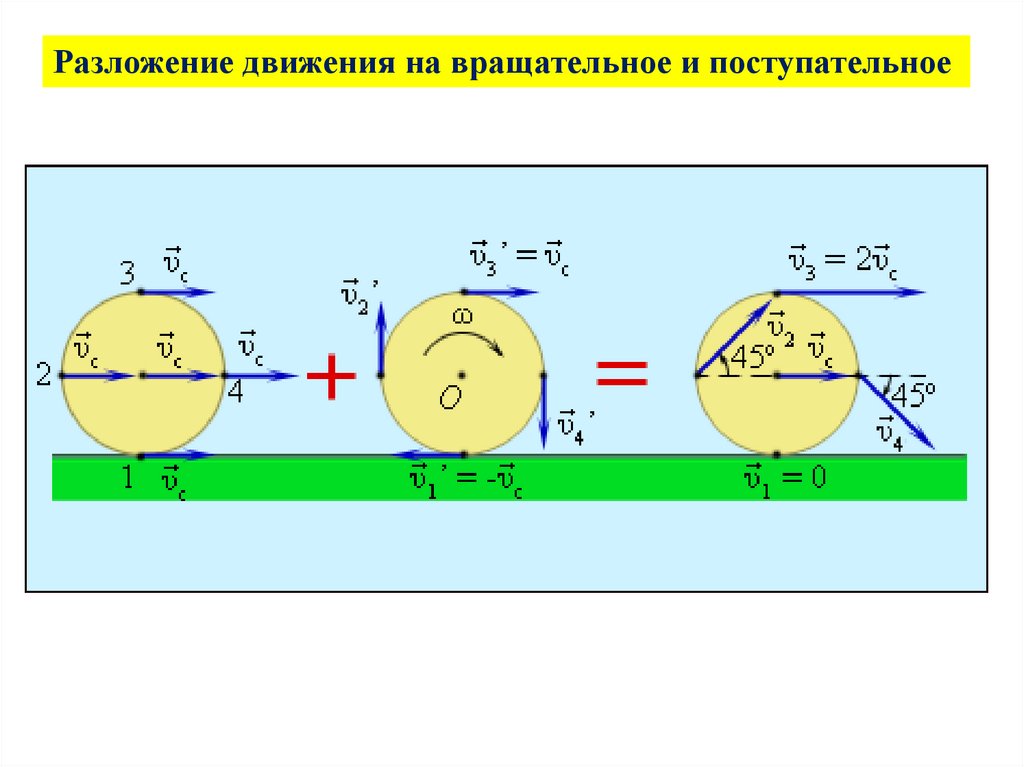
3.

Разложение движения на вращательное и поступательное

4.

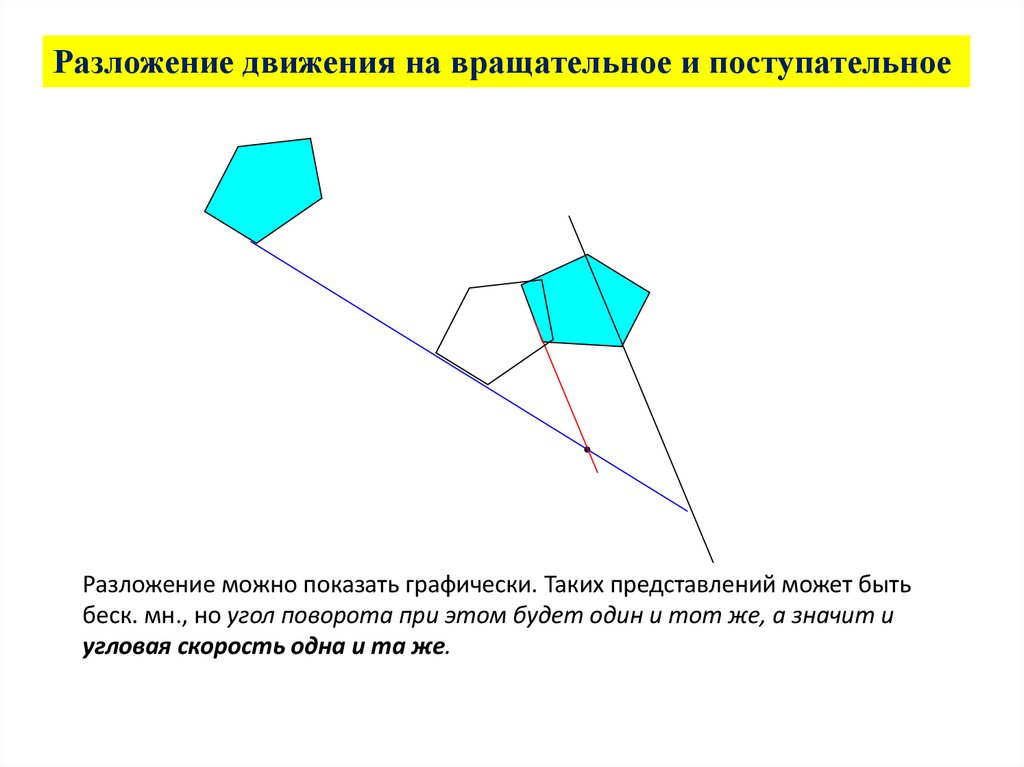
Разложение движения на вращательное и поступательное
Разложение можно показать графически. Таких представлений может быть
беск. мн., но угол поворота при этом будет один и тот же, а значит и
угловая скорость одна и та же.

5.

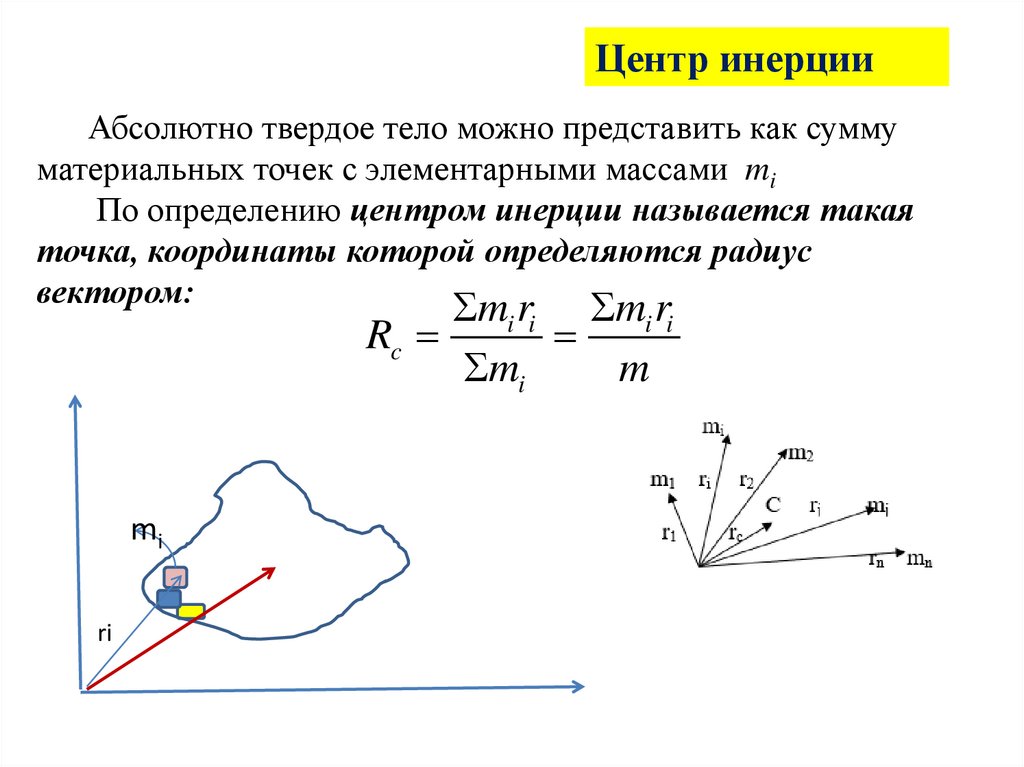
Центр инерции
Абсолютно твердое тело можно представить как сумму
материальных точек с элементарными массами mi
По определению центром инерции называется такая
точка, координаты которой определяются радиус
вектором:
mi ri mi ri
Rc
mi
m
mi
ri

6.

Центр инерции
mi аi = Fi + fi
по 2 з-ну Ньютона
mi аi = Fi + fi
fi =0
по 3 з-ну Н.
Таким образом
mi аi = Fi (*)
Продифференцировав определение центра инерции, получим:
d 2 (mi ri ) 1
d 2 ri 1
d 2R
1
ac
mi 2 mi ai
2
2
dt
m
dt
m
dt
m

7.

Центр инерции
Подставив полученное выражение в
получим
m ас = Fi
уравнение(*),
т.е. центр инерции твердого тела двигается так, как
двигалась бы материальная точка с массой равной массе
тела, под действием всех приложенных сил
В случае поступательного движения это уравнение
определяет движение всех точек, а не только центра
инерции.
Для описания любого движения твердого тела
необходимо знание 2-х векторов V и ω, каждый вектор
задается 3-мя координатами, всего необходимо 6
координат (проекций).
Система имеет 6 степеней свободы – 3
поступательных и 3 вращательных.

8.

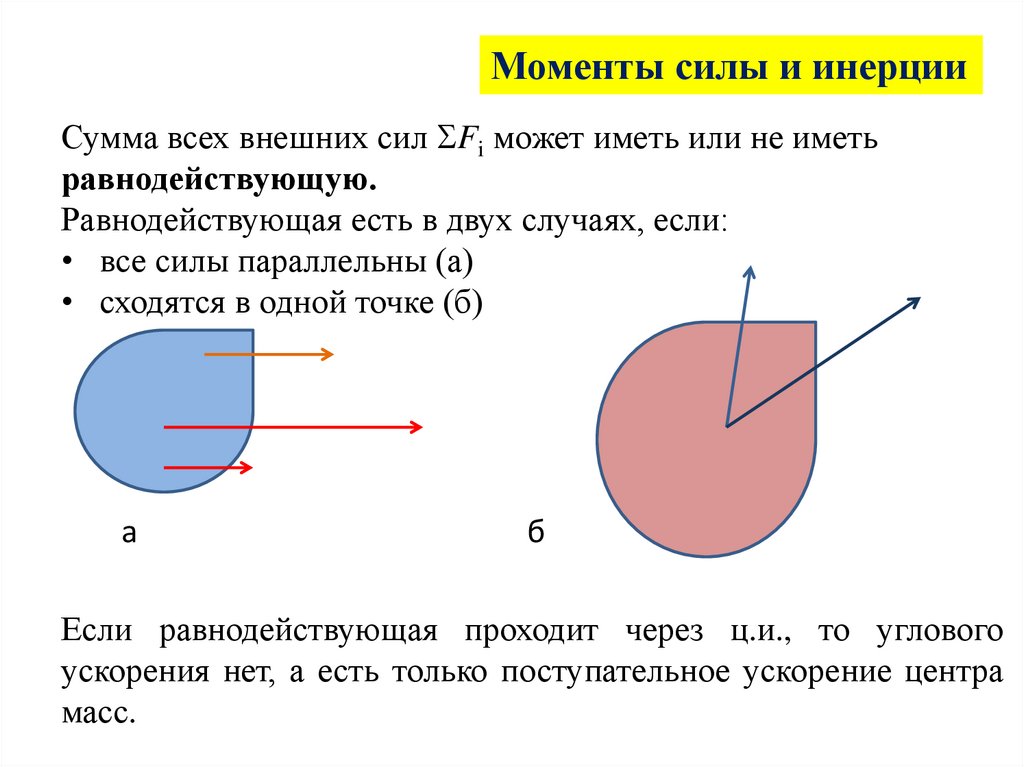
Моменты силы и инерции
Сумма всех внешних сил Fi может иметь или не иметь
равнодействующую.
Равнодействующая есть в двух случаях, если:
• все силы параллельны (а)
• сходятся в одной точке (б)
а
б
Если равнодействующая проходит через ц.и., то углового
ускорения нет, а есть только поступательное ускорение центра
масс.

9.

Моменты силы и инерции
Если равнодействующей нет, но при этом Fi =0, то это
сводится к наличию, так называемой, пары сил – две равные
по величине и противоположно направленные силы.
F1 = ‒F2
F2
R1
R2
Моментом силы относительно
некоторой точки О называется
О
векторная
величины
М,
F1
определяемая выражением
M= [R F] , где R – радиус
M= [R1 F 1]+ [R2 F 2]=
вектор проведенный из О в точку
=[R1 F 1]‒ [R2 F 1]=
приложения силы. Модуль равен:
= [(R1 ‒R2)F 1]= bF
M= F R sin α,
R sinα называется плечом силы
b - расстояние между
точками приложения
силы.

10.

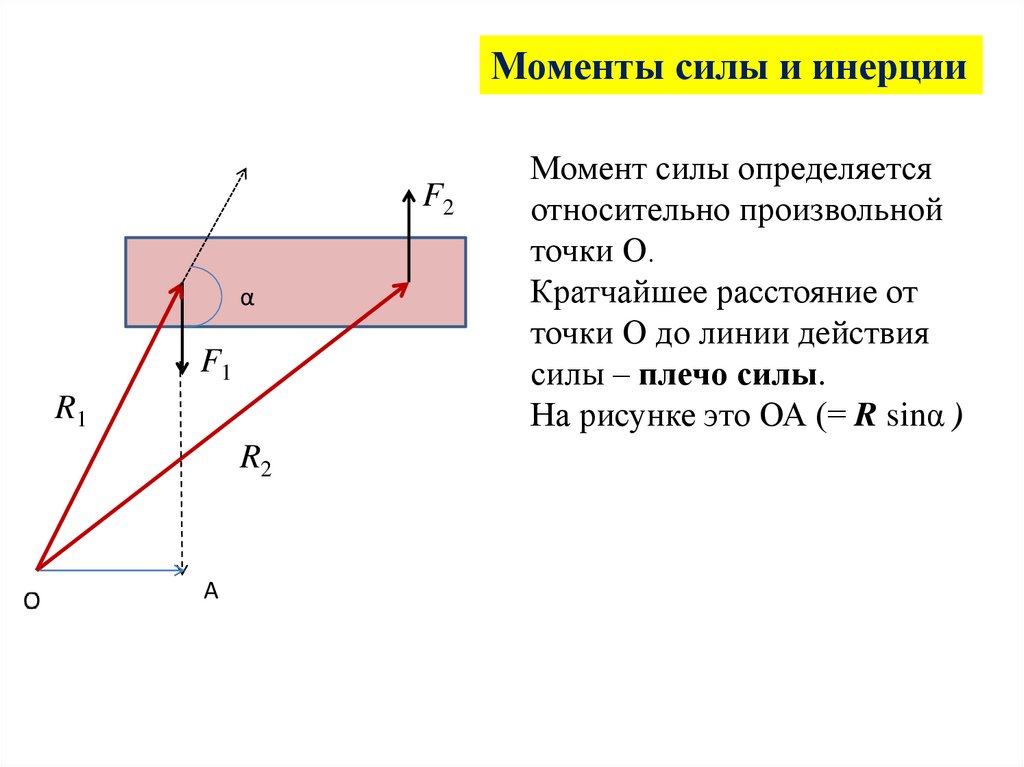
Моменты силы и инерции
F2
α
F1
R1
R2
А
Момент силы определяется
относительно произвольной
точки О.
Кратчайшее расстояние от
точки О до линии действия
силы – плечо силы.
На рисунке это ОА (= R sinα )

11.

Моменты силы и инерции
Моментом инерции системы материальных точек
относительно оси С называется физическая величина
равная сумме
произведений их масс на квадраты
расстояний до оси I = .miri2.
Момент инерции в динамике вращательного движения
играет ту же роль, что и масса тела в динамике
поступательного движения. Но есть и принципиальная
разница. Если масса – внутреннее свойство данного тела, не
зависящее от его движения, то момент инерции тела зависит
от того, вокруг какой оси оно вращается.
Для разных осей вращения моменты инерции одного
и того же тела различны.

12.

Моменты силы и инерции

13.

Моменты силы и инерции
Mb2 + I0 = I теорема Штейнера
Если твердое тело вращается относительно некоторой
неподвижной оси, то его момент инерции I можно выразить
через момент инерции I0 этого тела относительно оси,
проходящей через центр масс тела и параллельной первой.
b

14.

Моменты силы и инерции

15.

Кинетическая энергия при вращательном движении
mV 2
При поступательном движении Eкин
2
При вращательном движении V=ωR, следовательно для
2 2
элементарной массы
mi Ri
Eкин
2
Энергия аддитивна, следовательно Е= Еi
Тогда кинетическую энергию вращающегося тела можно
записать в виде:
2
mi 2 Ri2 2
I
2
E Ei
mi R1
2
2
2
I 2
E
2

16.

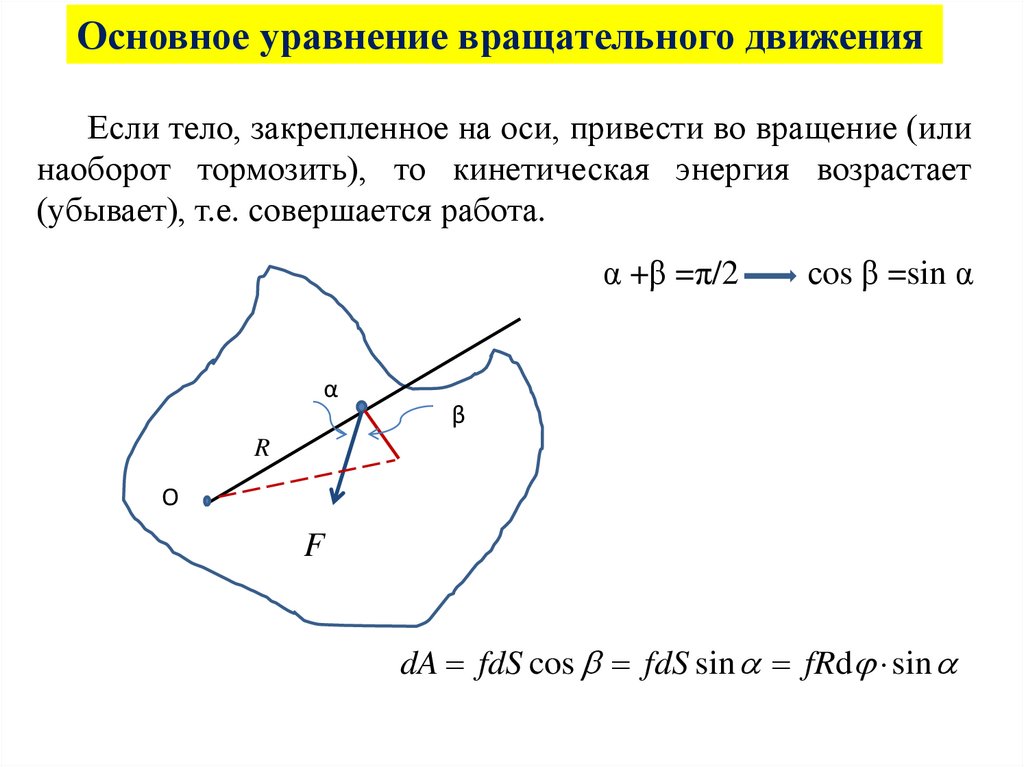
Основное уравнение вращательного движения
Если тело, закрепленное на оси, привести во вращение (или
наоборот тормозить), то кинетическая энергия возрастает
(убывает), т.е. совершается работа.
α +β =π/2
сos β =sin α
α
β
R
О
F
dA fdS cos fdS sin fRd sin

17.

Основное уравнение вращательного движения
Но fR sin M
Тогда dA =Mdφ
Эта работа идет на увеличение кинетической энергии тела,
то есть
I 2
Md d (
)
2
d
если I=const, то Mdφ=Iωdω, но
dt
d
тогда
Md I
d или
dt
d
M I
I
dt
Это и есть основное уравнение
вращательного движения.

18.

Момент импульса
Момент импульса момент количества движения
материальной точки относительно точки О, определяется
подобно моменту силы, как векторное произведение радиусвектора на импульс
L = [r p] =m [r V].
Здесь р = mV – импульс точки.
Проекция
(составляющая) момента L на ось z,
проходящую через точку О, называется моментом импульса
относительно этой оси Lz.
При вращательном движении тела момент импульса играет
роль аналогичную роли импульса при движении точки.

19.

Момент импульса
Момент импульса i-го элемента, Li = mi[RiVi], для твердого
тела:
L = mi[RiVi] == mi[Ri ωRi] = ω mi Ri 2
но последняя сумма – ни что иное, как момент инерции т.е.
получаем
L = I ω,
это уравнение аналогично уравнению p=mV для
материальной точки.

20.

Момент импульса
Продифференцируем выражение для момента импульса по
времени:
dL/dt =d[rp] /dt = [ dr/dt p] + [r dp/dt]
первое слагаемое =0, т.к. это векторное произведение
параллельных векторов.
dp/dt =f по 2 з-ну Н., следовательно
dL/dt = [r f ] =M
Это уравнение аналог второго закона Ньютона в виде
dp/dt =f.
или, учитывая, что Lz = Iω,
dL/dt = I dω/dt =M
отсюда следует, что если момент внешних сил равен 0, то
L=const - Это - Закон сохранения момента импульса.

21.

Момент импульса
Следует отметить, что все выше сказанное
относится к вращению вокруг неподвижной оси,
в других случаях связь L и ω значительно
усложняется.

22.

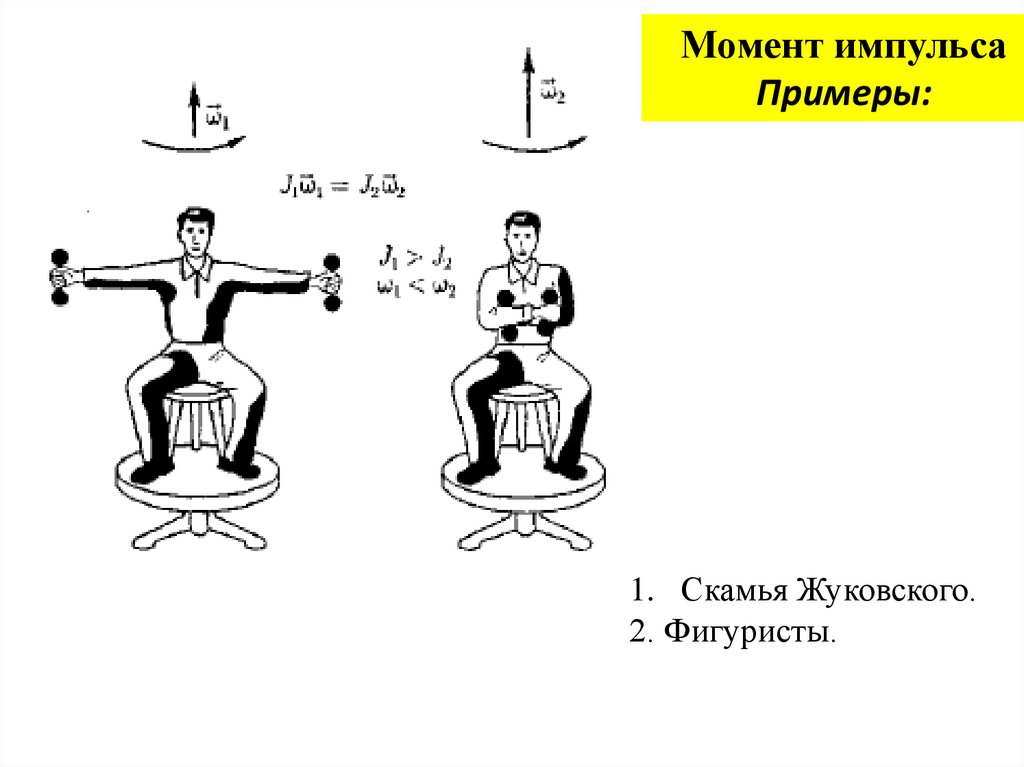
Момент импульса
Примеры:
1. Скамья Жуковского.
2. Фигуристы.

23.

Момент импульса
Примеры:
Если человек, стоящий на скамье Жуковского,
приводит во вращение колесо, то сам начинает
вращаться в противоположную сторону.

24.

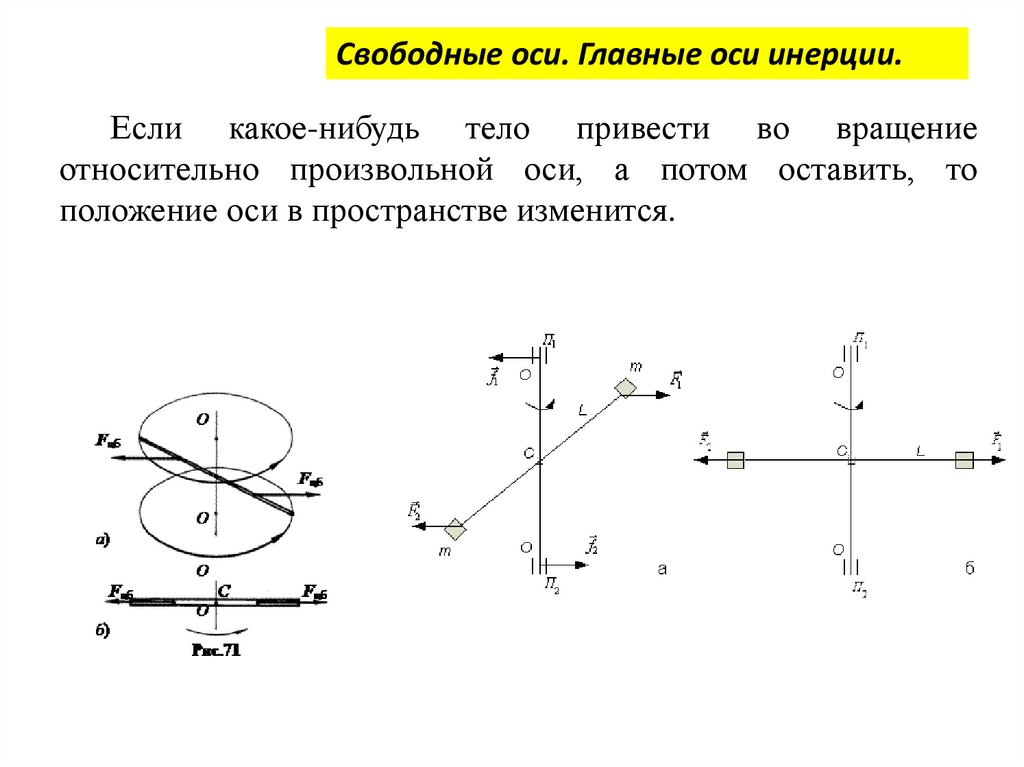
Свободные оси. Главные оси инерции.
Если какое-нибудь тело привести во вращение
относительно произвольной оси, а потом оставить, то
положение оси в пространстве изменится.

25.

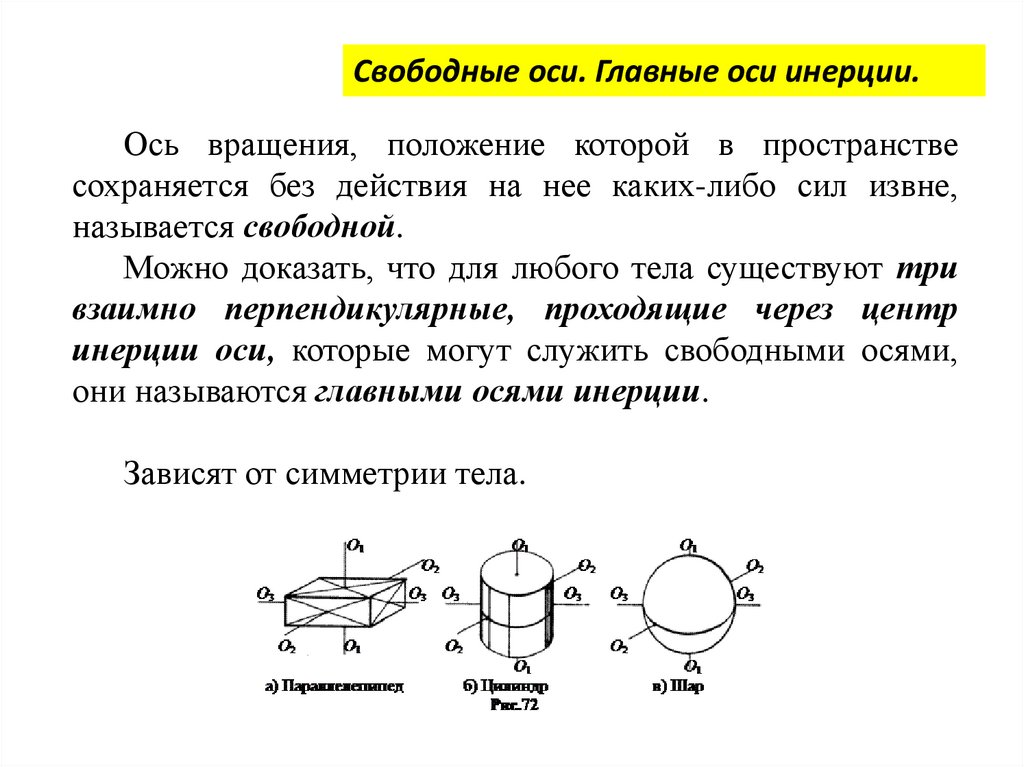
Свободные оси. Главные оси инерции.
Ось вращения, положение которой в пространстве
сохраняется без действия на нее каких-либо сил извне,
называется свободной.
Можно доказать, что для любого тела существуют три
взаимно перпендикулярные, проходящие через центр
инерции оси, которые могут служить свободными осями,
они называются главными осями инерции.
Зависят от симметрии тела.

26.

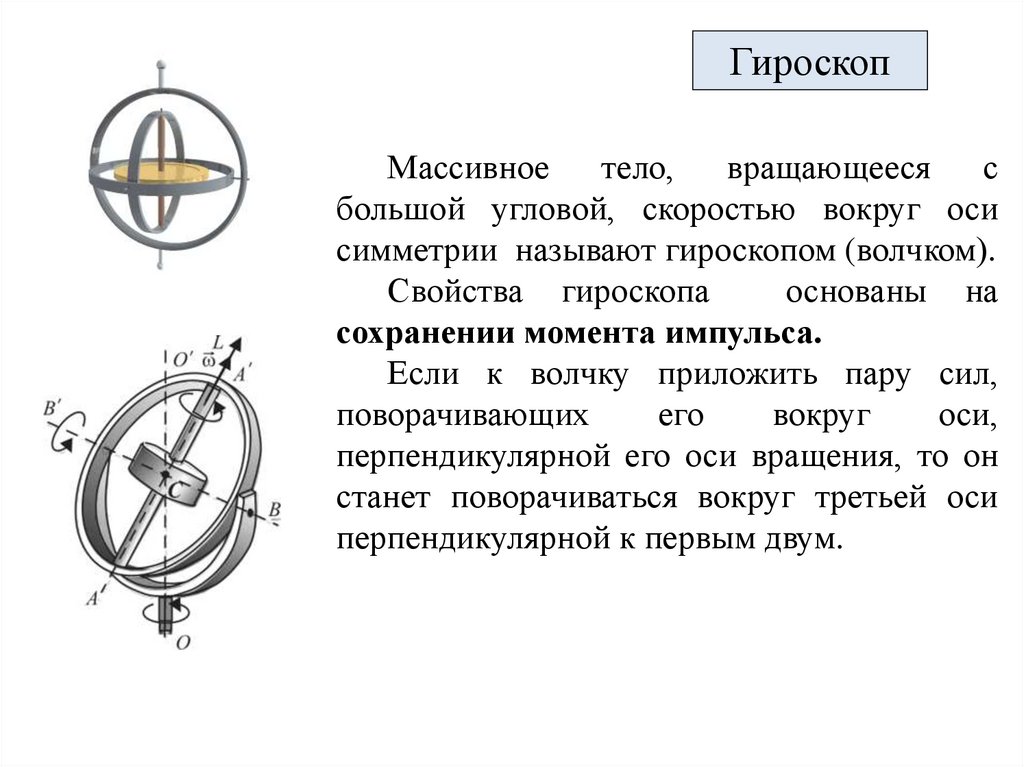
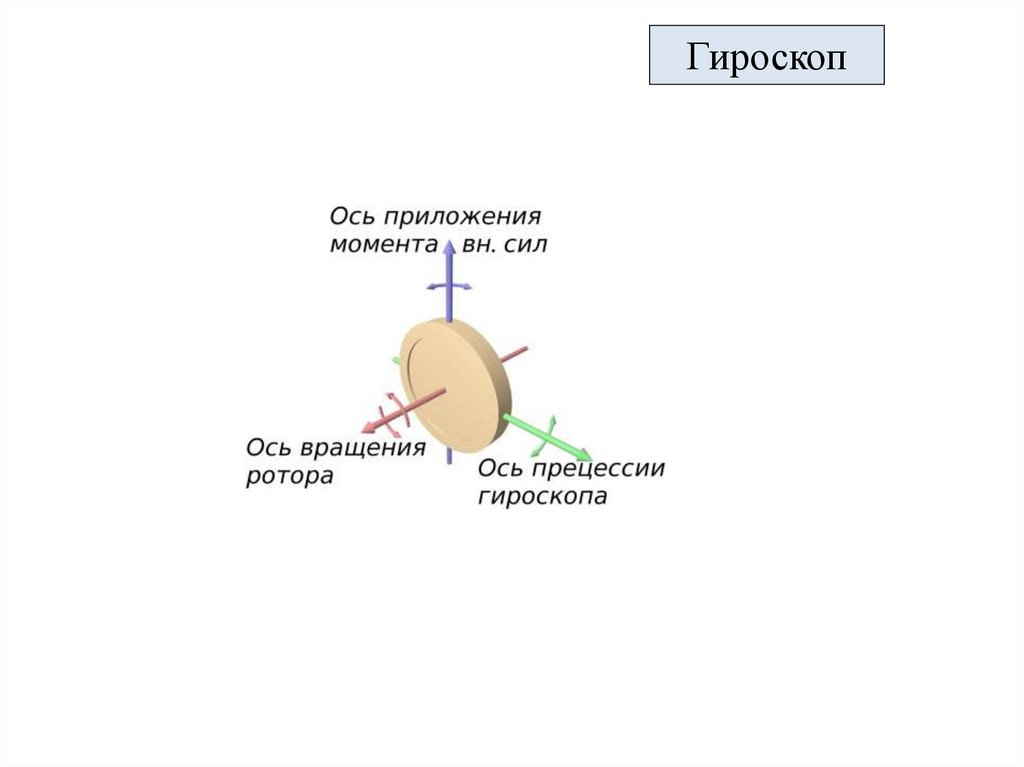
Гироскоп
Массивное
тело,
вращающееся
с
большой угловой, скоростью вокруг оси
симметрии называют гироскопом (волчком).
Свойства гироскопа
основаны на
сохранении момента импульса.
Если к волчку приложить пару сил,
поворачивающих
его
вокруг
оси,
перпендикулярной его оси вращения, то он
станет поворачиваться вокруг третьей оси
перпендикулярной к первым двум.

27.

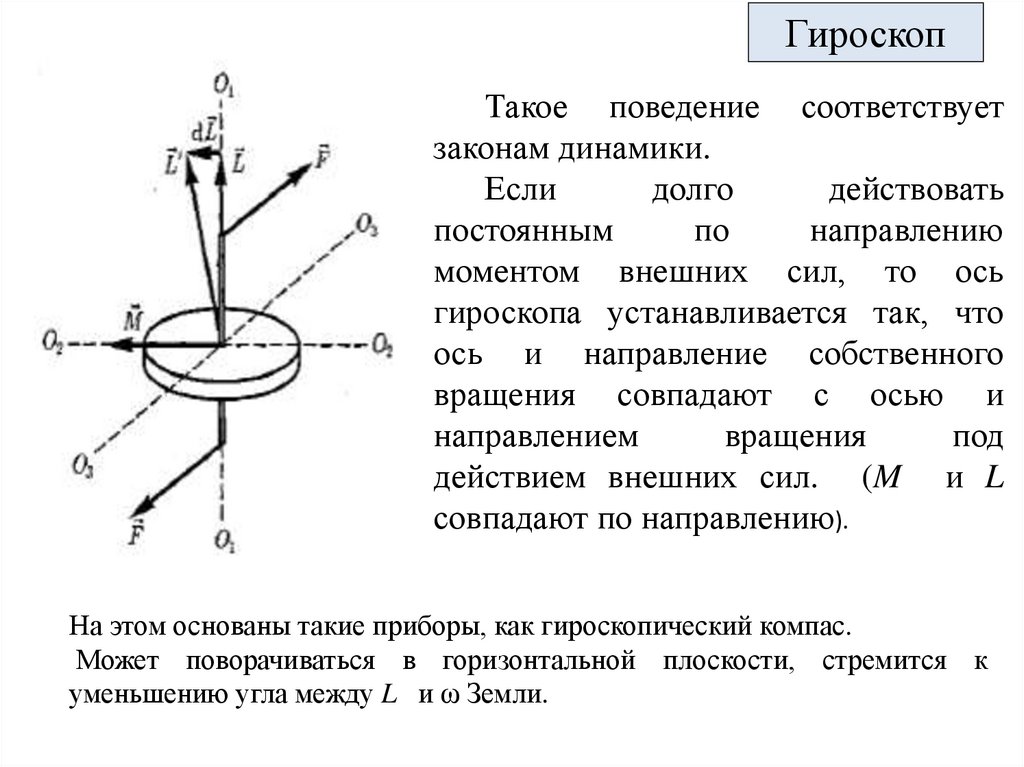
Гироскоп
Такое поведение соответствует
законам динамики.
Если
долго
действовать
постоянным
по
направлению
моментом внешних сил, то ось
гироскопа устанавливается так, что
ось и направление собственного
вращения совпадают с осью и
направлением
вращения
под
действием внешних сил. (M и L
совпадают по направлению).
На этом основаны такие приборы, как гироскопический компас.
Может поворачиваться в горизонтальной плоскости, стремится к
уменьшению угла между L и ω Земли.

28.

Гироскоп

29.

Аналогии между вращательным движением
твердого тела и движением точки
m
V
a
P=mV F=ma
I
ω
β
L=I ω
M=Iβ
M=dL/dt

30.

y
2
1
1
2
3
4
x
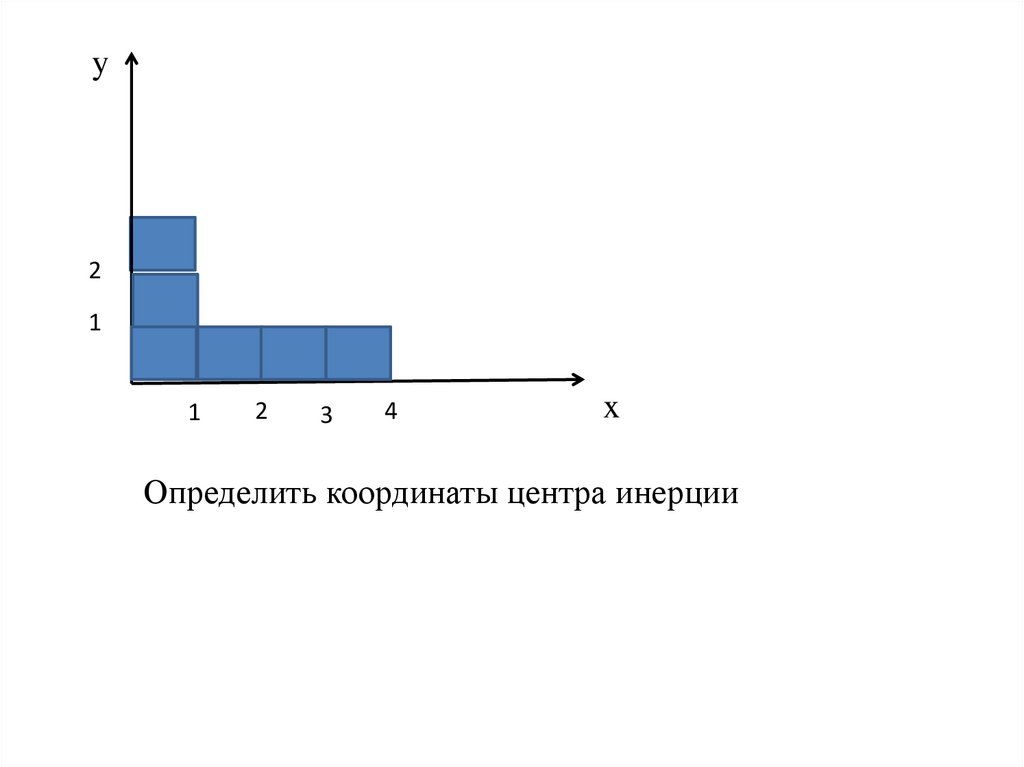
Определить координаты центра инерции

31.

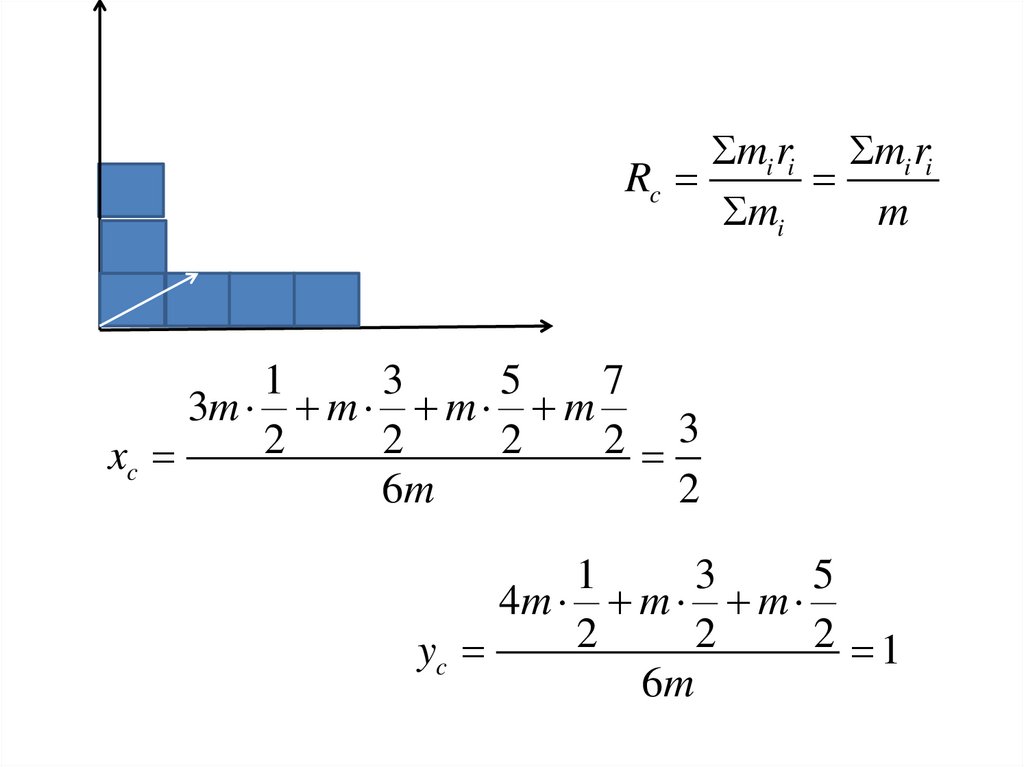
mi ri mi ri
Rc
mi
m
1
3
5
7
3m m m m
3
2
2
2
2
xc
6m
2
1
3
5
4m m m
2
2
2 1
yc
6m

32.

Вопросы
1. Сколько степеней свободы имеет твердое тело?
2. Как определяется центр инерции твердого тела?
3. Дайте определение момента силы
4. Как определяется момент инерции неточечного тела?
5. Может ли одно и тоже тело иметь несколько различных
моментов инерции?
6. Чему равен момент импульса (определение)?
7. Какое уравнение называется основным уравнением динамики
вращательного движения?
8. Как связаны момент импульса и момент силы?
9. Сформулируйте теорему Штейнера.
10.Как вычисляется работа внешних сил при вращении твердого
тела?
11.Чему равна кинетическая энергия вращающегося тела?
12.Как связаны момент импульса и момент инерции?
13. Какие оси называются свободными?