Тема №2. Векторная графика

1. Компьютерная графика

Москин Николай Дмитриевич
Институт математики и информационных
технологий
Петрозаводский государственный университет
1

2. § 2 Векторная графика

Рассмотрим два подхода к графическому моделированию: растровая и векторная графика.
• В растровой графике изображение моделируется с
помощью массива значений пикселей.
• В векторной графике изображение создается из
геометрических фигур, которые легко описываются с
помощью математических выражений. При этом
описания получаются компактными, изображения
можно легко редактировать и масштабировать
без потери качества.
2

3. Растровая и векторная графика

Векторное изображение
мака.
Растровое изображение
бабочки.
3

4. Документ на графическом языке SVG

Это описание красного квадрата с синими контурами:
<?xml version=“1.0” encoding=“utf-8”?>
<!DOCTYPE svg PUBLIC “-//W3C//DTD SVG 1.0//EN”
“http://www.w3.org/TR/2001/REC-SVG-20010904/
DTD/svg10.dtd”>
<svg xmlns=“http:www.w3.org/2000/svg”>
<path fill=“#F8130D” stroke=“#E338B” stroke-width=“20”
d=“M118, 118H10V10h108V118z”/>
</svg>
4

5. Геометрические фигуры

Линии и ломаные линии;
Многоугольники;
Окружности и эллипсы;
Класс гладких кривых – кривых Безье;
Текст (в некоторых компьютерных
шрифтах буквы создаются из кривых
Безье).
5

6. Кривые Безье

Кривые Безье были разработаны в 60-х годах XX
века независимо друг от друга Пьером Безье из
автомобилестроительной компании «Рено» и
Полем де Касталье (Кастельжо) из компании
«Ситроен», где применялись для проектирования
кузовов автомобилей.
Благодаря простоте задания и манипуляции,
кривые Безье нашли широкое применение в
компьютерной графике для представления
гладких линий. Являются частным случаем
многочленов С. Н. Бернштейна, описанных
1912 году.
в
6

7. Виды кривых Безье

Линейная кривая Безье
p(t)=(1-t)P0+tP1, 0≤t≤1
Квадратичная кривая Безье
задаётся тремя опорными
точками: P0, P1 и P2.
p(t)=(1-t)2P0+2t(1-t)P1+t2P2
Кубическая кривая Безье описывается
следующим уравнением:
p(t)=(1-t)3P0+3t(1-t)2P1+3t2(1-t)P2+t3P3
7

8. Многочлены Бернштейна

Кривую порядка m можно задать параметрически
следующим образом:
Здесь Bim(t) задаются формулами:
8

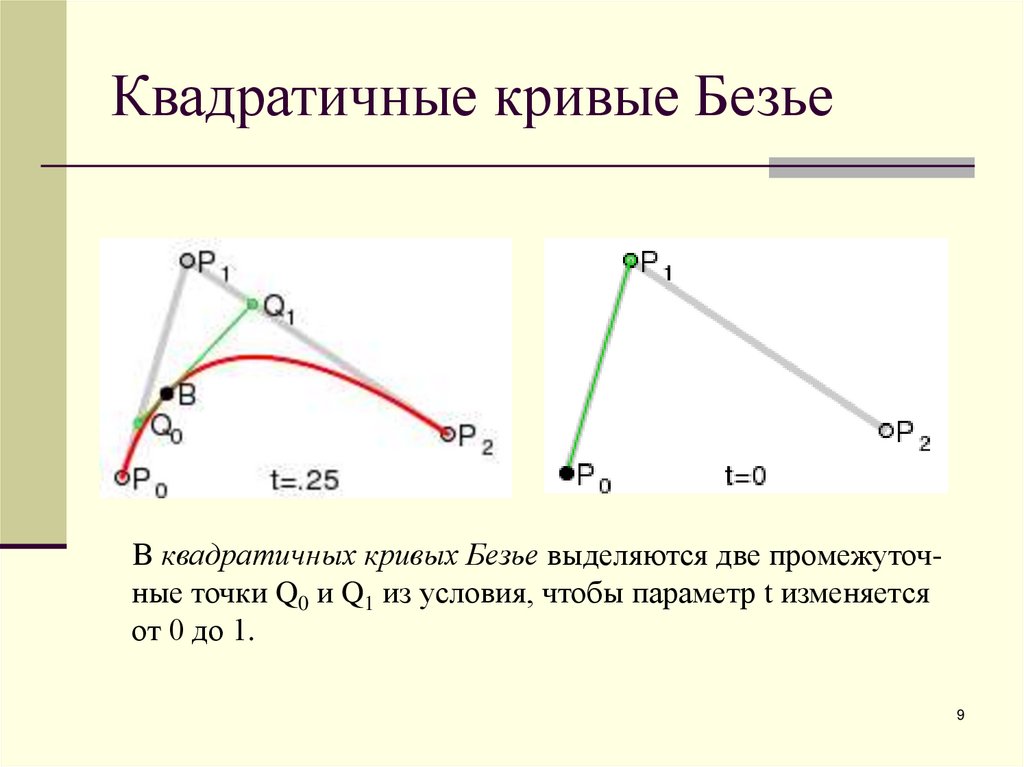
9. Квадратичные кривые Безье

В квадратичных кривых Безье выделяются две промежуточные точки Q0 и Q1 из условия, чтобы параметр t изменяется
от 0 до 1.
9

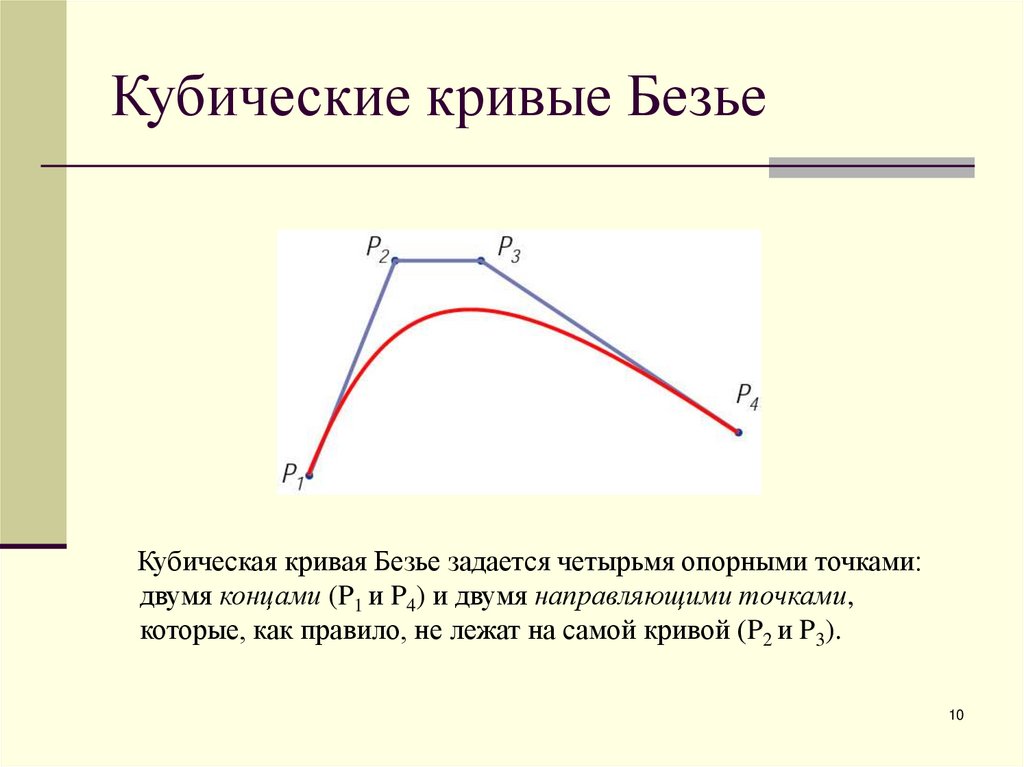
10. Кубические кривые Безье

Кубическая кривая Безье задается четырьмя опорными точками:
двумя концами (P1 и P4) и двумя направляющими точками,
которые, как правило, не лежат на самой кривой (P2 и P3).
10

11. Схема построения кривой Безье

1. Найдем середины отрезков P12,
P23 и P34, соединяющих точки P1 и
P2, P2 и P3, P3 и P4. Построим
отрезки, соединяющие точки P12 и
P23, а также P23 и P34.
2. Найдем середины P123 и P234,
соединим их и найдем середину
Q этого последнего отрезка (по
построению Q будет лежать на
кривой). Аналогично строим
левую и правую половины кривой
для точек P1, P12, P123, Q и Q, P234,
P34, P4 и т.д.
11

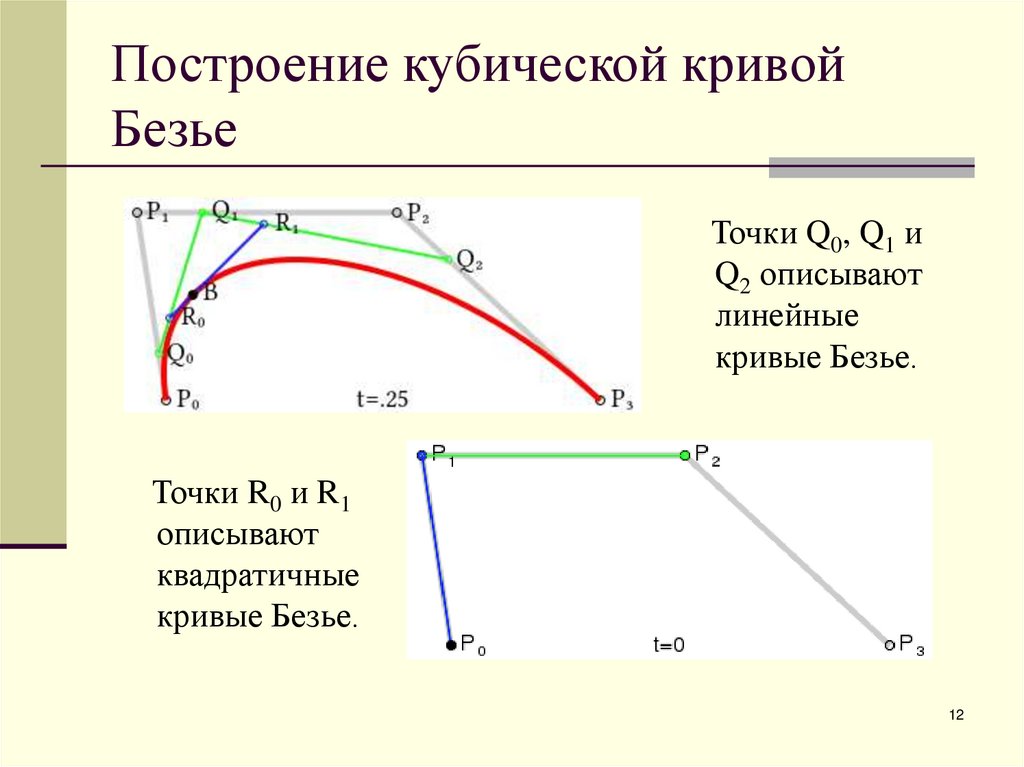
12. Построение кубической кривой Безье

Точки Q0, Q1 и
Q2 описывают
линейные
кривые Безье.
Точки R0 и R1
описывают
квадратичные
кривые Безье.
12

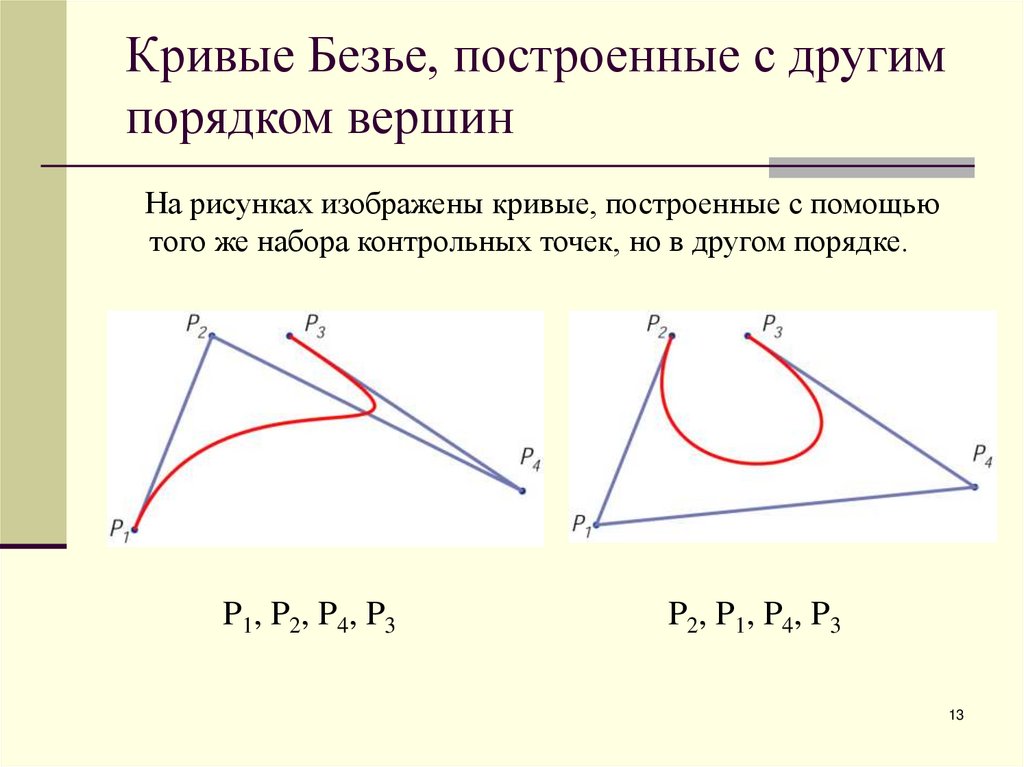
13. Кривые Безье, построенные с другим порядком вершин

На рисунках изображены кривые, построенные с помощью
того же набора контрольных точек, но в другом порядке.
P1, P2, P4, P3
P2, P1, P4, P3
13

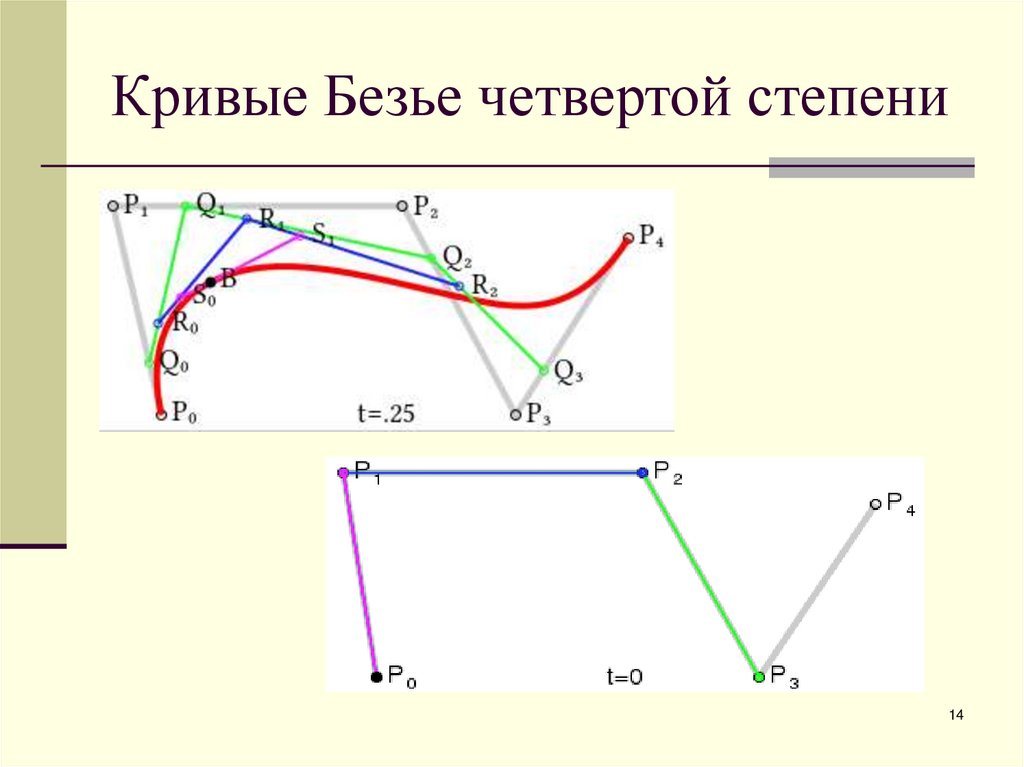
14. Кривые Безье четвертой степени

14

15. Траектории

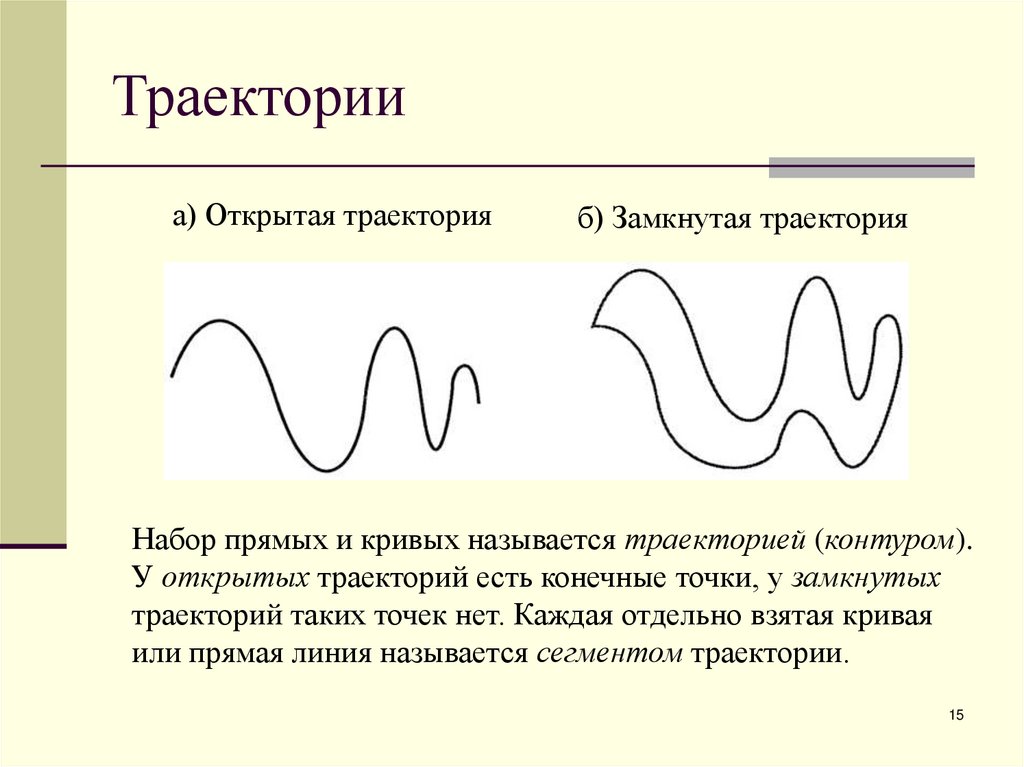
а) Открытая траектория
б) Замкнутая траектория
Набор прямых и кривых называется траекторией (контуром).
У открытых траекторий есть конечные точки, у замкнутых
траекторий таких точек нет. Каждая отдельно взятая кривая
или прямая линия называется сегментом траектории.
15

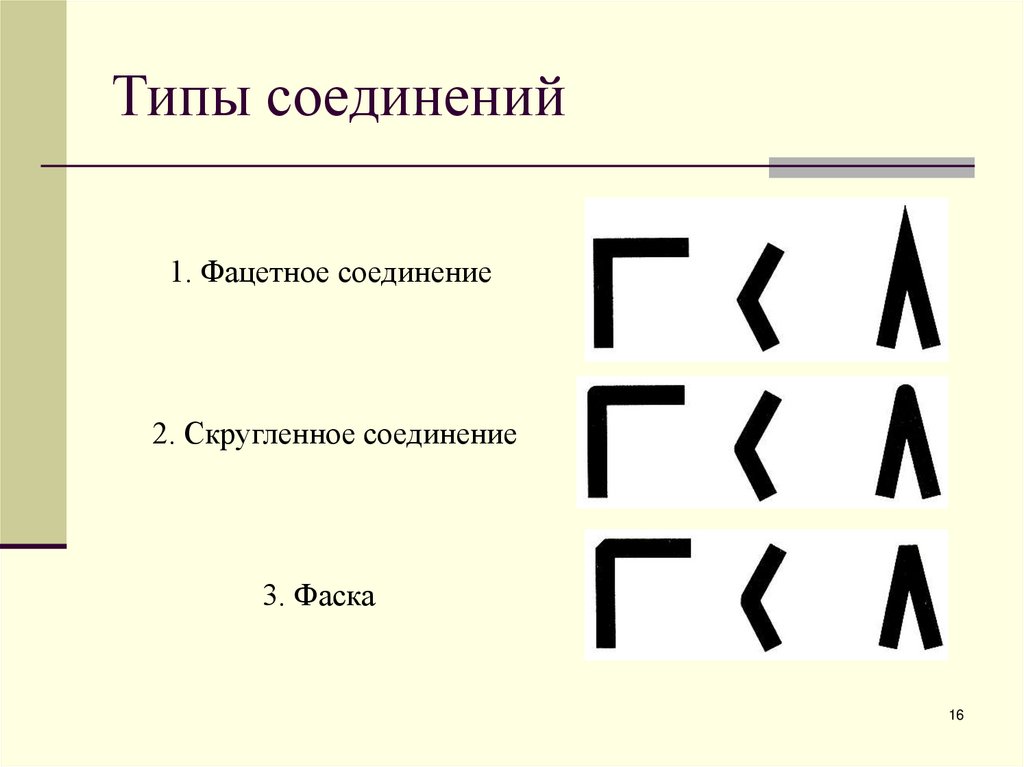
16. Типы соединений

1. Фацетное соединение
2. Скругленное соединение
3. Фаска
16

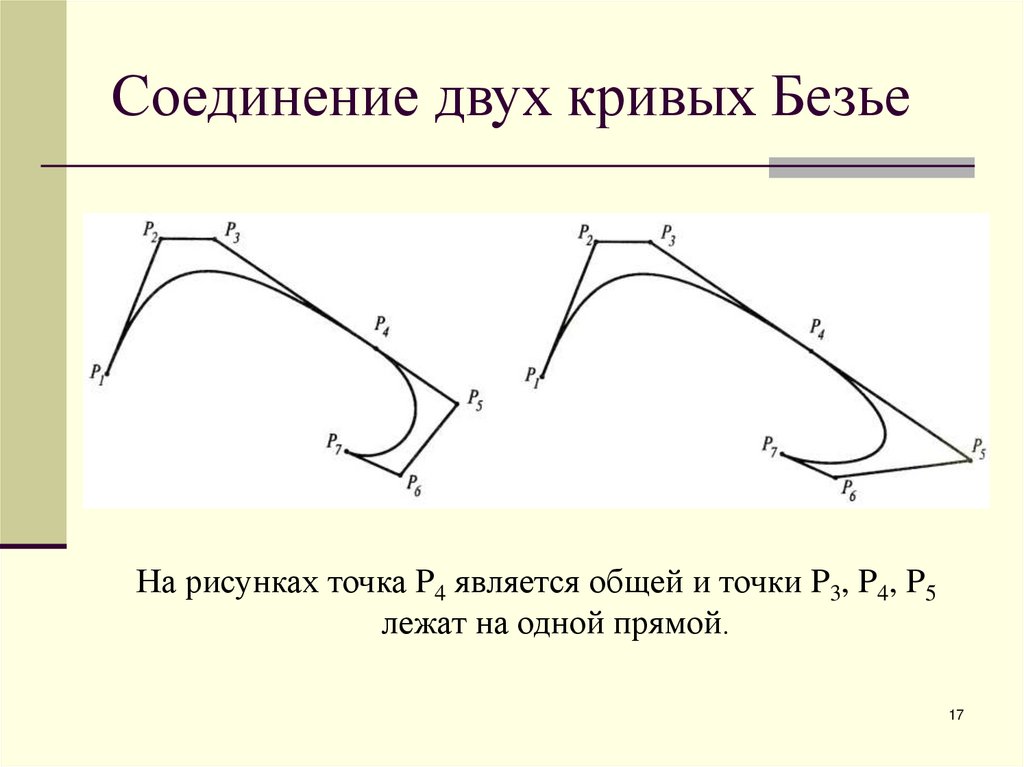
17. Соединение двух кривых Безье

На рисунках точка P4 является общей и точки P3, P4, P5
лежат на одной прямой.
17

18. Интерполяция

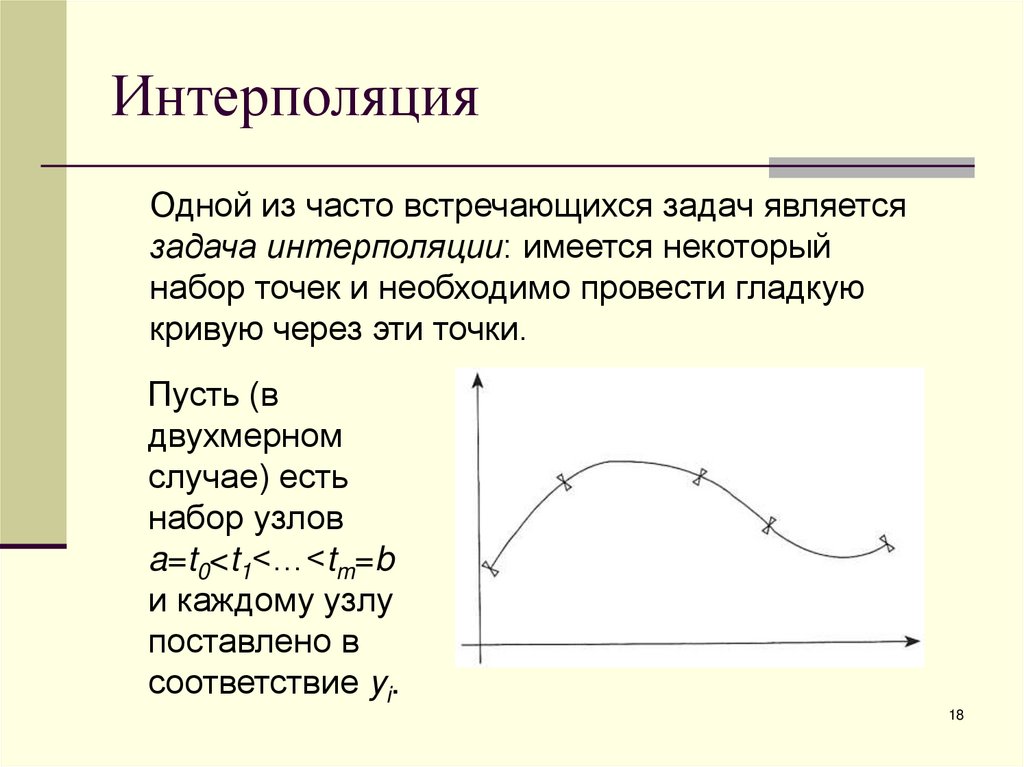
Одной из часто встречающихся задач является
задача интерполяции: имеется некоторый
набор точек и необходимо провести гладкую
кривую через эти точки.
Пусть (в
двухмерном
случае) есть
набор узлов
a=t0<t1<…<tm=b
и каждому узлу
поставлено в
соответствие yi.
18

19. Многочлен Лагранжа

Известно, что для этой задачи всегда существует
многочлен степени m (и притом единственный),
называемый интерполяционным многочленом
Лагранжа:
Здесь функция φ(t) задается следующим образом:
19

20. Многочлен Лагранжа

Однако использование интерполяционного
многочлена Лагранжа часто бывает неудобным
по следующим причинам:
порядок многочлена зависит от числа точек и
может быть очень высок;
изменение любой из точек ведет к изменению
всего многочлена;
добавление новой точки увеличивает степень
многочлена и приводит к необходимости его
полной перестройки.
20

21. Сплайны

Поэтому довольно часто для интерполяции
используют сплайны. Функция s(t) называется
сплайном, если:
на каждом частичном отрезке [ti, ti+1] эта функция
является многочленом степени p;
она имеет непрерывные производные вплоть до
порядка p-1 на всем отрезке.
Многочлен степени p задается с помощью p+1
коэффициента. Поэтому, если есть m+1 узлов, то
нужно m(p+1) коэффициентов, чтобы однозначно
определить сплайн.
21

22. Сплайны

Сплайны позволяют задавать довольно сложную
геометрию с помощью небольшого числа
контрольных точек. Для изменения полученных
моделей достаточно просто передвинуть одну или
несколько контрольных точек.
Большинство современных систем трехмерного
моделирования поддерживают работу с
различными сплайновыми поверхностями.
22

23. Штриховка и заполнение

Строго говоря, траектория – это абстрактный
математический объект, поскольку точки
бесконечно малы, траектория должна быть
бесконечно тонкой.
Увидеть траекторию можно двумя способами:
либо применить к траектории штриховку, либо
рассматривать траекторию как контуры
геометрической фигуры и заполнить ее
сплошным цветом (или более сложными
структурами: узорами и градиентами цвета).
23

24. Градиентное заполнение

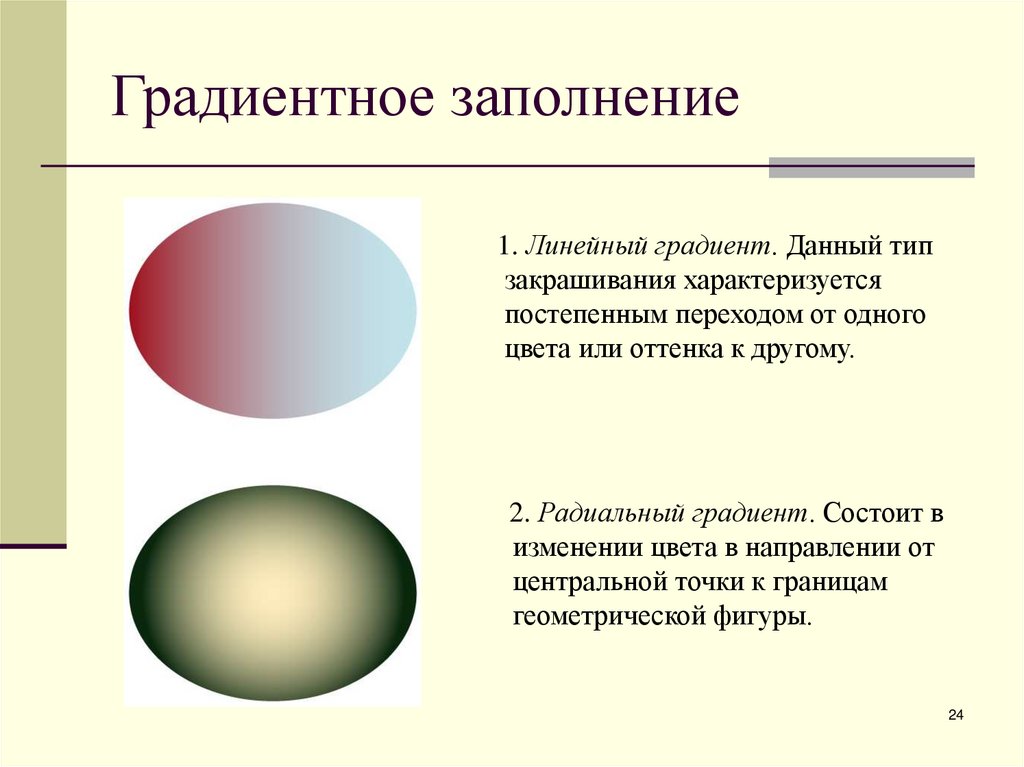
1. Линейный градиент. Данный тип
закрашивания характеризуется
постепенным переходом от одного
цвета или оттенка к другому.
2. Радиальный градиент. Состоит в
изменении цвета в направлении от
центральной точки к границам
геометрической фигуры.
24

25. Преобразования

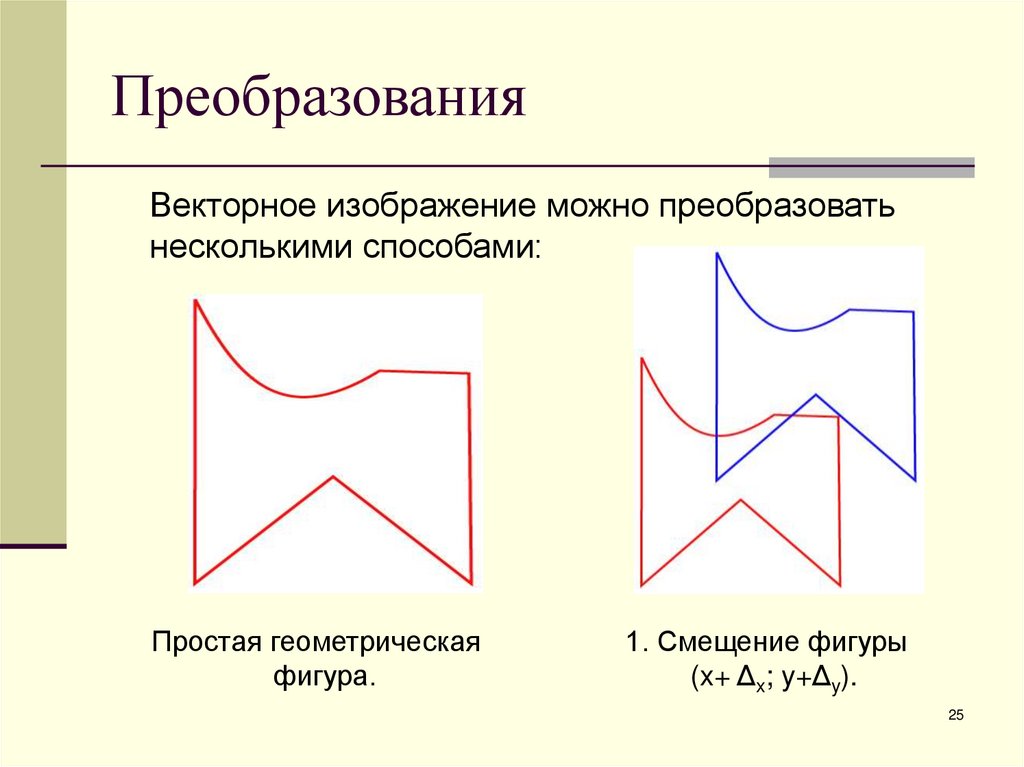
Векторное изображение можно преобразовать
несколькими способами:
Простая геометрическая
фигура.
1. Смещение фигуры
(x+ Δx; y+Δy).
25

26. Преобразования

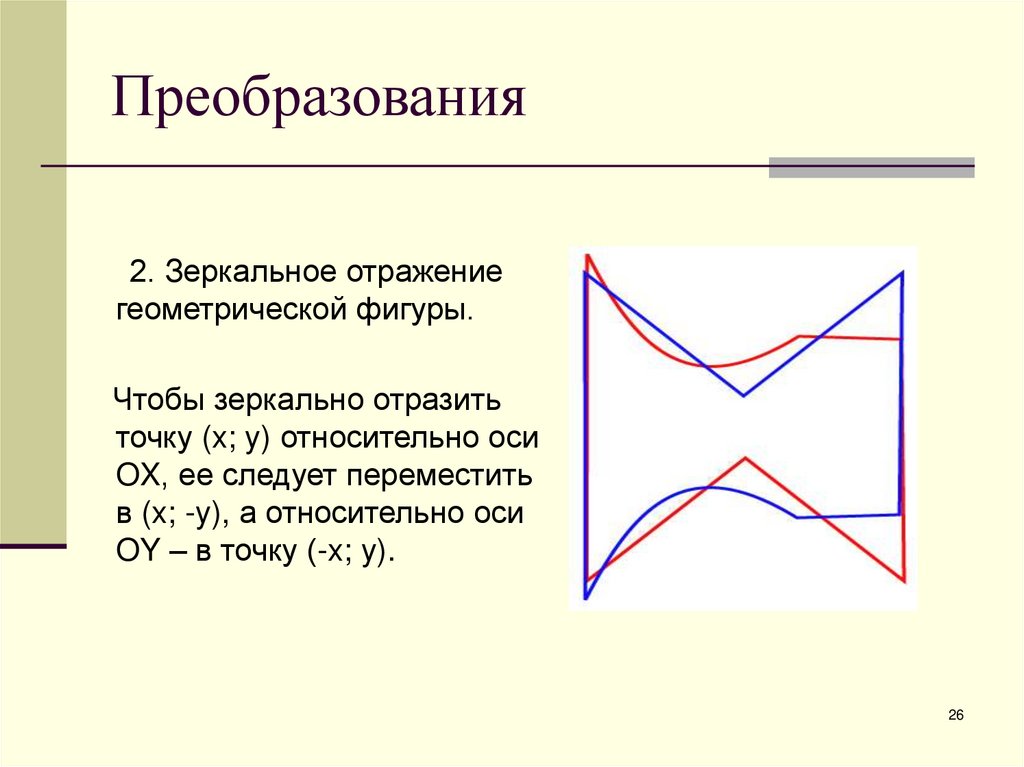
2. Зеркальное отражение
геометрической фигуры.
Чтобы зеркально отразить
точку (x; y) относительно оси
OX, ее следует переместить
в (x; -y), а относительно оси
OY – в точку (-x; y).
26

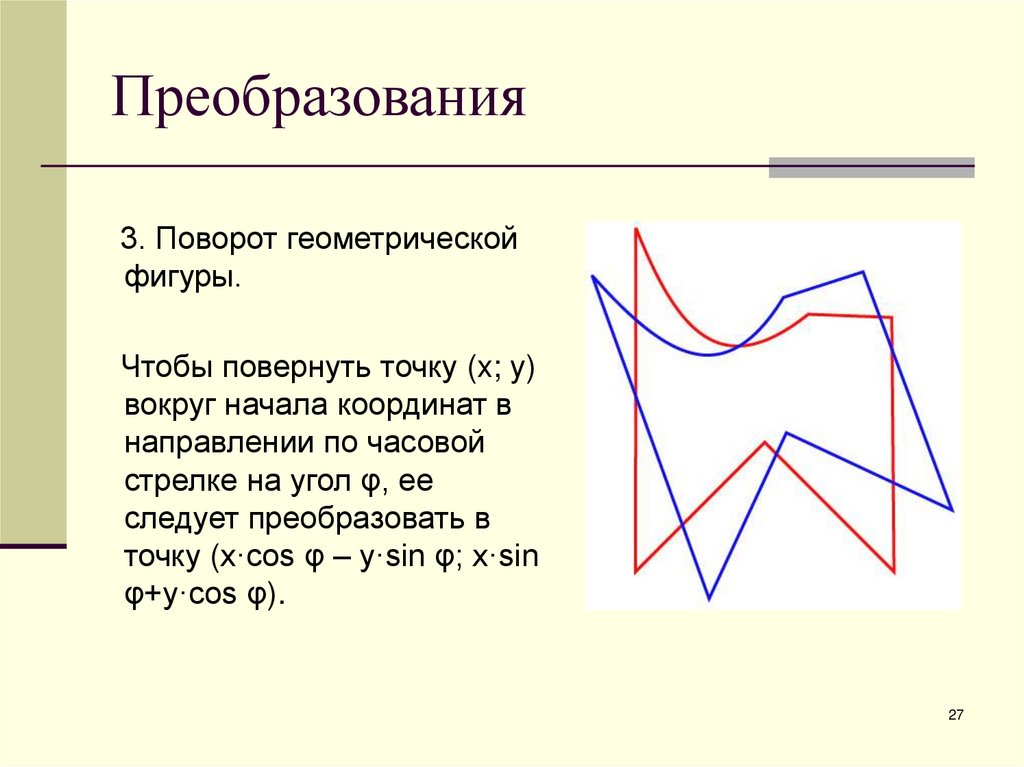
27. Преобразования

3. Поворот геометрической
фигуры.
Чтобы повернуть точку (x; y)
вокруг начала координат в
направлении по часовой
стрелке на угол φ, ее
следует преобразовать в
точку (x·cos φ – y·sin φ; x·sin
φ+y·cos φ).
27

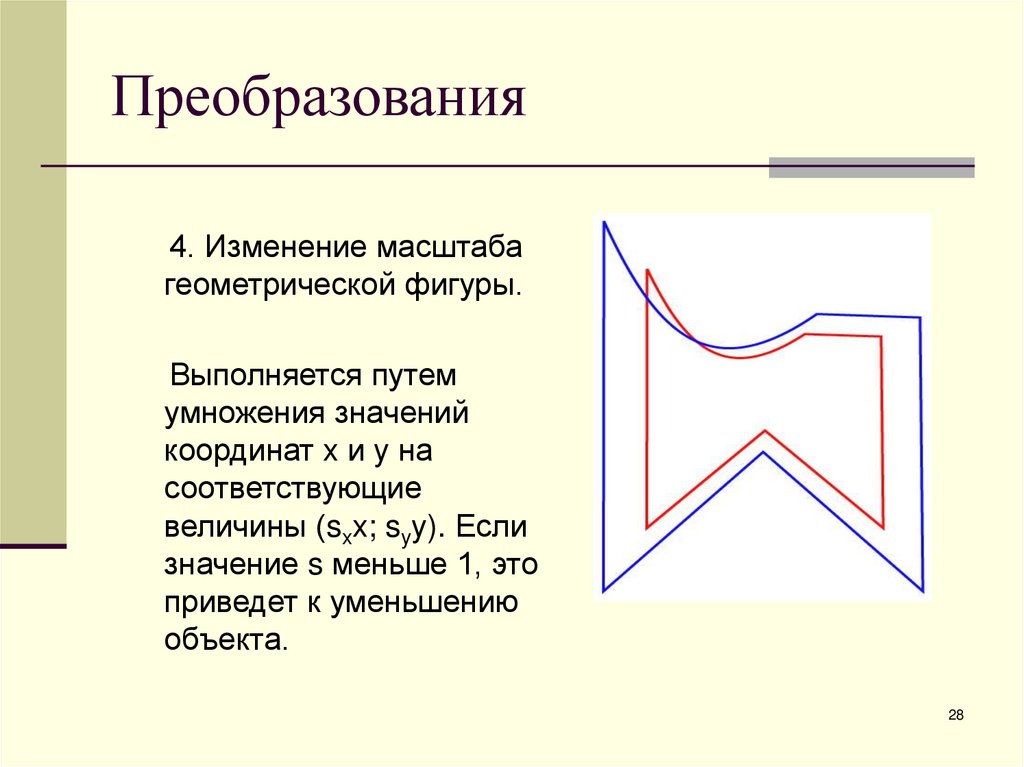
28. Преобразования

4. Изменение масштаба
геометрической фигуры.
Выполняется путем
умножения значений
координат x и y на
соответствующие
величины (sxx; syy). Если
значение s меньше 1, это
приведет к уменьшению
объекта.
28

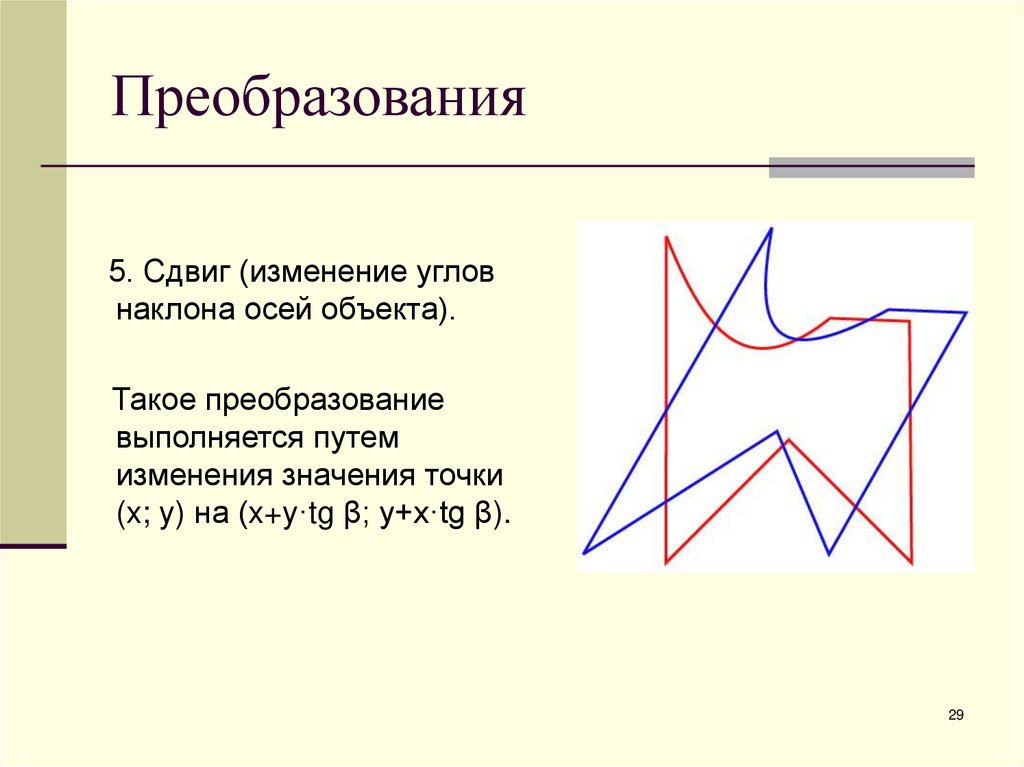
29. Преобразования

5. Сдвиг (изменение углов
наклона осей объекта).
Такое преобразование
выполняется путем
изменения значения точки
(x; y) на (x+y·tg β; y+x·tg β).
29

30. Преобразования в SVG: matrix

Matrix (в качестве значения атрибута transform)
представляет собой способ компактной записи
серии преобразований:
matrix(a, b, c, d, e, f)
Каждое из основных
преобразований
представляется
своей матрицей и
соответствующей
командой matrix.
30

31. Смещение

Смещение можно задать следующим образом:
Пример: <rect x="25" y="25" width="50" height="25"
fill="palegreen" stroke="red" stroke-width="2"
transform="matrix(1, 0, 0, 1, 100, 75)"/>
31

32. Поворот и масштабирование

32

33. Сдвиг: SkewX и SkewY

33

34. Произведение матриц

Несколько команд можно записать в виде одной
матрицы. Результирующая матрица представляет
собой произведение отдельных матриц.
34

35. Пример

Перемножим матрицы для translate(-6,0) и skewX(45):
Результирующая матрица: matrix(1, 0, 1, 1, -6, 0).
35

36. Визуализация прямой линии

При визуализации отрезка
можно задать значения
координат его концов (xa,ya),
(xb,yb) плюс общую форму
описания подобных кривых.
Если уравнение прямой линии
записывается как y=kx+b, то k
и b можно найти по формулам:
k=(yb-ya)/(xb-xa)
b=(xbya-xayb)/(xb-xa)
36

37. Алгоритм Брезенхэма

Алгоритм Брезенхэма определяет, какие точки
двумерного растра нужно закрасить, чтобы получить
близкое приближение прямой линии между двумя
заданными точками (xa, ya), (xb, yb).
Это один из классических алгоритмов в машинной
графике. Он был разработан Джеком Элтоном
Брезенхэмом в компании IBM в 1962 году. Алгоритм
широко используется, в частности, для рисования
линий на экране компьютера.
37

38. Алгоритм Брезенхэма

Отрезок проводится между
двумя точками - (xa, ya) и
(xb, yb), где в этих парах
указаны столбец и строка
соответственно. Сначала
предположим, что линия
идёт вправо и вниз, причём
горизонтальное расстояние
xb-xa > yb-ya.
Общая формула линии между двумя точками:
38

39. Простейший алгоритм растрового представления отрезка

Вычисления значений функции y=kx+b можно избежать.
39

40. Простейший алгоритм растрового представления отрезка

Для этого используем в цикле рекуррентные соотношения,
так как при изменении x на 1 значение y меняется на k.
40

41. Недостатки

Приведенные простейшие пошаговые алгоритмы
построения отрезка имеют ряд недостатков:
1. Выполняют операции над числами с
плавающей точкой, а желательно было бы
работать с целочисленной арифметикой;
2. На каждом шаге выполняется операция
округления, что также снижает быстродействие.
Эти недостатки устранены в следующем
алгоритме Брезенхэма.
41

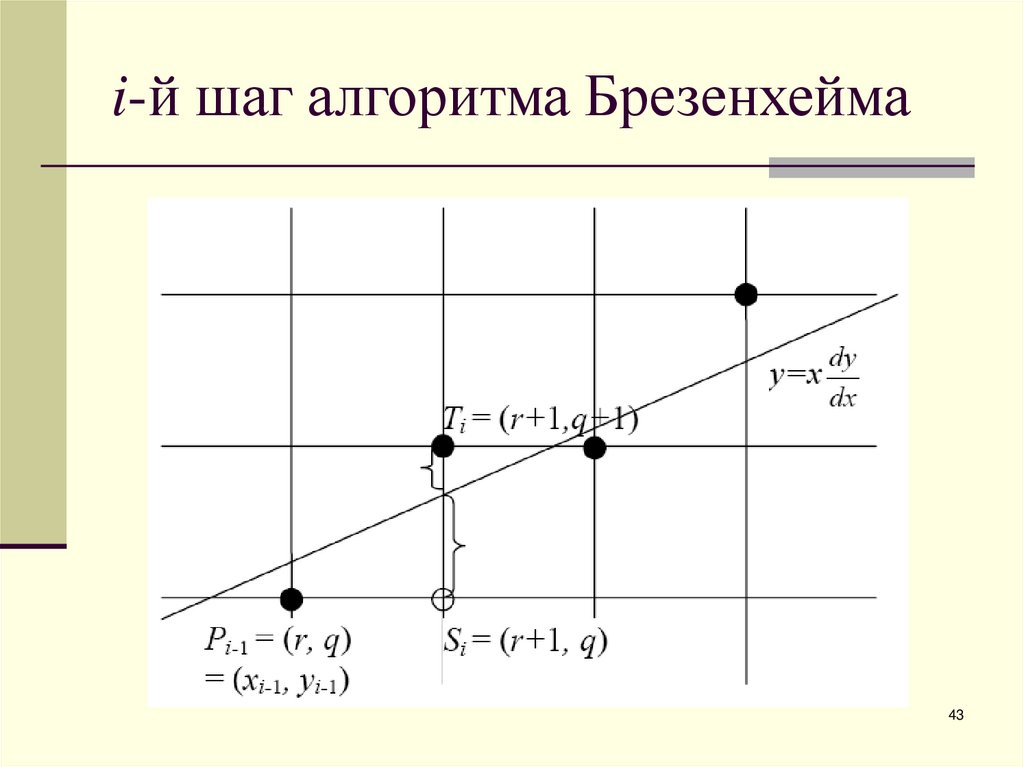
42. Алгоритм Брезенхэма

Будем считать, что тангенс угла наклона отрезка
принимает значение в диапазоне от 0 до 1.
Рассмотрим i-й шаг алгоритма. На этом этапе
пиксель Pi-1 уже найден как ближайший к
реальному отрезку. Требуется определить, какой из
пикселей (Ti или Si) будет установлен следующим.
В алгоритме используется управляющая
переменная di, которая на каждом шаге
пропорциональна разности между S и T. Если
S < T, то Si ближе к отрезку, иначе выбирается Ti.
42

43. i-й шаг алгоритма Брезенхейма

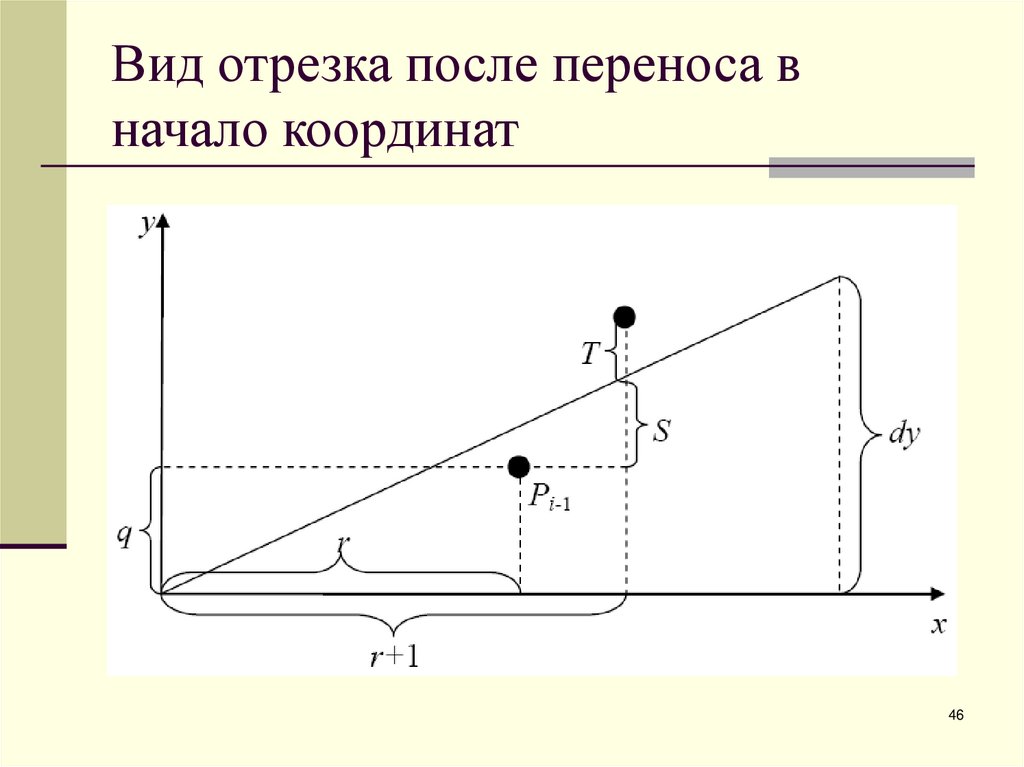
43

44. Перенос в начало координат

Пусть изображаемый отрезок проходит из точки
(xa, ya) в точку (xb, yb). Исходя из начальных
условий, точка (xa, ya) ближе к началу координат.
Тогда перенесем оба конца отрезка с помощью
преобразования T(–xa, –ya), так чтобы первый
конец отрезка совпал с началом координат.
Начальной точкой отрезка стала точка (0, 0),
конечной точкой (dx, dy), где dx = xb – xa, dy = yb – ya.
44

45. Перенос в начало координат

Уравнение прямой в этом случае будет иметь вид:
Обозначим координаты точки Pi-1 после переноса
через (r, q). Тогда Si = (r+1, q) и Ti = (r+1, q+1).
Из подобия треугольников на рисунке запишем:
45

46. Вид отрезка после переноса в начало координат

46

47. Алгоритм Брезенхэма

Выразим S:
T можно представить как T = 1 – S. Тогда:
Помножим левую и правую часть на dx:
47

48. Алгоритм Брезенхэма

Величина dx положительная, поэтому неравенство
dx(S – T) < 0 можно использовать в качестве проверки
при выборе пикселя. Обозначим di = dx(S – T), тогда
Поскольку r = xi -1 и q = yi -1, то
Прибавляя 1 к каждому индексу найдем di+1:
48

49. Итеративная формула

Вычитая di из di+1 получим
Известно, что xi – xi-1 = 1, тогда
Отсюда выразим di+1:
49

50. Итеративная формула

Таким образом, получили итеративную формулу
вычисления управляющего коэффициента di+1 по
предыдущему значению di. С помощью
управляющего коэффициента выбирается
следующий пиксель – Si или Ti.
Если di ≥ 0, тогда выбирается Ti и yi = yi–1+1, di+1 =
di +2 (dy – dx). Если di < 0, тогда выбирается Si и yi
= yi–1 и di+1 = di +2 dy.
50

51. Начальные значения

Начальные значения d1 с учетом того, что (x0, y0)
= (0, 0),
Преимуществом алгоритма является то, что для
работы алгоритма требуются минимальные
арифметические возможности: сложение,
вычитание и сдвиг влево для умножения на 2.
Реализация этого алгоритма выглядит
следующим образом.
51

52. Алгоритм Брезенхэма

52

53. Алгоритм Брезенхэма

53

54. Рисование окружностей

Также существует алгоритм
Брезенхэма для рисования
окружностей. По методу
построения он похож на
рисование линии. Здесь
строится дуга окружности
для первого квадранта, а
координаты точек
окружности для остальных
квадрантов получаются
симметрично.
На каждом шаге алгоритма рассматриваются три
пикселя, и из них выбирается наиболее подходящий
путём сравнения расстояний от центра до выбранного
пикселя с радиусом окружности.
54

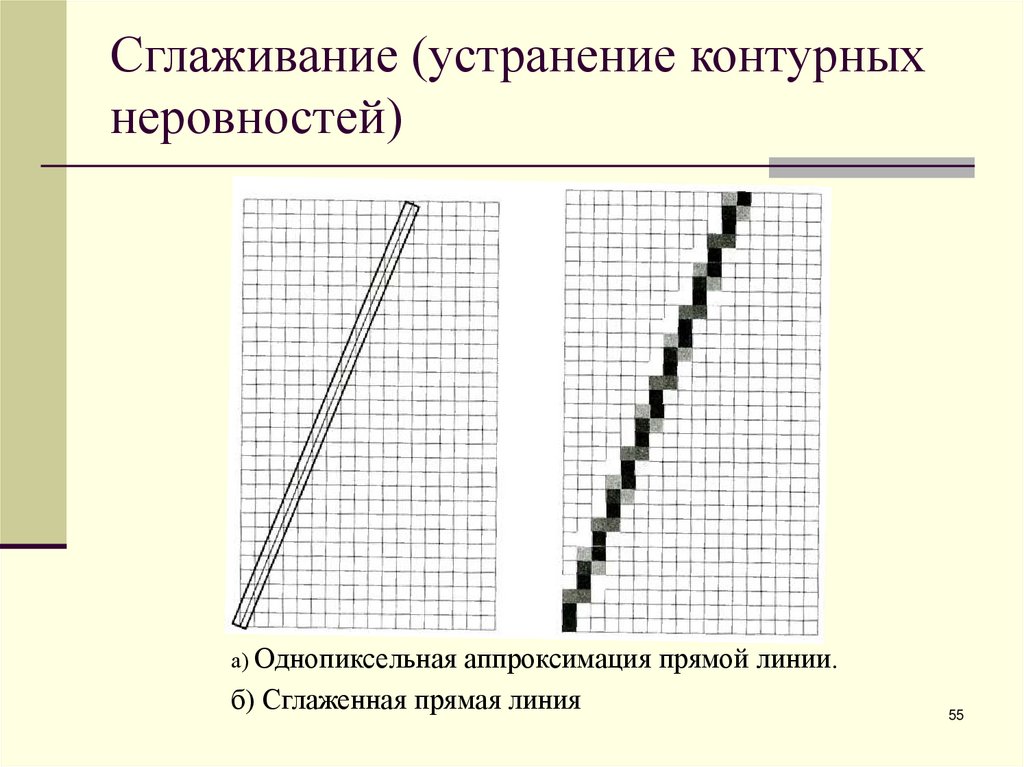
55. Сглаживание (устранение контурных неровностей)

а) Однопиксельная аппроксимация прямой линии.
б) Сглаженная прямая линия
55

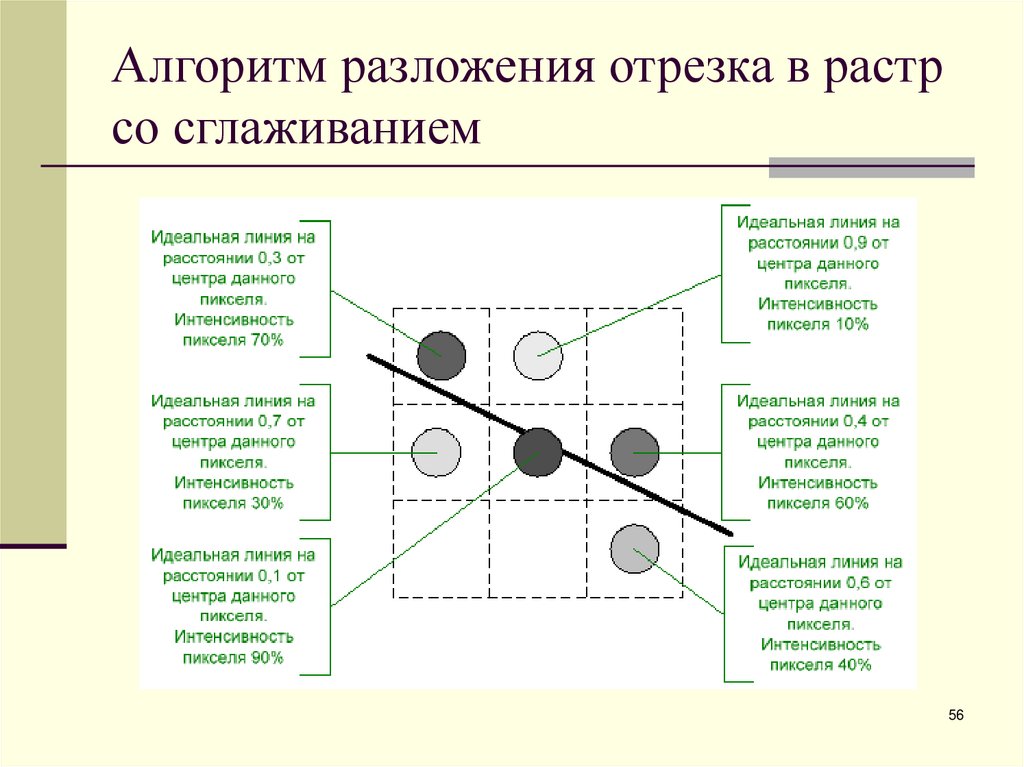
56. Алгоритм разложения отрезка в растр со сглаживанием

56

57. Текстовые объекты

Глифы – это маленькие изображения, которые можно
записать в шрифте, используя растровую графику
(широко использовались в эпоху матричных принтеров
и мониторов низкого разрешения) или векторную
графику, которая легко масштабируется.
Двумя наиболее распространенными векторными
форматами являются Type 1 от Adobe (часто
называемый просто шрифтами PostScript, хотя
существуют и другие типы шрифтов PostScript) и
TrueType. Пример растрового формата: BDF (Bitmap
Distribution Format) от компании Adobe.
57

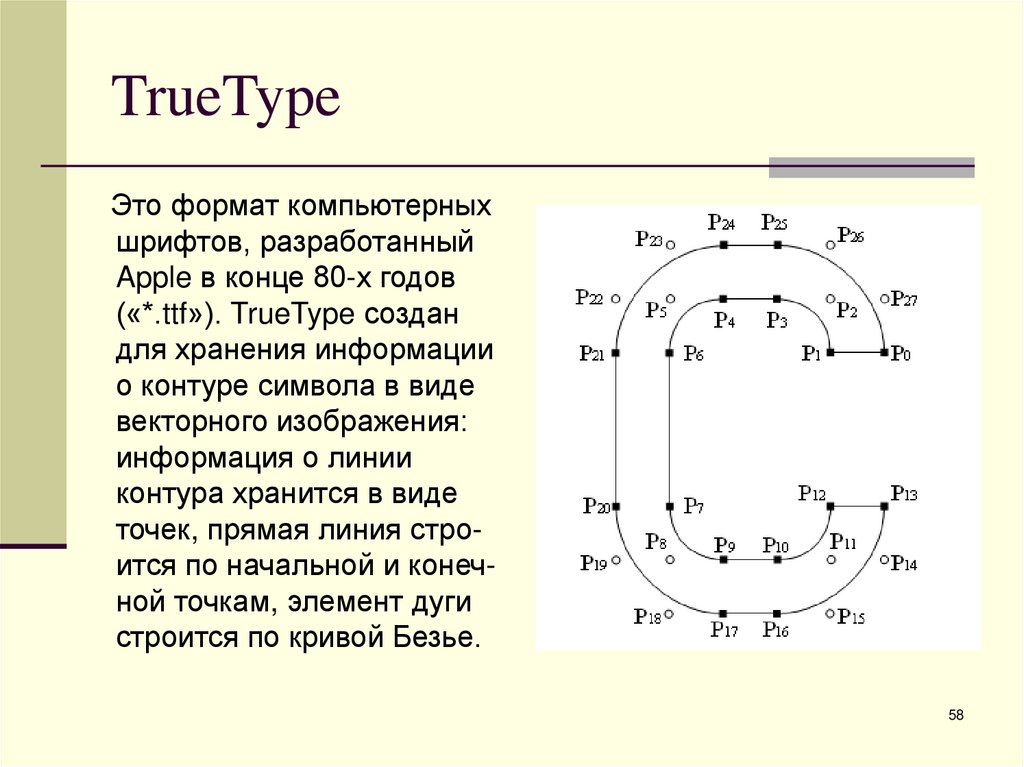
58. TrueType

Это формат компьютерных
шрифтов, разработанный
Apple в конце 80-х годов
(«*.ttf»). TrueType создан
для хранения информации
о контуре символа в виде
векторного изображения:
информация о линии
контура хранится в виде
точек, прямая линия строится по начальной и конечной точкам, элемент дуги
строится по кривой Безье.
58

59. Хинтинг

Хинтинг (хинтование) (англ. hint - намёк, совет) –
изменение контура шрифта при его растеризации
с помощью специальных программных
инструкций, заложенных в шрифтовой файл.
Используется для обеспечения более чёткой
формы букв на устройствах с низким разрешением экрана или при отображении текста в мелком кегле. TrueType позволяет хранить шрифты
как с инструкциями хинтинга, так и без них.
59

60. Хинтинг

Первая
строка без
хинтинга,
вторая с
ним. Снизу
то же самое
в масштабе
400%.
60

61. PostScript Type 1

Язык программирования PostScript был разработан
фирмой Adobe Systems для описания сложных
графических объектов. Наиболее известная
реализация языка PostScript – формат PDF (Portable
Document Format), поддерживаемый продуктами серии
Acrobat. Кроме распространенного PostScript Type 1
существуют и другие стандарты описания шрифтов –
Type 0, Type 2, Type 3 и др., однако сейчас они почти
не используются или используются для специальных
целей. В последние годы язык PostScript был
расширен, чтобы обеспечить поддержку шрифтовых
возможностей стандартов TrueType и OpenType.
61

62. OpenType

OpenType – это формат файла шрифтов, разработанный совместно Microsoft и Adobe для применения в различных операционных системах.
Преимущества:
Поддерживает Unicode-кодировку;
Могут эффективно сжиматься (это полезно для
pdf-файлов и web-страниц);
Улучшенная типографика: OpenType имеет
широкий набор глифов, включая лигатуры, дроби,
исторические символы (числа старого стиля,
капительные символы) и др.;
Улучшенный кернинг.
62

63. FreeType

FreeType – библиотека, которая используется для
растеризации шрифтов и операций над ними
(реализована на языке Си). Поддерживает форматы:
TrueType;
PostScript Type 1;
OpenType и др.
Выпускается с открытыми исходными кодами под
лицензиями GNU Public License и FreeType License.
http://www.freetype.org/
63