Лекция 10. Множества. Функции. Ч2

1. Множества. Функции.

Лекция №10 Часть 2
1

2. ПЛАН ЛЕКЦИИ

П О В Т О Р Е Н И Е И З У Ч Е Н Н О Г О М А Т Е Р ИА Л А
Виды множеств
Комбинаторика
Решение задач методом диаграмм Эйлера -Венна
Функции
2

3. ПОВТОРЯЕМ МАТЕРИАЛ

1. Что такое множество?
2. Назовите 3 способа, которыми можно задать множество.
3. Что такое универсальное множество и каково его
обозначение?
4. Дайте определение симметрической разности множеств.
5. Чем отличается разность A\B от B\A?
6. Что такое кортеж и чем он отличается от множества?
7. Что такое декартово произведение множеств, что
получается в результате этого произведения?
8. Что такое соответствие между множествами A и B? Что
называется образами и прообразами в соответствии?
9. Даны множества A = {1, 2, 3} и B = {a, b}. Найдите A × B
10.Для множества векторов V = {(1, 2, 3), (4, 5, 6), (7, 8, 9)}
найдите Pr₂V
3

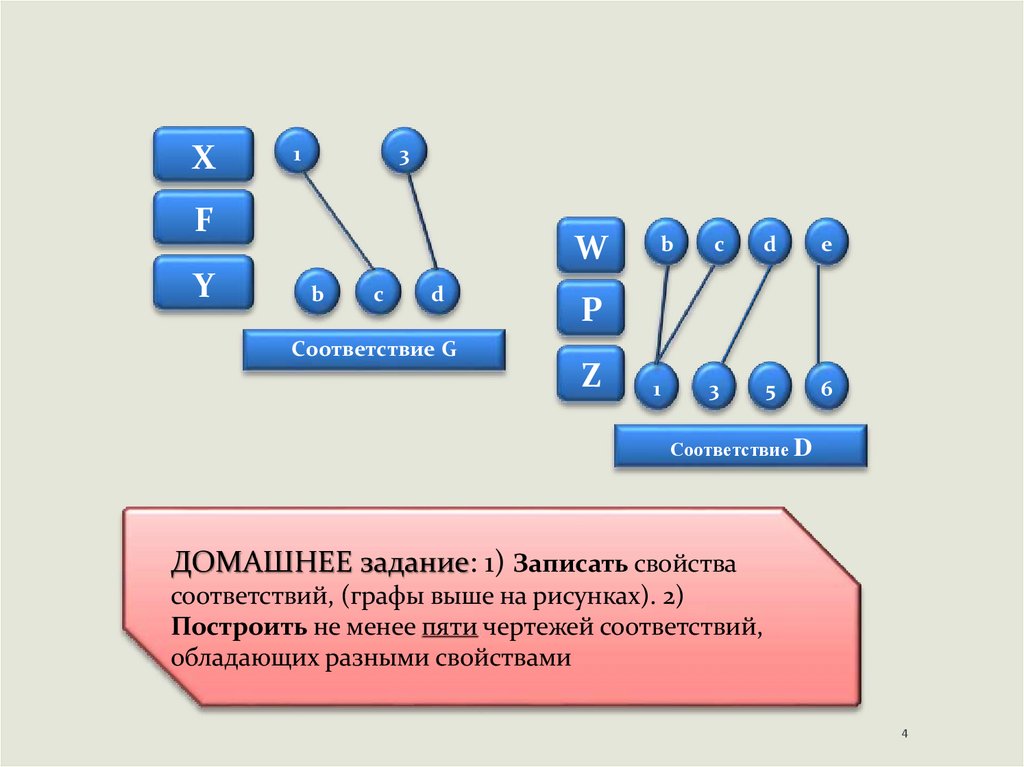
4.

X
1
3
F
Y
W
b
c
d
Соответствие G
b
c
d
e
1
3
5
6
P
Z
Соответствие D
ДОМАШНЕЕ задание: 1) Записать свойства
соответствий, (графы выше на рисунках). 2)
Построить не менее пяти чертежей соответствий,
обладающих разными свойствами
4

5.

5

6.

6

7. Виды множеств

7

8.

ПУСТОЕ МНОЖЕСТВО
8

9.

КОНЕЧНОЕ И БЕСКОНЕЧНОЕ
МНОЖЕСТВА
9

10.

Задача о «Гостинице Бесконечность»
(«Отель Гильберта»)
Условие:
Гостиница имеет бесконечное число номеров (№1, №2, №3,
…), последнего номера нет. Про свободные номера
информации нет.
Этап 1: Приезжает 1 новый гость. Как найти ему номер?
Решение:
Каждый текущий гость переезжает из номера n в номер n+1.
Гость из №1 → №2
Гость из №2 → №3
и т.д.
Результат: Номер №1 освобождается → новый гость
заселяется.
10

11.

Задача о «Гостинице Бесконечность»
(«Отель Гильберта»)
Этап 2: Приезжают 5 новых гостей. Как их заселить?
Решение:
Каждый текущий гость переезжает из номера n в номер n+5.
Гость из №1 → №6
Гость из №2 → №7
и т.д.
Результат: Номера №1–№5 освобождаются → 5 новых гостей
заселяются.
11

12.

Задача о «Гостинице Бесконечность»
(«Отель Гильберта»)
Этап 3: Приезжает бесконечно много новых гостей
Решение:
Каждый текущий гость переезжает из номера n в номер 2n
(чётные номера).
Гость из №1 → №2
Гость из №2 → №4
Гость из №3 → №6
и т.д.
Результат:
Все нечётные номера (№1, №3, №5, …) освобождаются
12

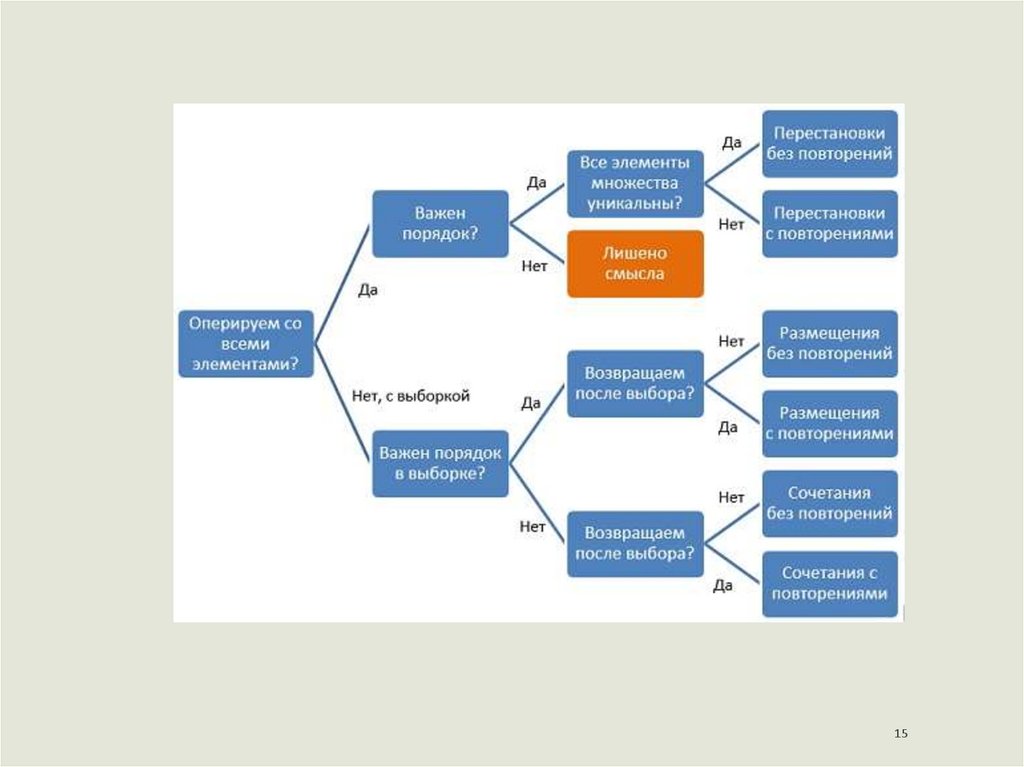
13. Комбинаторика

13

14.

14

15.

15

16.

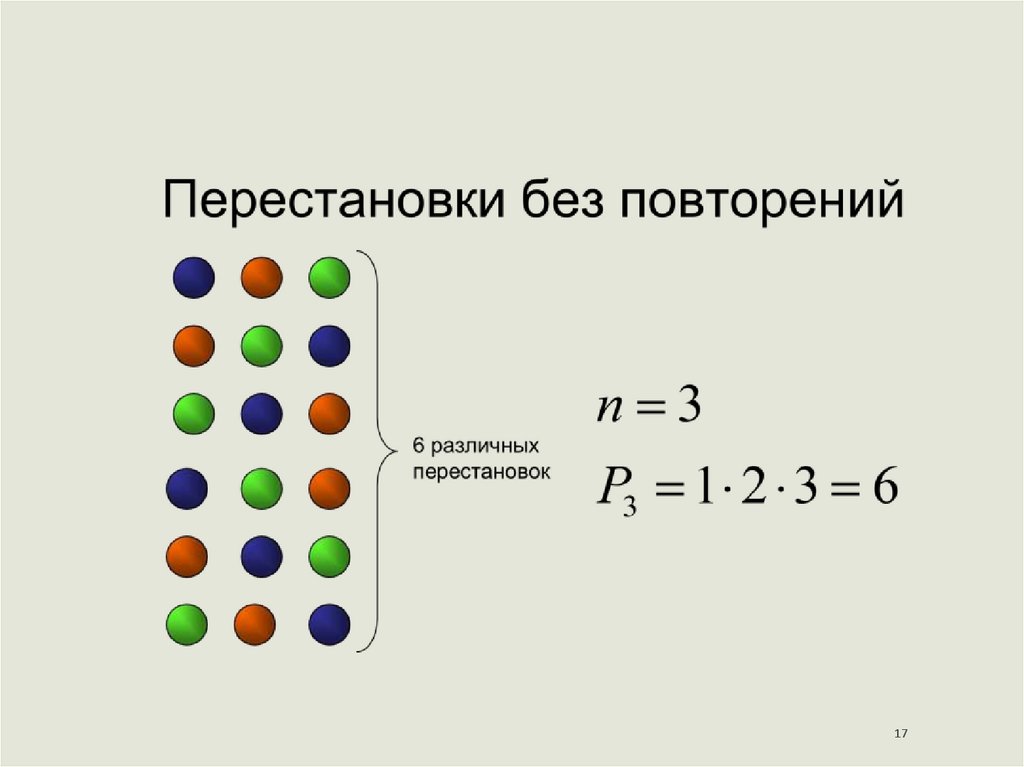
16

17.

17

18.

18

19.

19

20.

20

21.

21

22. ЗАДАЧИ

1. В группе 20 человек. Необходимо выбрать
старосту, заместителя старосты и профорга.
Сколько существует способов это сделать?
2. Расписание одного дня состоит из 4-х пар при
выборе из 11 дисциплин. Сколько существует
вариантов расписания при условии, что пары
не повторяются?
22

23.

23

24.

24

25.

25

26.

Сложение и умножение комбинаций
1) Знак «плюс» следует понимать и читать как союз
ИЛИ.
2) Знак «умножить» следует понимать и читать как
союз И
ЗАДАЧИ:
Студенческая группа состоит из 23 человек, среди
которых 10 юношей и 13 девушек. Сколько существует
способов выбора двух человек одного пола?
Рассмотрим ту же студенческую группу, которая пошла
на танцевальный конкурс среди пар. Сколько
существует способов составить пару из юноши и
девушки?
26

27.

Комбинации с повторениями
Расписание одного дня состоит из 4-х пар при выборе из 11
дисциплин. Сколько существует вариантов расписания при
условии, что пары могут повторяться?
Алексей занимается спортом, причём 4 дня в неделю – лёгкой
атлетикой, 2 дня – силовыми упражнениями и 1 день отдыхает.
Сколько существует способов составить ему расписание занятий
на неделю?
В студенческой столовой продают сосиски в тесте, ватрушки и
пончики. Сколько существует способов приобретения пяти
пирожков?
27

28.

Диаграммы Эйлера-Венна
Диаграммы Эйлера-Венна – геометрические представления
множеств. Построение диаграммы заключается в
изображении большого прямоугольника, представляющего
универсальное множество U, а внутри его – кругов (или какихнибудь других замкнутых фигур), представляющих
множества. Фигуры должны пересекаться в наиболее общем
случае, требуемом в задаче, и должны быть соответствующим
образом обозначены. Точки, лежащие внутри различных
областей диаграммы, могут рассматриваться как элементы
соответствующих множеств. Имея построенную диаграмму,
можно заштриховать определенные области для обозначения
вновь образованных множеств.
28

29.

Диаграммы Эйлера-Венна.
ПРИМЕР:
С помощью диаграмм Эйлера – Венна проиллюстрируем
справедливость соотношения
29

30.

Задачи на применение диаграмм ЭйлераВенна
30

31.

Отображения и функции
Определение 1: Функция (отображение, оператор,
преобразование) – математическое понятие,
отражающее однозначную парную связь
элементов одного множества с элементами
другого множества.
Определение 2 альтернативное: Функция – это
соответствие между элементами двух
множеств, установленное по такому правилу,
что каждому элементу одного множества
ставится в соответствие элемент другого
множества.
31

32.

Известная и неизвестная функция
Если хотят подчеркнуть, что правило f
известно, то говорят, что на множестве X
задана функция f, принимающая
значения из Y. Y= F (x)
Если f должна находится в результате
решения уравнения, то говорят, что f
неизвестная или неявная функция.
F (x,y)=0
32

33.

Область задания (определения) и область
значения функции
Функция y = f (x) представляет три объекта y,f,x где
X – множество, которое называют областью
определения функции.
Y – множество, которое называют областью
значений функции.
F – правило, по которому каждому элементу
множества X, сопоставляется элемент
множества Y.
33

34.

Функция
Каждый элемент множества X называется независимой
переменной или аргументом функции.
Элемент y, соответствующий фиксированному значению x,
называется частным значением функции в точке x.
f
1. f : X Yили x
y
2. y f ( x )или y y(x)
ОБОЗНАЧЕНИЕ функции
34

35.

Равенство двух функций
Две функции f и g равны, если совпадают их области
определения и если для каждого x имеет место
равенство: f (x) = g (x)
ПРИМЕР: Пусть x – элемент числового множества.
ВОПРОС – Равны ли функции F и G если:
f ( x ) x 1, а g(x) x 2 x 1
3
На этот вопрос нельзя ответить, так как не указаны области
определения функций.
35

36.

Способы задания числовой функции
Аналитический.
С помощью формулы и стандартных обозначений
Графический.
Табличный.
С помощью таблицы значений
Рекурсивный.
Словесный. Игрек равно целая часть от икс.
Реку́рсия — определение, описание, изображение какого-либо объекта или процесса
внутри самого этого объекта или процесса, то есть ситуация, когда объект является
частью самого себя
36