Занятие 2 n

1. Раздел 1 Алгебра и геометрия

2. Занятие 2

Учебные вопросы
1. Ранг матрицы.
2. Способы вычисления ранга матрицы.

3. 1. Ранг матрицы

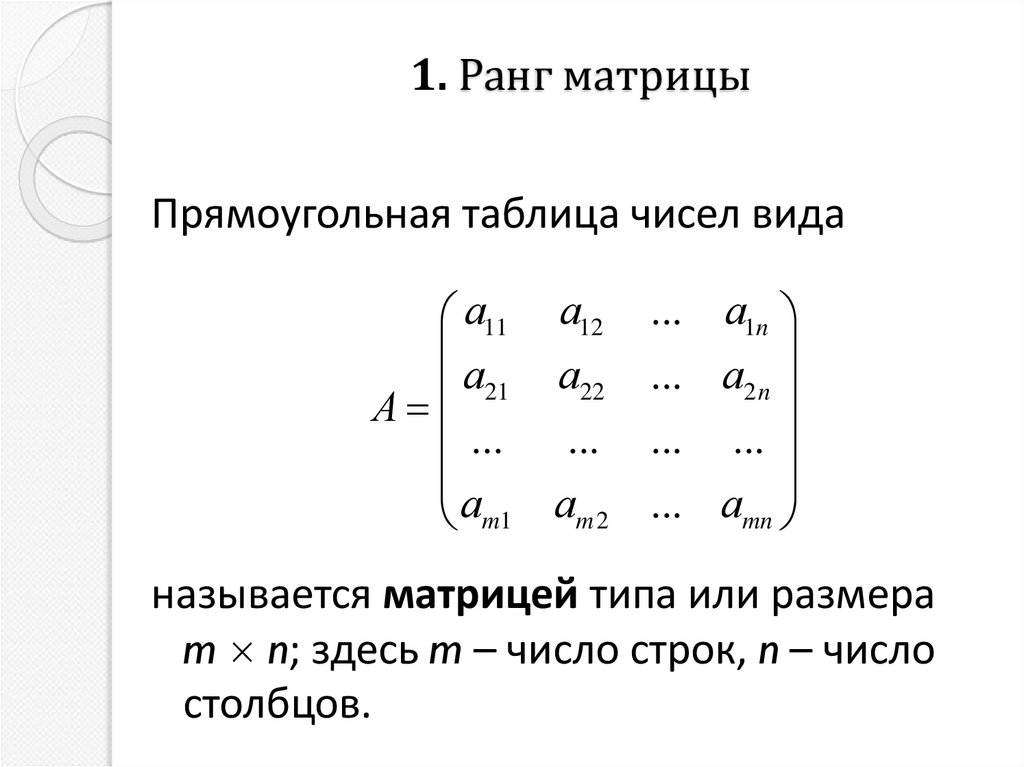
Прямоугольная таблица чисел вида
а11 а12
а
а22
21
А
... ...
а
m1 аm 2
... а1n
... а2 n
... ...
... аmn
называется матрицей типа или размера
m n; здесь m – число строк, n – число
столбцов.

4. Определение ранга матрицы

5. Вычисление ранга с помощью базисных миноров

6. 1. Матрицы и действия над ними

Если число строк и столбцов матрицы
одинаковое , то матрица называется
квадратной, порядка n.
Квадратная матрица, в которой все
элементы, не стоящие на главной
диагонали, равны нулю, называется
диагональной, например:
3 0 0
0 1 0
0 0 5

7. 1. Матрицы и действия над ними

Диагональная матрица, у которой все
элементы,
стоящие
на
главной
диагонали равны единице, называется
единичной, например
1 0 0
0 1 0
0 0 1
- единичная матрица 3-го порядка.

8. 1. Матрицы и действия над ними

Прямоугольная матрица, в которой
каждая строка заменена столбцом с
тем
же
номером,
называется
транспонированной по отношению к
Т
A
данной матрице, обозначается .
Например, если
1 4 5
1 2 3
A 2 3 7 то AT 4 3 6 .
3 6 8
5 7 8
Т
Т
Очевидно: А А

9. 1. Матрицы и действия над ними

Суммой двух матриц одинакового
типа называется матрица того же типа,
все элементы которой равны суммам
соответствующих элементов слагаемых
матриц.
Пример
5 4 1 3 6 5 8 10 4
2 6 3 2 1 3 0 7 0

10. 1. Матрицы и действия над ними

Произведением матрицы А на
число α называется матрица αА или
Аα, все элементы которой равны
соответствующим элементам матрицы
А, умноженным на α.
Пример
1 1 0 3 3 0
3 2 0 3 6 0 9
3 2 2 9 6 6

11. 1. Матрицы и действия над ними

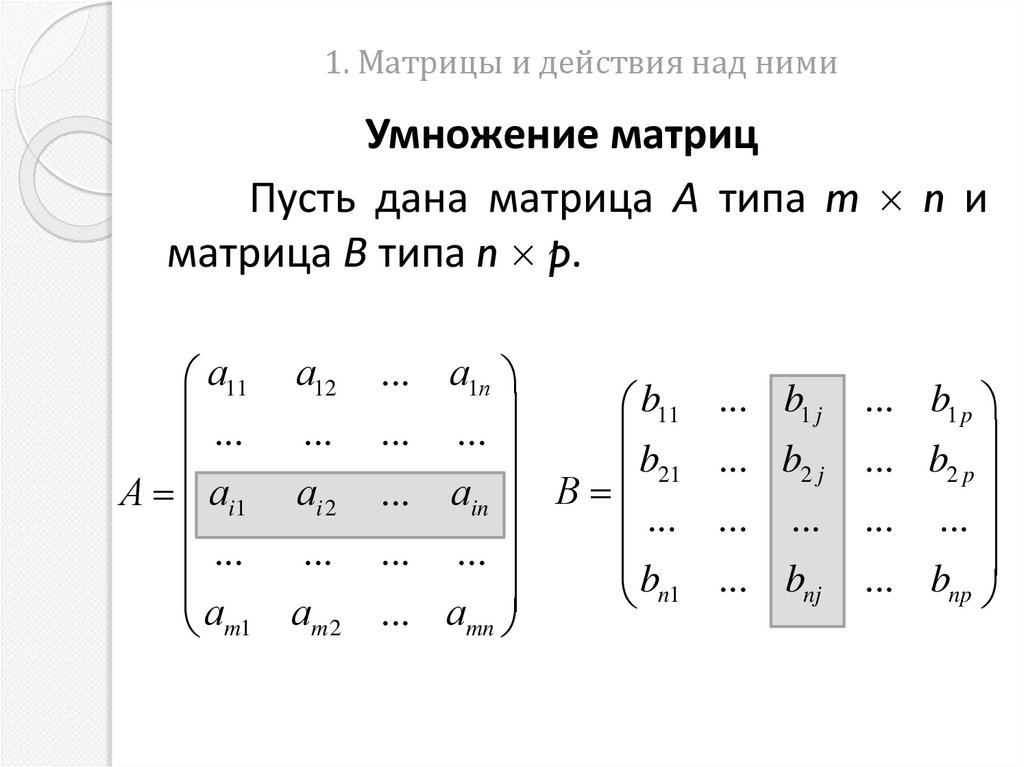
Умножение матриц
Пусть дана матрица А типа m n и
матрица В типа n p.
а11 а12
... ...
А аi1 аi 2
... ...
а
m1 аm 2
... а1п
b11
... ...
b
21
... аin В
...
... ...
b
n1
... amn
... b1 j
... b2 j
... ...
... bnj
... b1 p
... b2 p
... ...
... bnp

12. 1. Матрицы и действия над ними

Для таких двух матриц, у которых число
столбцов первой равно числу строк второй
определено понятие произведения матрицы
А на В следующим образом: С = А · В , где С
есть матрица типа m p
с11 с12 ... с1 p
с
с
...
с
21
22
2p
C
... ... ... ...
сm1 сm 2 ... сmp
где cij ai1b1 j ai 2b2 j ... ainbnj ,
i 1,2, , m; j 1,2, , p .

13. 1. Матрицы и действия над ними

A B
= C
( m n) ( n p ) ( m p )
2 1
1 3
3
2
8
1
Пример 1
1 4 0 3 0 1
3 1
3 2 2 1 8 0 1 3
3 1 2 3 8 1 1 1
1 2 4 1 0 0 3 3 1 1 4 3 0 1 3 1
11 0
7 14

14. 1. Матрицы и действия над ними

Произведение двух матриц НЕ
обладает свойством переместительности
(коммутативности): AB BA .
Пример 2
4 2
12 20 34
3 4 5
.
BA 7 1
21
30
42
0 2 7
9 3
27 42 66

15. 1. Матрицы и действия над ними

Пример 3
Найти значение матричного многочлена:
3 A 2E B , где
3 1
2 0 1
A
B
1
3
1
2 0
1 0
E
0
1
Решение
3 1
1 0 2 0 1
2
3
0 1 1 3 1
2 0
7 3 2 0 1 17 9 10
6
2
1
3
1
14
6
8

16. 2. Решение матричных уравнений

Пусть дана квадратная матрица А
порядка n.
Обратной матрицей по отношению к
данной А называется матрица, которая
будучи умноженной, как справа, так и
слева на данную матрицу, дает
единичную матрицу.
Для матрицы А обратная обозначается
1
символом A . По определению имеем:
A A 1 A 1 A E .

17. 2. Решение матричных уравнений

Квадратная матрица называется
неособенной или невырожденной,
если определитель ее отличен от нуля.
В
противном
случае
матрица
называется
особенной
или
вырожденной.
Всякая неособенная матрица имеет
обратную матрицу, которую можно
найти по формуле
1
1
A A.

18. 2. Решение матричных уравнений

A -
союзная
матрица
по
отношению к данной матрице А, в
которой элементы каждой строки
данной
матрицы
заменены
алгебраическими
дополнениями
элементов соответствующих столбцов.
Например,
A
A
A
11
A11
A
A12
A21 A A12
A
A22 ,
13
21
A22
A23
31
A32
A33 .

19. 2. Решение матричных уравнений

Пример 1
2 4
1
Для матрицы A
найти A .
1 3
Решение
1
1 A11 A21
A A
A12 A22 ,
2 4
6 4 10 0 ,
1 3
1
A11 3, A12 1, A21 4, A22 2 ,
1 3 4 0,3 0,4
A
10 1 2 0,1 0,2 .
1

20. 2. Решение матричных уравнений

Пример 2
1 2 3
Для матрицы A 2 4 5 найти A 1 .
3 5 6
Решение
A11
1
1
1
A A A A12
A
13
A21
A22
A23
A31
A32
A33

21. 2. Решение матричных уравнений

1 2 3
2 4 5 1 0
1 2
A33
4 4 0
2 4
3 5 6
4 5
A11
24 25 1
5 6
A13
2 4
A22
1 3
3 5
3 6
10 12 2
6 9 3
2 3
A31
10 12 2
4 5
2 5
A12
12 15 3
3 6
A21
A23
2 3
5 6
1 2
3 5
12 15 3
5 6 1
1 3
A32
5 6 1
2 5

22. 2. Решение матричных уравнений

1 3 2 1 3 2
1
1
A
3 3 1 3 3 1
1
2
1
0
2
1
0

23. 2. Решение матричных уравнений

Рассмотрим два случая.
1. Пусть дано уравнение
A X B ,
требуется найти Х.
Умножим левую и правую часть
матричного уравнения слева на
обратную матрицу A 1 , получим
A 1 AX A 1B
или
X A 1B .

24. 2. Решение матричных уравнений

X A B ,
2. Пусть дано уравнение
требуется найти Х.
Умножим левую и правую часть
матричного уравнения справа на
обратную матрицу A 1 , получим
XAA 1 BA 1 ,
или
1
X BA .

25. 2. Решение матричных уравнений

Пример
Решить уравнения 1) AX B , 2) XA B ,
1 0
2 1
если A
, B
.
2 3
0 4
Решение
1) 1 0 X 2 1 ,
2 3
1 A11
A
A12
1
0
4
X A 1B
A21 1 3 0
A22 3 2 1

26. 2. Решение матричных уравнений

Тогда
2 1
1 3 0 2 1 1 6 3
X
4 2
3 2 1 0 4 3 4 2
3 3
1 0 2 1
1
2) X
,
X BA , тогда
2 3 0 4
8
1 2 1 3 0 1 8 1
3
X
3 0 4 2 1 3 8 4 8
3
1
3
4
3