Презентация 2

1. Лекция № 2 Динамика поступательного и вращательного движения.

2. План:

1. Инерциальные системы отсчета. 1 закон Ньютона
2. 2 закон Ньютона
3. 3 закон Ньютона
4. Силы в механике
5. Центр масс
6. Момент инерции
7. Теорема Штейнера
8. Уравнение динамики вращательного движения
9. Момент импульса.
10. Кинетическая энергия вращающегося тела
11. Законы динамики в неинерциальных системах отсчета
12. Движение жидкостей. Уравнение Бернулли.

3. Введение

Динамика – раздел механики, изучающий
причины движения и взаимодействия тел.
Две основные задачи динамики:
1. Прямая задача: Задано движение (уравнения
движения, траектория). Требуется определить
силы, под действием которых происходит
заданное движение.
2. Обратная задача: Заданы силы, под
действием которых происходит движение.
Требуется найти параметры движения
(уравнения движения, траекторию движения).

4. Инерциальные системы отсчета. 1 закон Ньютона

Инерциальная система отсчета - система отсчета, в
которой ускорение материальной точки целиком
обусловлено только взаимодействием ее с другими
телами, а свободная частица, не подверженная
действию
никаких
других
тел,
движется
прямолинейно и равномерно (или покоится).
Свойства инерциальных систем отсчета:
• Однородность времени
• Однородность пространства
• Изотропность пространства

5. Инерциальные системы отсчета. 1 закон Ньютона

Существует не одна, а бесчисленное множество инерциальных
систем отсчета, движущихся относительно друг друга
прямолинейно и равномерно.
Системы отсчета, движущиеся с ускорением относительно
инерциальных систем, называют неинерциальными.
ИСО
НИСО
-Находятся в
-Движутся ускоренно
относительном покое или замедленно
(относительно Земли) -Вращаются
-Движутся
равномерно и
прямолинейно

6. Инерциальные системы отсчета. 1 закон Ньютона

Принцип относительности
Галилея:
• Все инерциальные системы по
своим механическим свойствам
эквивалентны друг другу.
• Во всех инерциальных системах
отсчета свойства пространства и
времени
одинаковы,
одинаковы также и все законы
механики.

7. Инерциальные системы отсчета. 1 закон Ньютона

1 закон Ньютона:
Всякое тело находится в состоянии покоя или
равномерного прямолинейного движения пока
воздействие со стороны других тел не заставит
его изменить это состояние.

8. 2 закон Ньютона

Сила – физическая величина, характеризующая
воздействие одних тел на другие, ведущее к
изменению состояния их движения
Действие тел друг на друга называют
взаимодействием.

9. 2 закон Ньютона

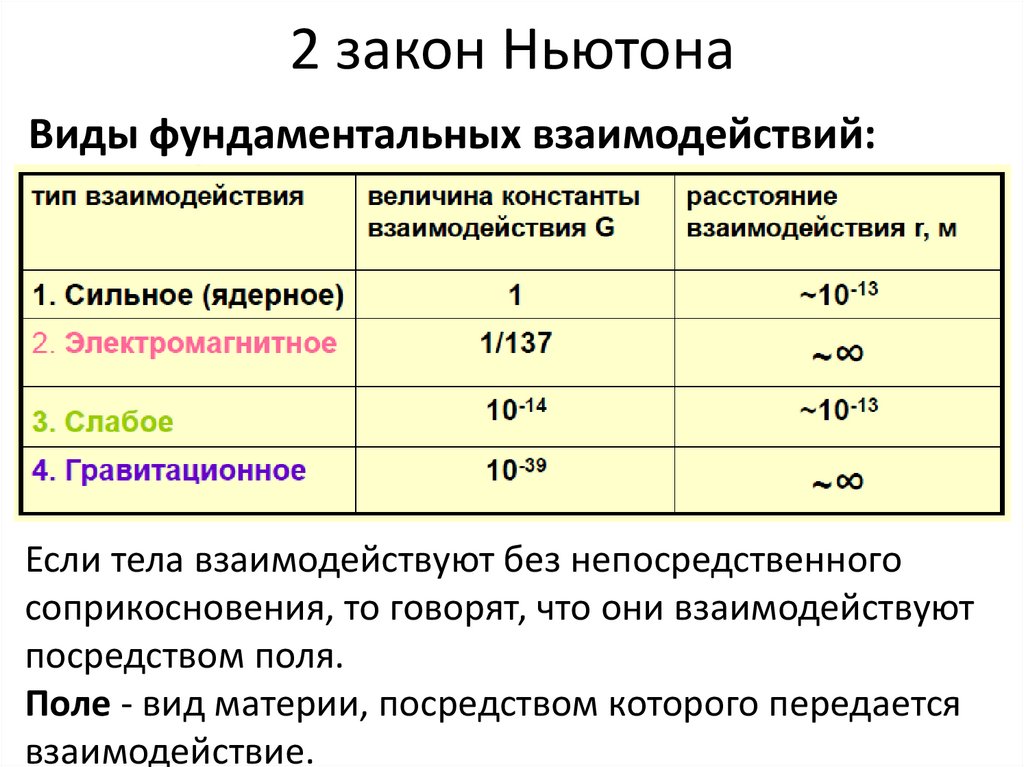
Виды фундаментальных взаимодействий:
Если тела взаимодействуют без непосредственного
соприкосновения, то говорят, что они взаимодействуют
посредством поля.
Поле - вид материи, посредством которого передается
взаимодействие.

10. 2 закон Ньютона

Силой называется всякое воздействие на данное
тело, сообщающее ему ускорение или
вызывающее его деформацию.
Единица измерения – Н (Ньютон)
Сила характеризуется:
1)природой взаимодействия;
2)телом, со стороны которого действует сила;
3)телом, на которое действует сила (точка приложения силы);
4)линией действия силы;
5)направлением силы;
6)величиной силы.

11. 2 закон Ньютона

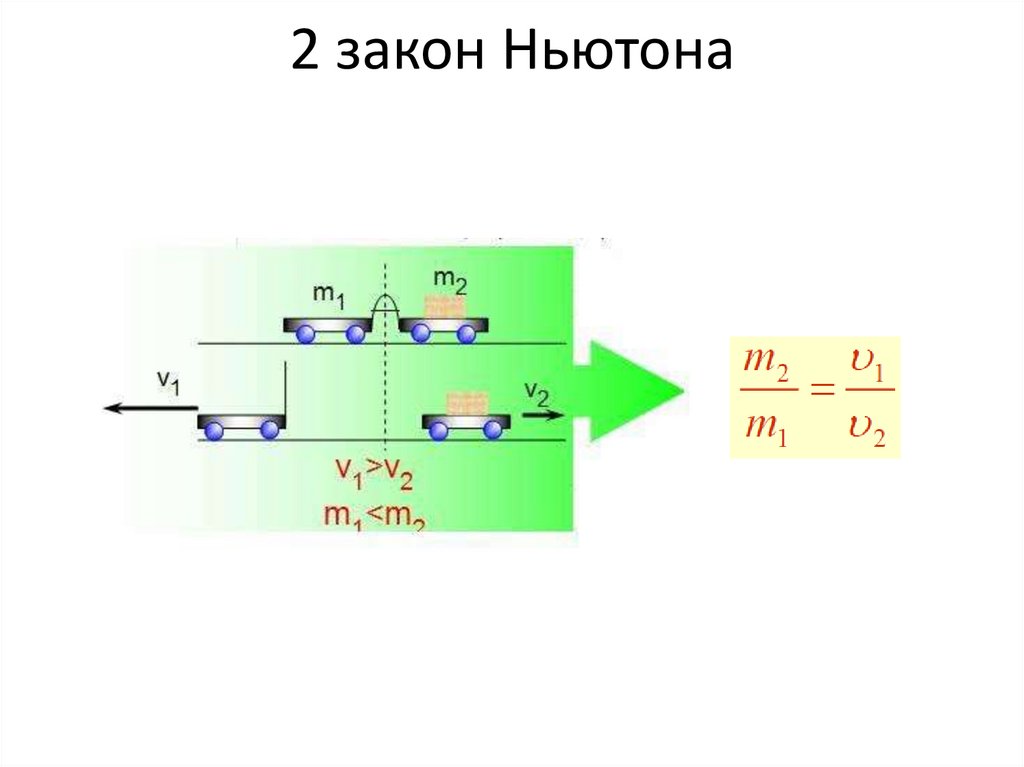
Свойство тел сопротивляться попыткам изменить
их скорость называется инертностью.
Масса – это свойство, которое определяет
величину ускорения а, приобретаемое телом
под воздействием силы.
Масса тела – это физическая величина,
являющаяся количественной мерой инертности
тел, т.е. свойство сохранять приобретенную
скорость движения V или состояние покоя (V=0).

12. 2 закон Ньютона

13. 2 закон Ньютона

2 закон Ньютона:
Ускорение, приобретаемое телом, прямо
пропорционально силе, действующей на тело, и
обратно пропорционально массе тела.
В инерциальной системе ускорение, которое сила
сообщает телу (материальной точке), определяется
формулой:

14. 2 закон Ньютона

Импульс материальной точки- вектор, равный
произведению массы точки на ее скорость
Импульсом или количеством движения системы
материальных точек назовем векторную сумму
импульсов отдельных
материальных точек, из которых эта система
состоит.

15. 2 закон Ньютона

Согласно второму закону Ньютона
- импульс силы

16. 2 закон Ньютона

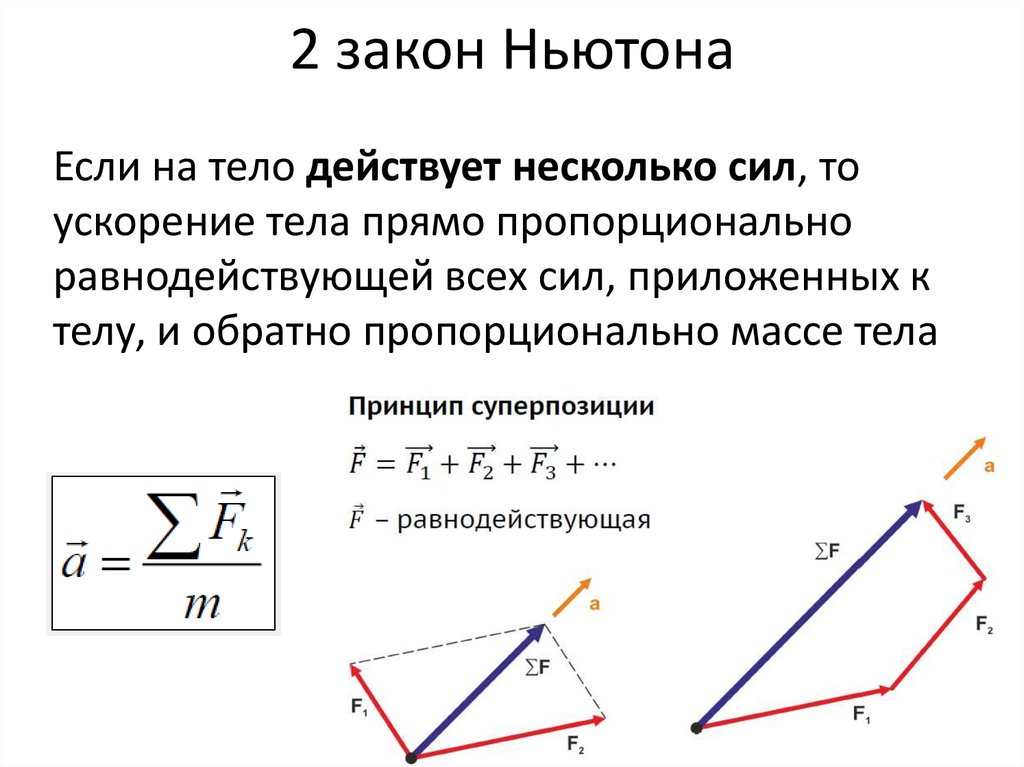
Если на тело действует несколько сил, то
ускорение тела прямо пропорционально
равнодействующей всех сил, приложенных к
телу, и обратно пропорционально массе тела

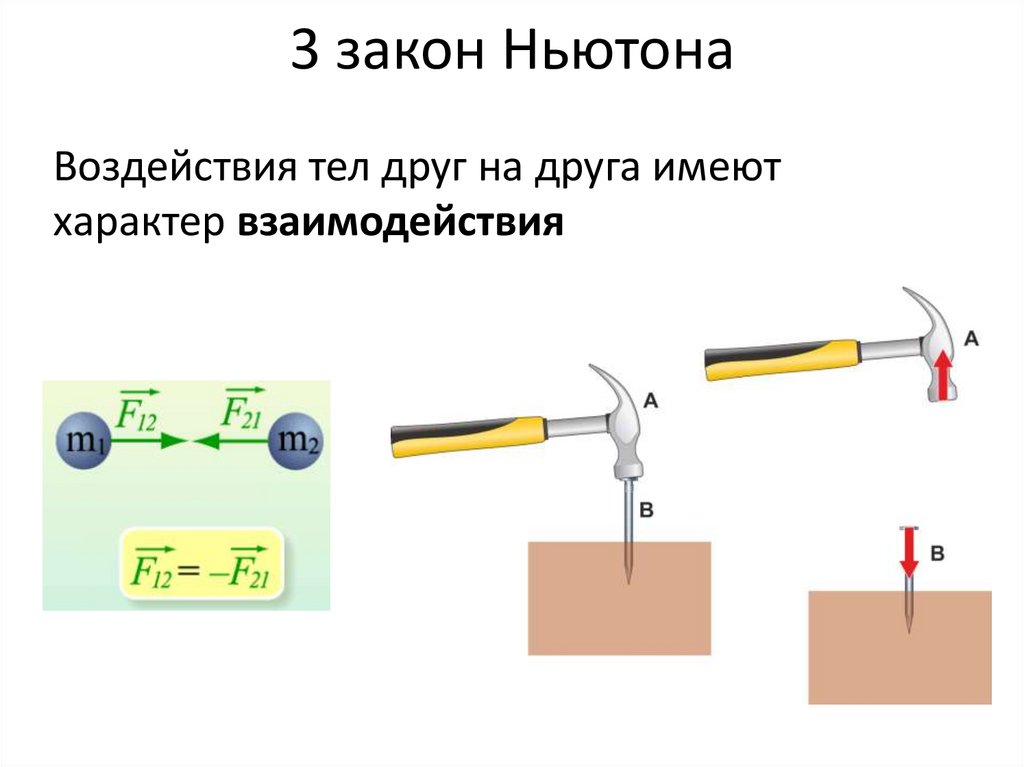
17. 3 закон Ньютона

Воздействия тел друг на друга имеют
характер взаимодействия

18. 3 закон Ньютона

Силы, с которыми две материальные точки
воздействуют друг на друга, всегда равны по
модулю и направлены в противоположные
стороны вдоль прямой, соединяющей эти точки

19. 3 закон Ньютона

1.Силы в природе возникают парами.
2.Эти силы одной природы.
3.Они равны по модулю и
противоположны по направлению.
4.Силы действуют вдоль одной прямой.
5.Приложены к разным телам.

20. Силы в механике

Сила гравитационного притяжения:
G – гравитационная постоянная
Сила тяжести – частный случай силы всемирного
тяготения

21. Силы в механике

Вес тела – сила, с которой тело вследствие
притяжения к Земле давит на опору или
растягивает подвес
тело в покое
тело движется с ускорением вверх
тело движется с ускорением вниз
тело движется с ускорением
свободного падения
Вес ≠ масса

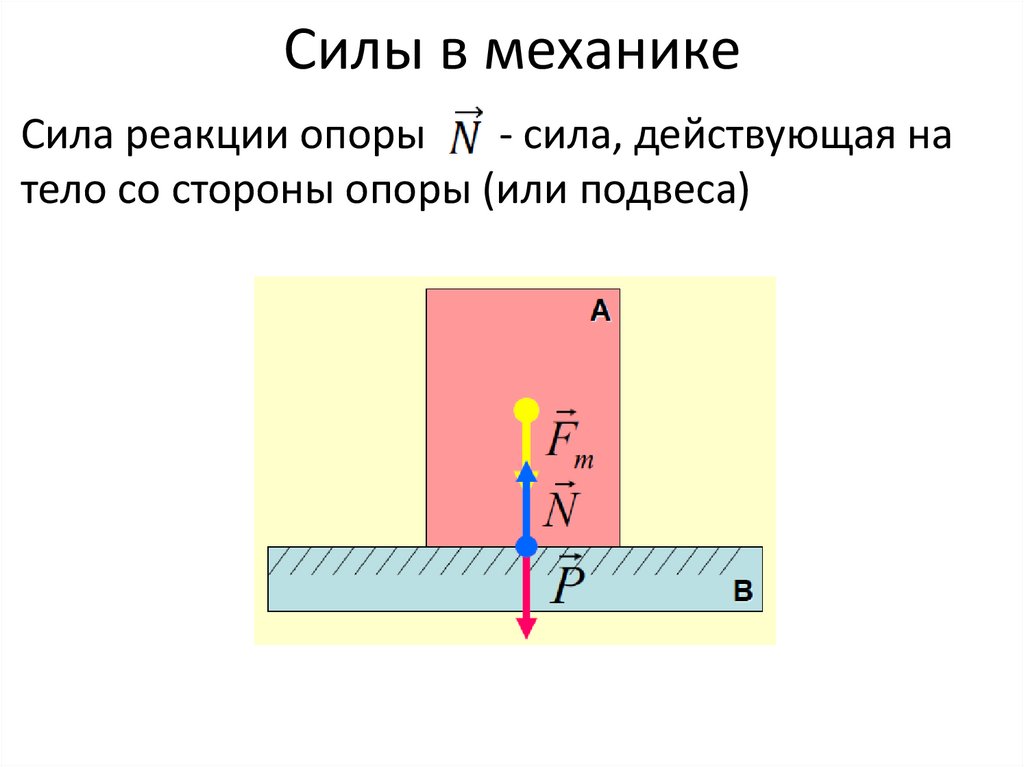
22. Силы в механике

Сила реакции опоры
- сила, действующая на
тело со стороны опоры (или подвеса)

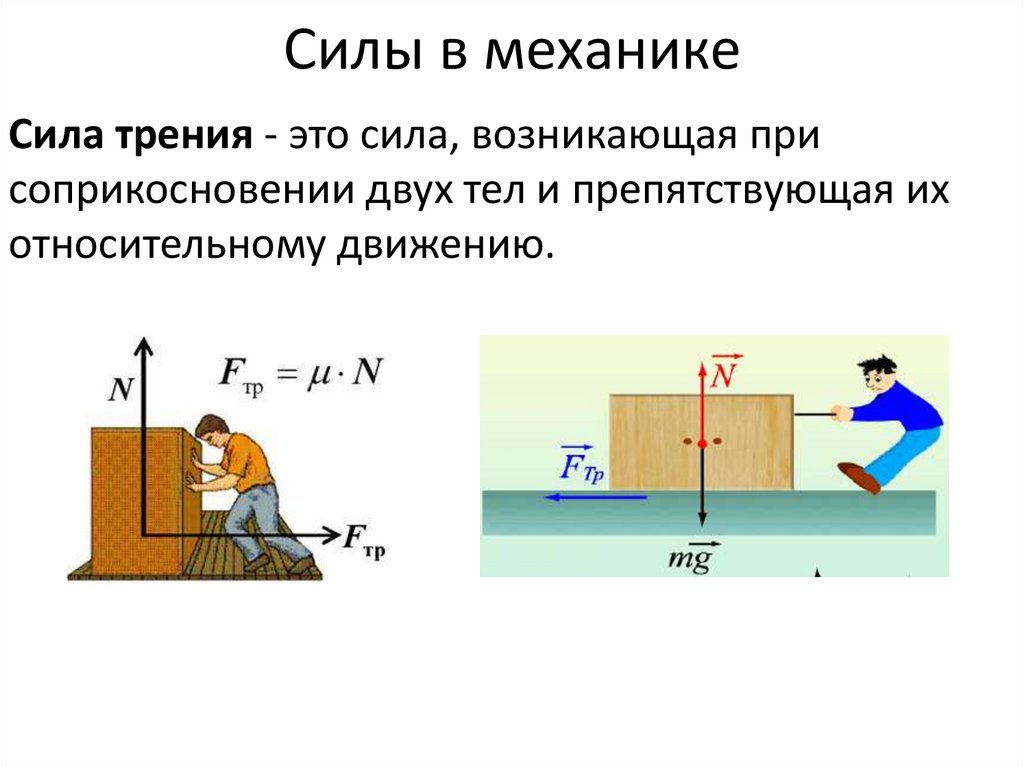
23. Силы в механике

Сила трения - это сила, возникающая при
соприкосновении двух тел и препятствующая их
относительному движению.

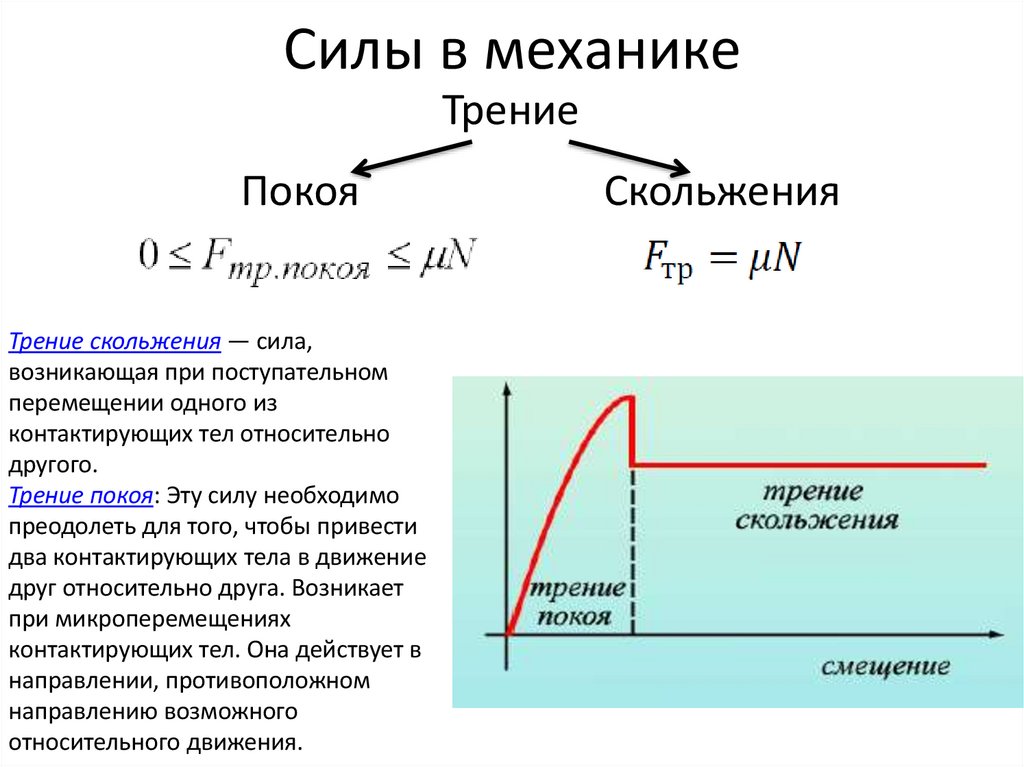
24. Силы в механике

Трение
Покоя
Трение скольжения — сила,
возникающая при поступательном
перемещении одного из
контактирующих тел относительно
другого.
Трение покоя: Эту силу необходимо
преодолеть для того, чтобы привести
два контактирующих тела в движение
друг относительно друга. Возникает
при микроперемещениях
контактирующих тел. Она действует в
направлении, противоположном
направлению возможного
относительного движения.
Скольжения

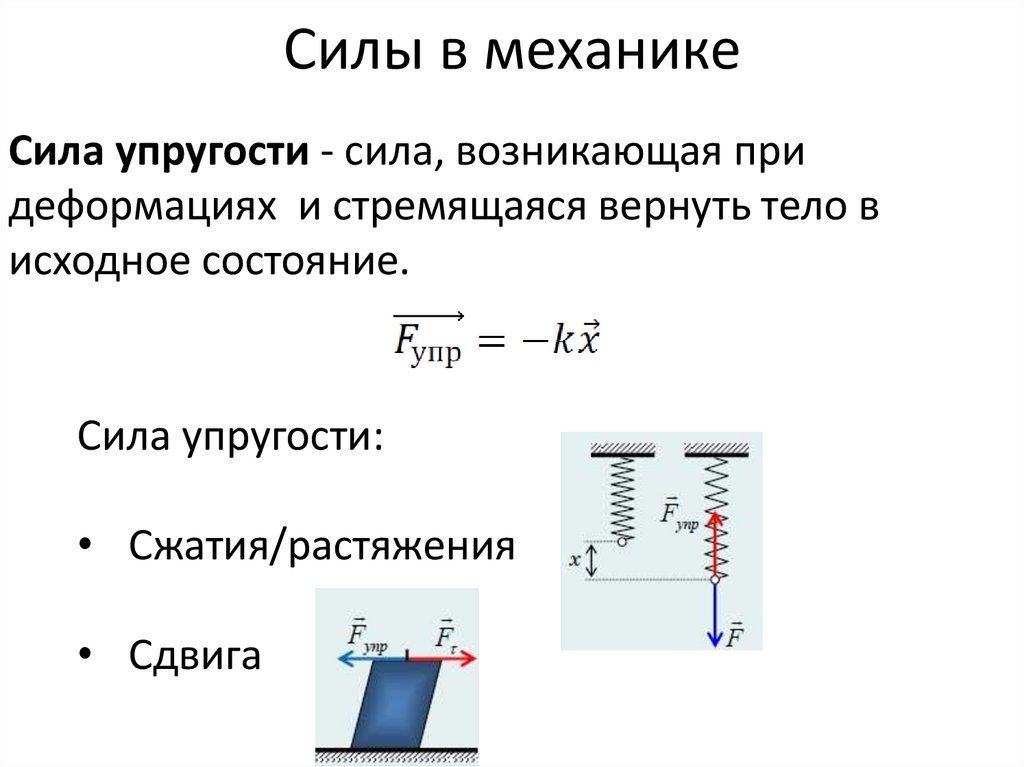
25. Силы в механике

Сила упругости - сила, возникающая при
деформациях и стремящаяся вернуть тело в
исходное состояние.
Сила упругости:
• Сжатия/растяжения
• Сдвига

26. Центр масс

Центр масс (или инерции) – это точка,
характеризующая движение тела как целого.
Положение центра масс задается радиусвектором:
где mi масса i-го тела, ri – его
радиус – вектор, M – масса
системы

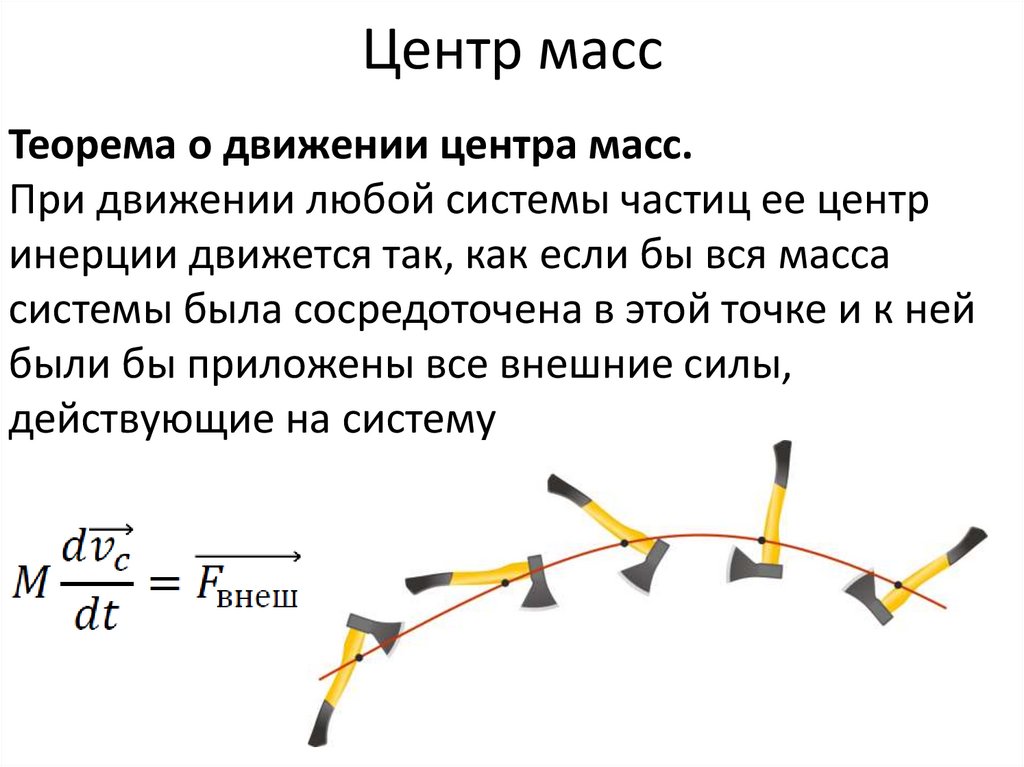
27. Центр масс

Теорема о движении центра масс.
При движении любой системы частиц ее центр
инерции движется так, как если бы вся масса
системы была сосредоточена в этой точке и к ней
были бы приложены все внешние силы,
действующие на систему

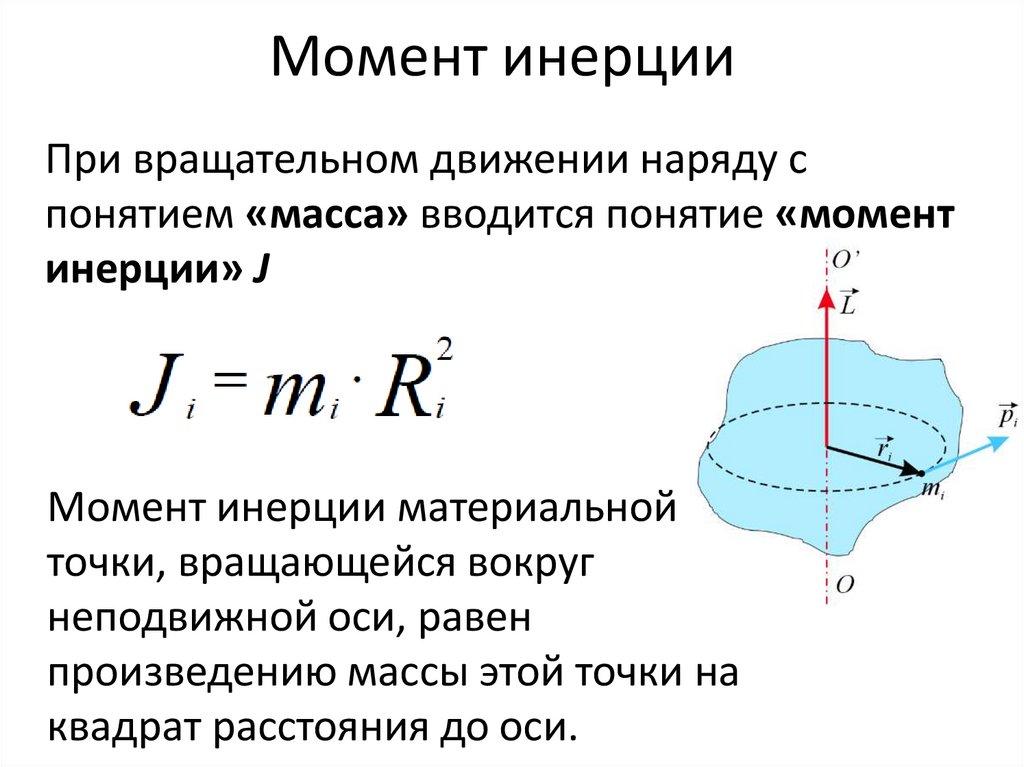
28. Момент инерции

При вращательном движении наряду с
понятием «масса» вводится понятие «момент
инерции» J
Момент инерции материальной
точки, вращающейся вокруг
неподвижной оси, равен
произведению массы этой точки на
квадрат расстояния до оси.

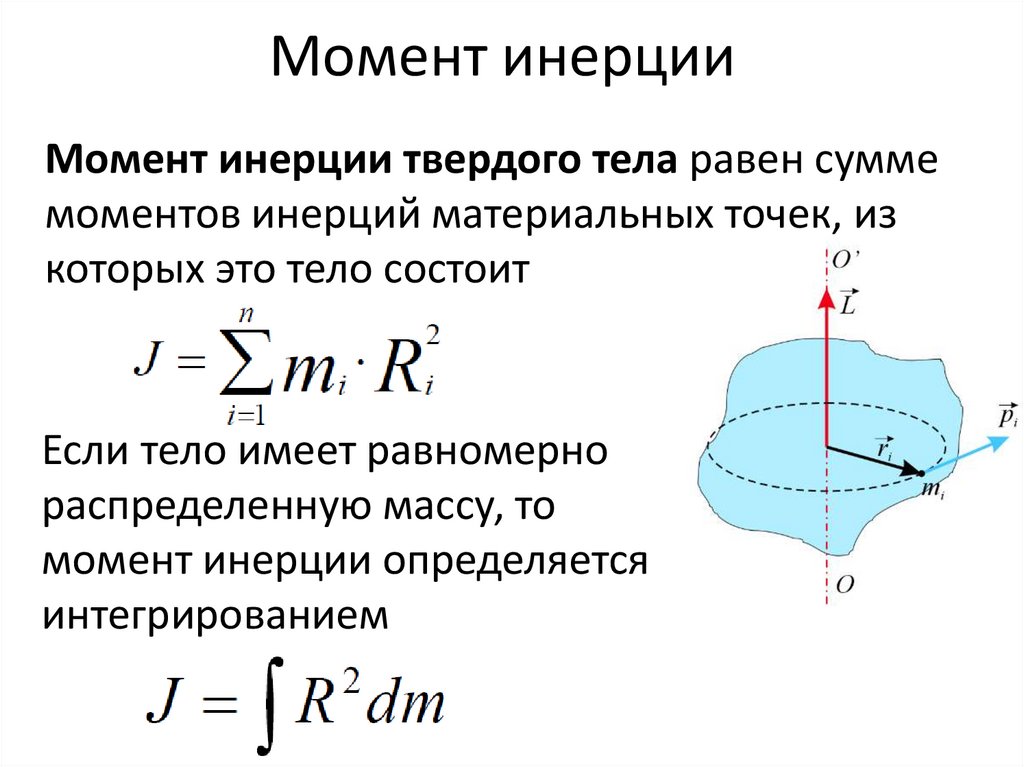
29. Момент инерции

Момент инерции твердого тела равен сумме
моментов инерций материальных точек, из
которых это тело состоит
Если тело имеет равномерно
распределенную массу, то
момент инерции определяется
интегрированием

30. Момент инерции

31. Момент инерции

Момент инерции является мерой инертности
тела при вращательном движении.
Момент инерции данного тела зависит от:
1) распределения массы в теле;
2) размеров тела;
3) формы тела;
4) положения оси вращения.

32. Теорема Штейнера

Если для какого-либо тела известен его момент
инерции относительно оси, проходящей через
центр тяжести, то легко может быть найден и
момент инерции относительно любой оси,
параллельной первой.

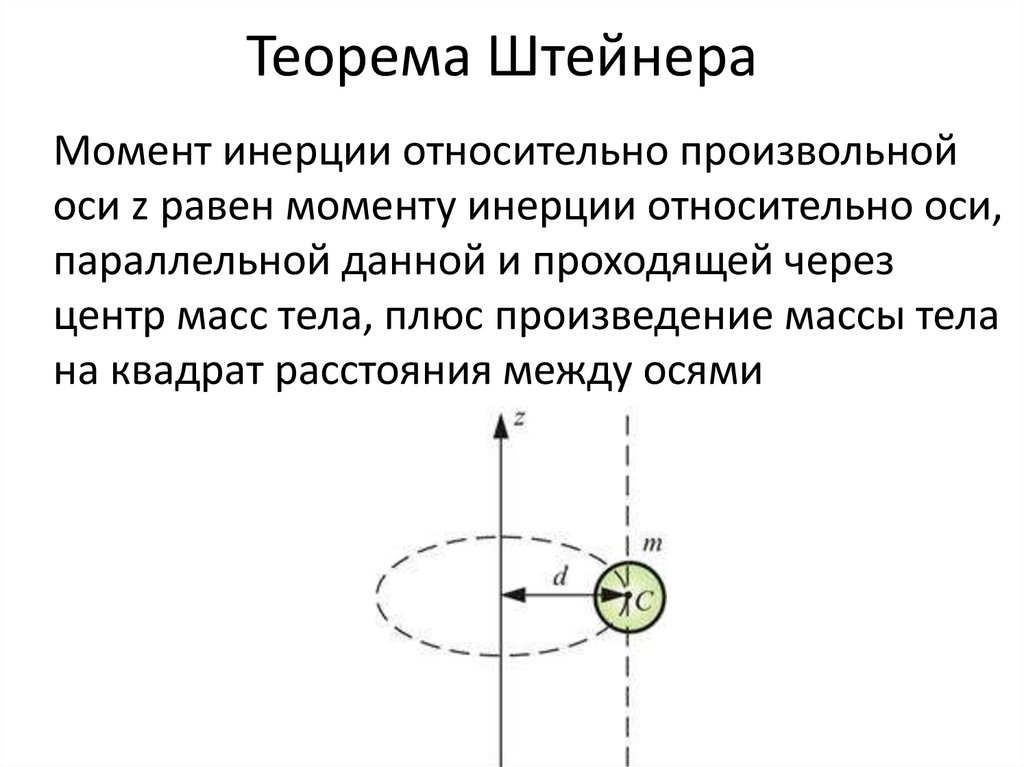
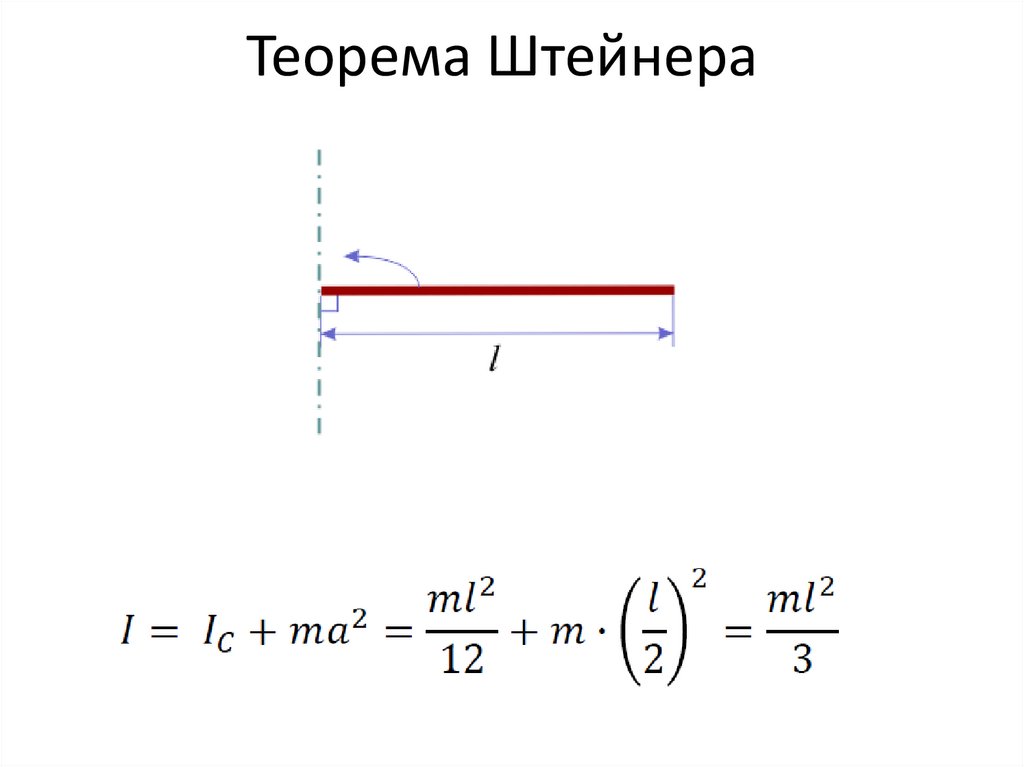
33. Теорема Штейнера

Момент инерции относительно произвольной
оси z равен моменту инерции относительно оси,
параллельной данной и проходящей через
центр масс тела, плюс произведение массы тела
нa квадрат расстояния между осями

34. Теорема Штейнера

35. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси

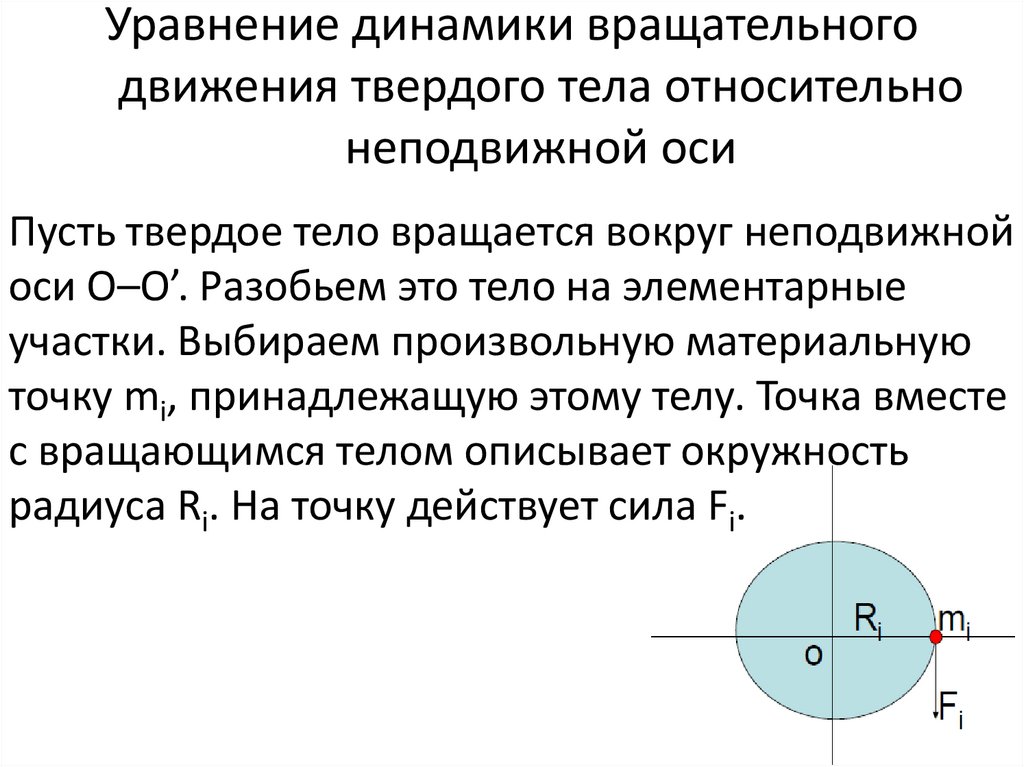
Пусть твердое тело вращается вокруг неподвижной
оси О–О’. Разобьем это тело на элементарные
участки. Выбираем произвольную материальную
точку mi, принадлежащую этому телу. Точка вместе
с вращающимся телом описывает окружность
радиуса Ri. На точку действует сила Fi.

36. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси

По второму закону Ньютона:
при этом
тогда

37. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси

Подставим значение ускорения во второй
закон Ньютона
умножим обе части последнего равенства
на ri и просуммируем его

38. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси

- суммарный момент силы М
- момент инерции
- угловое ускорение

39. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси

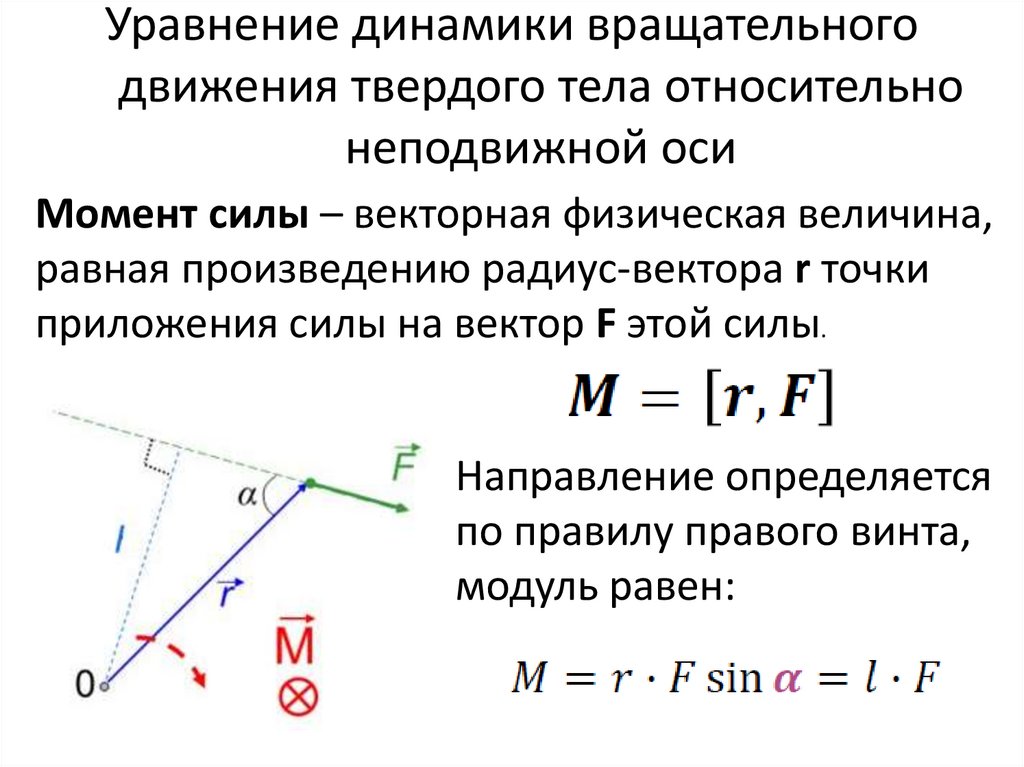
Момент силы – векторная физическая величина,
равная произведению радиус-вектора r точки
приложения силы на вектор F этой силы.
Направление определяется
по правилу правого винта,
модуль равен:

40. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси

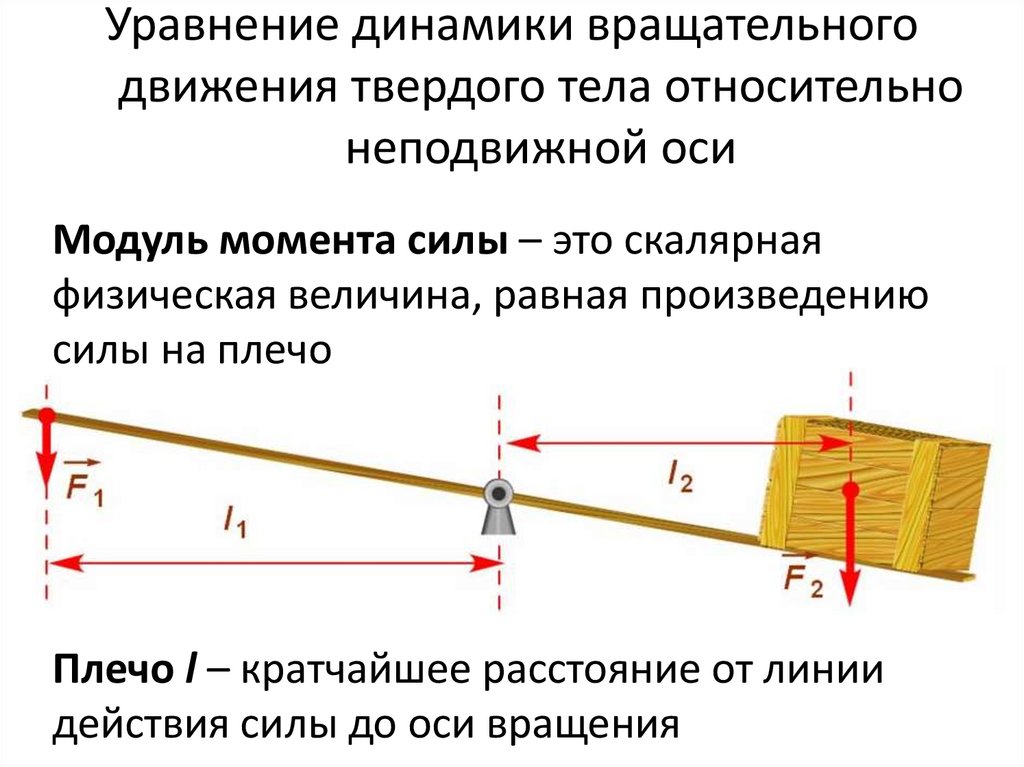
Модуль момента силы – это скалярная
физическая величина, равная произведению
силы на плечо
Плечо l – кратчайшее расстояние от линии
действия силы до оси вращения

41. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси

Основное уравнение динамики вращательного
движения или второй закон Ньютона для
вращательного движения.
Момент вращающейся силы приложенной к
телу, равен произведению момента инерции
тела на угловое ускорение.

42. Момент импульса

Момент импульса – это физическая величина,
равная произведению момента инерции тела на
угловую скорость
Основное уравнение динамики
вращательного движения можно
записать в виде (уравнение моментов):

43. Кинетическая энергия вращающегося тела

При поступательном движении кинетическая
энергия тела определяется по формуле (для
материальной точки):
Линейная скорость vi материальной точки mi,
вращающейся вокруг оси с, определяется

44. Кинетическая энергия вращающегося тела

Подставим значение линейной скорости в
формулу кинетической энергии.
Если тело одновременно участвует во
вращательном и поступательном движениях, то
его полная энергия определится по формуле:

45. Кинетическая энергия вращающегося тела

46. Законы динамики в неинерциальных системах отсчета

В неинерциальной системе
можно пользоваться
законами Ньютона, если
ввести фиктивные силы
инерции.
aн
Силы инерции обусловлены не взаимодействием
тел, а свойствами самих неинерциальных систем
отсчета. На силы инерции законы Ньютона не
распространяются.

47. Законы динамики в неинерциальных системах отсчета

Найдем количественное выражение для силы
инерции:
– ускорение тела относительно
неинерциальной системы;
– ускорение неинерциальной системы
относительно инерциальной (относительно
Земли).
Тогда ускорение тела относительно инерциальной
системы

48. Законы динамики в неинерциальных системах отсчета

В инерциальной системе:
Формально ускорение а* можно переписать как:
-
– сила, направленная в сторону,
противоположную ускорению неинерциальной
системы.
Тогда:

49. Законы динамики в неинерциальных системах отсчета

– уравнение Ньютона для неинерциальной
системы отсчета
Силы инерции:
• неинвариантны относительно перехода из одной
системы отсчета в другую
• не подчиняются закону действия и
противодействия
• движение тела под действием сил инерции
аналогично движению во внешнем силовом поле

50. Законы динамики в неинерциальных системах отсчета

В инерциальной системе:
Камень, вращающийся на веревке
связан ей с осью вращения. Веревка
растягивается, появляется упругая сила,
действующая на камень, направленная
вдоль веревки к центру вращения.
Это центростремительная сила.
Она приложена к телу.

51. Законы динамики в неинерциальных системах отсчета

Сила, приложенная к связи (к
веревке) и направленная по радиусу
от центра, называется центробежной.
В неинерциальной системе
(связанной с самим вращающимся
телом) центробежную силу вводят как
силу, уравновешивающую
центростремительную силу.

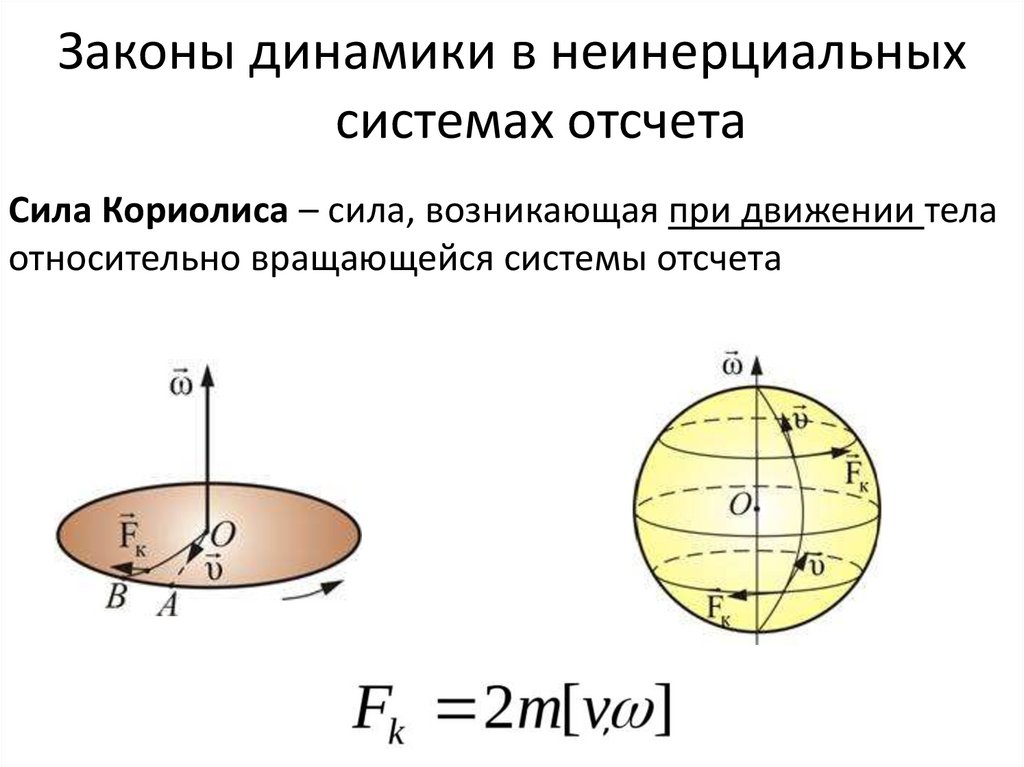
52. Законы динамики в неинерциальных системах отсчета

Сила Кориолиса – сила, возникающая при движении тела
относительно вращающейся системы отсчета

53. Движение жидкостей. Уравнение Бернулли

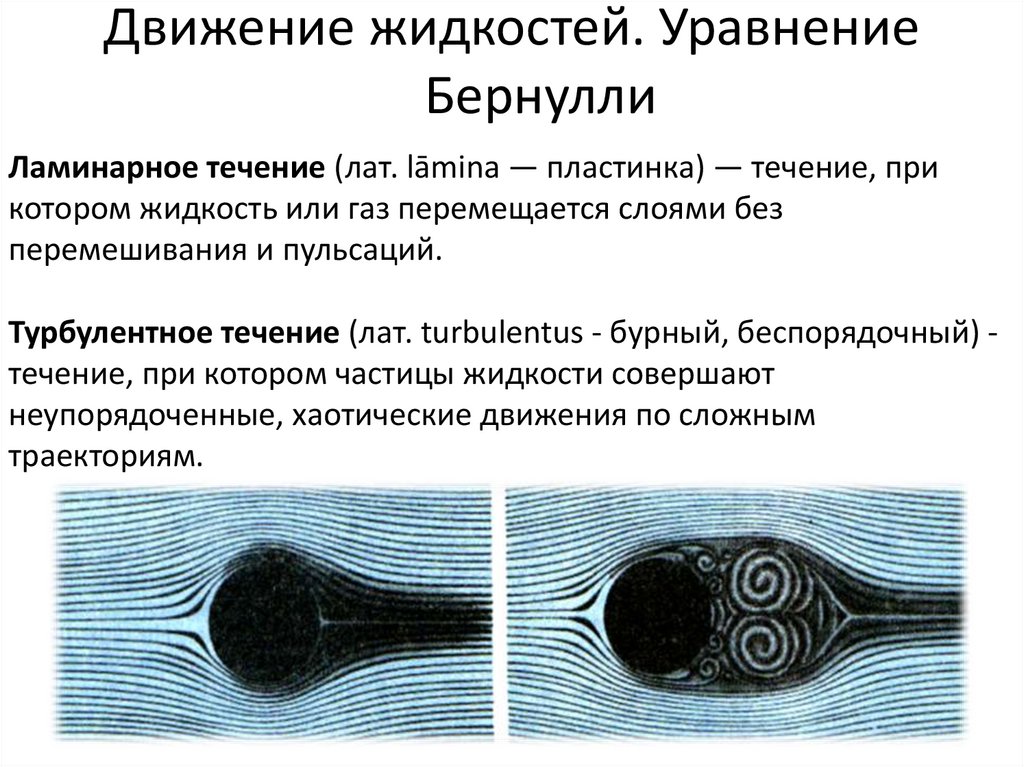
Ламинарное течение (лат. lāmina — пластинка) — течение, при
котором жидкость или газ перемещается слоями без
перемешивания и пульсаций.
Турбулентное течение (лат. turbulentus - бурный, беспорядочный) течение, при котором частицы жидкости совершают
неупорядоченные, хаотические движения по сложным
траекториям.

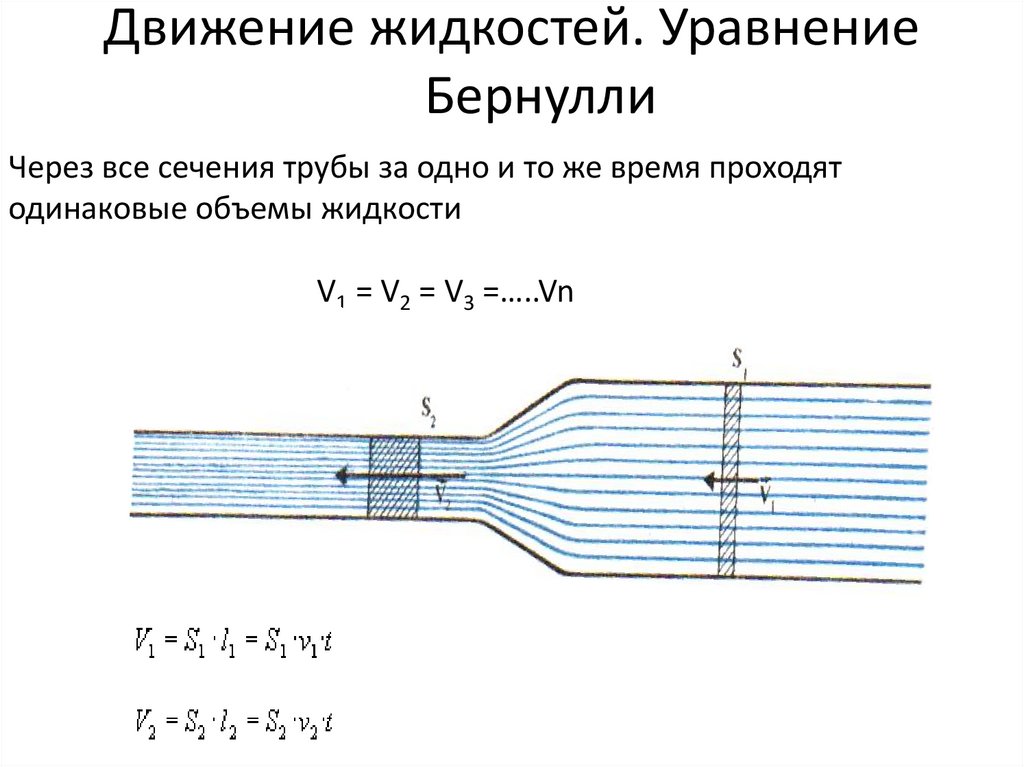
54. Движение жидкостей. Уравнение Бернулли

Через все сечения трубы за одно и то же время проходят
одинаковые объемы жидкости
V1 = V2 = V3 =…..Vn

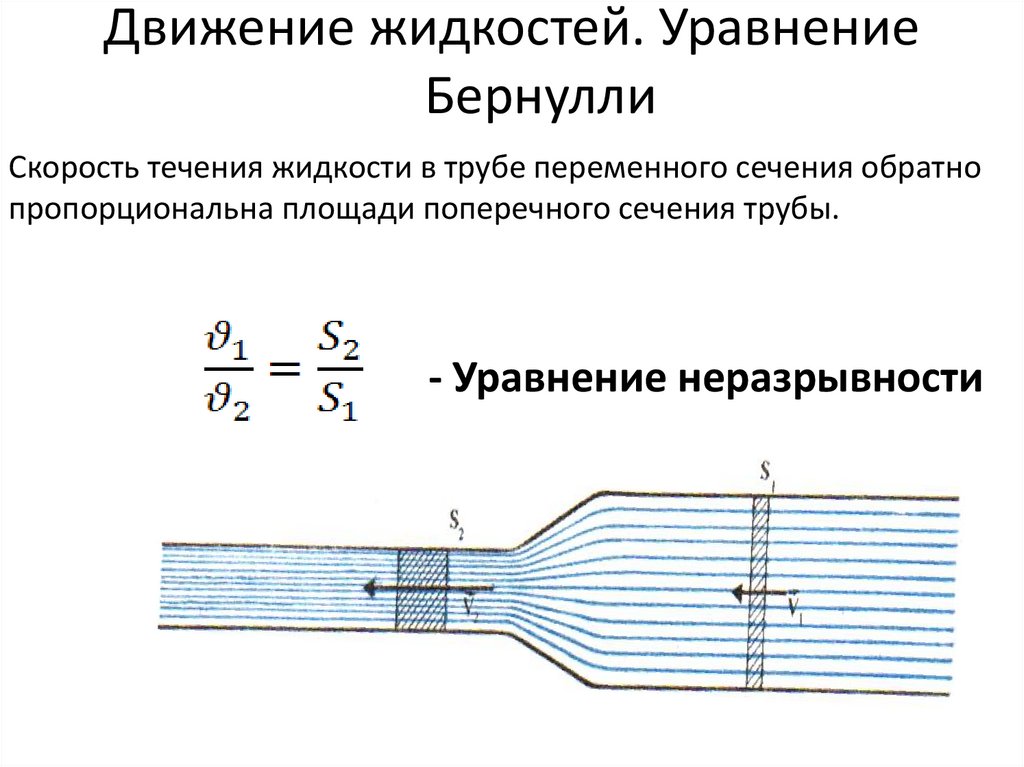
55. Движение жидкостей. Уравнение Бернулли

Скорость течения жидкости в трубе переменного сечения обратно
пропорциональна площади поперечного сечения трубы.
- Уравнение неразрывности

56. Движение жидкостей. Уравнение Бернулли

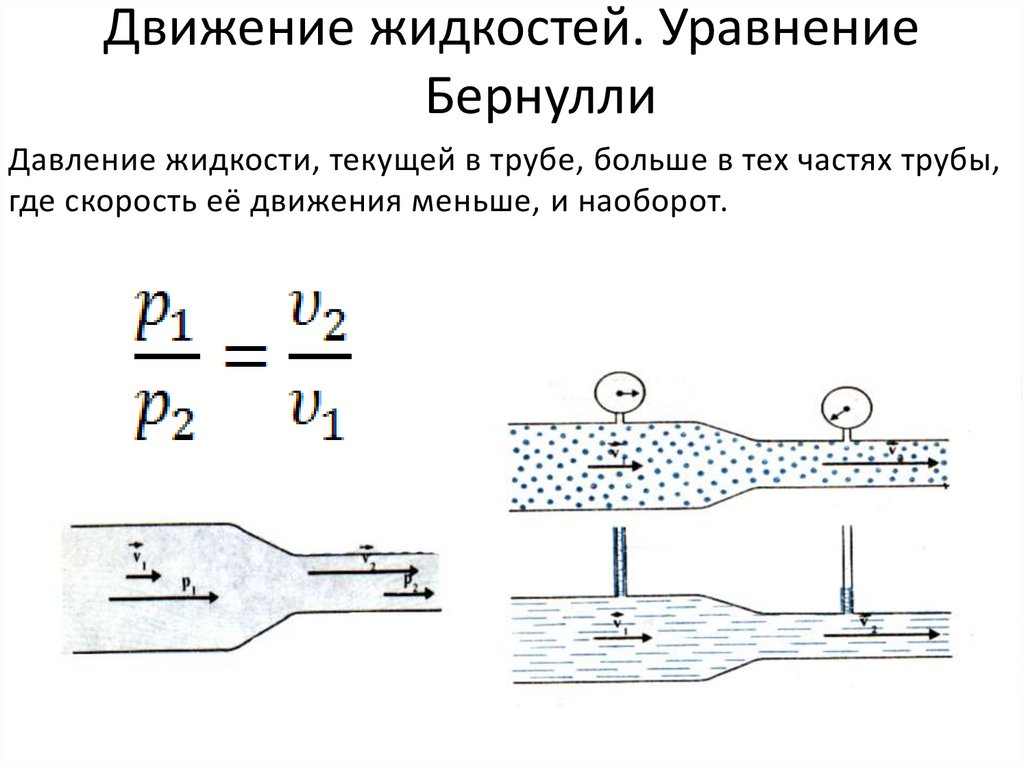
Давление жидкости, текущей в трубе, больше в тех частях трубы,
где скорость её движения меньше, и наоборот.

57. Движение жидкостей. Уравнение Бернулли

58. Движение жидкостей. Уравнение Бернулли

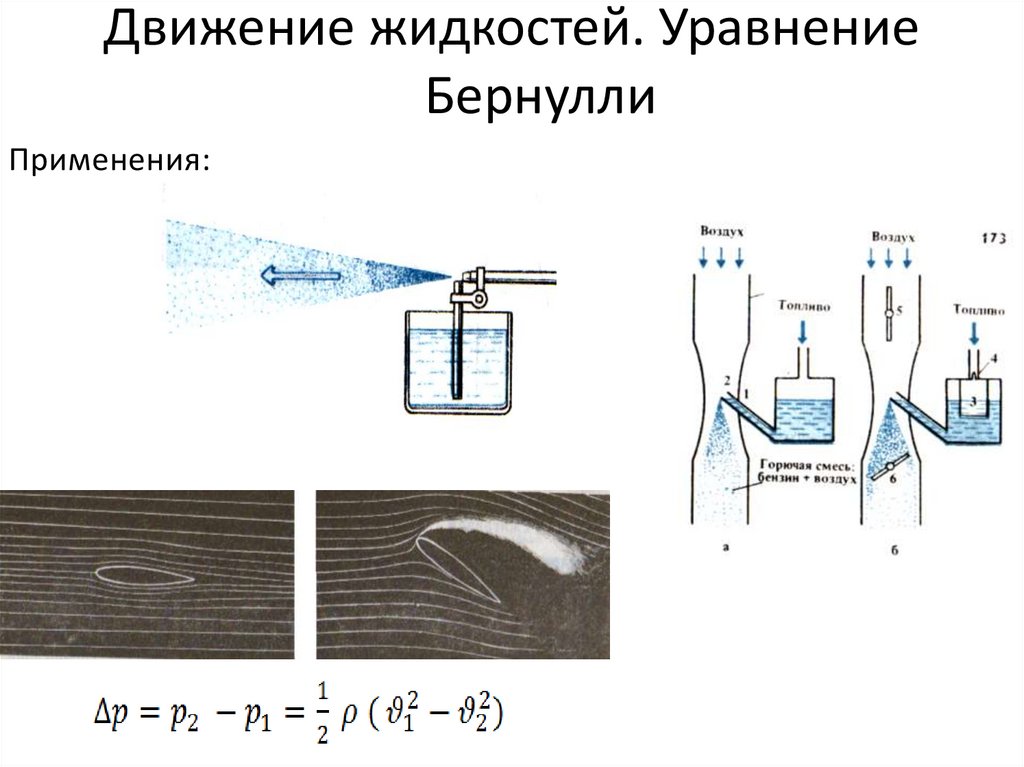
Применения:

59. Движение жидкостей. Уравнение Бернулли

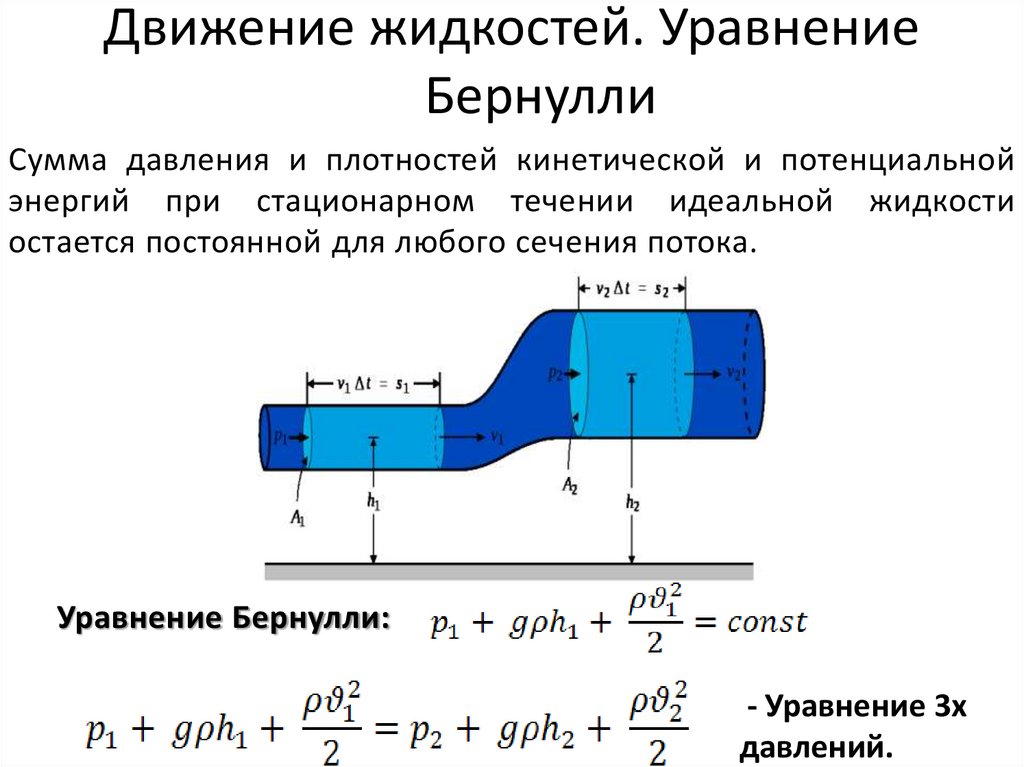
Сумма давления и плотностей кинетической и потенциальной
энергий при стационарном течении идеальной жидкости
остается постоянной для любого сечения потока.
Уравнение Бернулли:
- Уравнение 3х
давлений.