Лекция_5_формулы_01.10.2024

1. Лекция №5 Разработка программного обеспечения для моделирования физических процессов

Санкт-Петербургский политехнический университет Петра Великого
Лекция №5
Разработка программного обеспечения
для моделирования физических
процессов
Воскобойников С.П.
Доцент ВШ ПИ ИКНК, к.ф.-м.н.
voskob_sp@spbstu.ru
01.10.2024

2. Содержание

• Постановка задач на собственные значения.
• Применение ИИМ для численного решения
задач на собственные значения в декартовой,
цилиндрической и сферической системах
координат.
• Пример аналитического и численного
решения модельной задачи на собственные
значения.
• Оценка обусловленности матриц при решении
краевых задач для ОДУ второго порядка.

3. Постановка задач на собственные значения

d
du x
k x
q x u x u x ,
dx
dx
x a,b ,
0 C1 k x C2 ,
Однородные краевые условия первого рода
u x x a 0,
u x x b 0
Однородные краевые второго рода
k ( x)
du x
0,
dx x a
k ( x)
du x
0,
dx x b
Однородные краевые условия третьего рода
k x
du x
1u x x a ,
dx x a
k x
du x
2u x x b ,
dx x b
1 0,
2 0,
Комбинации однородных краевых условий
u x x a 0,
k x
собственны е
du x
2u x x b ,
dx x b
u x 0,
числа (значения)
если u x собственна я
2 0,
u x 0 собственные функции
функция, то с u x тоже собственна я
функция, с 0

4. Интегро-интерполяционный метод (ИИМ)

N число разбиений интервала a, b
x0 x1 ... xN ,
xi a, b ,
x0 a, xN b
hi xi xi 1 , i 1,2,..., N
xi 1/ 2
xi xi 1
,
2
i 1,2,..., N
hi 1
i 0
2 ,
h hi 1
i i
, i 1,2,..., N 1
2
hi
i N
2 ,
ui u xi
vi v xi
vi ui

5. ИИМ для задачи на собственные значения с краевыми условиями 1-ого рода

i 1 / 2
d
du
k x q x u dx udx,
dx
dx
xi 1 / 2
xi 1 / 2
xi 1 / 2
x
i 1,2,..., N 1,
xi 1 / 2
xi 1 / 2
du
du
k x
k x
qudx udx,
dx x xi 1 / 2
dx x xi 1 / 2 xi 1 / 2
xi 1 / 2
k x
u u
u u
du
k xi 1/ 2 i i 1 ki 1/ 2 i i 1 ,
h
dx x xi 1 / 2
hi
2 i
2
x i 1 / 2
x dx ,
i
i
x i 1 / 2
v v
v v
ki 1/ 2 i 1 i ki 1/ 2 i i 1 i qi vi i vi , i 1,2,..., N 1,
hi 1
hi
vi 0,
i 0,
vi 0,
i N,

6. ИИМ для задачи на собственные значения с краевыми условиями 1-ого рода

v v
v
ki 1 / 2 i 1 i ki 1 / 2 i i qi vi i vi , i 1,
hi 1
hi
v v
v v
ki 1 / 2 i 1 i ki 1 / 2 i i 1 i qi vi i vi , i 2,..., N 2,
hi 1
hi
v
v v
ki 1 / 2 i ki 1 / 2 i i 1 i qi vi i vi , i N 1,
hi 1
hi
ki 1/ 2 ki 1/ 2
k
i qi vi i 1/ 2 vi 1 i vi ,
hi 1
hi 1
hi
i 1
k
k
k
k
i 1 / 2 vi 1 i 1 / 2 i 1 / 2 i qi vi i 1 / 2 vi 1 i vi , i 2,..., N 2,
hi
hi 1
hi 1
hi
k
ki 1/ 2
k
vi 1 i 1/ 2 i 1/ 2 i qi vi i vi ,
hi
hi 1
hi
i N 1,

7. ИИМ для задачи на собственные значения с краевыми условиями 1-ого рода

ci
ki 1 / 2 ki 1 / 2
i qi ,
hi
hi 1
k
bi i 1 / 2 , di i ,
hi 1
k
k
k
ai i 1 / 2 , ci i 1 / 2 i 1 / 2 i qi ,
hi
hi
hi 1
k
bi i 1 / 2 , di i ,
hi 1
k
k
k
ai i 1 / 2 , ci i 1 / 2 i 1 / 2 i qi ,
hi
hi
hi 1
di i ,
ci vi bi vi 1 i vi , i 1
ai vi 1 ci vi bi vi 1 i vi ,
ai vi 1 ci vi
i 1
i 2,..., N 2
i vi , i N 1
i 2,..., N 2
i 1,2,..., N 1

8. ИИМ для задачи на собственные значения с краевыми условиями 1-ого рода

Av Dv ,
A N 1 N 1 ,
c1
a
2
A
b1
c2
.
D N 1 N 1 ,
b2
.
.
.
.
.
.
.
.
a N 2
c N 2
aN 1
,
bN 2
cN 1
1
D
v R ( N 1)
2
.
.
.
N 2
,
N 1
v1
v
2
.
v .
,
.
v
N 2
v
N 1

9. Переход от обобщённой задачи к классической

D 1 Av v,
1
2
Av Dv ,
A AT ,
D DT ,
B D 1 A,
Bv v,
B BT ,
1
D2
1
2
D D D ,
1
2
1
2
.
.
.
N 2
1
2
Av D D v,
1
2
1
2
C D AD ,
1
2
1
2
1
2
1
2
D AD D v D v,
1
2
w D v,
Cw w,
C CT ,
,
N 1

10. ИИМ для задачи на собственные значения с краевыми условиями 3-ого рода

d
du x
k x
q x u x u x ,
dx
dx
Краевое условие третьего рода
du x
1u x x a , 1 0,
dx x a
Краевое условие третьего рода
k x
du x
2u x x b ,
dx x b
i 1 / 2
d
du
k x q x u dx udx,
dx
dx
xi
xi
x i 1 / 2
2 0
x
i 0
xi 1 / 2
xi 1 / 2
du
du
k x
k x
qudx udx
dx
dx
x xi 1 / 2
x xi
xi
xi
du
u u
u u
k x
k xi 1 / 2 i 1 i ki 1 / 2 i 1 i ,
h
dx x xi 1/ 2
hi 1
2 i 1
2
i 0
xi 1 / 2
x dx ,
i
xi
du x
1u x x x , i 0
i
dx x xi
v v
ki 1 / 2 i 1 i 1vi i qi vi i vi , i 0
hi 1
k x
i

11. ИИМ для задачи на собственные значения с краевыми условиями 3-ого рода

Краевое условие третьего рода
k x
du x
2u x x b ,
dx x b
2 0
i
d
du
k x q x u dx udx,
dx
dx
x i 1 / 2
x i 1 / 2
xi
x
i N
xi
xi
du
du
k x
k x
qudx udx,
dx
dx
x xi
x xi 1 / 2
xi 1 / 2
xi 1 / 2
du
u ui 1
u ui 1
k x
k xi 1 / 2 i
ki 1 / 2 i
,
hi
dx x xi 1/ 2
h
i
2
2
k ( x)
du x
2u x x x ,
i
dx x xi
i N
xi
x dx ,
i
x i 1 / 2
i N
v v
2vi ki 1 / 2 i i 1 i qi vi i vi , i N
hi
i

12. ИИМ для задачи на собственные значения с краевыми условиями 3-ого рода

v v
ki 1 / 2 i 1 i 1vi i qi vi i vi , i 0
hi 1
v v
v v
ki 1/ 2 i 1 i ki 1/ 2 i i 1 i qi vi i vi , i 1,2,..., N 1
hi 1
hi
v v
2vi ki 1/ 2 i i 1 i qi vi i vi , i N
hi
ci
ki 1 / 2
i qi 1 ,
hi 1
k
k
k
ai i 1 / 2 , ci i 1 / 2 i 1 / 2 i qi ,
hi
hi
hi 1
k
k
ai i 1 / 2 , ci i 1 / 2 i qi 2 ,
hi
hi
k
bi i 1 / 2 , d i i ,
hi 1
i 0
k
bi i 1 / 2 , di i ,
hi 1
di i ,
i N
i 1,2,..., N 1

13. ИИМ для задачи на собственные значения с краевыми условиями 3-ого рода

Av Dv ,
c0
a
1
A
A N 1 N 1 ,
D N 1 N 1 ,
b0
c1
0
, D
bN 1
cN
.
b1
.
.
.
.
.
.
.
.
aN 1
cN 1
aN
Av Dv ,
1
2
1
2
C D AD ,
A AT ,
1
2
w D v,
v R ( N 1)
1
.
.
.
N 1
,
N
v0
v
1
.
v . ,
.
v
N 1
v
N
D DT ,
Cw w,
C CT ,

14. ИИМ для задачи на собственные значения в криволинейной системе координат

1 d
du r
n r n k r
q r u r u r ,
dr
r dr
0 C1 k r C2 ,
r 0, R
n 1 одномерный случай цилиндрическая системы координат
n 2 одномерный случай сферической системы координат
u r 0 ограничено
Краевые условия первого рода
u r r R 0
Краевое условие второго рода
k r
du r
0,
dr r R
Краевое условие третьего рода
k r
du r
u r r R ,
dr r R
0

15. ИИМ для задачи на собственные значения в криволинейной системе координат

N число разбиений интервала 0, R
r0 r1 ... rN , ri 0, R , r0 0, rN R
hi ri ri 1 , i 1,2,..., N
r r
ri 1 / 2 i i 1 ,
2
i 1,2,..., N
hi 1
i 0
2 ,
h hi 1
i i
, i 1,2,..., N 1
2
hi
i N
2 ,
u xi ui ,
v xi vi ,
vi ui ,

16. ИИМ для задачи на собственные значения в криволинейной системе координат

1 d
du r
n r n k r
q r u r u r ,
dr
r dr
i 1 / 2
d n
du r n
n
r k r
r q r u r dr r u r dr ,
dr
dr
ri 1 / 2
ri 1 / 2
ri 1 / 2
r
i 1,2,..., N 1
ri 1 / 2
ri 1 / 2
n
du r
du r
n
n
r k r
r k r
r q r u r dr r nu r dr
dr r ri 1/ 2
dr r ri 1/ 2 ri 1/ 2
ri 1 / 2
du r
u ui 1 ui ui 1
i
hi
dr r ri 1/ 2
hi
2
2
ri 1 / 2
r r dr r ,
n
n
i i
i
ri 1 / 2
v v
v v
ri n 1 / 2ki 1 / 2 i 1 i ri n 1 / 2ki 1 / 2 i i 1 i ri n qi vi i ri nvi ,
hi 1
hi
i 1,2,..., N 1

17. ИИМ для задачи на собственные значения с условием ограниченности

1 d
du r
n r n k r
q r u r u r ,
dr
r dr
du r
nk
r
d
du r
dr q r u r u r ,
k r
dr
dr
r
du r
dr ,
r
nk r
lim
r 0
k r
du r
0,
dr r 0
0
,
0
du r
dr n d k r du r ,
r
dr
dr
nk r
lim
r 0
d
du r
n 1 k r
q r u r u r r 0 ,
dr
dr
r 0
u r 0 ограничено k r
du r
0,
dr r 0

18. ИИМ для задачи на собственные значения с условием ограниченности

i 1 / 2
d n
du r n
n
r k r
r q r u r dr r u r dr ,
dr
dr
ri
ri
ri 1 / 2
r
i 0
ri 1 / 2
ri 1 / 2
n
du r
du
r
r k r
r n k r
r n q r u r dr r nu r dr ,
dr r ri 1 / 2
dr r ri
ri
ri
du r
u u u u
i 1 i i 1 i
h
dr r ri 1/ 2
hi 1
2 i 1
2
r ri 1 / 2
r n 1
n
n
r r r dr ri r r dx i n 1
r r
i
i
ri 1 / 2
ri 1 / 2
ri n 1 / 2
i i
,
n 1
i
n
vi 1 vi
ri n 1/ 2
ri n 1/ 2
ri 1 / 2 k i 1 / 2
0 i qi
vi i
vi ,
hi 1
n 1
n 1
i 0
i 0

19. ИИМ для задачи на собственные значения с условием 3-его рода

Краевое условие третьего рода : k r
du r
u r r R ,
dr r R
i
d n
du r n
n
r k r
r q r u r dr r u r dr ,
dr
dr
ri 1 / 2
ri 1 / 2
ri
0
r
i N
ri
ri
n
du r
du r
n
n
r k r
r k r
r q r u r dr r nu r dr
dr r ri
dr r ri 1/ 2 ri 1/ 2
ri 1 / 2
,
du r
u ui 1 ui ui 1
i
hi
dr r ri 1/ 2
hi
2
2
k r
du r
u r r r , i N
i
dr r ri
ri
n
n
r
r
dr
r
i ,
i
i
ri 1 / 2
v v
ri n vi ri n 1 / 2ki 1 / 2 i i 1 i ri n qi vi i ri nvi , i N
hi

20. Разностная схема для задачи на собственные значения с условием 3-его рода

n
vi 1 vi
ri n 1 / 2
ri n 1 / 2
ri 1/ 2 k i 1/ 2
0 i qi vi
, i 0
i vi
h
n
1
n
1
i 1
v v
v v
ri n 1 / 2ki 1 / 2 i 1 i ri n 1 / 2ki 1 / 2 i i 1 i ri n qi vi i ri nvi ,
hi 1
hi
i 1,2,..., N 1
v v
ri n vi ri n 1 / 2ki 1 / 2 i i 1 i ri n qi vi i ri nvi , i N
hi
ci ri n 1 / 2
ai ri n 1 / 2
ki 1 / 2
1
i ri n 1 / 2 qi ,
hi 1 n 1
ki 1 / 2
k
k
, ci ri n 1 / 2 i 1 / 2 ri n 1 / 2 i 1 / 2 i ri n qi ,
hi
hi
hi 1
ai rin 1 / 2
ki 1/ 2
,
hi
ci rin 1 / 2
ki 1/ 2
i ri n qi ri n ,
hi
bi ri n 1 / 2
ki 1 / 2
,
hi
bi ri n 1 / 2
ki 1 / 2
, d i i ri n ,
hi 1
di
1
i ri n 1 / 2 ,
n 1
d i ri n ,
i 0
i 1,2,..., N 1
i N

21. Матричная запись разностной схемы для задачи на собственные значения с условием 3-его рода

Av Dv ,
A N 1 N 1 ,
c0
a
1
A
b0
c1
.
b1
.
.
.
.
.
.
.
.
aN 1
cN 1
aN
D N 1 N 1 ,
,
bN 1
cN
0 r1n/ 2
n 1
D
Av Dv ,
1
2
1
2
C D AD ,
v R ( N 1)
1r1n
.
.
.
.
.
.
.
.
N 1rNn 1
A AT ,
1
2
w D v,
.
v0
v
1
.
, v .
,
.
vN 1
v
N
N rNn
D DT ,
Cw w,
C CT ,

22. Модельная задача на собственные значения. Аналитическое решение.

d 2u x
u x ,
2
dx
u x x 0 C2 0,
u x x L C1 sin
0,
k 0,
u x x 0 C1 0,
k 1, q 0, a 0, b L,
x 0, L
u x C1 sin
L 0,
2
C1 sin
L 0,
sin
L 0,
u x C1 C2 x,
C2 0,
u x 0,
0 не является собственным числом
k
k ,
L
2
k 1,2,...
u x x L 0,
x C cos x ,
d 2u x
0,
2
dx
u x x L C2 L 0,
u x x 0 0,
x
uk x C sin k ,
L
L k ,
k 0,1,2,...

23. Модельная задача на собственные значения. Численное решение.

d 2u x
u x ,
2
dx
x 0, L
u x x 0 0,
u x x L 0,
N число разбиений интервала 0, L
h
L
,
N
xi ih, i 0,1,..., N
xi 1 / 2
xi xi 1
,
2
h
2 ,
i h,
h
,
2
hi xi xi 1 h, i 1,2,..., N
i 1,2,..., N
i 0
i 1,2,..., N 1
i N

24. Модельная задача на собственные значения. Численное решение.

v v v
i 1 i i h vi , i 1,
h
h
v v v v
i 1 i i i 1 h vi , i 2,..., N 2,
h
h
v v v
i i i 1 hvi , i N 1,
h
h
v 2vi vi 1
i 1
vi , i 1,..., N 1,
2
h
v0 0,
vN 0,
2 1
1 2 1
.
.
1
A 2
.
h
.
.
.
.
,
.
.
1 2 1
1 2
Av v
v1
v
2
.
v .
,
.
v N 2
v
N 1

25. Модельная задача на собственные значения. Численное решение.

vi 1 2vi vi 1 h2vi , i 1,..., N 1,
v0 0,
vN 0,
vi 1 2 h2 vi vi 1 0, i 1,..., N 1,
v0 0,
vN 0,
vi q i ,
qi 1 2 h2 qi 1 qi 1 0,
q 2 2 h 2 q 1 0,
2 h 2 h 4 ,
q
2 h 2 h 4 ,
q
2 2
2
1
2
2 2
2
2
2
q2 q1 1 ,
q1q2 1,
vi C1q1i C2 q1 i ,

26. Модельная задача на собственные значения. Численное решение.

v0 0,
vi C1q1i C2 q1 i ,
C1 C2 0,
N
N
C1q1 C2 q1 0,
j
q1 e ,
1
1
N
1
N
1
q
q
0,
k 1,2,..., N 1,
2 h , 2 cos 2 h2,
cos
2
2
i
1 1
vi C q C q ,
i
1 1
q12 N 1 0,
q1 e j ,
cos 2N j sin 2N 1,
e j 2 N 1 0,
C2 C1,
q1 N q1N 0,
1,
j 1
2 N 2 k ,
vN 0,
k
N
,
2 2 cos 4
2
sin
,
2
2
h
h
2
vi C1e ji C1e ji ,
e ji e ji
C sin i ,
vi C
2j
k 1,2,..., N 1,
C1
ki
vik C sin
,
N
k
C
,
2j
4
2 k
sin
,
h2
2N
C R,

27. Модельная задача на собственные значения. Численное решение.

k
4
2 k
sin
,
h2
2N
k 1,2,..., N 1
k
sin
N
2 k
sin
N
.
vk C .
,
.
sin N 2 k
N
N
1
k
sin
N
x
uk xi C sin k i ,
L
ih
uk xi C sin k ,
L
ki
u k xi C sin
,
N
k
k ,
L
2
k 1,2,...,
ki
vik C sin
,
N

28. Число обусловленности для модельной задачи на собственные значения.

cond2 A A 2 A 1 ,
cond 2 A A 2 A 1
2
2
max N 1
sin
2
N 1
2N
4
2 N 1
sin
,
h2
2N
max
,
min
2
sin
sin
2 sin cos
4 cos 2 ....
2 2N
2
2 2N
2 2N
2
2
2
sin
2
N 1
2N
1
,
2N
max N 1
2
4
,
2
h
max A ,
4
4
4 2
2
2
min 1 2 sin
2 2 2
h
2N h2 2N
4h N
L
2
2
2
4
L
4
N
cond 2 A A 2 A 1 max 2 2 2 ,
2
min h
cond 2 A ~
1
,
2
h
cond 2 A ~ N 2 ,

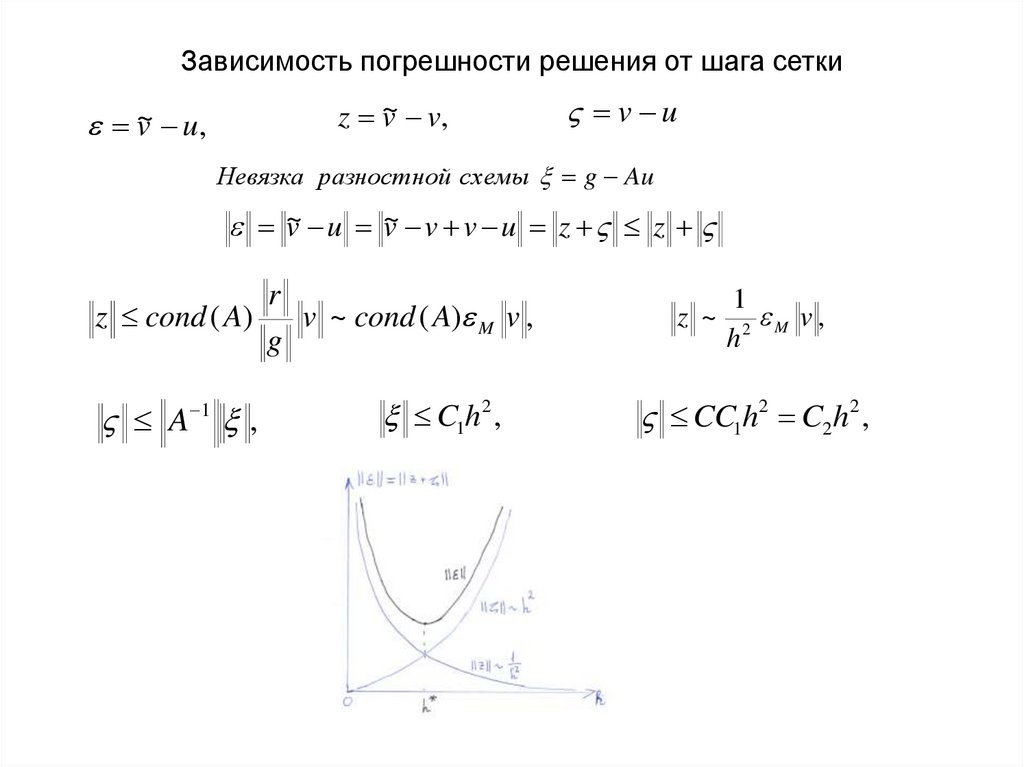
29. Зависимость погрешности решения от шага сетки

z v~ v,
v~ u,
v u
Невязка разностной схемы g Au
v~ u v~ v v u z z
r
z cond ( A)
v ~ cond ( A) M v ,
g
A 1 ,
C1h2 ,
z ~
1
v,
2 M
h
CC1h2 C2h2 ,