Похожие презентации:
затухающие и вынужденные лекция 2 2025
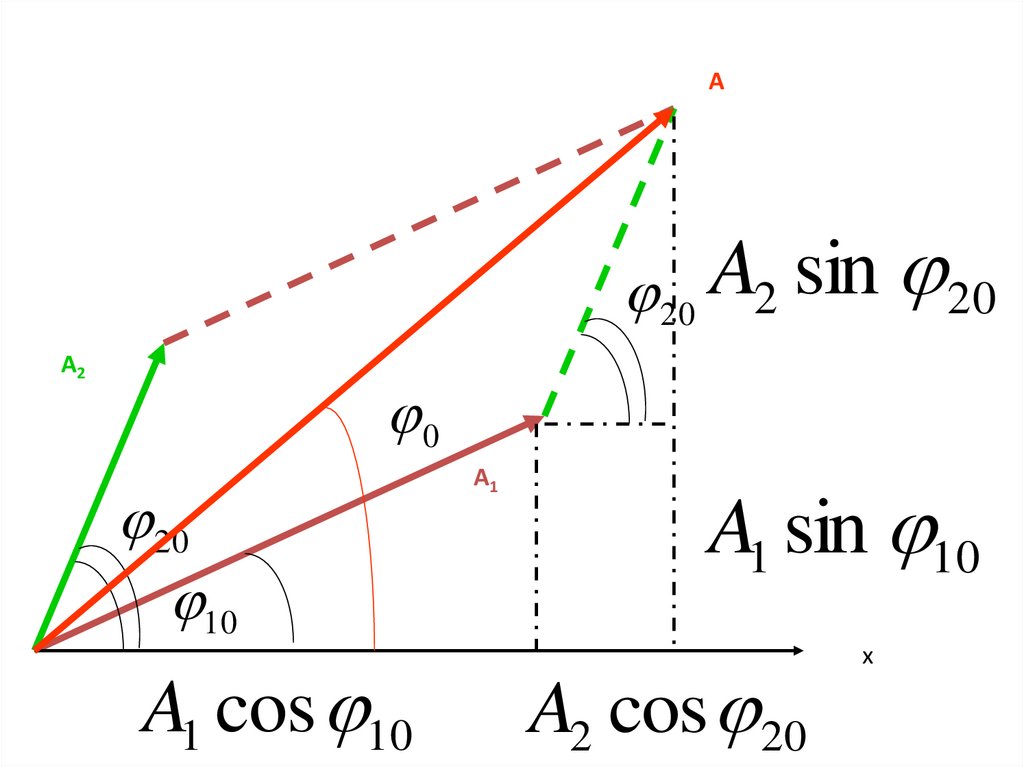
1. Сложение гармонических колебаний одного направления
+x1 A1 cos( 0t 10 )
x2 A2 cos( 0t 20 )
x A cos( 0t 0 )
2.
А20 A2 sin 20
А2
0
20
10
A1 cos 10
А1
A1 sin 10
A2 cos 20
х
3.
tg 0A1 sin 10 A2 sin 20
A1 cos 10 A2 cos 20
A A A2 2 A1 A2 cos( ( 20 10 ))
2
2
1
2
A A2 2 A1 A2 cos( 20 10 )
2
1
2
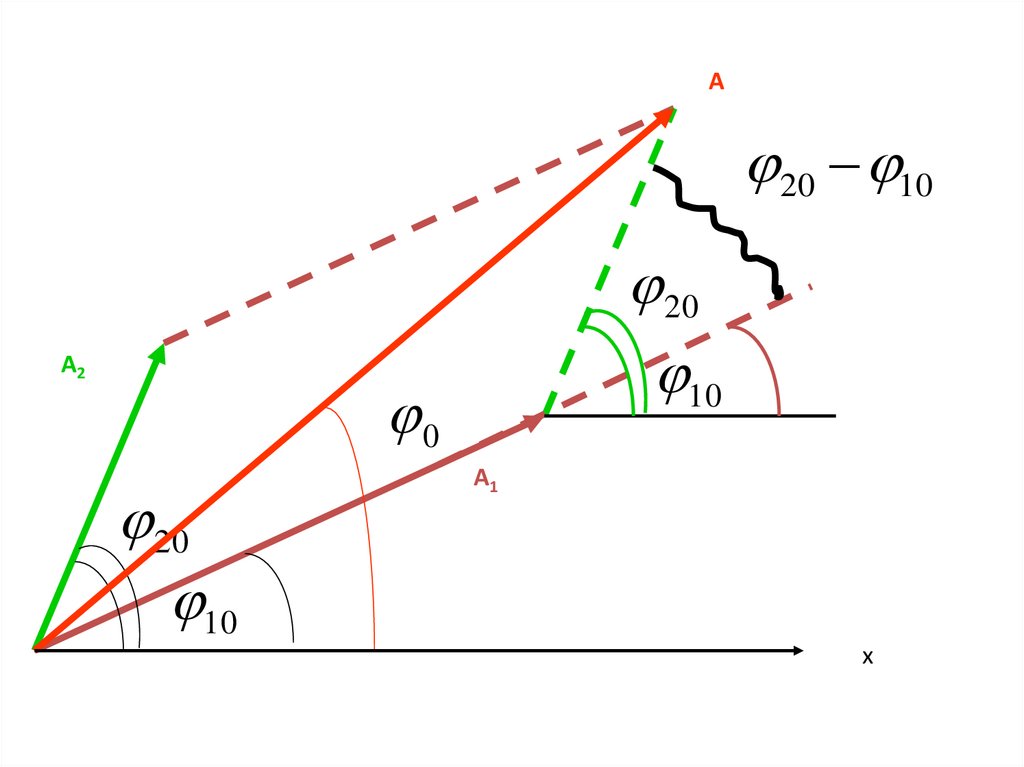
4.
А20 10
А2
20
10
0
20
10
А1
х
5.
20 10 2kA A1 A2 2 A1 A2
2
2
2
A A1 A2
20 10 (2k 1)
A A1 A2 2 A1 A2
2
2
2
A A1 A2
6. Затухающие колебания
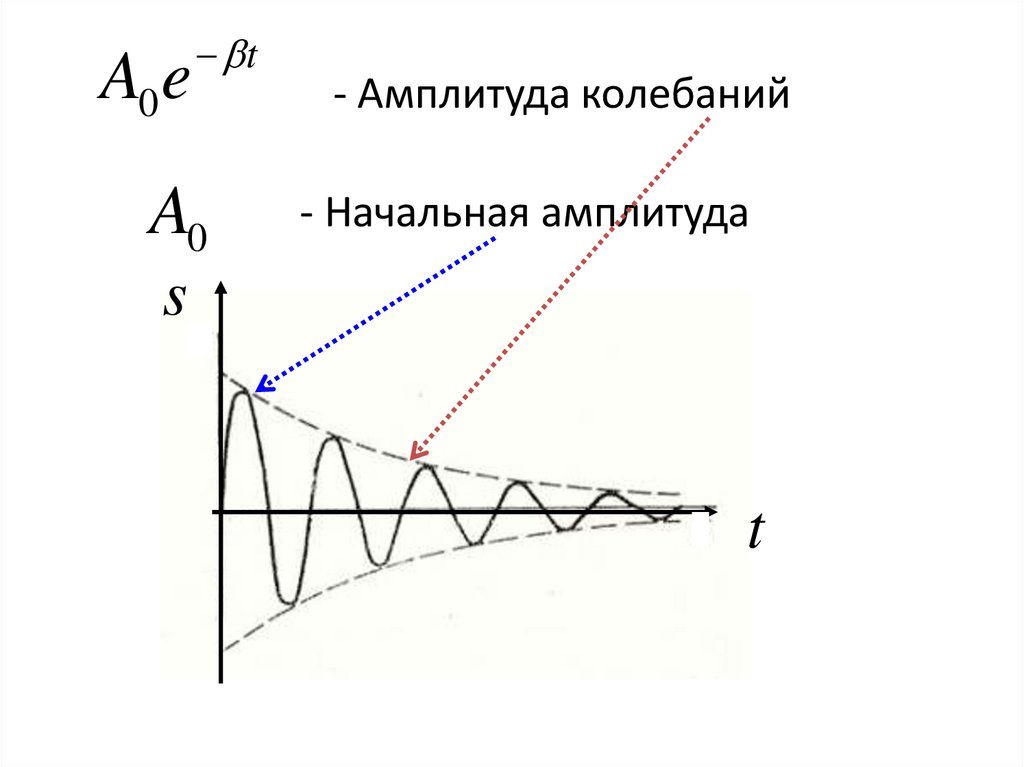
• Затухающие колебания –амплитудакоторых с течением времени уменьшается
7.
2d s
ds
2
2
s
0
0
2
dt
dt
s 2 s 0 s 0
2
s A0 e
t
cos( t )
Решение дифференциального уравнения
8.
A0 et
A0
- Амплитуда колебаний
- Начальная амплитуда
s
t
9.
коэффициент затухания0 собственная частота
2
0
T
2
2
2
0
2
частота затухающих
колебаний
период затухающих
колебаний
10.
1- время релаксации
t
A(t )
A0 e
( t T )
A(t T ) A0 e
- декремент затухания
t
A0 e
A(t )
T
ln
ln
( t T )
A0 e
A(t T )
-логарифмический декремент
-затухания
- добротность
11.
При малом затухании0
2
2
2
T T0
0
0
2
12. Затухающие колебания пружинного маятника
F kxFТР rV
X- смещение маятника от положения
равновесия
Сила трения пропорциональна скорости,
r- коэффициент сопротивления
Знак «-» указывает, что сила трения и
скорость противоположно направлены
13.
ma m x F FТрm x rx kx 0
r
k
x x x 0
m
m
x 2 x 0 x 0
2
14.
k0
m
r
2m
2
2
0
x A0 e
t
2
k r
m 2m
cos( t )
2
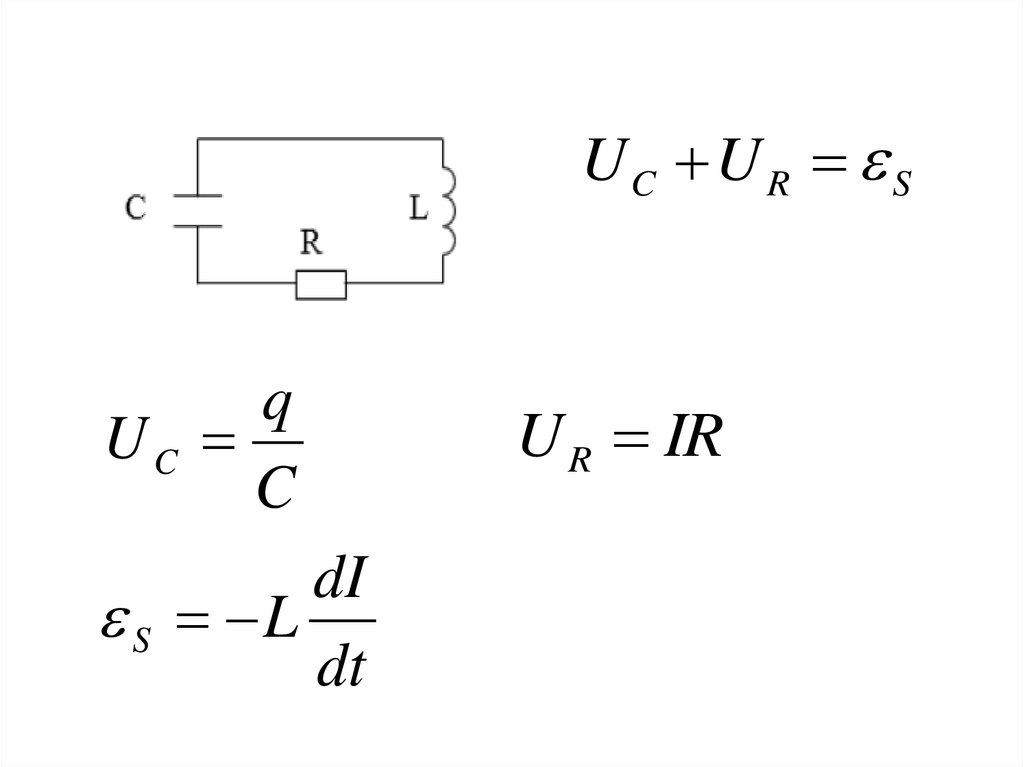
15. Затухающие колебания в колебательном контуре
16.
СL
q
UC
C
dI
S L
dt
R
UC U R S
U R IR
17.
qdI
IR L
C
dt
dq
I
dt
2
dq
q
d q
R L 2
dt
C
dt
18.
dq qd q
0
L 2 R
dt C
dt
2
d q R dq 1 q 0
2
L dt LC
dt
2
2
q 2 q 0 q 0
19.
10
LC
R
2L
2
q q0 e
t
cos( t )
2
0
2
0
R 0
0
2
1
R
2
LC 4 L
20.
T0
2
1 L
R C
1
1
LC 2 R
2L
21.
20
2
0
2
1
R
2
LC 4 L
L
RКР 2
C
Критическое сопротивление,
при котором прекращаются
колебания
22. Вынужденные колебания
23.
• Чтобы получить незатухающие колебания вреальной системе необходимо
компенсировать потери энергии
• Это можно осуществить с помощью
внешнего периодически меняющегося
фактора, изменяющегося по
гармоническому закону
X (t ) X 0 cos t
24.
Дифференциальное уравнениевынужденных колебаний
2
d s
ds
2
2
s
X
cos
t
0
0
2
dt
dt
Частота вынуждающего фактора ( силы или э.д.с)
X0
Амплитуда вынуждающего фактора
25.
Решение уравненияs A cos( t )
26.
2arctg 2
2
0
Фаза колебаний ( колебания в системе
не совпадают по фазе с колебаниями
вынуждающего фактора)
27.
AX0
4
2
0
2 2
2
-Амплитуда колебаний зависит
от частоты вынуждающей силы
2
28.
• Явление резкого возрастания амплитудыпри приближении частоты вынуждающей
силы к резонансной частоте называется
резонансом
29.
d 22 2
2 2
4
0
d
2 2 8 0
Точка
перегиба
0
2
0
2
2 0
2
0
2
2
• Экстремум
2
30.
рез2
2
0
2
• Резонансная частота зависит от
собственной частоты (конфигурация
системы) и коэффициента затухания (
потери энергии)
• С увеличением потерь энергии
(коэффициента затухания) резонансная
частота уменьшается
• При малом затухании резонансная частота
близка к собственной
31.
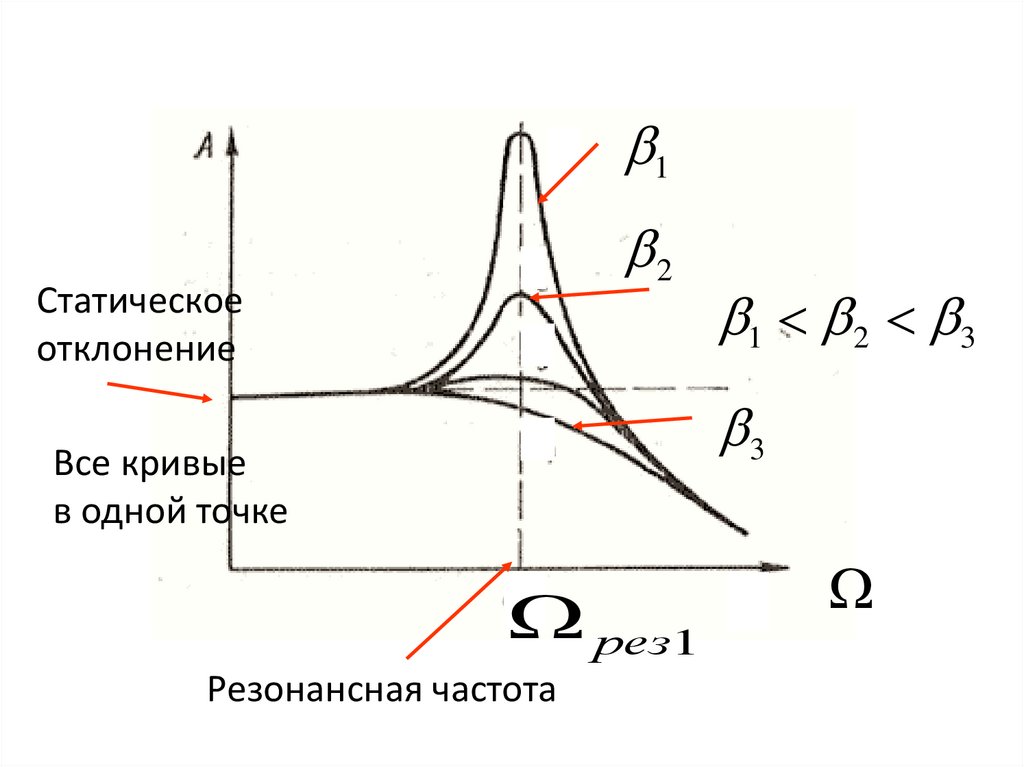
• Нарисуем график зависимости амплитудыколебаний от частоты вынуждающей силы
Амплитудно -частотная характеристика
32.
12
Статическое
отклонение
1 2 3
3
Все кривые
в одной точке
рез1
Резонансная частота
33.
Амплитуда в резонансеX0
Арез
2 4 2
2
0
2 2
2
0
2
X0
4 8 4
4
4
2
X0
2
2
0
2
2
0
2
0
2
34.
22
0
0
Aрез
X0
2 0
A 0
Aрез
А( 0)
0
2
X0
X0
0
2 0
2
X0
0
Добротность при
малом затухании
2
35.
• Добротность показывает свойства системыпри резонансе
• Чем больше добротность , тем выше
амплитуда при резонансе
36. Вредное влияние резонанса
• Солдаты• Поезд через мост сбрасывает скорость
• Корабль меняет курс
Полезное применение резонанса
• Муз инструменты
• Радиоприемники

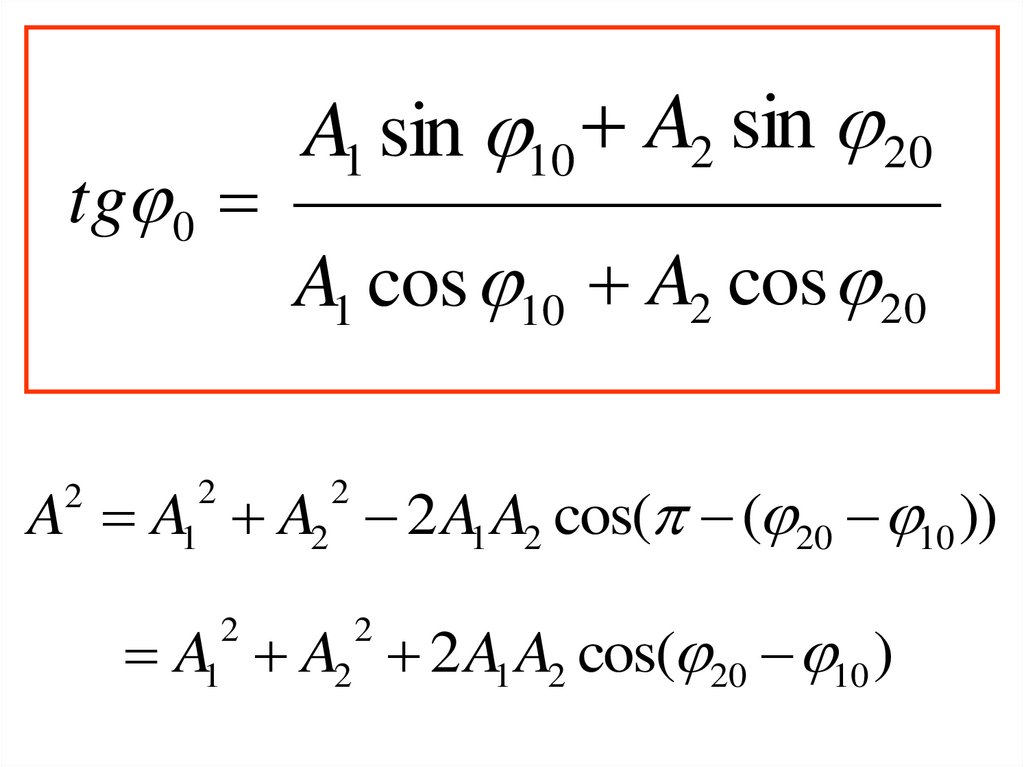
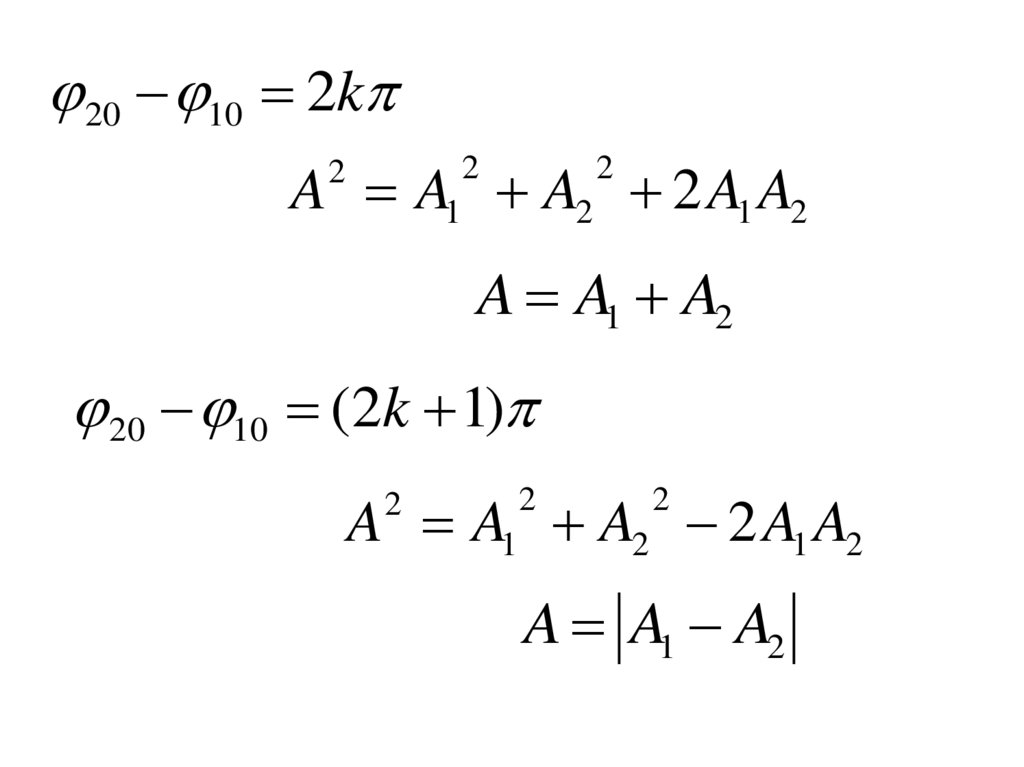






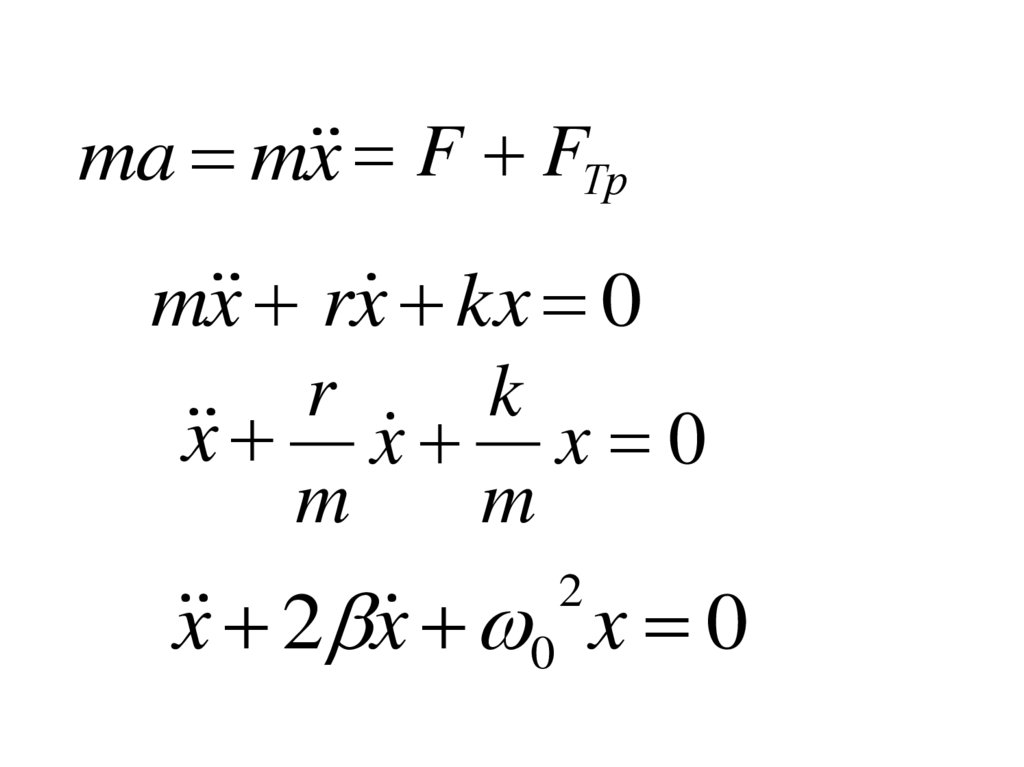
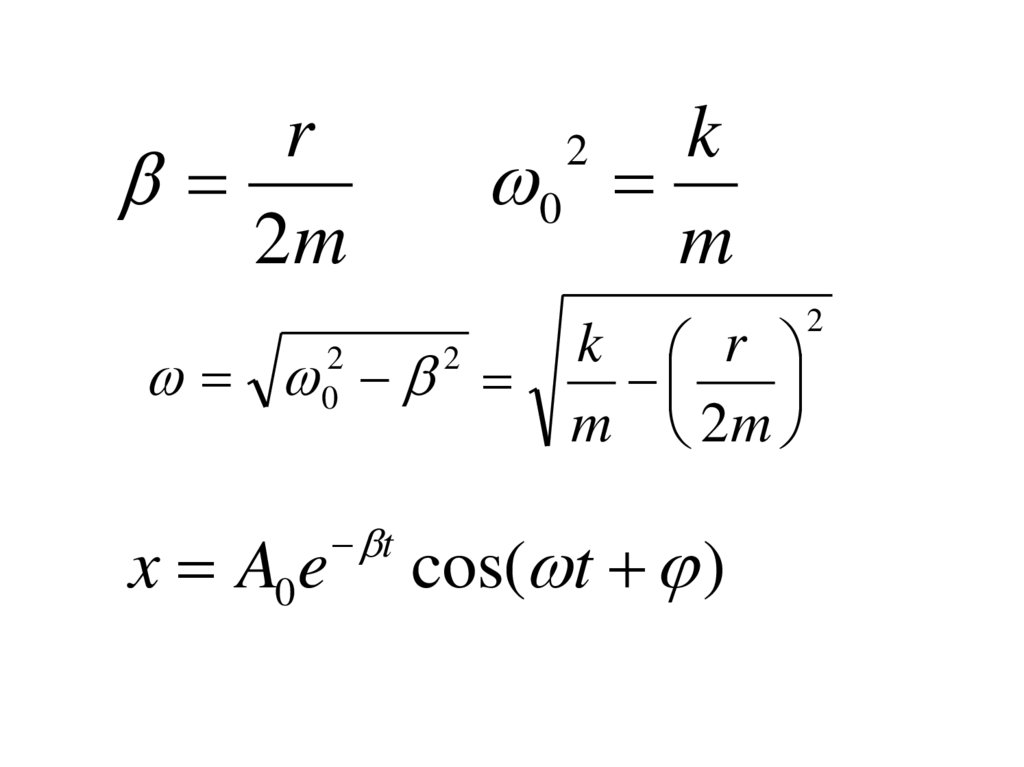

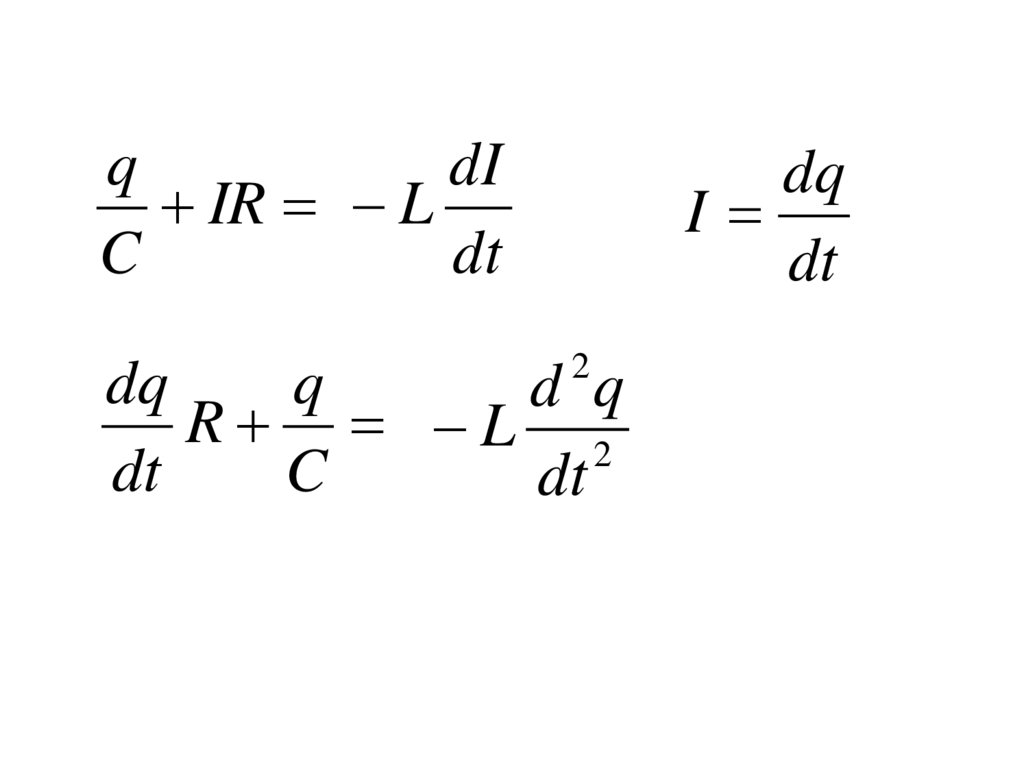
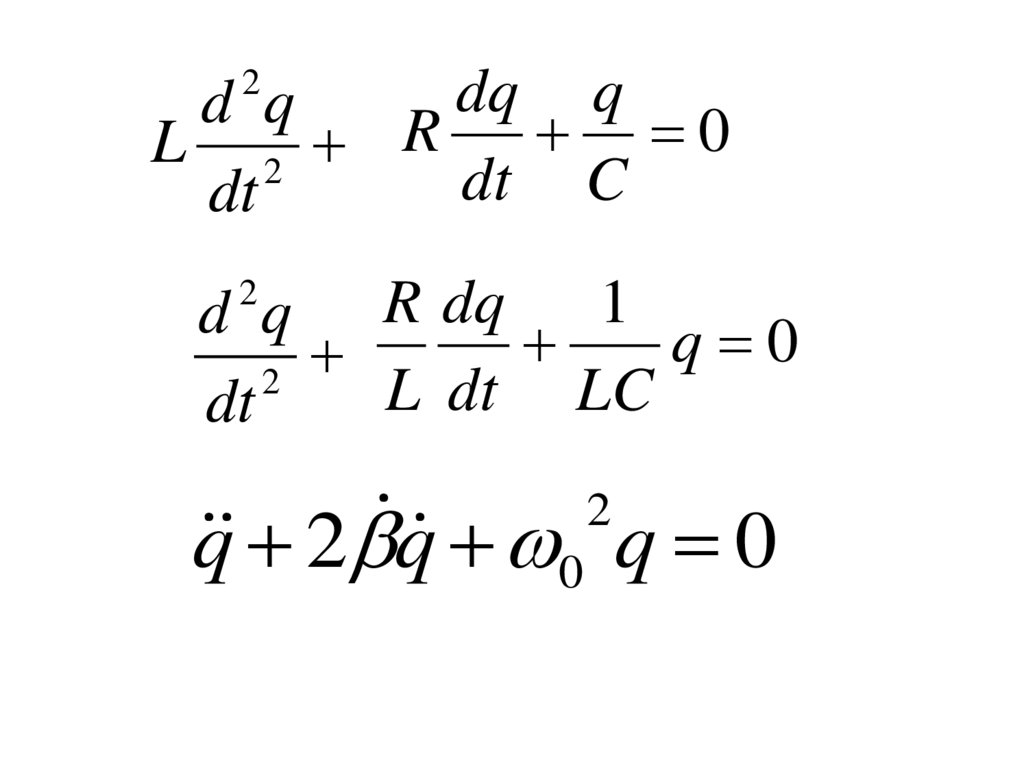

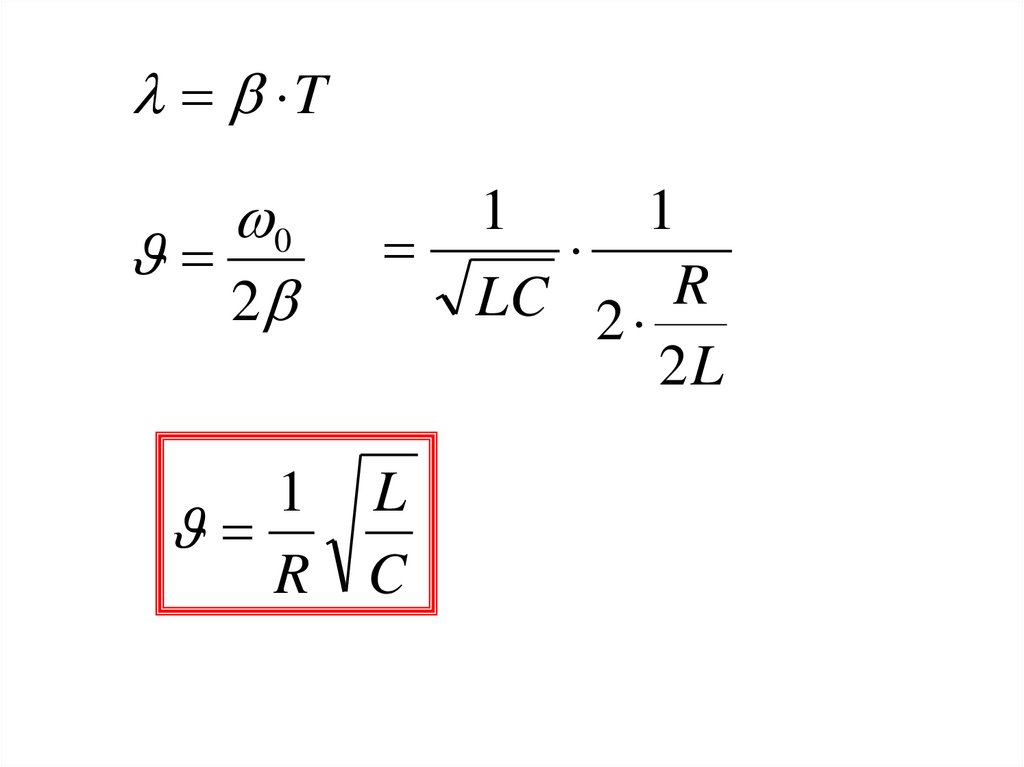








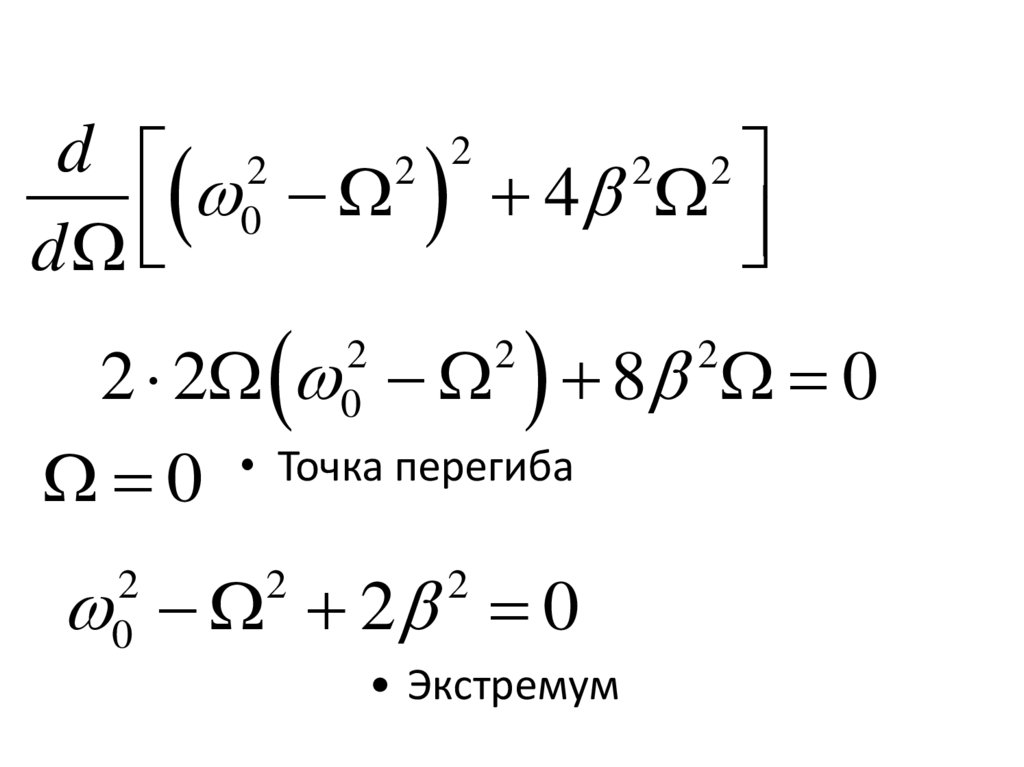



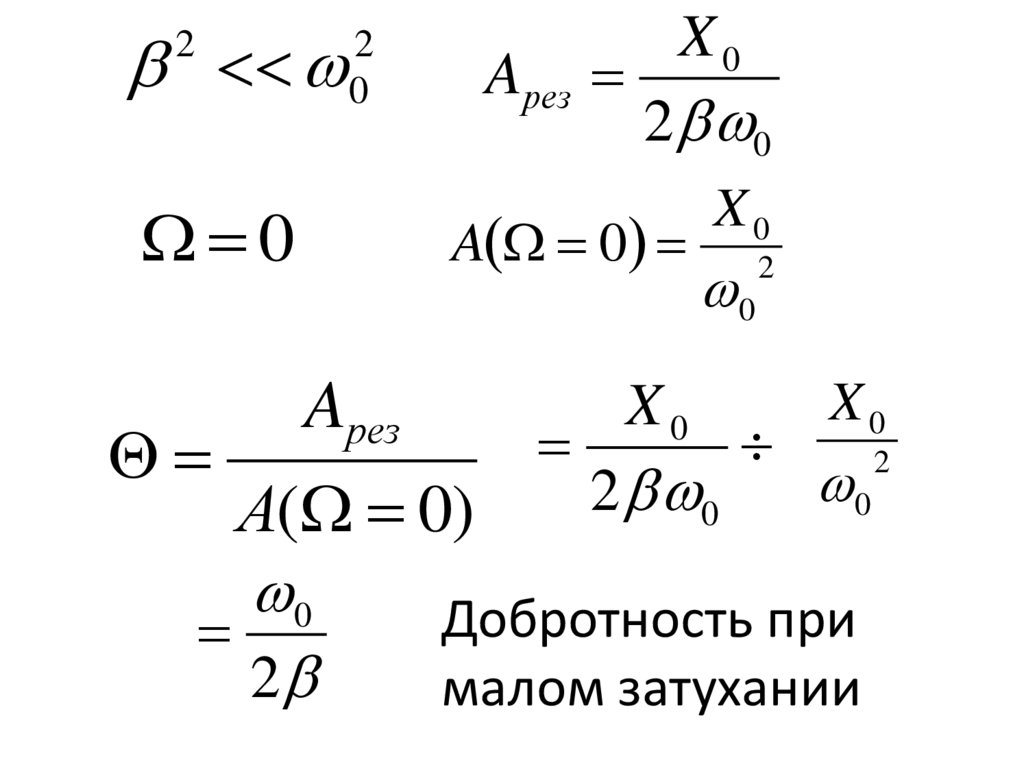


 Физика
Физика








