Похожие презентации:
Лекция 7. Свободные затухающие колебания
1. ЛЕКЦИЯ 7
2. СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
3.
СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ – колебания, амплитуда которых уменьшается с течение времени, изза потерь энергии реальной колебательной системой.(например, превращение энергии в теплоту при механических колебаниях).
Обычно рассматривают ЛИНЕЙНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ – идеализированные, реальные колебательные
системы, в которых параметры определяющие физические свойства системы, в ходе процесса не изменяются.
4. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СВОБОДНЫХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
d 2SdS
2
2
0S 0
2
dt
dt
Дифференциальное уравнение свободных затухающих
колебаний линейной системы.
Где:
• S – колеблющаяся величина описывающая физический процесс.
• const – коэффициент затухания
• 0 – циклическая частота свободных НЕЗАТУХАЮЩИХ
колебаний той же системы (то есть при отсутствии потерь энергии 0 ), иначе говоря – собственная циклическая частота системы.
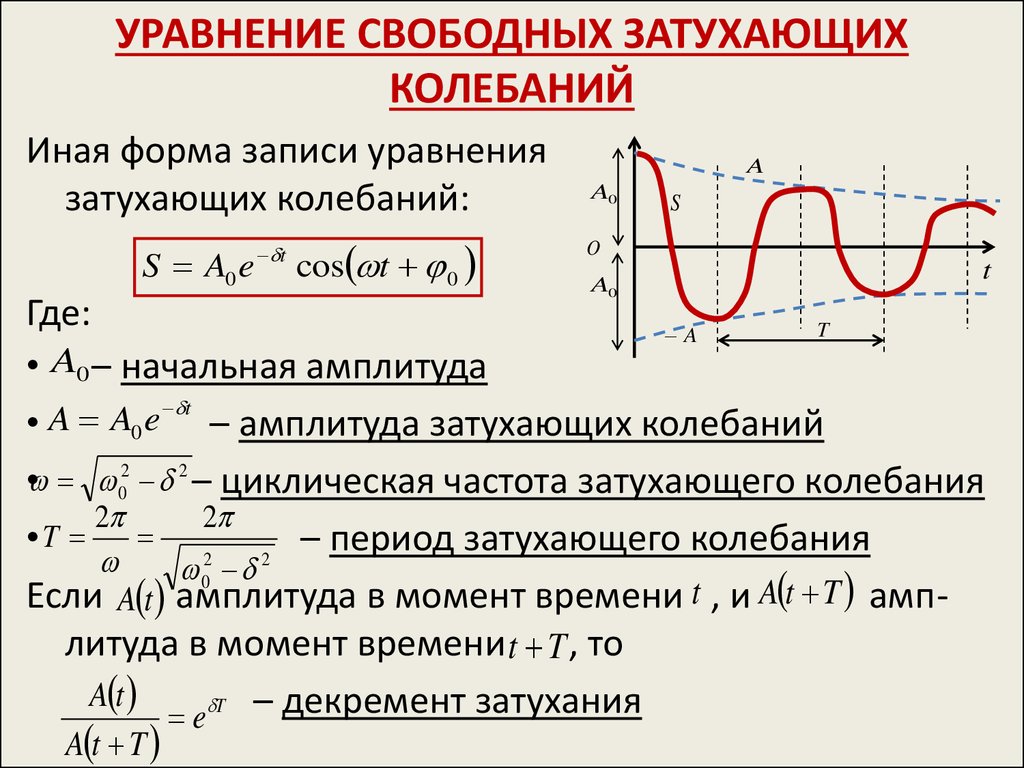
5. УРАВНЕНИЕ СВОБОДНЫХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Иная форма записи уравнениязатухающих колебаний:
S A0 e
t
cos t 0
A
A0
S
O
A0
t
Где:
T
A
• A0 – начальная амплитуда
t
A
A
e
– амплитуда затухающих колебаний
0
• 02 2 – циклическая частота затухающего колебания
2
2
• T 2 2 – период затухающего колебания
0
Если A t амплитуда в момент времени t , и A t T амплитуда в момент времени t T , то
A t
e T – декремент затухания
A t T
6.
A(t )T 1
ln
T
A(t T )
Ne
• – Логарифмический декремент затухания
• N e – число колебаний совершаемое за время
уменьшения амплитуды в е раз
1
• – время релаксации, (время за которое
амплитуда колебаний уменьшается в е раз).
0
• Q N e . – добротность (характеристика
T 2
колебательной системы, пропорциональна числу
колебанийN e , за время релаксации ).
7. СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ В ПРУЖИННОМ МАЯТНИКЕ
Для пружинного маятника массой m, совершающего малые колебания под действием упругой силы F kx ,сила трения пропорциональна скорости Fтр r rx ,где r коэффициент сопротивления.
Закон движения маятника будет иметь вид:
x 2 x 02 x 0 mx kx rx
• Коэффициент затухания: r 2m
• Собственная циклическая частота: 0 k m
• Циклическая частота: 2 r 2 4m 2
1
0
• Добротность пружинного маятника: Q r km
Уравнение колебаний маятника: x A e t cos t
0
8. СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ В ЭЛЕКТРИЧЕСКОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Дифференциальное уравнение свободных затухающихколебаний заряда в контуре имеет вид:
R
1
q q
q 0
R
L
LC
2L
• Коэффициент затухания
• Частота 1 LC R 2 4 L2
1 L
Q
• Добротность контура
R C
Колебания заряда совершаются по закону:
q q m e t cos t
При увеличении период затухающего колебанияT растет, и при 0 обращается в бесконечность T ,
то есть движение перестает быть периодическим.
9. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
10.
Что бы в реальной колебательной системе получить незатухающие колебания, необходимо компенсироватьпотери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X t , изменяющегося по периодическому закону
X t X 0 cos t
Например, если рассматривают механические колебания
то роль X t выполняет внешняя вынуждающая сила
.F (t ) F0 cos t , если электрический колебательный
контур, то внешняя, периодически изменяющаяся ЭДС,
или переменное напряжение U t U m cos( t ) .
Колебания возникающие под действием внешней периодически изменяющейся силы (или ЭДС) называются
соответственно: вынужденными механическими и вынужденными электромагнитными колебаниями.
11. ДИФФЕРЕНЦИАЛЬНАЯ ФОРМУЛА ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
Общая дифференциальная формула вынужденных колебанийd 2S
dS
dt 2
2
dt
02 S X 0 cos( t
• Для механических колебаний (пружинный маятник)
x 2 x 02 x F0 m cos( t )
• Для электромагнитных колебаний
Um
2
q 2 q 0 q
cos( t )
S
L
В установившемся режиме вынужденные колебания происходят с часто- O
той и являются гармоническими,
амплитуда и фаза колебаний, так же
t
12.
зависят от циклической частоты.Если период вынуждающей силы не равен периоду свободных колебаний системы, то в начале происходит
несколько биений, а затем устанавливаются вынужденные колебания с постоянной амплитудой.
13. АМПЛИТУДА И НАЧАЛЬНАЯ ФАЗА ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
Установившиеся вынужденные колебания можносчитать гармоническими, то есть для механических
колебаний, приблизительно можно считать:
x A cos t
Если вывести значения скорости x и ускорения a x ,
то дифференциальное уравнение колебаний:
mA 2 cos t rA cos( t 2) kAcos( t ) F0 cos( t )
Сократим все части уравнения на mA и ведём обозначения:
A1
2
r
k 2
A2 2 A3 0
m
m
F0
A4
mA
14.
В результате получим:A1 cos t A2 cos( t 2) A3 cos( t ) A4 cos( t )
Правую часть уравнения можно рассматривать как уравнение некоторого гармонического колебания, получившегося от сложения трёх гармонических колебаний,
определяемых левой частью равенA2
A1
ства. Для сложения воспользуемся
методом векторных диаграмм, так
A4 x
A3 A1
что A3 A1 A2 A4 . Отсюда можно
A3
определить амплитуду А:
F02
F0
2 2
2
2 2
4 ( 0 ) A
2 2
m A
m 02 2 4 2 2
Амплитуда установившихся вынужденных колебаний
прямо пропорциональна вынуждающей силе.
15.
– сдвиг фаз между скоростью колебаний и2
вынуждающей силой.
A2
2
tg
2
A3 A1
0 2
02 2
tg ctg
2
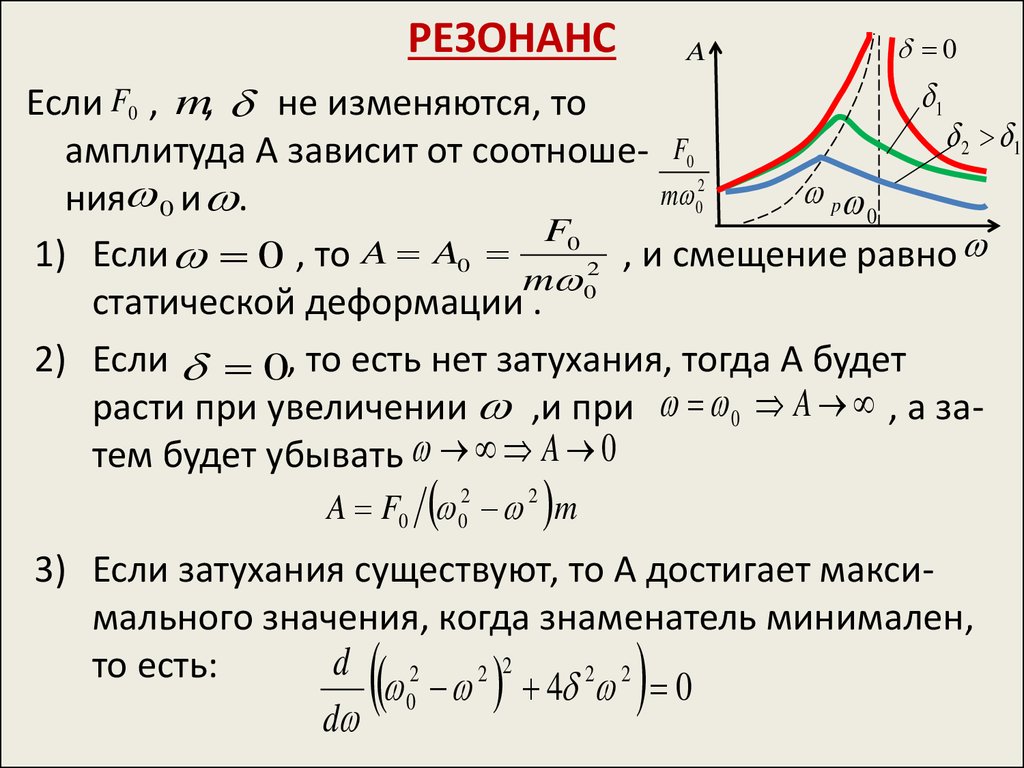
16. РЕЗОНАНС
A0
1
Если F0 , m, не изменяются, то
2 1
амплитуда А зависит от соотноше- F0
p
m 02
ния 0 и .
0
F0
1) Если 0 , то A A0
2 , и смещение равно
m 0
статической деформации .
2) Если 0, то есть нет затухания, тогда А будет
расти при увеличении ,и при 0 A , а затем будет убывать A 0
A F0 02 2 m
3) Если затухания существуют, то А достигает максимального значения, когда знаменатель минимален,
d 2 22
то есть:
0 4 2 2 0
d
17.
Введем понятие p– резонансная частота, - частота, прикоторой амплитуда смещения достигает своего
максимума:
p2 02 2 2
2
2
p 0 2 2 0 1
0
Явление резкого возрастания амплитуды вынужденных
колебаний, при приближении частоты возбуждающей
силы (частоты вынуждающего переменного напряжения)к частоте p называется – РЕЗОНАНС.
Ap
x0
2 02 2
18. ВОЛНЫ
19.
СПЛОШНАЯ СРЕДА– среда непрерывно распределенная впространстве и обладающая упругими свойствами.
ВОЛНОВОЙ ПРОЦЕСС – процесс распространения колебаний в сплошной среде.
Колеблющееся материальное тело, помещенное в упругую среду, увлекает за собой, и приводит в состояние
колебания прилегающие к нему, частицы среды. Те, в
свою очередь воздействуют на соседние частицы и
приводят их в колебательное движение. При распространении волны, частицы среды не движутся вместе с
волной, а колеблются около своего положения равновесия. Вместе с волной передаются лишь состояние
колебательного движения и его энергия. Основным
свойством всех волн независимо от их природы
является: перенос энергии без переноса вещества.
20.
ВОЛНОВАЯ ПОВЕРХНОСТЬ – совокупность точек колеблющихся в одинаковой фазе.ФРОНТ ВОЛНЫ – поверхность которая отделяет колеблющиеся частицы, от частиц ещё не пришедших в колебательное движение, или, иначе говоря, геометрическое место точек до которого дошли колебания в
момент времени t .
Волновых поверхностей огромное количество, но волновой фронт только один, и он так же является волновой поверхностью. Волновые поверхности могут
быть любой формы, в простейшем случае представляют собой совокупность плоскостей параллельных
друг другу, или совокупность концентрических сфер.
Соответственно волны бывают плоскими или сферическими.
21. ВИДЫ ВОЛН
Волны бывают различных типов:• Волны на поверхности жидкости
• Электромагнитные волны
• Механические (упругие) волны и т. д.
Упругие (механические) волны – механические возмущения распространяющиеся в упругой среде.
ПРОДОЛЬНЫЕ ВОЛНЫ – частицы среды колеблются в
направлении распространения волны.
ПОПЕРЕЧНЫЕ ВОЛНЫ – перпендикулярны направлению
распространения колебаний.
22. ГАРМОНИЧЕСКИЕ ВОЛНЫ
23.
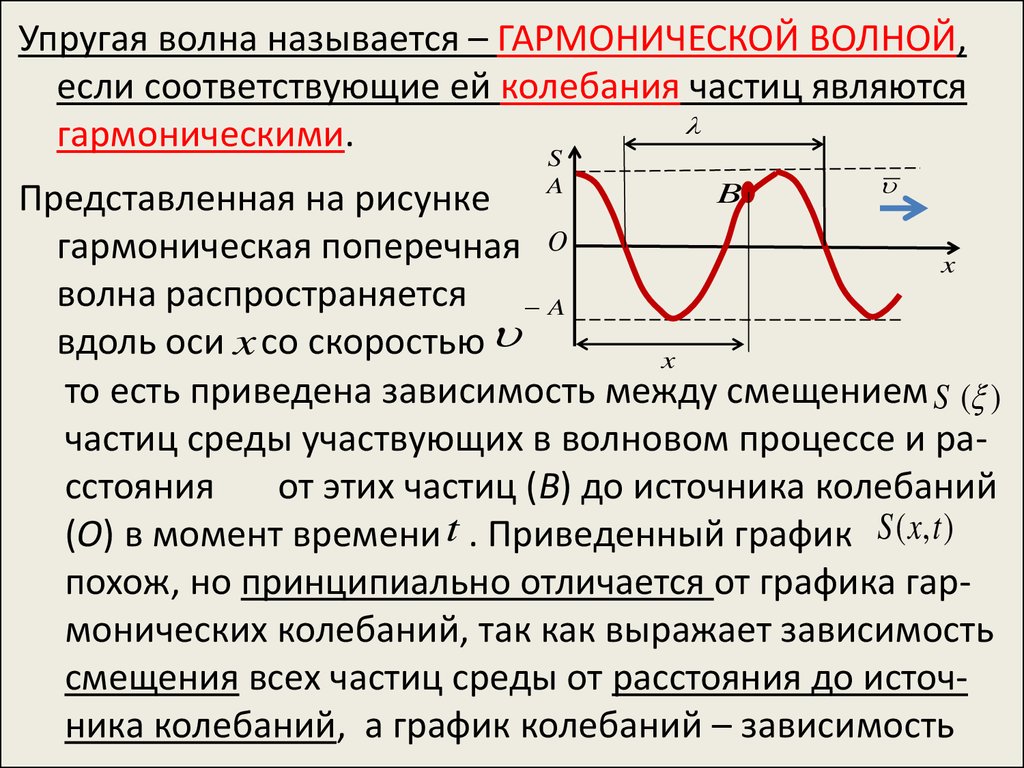
Упругая волна называется – ГАРМОНИЧЕСКОЙ ВОЛНОЙ,если соответствующие ей колебания частиц являются
гармоническими.
S
A
B
Представленная на рисунке
гармоническая поперечная O
x
волна распространяется A
вдоль оси x со скоростью
x
то есть приведена зависимость между смещением S ( )
частиц среды участвующих в волновом процессе и расстояния
от этих частиц (В) до источника колебаний
(О) в момент времени t . Приведенный график S ( x, t )
похож, но принципиально отличается от графика гармонических колебаний, так как выражает зависимость
смещения всех частиц среды от расстояния до источника колебаний, а график колебаний – зависимость
24.
колебания данной частицы от времени.ДЛИНА ВОЛНЫ – расстояние между ближайшими
частицами, колеблющимися в одинаковой фазе. Она
равна тому расстоянию, на которое распространяется
определённая фаза колебания за период T .
1
T v
T
ЧАСТОТА КОЛЕБАНИЙ (ВОЛНЫ) –
СКОРОСТЬ РАСПРОСТРАНЕНИЯ ВОЛНЫ –
Пусть частица в начальной точке О совершает колебания S (t ) A cos t , до некоторой точки В волна дойдет
за время x . Колебания в точке В начнутся с опозданием тем большим, чем дальше она отстоит от
исходной точки О.
25.
Смещение точки В в момент времени t , будет равносмещению точки О в момент времени t t t x
S A cos( (t x )) A cos( t x )
Уравнение плоской волны распространяющейся вдоль
положительного направления оси х в среде,не поглощающей энергию:
S ( x, t ) A cos( (t
x
) 0 )
A const – амплитуда волны
0 – циклическая частота волн
0 – начальная фаза колебаний (определяемая выбором
начала отсчета, x и t ).
26.
x( (t ) 0 ) – фаза плоской волны
2
2
– волновое число
k
T
Иная форма записи уравнения плоской волны
S ( x, t ) A cos( t kx 0 )
Представим, что в волновом процессе фаза постоянна:
dt
dx 0,
t kx 0 const , продифференцируем:
dx
dx
разделим на и получим dt
0
dt
Скорость распространения волны – это скорость перемещения фазы, и её называют ФАЗОВОЙ СКОРОСТЬЮ.
27.
Выше был рассмотрен случай плоской волны,уравнение СФЕРИЧЕСКОЙ ВОЛНЫ – волновые поверхности которой имеют форму концентрических сфер,
записывается как :
A
S (r , t )
cos( t kr 0 )
r
– расстояние от центра волны до рассматриваемой
точки
В случае сферической волны, даже если среда не поглощает энергию, амплитуда колебаний не остается постоянной, а убывает с расстоянием ( справедливо для
тех случаев, когда расстояния много больше размеров источника сигнала.
r
28. ВОЛНОВОЕ УРАВНЕНИЕ
Распространение волн в однородной изотропной среде,в общем случае записывается ВОЛНОВЫМ УРАВНЕНИЕМ – специальным дифференцированным уравнением в частных производных.
2S 2S 2S 1 2S
2 2 2 2
2
x
y
z
t
1 2S
S 2 2
t
2
2
2
2 2
2
x
y
z
– оператор Лапласа
– фазовая скорость
Решением этого уравнения является уравнение любой
волны (любого типа волн)
Волновое уравнение для одномерного (вдоль оси х)
распространения волны.
2S
1 2S
x
2
2 t 2
29. ПРИНЦИП СУПЕРПОЗИЦИИ ГРУППОВАЯ СКОРОСТЬ
30. ПРИНЦИП СУПЕРПОЗИЦИИ
Если среда, в которой одновременно распространяютсянесколько волн, линейна, то есть её свойства не изменяются под действием возмущений создаваемых волной, то к этим волнам применим ПРИНЦИП СУПЕРПОЗИЦИИ (НАЛОЖЕНИЯ) ВОЛН. При наложении в линейной среде нескольких волн, каждая из них распространяется независимо от других, как будто иные волны отсутствуют, а результирующее смещение частицы среды
в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в
каждом из слагаемых волновых процессов. Суперпозиция волн, мало отличающихся друг от друга по частоте,
занимающая в каждый момент времени ограниченную
область пространства называется – волновым пакетом.
31.
Пусть имеется волновой пакет из двух расположенныхвдоль оси х горизонтальных волн с одинаковыми амплитудами, близкими частотами и волновыми
числами т. е.: d dk k .
Тогда:
S A0 cos( t kx) A0 cos(( d )t (k dk ) x)
td xdk
2 A0 (cos
) cos( t kx)
2
Эта волна отличается от гармонической тем, что её
амплитуда есть медленно изменяющаяся функция
координаты x и времени t :
A 2 A0 (cos
td xdk
)
2
32. ГРУППОВАЯ СКОРОСТЬ
Результат сложения колебаний двигающихся в одномнаправлении определяется соотношением фаз этих
колебаний. Если фазы противоположны, то результирующая амплитуда минимальна, если совпадают то
максимальна. Каждый момент времени t максимальной амплитуды группы волн, соответствует тому участку пространства в котором сосредоточен максимум
энергии волны. Эта точка называется центром группы
волн, и так как фазы группы волн со временем меняются, то и центр группы волн, за некоторое время t , перемещается с некоторой скоростью u . Иначе говоря:
За ГРУППОВУЮ СКОРОСТЬ u принимают скорость
перемещения максимума амплитуды волн.
33.
Для уравнений выполняется условие:dx
d
0
dt
dk
d
Рассмотрим связь между групповой u dk
скоростями.
k
td xdk const
u
и фазовой
d
d k
d
d d
d
dk
k(
) k
dk
dk
dk
d dk
k d
d
u
d
Если фазовая скорость не зависит от фазы , то есть
нет дисперсии, то u .
Понятие групповой скорости u определяет скорость распространения сигнала который можно уловить каким
либо прибором. В теории относительности доказывается что групповая скорость u c . В то время как для
фазовой скорости ограничений не существует.
34. ИНТЕРФЕРЕНЦИЯ ВОЛН
35.
Согласованное во времени и пространстве протеканиенескольких волновых или колебательных процессов
наблюдается только в том случае, если волны имеют
одинаковую частоту.
КОГЕРЕНТНЫЕ ВОЛНЫ – волны которые имеют одинаковую частоту и постоянную разность фаз. При положении в пространстве нескольких когерентных волн происходит перераспределение энергии волн, то есть в
разных точках происходит усиление или ослабление
результирующей волны в зависимости от соотношения
между фазами этих волн. Данное явлеS1
ние называется – ИНТЕРФЕРЕНЦИЯ.
r1
Рассмотрим наложение двух когерентных
B
сферических волн, возбуждаемых истоr2
чниками S1 и S 2 , колеблющихся с одинаS
2
36.
ковыми амплитудами A0 и частотами , а так же постоянной разностью фаз.A0
S1
cos( t kx 1 )
r1
A
S 2 0 cos( t kx 2 )
r2
– расстояния от источников волн, до рассматриваемой точки В
1 , 2 – начальные фазы обеих складывающихся сферических волн
k – волновое число
Амплитуда результирующей волны в точке В:
r1 , r2
1
1
2
A A ( 2 2
cos( k (r 1 r2 ) ( 1 2 )))
r1 r2 r1 r2
2
2
0
37.
Так как для когерентных источников ( 2 1 const ) , то результат наложения двух волн в различных точках зависит от разности хода волн r1 r2 .• Там где k (r 1 r2 ) ( 1 2 ) 2 m m 0,1,2, – интеференционный максимум, амплитуда результирующего колебаA A
ния A ( 0 0 )
r1 r2
• Если k (r 1 r2 ) ( 1 2 ) (2m 1) m 0,1,2, – интеференционный минимум, амплитуда результирующего колебаA
A
ния A 0 0
r1
r2
m – порядок интерференционного максимума или
минимума.
38. СТОЯЧИЕ ВОЛНЫ
39.
СТОЯЧИЕ ВОЛНЫ – волны образованные при наложениидвух бегущих волн, распространяющихся навстречу
друг другу, с одинаковыми частотами и амплитудами.
Пусть две волны распространяются навстречу друг другу
без затухания, с одинаковыми амплитудами и частотами, вдоль оси х. При t 0 фазы 1 2 0 .
S1 A cos( t kt)
S A cos( t kt)
2
S
ACT
Уравнение стоячей волны:
S S1 S 2 2 A cos kx cos t 2 A cos
k
2
2 x
узел
пучность
cos t
– волновое число
ACT – амплитуда стоячей волны
– длина волны
x
ACT
4
2
40.
ACT 2 A cos2 x
2 x
m 0,1,2, – амплиcos
kx
1
kx
m
Если
туда максимальна xmax m ; ACT 2 A . – ПУЧНОСТЬ.
2
1
2 x
• Если cos kx 0 kx (m 2 )
1
x min (m ) ; ACT 0 . – УЗЕЛ.
2 2
m 0,1,2, . –



































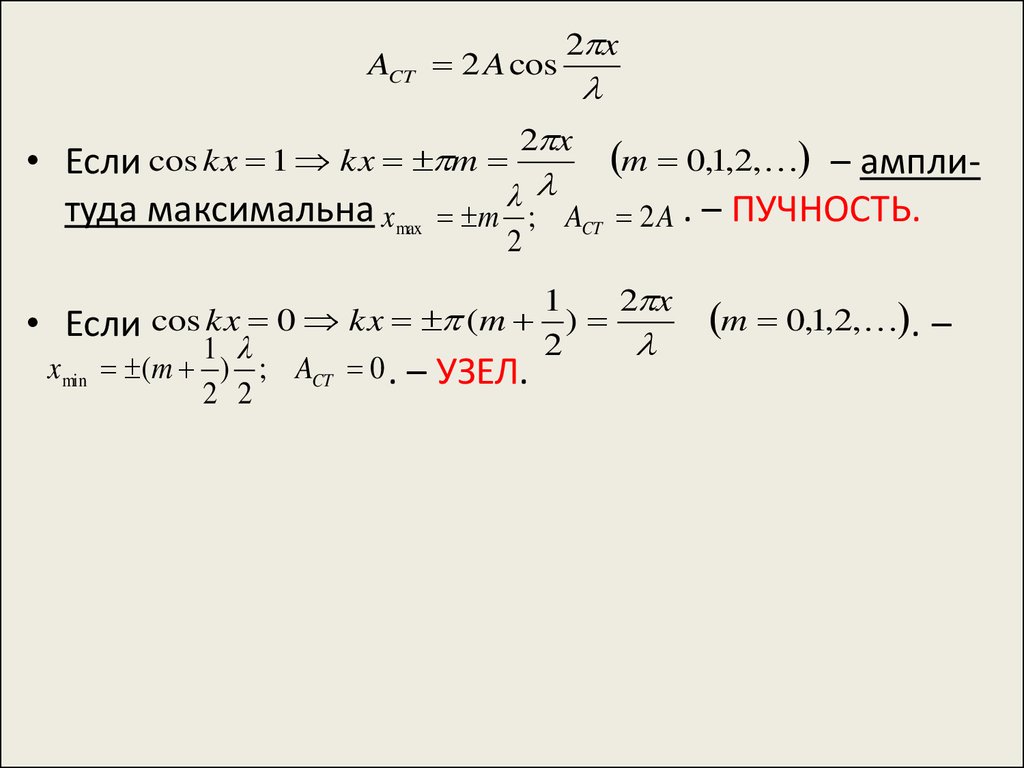
 Физика
Физика








