Похожие презентации:
Механические и электромагнитные колебания. Лекция 24
1.
Лекция 24.Механические и электромагнитные
колебания
Учебник:
Трофимова Т.И. Курс физики : учеб. пособ. для вузов / Т. И.
Трофимова. - М.: Академия, 2007.- с. 253-268.
к.ф.-м.н.
Курочкин А.Р.
2.
Общие сведенияКолебание – процесс любой физической природы,
характеризующийся повторяемостью во времени.
Колебания различают:
1) по физике процесса
механические
электромагнитные
R
L
C
Колебательный
контур
2
3.
2) по степени связи колеблющейся системы сокружающими телами
свободные
вынужденные
3) по характеру внутренних взаимодействий
в системе
незатухающие
затухающие
4) по математическому виду
зависимости возмущения от времени
гармонические
негармонические
3
4.
Период колебания T [c] – временной интервал, втечение которого совершается одно полное
колебание.
Периодическое колебание – колебание, период
которого постоянен.
Частота колебания ν [Гц=1/с] – число колебаний,
совершаемых за единицу времени:
1
.
T
Амплитуда – величина наибольшего отклонения
системы от положения равновесия.
4
5.
СВОБОДНЫЕ ГАРМОНИЧЕСКИЕКОЛЕБАНИЯ
Свободные (собственные) колебания – колебания
происходящие в системе, предоставленной самой себе
после того, как она была выведена из положения
равновесия.
Гармонические
колебания
–
периодическое
изменение физической величины во времени,
протекающее по закону синуса или косинуса.
5
6.
Гармонические колебания величины x описываютсяуравнением вида:
x A cos 0t ,
A – амплитуда колебания.
ω0 – циклическая частота. [рад/с=1/с]
(ω0t+φ) – фаза гармонического колебания –
определяет смещение колеблющейся величины от
положения равновесия в данный момент времени t.
[рад (радианы)]
φ – начальная фаза – определяет смещение
колеблющейся величины от положения равновесия в
начальный момент времени t=0. [рад (радианы)]
6
7.
Значение начальной фазыопределяется
выбором начала отсчёта времени.
Циклическая частота ω0 связана с частотой ν
соотношением:
0 2 .
Циклическая частота ω0 связана с периодом T
соотношением:
T
1
2
0
.
7
8.
Для колеблющейся м.т.кинематическое уравнение
описывает зависимость
координаты от времени:
x A cos 0t ,
скорость
dx
0 A sin 0t ,
dt
ускорение
A
A
0 A
0 A
02 A
02 A
d 2 x d
2
2
a 2
0 A cos 0t 0 x.
dt
dt
x
8
9.
1. Пружинный маятникЭто груз массой m, подвешенный на абсолютно упругой
пружине и совершающий гармонические колебания под
действием упругой силы.
9
10.
Рассмотрим систему, состоящую из шарика массы m,подвешенного на пружине, массой которой можно
пренебречь по сравнению с m .
В положении равновесия сила mg уравновешивается
упругой силой Fуп .
Проекция результирующий силы на ось x:
l
Fx mg k l x ,
Fуп
m
x
mg
Fуп mg
0
Fx k l k l x
x
k l k l kx kx
k l mg где l , k – удлинение и жёсткость пружины.
10
11.
Уравнение второго закона Ньютона для шарика имеет вид:2
2
d x
m 2 kx m
dt
d x k
x 0
2
dt
m
Пружинный маятник совершает гармонические колебания с
циклической частотой и периодом
0
m
T 2
.
k
k
.
m
Уравнение движения маятника в отсутствие сил трения
описывается дифференциальным уравнением:
x x 0
2
0
Решением этого уравнения является уравнение
x A cos 0t 0
11
12.
Гармонический осциллятор – систем, совершающаяколебания, описываемые уравнением вида
x 02 x 0
12
13.
km
Потенциальная
энергия
м.т.,
совершающей
гармонические колебания в поле упругих сил
2
0
m A cos ( 0t )
kx
Ep
.
2
2
2
2
0
2
2
Кинетическая
энергия
м.т.,
совершающей
гармонические колебания в поле упругих сил
2 2
2
m
A
sin
( 0t )
m
0
Eк
.
2
2
2
13
14.
m 02 A2E Eк E п
const
2
В
системе,
совершающей
гармонические
колебания,
выполняется закон сохранения полной механической энергии,
поскольку упругая сила консервативна.
E E p Eк
Ep
Eк
0
T
t
14
15.
2. Физический маятникЭто твёрдое тело, совершающее под действием силы
тяжести колебания вокруг неподвижной горизонтальной
оси (не совпадающей с центром масс).
15
16.
M r FО
M
r
M J
l
С
mg
Отклоним маятник на угол α.
Возникнет
вращающий
момент
стремящейся
вернуть
маятник
в
положение равновесия.
Спроецируем момент силы и угловое
ускорение на ось направленную от нас.
Тогда,
d
d 2
M J J
J 2
dt
dt
M mgl sin
J – момент инерции
маятника относительно т. О
d 2
J 2 mgl sin
dt
16
17.
При малых отклоненияхsin
d 2
J 2 mgl ,
dt
d 2 mgl
0,
2
dt
J
02
02 0.
Решением данного дифференциального уравнения
будет функция вида
max cos 0t
2
J
- период колебания физического
T
2
0
mgl маятника.
1
17
18.
3. Математический маятникЭто идеализированная система, состоящая из м.т. массой
m, подвешенной на нерастяжимой нити, и колеблющаяся
под действием силы тяжести.
Момент инерции математического маятника
J ml 2 ,
где l – длина маятника.
Период малых колебаний математического маятника
T 2
l
.
g
18
19.
Свободные гармонические колебанияв колебательном контуре
Электромагнитные колебания – колебания, при которых
электрические величины (заряды, токи) периодически
изменяются и которые сопровождаются взаимными
превращениями электрического и магнитного полей.
Колебательный контур – цепь, состоящая из включенных
последовательно
• катушки индуктивностью L,
• конденсатора ёмкостью С ,
• резистора сопротивлением R.
19
20.
Рассмотрим идеальный колебательный контур (R≈0).2
q
WE
2C
E E p max
1. В начальный момент времени (t=0) конденсатор
заряжают и между его обкладками возникает
электрическое поле с энергией WE.
20
21.
2.При
замыкании
конденсатора
на
катушку
индуктивности, он начнёт разряжаться, и в контуре
потечёт возрастающий со временем ток.
В результате WE буде уменьшаться, а WB будет возрастать.
Lq 2
WB
2
E Eк max
Но полная энергия будет сохраняться (т.к. R≈0):
q 2 Lq 2
W
const.
2C
2
Wэл
Wмаг
В момент времени t=T/4 конденсатор
разрядится (WE=0), а WB=max.
полностью
21
22.
3. Затем ток начнет убывать (магнитное поле катушкибудет ослабевать, что будет способствовать появлению
индукционного тока, направленного в также как и ток
разрядки конденсатора - согласно правилу Ленца).
Конденсатор
начнёт
перезаряжаться,
возникнет
электрическое поле, стремящееся ослабить ток. В конце
концов WE=max, а WB=0.
2
q
WE
2C
E E p max
4. Далее те же процессы начнут протекать в обратном
направлении и система к моменту времени t=T придёт в
первоначальное состояние.
22
23.
Рассмотрим колебательный контурR
IR U C s ,
где IR – напряжение на резисторе;
UC
q
C
s L
dI
dt
L
C
– напряжение на конденсаторе;
– ЭДС самоиндукции, возникающая в катушке при
протекании в ней переменного тока.
dI
q
dI
L IR 0. I q,
q
dt
C
dt
R
1
q q
q 0. - дифференциальное уравнение свободных
затухающих электрических колебаний
L
LC
23
24.
В данном колебательном контуре отсутствуют внешние ЭДС,поэтому такие колебания называются свободными.
Если R=0, то свободные электромагнитные колебания в
контуре являются гармоническими.
Тогда
1
q
q 0.
LC
q 02 q 0.
Заряд q совершает гармонические колебания по закону
q qmax cos 0t ,
где qmax – амплитуда колебаний заряда конденсатора с
циклической частотой ω0 (собственная частота контура),
24
25.
01
.
LC
и периодом
T 2 LC .
Формула Томпсона
Томсон
Джозеф Джон
(1856 - 1940)
I q 0 qmax sin 0t I max cos 0t ,
2
где Imax – амплитуда силы тока.
Q Qm
UC
cos 0t U m cos 0t ,
C C
где Umax – амплитуда напряжения.
Вывод: колебания тока I опережают по фазе колебания заряда q
на π/2, т.е., когда ток достигает максимального значения, заряд
25
(а также и напряжение) обращаются в ноль, и наоборот.
26.
Сложение колебаний. Векторная диаграммаA
A
0
x
x
t 0;
x A cos 0
0t 0
x
x
x A cos A cos t 0
Проекция вращающегося вектора изображает
гармоническое колебание.
26
27.
Сложение гармонических колебанийКогерентность
колебаний
–
согласованное
протекание нескольких колебательных процессов,
заключающееся в постоянстве или закономерном
изменении их направлений, амплитуд, частот и
начальных фаз.
Рассмотрим
однонаправленные
одночастотные
колебания с неизменными амплитудами и
постоянной разностью начальных фаз.
Воспользуемся
представлением
гармонических
функций в виде проекций вращающихся векторов A(t)
на оси декартовой системы координат.
27
28.
Сложим гармонические колебания• одного направления и
• одинаковой частоты:
y
x1 A1 cos 0t 1 ,
x2 A2 cos 0t 2 .
Т.к. колебания когерентны,
то (φ2-φ1)=const.
y1
A
A2
y2
2
1
x1
A1
x2
x
Результирующее
колебание x будет
x x1 x2 A cos 0t .
28
29.
yA A1 A2
A
y1
A2
y2
2
1
x1
cos 1 A
1
cos x2
2
x
A2
A1
x2
x1
y1
sin 1 A
1
sin y2
2
A2
A x1 x2 y1 y2
2
2
2
x 2 x1 x2 x y 2 y1 y2 y
2
1
2
2
2
1
2
2
A cos 1 2 A1 cos 1 A2 cos 2 A cos 2
2
1
2
2
2
2
A sin 1 2 A1 sin 1 A2 sin 2 A sin 2
2
1
2
2
2
2
29
30.
1sin sin 2 cos cos
cos cos 1 cos cos
2
A cos 1 A sin 1 A cos 2 A sin 2
1
2 A1 A2 cos 1 2 cos 1 2
2
1
2 A1 A2 cos 1 2 cos 1 2
2
2
2
A1 A2 2 A1 A2 cos 1 2
2
1
2
2
1
2
2
2
2
2
2
2
30
31.
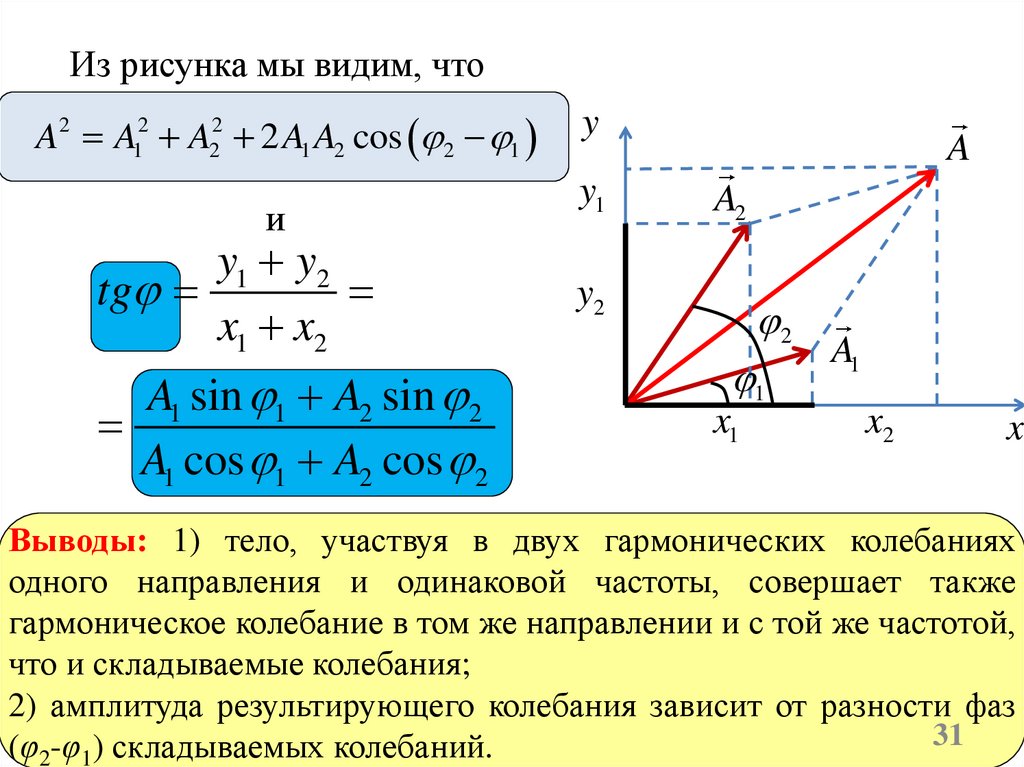
Из рисунка мы видим, чтоA2 A12 A22 2 A1 A2 cos 2 1
и
y1 y2
tg
x1 x2
A1 sin 1 A2 sin 2
A1 cos 1 A2 cos 2
y
y1
A
A2
y2
2
1
x1
A1
x2
x
Выводы: 1) тело, участвуя в двух гармонических колебаниях
одного направления и одинаковой частоты, совершает также
гармоническое колебание в том же направлении и с той же частотой,
что и складываемые колебания;
2) амплитуда результирующего колебания зависит от разности фаз
31
(φ2-φ1) складываемых колебаний.
32.
Рассмотрим выражение (4)1. 2 1 2m m 0,1, 2,... y
y1
В этом случае A=A1+A2, т.е.
амплитуда
результирующего колебания A y2
равна сумме
амплитуд
складываемых колебаний;
A
A2
2
1
x1
A1
x2
x
2. 2 1 2m 1 m 0,1, 2,...
В этом случае A=|A1-A2|,
т.е. амплитуда результирующего колебания A
равна разности амплитуд
складываемых колебаний.
32
33.
БиенияБиения – периодические изменения амплитуды колебаний,
возникающие при сложении двух гармонических
колебаний с близкими частотами.
Условия.
Пусть:
1) амплитуды
складываемых
колебаний равны A;
2) начальные фазы
колебаний равны 0.
1 2
и
2 1
.
x1 A cos t , 5
x2 A cos t
6 .
33
34.
Сложим выражения (5) и (6):x 2 A cos
t cos t
2
Амплитуда
колебаний
(штриховая линия)
изменяется по
периодическому
закону.
Сплошная линия –
график
результирующего
колебания
34
35.
Пояснение. За период сдвиг фаз меняется незначительно,вследствие чего на протяжении нескольких периодов
колебания складываются «в фазе» (∆φ≈0) – амплитуда фаз
максимальна;
затем, на протяжении нескольких периодов, колебания
складываются «в противофазе» (∆φ≈π) – амплитуда
минимальна.
На практике
эффект биения
используют для
определения
частоты тона.
Для этого сравнивают
эталонное колебание с
измеряемым.
35
36.
Сложение взаимно перпендикулярных колебанийПусть:
Запишем.
1) частоты
складываемых
колебаний равны ω;
2) начальные фазы
колебаний равны 0.
Произведём следующее:
x A cos t ,
y B cos t ,
где α – разность фаз
обоих колебаний,
A и B – амплитуды
складываемых колебаний.
x
1
A
2
x
cos t ;
A
y
cos t cos t cos sin t sin
B
36
37.
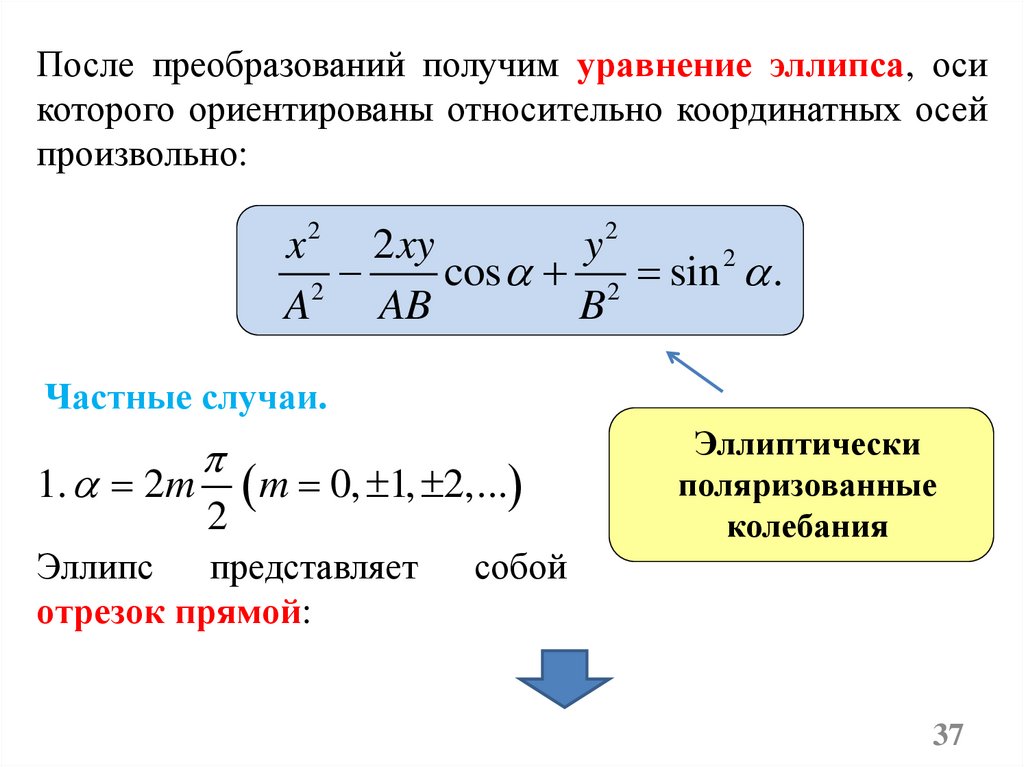
После преобразований получим уравнение эллипса, осикоторого ориентированы относительно координатных осей
произвольно:
x 2 2 xy
y2
2
cos 2 sin .
2
A
AB
B
Частные случаи.
1. 2m
2
m 0, 1, 2,...
Эллипс
представляет
отрезок прямой:
Эллиптически
поляризованные
колебания
собой
37
38.
By x,
A
«+» - соответствует нулю и чётным значениям m (левый
рисунок);
«–» - соответствует нечётным значениям m (правый
рисунок).
Линейно поляризованные колебания
38
39.
2. 2m 12
m 0, 1, 2,...
x2 y 2
2 1
2
A B
Если A=B, то эллипс вырождается в окружность.
Колебания, поляризованные по кругу
39
40.
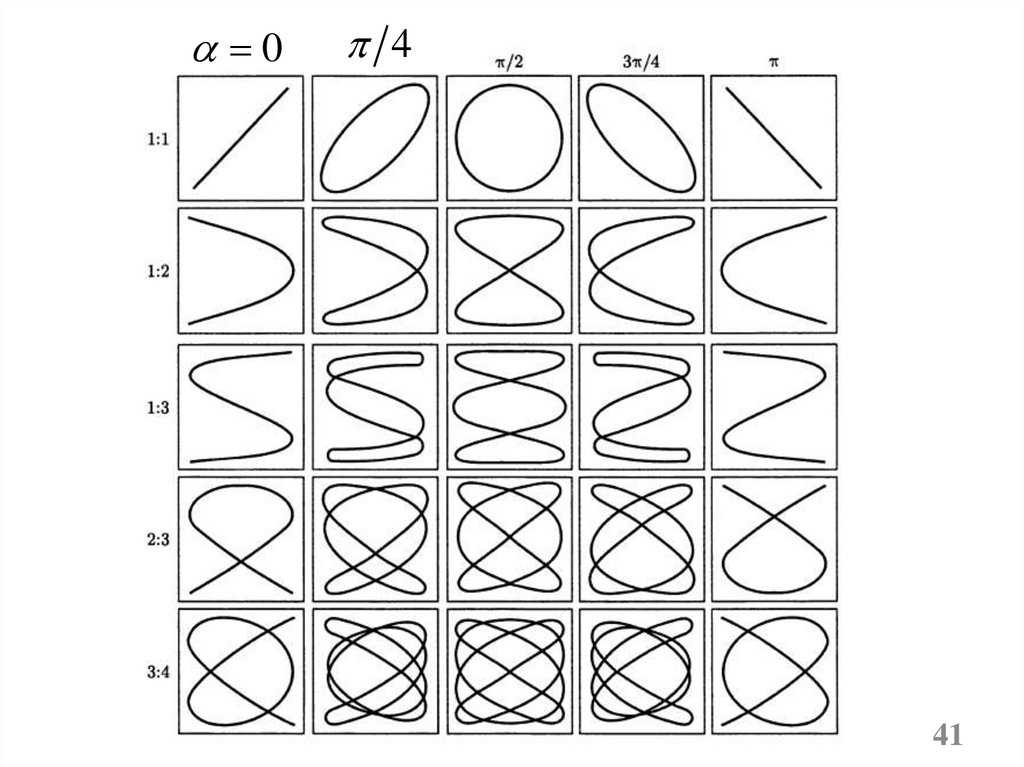
3. При различных частотах складываемыхвзаимно перпендикулярных колебаний,
замкнутые траектории,
прочерчиваемые точкой,
совершающей одновременно
два взаимно перпендикулярных колебания,
называются фигурами Лиссажу.
Вид кривых зависит от соотношения
амплитуд, частот и разности фаз
складываемых колебаний.
40
41.
04
41
42.
Свободные затухающие колебанияЗатухающие колебания – колебания, амплитуды которых
из-за потерь энергии колебательной системы с течением
времени уменьшаются.
Затухающие колебания описываются дифференциальным
уравнением
2
d s
ds
2
2
0 s 0
2
dt
dt
s 2 s 02 s 0
s – колеблющаяся величина;
β =const – коэффициент затухания;
ω0 – собственная частота системы (частота, с которой
совершались бы свободные колебания системы в
отсутствие сопротивления среды).
42
43.
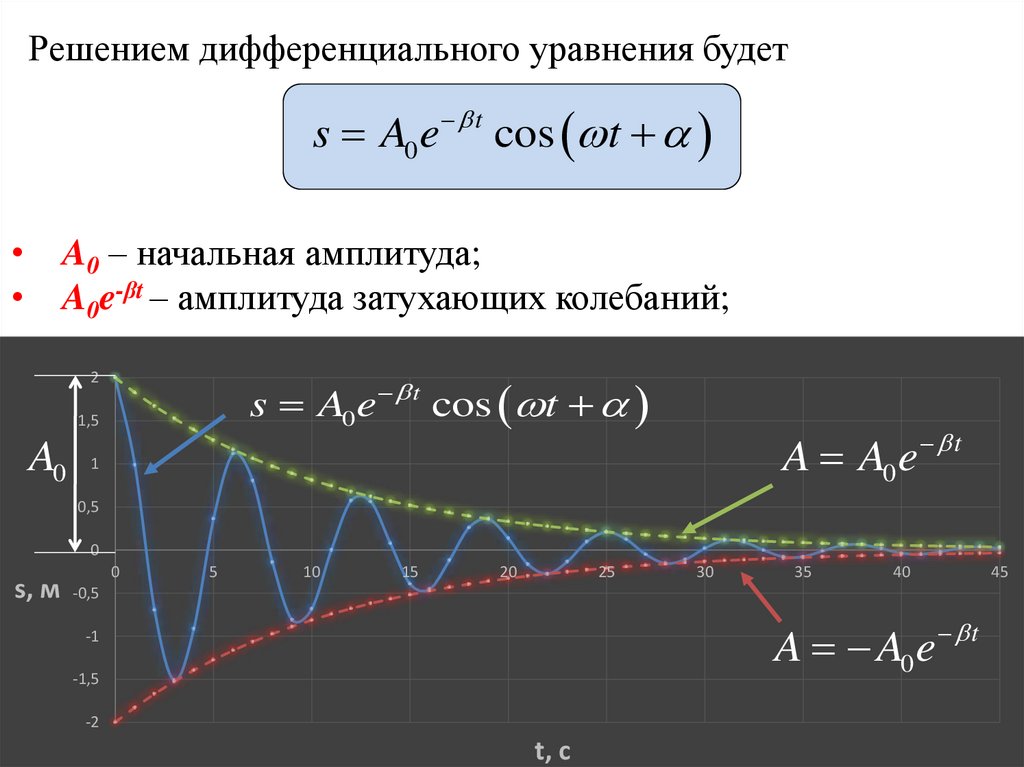
Решением дифференциального уравнения будетs A0 e
t
cos t
A0 – начальная амплитуда;
A0e-βt – амплитуда затухающих колебаний;
s A0 e t cos t
2
1,5
A0
A A0 e t
1
0,5
0
s, м
0
5
10
15
20
25
30
35
40
-0,5
A A0 e t
-1
-1,5
-2
t, c
45
44.
ω – частота затухающих колебаний.
02 2
Время релаксации – время, в течение которого амплитуда
затухающих колебаний уменьшается в е раз.
1
Затухающие колебания не являются периодическими (к ним не
применимы понятия периода и частоты)
Если затухание мало, то можно пользоваться понятием периода
как промежутка времени между двумя последующими
максимумами (или минимумами) колеблющейся величины.
T
1
2
2
2
0
2
44
45.
Декрементом затухания называют отношение амплитуд двухпоследовательных колебаний, соответствующих моментам
времени, отличающихся на период.
A t
A t T
e
T
Логарифмический декремент затухания
ln
A t
A t T
ln e
T
T
1
T
Ne
Ne – число колебаний, совершаемых за время уменьшения
амплитуды в е раз.
Ne
T
Логарифмический декремент затухания –
постоянная величина для данной колебательной
системы.
45
46.
Добротность колебательной системы пропорциональначислу колебаний Ne, совершаемых системой за то время τ, за
которое амплитуда колебаний уменьшается в е раз.
Q Ne
Свободные затухающие
колебания пружинного
маятника
ma kx r ,
d 2x
dx
m 2 kx r ,
dt
dt
2
d x r dx k
x 0.
2
dt
m dt m
k - коэффициент жесткости,
r - коэффициент трения.
Свободные затухающие
колебания в электрическом
колебательном контуре
IR U C s ,
q
dI
IR L ,
C
dt
2
d q R dq
1
q 0.
2
dt
L dt LC
46
47.
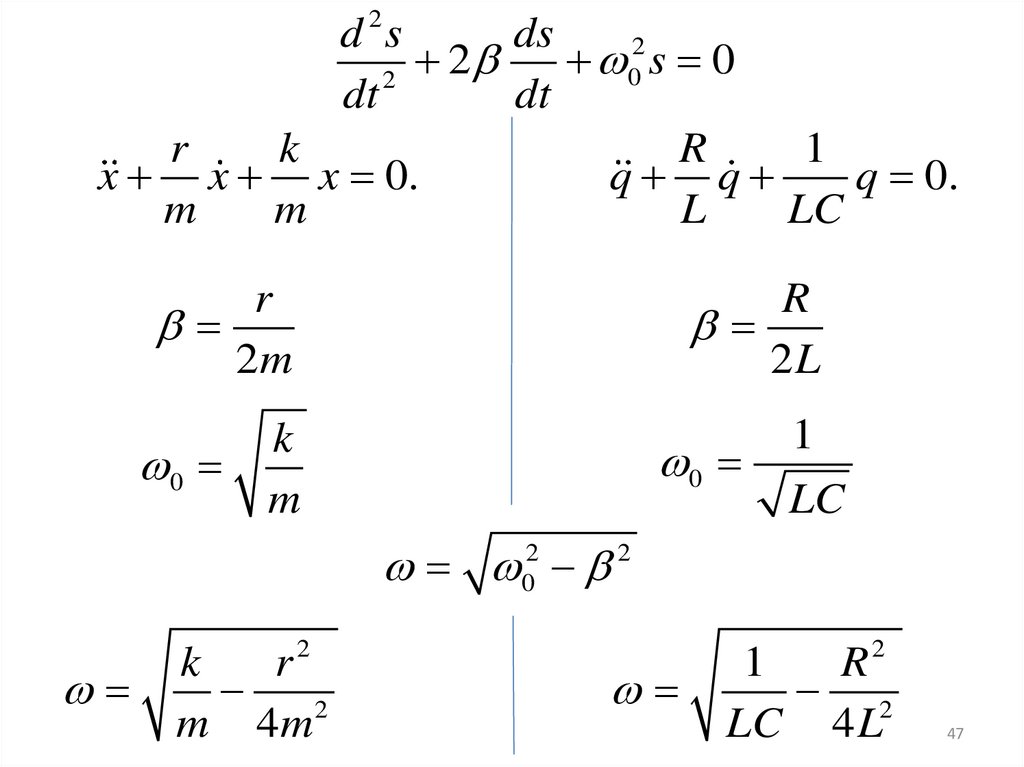
d 2sds
2
2
0 s 0
2
dt
dt
r
k
R
1
x x x 0.
q q
q 0.
m
m
L
LC
r
2m
0
R
2L
k
m
0
1
LC
02 2
k
r2
2
m 4m
1
R2
2
LC 4 L
47





























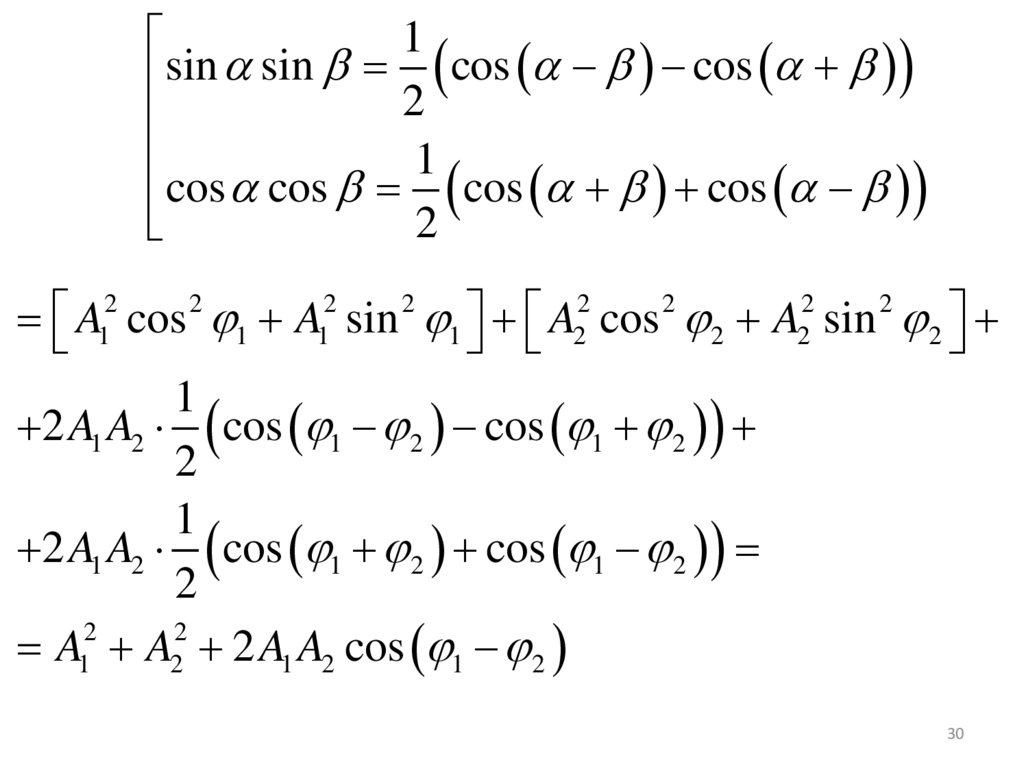












 Физика
Физика








