lection3-4_LMS

1. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ

Лекция 3-4
Титова Юлияна Францевна
1

2. Описание поведения системы

2

3. Система (повторение)

Система — это совокупность объектов
(элементов), например, людей или механизмов,
функционирующих и взаимодействующих друг с
другом для достижения определенной цели.
Состояние системы – совокупность параметров и
переменных , необходимых для описания системы
на определенный момент времени в соответствии с
задачами исследования.
Поведение системы – описание законов
изменения переменных.
3

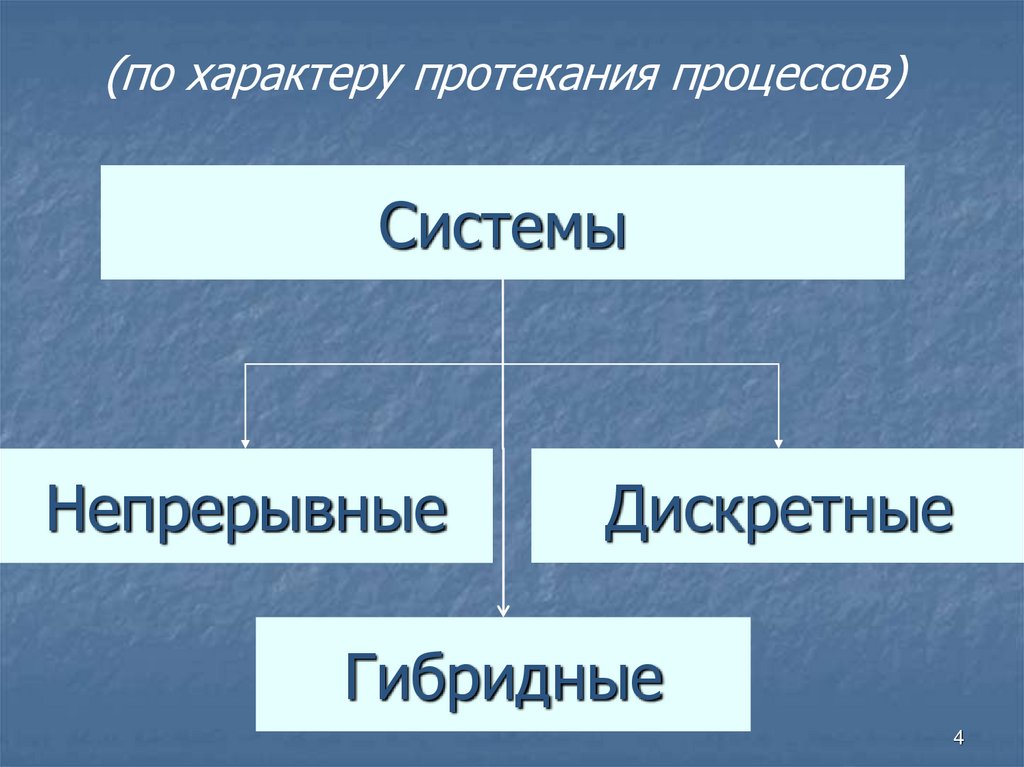
4. Системы

(по характеру протекания процессов)
Системы
Непрерывные
Дискретные
Гибридные
4

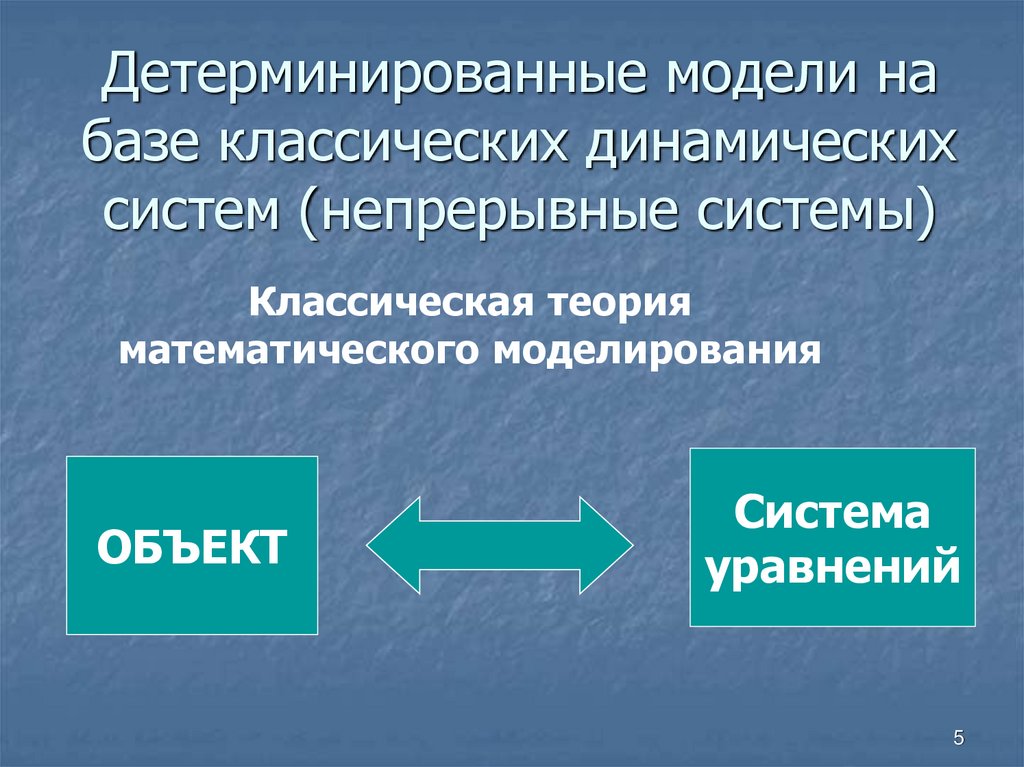
5. Детерминированные модели на базе классических динамических систем (непрерывные системы)

Классическая теория
математического моделирования
ОБЪЕКТ
Система
уравнений
5

6. ДУ как способ описания непрерывного поведения системы

x(t ) - исследуемая переменная
dx
F ( x, t )
dt
скорость изменения переменной
6

7. Накопление средств

Модель 1. В «банке» (В чулке)
A=const – приращение средств в единицу времен
dx
A
dt
x(0) x0 первоначальная сумма
м.б. равна нулю
x(t ) x0 At
7

8. Накопление средств

Модель 2. В банке
p=const – процент приращения капитала за
единицу времени
dx
px
dt
x(0) x0 ïåðâîíà÷àë üíàÿ ñóììà
ÍÅ ì .á. ðàâíà íóëþ
t
x (t ) x0e
8

9. Накопление средств

Модель 1+2. Гибридная схема: «В банке» и
в банке
Сначала деньги копятся дома (в чулке),
а затем когда накоплена сумма, достаточная
для вклада в банк, деньги копятся в банке.
A=const – приращение средств дома в единицу
времени
p=const – процент приращения капитала в банке
B=const – минимальная сумма для вклада в банк
D=const – сумма, которую надо накопить

10. Моделирование гибридного поведения

10

11. Описание непрерывного поведения

Непрерывное поведение на всем интервале времени
по одному закону описывается 1-й или несколькими
переменными типа накопитель или динамическая
переменная.
Накопитель
dx
f (t , x)
dt
Динамическая
переменная
f (t , x) 0
dxi
f (t , x1, x2, xn , )
dt
11

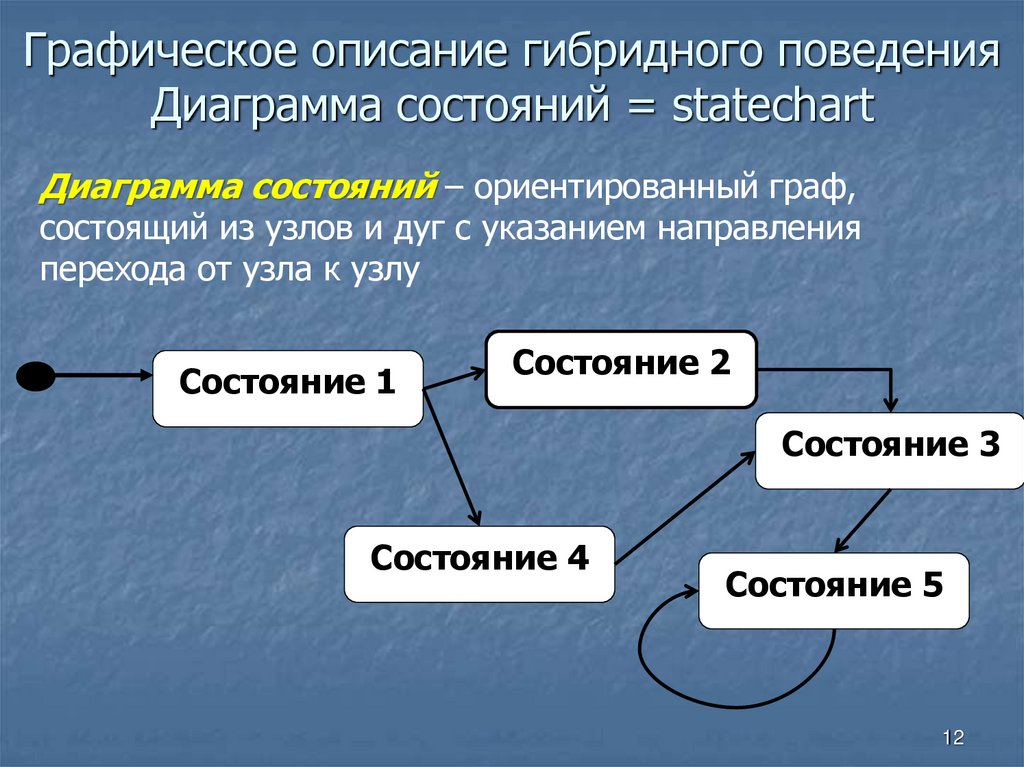
12. Графическое описание гибридного поведения Диаграмма состояний = statechart

Диаграмма состояний – ориентированный граф,
состоящий из узлов и дуг с указанием направления
перехода от узла к узлу
Состояние 1
Состояние 2
Состояние 3
Состояние 4
Состояние 5
12

13. Элементы диаграммы состояний (statechart)

Состояние
Длительное состояние (состояние)
Система находится в этом состоянии некоторый промежуток
времени.
• Переменные непрерывно изменяются во времени по
заданному закону;
• Значение переменной не изменяется.
Состояние может простым или сложным (если оно
содержит в себе другие состояния).
При описании состояния можно задать действия при входе и
при выходе.
Действие – мгновенное изменение значения переменной.
Действие описывается как операция присваивания.

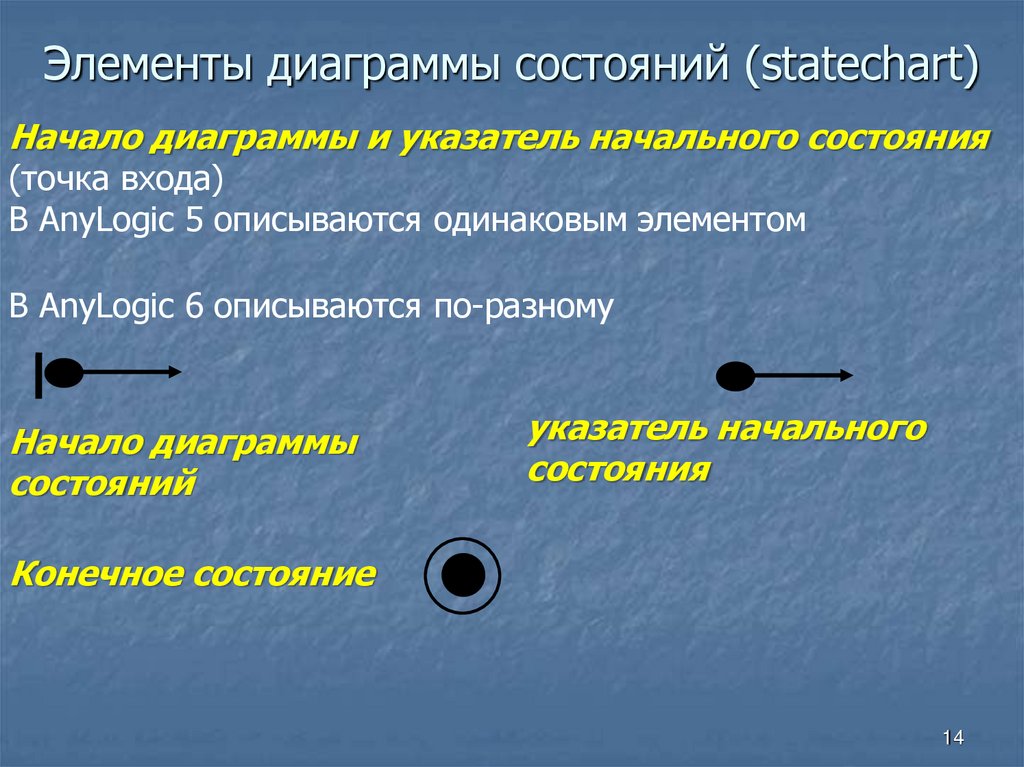
14. Элементы диаграммы состояний (statechart)

Начало диаграммы и указатель начального состояния
(точка входа)
В AnyLogic 5 описываются одинаковым элементом
В AnyLogic 6 описываются по-разному
Начало диаграммы
состояний
указатель начального
состояния
Конечное состояние
14

15. Элементы диаграммы состояний (statechart)

Дуга перехода определяет последовательность
смены состояний. Переход происходит мгновенно.
• По таймауту;
• При выполнении условия;
• При получении сообщения;
• И некоторые другие.
15

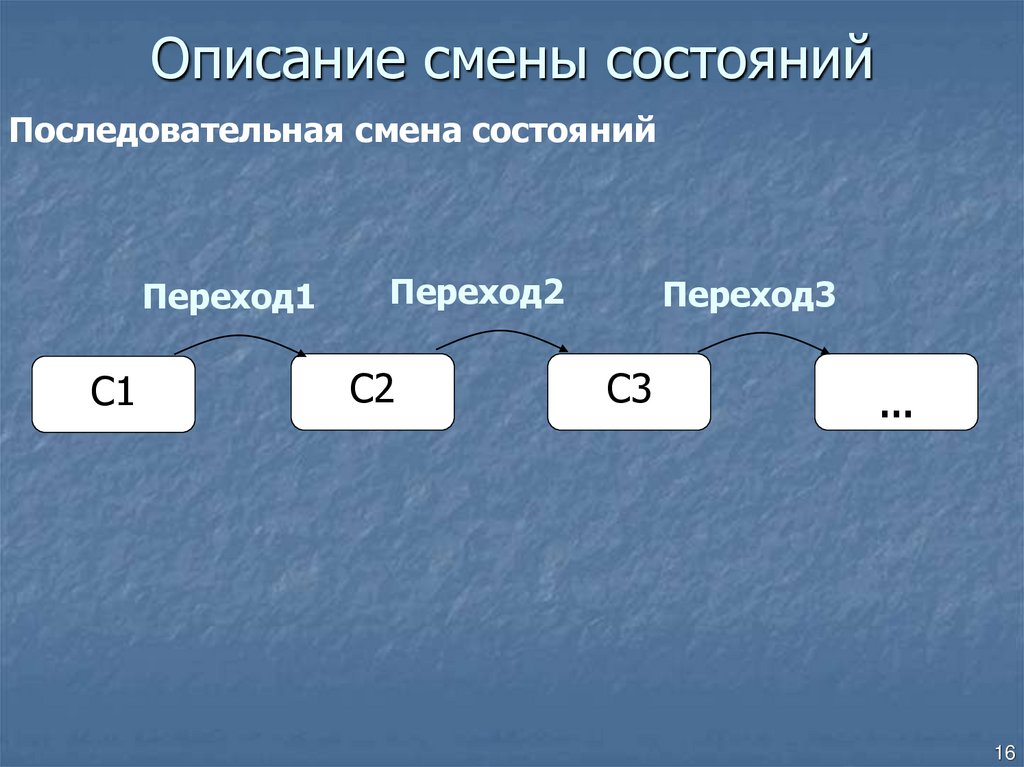
16. Описание смены состояний

Последовательная смена состояний
Переход1
C1
Переход2
C2
Переход3
C3
…
16

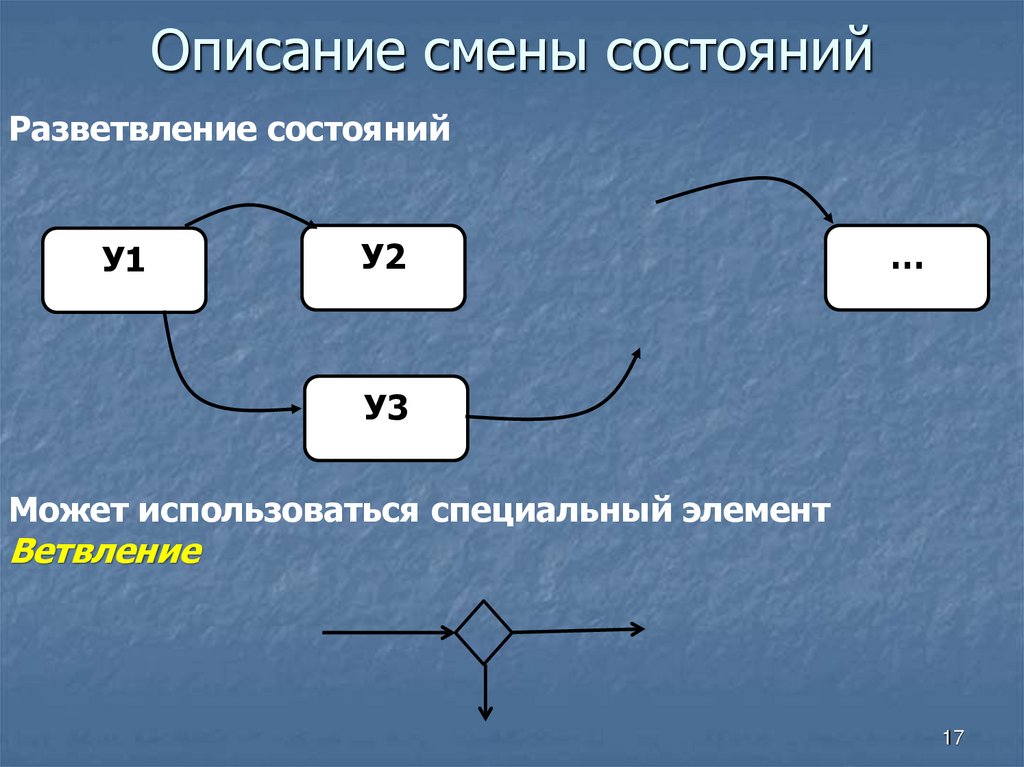
17. Описание смены состояний

Разветвление состояний
У1
У2
…
У3
Может использоваться специальный элемент
Ветвление
17

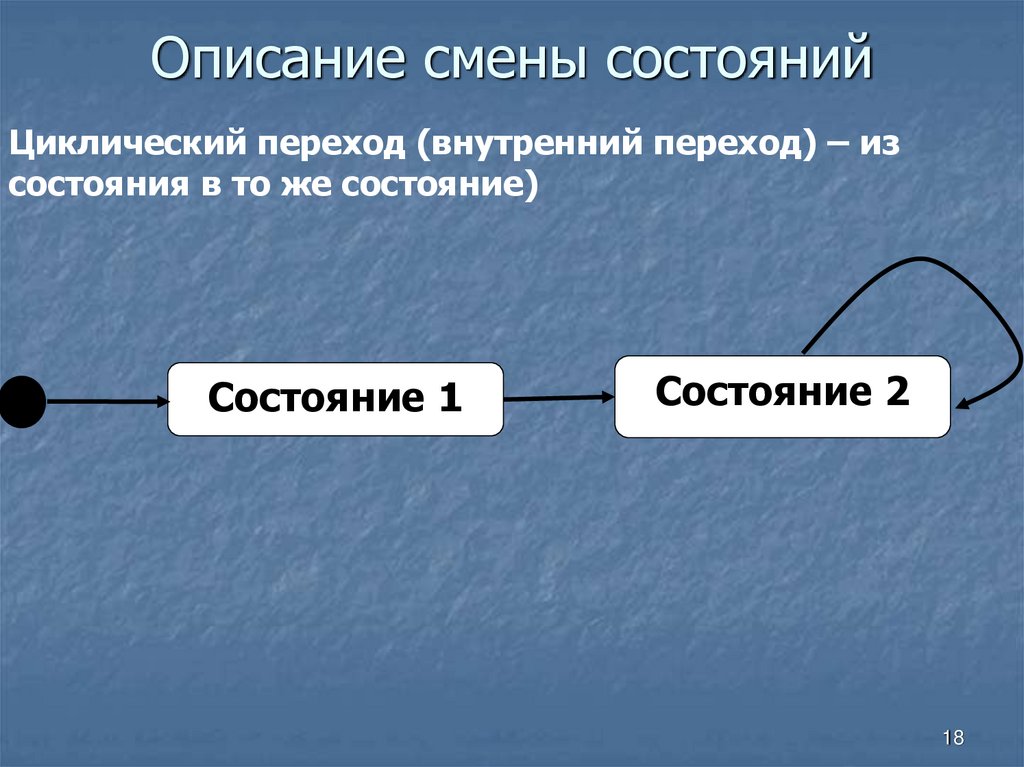
18. Описание смены состояний

Циклический переход (внутренний переход) – из
состояния в то же состояние)
Состояние 1
Состояние 2
18

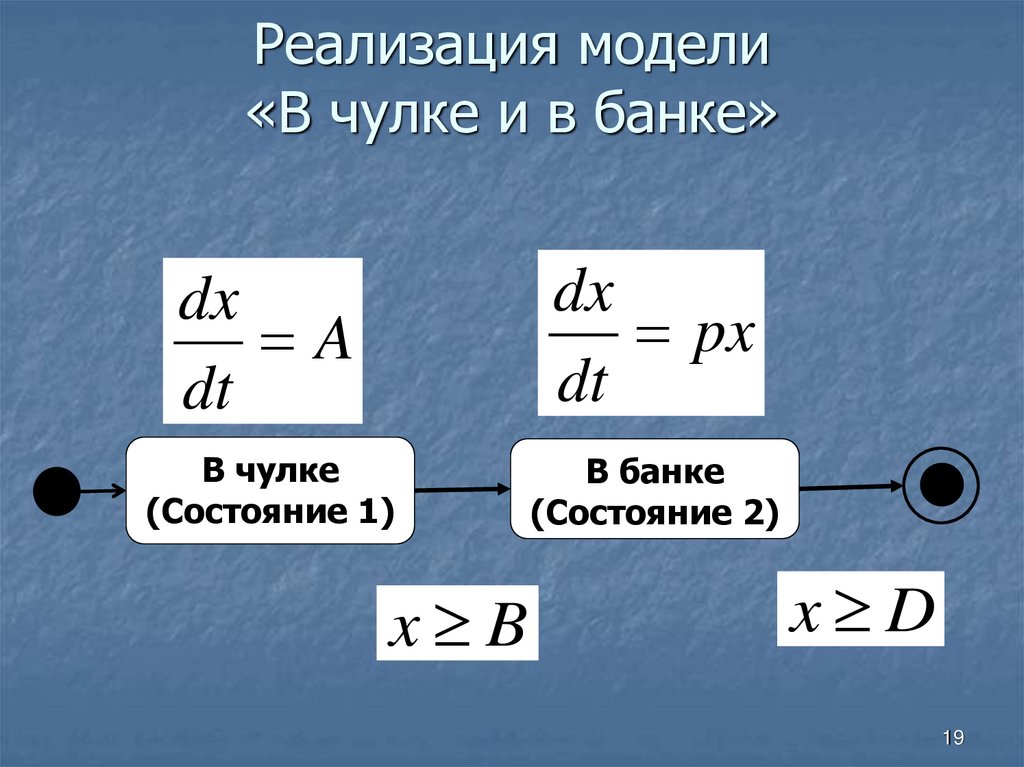
19. Реализация модели «В чулке и в банке»

dx
A
dt
dx
px
dt
В чулке
(Состояние 1)
В банке
(Состояние 2)
x B
x D
19

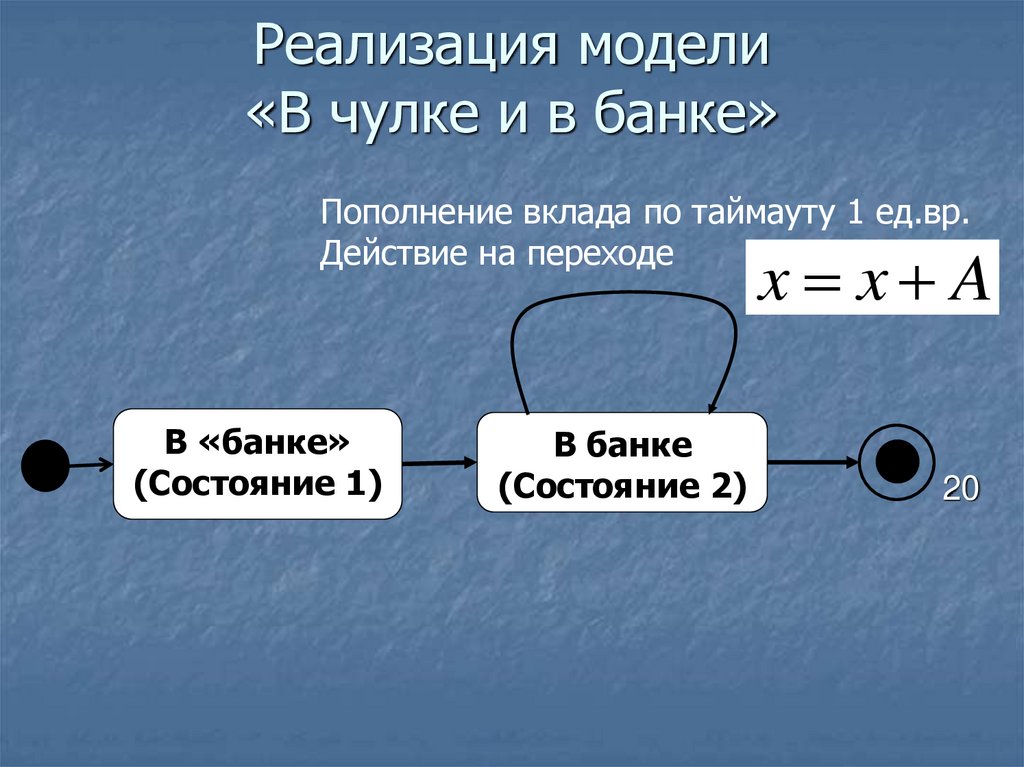
20. Реализация модели «В чулке и в банке»

Пополнение вклада по таймауту 1 ед.вр.
Действие на переходе
x x A
В «банке»
(Состояние 1)
В банке
(Состояние 2)
20

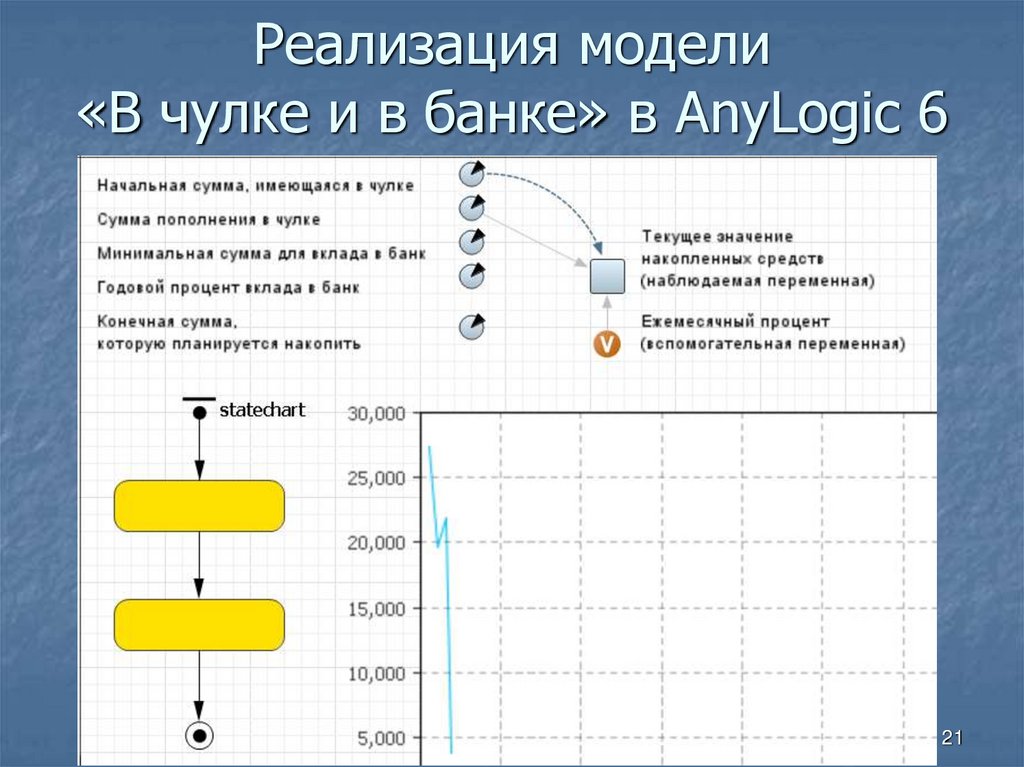
21. Реализация модели «В чулке и в банке» в AnyLogic 6

21

22. Описание гибридного поведения (AnyLogic 6)

Два состояния
d(капитал)/dt=
statechart.isStateActive(state1) ? формула1 : формула2
Больше, чем 2 состояния
d(капитал)/dt=
statechart.isStateActive(state1) ? формула1 :
(statechart.isStateActive(state2) ? Формула2 : (…))
22

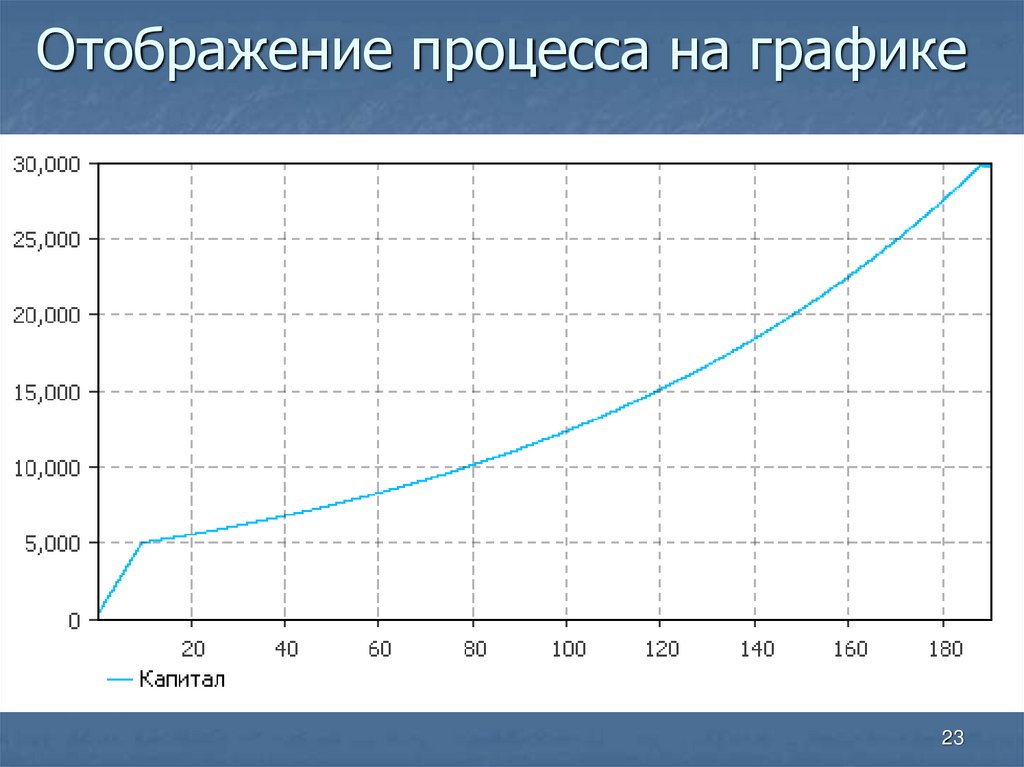
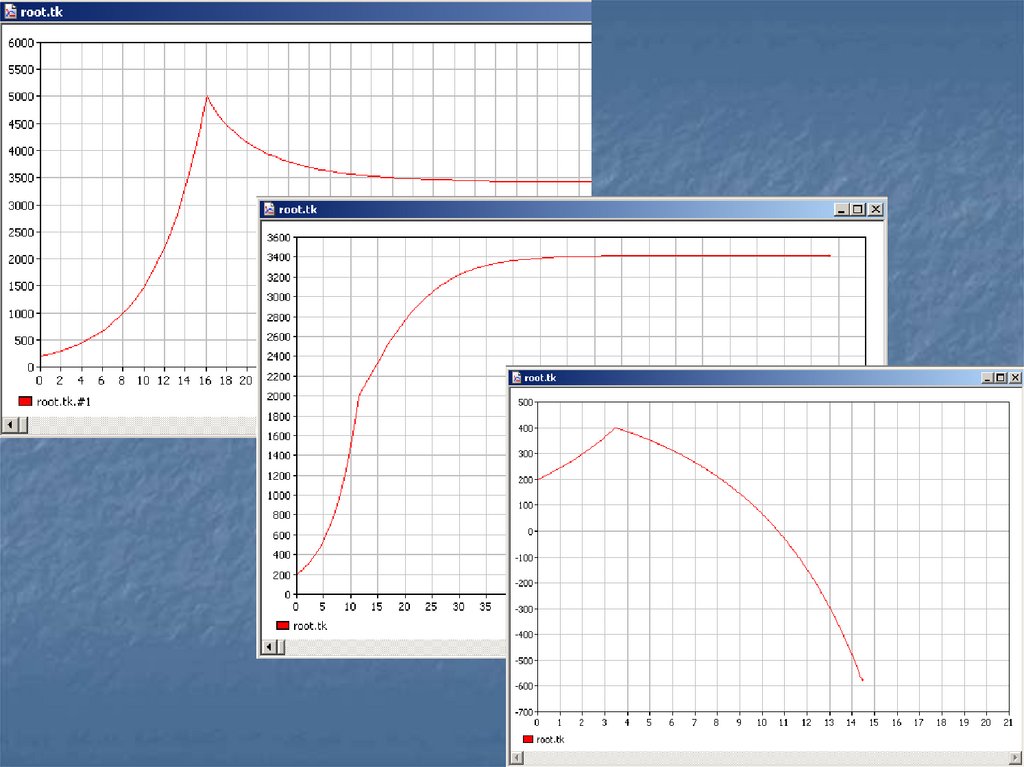
23. Отображение процесса на графике

23

24. Модели производства продукции

Лекция 4
24

25. Производство продукции

Модель 4. Монополия, неограниченные ресурсы
Производительность – скорость выпуска
изделий в ед.врем.
М.б. постоянной (см. модель 1)
Может увеличиваться пропорционально росту
производства
r=const – коэф. роста производства
Количество ресурса не ограничено
dx
rx
dt
Решение: см. модель 2
25

26. Производство продукции

Модель 5. Учет спроса и потерь
К=const – спрос, количество
товара, покрывающее
потребности населения в 1-цу
вр.
dx
rx f (x)
dt
Учет спроса – функция f(x), обладающая свойствами:
lim f ( x) 1
x 0
lim f ( x) 0
x K
dx
K x
rx
dt
K
26

27. Производство продукции

Модель 5. Учет спроса и потерь
Учет потерь – будем считать постоянной
величиной А за единицу времени
dx
K x
rx
A
dt
K
27

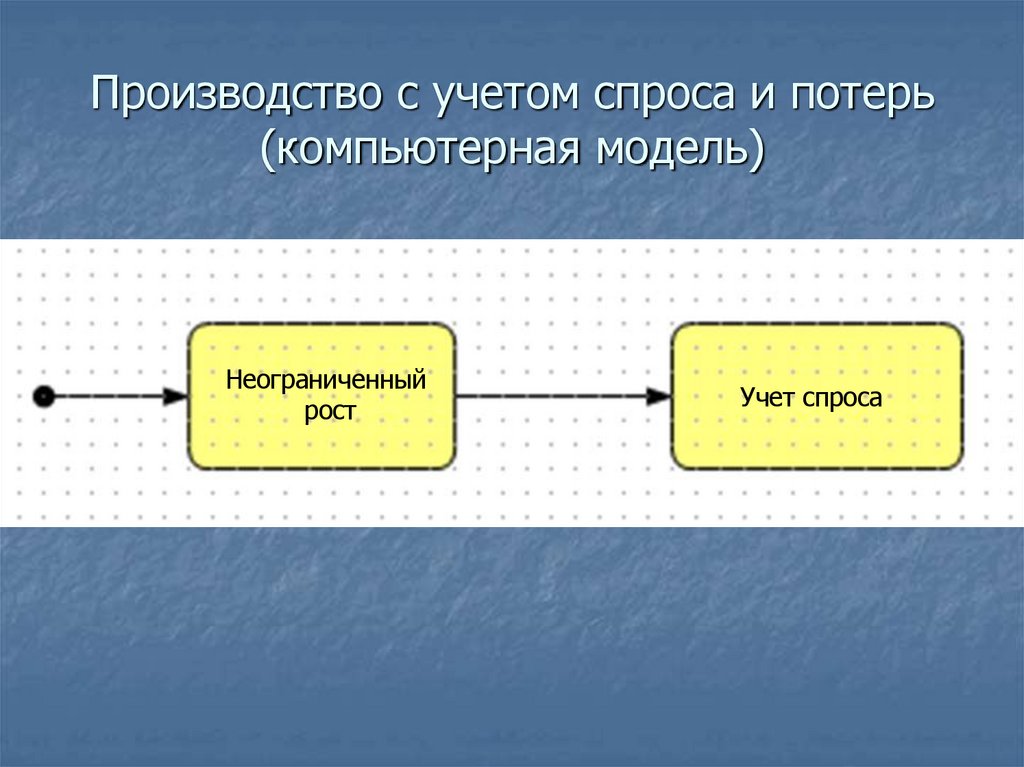
28. Производство с учетом спроса и потерь (компьютерная модель)

Неограниченный
рост
Учет спроса

29.

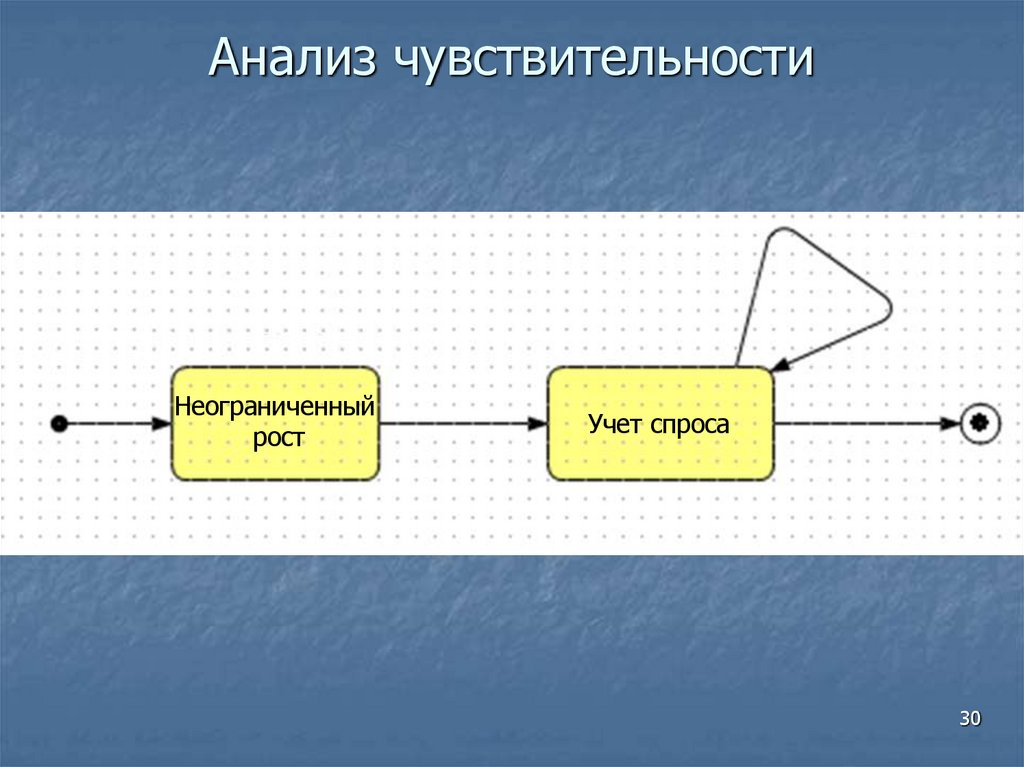
29

30. Анализ чувствительности

Неограниченный
рост
Учет спроса
30

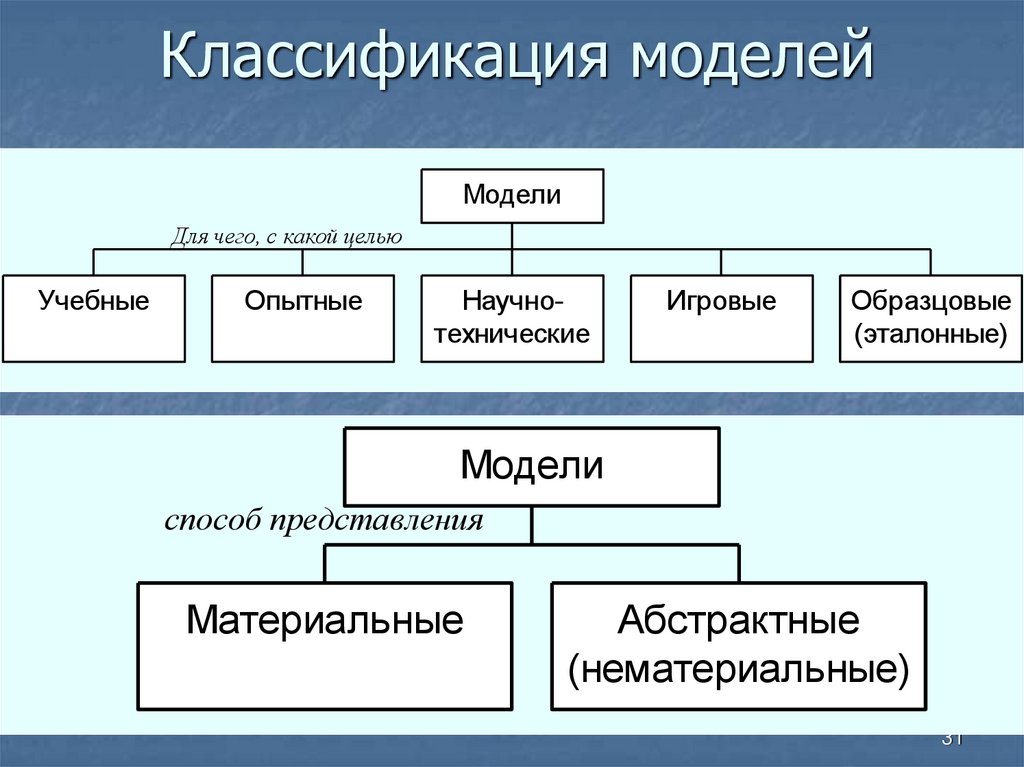
31. Классификация моделей

Модели
Для чего, с какой целью
Учебные
Опытные
Научнотехнические
Игровые
Образцовые
(эталонные)
Модели
способ представления
Материальные
Абстрактные
(нематериальные)
31

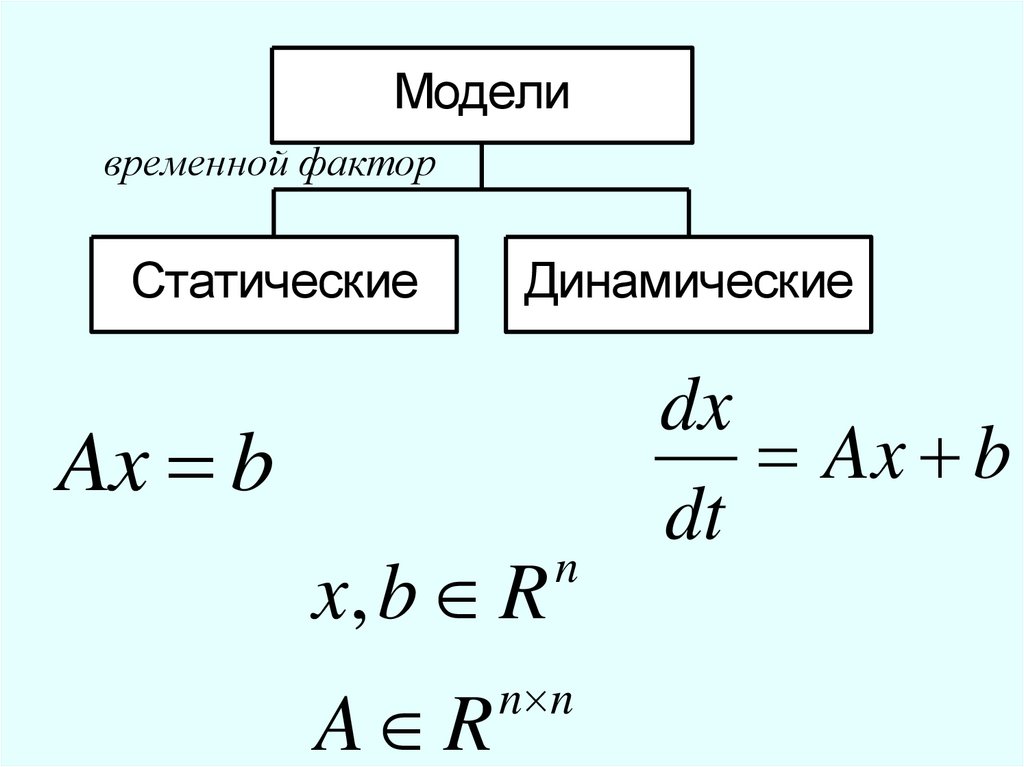
32.

Модели
временной фактор
Статические
Динамические
Ax b
x, b R
A R
n
dx
Ax b
dt
n n
32

33.

По характеру протекания процессов
Модели
Детерминированные
Случайные
Вероятностные
Стохастические
33