Похожие презентации:
ТМ_ПЗ_4_Кинематика_задачи_плоское_движение
1. Практическое занятие 4
Плоское движение твердого тела2.
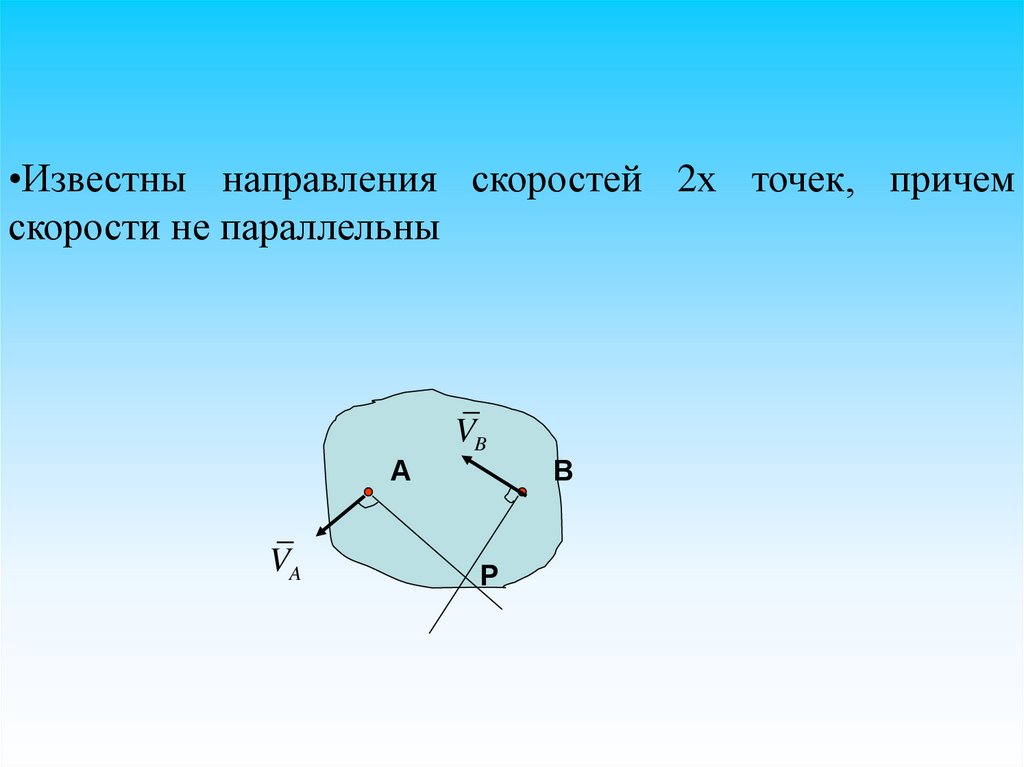
•Известны направления скоростей 2х точек, причемскорости не параллельны
А
VA
VB
Р
В
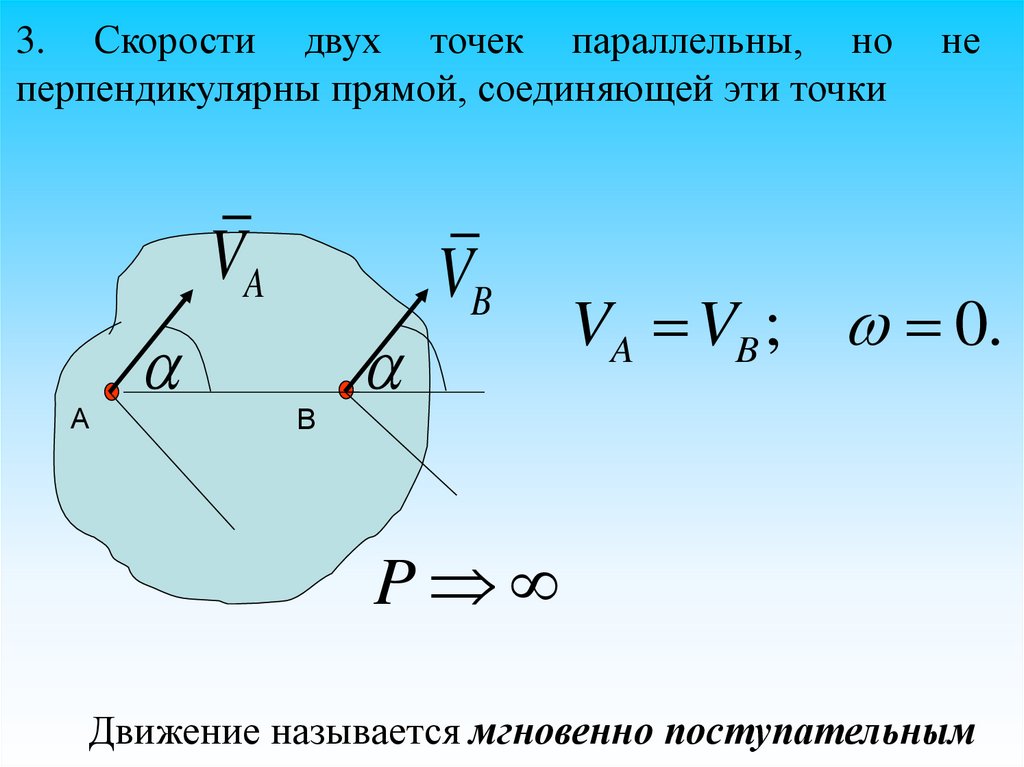
3.
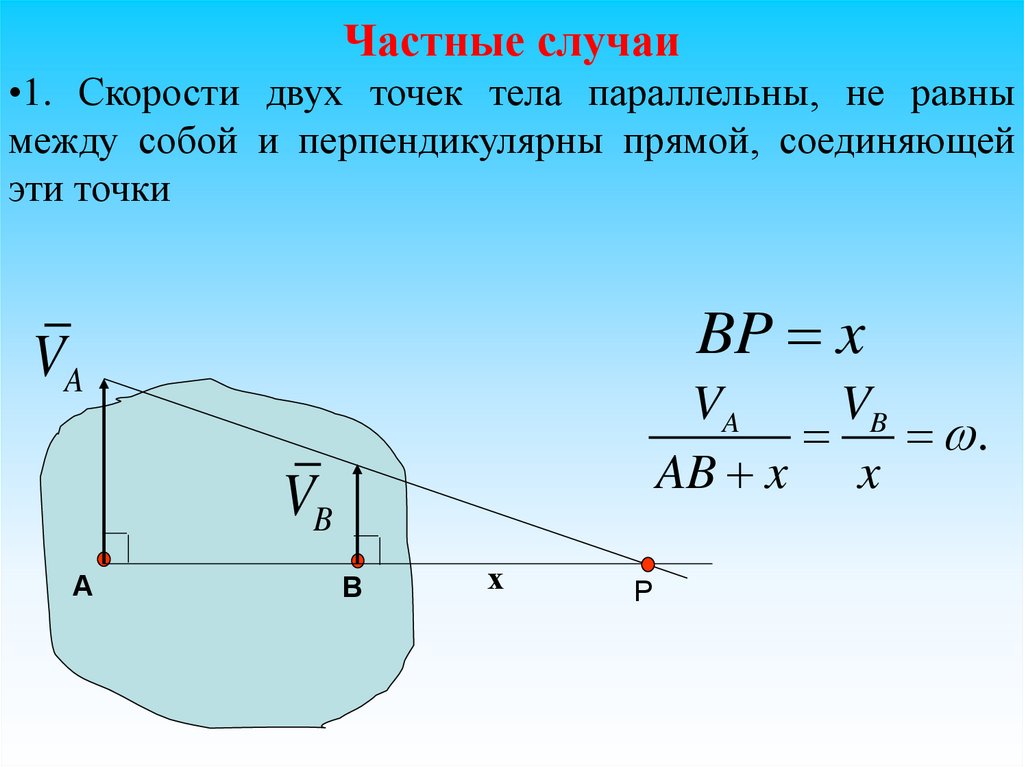
Частные случаи•1. Скорости двух точек тела параллельны, не равны
между собой и перпендикулярны прямой, соединяющей
эти точки
BP x
VA
VA
VB
.
AB x x
VB
А
В
х
Р
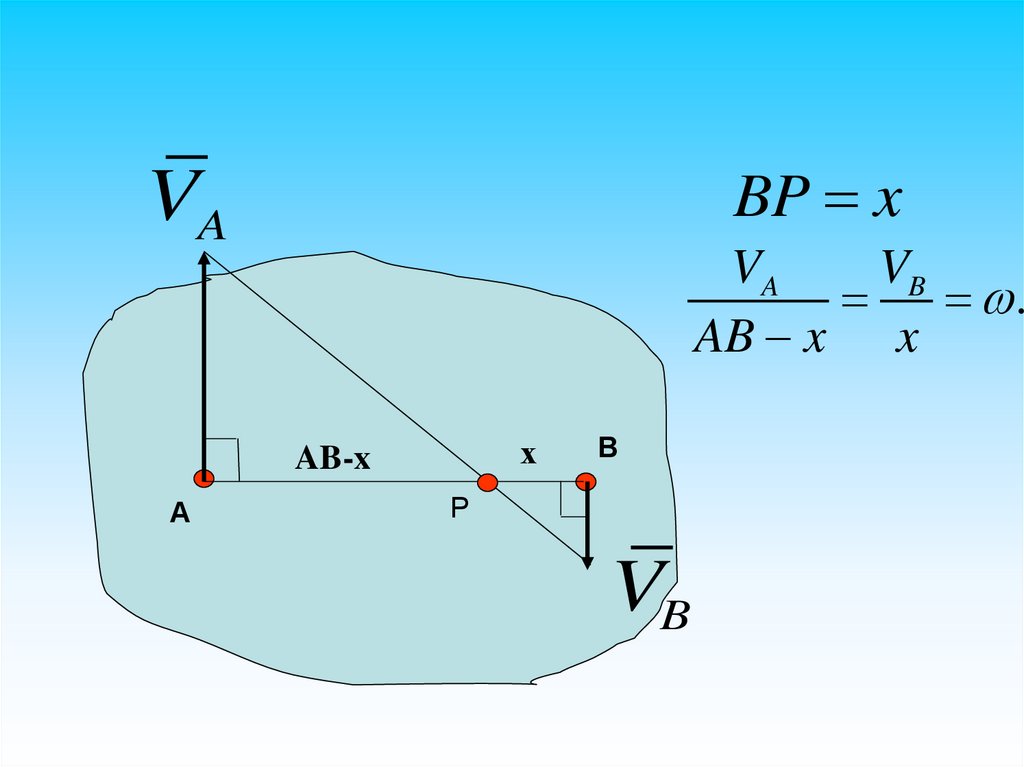
4.
BP xVA
VA
VB
.
AB x x
х
AB-x
А
В
Р
VB
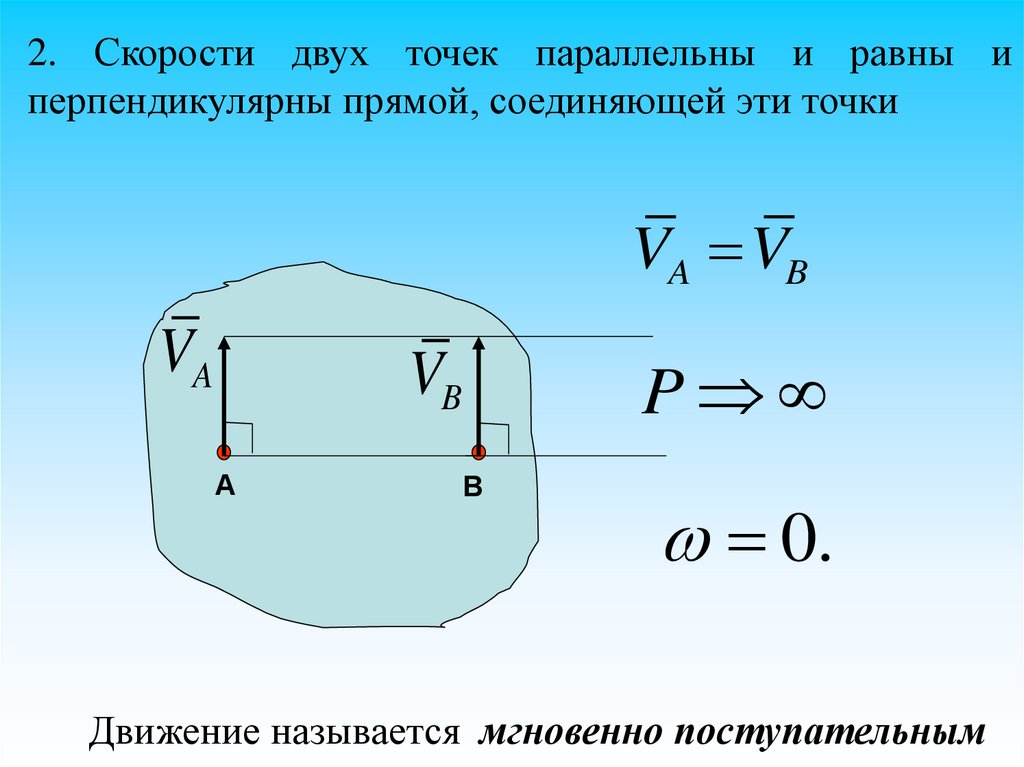
5.
2. Скорости двух точек параллельны и равны иперпендикулярны прямой, соединяющей эти точки
VA VB
VA
P
VB
А
В
0.
Движение называется мгновенно поступательным
6.
3. Скорости двух точек параллельны, ноперпендикулярны прямой, соединяющей эти точки
VA
А
В
VB
не
VA VB ; 0.
P
Движение называется мгновенно поступательным
7.
8.
• Принимаем:• Точки сочленения двух звеньев имеют одинаковые скорости и
одинаковые ускорения.
• При постоянном контакте двух звеньев проекции скоростей
точек их соприкосновения на нормаль к одному из звеньев в
точке контакта равны между собой.
• При отсутствии проскальзывания одного звена по другому
скорости точек соприкосновения одинаковы, нормальные
ускорения этих точек будут различными, а касательные
ускорения – равны.
• Размерами ползуна при решении задач пренебрегают, хотя на
рисунках ползун имеет размеры.
• Перед решением векторных уравнений, как и любых других
уравнений, необходимо убедиться в существовании его
решения (в корректности поставленной задачи).
9.
• Алгоритм решения задач по кинематикеплоских механизмов
• После того, как механизм в масштабе изображен на рисунке,
необходимо:
• 1. Назвать механизм и пространство, в котором
рассматривается его движение. Пронумеровать звенья
механизма и назвать вид их движения и кинематические
характеристики (КХ).
• 2. Указать особые кинематические точки механизма и их
траектории.
• 3. Задача скоростей. Определить скорости особых
кинематических точек, угловые скорости звеньев и скорости
точек, указанных в условии задачи. (Перед определением
скорости точки звена, траектория которой неизвестна,
необходимо знать угловую скорость этого звена.)
10.
• 4. Задача ускорений. Определить ускорения особыхкинематических точек, угловые ускорения звеньев и ускорения
точек, указанных в условии задачи. (Перед определением
ускорения точки звена, траектория которой неизвестна,
необходимо знать угловое ускорение этого звена.)
• Нумерацию звеньев следует начинать с ведущего звена.
Неподвижное звено (основание) считается нулевым.
• Важно правильно определить вид движения звена, чтобы знать –
теорию какого движения надо применить при нахождении
скоростей и ускорений точек того или иного звена механизма. В
плоских механизмах встречаются три вида движения твердого
тела: поступательное, вращательное вокруг неподвижной оси и
плоское.
• Определение скоростей (ускорений) ОКТ следует начинать с
точки сочленения (соприкосновения) ведущего звена с
последующим. Затем находится скорость (ускорение) точки
сочленения или соприкосновения этого звена с другим и т.д.
11.
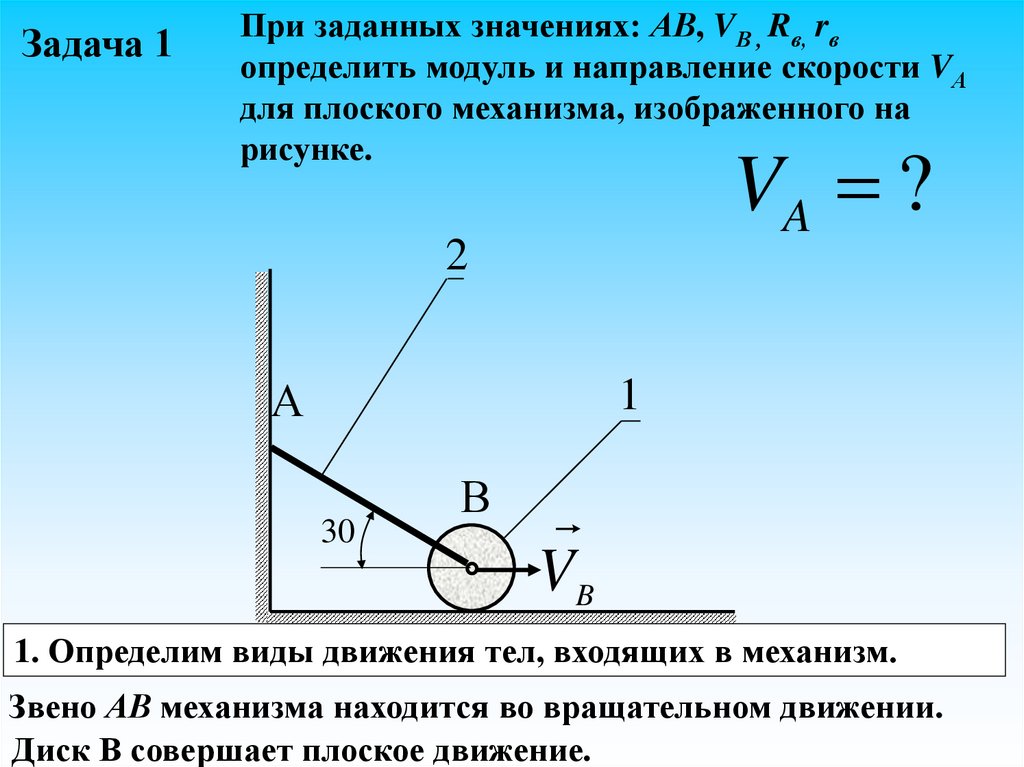
Задача 1При заданных значениях: АВ, VВ , Rв, rв
определить модуль и направление скорости VА
для плоского механизма, изображенного на
рисунке.
VA ?
2
А
1
30
В
VB
1. Определим виды движения тел, входящих в механизм.
Звено АВ механизма находится во вращательном движении.
Диск В совершает плоское движение.
12.
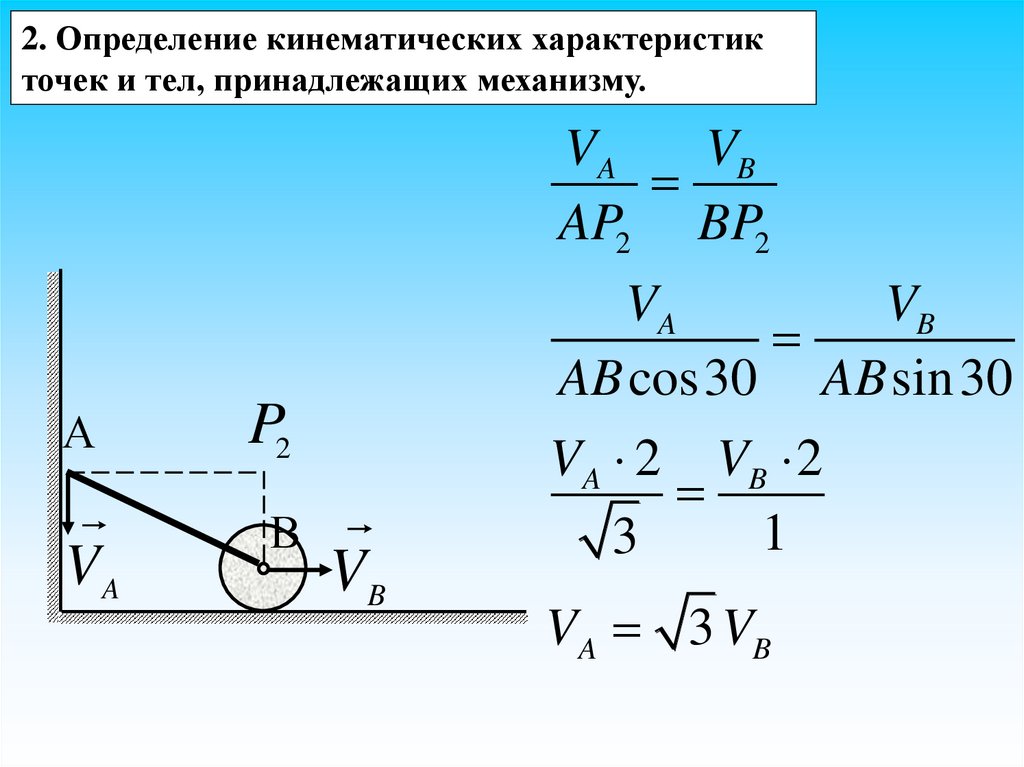
2. Определение кинематических характеристикточек и тел, принадлежащих механизму.
VA
VB
AP2 BP2
А
P2
VA
В
VB
VA
VB
AB cos30 AB sin 30
VA 2 VB 2
1
3
VA 3 VB
13.
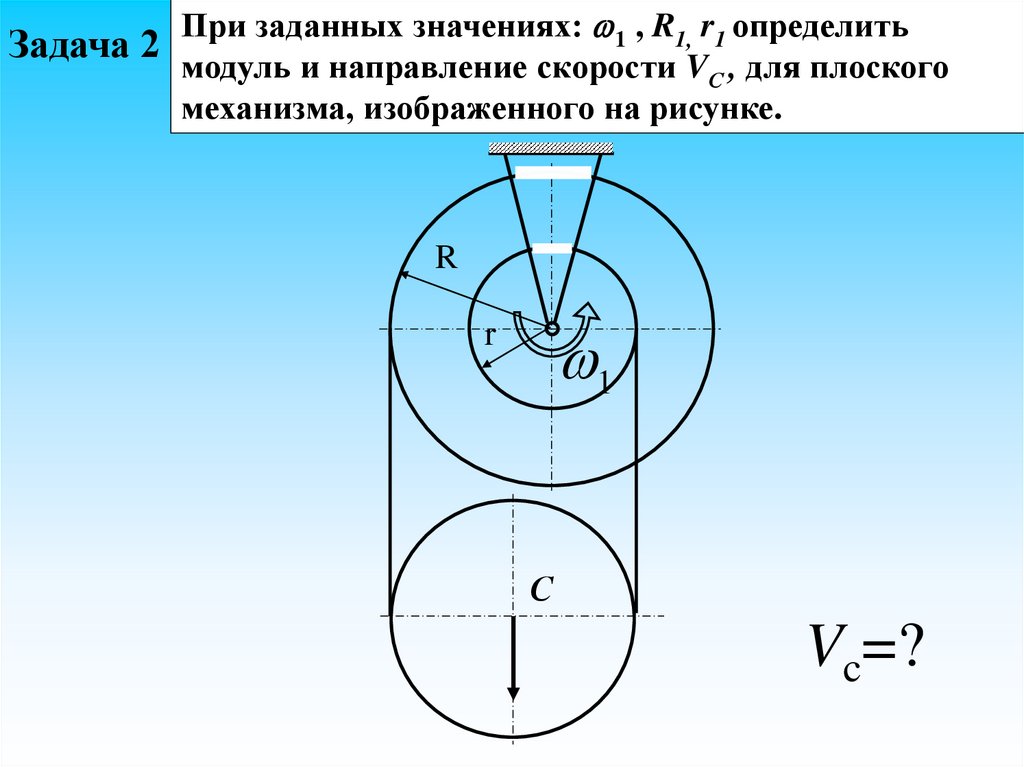
При заданных значениях: 1 , R1, r1 определитьЗадача 2
модуль и направление скорости VС , для плоского
механизма, изображенного на рисунке.
R
1
r
С
Vc=?
14.
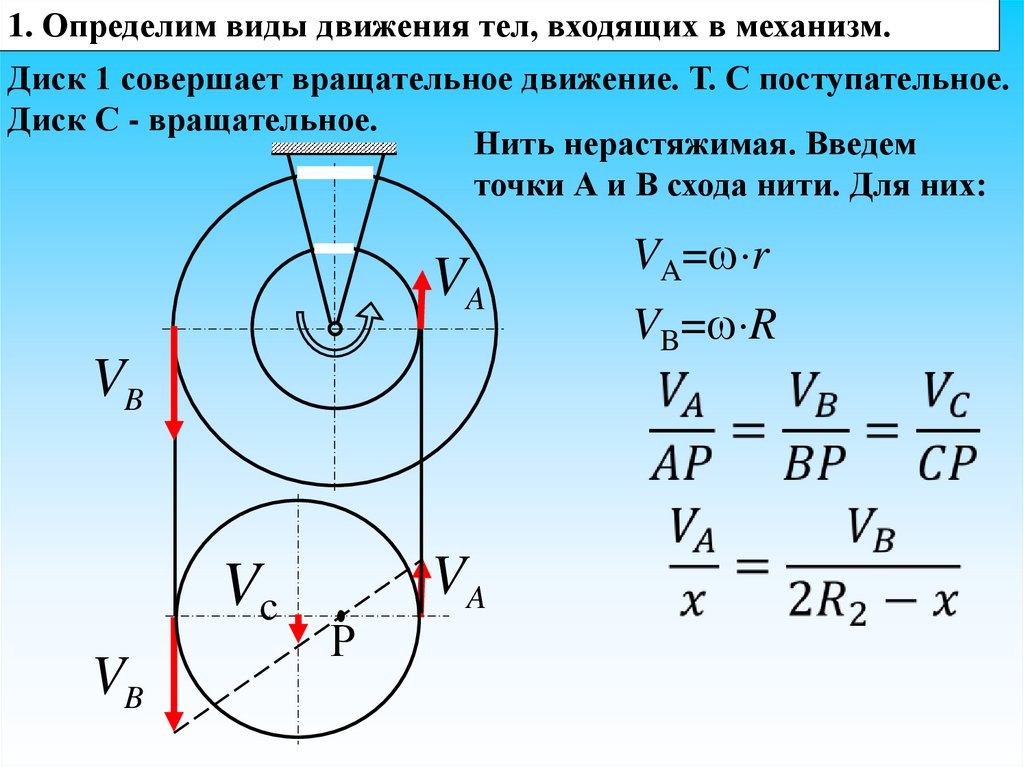
1. Определим виды движения тел, входящих в механизм.Диск 1 совершает вращательное движение. Т. С поступательное.
Диск С - вращательное.
Нить нерастяжимая. Введем
точки А и В схода нити. Для них:
VA
VB
Vc
VB
VA
Р
VA= r
VB= R
15.
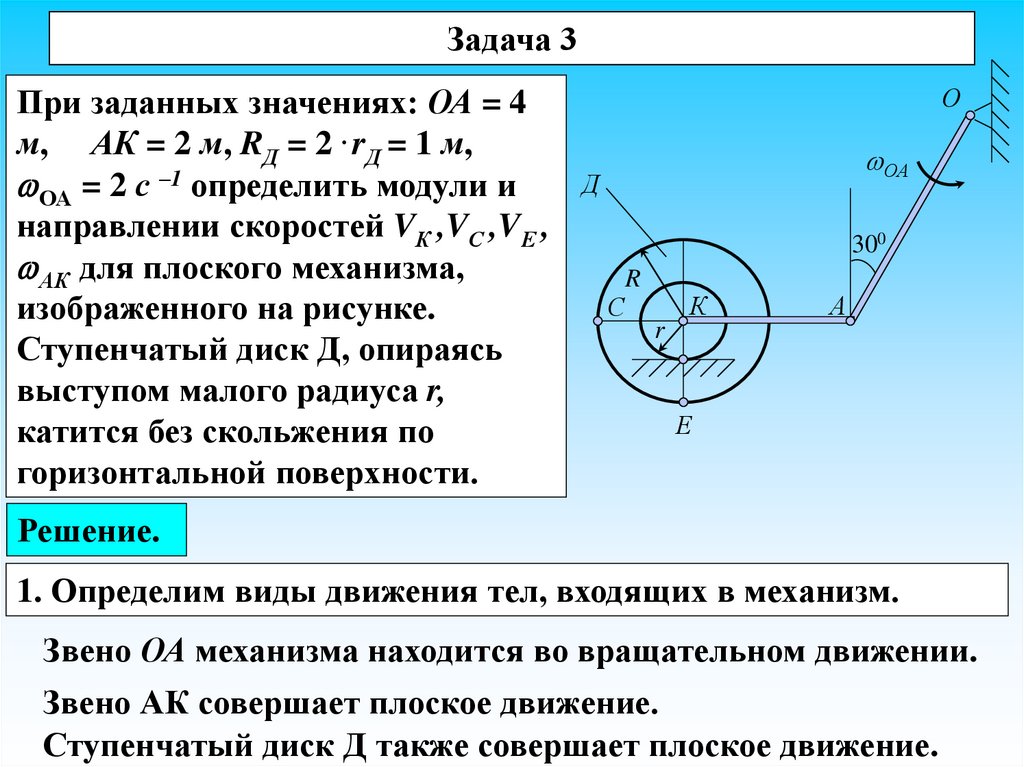
Задача 3При заданных значениях: ОА = 4
м, АК = 2 м, RД = 2 . rД = 1 м,
ОА = 2 с –1 определить модули и
направлении скоростей VК ,VС ,VЕ ,
АК для плоского механизма,
изображенного на рисунке.
Ступенчатый диск Д, опираясь
выступом малого радиуса r,
катится без скольжения по
горизонтальной поверхности.
О
ОА
Д
300
R
С
К
А
r
Е
Решение.
1. Определим виды движения тел, входящих в механизм.
Звено ОА механизма находится во вращательном движении.
Звено АК совершает плоское движение.
Ступенчатый диск Д также совершает плоское движение.
16.
2. Определение кинематических характеристикточек и тел, принадлежащих механизму.
Определение необходимо
начинать со звена механизма,
для которого они частично
заданы, а далее переходить к
другим звеньям через общие
для них точки.
О
ОА
Д
300
R
С
К
А
r
Е
В данной задаче известна ОА, что позволяет определить
скорость точки А, поэтому необходимо сначала рассмотреть
звено ОА.
а) Рассмотрим звено ОА.
Точка А принадлежит звену ОА, находящемуся во
вращательном движении, поэтому модуль ее скорости
найдется по формуле: VА = ОА . ОА = 2 . 4 = 8 м/с.
17.
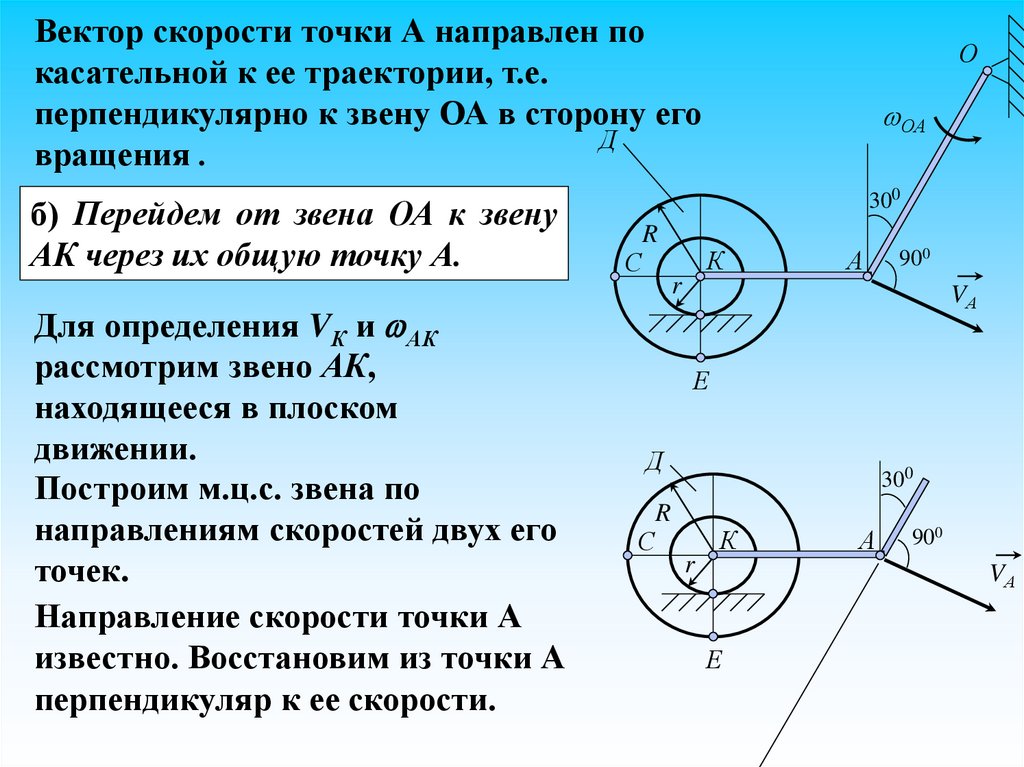
Вектор скорости точки А направлен покасательной к ее траектории, т.е.
перпендикулярно к звену ОА в сторону его
Д
вращения .
б) Перейдем от звена ОА к звену
АК через их общую точку А.
Для определения VК и АК
рассмотрим звено АК,
находящееся в плоском
движении.
Построим м.ц.с. звена по
направлениям скоростей двух его
точек.
Направление скорости точки А
известно. Восстановим из точки А
перпендикуляр к ее скорости.
О
ОА
300
R
С
К
А
900
r
VА
Е
Д
R
С
300
К
r
А
900
VА
Е
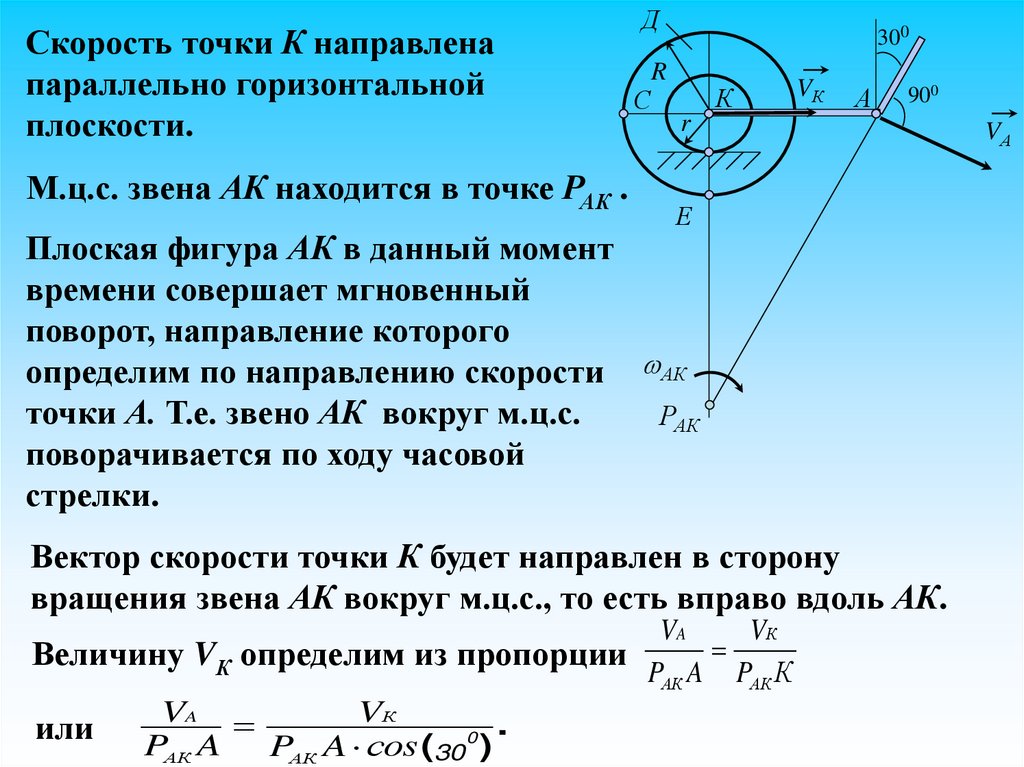
18.
Скорость точки К направленапараллельно горизонтальной
плоскости.
М.ц.с. звена АК находится в точке РАК .
Д
R
С
300
К
VК
А
900
r
Е
Плоская фигура АК в данный момент
времени совершает мгновенный
поворот, направление которого
определим по направлению скорости АК
точки А. Т.е. звено АК вокруг м.ц.с.
РАК
поворачивается по ходу часовой
стрелки.
Вектор скорости точки К будет направлен в сторону
вращения звена АК вокруг м.ц.с., то есть вправо вдоль АК.
VA
VК
Величину VК определим из пропорции
PАК A PАК К
К
или PVAA P A Vсоs
0 .
(
30 )
АК
АК
VА
19.
Откуда найдем VК = VА . соs(300) = 8 . 0,865 = 6,92 м/с.VА
8
4
АК P А 2 АК 2 2 с-1.
АК
в) Перейдем от звена АК к диску Д через общую точку К.
Д
Для нахождения скоростей точек С и Е
необходимо знать м.ц.с. ступенчатого диска
Д, который находится в плоском движении.
VК
К
С
Р
Е
Точка Р соприкосновения диска с неподвижной
поверхностью является в данный момент времени
неподвижной точкой, поэтому м.ц.с. ступенчатого диска Д
находится в этой точке.
20.
Угловая скорость диска Д Д направлена по ходу часовойстрелки, так как скорость VК направлена вправо.
Скорости точек С и Е перпендикулярны к
отрезкам, соединяющим эти точки с м.ц.с.,
и направлены в сторону вращения плоской
фигуры вокруг м.ц.с.
VС
Величины скоростей точек VС и VЕ
определим из пропорции, то есть:
К
С
Д
Д
VК
Р
VЕ
Е
VЕ
VС
VК
VЕ или VК VС
2
2
КP СP ЕP
r
R r
R r
Откуда получим: VС = VК . R 2 r 2 /r = 6,92 . 12 0,52 / 0,5 15,5 м/с,
VЕ = VК .(R - r)/r = 6,92 . 0,5/0,5 = 6,92 м/с.
21.
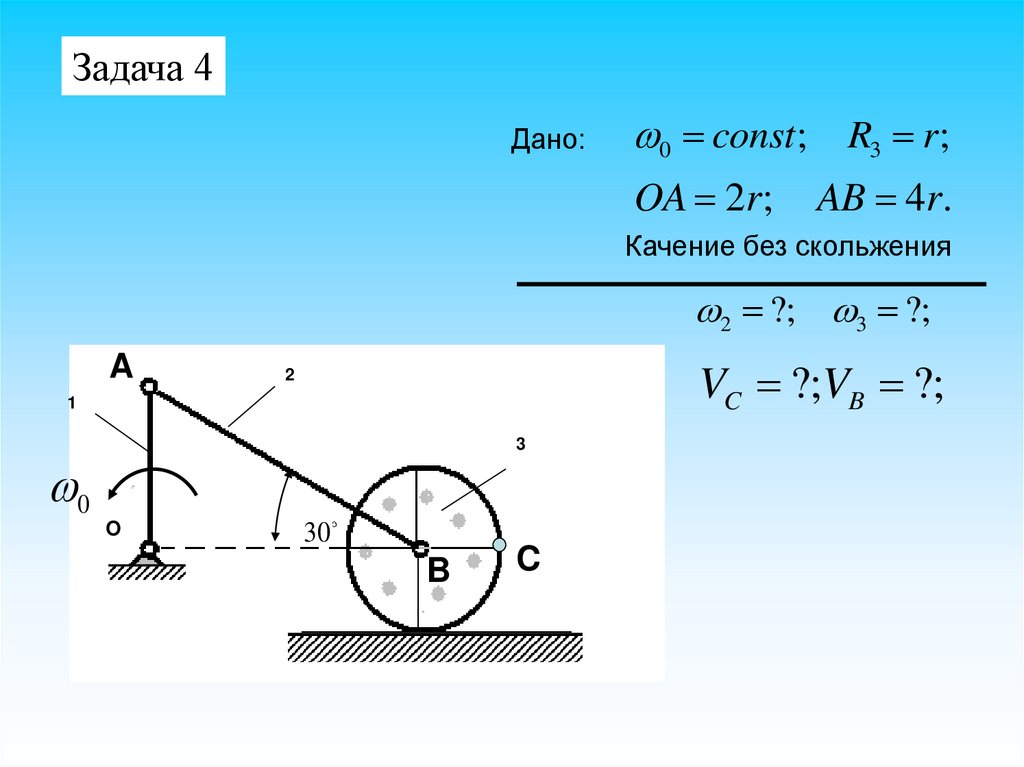
Задача 4Дано:
0 const; R3 r;
OA 2r;
AB 4r.
Качение без скольжения
2 ?; 3 ?;
A
VC ?;VB ?;
2
1
3
0
O
30
B
C
22.
VAA
VC
0
O
30
B
VB
C
3
P
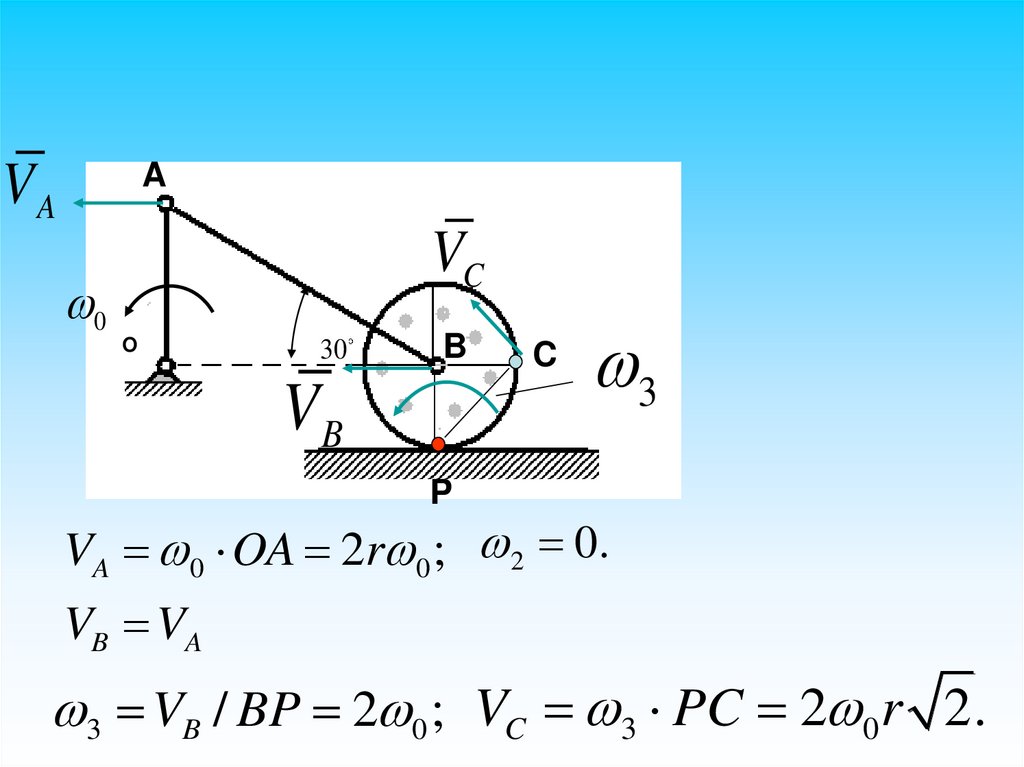
VA 0 OA 2r 0 ; 2 0.
VB VA
3 VB / BP 2 0 ; VC 3 PC 2 0 r 2.
23.
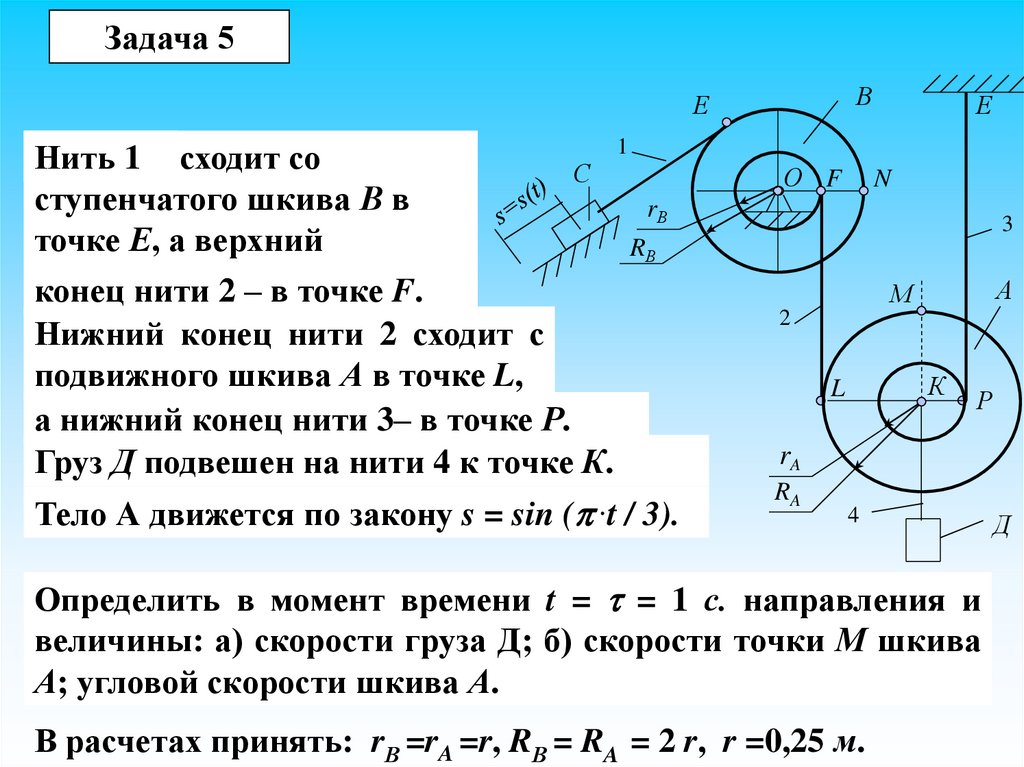
Задача 5В
Е
1
Нить 1 сходит со
С
ступенчатого шкива В в
rВ
точке Е, а верхний
RВ
конец нити 2 – в точке F.
Нижний конец нити 2 сходит с
подвижного шкива А в точке L,
а нижний конец нити 3– в точке Р.
Груз Д подвешен на нити 4 к точке К.
Тело А движется по закону s = sin ( .t / 3).
О F
Е
N
3
А
М
2
К
L
Р
rA
RA
4
Определить в момент времени t = = 1 с. направления и
величины: а) скорости груза Д; б) скорости точки М шкива
А; угловой скорости шкива А.
В расчетах принять: rВ =rA =r, RВ = RA = 2 r, r =0,25 м.
Д
24.
Решение.1. Определим вид
движения каждого тела,
входящего в механизм.
В
Е
Е
1
С
- нити – 1,2,4 движутся
поступательно, а участок 3ей нити ЕР – неподвижен;
О F
N
rВ
3
RВ
2
К
L
- тела С и Д движутся также поступательно;
- диск В совершает вращательное движение;
А
М
Р
rA
RA
4
- диск А совершает плоское движение.
Д
2. Определим искомые кинематические характеристики
точек и тел, принадлежащих механизму.
Начнем со звена механизма, для которого они частично
заданы или могут быть найдены.
25.
а) Рассмотрим тело С, движущееся поступательно.Определим скорость тела С, которое
движется по заданному закону.
Алгебраическое значение скорости найдем по
формуле V ds s .
С
VС
dt
VС s = /3 .cos ( .t / 3)|t=1 = / 3 . сos (600) = / 6 = 0,52 м/с.
Скорость точки VС 0, поэтому она будет направлена в
сторону возрастания координаты s, то есть вниз по наклонной
плоскости.
б) Рассмотрим нить 1.
Так как нить 1 движется
поступательно, то V Е V С ,
то есть V VC 0,52 м /с.
E
1
VЕ
С
VС
rВ
RВ
В
Е
О F
N
26.
а) Рассмотрим тело С, движущееся поступательно.Определим скорость тела С, которое
движется по заданному закону.
Алгебраическое значение скорости найдем по
формуле V ds s .
С
VС
dt
VС s = /3 .cos ( .t / 3)|t=1 = / 3 . сos (600) = / 6 = 0,52 м/с.
Скорость точки VС 0, поэтому она будет направлена в
сторону возрастания координаты s, то есть вниз по наклонной
плоскости.
б) Рассмотрим нить 1.
Так как нить 1 движется
поступательно, то V Е V С ,
то есть V VC 0,52 м /с.
E
1
VЕ
С
VС
rВ
RВ
В
Е
О F
N
27.
г) Рассмотрим нить 2.Скорость точки L по модулю и по
направлению будет совпадать со
скоростью точки F, так как нить 2
находится в поступательном
движении.
Точка F является общей для нити 2 и
блока В, поэтому ее скорость
представим в виде:
В
Е
VF
О F
N
rВ
RВ
2
VL
L
VL = VF = 0,26 м/с.
д) Рассмотрим ступенчатый шкив А.
Точка L одновременно принадлежит нити 2 и шкиву А,
который находится в плоском движении.
28.
Зная скорость VL и м.ц.с. шкива А, можноопределить скорости других его точек.
Е
М.ц.с. шкива А совпадает с точкой схода Р нити 3 со
шкива, так как нить 3 неподвижна, то есть VР = 0.
Скорости точек плоской фигуры А
пропорциональны расстояниям до м.ц.с., то
есть справедливо выражение:
Откуда VК = VL
= VL
LP
rА
R А rА
= 0,26 .
r
r 2 r
А
М
VL
VК
L
VL VК .
LP
КР
. КР
3
А
К
Р
rA
RA
4
Д
= 0,26 .0,33 =0,087 м/с.
VK VК 0,087
0,22 с 1 .
Угловая скорость шкива А: А =
r
0,25
КР
Ее направление определяется направлением VL.
Вектор скорости точки К направлен вверх, перпендикулярно к
отрезку КР, соединяющему точку К и м.ц.с., в сторону вращения
шкива А вокруг м.ц.с.
29.
Величина скорости точки М определиться по формулеVМ = А · РМ = 0,22 · r 2 ( 2r )2 = 0,22 · r · 5
Е
= 0,22 • 0,25 • 2,24 = 0,12 м/с.
3
Вектор скорости точки М направлен
перпендикулярно к отрезку МР,
соединяющему точку М и м.ц.с., в сторону
вращения шкива А вокруг м.ц.с.
е) Рассмотрим нить 4.
Нить
находится
движении, поэтому
М
VL
VК
L
VМ
А
А
К
Р
rA
в
поступательном
RA
V Д V К ,
то есть величина VД = 0,087 м/с,а вектор
скорости тела Д направлен вертикально вверх.
4
VД
Д
30.
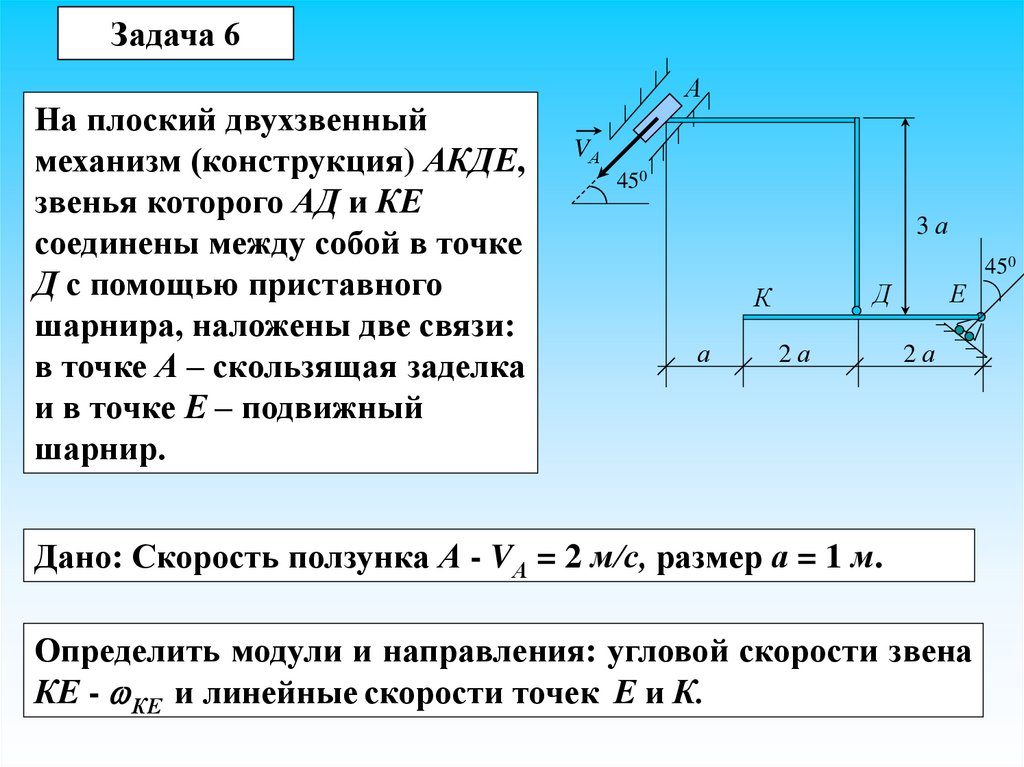
Задача 6На плоский двухзвенный
механизм (конструкция) АКДЕ,
звенья которого АД и КЕ
соединены между собой в точке
Д с помощью приставного
шарнира, наложены две связи:
в точке А – скользящая заделка
и в точке Е – подвижный
шарнир.
А
VА
450
3а
450
Д
К
а
2а
Е
2а
Дано: Скорость ползунка А - VА = 2 м/с, размер а = 1 м.
Определить модули и направления: угловой скорости звена
КЕ - КЕ и линейные скорости точек Е и К.
31.
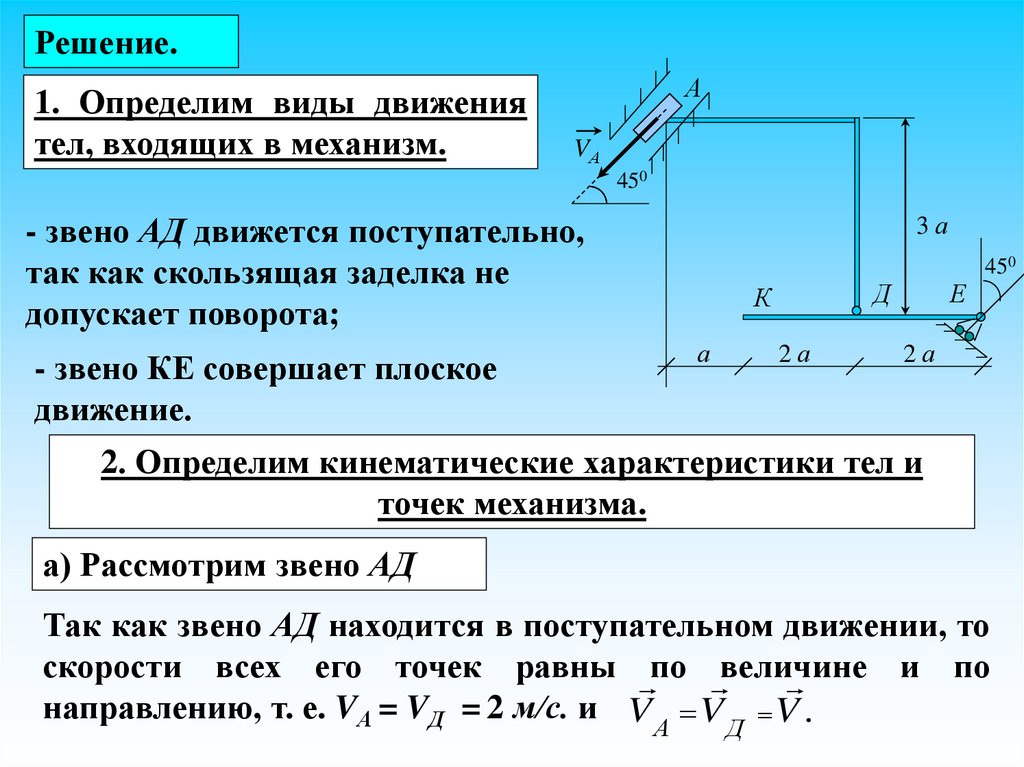
Решение.1. Определим виды движения
тел, входящих в механизм.
А
VА
450
3а
- звено АД движется поступательно,
так как скользящая заделка не
допускает поворота;
450
Д
К
а
- звено КЕ совершает плоское
движение.
2а
Е
2а
2. Определим кинематические характеристики тел и
точек механизма.
а) Рассмотрим звено АД
Так как звено АД находится в поступательном движении, то
скорости всех его точек равны по величине
и по
направлению, т. е. VА = VД = 2 м/с. и V V V .
А
Д
32.
VА V Д V .А
б) Рассмотрим звено КЕ
VА
Посмотрим для него м.ц.с.
Для этого восстановим
перпендикуляр из точки Д к
вектору ее скорости.
V
450
2а
а
VЕ 450
Е
К
Д
900
900
1,41 с-1.
а
КЕ
Второй перпендикуляр восстановим
VК
VД
Р
из точки Е к ее прямолинейной
траектории, вдоль которой направлен вектор скорости VЕ .
М.ц.с. для звена КЕ будет находиться в точке Р.
Угловая скорость КЕ =
VД
VА
2
2
ДР
2 а cos( 450 )
Скорость VE направлена вверх
по наклонной плоскости и
VЕ = VД = 2 м/с. Скорость VK направлена отрезку РК в
сторону вращения звена и VК = КЕ · РК = 1,41 · (3 а)2 (а)2
= 1,41 . 3,16 = 4,46 м/с.
33.
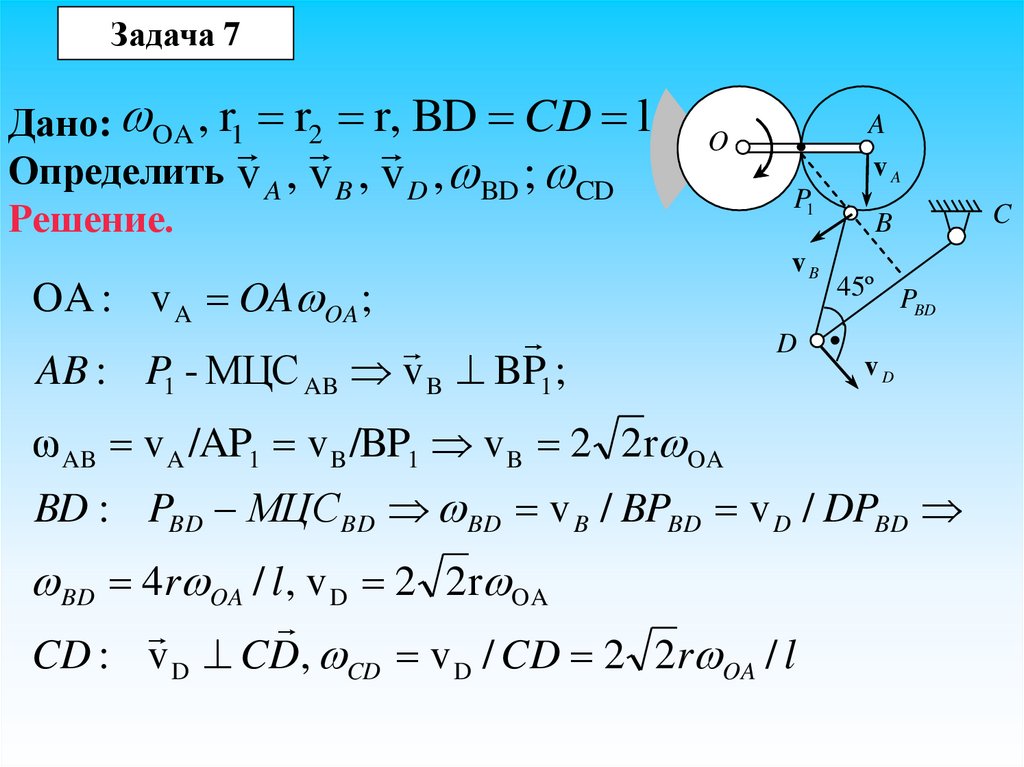
Задача 7Дано: OA , r1 r2 r, BD CD l
Определить v A , v B , v D , BD ; CD
Решение.
A
O
OA : v A OA OA ;
AB : P1 - МЦС AB v B BP1 ;
vA
P1
vB
D
B
45º P
BD
vD
ω AB v A /AP1 v B /BP1 v B 2 2r OA
BD : PBD МЦСBD BD v B / BPBD v D / DPBD
BD 4r OA / l , v D 2 2r OA
CD : v D CD, CD v D / CD 2 2r OA / l
C
34.
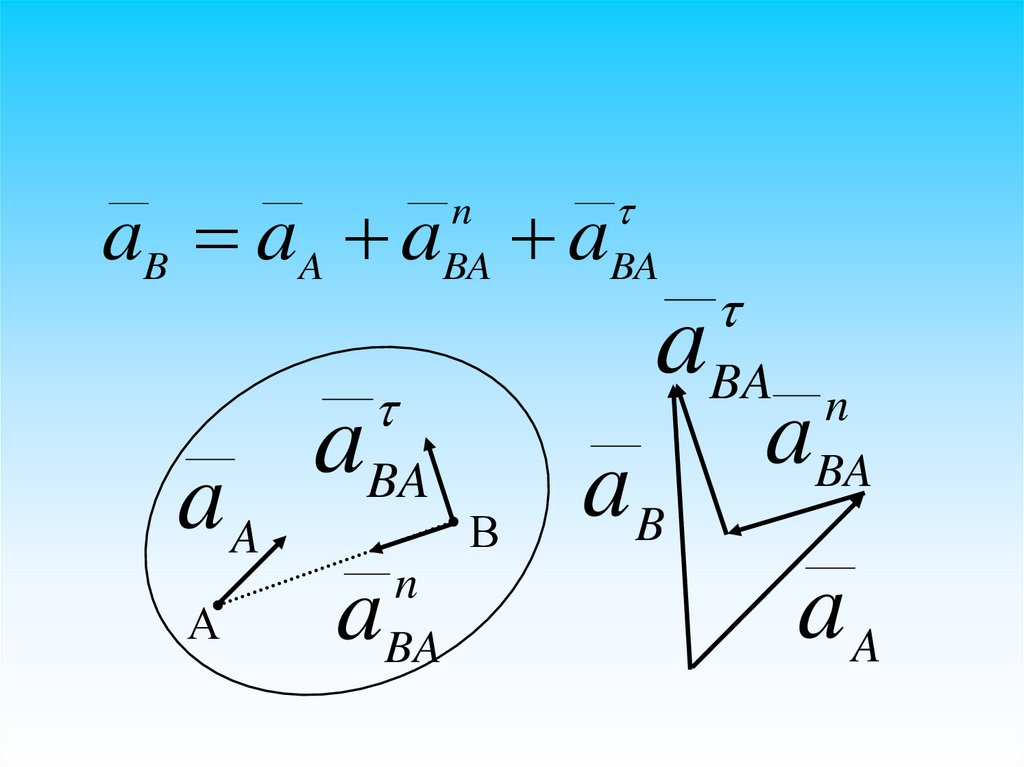
Ускорения точек плоской фигурыa
O
AO
a
aO
aA aO aAO a ;
A
n
AO
a AO OA; a
n
AO
n
AO
OA;
aAO OA;
n
2
a AO OA.
Ускорение любой точки А геометрически складывается
из ускорения полюса
О
и осестремительного и
вращательного ускорений во вращении тела вокруг
полюса
35.
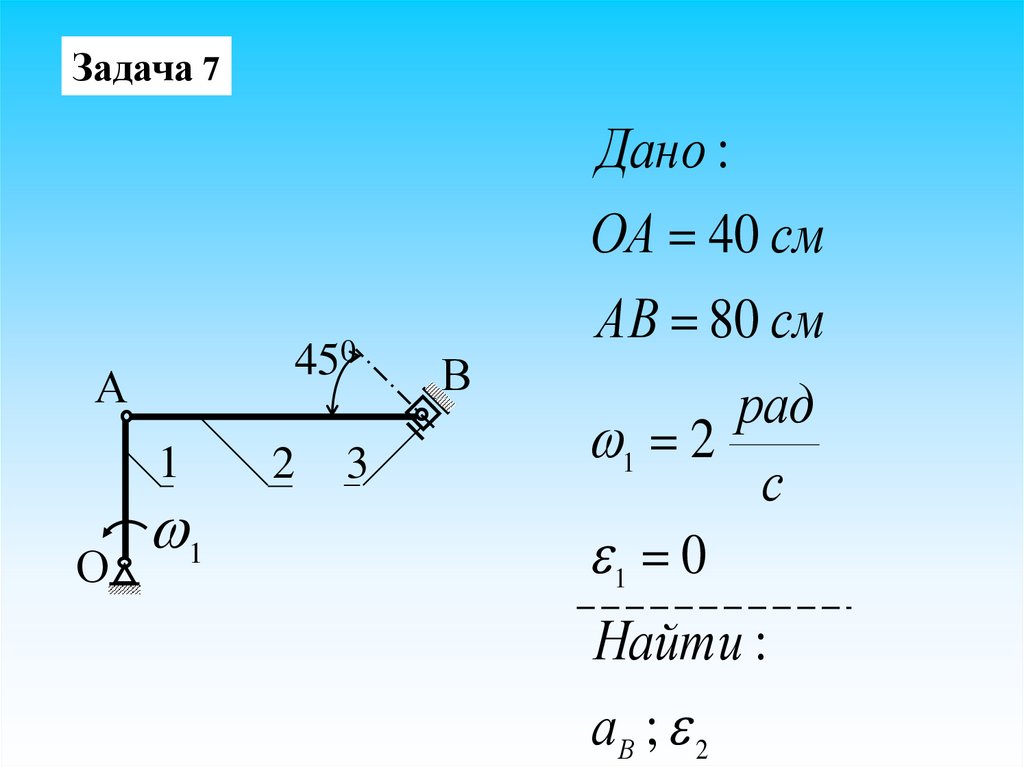
Задача 7450
А
1
О
1
2
3
В
Дано :
ОА 40 см
АВ 80 см
рад
1 2
с
1 0
Найти :
аВ ; 2
36.
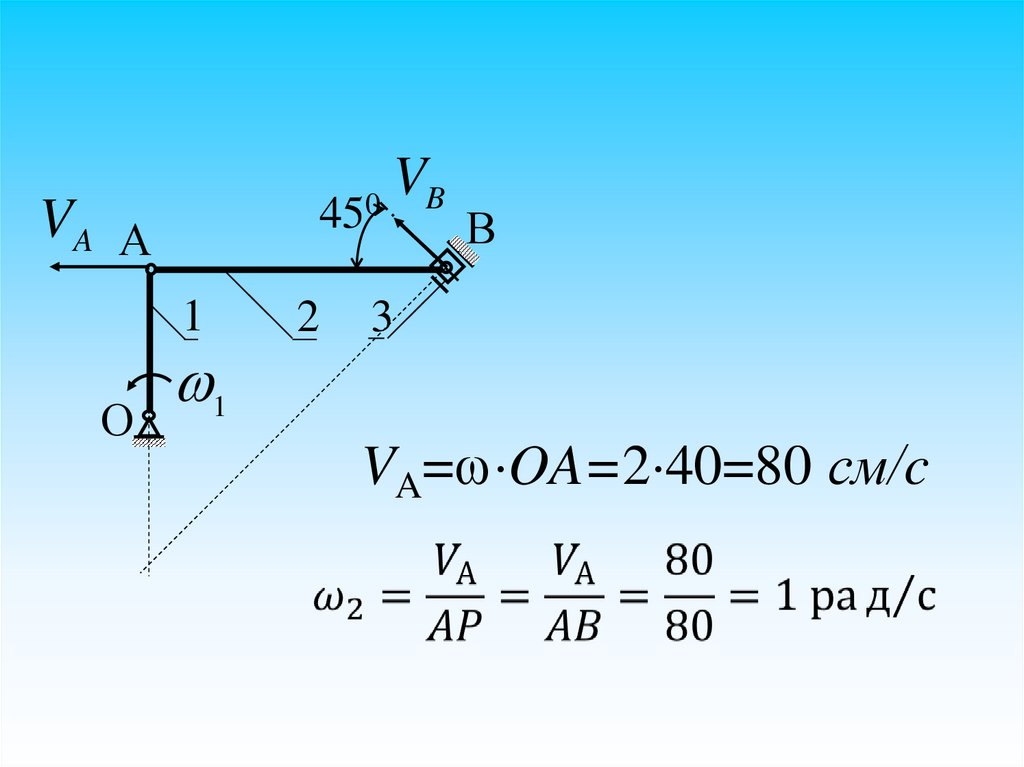
450VA А
1
О
1
2
VB
В
3
VA= OA=2 40=80 см/c
37.
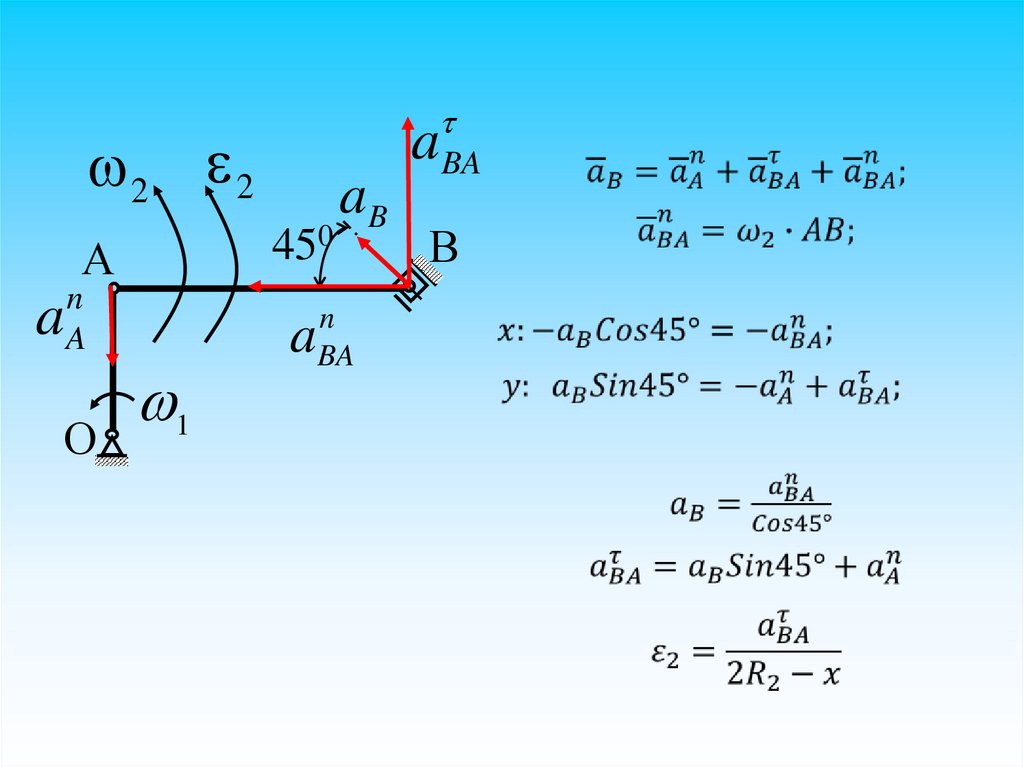
2 2450
А
a
n
A
О
1
a
aB
n
BA
aBA
В
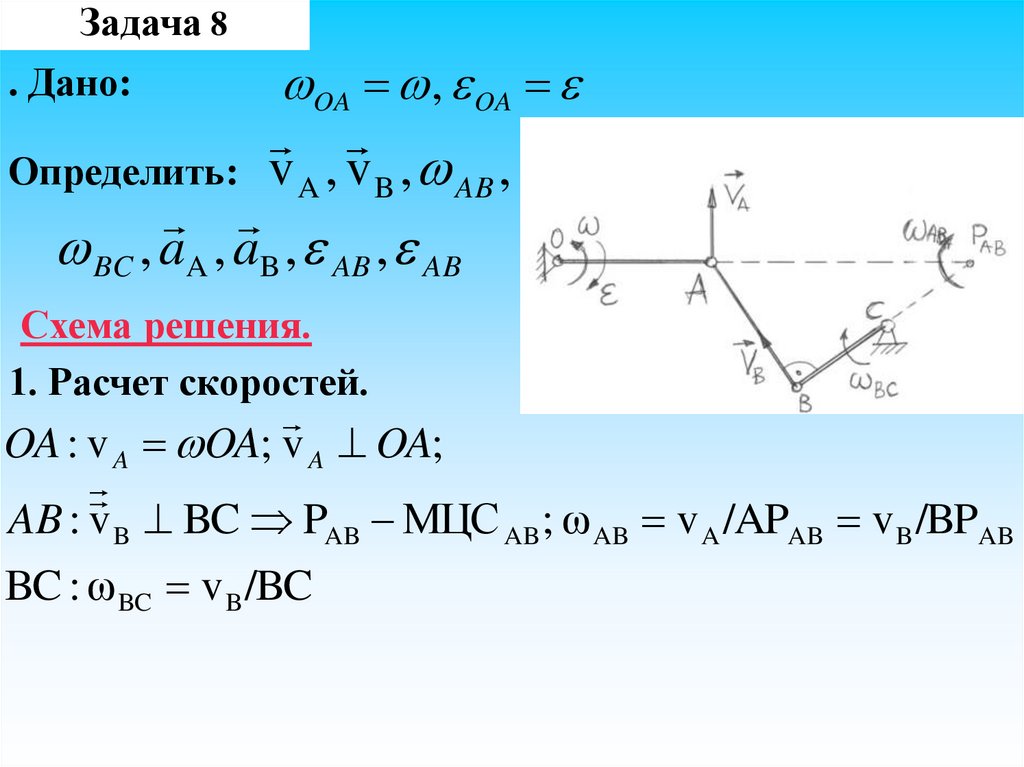
38. Задача 8
. Дано:OA , OA
Определить: v A , v B , AB ,
BC , aA , aB , AB , AB
Схема решения.
1. Расчет скоростей.
OA : v A OA; v A OA;
AB : v B BC PAB МЦС AB ; ωAB v A /APAB v B /BPAB
BC : ωBC v B /BC
39.
2. Расчет ускорений.OA : a OA; a A OA;
n n
2
AB : aB a A aBA aBA ; aBA AB
AB; a BA AB AB;
n
2
BC : aB aB aB (*); aBn BC
BC ; a B BC BC
n n
n
aB aB a A a A aBA aBA (**)
n
A
2
В (**) две неизвестные : AB , BC . Проецируя (**) на
две оси, найдем их. Ускорение aB найдем из (*).
40.
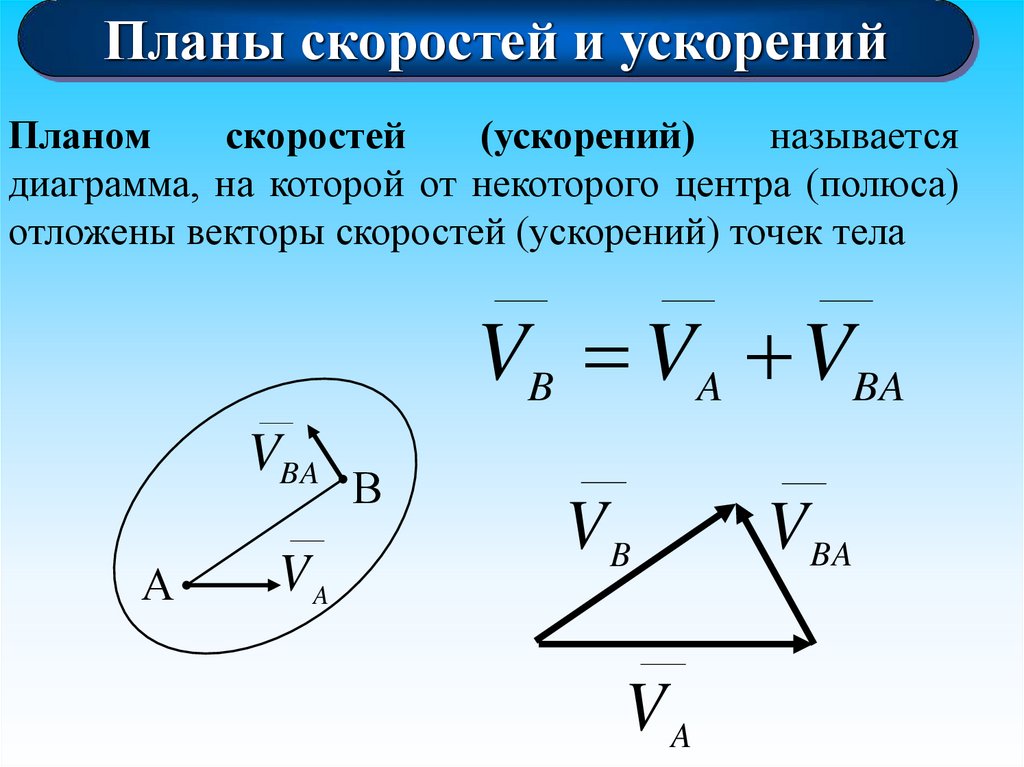
Планы скоростей и ускоренийПланом
скоростей
(ускорений)
называется
диаграмма, на которой от некоторого центра (полюса)
отложены векторы скоростей (ускорений) точек тела
VB VA VBA
VBA
А
VA
В
VB
VA
V BA
41.
aB aA a aBAn
BA
aA
А
a
n
BA
aBA n
aBA
В
aB
aBA
aA
42.
Свойства планов скоростей и ускорений1. Векторы выходящие из полюса плана скоростей
(ускорений) изображают в масштабе векторы
абсолютных
скоростей
(ускорений)
соответствующих точек
2. Отрезки, соединяющие концы векторов, выходящих
из полюса, изображают в масштабе векторы
относительных
скоростей
(ускорений)
соответствующих точек
3. Сходственные фигуры звеньев на плане механизма и
плане скоростей (ускорений) – подобны
Примечание (правило обхода букв): направление
обхода букв сходственных фигур на плане механизма
и плане скоростей (ускорений)- одинаково
43.
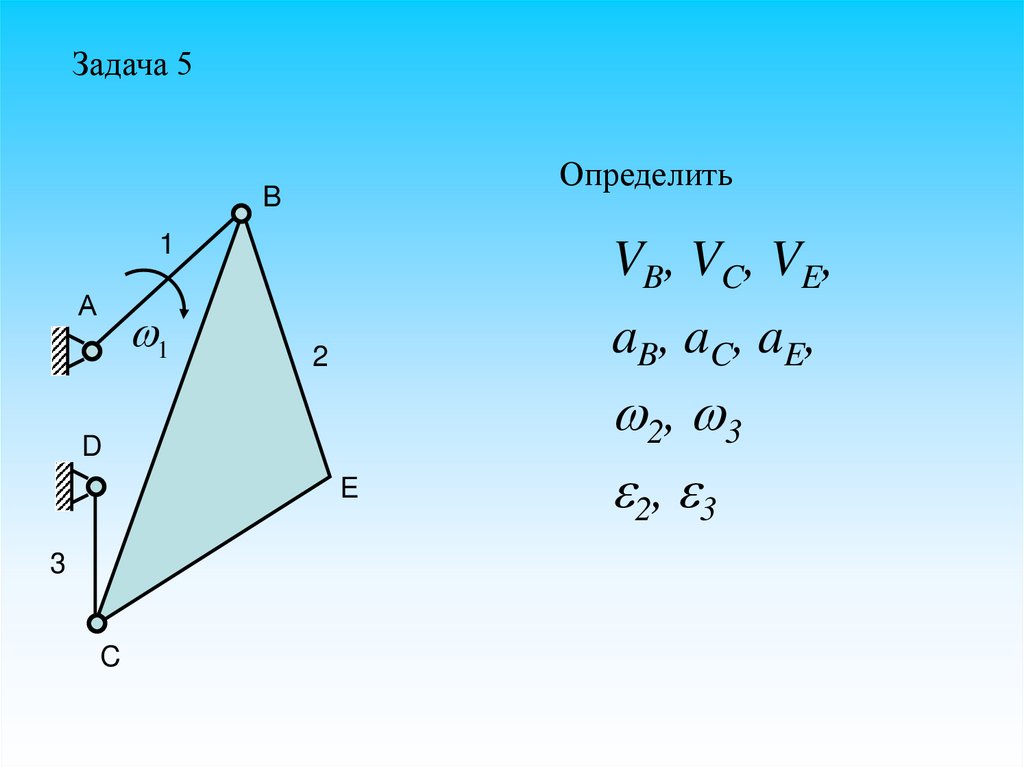
Задача 5Определить
B
1
А
1
VB, VC, VE,
aB, aC, aE,
2
D
E
3
C
2 , 3
2, 3
44.
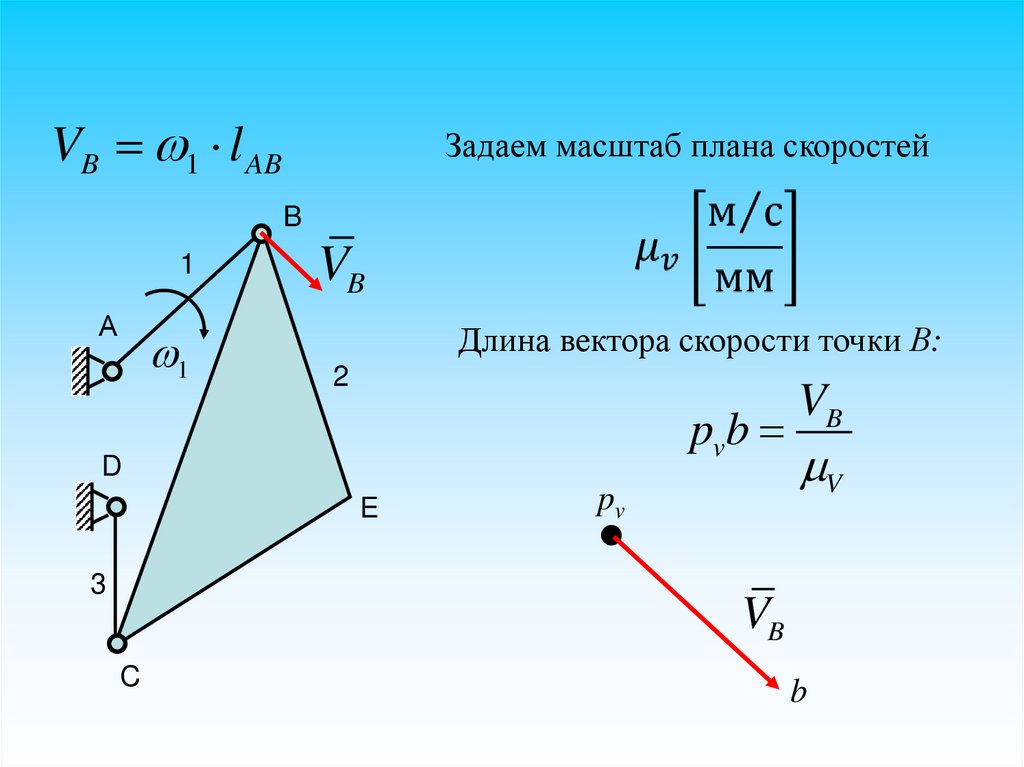
VB 1 l ABЗадаем масштаб плана скоростей
B
1
А
1
VB
Длина вектора скорости точки В:
2
pvb
D
E
3
pv
VB
V
VB
C
b
45.
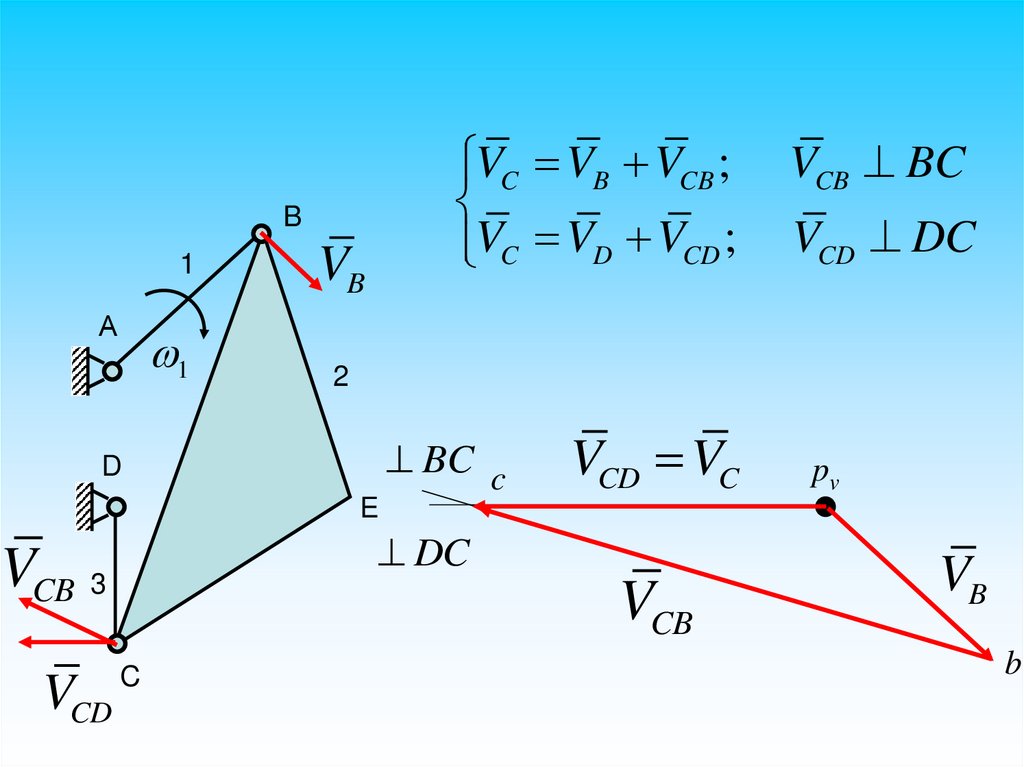
VC VB VCB ;VC VD VCD ;
B
1
А
1
VB
VCB BC
VCD DC
2
BC c
D
VCD VC
pv
E
DC
VCB 3
VCD
VCB
C
VB
b
46.
BC cB
VB
1
А
1
D
pv
DC
VCB
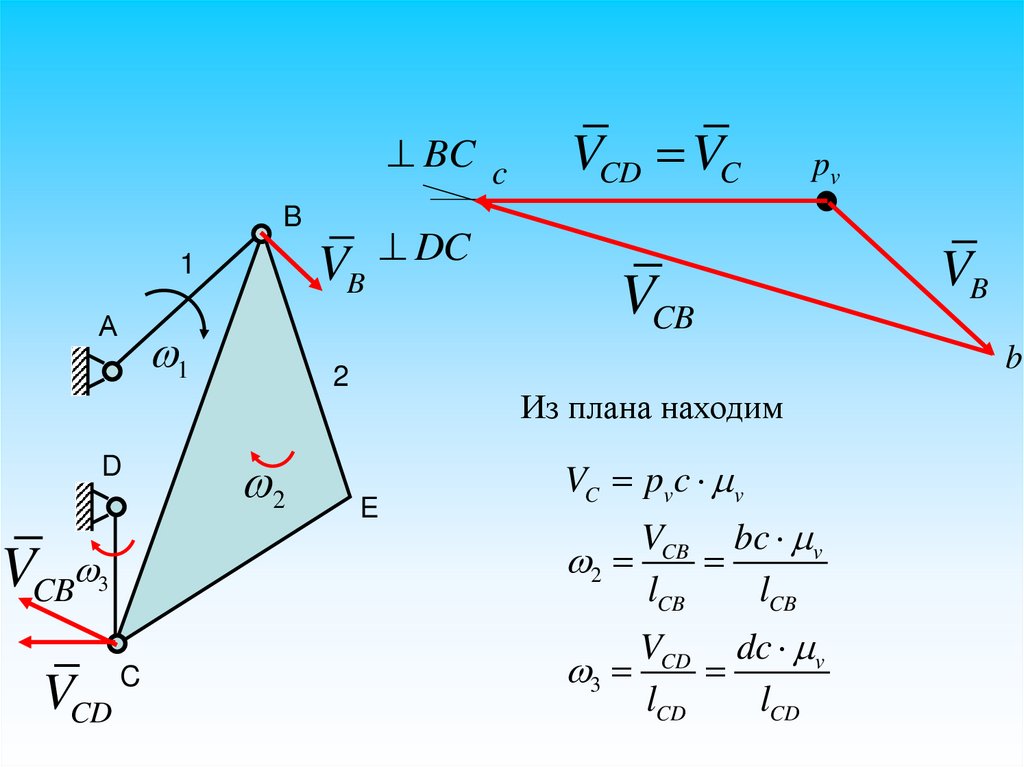
Из плана находим
E
VC pv c v
VCB
VCB bc v
2
lCB
lCB
VCD
VCD dc v
3
lCD
lCD
3
C
VB
b
2
2
VCD VC
47.
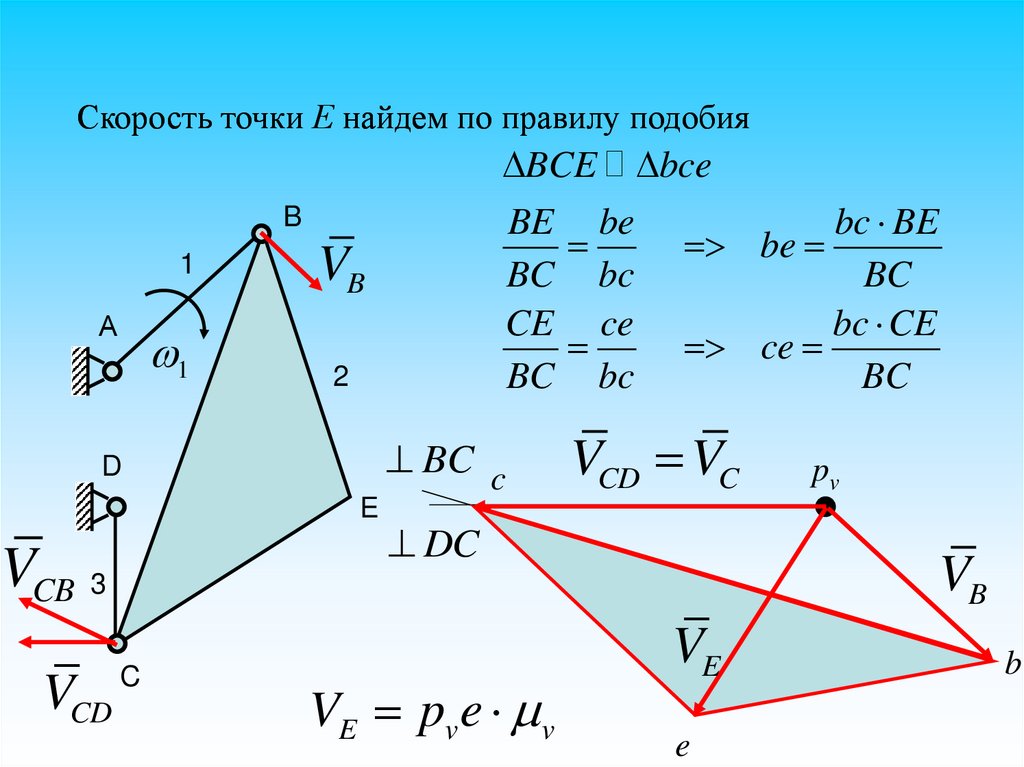
Скорость точки Е найдем по правилу подобияBCE bce
BE be
bc BE
be
BC bc
BC
CE ce
bc CE
ce
BC bc
BC
B
1
А
1
VB
2
BC c
D
E
VCB 3
VCD
VCD VC
DC
VCB
C
VE pve v
VE
e
pv
VB
b
48.
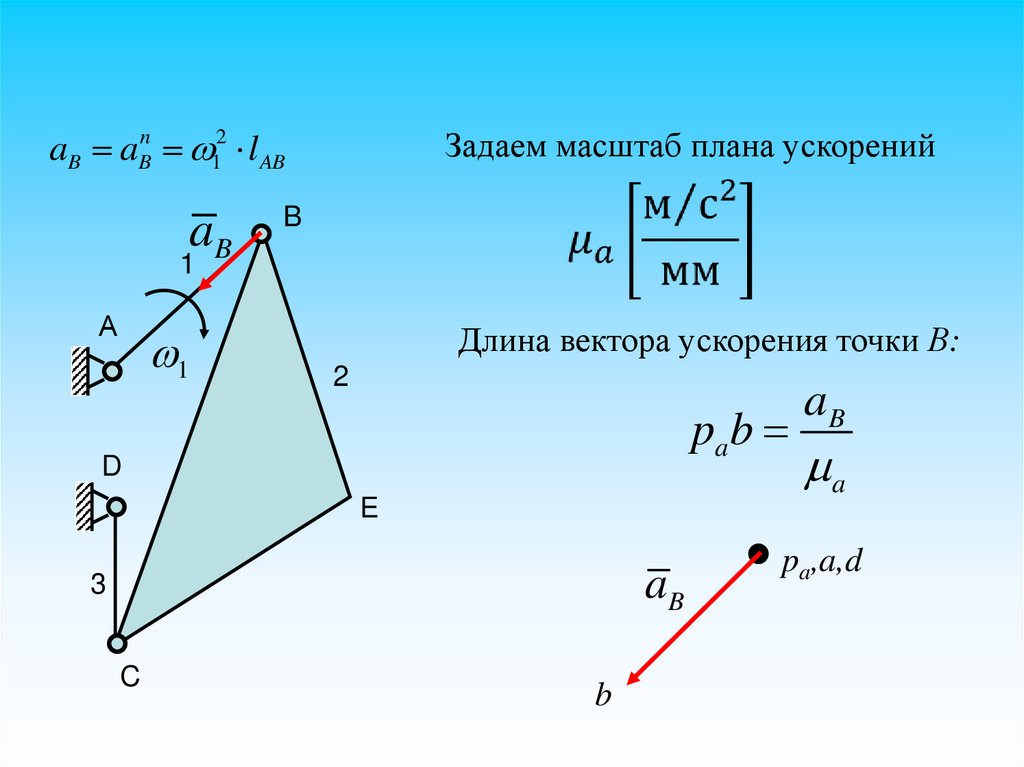
aB aBn 12 l ABaB
Задаем масштаб плана ускорений
B
1
А
1
Длина вектора ускорения точки В:
2
pab
D
E
aB
3
C
b
aB
a
pa,a,d
49.
aC aB a aCB ; aBC , aCB BC
n
n
a
a
a
a
;
a
DC
,
a
C
D
CD
CD
CD
CD DC
n
a
n
2
aCB 2 lBC bn1 CB
n
CB
n
CB
a
n
aCD
32 lDC
aCB 2 lBC
aCD
3 lDC
dn2
n
aCD
a
50.
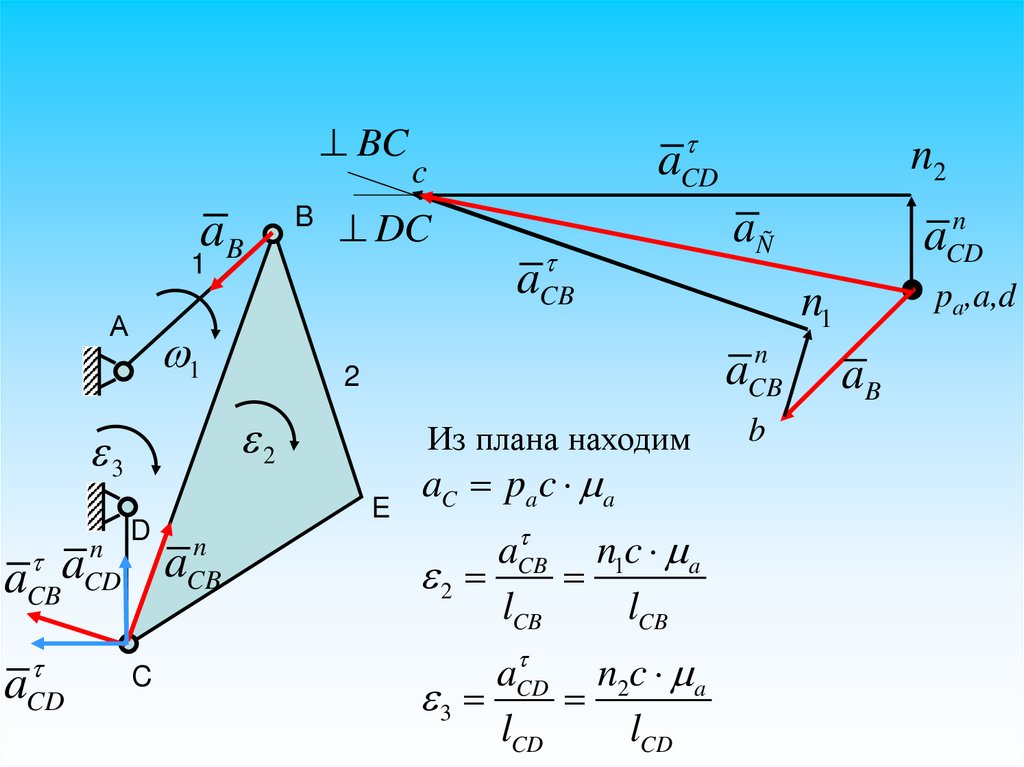
BCaB
B
1
n
CD
D
aCBa
aCD
C
a
aÑ
a
2
Из плана находим
aC pa c a
aCB
n1c a
2
lCB
lCB
aCD
n2c a
3
lCD
lCD
n
CD
a
pa,a,d
n1
n
CB
E
n
CB
n2
aCB
2
3
c
DC
1
А
aCD
b
aB
51.
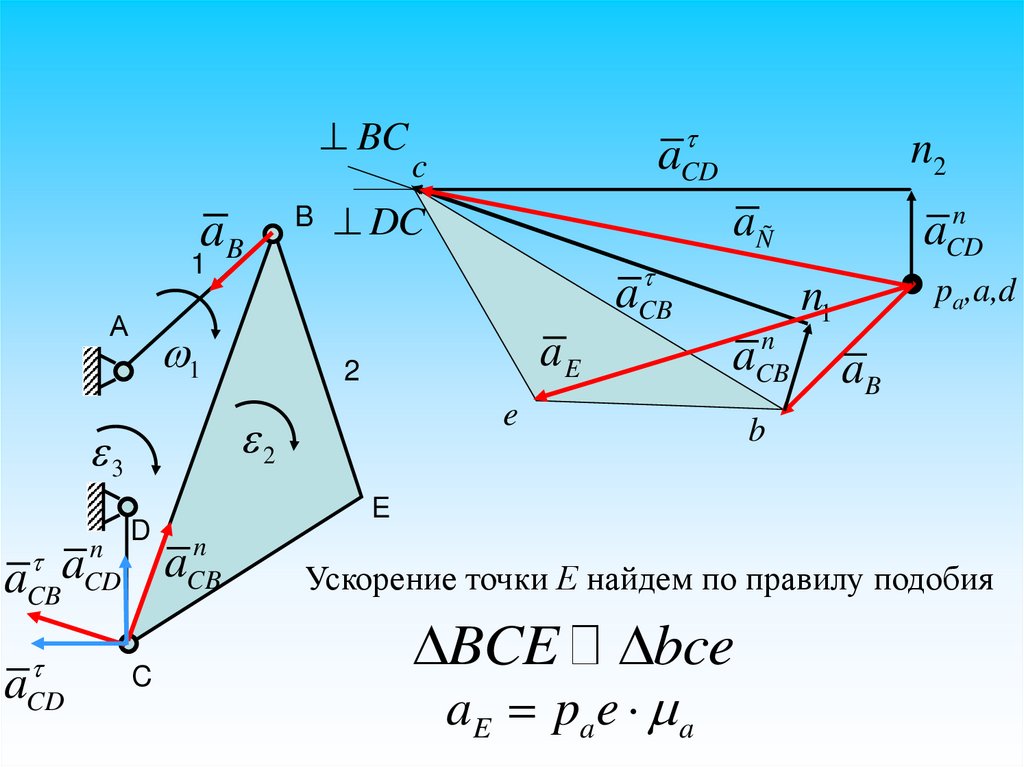
BCaB
aCD
c
B DC
aÑ
1
А
n
CD
aCD
2
D
C
n
CD
a
pa,a,d
n1
n
CB
aE
a
e
2
aCBa
aCB
1
3
n2
aB
b
E
n
CB
a
Ускорение точки Е найдем по правилу подобия
BCE
bce
aE pa e a

















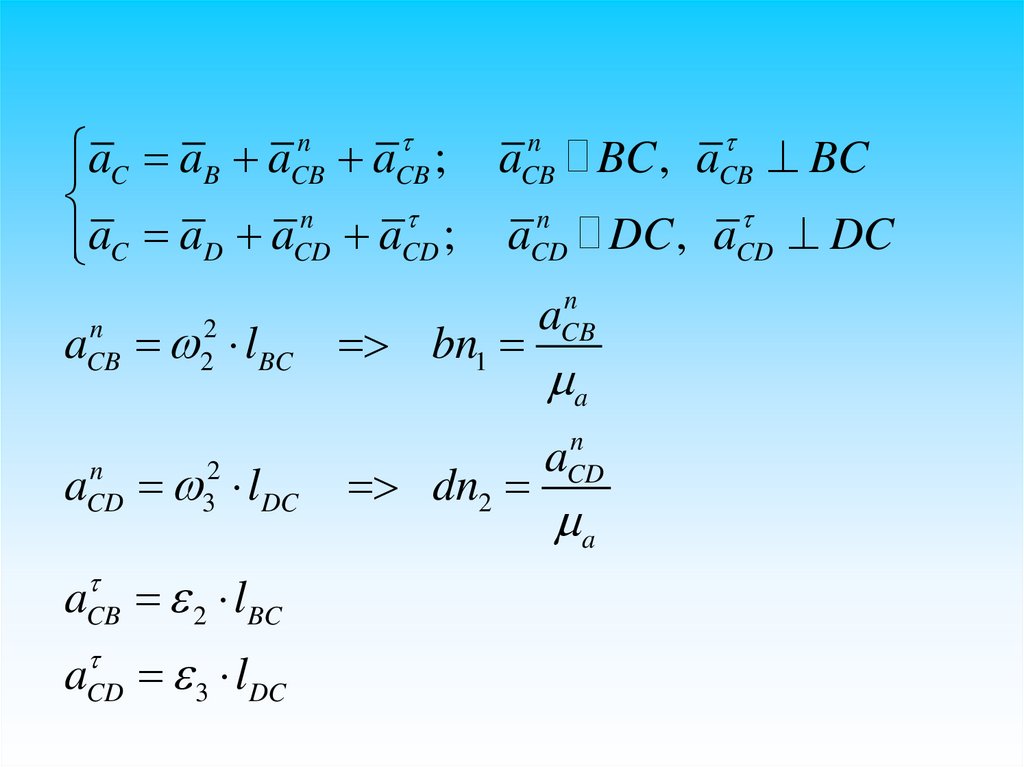
 Физика
Физика








