3_2 Ан_Геом_На плоскости_Кривые2 24

1.

§ 3. Прямая на плоскости
Различные виды уравнения прямой на плоскости
Прямая на плоскости может быть задана двумя
точками либо точкой и направляющим вектором,
точкой,
лежащей
на
ней,
и
вектором,
перпендикулярным прямой. Рассмотрим различные
способы записи уравнения прямой на плоскости.

2.

1. Уравнение прямой, проходящей через две заданные точки
M1(x1; y1), M2(x2; y2) записывается из условия коллинеарности
векторов M M M M
1
1
2
x x1
y y1
.
(1)
x2 x1 y2 y1
M
M2
M (x,y)- произвольная точка этой прямой
M1
2. Каноническое уравнение прямой
записывается как уравнение прямой, проходящей через данную
s
точку M0(x0; y0) параллельно заданному вектору
M
s {m; n} (направляющему вектору прямой)
M0
x x0 y y0
.
M 0M s
m
n
x x0 mt ,
3. Параметрические уравнения прямой
y y0 nt ,
где (x0; y0) – координаты точки, лежащей на прямой, а s {m; n} –
направляющий вектор прямой.

3.

Заметим, что одна из координат вектора s {m; n} может
быть равна нулю.
В этом случае запись уравнения прямой в каноническом
виде остается прежней, например,
x x0 y y0
0
m
что означает, что вектор s параллелен оси Y и уравнение
можно записать как
m ( x x0 ) 0 ( y y0 ) 0
т.е. x=x0 уравнение прямой, параллельной оси Y, пересекающей
ось X в точке x=x0 .

4.

4. Уравнение прямой, проходящей через данную точку M0(x0; y0)
перпендикулярно заданному вектору n { A; B}.
n
Вектор n , перпендикулярный данной прямой,
M
называется нормальным вектором этой прямой.
M
n M 0M
n M 0 M 0,
A( x x0 ) B( y y0 ) 0.
0
5. Общее уравнение прямой на плоскости – это уравнение вида
Ax + By + C = 0,
(2)
в котором хотя бы один из коэффициентов A или B не равен 0, т. е.
A2 + B2 ≠ 0.
(A,B) - координаты нормального вектора.
Утверждение. Любое уравнение вида (2), где A2 + B2 ≠ 0, задает
некоторую прямую на плоскости. И обратно, любая прямая на
плоскости может быть задана уравнением вида (2).
В общем уравнении прямой Ax + By + C = 0, A,B,C могут
принимать различные действительные значения, исключая
одновременное равенство нулю A и B.

5.

Пусть в уравнении Ax + By + C = 0, A=0
y =b
By + C = 0
Если кроме того, C=0, то уравнение y=0 (Ox)
Пусть B=0, тогда уравнение примет вид
x=a
Ax+C=0
Если кроме того, C=0, то уравнение x=0 (Oy)
Пусть в уравнении Ax + By + C = 0, C=0
Ax + By = 0 , By = -Ax
y
A
x
B
x y
1. (3)
6. Уравнение прямой в отрезках
a b
y
M2
b
Это уравнение прямой, пересекающей ось Ox в
M1
точке a, а ось Oy – в точке b.
O
a
x
x
y x y
M1(a; 0), x a y 0 x a y
;
; 1 ; 1.
M2(0; b). 0 a b 0 a
b
a
b a b

6.

Пример 1. Построим прямую 2x – 3y – 6 = 0.
y
Преобразуем к виду (3): 2x – 3y = 6. x y 1.
O
3 x
3
2
Тогда a = 3 и b = –2.
-2
Прямая пересекает ось Ox при x = 3, а ось Oy – при y = –2.
7. Уравнение прямой с угловым коэффициентом.
Прямая, пересекающая ось Oy, может быть задана точкой M0(0; b)
пересечения с осью Oy и углом φ наклона прямой к оси Ox.
Опр. 1. Угловым коэффициентом прямой на плоскости
называется число k = tg φ, где φ – угол наклона прямой к оси Ox.
N ( x; b). Из прямоугольного M0MN получим
y
M
MN
b φ
y
b
(4)
y
kx
b
.
k tg
.
φ M0 N
M0N
x
O
x
8. Уравнение прямой, проходящей через данную точку M0(x0; y0)
с заданным угловым коэффициентом k.
Координаты точки M0(x0; y0) должны удовлетворять уравнению,
т. е. y0 kx0 b.
y y0 k ( x x0 ). (5)
b y0 kx0 . y kx y0 kx0 .

7.

Рассмотрим теперь произвольную
прямую L.
Проведем из начала координат
перпендикулярно прямой L луч
с единичным вектором n
и пусть P - точка его пересечения
с прямой L.
Направляющие косинусы вектора n
cos cos ,
cos cos( / 2 ) sin n cos ,sin
Тогда для любой точки M, лежащей на прямой L, прn OM p
где p – длина отрезка OP (всегда неотрицательная величина!)
или
n OM
прn OM
OM n x cos y sin
|n|
откуда получаем нормированное уравнение прямой или
уравнение прямой в нормальном виде
x cos y sin p 0

8.

Взаимное расположение двух прямых на плоскости
1. Если прямые заданы своими каноническими уравнениями, то
известны их направляющие векторы. Тогда формула для нахождения
угла между прямыми и условия параллельности и перпендикулярности
прямых аналогичны случаю прямых в пространстве.
Упражнение 1. Записать формулу для нахождения угла между
прямыми и условия параллельности и перпендикулярности прямых в
случае, когда известны канонические уравнения прямых на плоскости.
2. Если прямые заданы своими общими уравнениями, то известны их
нормальные векторы. Тогда формула для нахождения угла между
прямыми и условия параллельности и перпендикулярности прямых
аналогичны случаю плоскостей в пространстве.
Упражнение 2. Записать формулу для нахождения угла между
прямыми и условия параллельности и перпендикулярности прямых в
случае, когда известны общие уравнения прямых на плоскости.

9.

Взаимное расположение двух прямых на плоскости
1. Если прямые заданы своими каноническими уравнениями, то
известны их направляющие векторы. Тогда формула для нахождения
угла между прямыми и условия параллельности и перпендикулярности
прямых аналогичны случаю прямых в пространстве.
Упражнение 1. Записать формулу для нахождения угла между
прямыми и условия параллельности и перпендикулярности прямых в
случае, когда известны канонические уравнения прямых на плоскости.
2. Пусть даны две прямые, определяемые уравнениями
A1 A2 B1 B2
A1x+B1y+C1=0 и A2x+B2y+C2=0
cos
A12 B12 A22 B22
A1 B1 - условие параллельности прямых
A2 B2
A1 B1 C1
A2 B2 C2
- условие совпадения прямых
A1 A2 B1 B2 0
- условие перпендикулярности прямых

10.

k1 = tg φ1,
k2= tg φ2.
3. l1: y = k1x + b1,
l2: y = k2x + b2.
φ =φ2 – φ1
угол между прямыми l1 и l2.
tg 2 tg 1
,
tg tg( 2 1 )
1 tg 1 tg 2
k2 k1
tg
.
1 k1k2
(6)
Замечание. По этой формуле определяется тангенс угла φ, на который
нужно повернуть прямую l1 в положительном направлении (т. е. против
часовой стрелки) до совпадения с прямой l2. Для нахождения острого угла
между прямыми следует взять правую часть формулы по модулю.
Условие параллельности двух прямых на плоскости.
l1 l2
k1 k2 .
Прямые параллельны тогда и только
тогда, когда их угловые коэффициенты
равны между собой.
Условие перпендикулярности двух прямых на плоскости.
l1 l2
k1k2 1.
Прямые перпендикулярны тогда и
только тогда, когда их угловые
коэффициенты обратные по величине
и противоположны по знаку.

11.

Расстояние от точки до прямой на плоскости
Утв. 1. Расстояние от точки M0(x0; y0) до прямой Ax + By + C = 0
вычисляется по формуле
d
Ax0 By0 C
A2 B 2
.
Упражнение 3. Доказать аналогично формуле для расстояния
от точки до плоскости.

12.

Пример 2. Даны координаты вершин треугольника: A(1; 3),
B(–1; 2), C(2; –2). Запишем уравнения сторон AB и BC, высоты
CH, медианы AM; найдем угол ABC.
H B
x x1
y y1
1) AB
.
x2 x1 y2 y1
A
x 1 y 3 x 1 y 3
;
; x 1 2 y 6; x 2 y 5 0.
1 1 2 3 2
1
2) BC
C
x 1 y 2
x 1 y 2
; 4 x 4 3 y 6; 4 x 3 y 2 0.
;
3
4
2 1 2 2
3) Высоту CH построим как прямую, проходящую через точку C
перпендикулярно прямой AB.
1
5
kCH k AB 1. AB : x 2 y 5 0 2 y x 5 y x .
2
2
1
k AB ; kCH 2. y y0 k ( x x0 ).
2 x y 2 0.
2
y 2 2( x 2);
y 2 2 x 4;

13.

Пример 2. Даны координаты вершин треугольника: A(1; 3),
B(–1; 2), C(2; –2). Запишем уравнения сторон AB и BC, высоты
CH, медианы AM; найдем угол ABC.
H B
4) AM
φ
M
yB yC 2 ( 2)
xB xC 1 2
0.
y
xM
0,5; M
2 A
2
2
2
x 1 y 3
x x1
y y1
x 1
y 3
.
; 3x 3 0,5 y 1,5;
;
x2 x1 y2 y1
0,5
3
0,5 1 0 3
3x 0,5 y 1,5 0; 6 x y 3 0.
5) Найдем угол φ = ABC
1
k k
tg 2 1 .
2
1 k1k2 ВС : 4 x 3 y 2 0 3 y 4 x 2 y 4 x 2 ,
3
3
4
k1 k BC .
3
1 4
11
11
tg 2 3 6 11 ,
ABC
arctg
.
2
1 4
2
2
1 1
3
2 3
k1 k BC ; k2 k AB . k2 k AB .
C

14.

§ 4. Кривые второго порядка на
плоскости, их канонические
уравнения
Опр. 1. Линией (кривой) 2-го порядка называется линия,
определяемая в декартовой прямоугольной системе координат
на плоскости алгебраическим уравнением 2-й степени, т. е.
уравнением вида
a11x2 + 2a12xy + a22y2 + 2a1x + 2a2y + a0 = 0,
в котором хотя бы один из коэффициентов a11, a12, a22 не равен
0.
К линиям 2-го порядка относятся окружность, эллипс,
гипербола, парабола.
Рассмотрим их канонические уравнения, т. е. их простейшие
уравнения, которые получаются при определенном выборе
системы координат.

15.

Окружность
Опр. 2. Окружностью называется множество точек плоскости,
расстояние от каждой из которых до данной точки (центра
окружности) постоянно и равно R (число R называется радиусом
окружности).
Выведем уравнение окружности с центром в точке M0(x0; y0) и
радиусом R.
Пусть M(x; y) – произвольная точка этой окружности.
Расстояние от точки M до точки M0 должно быть равно R,
поэтому
( x x0 ) 2 ( y y0 ) 2 R;
( x x0 ) ( y y0 ) R .
2
2
2
Если x0 = 0; y0 = 0, то уравнение
окружности примет наиболее простой
вид: x 2 y 2 R 2 .

16.

Эллипс
Опр. 3. Эллипсом называется множество всех точек плоскости, сумма
расстояний от каждой из которых до двух данных точек, называемых
фокусами, есть величина постоянная и большая, чем расстояние между
фокусами.
y
Вывод канонического уравнения эллипса.
M(x;y)
Расстояние между фокусами F1F2 обозначим через 2c,
сумму расстояний от точек эллипса до фокусов – через 2a.
Пусть точка M(x; y) – произвольная точка эллипса.
F (-c;0) O F (c;0) x
( x c) y ( x c) y 2a;
F1M F2 M 2a.
2
2
2
2
( x c)2 y 2 2a ( x c)2 y 2 ;
( x c)2 y 2 4a 2 ( x c)2 y 2 4a ( x c)2 y 2 ;
x2 2cx c2 4a 2 x2 2cx c 2 4a ( x c)2 y 2 ;
4a ( x c)2 y 2 4a 2 4cx;
a ( x c) y a cx;
a 2 ( x 2 2cx c 2 y 2 ) a 4 2a 2cx c 2 x 2 ;
a 2 x 2 2a 2cx a 2c 2 a 2 y 2 a 4 2a 2cx c 2 x 2 ;
a 2 x 2 c 2 x 2 a 2 y 2 a 4 a 2c 2 ;
(a 2 c 2 ) x 2 a 2 y 2 a 2 (a 2 c 2 ).
Поскольку a > c, то a2 > c2; обозначим b2 a 2 c 2 .
2
2
2
1
2
b 2 x 2 a 2 y 2 a 2b 2 ,
x2 y 2
2 1. (1)
2
a
b
Это уравнение называется
каноническим уравнением
эллипса; величины a и b
называются
полуосями,
причем a – большая, b –
малая полуось эллипса.

17.

Исследование формы эллипса по его уравнению.
1. Уравнение (1) содержит переменные x и y только в четных степенях,
поэтому оси координат являются осями симметрии эллипса (осями эллипса), а
начало координат O(0; 0) – центром симметрии (центром) эллипса.
2. Точки пересечения эллипса с его осями симметрии называются его
вершинами. В данном случае это точки (a; 0), (–a; 0), (0; b), (0; –b).
3. Из уравнения (1) следует, что каждое слагаемое в левой части не
x2
y2
превосходит 1: 2 1; 2 1, поэтому | x | a; | y | b.
a
b
Следовательно, эллипс лежит внутри прямоугольника, ограниченного прямыми
Для эллипса эксцентриситет определяется
как отношение половины расстояния между
фокусами к большой полуоси эллипса:
x a; y b.
y
b
M(x; y)
c
.
a
Поскольку a > c, то 0 ≤ ε < 1.
В предельном случае при ε = 0 эллипс
превращается в окружность.
-a F1(-c; 0)
-b
F2(c; 0) a x

18.

Гипербола
Опр. 4. Гиперболой называется множество всех точек плоскости, модуль
разности расстояний от каждой из которых до двух данных точек, называемых
фокусами, есть величина постоянная и меньшая, чем расстояние между
фокусами.
y
Вывод канонического уравнения гиперболы.
M(x;y)
Расстояние между фокусами F1F2 обозначим через 2c, модуль
разности расстояний от точки гиперболы до фокусов – через 2a.
Пусть точка M(x; y) – произвольная точка эллипса.
F (-c;0) O F (c;0) x
F1M F2 M 2a.
( x c) y ( x c) y 2a;
2
2
2
2
( x c) 2 y 2 ( x c) 2 y 2 2a;
( x c ) 2 y 2 4a 2 ( x c ) 2 y 2 4a ( x c ) 2 y 2 ;
x 2 2cx c 2 4a 2 x 2 2cx c 2 4a ( x c) 2 y 2 ;
4a ( x c) 2 y 2 4cx 4a 2 ;
1
2
b 2 x 2 a 2 y 2 a 2b 2 ,
x2 y 2
2 1. (2)
2
a
b
Это уравнение называется
a ( x c) y cx a ;
каноническим
уравнением
гиперболы; величины a и b
a 2 ( x 2 2cx c 2 y 2 ) c 2 x 2 2a 2cx a 4 ;
полуосями,
a 2 x 2 2a 2cx a 2c 2 a 2 y 2 c 2 x 2 2a 2cx a 4 ; называются
причем a – действительная, b
a 2 x 2 c 2 x 2 a 2 y 2 a 4 a 2c 2 ;
– мнимая полуось гиперболы.
2
2
2
2 2
2
2
2
2
2
2
(a c ) x a y a (a c ).
Поскольку a < c, то a2 < c2; обозначим b 2 c 2 a 2 .

19.

Исследование формы гиперболы по ее уравнению.
1. Уравнение (2) содержит переменные x и y только в четных степенях,
поэтому оси координат являются осями симметрии гиперболы (осями
гиперболы), а начало координат O(0; 0) – центром симметрии (центром)
гиперболы.
2. Точки пересечения гиперболы с ее осями симметрии называются
вершинами гиперболы. В данном случае это точки (a; 0), (–a; 0).
Отметим, что гипербола (2) пересекает ось Ox (действительную ось
гиперболы) и не пересекает ось Oy (мнимую
ось гиперболы).
2
3. Из уравнения (2) следует, что x 1, поэтому | x | a, т. е. точки гиперболы
a2
расположены либо правее прямой x = a, либо левее прямой x = –a.
Прямоугольник, заключенный между прямыми x a; y b
y
называется основным прямоугольником гиперболы.
b
b
b
4. Прямые y x и y x, проходящие через
a
a
противоположные
вершины
основного F (-c; 0) -a
прямоугольника
гиперболы,
являются 1
-b
асимптотами гиперболы.
M(x; y)
a
F2(c; 0) x

20.

Эксцентриситет гиперболы определяется как отношение половины
расстояния между фокусами к действительной полуоси гиперболы:
c
.
a
Поскольку a < c, то ε >1.
y 2 x2
Замечание. Для гиперболы 2 2 1
b
a
действительной осью является ось Oy, так как эта
гипербола пересекает ось Oy и не пересекает ось
Ox. Поэтому точки (0; b); (0; –b) – вершины
гиперболы, b – действительная, a – мнимая
полуоси; фокусы гиперболы F1(0; –c); F2(0;c)
лежат на ее действительной оси.
y
F2(0; c)
b
-a
O
a
-b
F1(0; -c)
x

21.

Парабола
Опр. 7. Парабола – множество всех точек плоскости, равноудаленных от
данной точки, называемой фокусом, и данной прямой, называемой
директрисой.
Обозначим фокус параболы через F, расстояние между фокусом и
директрисой через p.
p
F ; 0 ;
2
p
x .
2
Пусть M(x; y) – произвольная точка этой параболы.
2
p
p
2
x
y
x
.
2
2
2
y
p
x .
2
2
p
p
x px
y 2 x 2 px .
4
4
2
M(x; y)
Получим каноническое уравнение параболы
y 2 2 px,
(3)
где p – расстояние от фокуса до директрисы
параболы – называется параметром параболы.
O
p
F ; 0 ;
2
x

22.

Исследование формы параболы по ее уравнению.
1. В уравнение (3) переменная y входит в четной степени,
поэтому ось Ox является осью симметрии параболы (осью
параболы).
2. Точка пересечения параболы с ее осью симметрии
называются вершиной параболы. В данном случае это O(0; 0).
3. Из (3) следует, что x ≥ 0, т. е. парабола расположена правее
оси Oy.
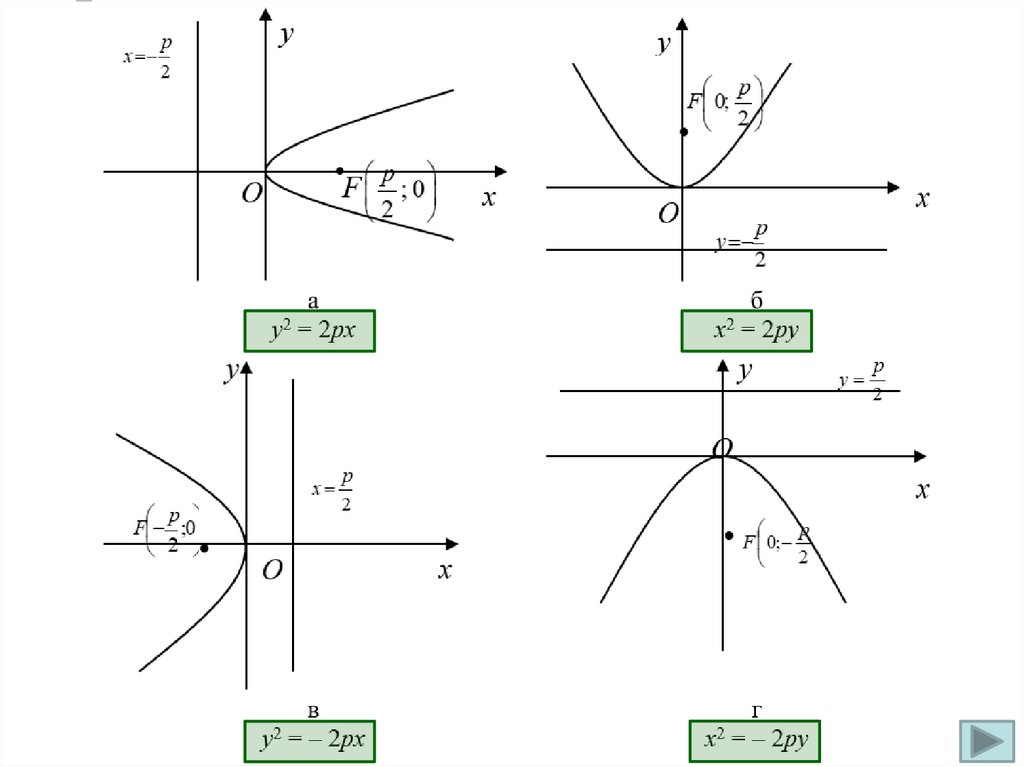
Замечание 1. Каноническое уравнение параболы может быть
записано в одной из четырех форм.

23.

24.

Исследование формы параболы по ее уравнению.
1. В уравнение (3) переменная y входит в четной степени,
поэтому ось Ox является осью симметрии параболы (осью
параболы).
2. Точка пересечения параболы с ее осью симметрии
называются вершиной параболы. В данном случае это O(0; 0).
3. Из (3) следует, что x ≥ 0, т. е. парабола расположена правее
оси Oy.
Замечание 1. Каноническое уравнение параболы может быть
записано в одной из четырех форм.
Замечание 2. Параметр p > 0 отвечает за форму параболы, чем
больше p, тем шире область, ограниченная параболой.

25.

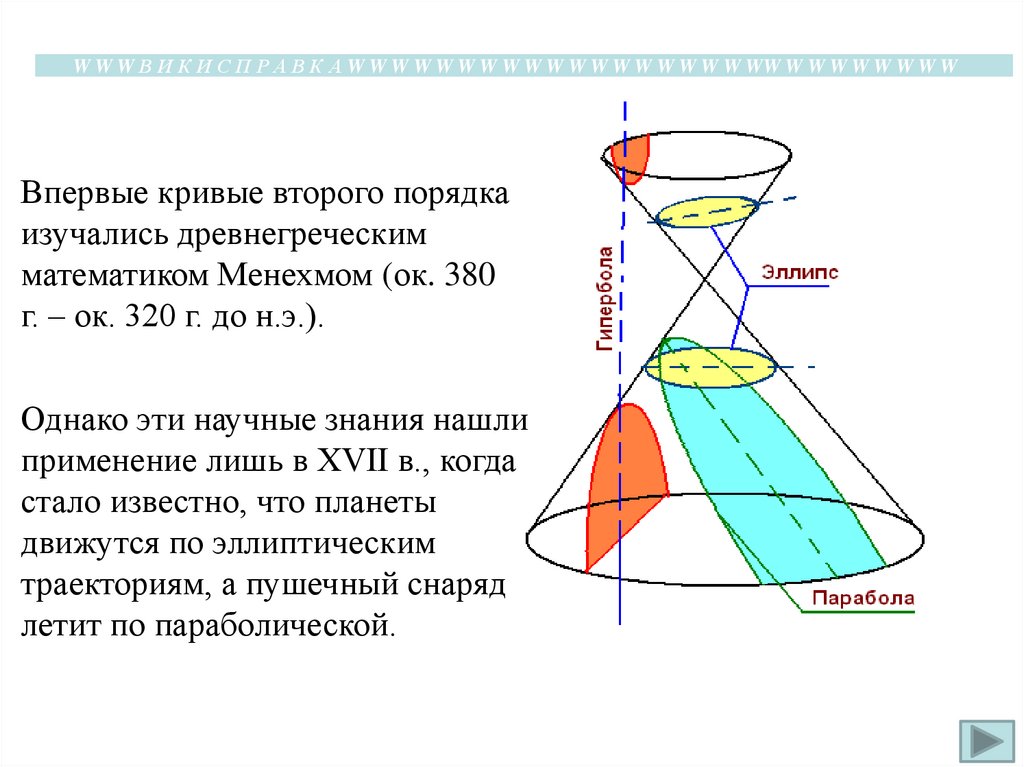
W W W В И К И С П Р А В К А W W W W W W W W W W W W W W W W W W WW W W W W W W W W
Впервые кривые второго порядка
изучались древнегреческим
математиком Менехмом (ок. 380
г. – ок. 320 г. до н.э.).
Однако эти научные знания нашли
применение лишь в XVII в., когда
стало известно, что планеты
движутся по эллиптическим
траекториям, а пушечный снаряд
летит по параболической.

26.

Кривые второго порядка с осями симметрии, параллельными
координатным осям
Пусть даны две системы Oxy и O1XY декартовых координат на плоскости с
разными началами O и O1 и одинаковым направлением осей.
Пусть O1(x0; y0) в системе координат на Oxy.
Пусть M – произвольная точка на плоскости. Обозначим через M(x; y) ее
координаты в системе координат Oxy; через M(X; Y) – в системе координат
O1XY. Тогда X x x0 ,
Y y y0 .
Пусть имеется эллипс с центром O1(x0; y0) и осями
симметрии, параллельными координатным осям Ox и Oy,
y Y
y
y0
O
X2 Y2
( x x0 )2 ( y y0 )2
1.
2 1,
2
2
2
a
b
a
b
M
Y
O1
X
Аналогично для гиперболы с центром O1(x0; y0) и
осями симметрии, параллельными координатным
X осям Ox и Oy (если действительная ось параллельна
Ox), имеем:
x0
x
x
2
2
(
x
x
)
(
y
y
)
X
Y
0
0
1;
1
2
2
2
2
a
b
a
b
2
2

27.

Для параболы с вершиной O1(x0; y0) получим
Y 2 2 pX
( y y0 ) 2 2 p ( x x0 ),
если ось симметрии параллельна Ox;
X 2 2 pY
2
( x x0 ) 2 p ( y y0 ),
если ось симметрии параллельна Oy.
Заметим, что после преобразований все эти уравнения могут быть
записаны в виде
a11x2 + a22y2 + 2a1x + 2a2y + a0 = 0,
(4)
в котором хотя бы один из коэффициентов a11, a22 не равен 0.
Чтобы получить каноническое уравнение, нужно выделить полный квадрат
по каждой переменной.
Уравнение (4) приводится к каноническому виду с помощью замены
переменных X x x0 ,
Y y y0 ,
которая сводится к параллельному переносу системы координат.

28.

Пример 1. Построим линию 9x2 + 4y2 – 18x + 24y + 9 = 0.
9(x2 – 2x) + 4(y2 + 6y) + 9 = 0;
y
9(x2 – 2x + 1) – 9 + 4(y2 + 6y + 9) – 36 + 9 = 0;
O 1F
9(x – 1)2 + 4(y + 3)2 = 36;
( x 1)2 ( y 3)2
1.
4
9
a = 2 – малая полуось, а b = 3 – большая.
1
x
O1
F2
Найдем дополнительно координаты фокусов эллипса. Эти точки будут
расположены симметрично относительно центра O1(1; –3) эллипса на
расстоянии c от него, поэтому F1(1; –3 + c); F2(1; –3 – c). Величину c найдем
из условия c2 = 32 – 22 = 5, поэтому c 5, F1 (1; 3 5); F2 (1; 3 5).
Пример 2. Построим линию x2 + 3y2 – 4x + 20 = 0.
(x2 – 4x + 4) – 4 + 3y2 + 20 = 0.
(x– 2)2 + 3y2 = –16.
Очевидно, что этому уравнению никакая линия не соответствует.

29.

Пример 3. Построим линию x2 – 4y2 + 16y = 0.
y
F1
4
O1 2
x2 – 4(y2 – 4y) = 0;
x2 – 4(y2 – 4y + 4) + 16= 0;
x2 – 4(y – 2)2 = –16;
x 2 ( y 2)2
1.
16
4
-4
4
O
x
F2
Получили уравнение гиперболы с центром в точке O1(0; 2) и полуосями
a = 4; b = 2, причем a – мнимая; b – действительная полуоси.
Отметим, что фокусы гиперболы лежат на ее действительной оси
симметрично относительно центра O1(0; 2) гиперболы на расстоянии c от
него, поэтому F1(0; 2 + c); F2(0; 2 – c). Величину c найдем из условия
c2 = 42 + 22 = 20, поэтому c 2 5, F1 (0; 2 2 5); F2 (0; 2 2 5).

30.

y
Пример 4. Построим линию y2 – 4x – 4y –8 = 0.
(y2 – 4y + 4) – 4 – 4x – 8 = 0;
2
(y – 2)2 = 4x + 12;
(y – 2)2 = 4(x + 3).
O1
-3
O
x
Получили уравнение параболы с вершиной O1(–3; 2) и осью симметрии y = 2.
Поскольку левая часть уравнения неотрицательна, то x ≥ –3, а значит, ветви
параболы направлены вправо.
На оси Ox переменная y = 0, поэтому из исходного уравнения получим
–4x – 8 = 0; x = –2.
На оси Oy переменная x = 0, из последнего уравнения получаем (y – 2)2 = 12;
y 2 2 3.

31.

Пример 5. Построим линию x2 – y2 – 2x + 1 = 0.
x 1 y 0,
(x – 1) 2 – y2 = 0.
x 1 y 0.
(x – 1– y) (x – 1 + y) = 0.
y
1
O
1
x
Таким образом, исходное уравнение задает на
плоскости две пересекающиеся прямые x – y = 1 и
x + y = 1.
Тh 1. Всякое алгебраическое уравнение 2-го порядка
a11x2 + 2a12xy + a22y2 + 2a1x + 2a2y + a0 = 0,
(в котором хотя бы один из коэффициентов a11, a12, a22 не равен 0) задает одну
из следующих линий на плоскости: эллипс (возможно, вырожденный эллипс
вида x2 + y2 = 0 (точка) или мнимый эллипс вида x2 + y2 = –1), гиперболу,
параболу или пару прямых (пересекающихся, параллельных или
совпадающих).
Преобразование уравнения к каноническому виду осуществляется с
помощью замены переменных вида
X 11 x 12 y c1 ,
Y 21 x 22 y c2 ,
которая сводится к повороту и параллельному переносу системы координат.