Элементы векторной алгебры. Тема 3

1. Тема 3: «Элементы векторной алгебры»

© Компьютерное оформление: Головко Р.С.
студент СтГАУ факультет ФБД
Тема 3: «Элементы
векторной алгебры»
§1. Векторы на плоскости и в пространстве
§2. Скалярное произведение векторов
Линии на плоскости
§1. Уравнение прямой на плоскости
§2. Угол между прямыми
§3. Точка пересечения двух прямых
§4. Расстояние от точки до прямой
Кривые 2-го порядка
§1. Эллипс
§2. Простейшие задачи аналитической геометрии
§3. Гипербола
§4. Парабола
§5. Приведение общего уравнения кривой 2-го
© Компьютерное оформление: Головко Р.С.
студент СтГАУ факультет ФБД
порядка к каноническому виду(частные случаи)

2. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости
в пространстве
(обобщающие сведения
о векторах из школьного курса)
и
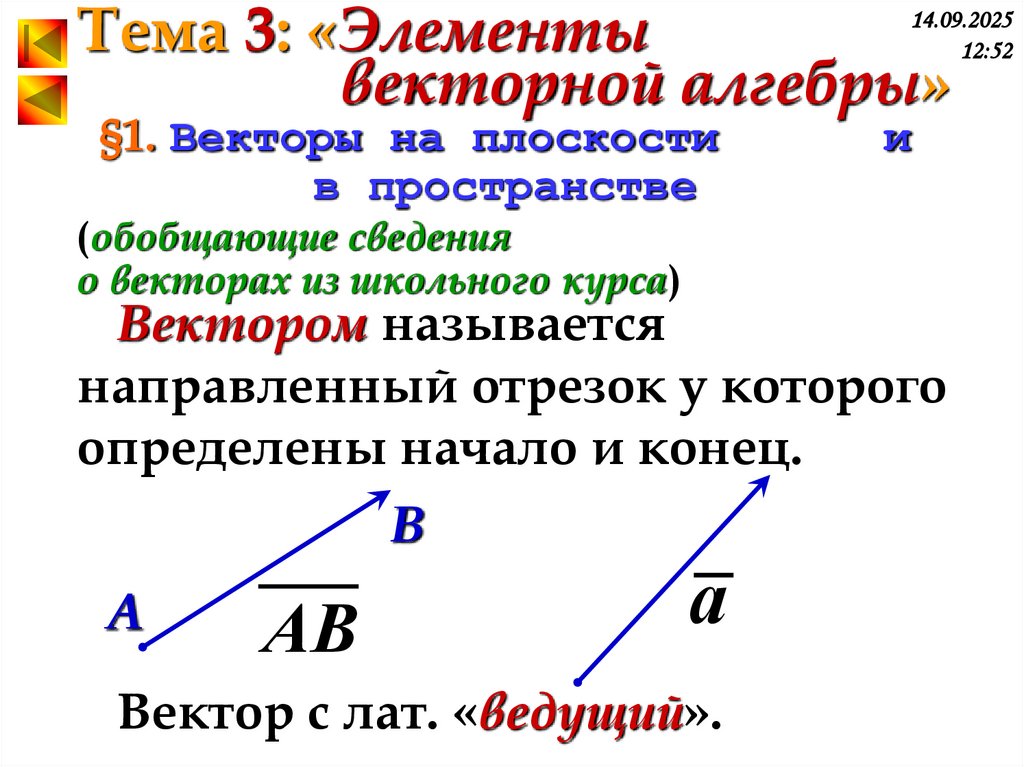
Вектором называется
направленный отрезок у которого
определены начало и конец.
В
А
АВ
а
Вектор с лат. «ведущий».

3. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
Длиной или модулем вектора
называется длина порождающего
его отрезка.
В математике рассматриваются
свободные векторы, которые в
пространстве можно перемещать
параллельно самим себе.

4. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
Определение. Векторы
лежащие на параллельных
прямых или на одной прямой
называются коллинеарными.
а
в

5. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
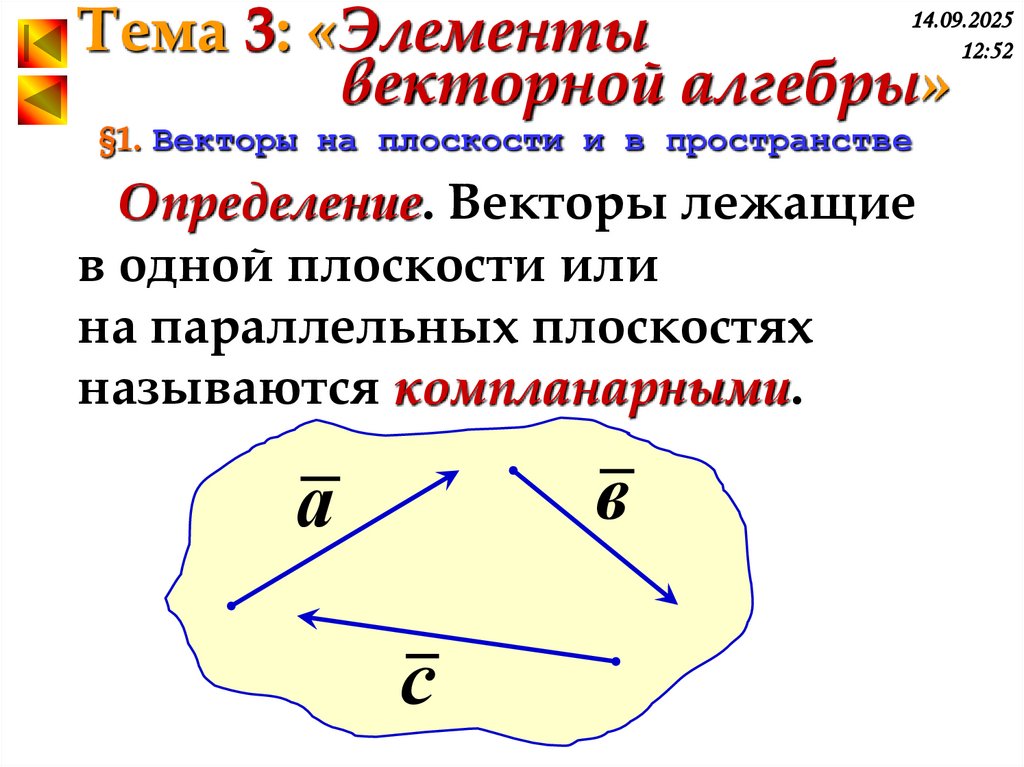
Определение. Векторы лежащие
в одной плоскости или
на параллельных плоскостях
называются компланарными.
в
а
с

6. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
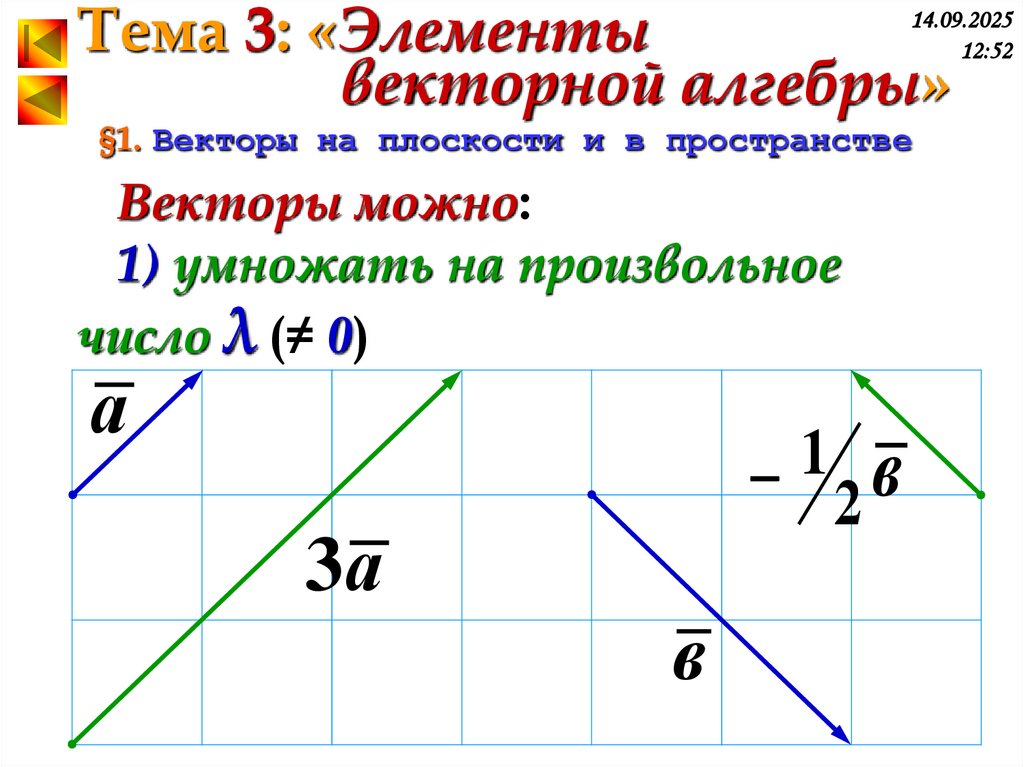
Векторы можно:
1) умножать на произвольное
число λ (≠ 0)
а
1
2в
3а
в

7. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
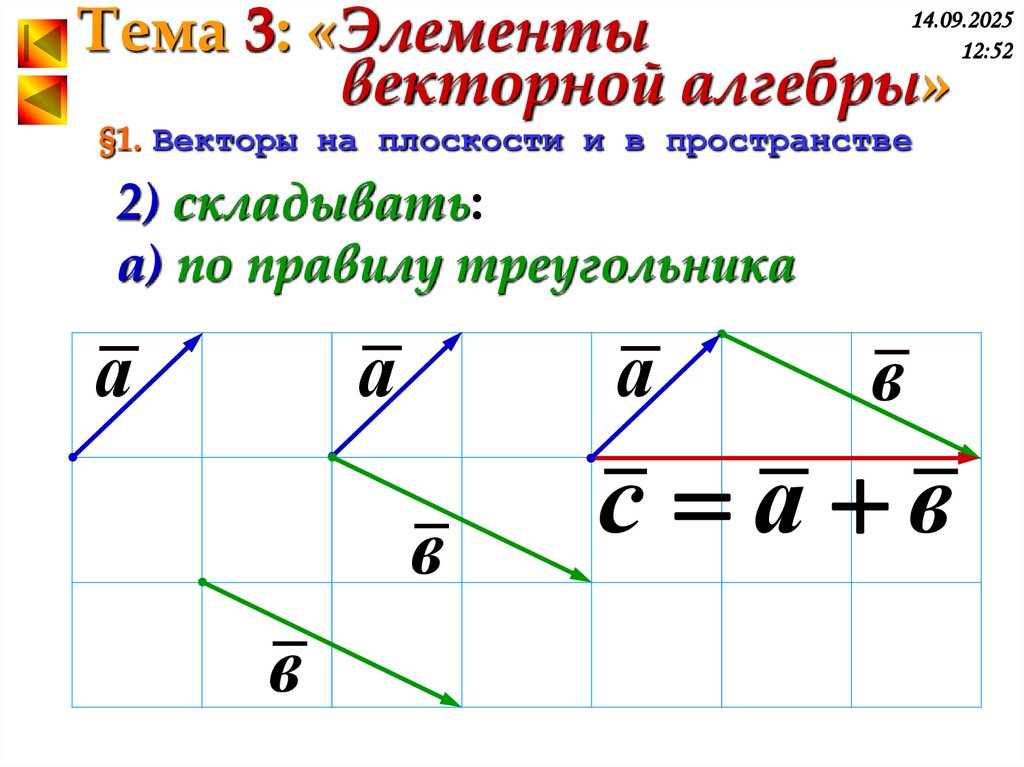
2) складывать:
а) по правилу треугольника
а
а
а
в
в
в
с а в

8. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
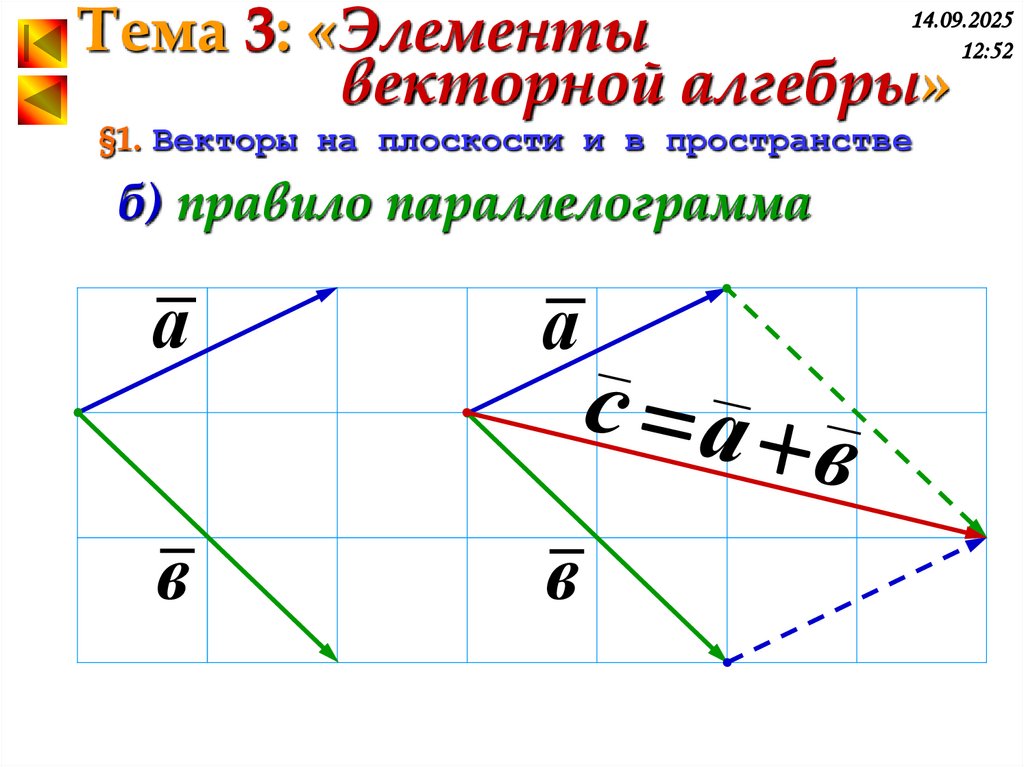
б) правило параллелограмма
а
в
а
в
с а
в

9. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
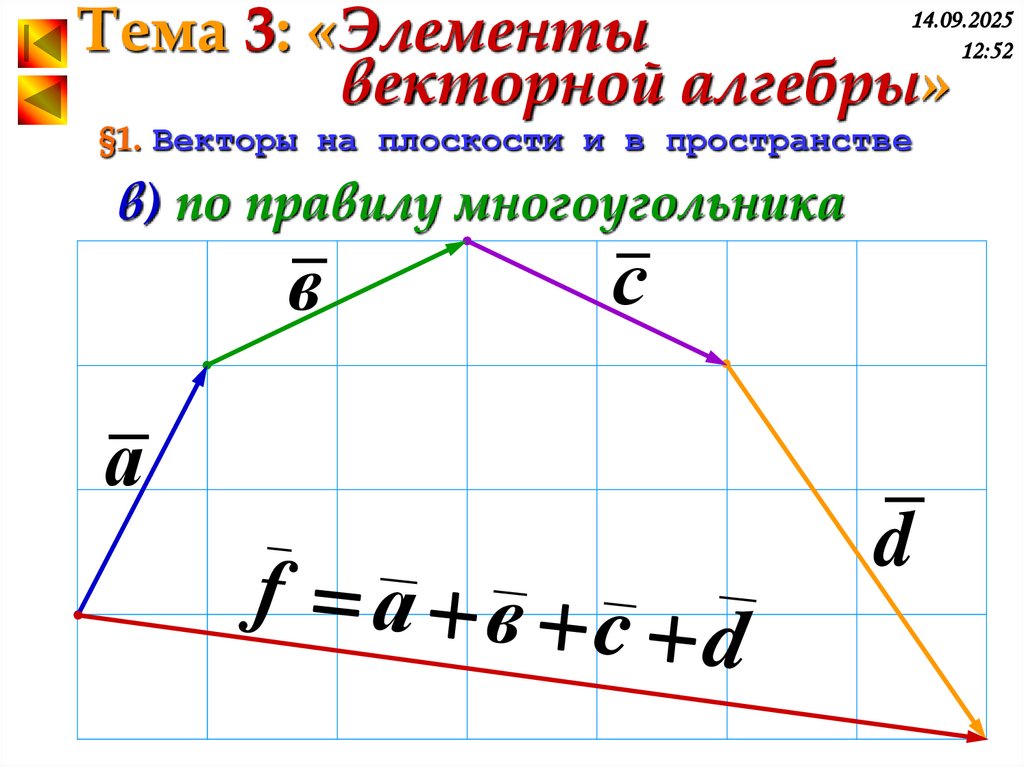
в) по правилу многоугольника
в
с
а
f а в c
d
d

10. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
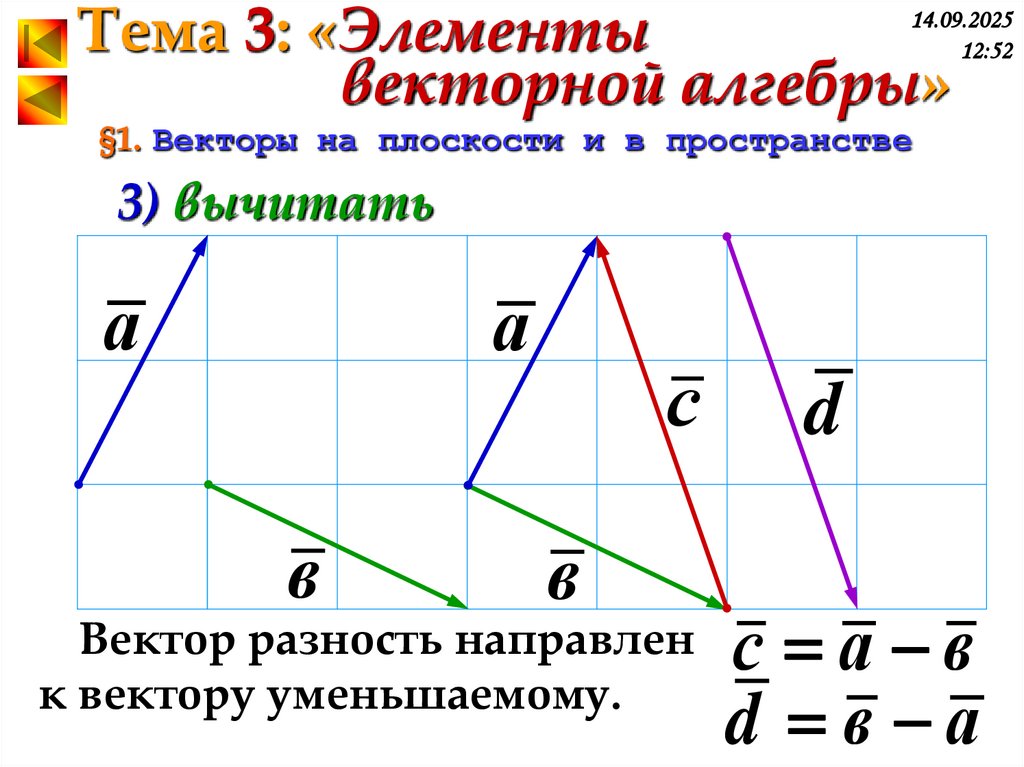
3) вычитать
а
а
в
с
в
Вектор разность направлен
к вектору уменьшаемому.
d
с а в
d в а

11. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
Замечания:
1) вектор ā * (-1) называется ему
противоположным.
а
а
2) Если при сложении векторов
конец последнего совпадает с
началом первого, то сумма этих
векторов равна 0 (и называется
нульвектором ( 0 )).

12. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
a
Y
y0 3
a
i
0
j
Перенесём ā
параллельно самому
себе так, чтобы его
начало совпало с
началом координат:
a 5i 3 j
5
x0
X

13. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
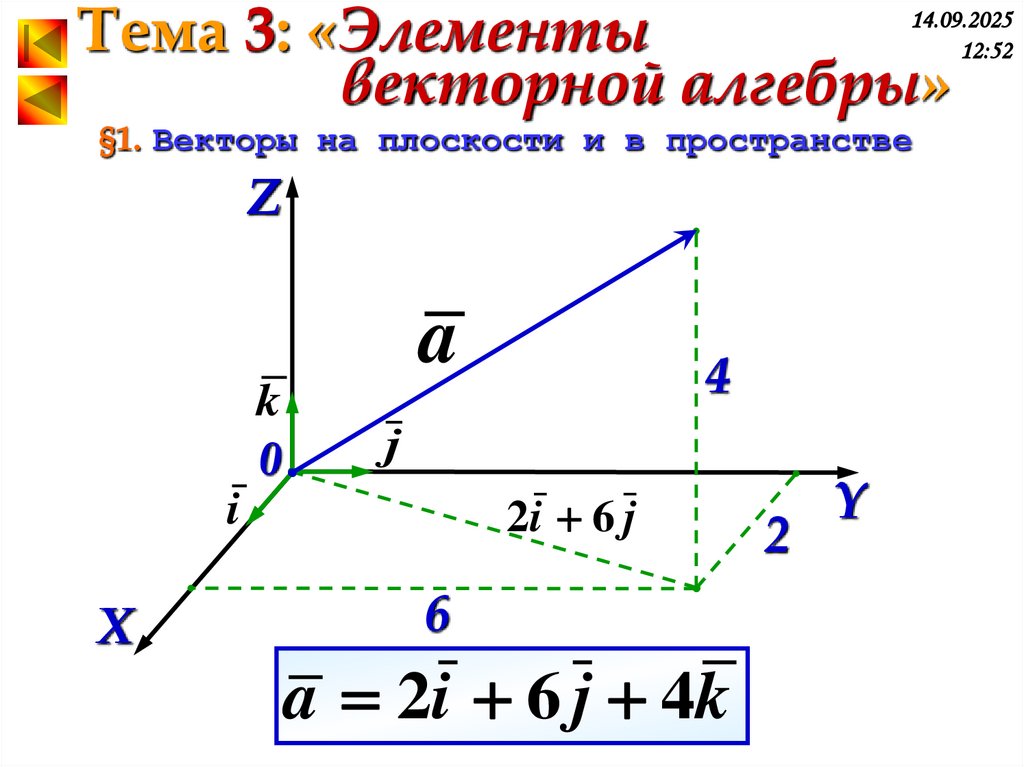
Z
a
k
0
j
2i 6 j
i
X
4
6
a 2i 6 j 4k
2
Y

14. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
Определение. Координатами
вектора ā называются координаты
его конечной точки, т.е. если M(x, y)
– конечная точка ā, то ā(x, y) (,z).
Если A(x1, y1, z1), а B(x2, y2, z2), то
AB = (x2 – x1; y2 – y1; z2 – z1).
Чтобы найти координаты вектора
с заданными координатами начала
и конца нужно из координат конца
вычесть координаты начала.

15. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
Если ā(x1, y1, z1) и в(x2, y2, z2):
1) λā = (λx1, λy1, λz1).
2) ā ± в = (x1 ± x2; y1 ± y2; z1 ± z2).
Из рисунка видно: по т. Пифагора
Y
А
OA2 = OB2 + AB2
|a|2 = x2 + y2
a
0
|a| x y
2
2
В X |c| x y z
2
2
2

16. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
Модуль вектора равен корню
квадратному из суммы квадратов
его координат.
В векторной алгебре принято на
всех осях координат наносить
единичные векторы (i, j, k) – орты.
Таким образом (i, j) – являются
базисом пространства Е2; (i, j, k) –
базисом пространства Е3.

17. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
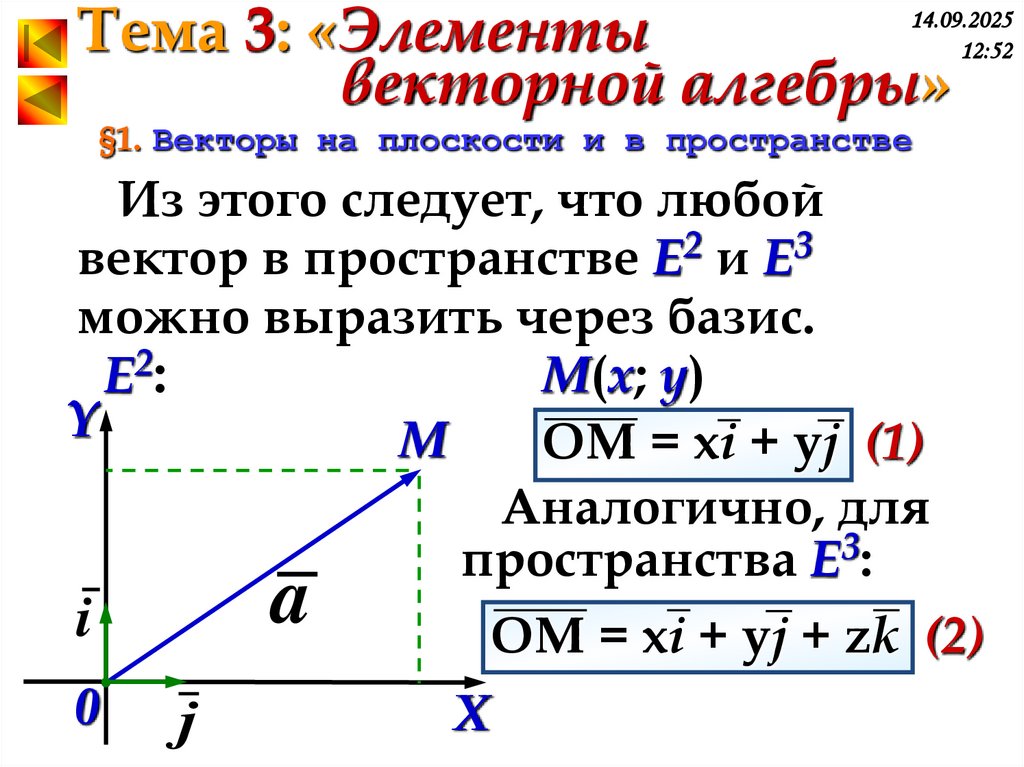
Из этого следует, что любой
вектор в пространстве Е2 и Е3
можно выразить через базис.
М(x; y)
Е2:
Y
М
OМ = xi + yj (1)
Аналогично, для
пространства Е3:
a
i
OМ = xi + yj + zk (2)
0
X
j

18. §1. Векторы на плоскости и в пространстве

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Векторы на плоскости и в пространстве
Вектор который начинается в
начале координат называется
радиус-вектор.
Векторы xi, yj, zk называются
компонентами ветора ОМ.
Выражение (1) и (2) называется
разложением вектора по базису.

19. §2. Скалярное произведение векторов

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Скалярное произведение векторов
Скалярным
произведением двух
a
у
ненулевых векторов
называется
в
произведение их
модулей на косинус
угла между векторами.
a * в = |a|*|в|* cosy
cosy = cos(a; в)

20. §2. Скалярное произведение векторов

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Скалярное произведение векторов
Свойства скалярного произведения:
1о) Скалярный квадрат вектора
равен квадрату его модуля:
ā2 = ā * ā = |ā|*|ā|* cos0o = |ā|2
Из этой формулы можно
определить длину вектора.
2о) Если векторы
перпендикулярны
(ā ┴ в): |ā|*|в|* cos90o = 0

21. §2. Скалярное произведение векторов

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Скалярное произведение векторов
Покажем скалярные квадраты
единичных векторов:
i2 = |i|*|i|* cos0o = |i|2 = 1
i * j = |i|*|j|* cos90o = 0
i
j
k
i
1
0
0
j
0
1
0
k
0
0
1

22. §2. Скалярное произведение векторов

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Скалярное произведение векторов
3o) Если векторы заданы
координатами
ā(x1, y1, z1); в(x2, y2, z2)
ā * в = x1 * x2 + y1 * y2 + z1 * z2
Т.е. скалярное произведение
двух векторов равно сумме
произведений одноимённых
координат.

23. §2. Скалярное произведение векторов

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Скалярное произведение векторов
Доказательство: ā = x1i + y1j + z1k
в = x2i + y2j + z2k
ā * в = (x1i + y1j + z1k) * (x2i + y2j + z2k)=
= x1 * x2 * i * i + y1 * y2 * j * j +
+ z1 * z2 * k * k + x1 * y2 * i * j +
+ x1 * z2 * i * k + y1 * x2 * j * i +
+ y1 * z2 * j * k + z1 * x2 * k * i +
+ z1 * y2 * k * j =
= x1 * x2 + y1 * y2 + z1 * z2

24. §2. Скалярное произведение векторов

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Скалярное произведение векторов
4o) Из скалярного произведения
векторов следует:
a *в
cos
a *в
или если вектора заданы в
координатной форме, то:
cos
x1 x2 y1 y2 z1 z 2
x y z * x y z
2
1
2
1
2
1
2
2
2
2
2
2

25. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
Линии на плоскости
§1. Уравнение прямой на плоскости
Самая простая линия на
плоскости прямая, ей
соответствует самое простое
уравнение – линейное или 1-й
степени, т.к. прямую можно задать
различными способами, то у
прямой может быть несколько
различных уравнений:

26. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
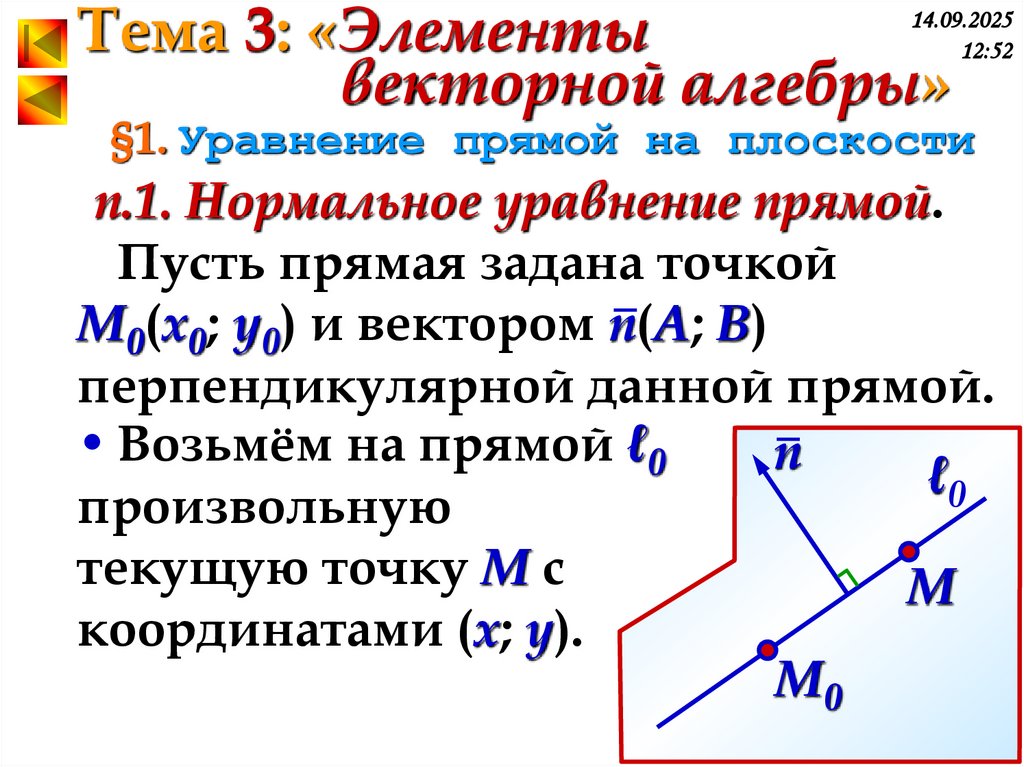
п.1. Нормальное уравнение прямой.
Пусть прямая задана точкой
M0(x0; y0) и вектором n(A; B)
перпендикулярной данной прямой.
• Возьмём на прямой ℓ0
n
ℓ0
произвольную
текущую точку M c
M
координатами (x; y).
M0

27. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
•Получим вектор M0 M (x – x0 ; y – y0)
•Т.к. ℓ0 ┴ n и M0 M ℓ0 M0 M ┴ n
M0 M * n = 0 – это векторное
уравнение прямой.
В координатной форме: n
ℓ0
A * (x – x0) + B * (y – y0) = 0
– это нормальное
M
уравнение прямой
M0

28. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
п.2. Общее уравнение прямой.
• Раскроим скобки в нормальном
уравнении прямой:
Ax – Ax0 + By – By0 = 0
• Заменим –Ax0 и –By0 через C,
где С – константа

29. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
• Тогда уравнение примет вид:
Ax + By + C = 0 – это общее
уравнение прямой, где A, B, C
принадлежат множеству
действительных чисел и
являются константами;
А и B одновременно не должны
равняться 0.

30. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
Частные случаи:
1) A = 0, B ≠ 0, C ≠ 0, тогда By + C = 0,
C
y – уравнение прямой
B параллельной оси OX.
2) A ≠ 0, B = 0, C ≠ 0, тогда Ax + C = 0,
C
x – уравнение прямой
B параллельной оси OY.

31. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
3) A ≠ 0, B ≠ 0, C = 0; Ax + By = 0,
– уравнение прямой
A
y x проходящей через
B
начало координат.
4) A = 0, B ≠ 0, C = 0; By = 0; y 0
– ур-ние прямой совпадающей с осью OX.
5) A ≠ 0, B = 0, C = 0; Ax = 0; x 0
– ур-ние прямой совпадающей с осью OY.

32. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
п.3. Каноническое и
параметрическое уравнения прямой.
Пусть прямая задана
М0(x0, y0), которая
принадлежит прямой ℓ0
и вектором q(m; n),
параллельным этой прямой.

33. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
• Возьмём на прямой ℓ0 текущую
точку M(x; y), получим вектор
М0 М (x – x0; y – y0), т.к. вектор
М0 М ℓ0 М0 М║q.
• По условию параллельных
векторов, векторы параллельны,
когда их координаты
пропорциональны.

34. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
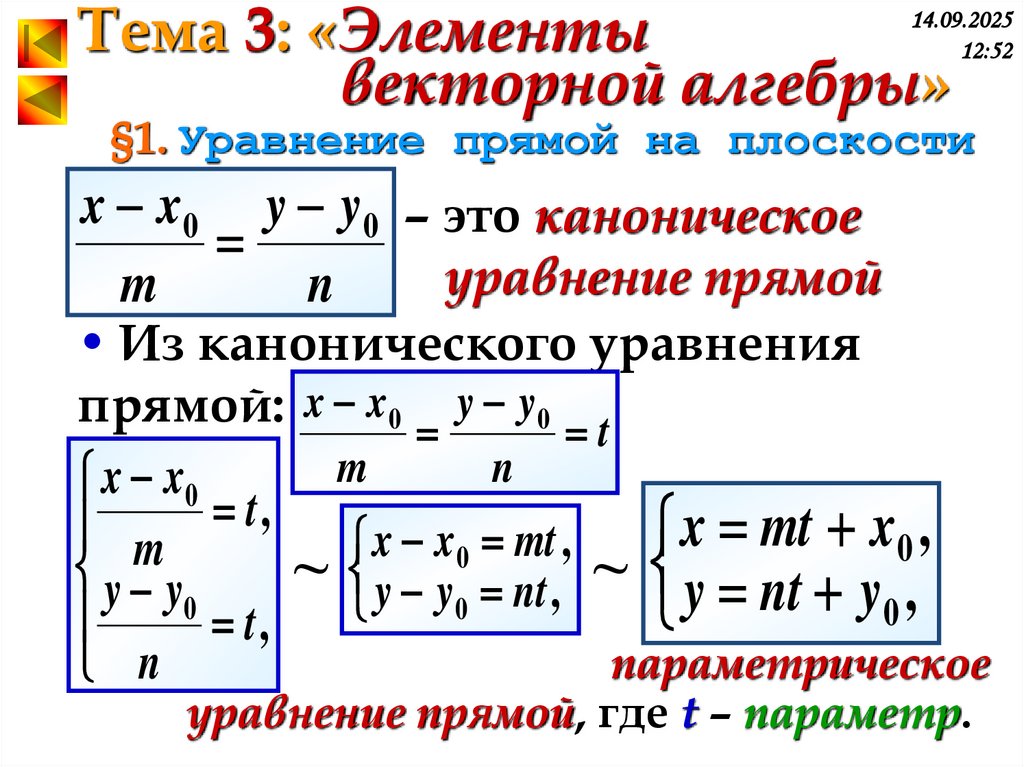
x x0 y y0 – это каноническое
уравнение прямой
m
n
• Из канонического уравнения
прямой: x x0 y y0 t
m
n
x x0
t
,
m
x mt x0 ,
x x0 mt ,
y y
y y nt , ~ y nt y ,
~
0
0
0
t,
параметрическое
n
уравнение прямой, где t – параметр.

35. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
п.4. Уравнение прямой с угловым
коэффициентом.
Пусть в общем уравнении прямой
B ≠ 0; выразив из него y.
Ax + By + C = 0,
A
C
y x
By = –Ax – C,
B
B
• Введём обозначения:
A
k
;
B
С
в
.
B

36. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
• Тогда получим:
y kx в – это
уравнение прямой
с угловым коэффициентом.

37. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
Определение. Угловым
коэффициентом называется
тангенс угла наклона этой прямой
к положительному направлению
оси OX.
Y
ℓ
k = tg
0
X

38. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
Коэффициент в равен ординате
точки пересечения прямой
с осью OY.
Если - острый угол, то
коэффициент k > 0.
Если - тупой угол, то
коэффициент k < 0.
Если = 90o, то не существует
уравнения с угловым
коэффициентом для такой прямой.

39. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
Частные случаи:
1) k = 0, в ≠ 0; y в – уравнение
прямой параллельной оси OX.
2) k ≠ 0, в = 0; y kx – уравнение
прямой проходящей через начало
координат.
3) k = 0, в = 0; y 0 – уравнение
оси OX.

40. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
п.5. Уравнение пучка прямых.
Пусть дана точка M0(x0; y0) и
прямая проходящая через эту
точку, тогда координаты точки M0
удовлетворяют уравнению
y = kx + в (1), т.е. y0 = kx0 + в (2)
• Вычтем из 1 уравнения 2-е:
y – y0 k * (x – x0 ) – уравнение пучка
прямых проходящих через точку M0(x0; y0)

41. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
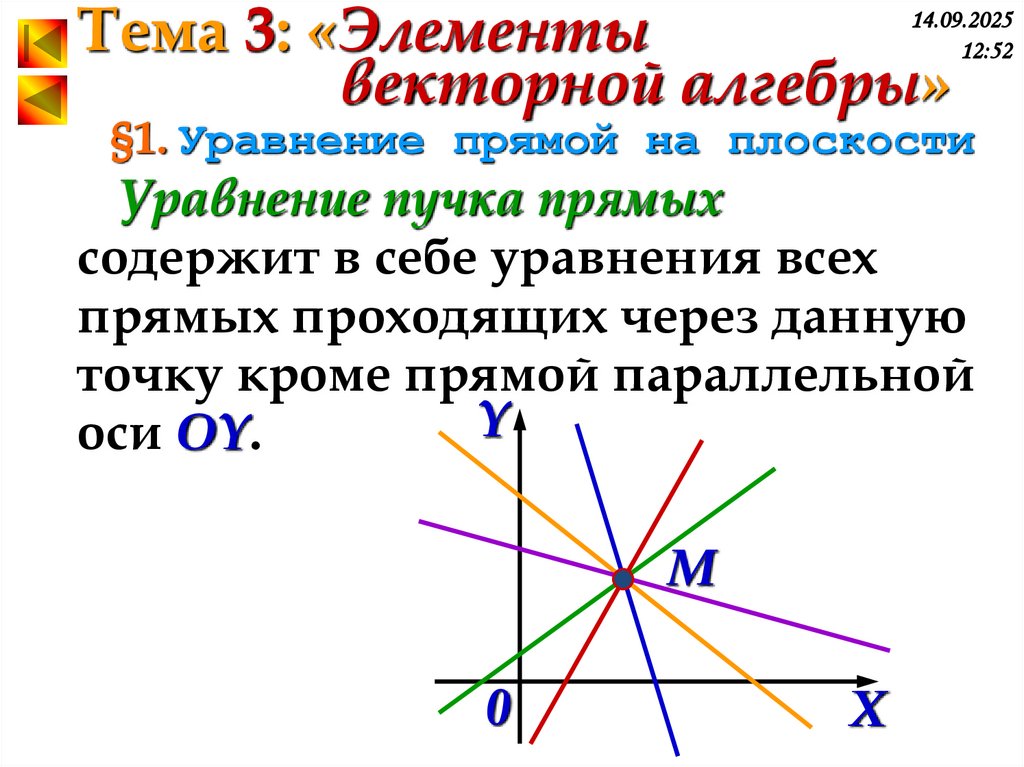
Уравнение пучка прямых
содержит в себе уравнения всех
прямых проходящих через данную
точку кроме прямой параллельной
Y
оси OY.
M
0
X

42. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
Если известны координаты
точки M0 из значения k, то
уравнение пучка прямых
будет называться уравнением
прямой проходящей через
данную точку в данном
направлении.

43. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
п.6. Уравнение прямой
проходящей через две точки.
Пусть прямая проходит через
точки M1(x1; y1) и M2(x2, y2), т.к.
прямая проходит через точку M1,
то координаты M1 удовлетворяют
уравнению пучка прямых:
y – y1 = k * (x – x1). (1)

44. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
Т.к. прямая проходит и через M2,
то координаты M2 также
удовлетворяют уравнению (1), то
получим:
y2 – y1 = k * (x2 – x1). (2)
• Разделим 1 уравнение на 2-е:
y y1
x x1 – уравнение прямой
проходящей через две
y2 y1 x2 x1 заданные точки

45. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
Частные случаи:
1) y1 = y2; тогда y y1 – это
уравнение прямой параллельной
оси OX.
2) x1 = x2; тогда x x1 – это
уравнение прямой параллельной
оси OY.

46. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
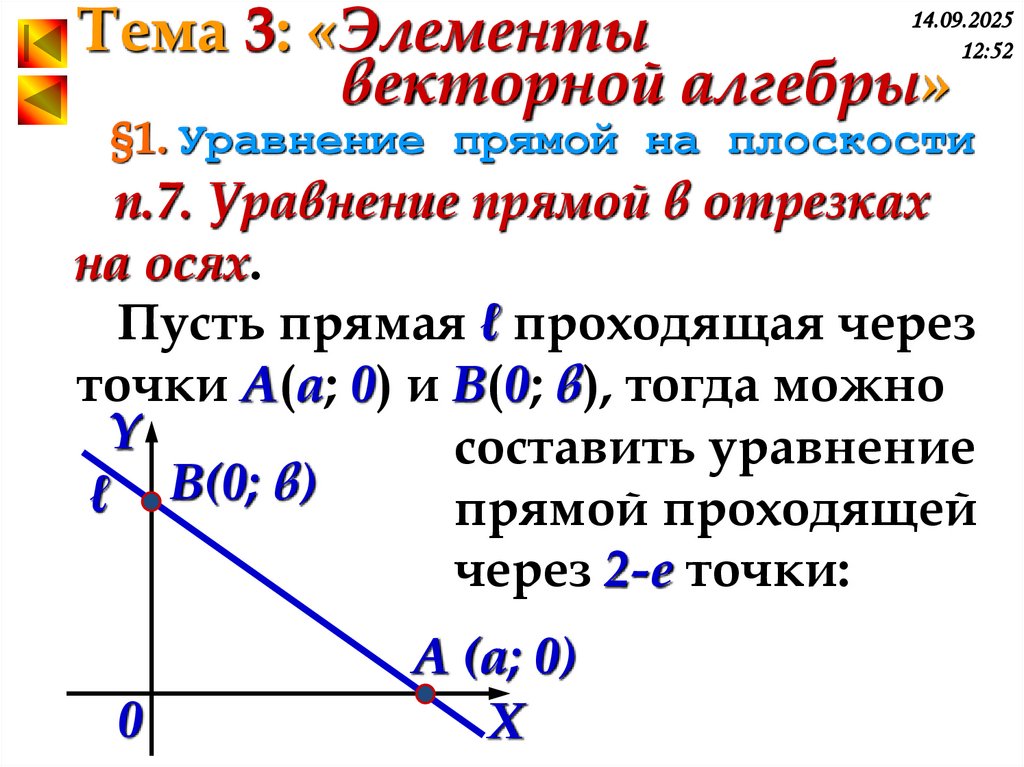
п.7. Уравнение прямой в отрезках
на осях.
Пусть прямая ℓ проходящая через
точки А(a; 0) и B(0; в), тогда можно
Y
составить уравнение
ℓ B(0; в)
прямой проходящей
через 2-е точки:
0
A (a; 0)
X

47. §1. Уравнение прямой на плоскости

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Уравнение прямой на плоскости
y 0 x a y x a y x
;
;
1;
в 0 0 a в a в a
– это уравнение прямой в
x y
отрезках на осях;
1 где a – отрезок
a в отсекающий на оси OX;
в – отрезок отсекающий на оси OY.
Это уравнение наиболее удобно
для построения прямой.

48. §2. Угол между прямыми

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Угол между прямыми
Углом между 2-мя прямыми
называется угол на который нужно
повернуть одну прямую до
совпадения с другой.
ℓ1: y = k1x + в1
Y
φ
ℓ2: y = k2x + в2
ℓ1
φ1 φ 2
φ = φ 1 – φ2
ℓ2
0
φ2 k2 = tg φ2
φ1
k1 = tg φ1
X

49. §2. Угол между прямыми

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Угол между прямыми
Необходимо найти φ ; на
практике удобнее искать не сам
угол, а его тангенс.
tg 1 tg 2
k1 k2
tg tg( 1 2 )
1 tg 1 * tg 2 1 k1 * k2
k1 k2 – это тангенс угла
tg
1 k1 * k2 между двумя прямыми.

50. §2. Угол между прямыми

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Угол между прямыми
Таким образом один угол
k1 k 2 , а второй угол
arctg
1 k1 * k 2 равен π – φ.
Частные случаи:
1) ℓ1║ℓ2 tg0o = 0 k1 – k2 = 0
k1 k2 – это
условие параллельности двух
прямых.

51. §2. Угол между прямыми

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Угол между прямыми
2) ℓ1 ┴ ℓ2 tg90o – не существует
1 + k1 * k2 = 0
1
k1
k2 – это
условие перпендикулярности
прямых.
Прямые перпендикулярны если их
коэффициенты противоположны по
знакам и обратны по величине.

52. §3. Точка пересечения двух прямых

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§3. Точка пересечения
двух
прямых
Точка пересечения 2-х прямых
находится при решении системы
линейных уравнений с 2-мя
переменными:
y k2 x в1 ,
или
y k2 x в2 ; A x B y C 0,
1 1
1 1
1
A2 x2 B2 y2 C 2 0;

53. §3. Точка пересечения двух прямых

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§3. Точка пересечения двух прямых
Возможны случаи:
1) Единственное решение –
прямые пересекаются;
2) Множество решений –
прямые совпадают;
3) Нет решений –
прямые параллельны.

54. §2. Простейшие задачи аналитической геометрии

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Простейшие задачи аналитической
геометрии
п.1. Расстояние между 2-мя точками.
Теорема. Расстояние между 2-мя
точками M1(x1; y1), M2(x2; y2)
вычисляется по формуле:
d M1 M 2 ( x2 x1 ) ( y2 y1 )
2
2

55. §2. Простейшие задачи аналитической геометрии

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Простейшие задачи аналитической геометрии
Доказательство: Рассмотрим
∆M1PM2 по т. Пифагора:
2
2
2
M1 M 2 M1 P M 2 P M1 M 2
Y
y2–y1
0
( x2 x1 )2 ( y2 y1 )2
M2
M1
P
x2 – x1 X

56. §2. Простейшие задачи аналитической геометрии

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
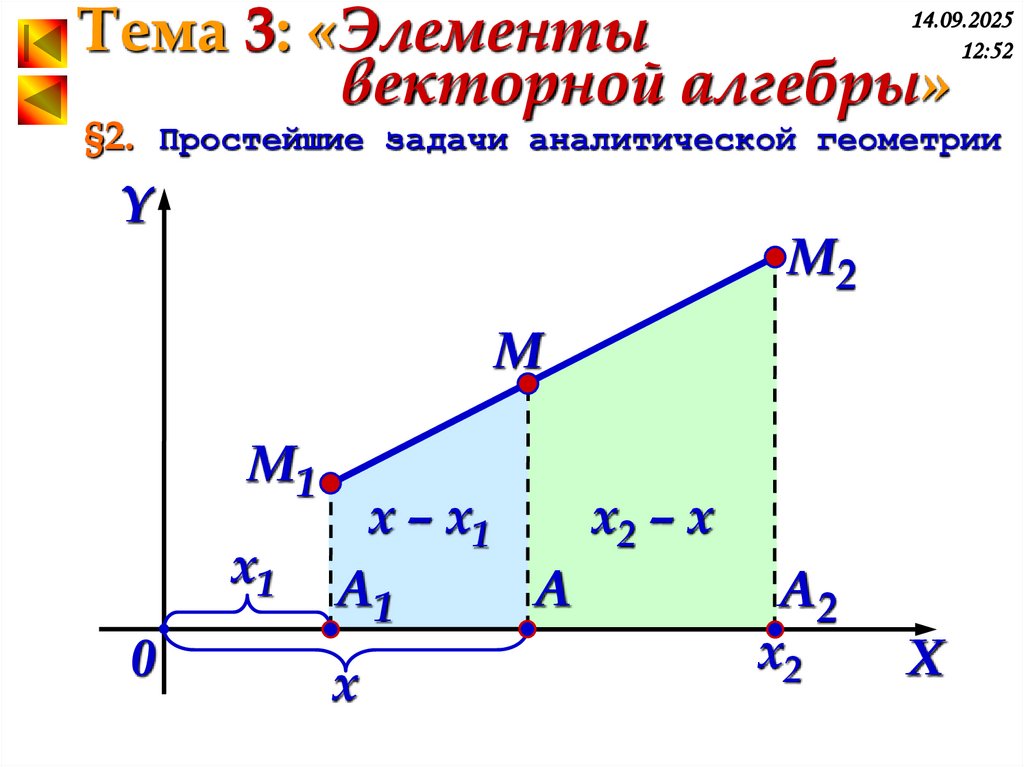
§2. Простейшие задачи аналитической геометрии
п.2. Деление отрезка в заданном
отношении.
Пусть даны точки M1(x1; y1) и
M2(x2; y2). Надо найти M(x; y),
чтобы выполнялось соотношение:
M1 M
Из точек M1, M, M2
MM 2
опустим перпендикуляры
на ось OX1, точки пересечения
обозначим соответственно A1, A, A2.

57. §2. Простейшие задачи аналитической геометрии

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Простейшие задачи аналитической геометрии
Y
M2
M
M1
x1
0
x – x1
x2 – x
A1
A
x
A2
x2
X

58. §2. Простейшие задачи аналитической геометрии

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Простейшие задачи аналитической геометрии
По т. Фалеса: M1 M A1 A
x x1
x2 x
x x1 * ( x2 x )
x x1 x2 x
x x x2 x1
x * (1 ) x2 x1
MM 2
AA2

59. §2. Простейшие задачи аналитической геометрии

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Простейшие задачи аналитической геометрии
x1 x 2
x
1
Аналогично
находится
координата y:
y1 y 2
y
1
Координаты
точки M,
делящей
отрезок M1M2
в отношении λ

60. §2. Простейшие задачи аналитической геометрии

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Простейшие задачи аналитической геометрии
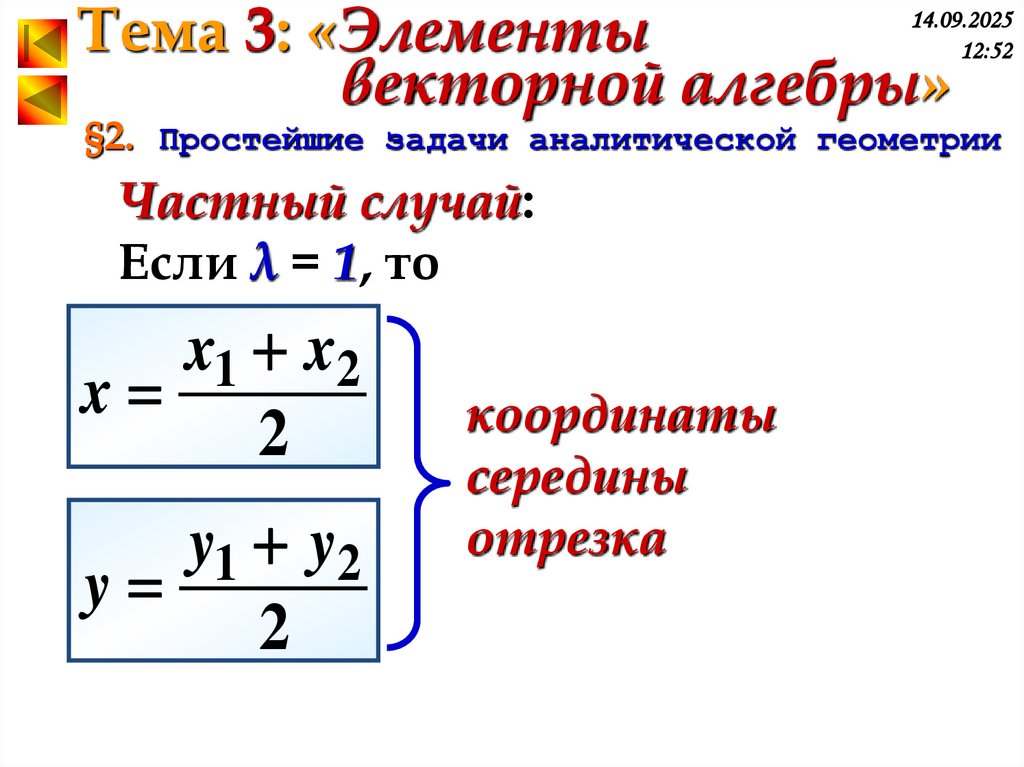
Частный случай:
Если λ = 1, то
x1 x2
x
2
y1 y2
y
2
координаты
середины
отрезка

61. §2. Простейшие задачи аналитической геометрии

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§2. Простейшие задачи аналитической геометрии
Если точка M находится
между точками M1 и M2,
то говорят что M делит
отрезок внутренним
образом, а если левее
или правее, то внешним
образом.

62. §4. Расстояние от точки до прямой

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§4. Расстояние от точки
до прямой
Пусть прямая задана общим
уравнением и пусть дана точка
P0(x0; y0), которая прямой ℓ.
Без доказательств примем:
d
Ax0 By0 C
A B
2
2
P0
d
ℓ

63. Кривые 2-го порядка

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
Кривые 2-го порядка
Уравнение вида:
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0,
где A, B, C, D, E, F – это
действительные числа и A ≠ 0, C ≠ 0
(одновременно).

64. Кривые 2-го порядка

Тема 3: «Элементы векторной
алгебры»
Кривые 2-го порядка
Существует 8 видов кривых 2-го
порядка:
1) эллипсы;
2) гиперболы;
3) параболы;
4) пара пересекающихся прямых;
5) пара параллельных прямых;
6) одна прямая (в пространстве);
7) одна точка;
8) пустое множество.

65. Кривые 2-го порядка

Тема 3: «Элементы векторной
алгебры»
Кривые 2-го порядка
Все кривые второго
порядка являются
результатом конусного
сечения.

66. §1. Эллипс

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
Кривые 2-го порядка
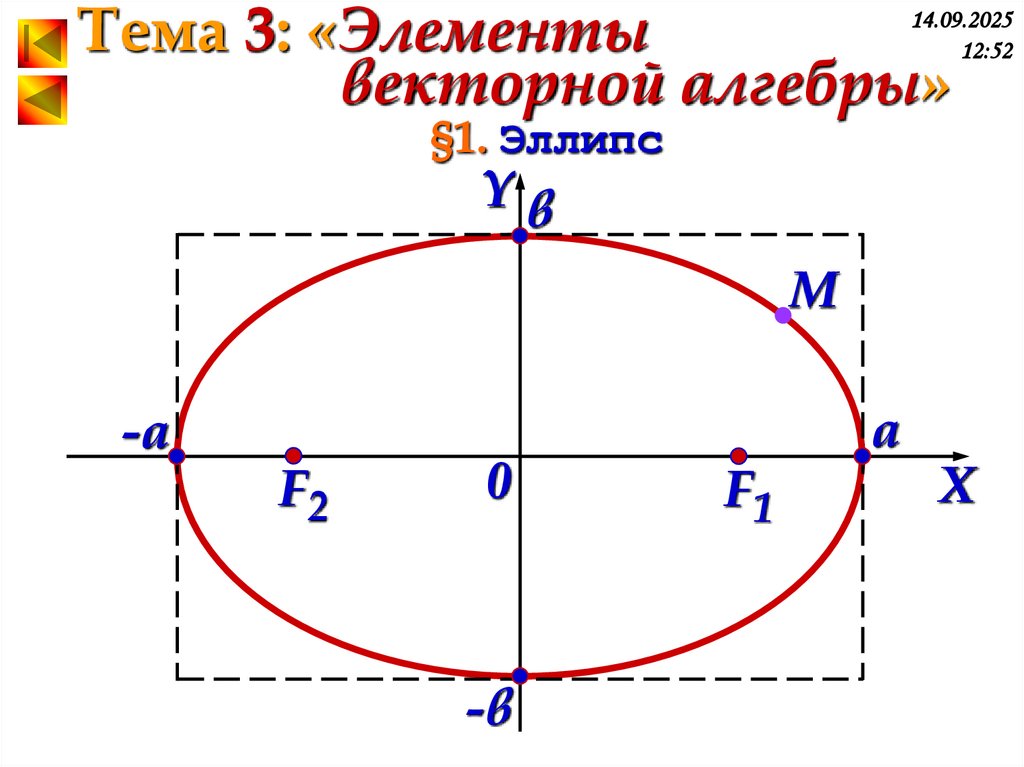
§1. Эллипс
Определение. Эллипсом
называется множество точек
плоскости сумма расстояний
от каждой из которых до 2-х
данных точек (фокусов) есть
величина постоянная
равная 2а.

67. §1. Эллипс

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Эллипс
Yв
M
-a
F2
0
-в
F1
a
X

68. §1. Эллипс

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Эллипс
Выведем формулу эллипса:
Возьмём на эллипсе
произвольную точку M(x; y).
|MF1|+|MF2| = 2a,
MF1
(c x ) (0 y )
MF2
( c x ) (0 y )
2
2
(c x )2 y 2 (c x )2 y 2
2
2
2
( 2a )
2

69. §1. Эллипс

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Эллипс
c 2cx x y
2
2
c 2cx x y
2
2
2
2
2 (c x ) y * (c x ) y 4a
2
2
2
2
2
2 (c x ) y * (c x ) y 4a 2c 2 x 2 y
2
2
2
2
(c x )2 y 2 * (c x )2 y 2
2
2
2
2
2a c x y
2
2
2
2
2 2
(c x) y * (c x) y 2a c x y
2
2
2
2
2
2
2
2 2

70. §1. Эллипс

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Эллипс
(a c ) * x a y a * (a c ) ||: a * (a c )
2
x
a
2
2
2
2
2 2
y
2
2
2
2
2
2
2
1
2
a c
Обозначим a2 – c2 = в2
2
2
2
←
каноническое
x
y
уравнение эллипса
1
2
2
где
a
>
0,
в
>
0,
c
>
0.
a
в

71. §1. Эллипс

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Эллипс
Свойства:
1о) a – большая полуось
2о) в – малая полуось
3о) OF1 = OF2 = c – фокальное
расстояние
Если a < в , то фокусы
расположены по оси OY, тогда
а2 – с2 = в2, т.е. эллипс вытянут
вдоль оси OY.

72. §1. Эллипс

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Эллипс
4о) Точки (-a; 0); (a; 0); (0; в); (0; -в) –
вершины эллипса
5о) Эллипс расположен в
прямоугольнике, ограниченном
прямыми x = ±a и y = ±в.
Определение. Эксцентриситетом
( ) эллипса называется отношение
фокального расстояния к большой
полуоси:
с
a

73. §1. Эллипс

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Эллипс
Эксцентриситет характеризует
форму эллипса (меру сжатия или
степень вытянутости): чем ближе
к 1, тем значение в меньше, т.е.
эллипс сжат к оси OX.
Если = 1, тогда в = 0, т.е.
эллипс вырождается в отрезок.

74. §1. Эллипс

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§1. Эллипс
Если = 0, тогда а = в, т.е. эллипс
вырождается в окружность при
этом фокусы сливаются с центром
окружности: x2 + y2 = R2.
C другой стороны эллипс можно
рассматривать как результат
равномерного сжатия к оси OX.

75. §3. Гипербола

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§3. Гипербола
Определение. Гиперболой
называется множество точек
плоскости модуль разности
расстояний от каждой из
которых до 2-х данных точек
есть величина постоянная
равная 2а.

76. §3. Гипербола

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
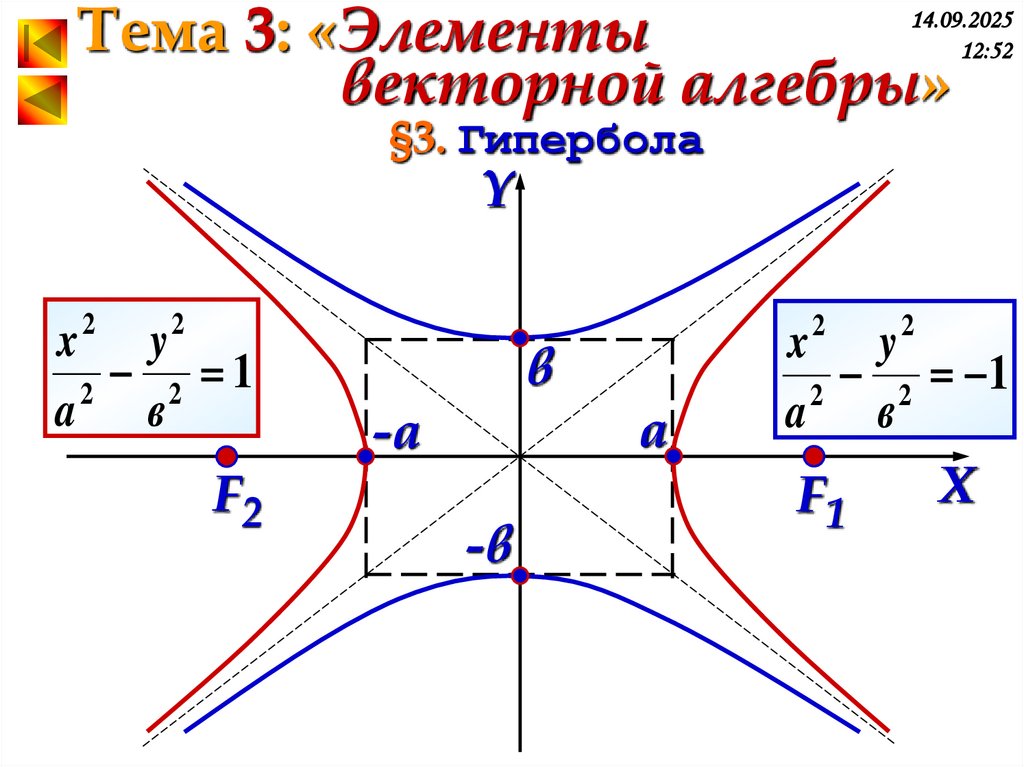
§3. Гипербола
Y
2
2
x y
2 1
2
a в
F2
в
a
-a
-в
x2 y2
2 1
2
a в
F1
X

77. §3. Гипербола

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§3. Гипербола
Выведем формулу гиперболы:
Возьмём на гиперболе
произвольную точку M(x; y).
|MF1|–|MF2| = 2a,
MF1
(c x ) y
2
MF2
(c x ) y
2
2
2
(c x )2 y 2 (c x )2 y 2
2
( 2a )2

78. §3. Гипербола

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§3. Гипербола
c 2cx x y
2
2
2
c 2cx x y
2
2
2
2 ( c x ) y * ( c x ) y 4a
2
2
2
2
Обозначим c2 + x2 + y2 = t :
t 2 xc * t 2 xc t 2a
2
2
2
2 2
2
2
t
4
x
c
t
2
a
2

79. §3. Гипербола

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§3. Гипербола
2 2
2
2
2
t 4 x c t 4a t 4a
2 2
2
x c a t a
4
4
Вернёмся от t к c2 + x2 + y2 :
2 2
2 2
2 2
2 2
4
2
2
x c a x a y a c a
2 2
2 2
2 2
2
x c a x a y a * (a c )
2
2
2
2 2
2
2
2
2
2
2
x * (a c ) a y a * (a c ) ||: a * (a c )

80. §3. Гипербола

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§3. Гипербола
2
2
2
2
y
y
x
x
1
1
2
2
2
2
2
2
a
a c
a
c a
Заменим в2 = c2 – a2 :
2
2
y
x
1
2
2
a
в

81. §4. Парабола

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§4. Парабола
Определение. Параболой
называется множество точек
плоскости равноудалённых от
данной точки (фокуса) и данной
прямой (директрисы).
Возьмём на параболе некоторую
точку M(x; y).

82. §4. Парабола

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
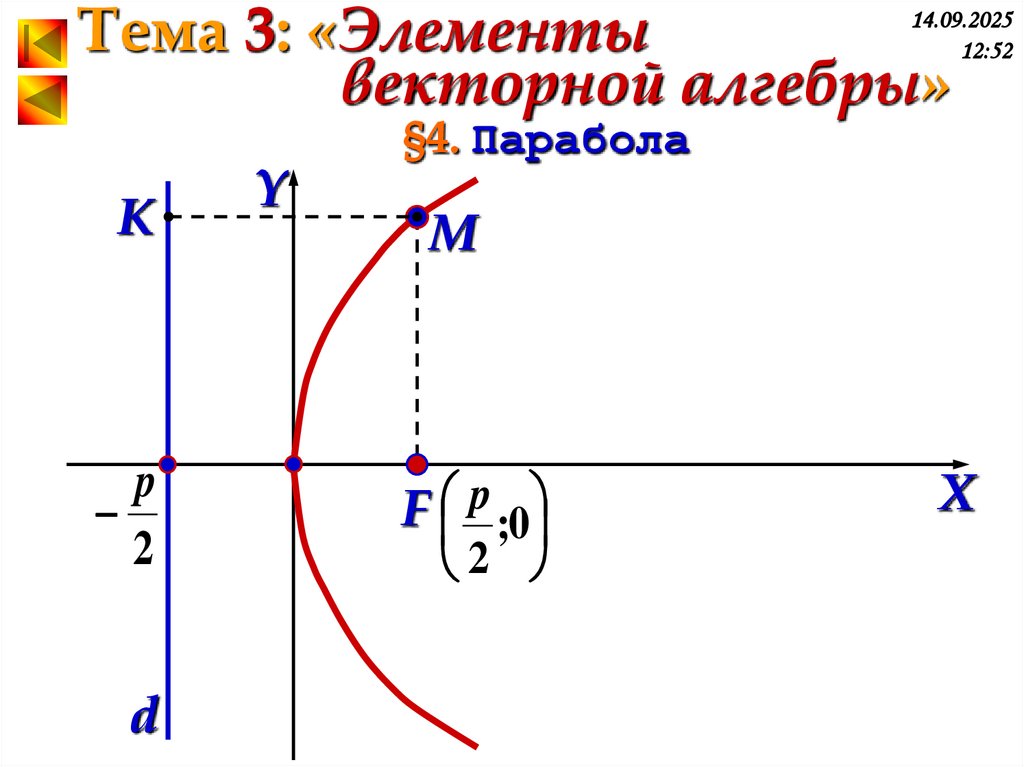
K
p
2
d
Y
§4. Парабола
M
F p ;0
2
X

83. §4. Парабола

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§4. Парабола
По определению параболы
имеем, что |MK|=|MF|.
p
F ;0
2
2
p
2
MK x ( y y )
2
M ( x; y )
p
K ; y
2
2
p
2
MF x (0 y )
2
2
2
p
p
2
2
x ( y y ) x (0 y )
2
2

84. §4. Парабола

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§4. Парабола
2
2
p
2 p
2
2
px x px x y
4
4
y 2 px
2
каноническое
← уравнение
параболы

85. §4. Парабола

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§4. Парабола
d
Y
Виды парабол и их
канонические уравнения.
y 2 px
p
F ;0
2
2
0
F
p X
;0
2
p
d:x
2

86. §4. Парабола

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§4. Парабола
y 2 px
p
F ;0
2
p
d:x
2
Y
2
F
p
;0
2
d
0
X

87. §4. Парабола

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
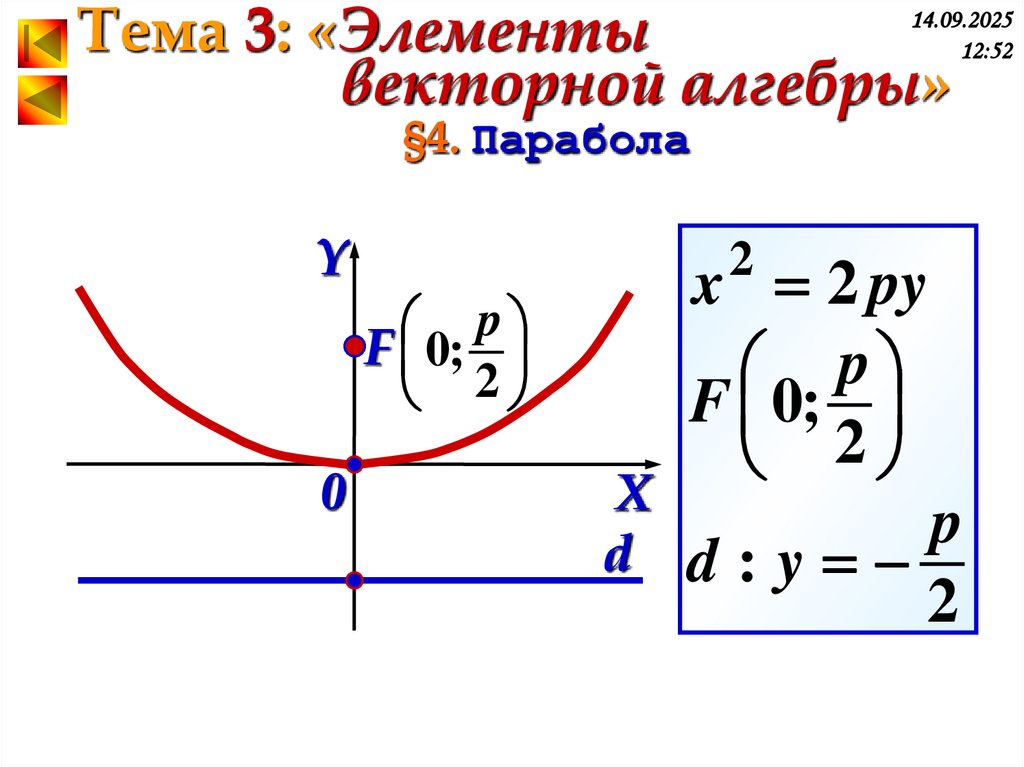
§4. Парабола
Y
p
F 0;
2
0
x 2 py
p
F 0;
2
2
X
p
d d:y
2

88. §4. Парабола

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
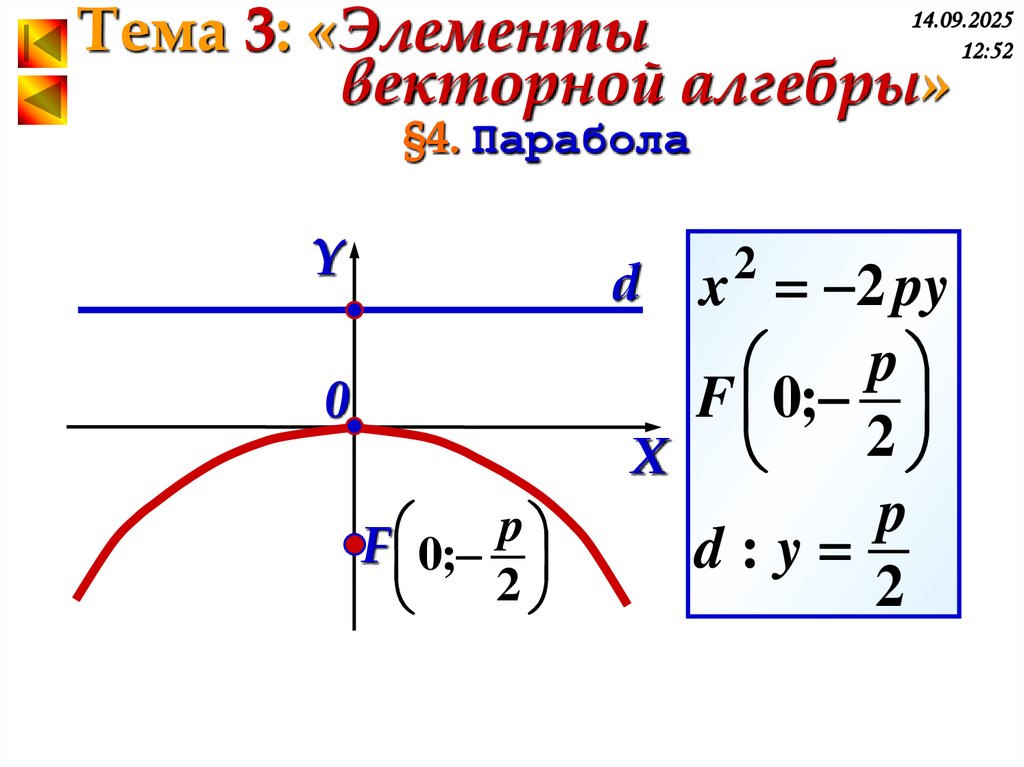
§4. Парабола
Y
x 2 py
p
F 0;
2
X
p
d:y
2
d
0
F 0; p
2
2

89. §4. Парабола

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§4. Парабола
Точка O(0; 0) называется
вершиной параболы. Ось
координат на которой лежит
фокус параболы называется
осью параболы.
Оптическое свойство параболы:
Луч исходящий из фокуса после
отражения от линии параболы
движется параллельно оси параболы.

90. §5. Приведение общего уравнения кривой 2-го порядка к каноническому виду(частные случаи)

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§5. Приведение общего уравнения
кривой 2-го порядка к
каноническому виду(частные случаи)
Чаще всего уравнение кривой
2-го порядка задано в общем виде,
следовательно, для изображения
кривой и её исследования данное
уравнение необходимо привести
к каноническому виду;
для этого достаточно выделить полный
квадрат при каждой переменной
или нескольких множителей
и затем произвести замену.

91. §5. Приведение общего уравнения кривой 2-го порядка к каноническому виду(частные случаи)

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§5. Приведение общего уравнения кривой 2-го порядка к каноническому виду(частные случаи)
Рассмотрим некоторые виды кривых:
1) окружность: (x – a)2 + (y – в)2 = R2
– уравнение окружности радиуса R
со смещенным центром O′(a; в).
Y′
Y
O(0; 0) → O′(a; в)
(XOY)
→
(X
′
O
′
Y
′
)
O′(a; в)
X′
O
X

92. §5. Приведение общего уравнения кривой 2-го порядка к каноническому виду(частные случаи)

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§5. Приведение общего уравнения кривой 2-го порядка к каноническому виду(частные случаи)
2) эллипс: ( x x )2
0
a
Y0
2
( y y0 )
в
2
2
1
Y O(0; 0) → O′(x0; y0)
O
O′
X
X0

93. §5. Приведение общего уравнения кривой 2-го порядка к каноническому виду(частные случаи)

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§5. Приведение общего уравнения кривой 2-го порядка к каноническому виду(частные случаи)
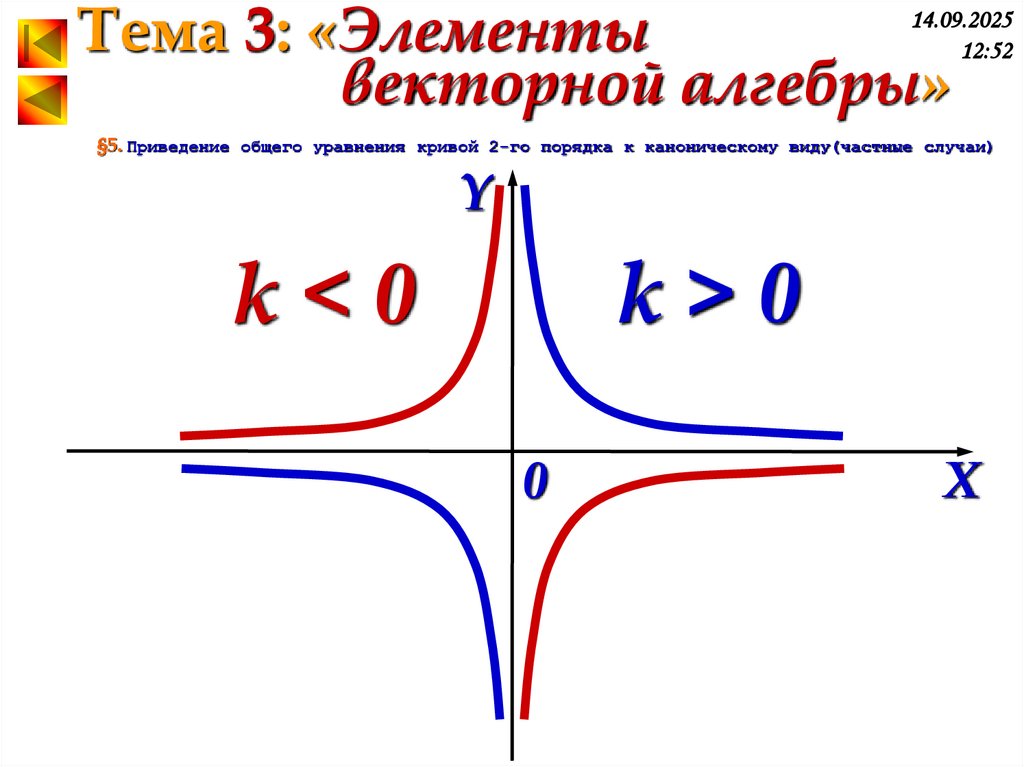
3) гипербола:
k
y
x – уравнение
гиперболы как графика обратной
пропорциональности получена
поворотом равнобочной
гиперболы вокруг начала
координат.

94. §5. Приведение общего уравнения кривой 2-го порядка к каноническому виду(частные случаи)

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§5. Приведение общего уравнения кривой 2-го порядка к каноническому виду(частные случаи)
Y
k>0
k<0
0
X

95. §5. Приведение общего уравнения кривой 2-го порядка к каноническому виду(частные случаи)

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§5. Приведение общего уравнения кривой 2-го порядка к каноническому виду(частные случаи)
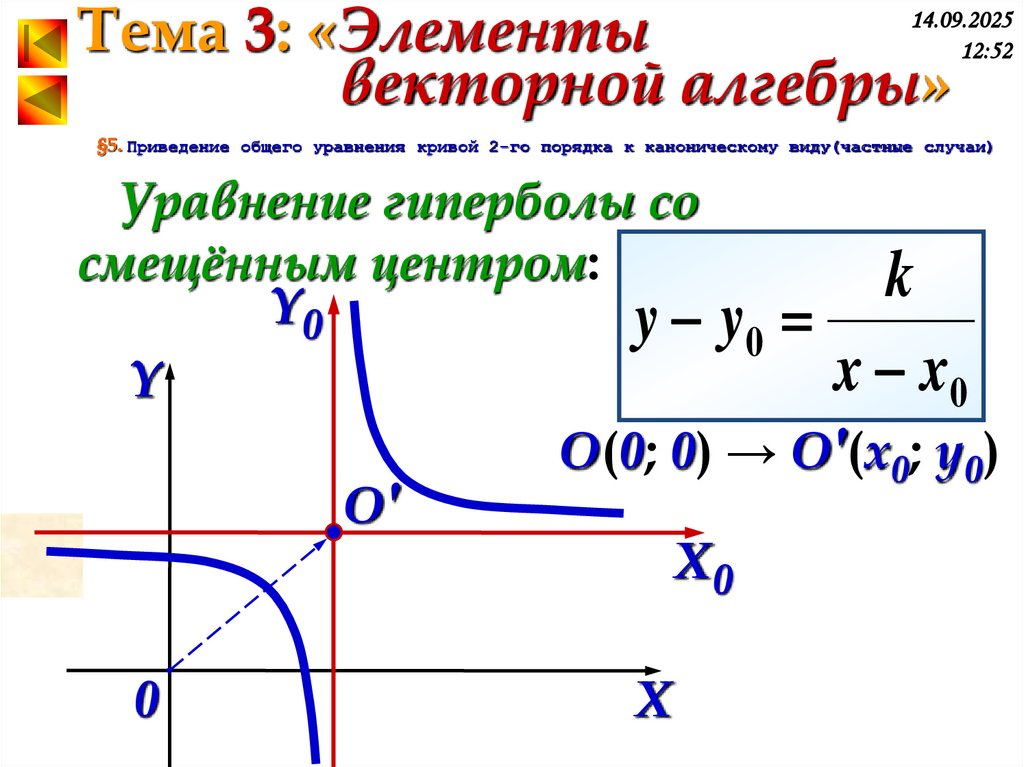
Уравнение гиперболы со
смещённым центром:
k
Y0
y y0
x x0
Y
O(0; 0) → O′(x0; y0)
O′
X0
0
X

96. §5. Приведение общего уравнения кривой 2-го порядка к каноническому виду(частные случаи)

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§5. Приведение общего уравнения кривой 2-го порядка к каноническому виду(частные случаи)
Ax B
y
Cx D – уравнение
гиперболы как графика
дробно-линейной функции.
Путём выделения целой
части дроби приводим её к виду:
k
y в
x a
O(0; 0) → O′(a; в)

97. §5. Приведение общего уравнения кривой 2-го порядка к каноническому виду(частные случаи)

Тема 3: «Элементы
векторной алгебры»
14.09.2025
12:52
§5. Приведение общего уравнения кривой 2-го порядка к каноническому виду(частные случаи)
4) парабола:
y Ax Bx C – уравнение
2
параболы как графика квадратного
трёхчлена. Сводим к каноническому
виду путём выделения полного
квадрата, а далее приводим к виду:
y в A * ( x a)
2