11_1 Кратные24(1)

1.

Раздел 8.
Кратные и криволинейные
интегралы. Элементы теории поля
1

2.

§ 1. Интеграл по фигуре
Интеграл по фигуре (ИФ) является обобщением понятия
определенного
интеграла
на
случай
различных
геометрических фигур.
Опр. 1. Множество точек называется связным, если любые
две его точки можно соединить линией, все точки которой
принадлежат данному множеству.
Связное множество
Несвязное множество
2

3.

Опр. 2. Под геометрической фигурой Φ будем понимать одно из
следующих связных (включая границу) множеств:
(А) отрезок [a; b] на числовой прямой;
(Б) область D на плоскости (плоская область);
(В) пространственная область Ω, ограниченная замкнутой
поверхностью, – тело в пространстве;
(Г) линию L на плоскости или в пространстве;
(Д) поверхность σ в пространстве.
Опр. 3. Диаметром d(Φ) фигуры Φ называется максимальное
расстояние между двумя точками этой фигуры.
Будем рассматривать фигуры конечного диаметра, т. е.
ограниченные фигуры.
Опр. 4. Под мерой μ(Φ) геометрической фигуры будем понимать:
(А) длину отрезка [a; b];
(Б) площадь SD плоской области D;
(В) объем VΩ тела Ω;
(Г) длину lL линии L;
(Д) площадь Sσ поверхности σ.
3

4.

Пусть во всех точках множества определена и непрерывна
функция f ( M ), M .
Разобьем фигуру на n частичных
(элементарных) фигур i , 1 i n, с
мерами i ; обозначим d ( i ) - диаметр
фигуры i ; на каждой элементарной
фигуре выберем произвольную точку
M i i , вычислим значение функции в
этой точке: f ( M i ).
Составим интегральную сумму
для функции f ( M ) по фигуре :
n
Sn f ( M i ) i .
(1)
i 1
Обозначим через d n max d ( i )
1 i n
диаметр разбиения –
наибольший из диаметров элементарных фигур, составляющих
4
разбиение.

5.

Опр. 5. Интегралом от функции f ( M ) по фигуре
называется предел интегральной суммы (1) при измельчении
разбиения, т. е. при диаметре разбиения, стремящемся к нулю:
Sn
f ( M )d dlim
0
n
при условии, что этот предел существует, конечен и не зависит ни
от способа разбиения фигуры на элементарные фигуры, ни от
выбора точек M i на элементарных фигурах.
Опр. 6. Функция f ( M ) называется интегрируемой по фигуре
с мерой , если существует интеграл от функции f ( M ) по
фигуре .
Т 1. Если фигура связная, ограниченная и содержит
граничные точки, а функция f ( M ) непрерывна на множестве ,
то эта функция интегрируема на .
5

6.

Названия и обозначения интегралов по фигуре
(А) Φ - отрезок [a; b] на числовой прямой
b
⇒ ИФ – это определенный интеграл по отрезку [a; b]: f ( x)dx
a
(Б) Φ - плоская область D
⇒ f ( x; y)dxdy - двойной интеграл по области D
D
(В) Φ - тело в пространстве
кратные интегралы
⇒ f ( x; y; z )dxdydz - тройной интеграл по телу
(Г) Φ - линия L на плоскости или в пространстве
⇒ f ( x; y; z )dl - криволинейный интеграл 1-го рода,
L
или криволинейный интеграл по длине дуги
(Д) Φ - поверхность σ в пространстве
⇒ f ( x; y; z )dS - поверхностный интеграл 1-го рода,
или поверхностный интеграл по площади поверхности
6

7.

Свойства ИФ
1. ИФ от единицы равен мере фигуры: d ( ).
2. Линейность:
kf ( M )d k f ( M )d (k const);
( f ( M ) g ( M ))d f ( M )d g ( M )d .
3. Аддитивность: если фигуру можно разбить на две фигуры
1 и 2 так, что их общая часть имеет меру 0: 1 2 ,
( 1 2 ) 0 , то
f ( M )d f ( M )d f ( M )d .
1
2
7

8.

4. Если f ( M ) 0 при всех M , то f ( M )d 0.
5. Монотонность:
если f ( M ) g ( M ) при всех M , то f ( M )d g ( M )d .
6. f ( M )d | f ( M ) | d .
7. Оценка ИФ: если m f ( M ) M при всех M , то
m ( ) f ( M )d M ( ).
8. (Теорема о среднем). Если функция f ( M ) непрерывна на
фигуре , то существует такая точка M 0 , что
f ( M )d f ( M 0 ) ( ).
8

9.

Геометрический смысл ИФ
Свойство 1: ИФ от единицы равен мере фигуры:
d ( ).
⇔
b
(А) dx b a - длина отрезка интегрирования;
a
(Б) dxdy S D - площадь области интегрирования;
D
(В) dxdydz V - объем тела интегрирования;
(Г) dl lL - длина кривой интегрирования;
L
(Д) dS S - площадь поверхности интегрирования.
9

10.

Геометрический смысл ИФ
(Б) Пусть f ( x; y ) 0 при всех M ( x; y ) D. Назовем
криволинейным цилиндром тело, ограниченное сверху
поверхностью z f ( x; y ), снизу областью D, лежащей в
плоскости Oxy, а по бокам – цилиндрической поверхностью,
направляющей которой служит граница области D, а образующие
параллельны оси Oz
интеграл от
функции f (x; y) по области D
выражает объем криволинейного
цилиндра:
⇒
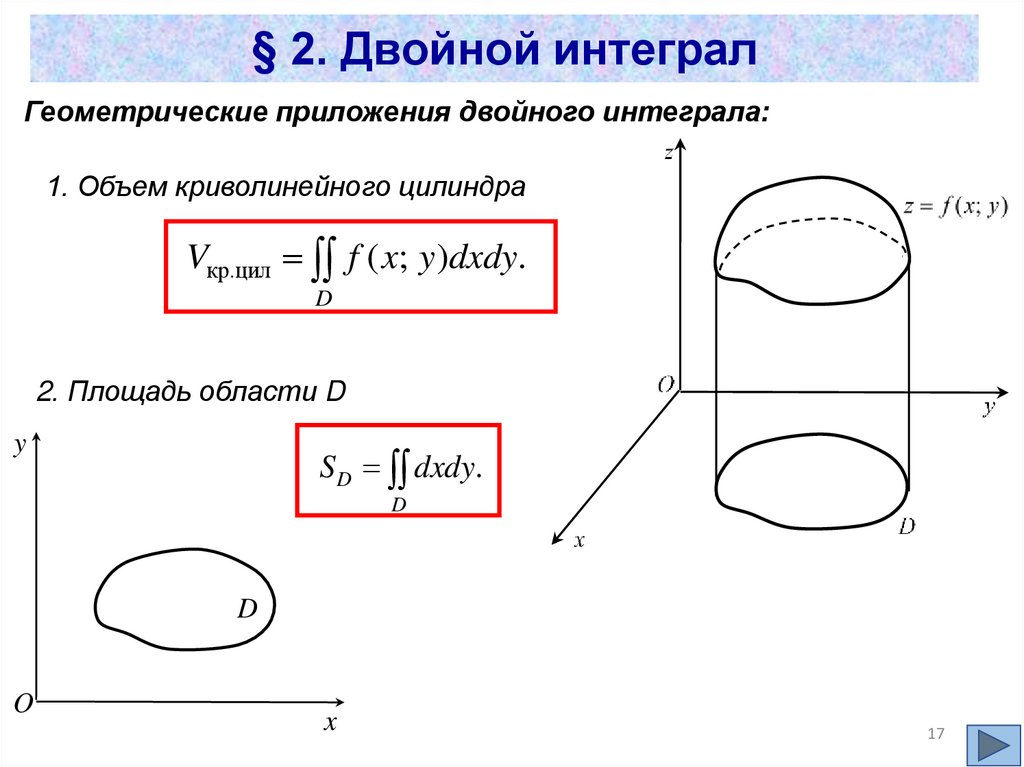
Двойной
Vкр.цил f ( x; y )dxdy.
D
10

11.

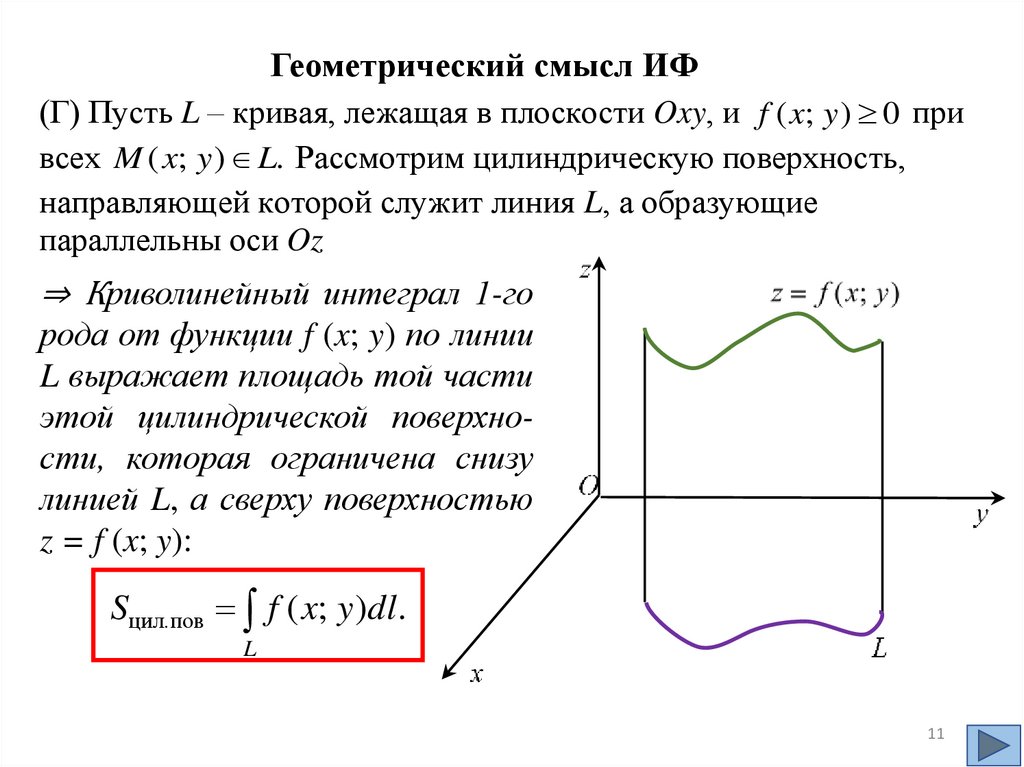
Геометрический смысл ИФ
(Г) Пусть L – кривая, лежащая в плоскости Oxy, и f ( x; y ) 0 при
всех M ( x; y ) L. Рассмотрим цилиндрическую поверхность,
направляющей которой служит линия L, а образующие
параллельны оси Oz
⇒ Криволинейный интеграл 1-го
рода от функции f (x; y) по линии
L выражает площадь той части
этой цилиндрической поверхности, которая ограничена снизу
линией L, а сверху поверхностью
z = f (x; y):
Sцил.пов f ( x; y )dl.
L
11

12.

Физический смысл ИФ
Пусть неотрицательная функция ( M ) выражает плотность
фигуры в точке M. Тогда ИФ от плотности ( M ) равен массе
фигуры: ( M )d m .
(А) Масса стержня равна определенному интегралу от
b
линейной плотности стержня: m[ a ; b] ( x )dx.
a
(Б) mD ( x; y)dxdy - масса плоской пластинки
D
(В) m ( x; y; z )dxdydz - масса пространственного тела.
(Г) mL ( x; y; z )dl - масса кривой.
L
(Д) m ( x; y; z )dS - масса поверхности.
12

13.

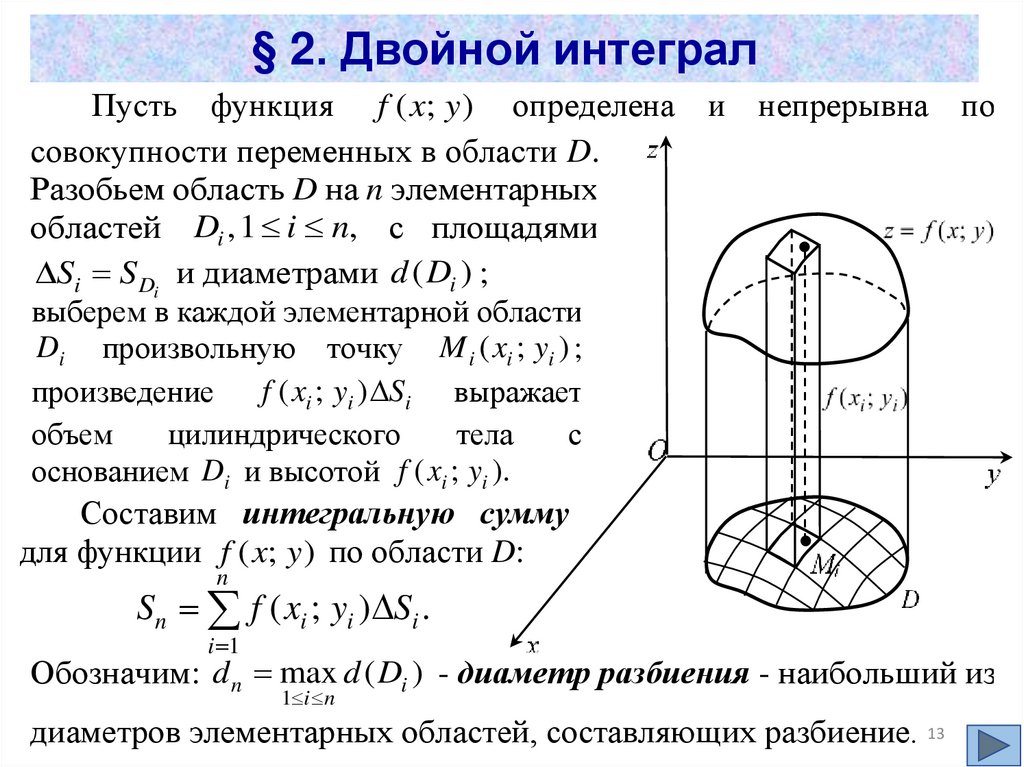
§ 2. Двойной интеграл
Пусть функция f ( x; y ) определена и непрерывна по
совокупности переменных в области D.
Разобьем область D на n элементарных
областей Di , 1 i n, с площадями
Si SDi и диаметрами d ( Di ) ;
выберем в каждой элементарной области
Di произвольную точку M i ( xi ; yi ) ;
f ( xi ; yi ) Si выражает
произведение
объем
цилиндрического
тела
с
основанием Di и высотой f ( xi ; yi ).
Составим интегральную сумму
для функции f ( x; y ) по области D:
n
Sn f ( xi ; yi ) Si .
i 1
Обозначим: d n max d ( Di ) - диаметр разбиения - наибольший из
1 i n
диаметров элементарных областей, составляющих разбиение. 13

14.

Опр. 1. Двойной интеграл от функции f ( x; y ) по области D
определяется как предел интегральных сумм для функции f ( x; y )
по области D при измельчении разбиения:
n
f ( xi ; yi ) Si ,
f ( x; y )dxdy dlim
0
D
n
i 1
если этот предел существует, конечен и не зависит ни от способа
разбиения области D на элементарные области, ни от выбора точек
M i на элементарных областях.
14

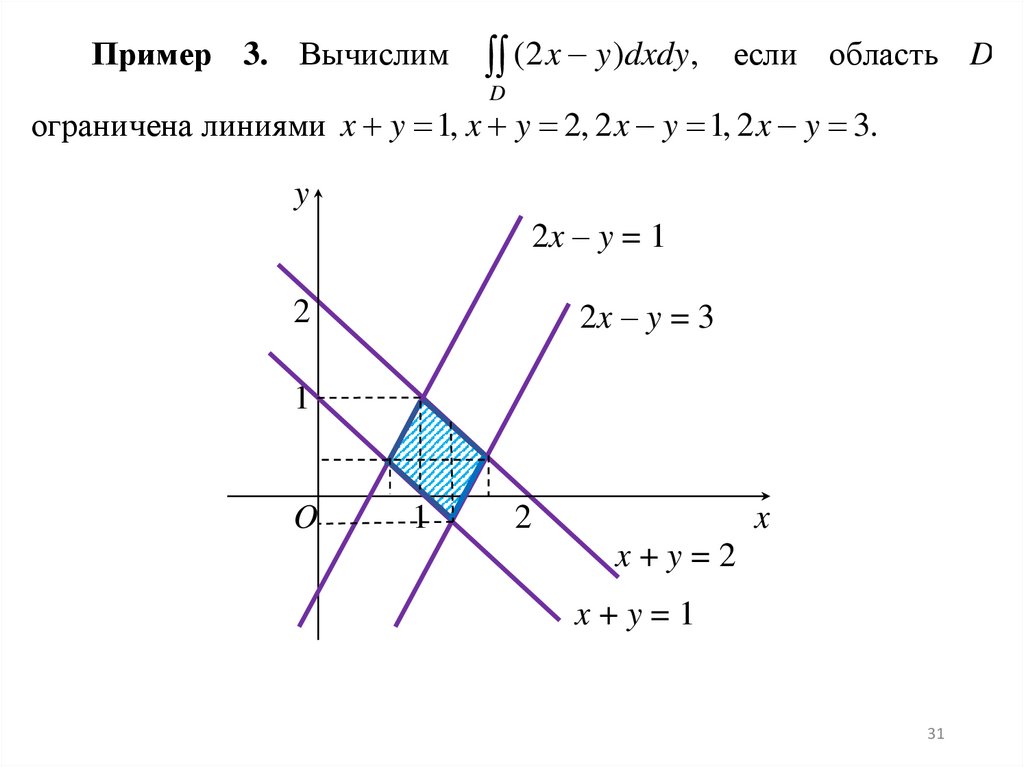
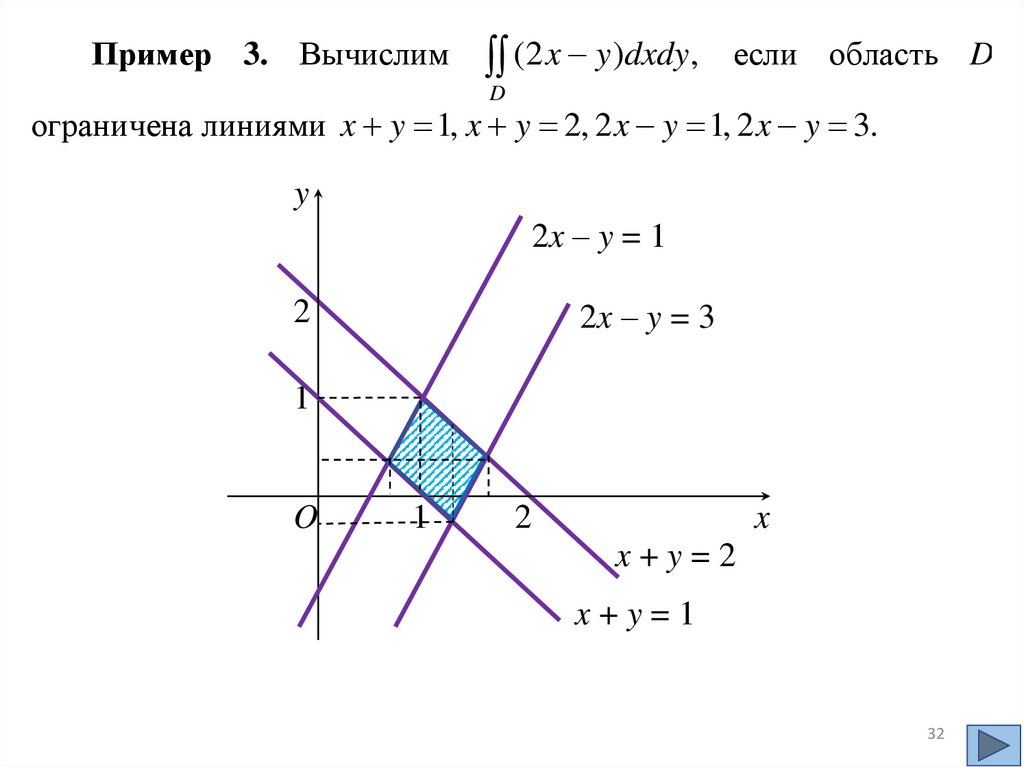
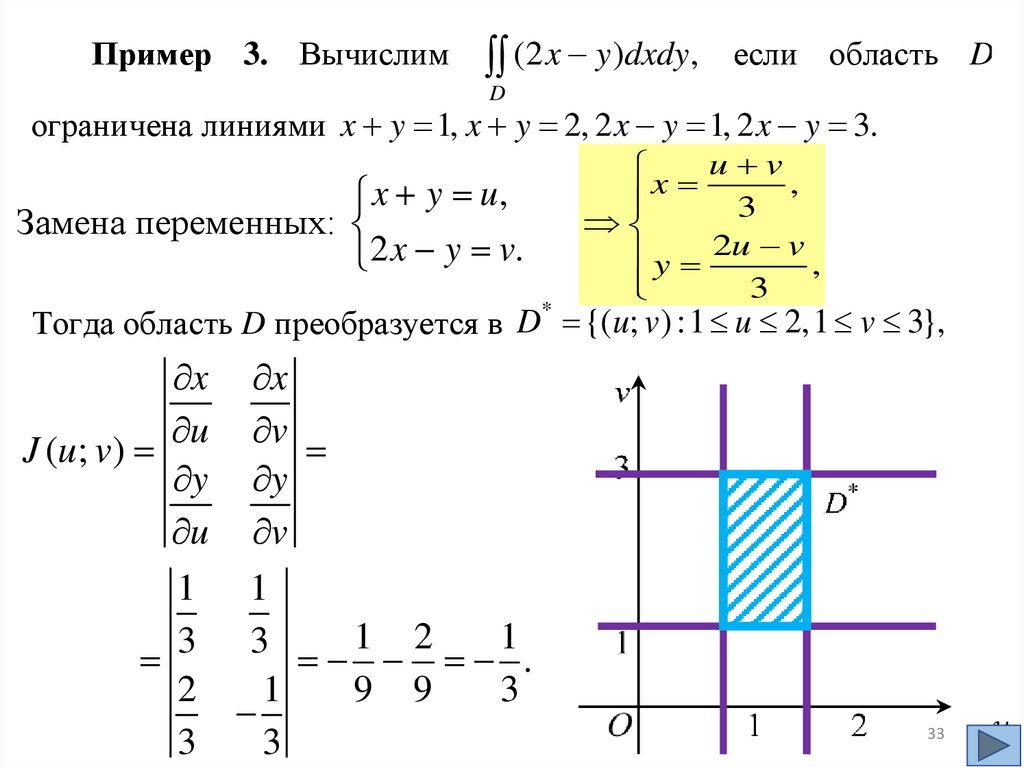
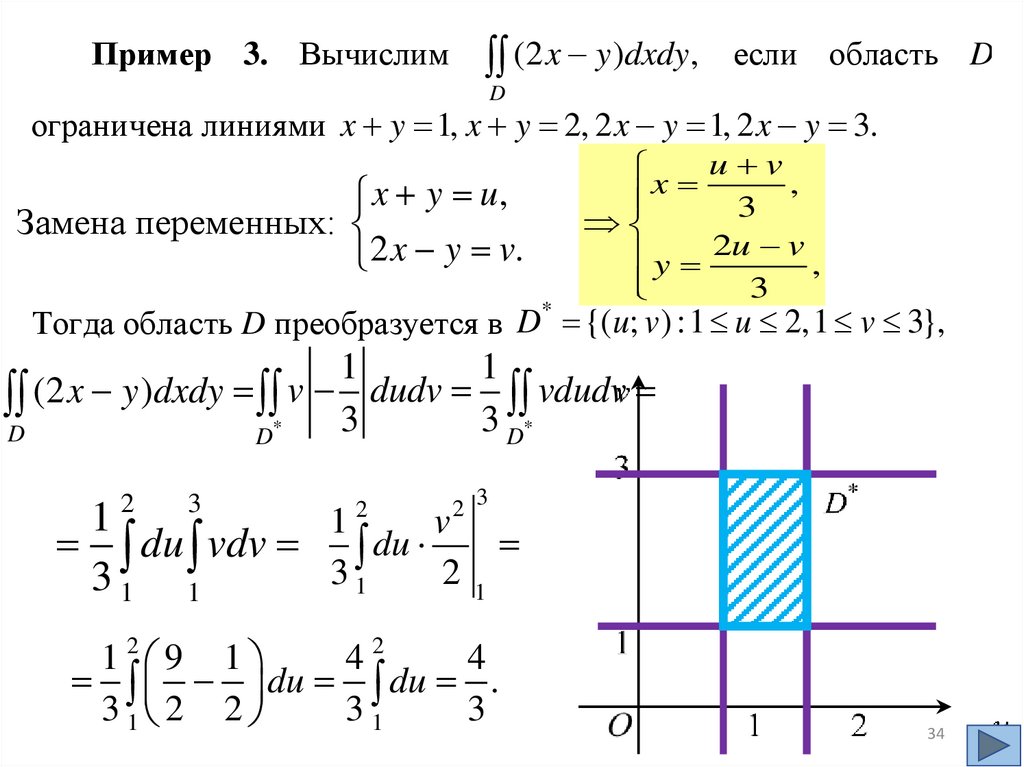
15.

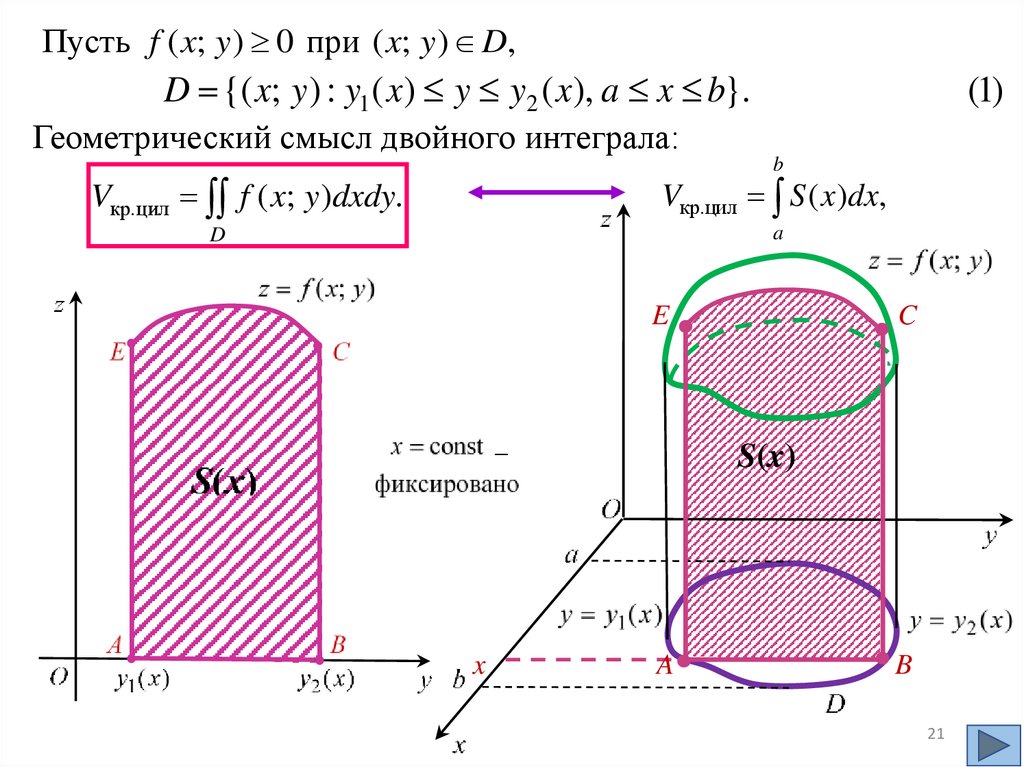
Геометрический смысл двойного интеграла.
Двойной интеграл от неотрицательной функции