Похожие презентации:
Математический анализ ВИТ-11, весенний семестр 2024-2025 уч. г
1.
Математический анализ ВИТ-11, весенний семестр 2024-2025 уч. г. Лектор проф. А.В.БратищевНеделя
Тема лекции
1. 3.02
Неопределённый интеграл и методы интегрирования.
2. 10.02 Дифференциальные уравнения и классы уравнений,
интегрируемых в квадратурах.
3. 17.02 Линейные дифференциальные уравнения и системы.
4. 24.02 Математические модели процессов и
дифференциальные уравнения
5. 3.03 Определённый интеграл.
6. 10.03 Приложения определённого интеграла.
Практика
Методы замены переменных и интегрирования по частям.
Интегрирование простейших рациональных и тригонометриче
ских выражений.
Уравнения с разделяющимися переменными и однородных.
Интегрирование линейных уравнений первого порядка и
линейны второго порядка с постоянными коэффициентами.
Контрольная работа 1.
Решение однородной НСЛДУ второго порядка с постоянными
коэффициентами с помощью собственных чисел матрицы.
7. 17.03 Числовые ряды. Признак сравнения для положительных Простейшие замены переменной. Интегрирование по частям.
рядов. Признак Лапласа знакопеременного ряда.
Вычисление площади криволинейной трапеции.
8. 24.03 Теоретическая контрольная 1.
Вычисление площади криволинейной трапеции.
9. 31.03 Комплексные числа и операции с ними.
Контрольная работа 2.
10. 7.04 Комплексная плоскость и функции комплексного
Исследование сходимости числовых рядов.
переменного.
11. 14.04 Ряды Фурье и их свойства.
Исследование сходимости числовых рядов.
Нахождение коэффициентов ряда Фурье.
12. 21.04 Мера Жордана. Двойной интеграл и его свойства.
Нахождение коэффициентов ряда Фурье. График суммы ряда.
13. 28.04 Геометрические и физические приложения.
Контрольная работа 3. Двойной интеграл на прямоугольнике.
14. 5.05 Криволинейный интеграл второго рода. Вычисление.
Прикладные задачи с двойным интегралом. 3649, 3653
Приложения.
15. 12.05 Контрольная работа 2
Вычисление работы с помощью криволинейного интеграла.
16. 19.05 Прикладные задачи, решаемые методами семестра.
Контрольная работа 4.
Берман Г. Сборник задач по математическому анализу
2.
А.В.БратищевОпорный конспект лекций по математике. Семестр 1.
Опорный конспект лекций по математике. Семестр 2.
На сайте de@donstu.ru факультет ИВТ кафедра
прикладной математики
Учебники:
Бугров Я.С., Никольский С.М. Высшая математика.
Аналитическая геометрия. Т.1.
Бугров Я.С., Никольский С.М. Высшая математика. Дифференци
альное и интегральное исчисление.Т.2.
Задачники:
Берман Г.Н. Сборник задач по курсу математического анализа.
Решебники:
Данко П.Е. и др. Высшая математика в упражнениях и задачах. Т.1,2.
Взять на абонементе или скачать на сайте www. techlibrary
3.
"Понять" означает: 1) привыкнуть и 2) уметь пользоваться" - принцип ФермиВОПРОСЫ К ПЕРВОМУ БЛОКУ, 2024-2025
1. Опр. первообразной, неопределенного интеграла и замечание. Пр. 2. Формулы интегрирования по частям и замены переменных Пр. 3.Опр. кратности нуля функции и теорема Гаусса. Пр. 4.
Опр. ДУ, ОДУ. Пр. 5. Опр. ОДУ n -го порядка, разрешенного (неразрешенного) относительно
производной. Пр. 6. Опр. решения ОДУ и интегральной кривой. Пр. 7. Опр. задачи Коши,
условий и данных Коши. Пр. 8. Опр. общего, частного и особого решений. Пр. 9. Что значит
проинтегрировать в явном виде и в квадратурах? Пр. 10. Уравнение с разделяющимися переменОпр. и метод решения. Пр. 11. Уравнение Линейной, Бернулли. Опр. и метод решения. Пр.
12. Опр. линейного ДУ с постоянными коэффициентами. Метод решения. Пр. 13. Опр. НСОДУ,
его порядка и задачи Коши. Пр. 14. Опр. НСЛДУ, однородной и неоднородной НСЛДУ. Пр. 15.
Характеристический многочлен, собственные числа и собственные векторы матрицы. Пр. 16.
Опр. кривой, спрямляемой кривой, гладкой кривой и длины кривой. Пр.
ВОПРОСЫ КО ВТОРОМУ БЛОКУ, 2024-2025
1. Опр. разбиения, диаметра разбиения. Пр. 2. Опр. интегральной суммы и определенного
интеграла. Пр. 3. Опр. криволинейной трапеции. Свойства определённого интеграла. Пр.
4. Опр. числового ряда, частичной сумм и сходящегося ряда. Пр. 5. Формулировка признаков
сходимости Даламбера и Лейбница. Пр. 6. Формулировка необходимого признака сходимости и
признаков сравнения. Пр. 7.Опр. тригонометрического ряда, ряда Фурье в комплексной форме и
к-ой гармоники. Пр. 8. Опр. спектра периодической функции, амплитуд, фаз, гармонических и
круговых частот. Пр. 9. Свойства поточечной сходимости ряда Фурье. Пр. 10. Опр. диаметра
множества, интегральной суммы и двойного интеграла функции. Пр. 11. Приложения двойного
интеграла. Пр.12. Опр. КИВР второго рода. Приложение. Пр.
4.
ТИПЫ ЗАДАЧ К ЭКЗАМЕНУ, 2024-20251. Вычислить неопределённый интеграл от рациональной функции методом неопределённых коэффициентов. 2. Найти площадь
криволинейной трапеции. 3. Решить однородное, линейное,
Бернулли ОДУ. 4. Решить линейное ОДУ второго порядка с
постоянными коэффициентами. 5. Решить однородную НСЛДУ
второго порядка с постоянными коэффициентами с помощью
собственных чисел матрицы. 6. Исследовать на сходимость
числовой ряд методами Лагранжа, Лейбница, сравнения. 7.
Разложить в ряд Фурье по синусам (косинусам) функцию,
заданную графически и нарисовать график суммы ряда. 8.
Вычислить двойной интеграл на многоугольнике, круге. 9.
Вычислить массу однородной пластинки. 10. Вычислить работу
силового поля с помощью криволинейного интеграла.
5.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛПусть функция f ( x) определена на интервале (a, b) . Первообразная
функции f ( x) это дифференцируемая на (a, b) функция F ( x) со
свойством x (a, b) F ( x) f ( x) .
F ( x) f ( x)
0
x , 1
1
x
a , a 0, 1
x
cos x
sin x
1
cos 2 x
1
sin 2 x
1
1 x2
1
1 x2
F ( x)
C
x 1
1
F ( x) f ( x)
ln x
1
1 x2
ax
ln a
sin x
cos x
tg x
ctg x
arcsin x
arctg x
1
x2 a
F ( x)
, a 0 ln x x 2 a
1 1 x
ln
2 1 x
6.
ЛЕММА Если f ( x) 0 на (a, b) ,то f ( x) const на (a, b) . ЛЕКЦИЯ 20СЛЕДСТВИЕ Если F ( x) есть первообразная функции f ( x) на (a, b) ,
то любая другая первообразная имеет вид F ( x) C , где C произвольная постоянная.
Неопределенный интеграл функции – это множество всех ее
первообразных.
Обозначение f ( x)dx : F ( x) C .
СЛЕДСТВИЕ Равносильны утверждения:
1) два интеграла совпадают;
2) они имеют общую первообразную;
3) их подынтегральные функции совпадают.
Проинтегрировать функцию это значит найти ее первообразную.
sin x x2
, e , sin x 2 не имеют первообразных среди
Кпр. Функции
x
элементарных функций.
7.
ТЕОРЕМА 4.1 (правила и формулы интегрирования)1) (линейность) , R ( f ( x) g ( x)dx f ( x)dx g ( x)dx ,
если хотя бы два из трех интегралов существуют.
2) (формула замены переменных) Если f ( x)dx : F ( x) C и
функция (t ) : ( , ) (a, b) непрерывно дифференцируема на ( , ) , то
на ( , ) интеграл функции f ( (t )) (t ) вычисляется по формуле
ЛЕКЦИЯ 21 30.11.15
f ( (t )) (t )dt : F ( (t )) C .
◄ f ( (t )) (t )dt f ( (t ))d (t ) f (u )du F (u ) C F ( (t )) C .
sin 2 x
C
Пр. sin x cos xdx sin xd sin x
2
3) (формула интегрирования по частям) Если функции u ( x), v( x)
дифференцируемы на ( , ) , то интегралы u ( x) v ( x)dx, v( x) u ( x)dx
связаны равенством u ( x) v ( x)dx u ( x) v( x) v( x) u ( x)dx .
◄ u ( x) v( x)
v( x) u ( x)dx
u ( x) v( x) u( x) v ( x) u ( x) v( x) u( x) v ( x)
x
u ( x) v ( x)dx u ( x) v( x) v( x) u ( x)dx ► ЛЕКЦИЯ 18 12.12.19
Пр. ln x x dx
8.
12
Пр. x cos x 2 dx cos x 2 ( x 2 ) x dx x 2 : u, du ( x 2 ) x dx
9.
Пусть функция f ( x) имеет производную порядка s в точке x0 .x0 называется нулем кратности s функции f ( x) (или корнем
кратности s уравнения f ( x) 0 ), если
f ( x0 ) f ( x0 ) ... f ( s 1) ( x0 ) 0, f ( s ) ( x0 ) 0 .
Пр.1 Функция 1 cos x имеет ноль кратности 2 в точке x0 0
Пр.2 Функция f ( x) ( x x0 )n имеет ноль кратности n в точке x0 .
ЛЕКЦИЯ 18 16.12.19
ТЕОРЕМА (Гаусс, 1802) Многочлен n -ой степени
p( x) a0 x n a1 x n 1 ... an , a0 0 ,
имеет ровно n нулей, если учитывать кратность каждого нуля и все
комплексные нули. Если 1 ,..., n его нули, то имеет место
представление p( x) a0 ( x 1 ) ... ( x n ) .ЛЕКЦИЯ 20 6.12.14 ЛЕКЦИЯ 21 12.12.16
Пр. p( x) x5 x 4 x 1.
10.
Иоганн Карл Фри́дрих Га́усс (1777-1855) – немецкийматематик, астроном и физик, считается одним из
величайших математиков всех времён, «королём
математиков». Колмогоров Понятие потенциала электрического поля
Дал первые строгие доказательства основной теоремы
алгебры. Указал геометрическую модель комплексных
чисел и действий с ними. Открыл кольцо целых комплексных гауссовых чисел, создал теорию делимости, и
с их помощью решил ряд алгебраических проблем.
Дал классическую теорию сравнений, открыл конечное поле вычетов по
простому модулю, глубоко проник в свойства вычетов. (17-ти угольник на
надгробии) 1820 год - геодезическая съёмка королевства Ганновера. Электромагнитный телеграф. Фильм «Измеряя мир»
Впервые начал изучать внутреннюю геометрию поверхностей. Открыл
характеристику поверхности (гауссову кривизну), которая не изменяется
при изгибаниях, тем самым заложив основы римановой геометрии.
Продвинул теорию специальных функций (эллиптические функции),
рядов, численные методы, решение задач математической физики. Создал
математическую теорию потенциала. Критерий возможности построения правильного n-угольника с
2k
помощью циркуля и линейки: если n — простое число, то оно должно быть вида n 2
1 (числом Ферма).
11.
СЛЕДСТВИЕ Многочлен единственным образом представим ввиде произведения степеней двучленов ( x )k , R и квадратных
трехчленов с действительными коэффициентами ( x 2 px q)l ,
имеющих сопряженные комплексные нули a bi .
Правильная дробь - рациональная функция r ( x)
p( x)
с deg p deg q .
q( x)
Дробь неправильная, если deg p deg q .
ЗАМЕЧАНИЕ Неправильную дробь с помощью деления
числителя на знаменатель можно представить в виде суммы
многочлена и правильной дроби.
x4 x 1
x 5
Пр. 2
.
x2 2 2
x 2
x 2
12.
Простейшие дроби это рациональные функции видавида
a
или
k
(x )
ax b
, k N , где квадратный трехчлен имеет комплекс2
k
( x px q )
ные сопряженные нули. ЛЕКЦИЯ 18 24.11.17
ЗАМЕЧАНИЕ (Эйлер) Каждая правильная дробь единственным
образом представима в виде суммы простейших дробей.
Метод неопределенных коэффициентов - алгоритм Эйлера
представления в виде суммы простейших дробей. ЛЕКЦИЯ 20 5.12.18
13.
11
1
.
Имеем
dx
4
2
2
2
2
x x
x ( x 1)
x x
Пр.1 Вычислить интеграл 4
ЗАМЕЧАНИЕ 1 Пусть r ( x, y )
p ( x, y )
- рациональная функция двух
q ( x, y )
ax b
- дробно-линейная функция. Тогда интеcx d
ax b
m
грал вида r x,
dx сводится к интегралу от рациональной
cx
d
ax b
функции с помощью замены переменной t m :
. ЛЕКЦИЯ 2 10.02.25
cx d
1 x dx
Пр.
1 x x
переменных, а y
14.
ЗАМЕЧАНИЕ 2 Интеграл вида r (sin x,cos x)dx приводится кинтегралу о рациональной функции с помощью универсальной
x
подстановки t tg .
2
Пр.
dx
cos x sin x
15.
ЗАМЕЧАНИЕ 3 Следующие интегралы специального видаприводятся к интегралам от рациональных функций с помощью
соответствующих замен: r (sin 2 x,cos 2 x)dx t tgx ,
r (sin x) cos xdx t sin x, r (cos x)sin xdx t cos x .
dx
Пр.1
1 sin 2 x
Пр.2
cos dx
2
(1 sin x)
16.
ЗАМЕЧАНИЕ 4 К интегралам от рациональных функций спомощью двух последовательных замен приводятся интегралы
t
2
;
r
(
x
,
1
x
)
dx
x
:
sht
u
:
th
2
t
2
;
r
(
x
,
1
x
)
dx
x
:
sin
t
u
:
tg
2
1
t
2
r
(
x
,
x
1)
dx
x
:
u
:
tg
.
sin t
2
Пр.
dx
x 1 x
2
ЛЕКЦИЯ 19 4.12.23 6.12.24
17.
§ 7.2 Основные понятияДифференциальное уравнение (ДУ) - уравнение, содержащее
неизвестную функцию, независимые переменные и производные
этой функции.
ЗАМЕЧАНИЕ Термин -впервые в письме Лейбница к Ньютону,
1676. В печати - 1684 г.
Пр. Дифференциальное уравнение Риккати
y x a( x) y 2 b( x) y c( x) (1724).
Дифференциальное уравнение в частных производных (ДУЧП) –
ДУ, в котором независимых переменных
более одной;
обыкновенное дифференциальное уравнение (ОДУ) - ДУ, в
котором одна независимая переменная (термин на русском языке –
1869).
Пр. ДУЧП Лапласа
2u 2u 2u
2 2 0.
2
x
y
z
18.
Дифференциальное уравнение n-ого порядка - ОДУ, в которомсамый высокий порядок производной неизвестной функции равен
n (термин – Эйлер).
ОДУ вида yx( nn ) f ( x, y, y x ,..., yx( nn 11) ) - уравнение, разрешенное
относительно старшей производной yx( nn ) .
ОДУ вида F ( x, y, y x ... yx( nn ) ) 0 - уравнение общего вида.
Здесь f , F - известные функции.
Пр. y x 2 y 2 0 .
19.
Решение ОДУ n -ого порядка на интервале (a, b) это n раздифференцируемая на (a, b) функция, которая при подстановке в
уравнение обращает его в тождественное равенство.
Интегральная кривая - график решения
ОДУ. ЛЕКЦИЯ 8 14.03.19 ЛЕКЦИЯ 6
Пр.1. Если F ( x) - первообразная функции
f ( x) на (a, b) , то f ( x)dx F ( x) C : C R все решения ОДУ y f ( x) .
Пара чисел ( x0 , y0 ) , где x0 (a, b), y0 R ,
выделяют из этого семейства решений
одно со свойством y( x0 ) y0 : y0 F ( x0 ) C y( x) F ( x) ( y0 F ( x0 )) .
Пр.2 Произвольное решение ДУ y 2 есть двухпараметрическое
семейство функций y( x) x2 C1x C2 . Произвольная тройка чисел
( x0 , y0 , y1 ), x0 (a, b), y0 , y1 R определяет единственное решение
x02 C1 x0 C2 y0
y ( x0 ) y0
этого уравнения со свойством
.
2 x0 C1 y1
y ( x0 ) y1
20.
1не имеет решения с условием y(0) y0 .
x
Кпр.2 ОДУ yy xy с условием y( x0 ) 0 имеем два решения в
1
окрестности точки x0 0 : y 0, y ( x 2 x02 ) .
2
Пусть дано ОДУ n -ого порядка и числа x0 , y0 , y1 ,..., yn 1 .
Кпр.1 ОДУ y
Задача Коши - задача нахождения решения ОДУ в окрестности
точки x0 , которое удовлетворяет равенствам y( x0 ) y0 ,..., y ( n 1) ( x0 ) yn 1
называемым условиями Коши. Числа x0 , y0 , y1 ,..., yn 1 - данные Коши.
1) Общее решение ОДУ n -ого порядка в окрестности точки x0 это
функция y y( x, C1 ,...Cn ) , зависящая от n параметров C1 ,..., Cn , которая при подстановке в уравнение обращает его в тождество.
2) Решение, получаемое из общего при конкретных значениях
параметров, называется частным (понятия – Эйлер, 1743).
3) Решение ОДУ, в каждой точке которого нарушается единственность решения задачи Коши, называется особым.
Пр. Решение y 0 из Кпр.2. является особым.
21.
Огюсте́н Луи́ Коши́ (1789 - 1857) - великийфранцузский математик.
К. написал свыше 800 работ. Много работал в обла
сти комплексного анализа, в частности, создал тео
рию интегральных вычетов. В математической фи
зике глубоко изучил краевую задачу с начальными
условиями, которая с тех пор называется «задача
Коши». Ему принадлежат также исследования по
геометрии (о многогранниках), по теории чисел,
алгебре, астрономии, механике и во многих других областях науки.
Впервые дал строгое определение основным понятиям математиче
ского анализа - предел, непрерывность, производная, дифференциал,
интеграл, сходимость ряда и т. д. Его определение непрерывности
опиралось на понятие бесконечно малого, которому он придал новый
смысл: у К. бесконечно малое — переменная величина, стремящаяся к
нулю. Ввёл понятие радиус сходимости ряда.
Учебники по анализу К., основанные на систематическом исполь
зовании понятия предела, послужили образцом для большинства
курсов позднейшего времени.
22.
Общий интеграл - решение, заданное в виде неявной функцииG( x, y, C1 ,..., Cn ) 0 , и зависящее от n произвольных параметров.
Пр. x 2 y 2 C - общий интеграл ОДУ yy x x 0 .
Проинтегрировать ОДУ в явном виде - значит найти его общее
решение в виде элементарной функции.
Проинтегрировать ОДУ в квадратурах - найти его общее
решение в виде интегралов от элементарных функций.
y
sin x
x .
Пр.
ЗАМЕЧАНИЕ (Лиувилль) Уравнение Риккати
y x a( x) y 2 b( x) y c( x) не может быть решено в квадратурах.
Ключевые понятия подкластера «Основные понятия»:
1)Дифференциальное уравнение (ДУ), 2) ДУЧП, 3) ОДУ, 4)
интегральная кривая, 4) задача Коши, 5) общее, частное и особое
решение ОДУ, 6) общий интеграл.
23.
§ 7.3 Интегрируемые в квадратурах ОДУпервого и второго порядков
ОДУ с разделяющимися переменными - ОДУ вида y x f ( x) g ( y)
или вида f1 ( x) g1 ( y)dx f 2 ( x) g2 ( y)dy 0 .
ОДУ
dy
с разделенными переменными - ОДУ вида g ( y) f ( x)dx или
вида
f1 ( x)
g ( y)
dx 2
dy 0 .
f 2 ( x)
g1 ( y )
ЗАМЕЧАНИЕ Решения в квадратурах ОДУ с разделяющимися
dy
f 1 ( x)
g 2 ( y)
dy
f
(
x
)
dx
dx
g1 ( y) dy 0
переменными: g ( y )
, f 2 ( x)
(впервые –Лейбниц).
24.
ЗАДАЧА Скорость лодки в стоячей воде равна 10 км/час. Силасопротивления воды пропорциональна скорости. Через 20 сек.
после отключения мотора она равна 6 км/час. Какое расстояние
пройдет лодка через 1 минуту? vt 180ln(0.6) v , v(0) 10 .
25.
F ( x, y) - однородная функция степени k , если ЛЕКЦИЯ 6 10.03.170 ( x, y ) F ( x, y ) k F ( x, y ) .
Пр. F ( x, y )
x y
; F ( x, y ) x 2 xy y 2 .
x y
ЛЕКЦИЯ 2 .09.24
Однородное дифференциальное уравнение - ОДУ вида y x f ( x, y) ,
если f ( x, y) есть однородная функция нулевой степени, или вида
M ( x, y )dx N ( x, y )dy 0 , если M ( x, y ), N ( x, y) - однородные
функции одинаковой степени.
ЗАМЕЧАНИЕ (И.Бернулли, 1693) Замена зависимой переменной по
формуле y x z преобразует однородное ОДУ в ОДУ с
разделяющимися переменными.
26.
ОДУ в полных дифференциалах - дифференциальное уравнениевида P( x, y)dx Q( x, y)dy 0 , если функции P( x, y), Q( x, y) имеют
непрерывные частные производные и
P Q
(определение
y x
полного дифференциала, термин и метод – Клеро,1739).
ЗАМЕЧАНИЕ Последнее условие равносильно существованию
функции U ( x, y) с дифференциалом dU Pdx Qdy 0 . U ( x, y) C общий интеграл ОДУ.
ЛЕКЦИЯ 2 17.02.21
Пр. 3 y 2 2 xy 2 x dx 6 xy x 2 3 dy 0 .
ЛЕКЦИЯ 15.03.23
27.
ОДУ вида y x p( x) y q( x) y , 0,1 - уравнение Бернулли. Здесьфункции p( x), q( x) заданы и непрерывны (Я.Бернулли, 1695).
ОДУ вида y x p( x) y q( x) - линейное уравнение (ЛДУ).
ЗАМЕЧАНИЕ (метод вариации произвольной постоянной, в
общем случае - Эйлер, 1739, Лагранж, 1775).
1) Сначала решается ОДУ с разделяющимися переменными
y ' p( x) y 0 y Ce P ( x ) , где P ( x) p( x) .
2) Общее решение исходного уравнения y x p( x) y q( x) y ищется в
виде y C ( x)e P ( x ) ,( C ( x) - искомая функция - вариация постоянной C )
ЛЕКЦИЯ 7 20.05.15
ЛЕКЦИЯ 2 17.02.20 УТС-11, 11.02.22
28.
Я́коб Берну́лли (1654, Базель- 1705, там же) швейцарский математик, профессор математики Базельского университета (с 1687 года).Один из основателей теории вероятностей и
математического анализа.
Б. решает (1690) задачу Лейбница о форме
кривой, по которой тяжелая точка опускается
за равные промежутки времени на равные вер
тикальные отрезки (полукубическая парабола)
Доказательство проведено интегрированием
дифференциального уравнения. При этом
впервые появился в печати термин «интеграл».
Монография «Искусство предположений»,1713
Закон больших чисел. Распределение Б. Числа
Б. Лемниската Б.
29.
Пр. Уравнение фильтра нижних частотЛЕКЦИЯ 7, 2014, 2016
uo
1
A
uo
uo
sin t . ЛЕКЦИЯ 9 21.03.19 ЛЕКЦИЯ 2 УА11 17.02.22
RC
RC
C
ui
u0 (t ) C (t ) e
t
RC
A
1 ( RC )
2
R
sin( t 0 ) C0e
t
RC
30.
uo1
A
uo
sin t
RC
RC
Случай 1.
A R C 1, 0,2 T 10 .
Желтый цвет - напряжение источника
u (t ) A sin t .
Красный цвет - напряжение на
обкладках конденсатора uo (t ) .
Случай 2. A R C 1, 5 T 0,4 .
uo
C
ui
R
31.
ЗАМЕЧАНИЕ 1 Решение ОДУ второго порядка вида y '' f ( x, y ')сводится к решению ОДУ первого порядка z ' f ( x, z ) с помощью
замены z y ' .
Пр. yt 2 yt t 3 5.
ЗАМЕЧАНИЕ 2 (метод Я.Бернулли) Решение ОДУ второго
порядка вида y '' f ( y, y ') сводится к решению ОДУ первого
порядка с помощью замены y ' на зависимую переменную p : y ' .
Пр. l '' g sin - уравнение математического маятника.
Ключевые понятия подкластера «Интегрируемые ОДУ
первого и второго порядков»: 1) ОДУ с разделяющимися
переменными, 2) уравнение Бернулли и линейное уравнение.
32.
ЗАДАЧА Вывести уравнение колебаний маятника.Материальная точка массы m подвешена на
X нерастяжимой нити длины l . На неё действуют
(t )
две силы: вертикальная сила тяжести m g и сила
реакции нити. AB mg sin (t ) .
A
По второму закону Ньютона m a
B
Y
C
mg
m xt 2 , yt 2 F AB mg sin (t )cos (t ), mg sin 2 (t )
xt 2 g sin cos
2
y
g
sin
2
t
x cos y sin g sin .
Запишем закон колебаний маятника в виде
x l sin 2 l cos
x(t ) l sin (t )
x (t ) l cos (t )
2
y
(
t
)
l
cos
(
t
)
y
(
t
)
l
sin
(
t
)
y l cos l sin
l '' g sin x cos y sin l
- уравнение колебаний математического маятника.
33.
§ 7.4 Нормальная система обыкновенныхдифференциальных уравнений
Пр. Рассмотрим RLC -цепь. Закон
изменения напряжения источника e(t )
считаем известным, а ток в катушке
индуктивности iL (t ) и падение напряжения на конденсаторе uC (t ) - искомыми.
Применяя закон Кирхгофа для напряжений к контуру с учетом
uL = LiLў: e = RiL + LiLў + uC .
Применяя закон Кирхгофа для тока – к узлу между емкостью и
индуктивностью с учетом iL = iC = CuCў.
м
R
1
1
п
ў
п
i
=
i
u
+
e
L
C
пL
L
L
L
Получаем такое уравнение RLC -цепи пн
.
п
1
п
ў
u
=
iL
п
C
п
C
п
о
34.
Нормальная система обыкновенных дифференциальныхуравнений (НСОДУ) порядка n это система уравнений вида
x1 f1 (t , x1 ,..., xn )
............................ ,
x f (t , x ,..., x )
n
1
n
n
где функции f1 (t ),..., f n (t ) непрерывны на открытом множестве
G R n 1 , а последовательность неизвестных функций x1 (t ),..., xn (t ) решение системы.
xt a11 x a12 y f1 (t )
- НСОДУ второго порядка.
Пр.
)
t
(
f
y
a
x
a
y
2
22
21
t
Если x1 (t ),..., xn (t ) - решение НСОДУ в окрестности точки t0 , то
кривая l : t , x1 (t ),..., xn (t ) R n 1 : t (t0 , t0 ) в R n 1 - интегральная
кривая.
35.
00
(
t
,
x
,...,
x
Пусть 0 1
n ) G . Задача Коши для НСОДУ с начальными
x1 (t0 ) x10
условиями . . . - задача нахождения решения системы в
x (t ) x 0
n
n 0
окрестности точки t0 , которое удовлетворяет этим условиям.
( n)
( n 1)
Пр. Решение задачи Коши для ОДУ n -го порядка y f (t, y,..., y )
с начальными условиями y(t0 ) x10 ,..., y ( n 1) (t0 ) xn0 равносильно
нахождению решения задачи Коши для НСОДУ
x1 x2
...........
xn 1 xn
xn f (t , x1 ,..., xn )
с начальными условиями x1 (t0 ) x10 ,..., xn (t0 ) xn0 . ЛЕКЦИЯ 8,9
27.02.15
36.
Функция f (t , x1 ,..., xn ) удовлетворяет условию Липшица попеременным x1 ,..., xn на множестве K R n 1 , если
C 0 (t , x1 ,..., xn ), (t , y1,..., yn ) K
f (t , x1 ,..., xn ) f (t , y1 ,..., yn ) C ( x1 y1 ) 2 ... ( xn yn ) 2
ЗАМЕЧАНИЕ 1) Если функция f (t , x1 ,..., xn ) дифференцируема в
каждой точке области G R n 1 , то она удовлетворяет условию
Липшица на любом ограниченном замкнутом множестве
(компакте) из G .
2) Обратно, если f (t , x1 ,..., xn ) удовлетворяет условию Липшица,
то она непрерывна по совокупности переменных x1 ,..., xn в каждой
точке из G .
Кпр. Функция f (t , x) t ln x на K : (0,1] (0,1] R 2 не удовлетворяет
условию Липшица. ЛЕКЦИЯ 3 21.02.20 18.02.21 УТС-11 17.02.22
37.
ТЕОРЕМА 7.1 (теорема существования и единственностирешения)
Пусть функции f1 (t , x1 , ... , xn ),..., f n (t , x1, ... , xn )
непрерывны на открытом множестве G R n 1 и удовлетворяют
условию Липшица по x1 ,..., xn на любом замкнутом ограниченном
подмножестве ( компакте) в G . Тогда (t0 , x10 ,..., xn0 ) G в окрестности точки t0 существует единственное решение x1 (t ),..., xn (t ) задачи
Коши для НСОДУ с начальным условием x1 (t0 ) x10 ,..., xn (t0 ) xn0 .
Если отказаться от условия Липшица, то решение задачи Коши
существует, но оно, вообще говоря, неединственное.
ЗАМЕЧАНИЕ Коши, 1844; Липшиц; Пикар, 1890.
Кпр. Правая часть ОДУ xt 2 | x | непрерывна при всех t , x . Но не
удовлетворяет условию Липшица на компактах K , содержащих
окрестность нуля: | f (t , x) f (t ,0) | 2 | x | 0 2 для x K , x 0 .
| x 0|
| x|
| x|
Задача Коши с начальным условием x(t0 ) 0 имеет два решения:
x1 (t ) 0 и
(t t0 )2 , t t0
.
x2 (t )
2
(t t0 ) , t t0
ЛЕКЦИЯ 3 14.02.24
38.
39.
Ру́дольф О́тто Си́гизмунд Ли́пшиц(1832-1903) немецкий математик. Был учеником Дирихле.Профессор Боннского университета с 1864.
Основные работы в области математического
анализа, теории дифференциальных уравнений,
теоретической механики и алгебры.
Его учеником был Ф. Клейн.
Шарль Эми́ль Пика́р ( 1856-1941) –французский
математик. Иностранный чл.-корр. Петербургской
Академии наук (1895), почётный член АН СССР
(1925). Внёс существенный вклад в теорию диффе
ренциальных уравнений, теорию функций, тополо
гию, теорию групп. Для линейных дифференциаль
ных уравнений разработал аналог теории Галуа.
Результаты П. нашли широкое применение в прик
ладных науках: теория упругости,телеграфия и др.
Классический учебник анализа (Traité d'Analyse).
40.
Нормальная система линейных дифференциальных уравненийx1 a11 (t ) x1 ... a1n (t ) xn b1 (t )
. . . . .
(НСЛДУ) - система уравнений вида
x a (t ) x ... a (t ) x b (t )
n1
1
nn
n
n
n
или в матричной форме X t A(t ) X B(t ) , где
x1 (t )
xt (t )
X (t ) : .... - искомое решение на ( , ) ,
X t : ..... ,
x (t )
x (t )
n
t
a11 (t ) ... a1n (t )
-матрица непрерывных на ( , ) коэффициентов,
A(t ) :
......
a (t ) ... a (t )
nn
n1
b1 (t )
B (t ): ..... - матрица непрерывных на ( , ) свободных членов.
b (t )
n
НСЛДУ однородная, если t ( , ) B(t ) 0 , и неоднородная в
противном случае. ЛЕКЦИЯ 10,11 25.03.18
ЛЕКЦИЯ 8.14
41.
Пр. Рассмотрим RLC -цепь. Законизменения напряжения источника e(t )
считаем известным, а ток в катушке
индуктивности iL (t ) и падение напряжения на конденсаторе uC (t ) - искомыми.
Применяя закон Кирхгофа для напряжений к контуру с учетом
uL = LiLў: e = RiL + LiLў + uC .
Применяя закон Кирхгофа для тока – к узлу между емкостью и
индуктивностью с учетом iL = iC = CuCў.
м
R
1
1
п
ў
п
i
=
i
u
+
e
L
L
C
п
L
L
L
Получаем такое уравнение RLC -цепи пн
.
п
1
п
uCў = iL
п
п
C
п
о
42.
x11 (t )x1n (t )
Последовательность n решений X 1 (t ) ... ,..., X n (t ) ...
x (t )
x (t )
n1
nn
однородной НСЛДУ называется фундаментальной системой,
если t0 ( , ) векторы X1 (t0 ),..., X n (t0 ) линейно независимы.
dx
dt 2 x y
Пр.
.
dy 3 x 4 y
dt
x11 (t ) ...
W (t ) :
et
X 1 (t ) t ,
e
e5 t
X 2 (t ) 5t - решения НСЛДУ.
3e
x1n (t )
- определитель Вронского (вронскиан),
xn1 (t ) ... xnn (t )
x11 (t ) ... x1n (t )
W (t ) :
- фундаментальная матрица НСЛДУ.
x (t ) ... x (t )
nn
n1
43.
Ю́зеф Вро́ньский (1776 - 1853), польскийматематик и философ-мистик. Современник
К.Ф.Гаусса.
Математические работы В. отмечены
широтой охвата материала и общностью
постановки задач. Лагранж был того мнения,
что теории В. могут произвести переворот в
науке. Но болезненная гордость В., его склонность к мистицизму
и, наконец, сложность обозначений, использованных в его сочинениях, привели к тому, что его труды остались незамеченными
современниками. Уже после смерти В. исследователи его трудов
во второй половине XIX века обнаружили, что ему принадлежит
авторство значительного числа методов и некоторых
утверждений, которые к тому времени были заново открыты
другими математиками.
В. ввел функциональный определитель (вронскиан) в 1812 году.
44.
Производная функциональной матрицы A(t ) : (ai j (t )) -этофункциональная матрица At (t ) : (ai j (t )) . ЛЕКЦИЯ 10 25.03.19
Интеграл функциональной матрицы A(t ) : (aij (t )) на отрезке [ , ]
- числовая матрица вида A(t )dt : ai j (t )dt .
Пр.
1 2t
0 0 cos t dt
1
ЗАМЕЧАНИЕ 1) Постоянную матрицу-множитель C можно
выносить за знак интеграла и производной: CA(t )dt C A(t )dt ,
(CA(t )) CA (t ) . 2) ( A(t ) B(t )) A (t ) B(t ) A(t ) B (t ) .
45.
ТЕОРЕМА 7.2 (свойства решений НСЛДУ)x10
1) t0 ( , ) X 0 ... R n существует единственное решение на
x0
n
( , ) задачи Коши с начальным условием x1 (t0 ) x10 ,..., xn (t0 ) xn0 .
2) Систем n решений-столбцов X1 (t ),..., X n (t ) фундаментальная на
( , ) t0 ( , ) W (t0 ) 0 ;
3) Если система решений X1 (t ), ... , X n (t ) фундаментальная на ( , ) ,
то общее решение однородной НСЛДУ X t/ A(t ) X имеет вид
c
c1 X 1 ... cn X n W C , где C : ... c1 ,..., cn R .
c
1
n
4) Если X 0 (t ) - какое-либо (частное) решение неоднородной
НСЛДУ, то общее (любое) решение этой НСЛДУ имеет вид
X 0 (t ) c1 X1 (t ) .... cn X n (t ) c1 ,...., cn R ,
где X1 (t ),..., X n (t ) - фундаментальная система.
46.
5) (Лагранж) Если известна фундаментальная система X1 (t ),..., X n (t ) ,то частное решение неоднородной НСЛДУ X A(t ) X B(t ) находится
методом вариации произвольных постоянных X (t ) : W (t ) C (t ) из
системы уравнений W C B , и имеет явный вид
t
0
t
t
X 0 (t ) W (t ) W 1 ( ) B ( )d ,
ЛЕКЦИЯ 7 15.03.2017
t0
а решение задачи Коши с начальным условием X (t ) X имеет вид
0
t
0
X (t ) W (t ) W 1 (t0 ) X 0 W (t ) W 1 ( ) B ( )d - формула Коши,
t0
x10
где X 0 : ... .
xn0
ЛЕКЦИЯ 3 18.02.2022
47.
Линейное дифференциальное уравнение n -го порядка (ЛДУ) ОДУ видаy0( n ) a1 ( x) y ( n 1) .... an ( x) y f ( x) ,
(1)
где функции a1 ( x) ,..., an ( x), f ( x) непрерывны на ( , ) .
ЛДУ однородное, если x ( , ) f ( x) 0 и ЛДУ неоднородное в
противном случае.
Последовательность решений y1 ( x) ,..., yn ( x) однородного ЛДУ n го порядка линейно независимая на ( , ) , если не существует такой
ненулевой n -ки чисел 1 ,..., n , что на ( , ) 1 y1 ( x) ... n yn ( x) 0 .
y1 ( x)
...
yn ( x )
- определитель Вронского однородного ЛДУ
W ( x)
y1( n 1) ( x) ... yn( n 1) ( x)
Здесь y1 ( x),..., yn ( x) - последовательности линейно независимых решений
(фундаментальная последовательность решении ЛДУ) (Вронский,
1812).
48.
yn ( x )...
y1 ( x)
- фундаментальная матрица
W ( x)
(
n
1)
(
n
1)
y ( x) ... y ( x)
n
1
(матрица Вронского) однородного ЛДУ.
ЗАМЕЧАНИЕ Последовательность n решений ЛДУ (1) линейно
независима последовательность соответствующих решений
yn ( x )
y1 ( x)
. . . , ..., . . . ассоциированной с (1) НСЛДУ
y ( n 1) ( x)
y ( n 1) ( x)
1
n
y1 y2
. . .
yn 1 yn
yn an ( x) y1 ... a1 ( x) yn 1 f ( x)
фундаментальная.
49.
ТЕОРЕМА 7.3 (свойства решений ЛДУ n -го порядка)1) x0 ( , ) { y10 ,..., yn0 } R n задача Коши с начальным условием
y ( x0 ) y10 ,..., y ( n 1) ( x0 ) yn0 имеет единственное решение на ( , ) .
2) Решения y1 ( x)1 ,..., yn ( x) однородного ЛДУ линейно независимы
на ( , ) x0 ( , ) W ( x0 ) 0 .
3) Если y1 ( x),..., yn ( x) - фундаментальная последовательность
решений однородного ЛДУ, то любое (общее) его решение
имеет вид c1 y1 ( x) ... cn yn ( x) .
4) Если y0 ( x) -какое-либо решение ЛДУ (1) и y1 ( x),..., y n ( x) фундаментальная последовательность решений, то любое
(общее) решение ЛДУ можно записать в виде
y0 ( x) c1 y1 ( x) ... cn yn ( x) .
50.
ЗАМЕЧАНИЕ ( алгоритм решения ЛОДУ y x py x qy f ( x) )2
1) Найти фундаментальную систему решений однородного ЛОДУ
y x py x qy 0 .
2 p q 0 - характеристическое уравнение с корнями 1 , 2 .
а) 1 , 2 R , 1 2 yo ( x) : C1e x C2e x - общее решение
однородного ЛОДУ. h1 ( x) : e x , h2 ( x) : e x . ЛЕКЦИЯ 9. 2016
2
1
2
1
2
б) 1 2 : R yo ( x) : C1e x C2 xe x .
1
2
h1 ( x) : e x , h2 ( x) : xe x .
в) 1,2 i, i : 1 yo ( x) e x (C1 cos x C2 sin x) .
h1 ( x) : e x cos x, h2 ( x) : e x sin x .
2) Общее решение методом вариаций ищется в виде
y( x) : C1 ( x)h1 ( x) C2 ( x)h2 ( x) ,
h C h C 0
2 2
где C1 ( x), C2 ( x) есть общее решение СЛДУ 1 1
.
h1 C1 h2 C2 f
51.
Харакеристический многочлен матрицы A M n ,n - многочлен n ой степени p( ) : det( E A) (ввел Коши,1826; термин Фробениус, 1896).Нули этого многочлена 1 ,..., r порядков p1 ,..., pr соответственно
называются собственными числами матрицы A .ЛЕКЦИЯ 4 28.02.20
Ненулевые решения СЛАУ ( A i E) X 0 называются собственны
ми векторами матрицы A , соответствующими собственному
числу i .
1 2
1 2
Пр. A
E A 2 1
2
1
1 2
det E A
1 3 0 1 1, 2 3 .
2 1
1
2 2
2 x 2 y 0
X1 .
1 1 E A
1
2 2
2 x 2 y 0
1
2 2
2 x 2 y 0
X
.
2 3 3E A
2
1
2 2
2 x 2 y 0
ЗАМЕЧАНИЕ 1 ,..., k попарно различны X1 ,..., X k лин. независимы.
52.
ТЕОРЕМА 7.4 (решение НСЛДУ с постоянными коэффициентами методом вариаций. Д’Аламбер, Л.Эйлер, 1743; Лагранж, 1762)
Пусть собственные числа 1 ,..., n матрицы коэффициентов НСЛДУ
x1k
X ' AX B(t ) попарно различны, X k . . . - соответствующие им соб
x
nk
ственные векторы, и элементы матрицы B(t ) непрерывны. Тогда:
1) общее решение однородной НСЛДУ имеет вид c1 X1e 1t ... cn X ne nt ;
2) матрица W (t ) : ( xij e j t ) является фундаментальной, и решение
задачи Коши однородной НСЛДУ находится по формуле
W (t ) W 1 (t0 ) X 0 ;
3) общее решение НСЛДУ ищется методом вариаций в виде
c1 (t )
X 0 W (t )C (t ) c1 (t ) X 1 (t ) ... cn (t ) X n (t ) , где C (t ) . . . есть общее
c (t )
n
t
t
x11e 1 c1 ... x1n e n cn b1 (t )
решение СЛДУ
. ЛЕКЦИЯ 9. 2014
nt
1t
xn1e c1 ... xnn e cn bn (t )
~
53.
Лагранж Жозеф Луи (1736-1813), французскийматематик и механик, член Парижской АН (1772).
Родился в семье обедневшего чиновника.
Самостоятельно изучал математику.
Наиболее важные труды Лагранжа относятся к 1)
вариационному исчислению, 2) аналитической и
теоретической механике. Опираясь на результаты Л.
Эйлера, разработал основные понятия вариацион
ного исчисления и предложил общий аналитический
метод (метод вариаций) для решения вариационных задач.
Выдающиеся исследования в следующих разделах математики:
математический анализ (формула остаточного члена ряда Тейлора,
формула конечных приращений, теория условных экстремумов,
формула интерполяции),
теории чисел, алгебра (симметрической функции корней уравнения,
теория и приложения непрерывных дробей),
дифференциальные уравнения (теория особых решений, метод вариации постоянных), математическая картографии, астрономии и пр.
54.
Пр. Рассмотрим RLC -цепь. Законизменения напряжения источника e(t )
считаем известным, а ток в катушке
индуктивности iL (t ) и падение напряжения на конденсаторе uC (t ) - искомыми. ЛЕКЦИЯ 4 УТС-11 24.02.22
Применяя закон Кирхгофа для напряжений к контуру с учетом
uL = LiLў: e = RiL + LiLў + uC .
Применяя закон Кирхгофа для тока – к узлу между емкостью и
индуктивностью с учетом iL = iC = CuCў.
м
R
1
1
п
ў
п
i
=
i
u
+
e
L
L
C
п
L
L
L
Получаем такое уравнение RLC -цепи пн
.
п
1
п
uCў = iL
п
п
C
п
о
55.
xt x 2 y etПр. Найти общее решение НСЛДУ
.Подробно решен
yt 2 x y 2t
1 2
1
1
A
1 1, 2 3 X 1 , X 2 .
2 1
1
1
56.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛРазобьем отрезок [a, b] точками a : x0 ... xn : b на n попарно
непересекающихся отрезков, и обозначим T : {xk } это разбиение.
Длина наибольшего из отрезков d (T ) : max xk , где xk : xk xk 1 ,
1 k n
называется диаметром разбиения T отрезка [a, b] .
ЗАМЕЧАНИЕ При d (T ) 0 число n отрезков разбиения стремится
к бесконечности, а длины всех этих отрезков равномерно стремятся
к нулю.
Пусть на отрезке [a, b] задана
функция f ( x) . Произведем разбиение [a, b], и выберем на k -ом
отрезке разбиения точку k , k n .
Обозначим E E (T ) : { k }.
n
Сумма вида S f (T , E ) : f ( k ) xk
k 1
- интегральная сумма.
57.
Определенный интеграл (Римана) функции f ( x) на отрезке [a, b]это конечный предел s : lim S f (T , E ) , равномерный относительно
d (T ) 0
выбора точек E : 0 0 d (T ) E E (T ) S f (T , E ) s ,
f ( x) - интегрируемая по Риману функция.
b
Обозначение f ( x)dx : s .
b
a
a
Пр. Для f ( x) C
b
Cdx C (b a) .
a
ЛЕКЦИЯ 21 9.12.2014 11.12.2015
ЛЕКЦИЯ 19 16.12.2019
58.
ЗАМЕЧАНИЕ Если функция f ( x) интегрируемая и четнаяa
(нечетная) на отрезке [ a, a] , то f ( x)dx 2 f ( x)dx f ( x)dx 0 .
a
0
a
a
a
Пр. (квадратура кубической параболы) Площадь
криволинейной трапеции между кубической
параболой и осью OX равна
1 n 3
k 1
3
3
s x dx lim k xk lim lim 4 k
d (T )
n
n n
k 1
k 1 n n
k 1
0
1
n
n
3
n 2 n 1 2 1
lim
.
n
4
4n 4
Это одна из многочисленных задач со времен Древней Греции до
XVII века (Джон Валлис).
3
1
1
1
1 4
k 1
3
x
dx
По формуле Ньютона-Лейбница s nlim
.
x
n
4
4 0
k 1 n
0
n
ЛЕКЦИЯ 23 14.12.15
59.
Исаак Барроу (1630-1677) – английский математик,физик, богослов. Читал лекции второкурснику Ньютону
(1665). Впоследствии они были изданы книгой и куплены
Лейбницем в 1673г. В книге изложен принцип: между
задачами о касательных и задачами о площадях имеется
двойственность (изложенная на языке геометрии, но не в
терминах переменной и функции).
Ньютон никогда не оспаривал приоритет Барроу 1) в откры
тии формулы Ньютона-Лейбница и 2) интегрировании диффе
ренциального уравнения с разделяющимися переменными.
Издал труды Евклида, Архимеда, Аполлония со своими комментариями.
Термин интеграл ввел И. Бернулли (1690). Обозначение дал Лейбниц (1686).
Бернгард Риман (1826-1866) - немецкий математик. В
1854 г. определил процедуру интегрирования, которую
впоследствии назвали его именем.
Обобщая геометрию Евклида и Лобачевского, развил
теорию обобщенных римановых пространств - источник
теории относительности.
Прорывные результаты в теории чисел, теории функций
комплексного переменного, теории уравнений в частных
производных, теории тригонометрических рядов.
60.
Функция кусочно непрерывна на [a, b] , если она непрерывна наэтом отрезке за исключением конечного числа точек разрыва
первого рода.
Функция кусочно монотонна на [a, b] , если она ограничена и
отрезок можно разбить на конечное число интервалов, на каждом
из которых функция монотонна.
ТЕОРЕМА 4.2 (существования определенного интеграла)
1) Если функция f ( x) кусочно непрерывна или кусочно монотонна
b
на [a, b], то определённый интеграл f ( x)dx существует.
a
2) Если функция f ( x) интегрируема на [a, b] , то она ограничена на
[ a, b] .
61.
ТЕОРЕМА 4.3 (свойства определенного интеграла)b
b
b
a
a
a
1) , R ( f ( x) g ( x))dx f ( x)dx g ( x)dx , если хотя бы два
из этих интегралов существуют , , 0.
b
b
a
a
2) Если x [a, b] g ( x) f ( x) , то g ( x)dx f ( x)dx .
ЛЕКЦИЯ 22 14
3) Если f ( x) интегрируема на [a, b] и m : inf f ( x), M : sup f ( x) ,
x [ a ,b ]
x [ a ,b ]
b
то m(b a) f ( x)dx M (b a) .
a
4) (теорема о среднем значении) Если f ( x) непрерывна, а g ( x)
b
b
a
a
знакопостоянна на [a, b] , то (a, b) f ( x) g ( x)dx f ( ) g ( x)dx
при условии существования интегралов.
b
c
b
a
a
c
5) c [a, b] f ( x)dx f ( x)dx f ( x)dx . ЛЕКЦИЯ 3 21. 02. 23
62.
ТЕОРЕМА 4.4 1) (формула первообразной) Если f ( x) непрерывxна на [a, b], то функция ( x) : f (t )dt является первообразной f ( x) .
a
2) (формула Ньютона-Лейбница) Если f ( x) непрерывна на [a, b] и
b
F ( x) какая-либо ее первообразная, то f (t )dt F (b) F (a ) .
a
3) (формула замены переменной) Если f ( x) непрерывна на [a, b] , а
функция x (t ) непрерывно дифференцируема на [ , ] и
t [ , ] (t ) [a, b], ( ) a, ( ) b , то
b
f ( x)dx f ( (t )) (t )dt .
a
4) (формула интегрирования по частям) Если функции u ( x), v( x)
непрерывно дифференцируемы на [a, b] , то
b
b
u( x)v ( x)dx u ( x)v( x) | u ( x)v( x)dx ,
b
a
a
где u( x)v( x) |ba : u(b)v(b) u(a)v(a) .
a
63.
ЗАМЕЧАНИЕ Если f ( x) непрерывно дифференцируема на [a, b] ,то для любого разбиения T этого отрезка по теореме о среднем
найдется последовательность точек k [ xk 1 , xk ], k 1,...n со свойством
b
n
xk
n
f ( x)dx f ( k ) xk S (T , E ) ,
a f ( x)dx
k 1 x
k 1
k 1
то есть определенный интеграл совпадает с некоторой интегральной
суммой функции.
Пусть f ( x) определена на [a, b] .
n
Сумма вида S ( A, E ) : f (xk( n ) ) Ak( n ) - квадратурная формула, где
k 1
a x1( n) ... xn( n) b, A : { Ak( n) } R ,
числа xk( n ) - узлы квадратурной формулы, ЛЕКЦИЯ 21 25.12.19
числа Ak( n ) - коэффициенты квадратурной формулы,
b
число R f ( A, E ) : f ( x)dx S ( A, E ) - остаточный член квадратурной
a
формулы.
64.
ЗАМЕЧАНИЕ (формула прямоугольников) Разобьем [a, b]b a
, k 0,1,..., n , на n
n
отрезков одинаковой длины. Если функция f ( x) имеет
непрерывную производную второго порядка на [a, b] , то
равноотстоящими точками xk : a hk , где h :
квадратурная формула прямоугольников имеет вид
b
n
a
k 1
f ( x)dx f (x ) h R ( A, E ) ,
k
f
3
xk xk 1
(
b
a
)
[
a
,
b
]
где xk :
и
R f ( A, E )
f ( ) .
2
24n 2
65.
2sin x
dx с точностью 10 2 .
Пр. Вычислить интеграл
x
0
а) Оценим модуль остаточного члена квадратурной формулы
(b a )3
R f ( A, E )
f ( ) .
2
24n
sin x
sin x
x cos x sin x
sin x 2 sin
(0, x ), ф.Коши
f ( x)
.
2
3
x
x
3
x
x
sin x
2 sin x
Функция
монотонно убывает на [0, ].
1
2
x
x
1
1 sin x
sin x 2 sin x
2 2 1
1
f ( x)
| f ( x) | .
3
3 x
x
3 x
3 3
3
б) Найдем число узлов формулы, обеспечивающее точность.
1
3
1
при n 3.
| R f (T , A) |
|
f
(
)
|
2
2
100
576 n
2 24 n
3
5
sin
sin
sin
3
в) S ( A, E ) sin xk 12 4 12 1,38
5
xk
6
6
k 1
4
12
12
с точностью 0,01. ЛЕКЦИЯ 20 6.12.23
2
sin x
0 x dx 1,38
66.
§ 5.3 Свойства кривых. Приложения определенного интеграла.x x(t )
, t [ , ]
Пусть кривая l задана параметрическим уравнением
y
y
(
t
)
Фиксируем разбиение T {tk }отрезка [ , ] и выберем точки кривой
M k : ( x(tk ), y(tk )) l , k 0,1,..., n . Длина k -го отрезка
равна sk : ( x(tk ) x(tk 1 )) 2 ( y (tk ) y (tk 1 )) 2
длина ломаной lT , составленной из этих
M k 1M k
n
отрезков и вписанной в l , равна s (lT ) : sk .
M k 1
M0
Mn
Mk
k 1
Кривая l спрямляемая, если существует конечный sup s(lT ) : s(l ) .
T
Он называется длиной кривой. ЛЕКЦИЯ 23 23.12.16
Кривая l кусочно гладкая, если ее можно разбить на конечное
число гладких кусков.
67.
x cos tx t
, t [0, ] , и l2 :
, t [ 1,1] ,
y sin t
y 0
Пр. Кривая l , составленная из l1 :
l1
кусочно гладкая.
l2
ТЕОРЕМА 4.5 1) (длина дуги) Если кривая l кусочно гладкая, то
она спрямляемая. Ее длина вычисляется по формуле
s (l ) x 2 (t ) y 2 (t )dt .
ЛЕКЦИЯ 23.13
b
Если l задана функцией y f ( x) , x [a, b], то s(l ) 1 f 2 ( x)dx .
a
(И. Барроу,1670).
Если l задана в полярной системе координат:
( ), [ , ], то s (l ) 2 ( ) 2 ( )d
(И. Барроу,1670)
ЛЕКЦИЯ 23
68.
2) (площадь криволинейной трапеции) Пусть на отрезке [a, b] заданынепрерывные функции g ( x) f ( x) . множество точек
Gg , f [a, b] : ( x, y ) : a x y, g ( x) y f ( x) называется криволинейной
трапеций.
Прощадь криволинейной трапеции вычисляется по формуле
b
s f ( x) g ( x) dx .
a
Пр. Найти площадь криволинейной
трапеции, ограниченной кривыми
y x 2 2 x 3, y x 2 1.
ЛЕКЦИЯ 22 14.12.14
ЛЕКЦИЯ 22 19.12.18
69.
3) (площадь углового сектора)Пусть дан криволинейный сектор
D : ( , ) : [ , ], 0 ( ) ,
где функция ( ), [ , ],
непрерывна. Тогда площадь
сектора существует и вычисляется
по формуле
1
s ( D) 2 ( )d .
2
Пр. D : ( , ) : [0,2 ], 0 ln(1 ) .
70.
4) (объем тела вращения) Пусть функция y f ( x), x [a, b], непрерывна и неотрицательна. Тогда объем тела, получаемого вращением
криволинейной трапеции D : ( x, y) : x [a, b], 0 y f ( x) вокруг отрезb
ка [a, b] OX , существует и вычисляется по формуле v(G ) : f 2 ( x)dx
a
5) (площадь поверхности вращения) Пусть функция y f ( x), x [a, b],
кусочно гладкая и неотрицательна. Тогда площадь боковой поверх
ности L тела, получаемого вращением криволинейной трапеции
D : ( x, y ) : x [a, b], 0 y f ( x) вокруг отрезка [a, b] OX , существует и
b
вычисляется по формуле s(L ) 2 f ( x) 1 f 2 ( x)dx .
a
71.
x2 y 2 z 2Пр. Найти объем эллипсоида G ( x, y, z ) : 2 2 2 1 , полученно
a
b b
x2 y 2
го вращением эллипса 2 2 1 вокруг его оси [ a, a]
a
b
ЛЕКЦИЯ 8.12.20
ЛЕКЦИЯ 19 13.12.24
ЛЕКЦИЯ 24 21.12.15
72.
Статический момент материальной точки A( x, y) массы mотносительно оси OX M OX ( A) : m y .
6) Статический момент системы материальных точек
T : Ak ( xk , yk ) , k 1,2,..., n , соответствующих масс mk относительно
n
оси OX M OX (T ) : mk yk .
k 1
Пусть однородная пластинка в форме криволиней
ной трапеции G : ( x, y) : a x b, ( x) y f ( x) имеет
плотность . Разобьем ее сетью вертикальных прямых x xk на узкие трапеции Gk , k 1,2,..., n . Фиксируем k [ xk 1, xk ] и
разобьем прямоугольник Gk : ( x, y) : xk 1 x xk , ( k ) y f ( k ) прямыми
f ( k ) ( k )
, на n прямоугольников Gk ,i . s Gk ,i hk xk .
n
Выберем материальные точки Ak ,i : k , ( k ) (i 1 2) hk Gk ,i с массой
y ( k ) ihk , hk
m Gk ,i hk xk .
n
Статический момент системы этих точек равен
n
n
n
k 1 i 1
k 1
i 1
hk xk ( k ) (i 1 2) hk hk xk ( k ) (i 1 2) hk
73.
b1 n
1
f ( k ) 2 ( k ) 2 xk f ( x) 2 ( x) 2 dx
2 k 1
2 a
b
1
M OX G : f ( x ) 2 ( x) 2 dx
2 a
- статический момент
криволинейной трапеции G относительно оси OX.
b
Аналогично, M OY G : x f ( x) ( x) dx - статический момент
a
криволинейной трапеции G относительно оси OY.
Пр. Вычислить статический момент инерции круга
DR : ( x, y) : x 2 y 2 R 2 относительно оси OX.
DR - верхний (нижний) полукруг.
M OX DR M OX DR M OX DR
b
b
1
1
( R 2 x 2 ) 02 dx 02 ( R 2 x 2 ) dx 0 .
2 a
2 a
74.
m1x1 m2 x2m y m y
Пр. Для двух точек имеем xц (T )
, yц (T ) 1 1 2 2 .
m1 m2
m1 m2
Проверим равенство m1 ( A1, Ac ) m2 ( A2 , Ac ) .
Координаты центра масс системы материальных точек
T : Ak ( xk , yk ) , k 1,2,..., n , соответствующих масс mk вычисляются
по формулам xц (T )
1
n
m
k 1 k
M OY (T ) , yц (T )
1
n
m
k 1 k
M OX (T ) .
7) Координаты центра масс однородной пластины
G : ( x, y ) : a x b, ( x) y f ( x) с постоянной плотностью
плотностью вычисляются по формулам
b
1
1
M OY G b
x f ( x ) ( x ) dx
xц (G )
m(G )
a f ( x) ( x)dx a
.
b
1
1
y
(
G
)
M
G
f ( x ) 2 ( x ) 2 dx
OX
b
ц
m(G )
2 f ( x) ( x)dx a
a
75.
Момент инерции материальной точки A( x, y) массы mотносительно оси OX IOX ( A) : m y 2 .
Момент инерции системы материальных точек T : Ak ( xk , yk ) ,
k 1,2,..., n , соответствующих масс mk относительно оси OX
n
I OX (T ) : mk yk2 .
k 1
b
1
8) M OX G : f ( x)3 ( x)3 dx - момент инерции однородной
3 a
криволинейной трапеции G : ( x, y) : a x b, ( x) y f ( x) с
плотностью относительно оси OX.
b
M OY G : x 2 f ( x) ( x) dx - момент инерции однородной кривоa
линейной трапеции G с плотностью относительно оси OY.
76.
Пр. Вычислить момент инерции однородной треугольнойпластины D ( x, y) : 0 x 1, 0 y 1 x относительно осей OX и OY .
ЛЕКЦИЯ 24. 13
ЛЕКЦИЯ 21. 11.12.23
77.
9) Работа переменной силы F ( x) , действующей в направленииx
оси OX на отрезке [ x1, x2 ] , вычисляется по формуле A x 2 F ( x)dx .
1
УА 8.12.21
Пр. Вычислить работу переменной силы F ( x) sin x на отрезке [0,2 ] .
A
2
0
2
sin xdx cos x 0 (1 1) 0 .
78.
x dx(2 x 5)dx
,
( x 3)( x2 6 x 6) x3 3x2 3x 1
79.
22
2x
ln(
x
1)
dx
,
cos
2
x
x
dx
,
e
sin x dx
80.
ЧИСЛОВЫЕ РЯДЫ И РЯДЫ ФУРЬЕЧисловой ряд - выражение вида a1 a2 ... an ... an , где a1, a2 ,... R .
n 1
Пр. Геометрический ряд a aq ... aq
n 1
... aq aq k 1 ;
n 0
n
k 1
1
1
1
гармонический ряд 1 ... ... ;
2
n
n 1 n
1
1
обобщенный гармонический ряд 1 p ... p ... 1p , p R .
2
n
n 1 n
N -ая частичная сумма ряда an - сумма S N : a1 ... aN , N 1,2,...
n 1
Пр.1 Для ряда 1
n 1
S1 1, S2 S1
1
1
1 1
1
1 1
9
1 , S4 S2 2 , S6 S4 2 , ...
2
2
3 4
12
5 6
20
Пр.2 Для aq
n 1
n
n 1
S N a ... aq
N 1
1 qN
.
a
1 q
81.
Числовой ряд сходится, если существует конечный предел S : lim S NN
Этот предел S называется суммой ряда. ЛЕКЦИЯ 11 6.11.19
Обозначение S : an .
n 1
Пр. Если a 0, q 1, то aq n 1 lim a 1 q a
N
1 q
N
n 1
1 lim q N
N
1 q
a
.
1 q
Числовой ряд расходится, если lim S N равен или не существует.
N
Пр1 Знакочередующийся ряд 1 1 1 ... ( 1) ... ( 1) n 1 расходится,
n
n 1
так как N 1 S2 N 1 1, S2 N 0 . ЛЕКЦИЯ13 1.11.14
Пр. 2 (Орем ,1350, Менголи, 1650 г.) Гармонический 1 1 ... 1 ... ряд
2
расходится ◄ m N S2m 1 1 11 2 1
1 2
2m 1
m
1 2 ... m 1
2 2
2
2
n
1
1
...
...
m 1
m
m 1
m 1
2 2 1 2 2 2
2 2 2
2 1
m
lim S2m lim 1
m
m
2
lim S N .
N
82.
ЗАМЕЧАНИЕ Первое корректноеопределение предела последовательности
дано Больцано (1817) и Коши (1821).
Графический способ доказательства
предела (Менголи, около 1650 г.)
1 1 1
2 3 ... 1
2 2
2
Аналитический способ доказательства
◄
?
1 1 1
... 1.
2 2 2 23
1
1
2 2n 1
1
1
1
) 1.
(1
lim
lim Sn lim ... n lim
n
1
n
n
n 2
n
2
2
1
2
83.
Вавилонские математики умели суммировать геометрическую и арифметическую прогрессии. Архимед (287-212 дон.э.) в «Квадратуре параболы» приводит бесконечный ряд.
Принципиальный шаг в создании теории сделал Ньютон
(1643-1727): он указал приемы разложения дробей и корней
в степенные ряды (первые открытия в 1673г.):
( 1)...( k 1) k k
a x ... - обобщённая
a x a a 1x ...
формула Ньютона.
k!
Готфрид Лейбниц (1646-1716) в теории рядов - это
1
3
1
5
1
7
разложение для arctg x x x3 x5 x7 ... и вычисление
1 1 1
1 ....
4
3 5 7
Брук Тэйлор (1685-1731) ввел одноименный ряд в 1715 г.
84.
ТЕОРЕМА (признаки сходимости числового ряда)1) (необходимый) Если ряд an сходится, то lim an 0 .
n
n 1
a
n a
n
2) (Даламбера,1768) Пусть n 1 an 0 . Если lim n 1 q , то при q 1
ряд an сходится, при q 1 расходится и lim an .
n
n 1
n a q , то при
3) (Коши-Маклорена,1742) Пусть n 1 an 0 . Если nlim
n
q 1 ряд an сходится, при q 1 расходится и lim an .
n
n 1
a
bn
n
0, , то ряды
4) (сравнения) Пусть n 1 0 an bn . Если nlim
a , b одновременно сходятся или расходятся. Если b схо
n 1
n
n 1
n
n 1
n 1
n 1
n 1
n
дится, то an сходится. Если an расходится, то bn расходится.
5) (Лейбница,1682) Пусть n 1 an 0, lim an 0, an 0 . Тогда
n
знакопеременный ряд 1 an сходится.
n 1
n 1
85.
Пр. (Фурье, 1805) Коэффициенты Фурье f ( x) на отрезке [a, a 2l ]по системе 1 , 1 cos x, 1 sin x,... имеют вид , ЛЕКЦИЯ 8 17.03.21
2l
1
1
k
f,
cos
t
l
l
l
a 2l
a
l
l
k
f (t ) cos
t dt ,
l
a0
k
k
ak cos x bk sin
x
2 k 1
l
l
l
l
1
1
k
f,
sin
t
l
l
l
a 2l
f (t )sin
a
k
t dt .
l
- тригонометрический ряд Фурье
функции f ( x) по ортогональной системе 1, cos x, sin x,... с ко
a 2l
эффициентами a0 , a1, b1,... , где ak 1 f (t )cos k t dt ,
l a
l
k
k
xi
l
ck e
l
a 2l
k
1
bk f (t )sin
t dt
l a
l
- ряд Фурье в комплексной форме функции f ( x) по
ортогональной системе
где ck 1
2l
l
a 2l
a
k
ti
l
f (t )e
dt
k
xi
l
{e
}|
k
. ЛЕКЦИЯ 8.04.16
с коэффициентами {c0 , c1,...},
УА-11 ЛЕКЦИЯ 6 4.03.22
86.
Жан Батист Жозеф Фурье (1768-1830)- французский математик и физик.
Родился в семье портного. В 9 лет потерял обоих родителей. Окончил военную
школу при монастыре. В 1795-1798годах
преподавал в Политехнической школе.
Ф. получает от Наполеона титул барона,
награжден орденом Почётного легиона.
Свои методы (ряды и интегралы Фурье) Ф. использовал
в теории распространения тепла. Доказал, что всякую
произвольно начерченную линию, составленную из отрез
ков дуг разных кривых, можно представить единым аналитическим выражением - рядом Фурье
a0
k
k
ak cos x bk sin
x
2 k 0
l
l
Имя Ф. внесено в список величайших учёных Франции,
помещённый на первом этаже Эйфелевой башни.
87.
kk
x bk sin
x - k -ая гармоника тригонометрического ряда.
l
l
cos k : ak Ak
k
2
2
x k
Для Ak : ak bk и угла k ( , ] :
Ak cos
l
sin k : bk Ak
k
k
k
k
Ak cos k cos
x Ak sin k sin
x ak cos
x bk sin
x - k -ая гармоника.
l
l
l
l
ak cos
k
k
xi
l
ck e
Ak ck - амплитуда; k arg ck - фаза.
a0
a0
k
k
k
Пусть ak cos x bk sin x = Ak cos x k есть три2 k 1
l
l
2 k 1
l
гонометрический ряд Фурье T : 2l - периодической функции f ( x) .
{ak , bk }, { Ak , k } или {ck ,arg ck } - спектр периодической функции f ( x) ;
Ak - амплитуда k -ой гармоники; k - фаза k -ой гармоники;
k k
1 1
:
основная
частота;
- k -ая гармоническая
0 :
k
T 2l
T 2l
частота; 0 : 2 - основная круговая частота; k : 2 k k - k T
l
T
l
ая круговая частота функции f ( x) .ЛЕКЦИЯ 11 12.04.17
88.
Пр. График и спектр ряда Фурьефункции
bk
2
1 sin kx dx
0
N
2
1 ( 1) k .
k
2
1 ( 1) k sin kx . ЛЕКЦИЯ 3 22.09.23
k 1 k
S N ( x)
2
1 ( 1) k ikt
k
S ( x)
1 ( 1) sin kx
e
k 1 k
k , k 0 ki
2
2
cos (2l 1) x
cos (2l 1) x
2 l 0 ( 2l 1)
2
l 0 (2l 1)
89.
90.
91.
ЗАМЕЧАНИЕ (электротехнический смысл) Для функцииf ( x) L2 (a, a 2l ) равенство Парсеваля принимает вид
a 2l
2
1 2
1
1
2
a0
2
2
(
a
b
).
=
f 2
f
(
t
)
dt
k
k
2l
2l a
2 k 1 2
Для периодического с периодом T на [0, ) аналогового
сигнала f (t ) (тока, напряжения) величина A 1
T
a 2l
f 2 (t )dt
a
1
f 2 T
квадратическое (действующее) значение сигнала.
k
x k квадрат действующего
l
Пр. Для k -ой гармоники Ak cos
2
1 2
ak2 bk2 Ak2 a0
2
2
Ak - равенство
значения равен
, A02 A A0
2
2 2
k 1 2
Парсеваля.
ВЫВОД Квадрат действующего значения сигнала равен сумме
квадратов действующих значений составляющих его гармоник.
92.
ТЕОРЕМА 8.2 (свойства сходимости ряда Фурье)1) (Дирихле, 1829-37) Пусть 2l -периодическая на всей оси функция f ( x)
а) имеет разрывы только первого рода и б) имеет правые и левые
производные в каждой точке. Тогда ее тригонометрический ряд Фуре
в каждой точке x сходится к числу f ( x 0) f ( x 0) .
2
2) В условиях предыдущего пункта f ( x) представима в том же смысле
в виде ряда Фурье в комплексной форме ck
k
xi
e l
, причем c k ck , и
k
коэффициенты ak , bk , ck связаны равенством ck ak bk i .
2
3) Если функция f ( x) четная (нечетная) на [ l , l ] и удовлетворяет условиям пункта 3), то k 1 bk 0 ( k 0 ak 0) , то есть она разлагается
в ряд по косинусам (по синусам) на оси. При этом
2
k
2
k
ak f (t )cos( t )dt , bk f (t )sin( t )dt .
l0
l
l0
l
l
l
93.
Пр. Разложить в тригонометрический ряд Фурье по синусамкратных дуг функцию f ( x) x 2 , x [1,3]. ЛЕКЦИЯ 12 14.04.17 ЛЕКЦИЯ 3 21.02.19
94.
Виктор Фёдорович Шаталов(1.05.1927 - 20.12.2020) - педагог- новатор.
г. Донецк. Донецкая обл.
Народный учитель СССР (1990).
Создатель нового направления в педагогике
«педагогика сотрудничества».
Разработал систему обучения с
использованием опорных сигналов –
взаимосвязанных
1) ключевых слов, 2) условных знаков,
3) рисунков, 4) формул с кратким выводом.
95.
Оригинальная система интенсивного обучения Шаталова, разработаннаядля средних и старших классов общеобразовательной школы включает
около 200 педагогических открытий, самые важные из которых:
1) Авторские учебные пособия, представляющие программный материал
главным образом в вербально-графических формах, упрощающих процесс
изложения, восприятия и запоминания.
2) Принцип открытых перспектив, ориентированный на развитие творческого мышл-я
3) Принцип систематической обратной связи, на базе разнообразных нестандартных
форм объективного учёта и контроля знаний каждого учащегося на каждом уроке,
позволяющий отказаться от ученических дневников и классных журналов.
4) Вместо домашних заданий учащиеся получают обширные «предложения», объём и
сложность которых варьируются на этапах обучения с учётом индивидуальных
особенностей, а к окончанию курса приближаются к конкурсным и олимпиадным.
5) Практикуются оригинальные формы взаимопроверки учащихся, в том числе в интере
сах увеличения времени для решения задач высокой сложности и развития продуктив
ного мышления.
6) Традиционные экзамены заменены работами по «листам группового контроля» и так
называемыми релейными, выявляющими результат самостоятельной деятельности над
всеми видами заданий.
7) Устранению дидактических противоречий способствует принцип бесконфликтности
учебной ситуации, то есть создание при участии родителей школьников соответствую
щих условий для занятий. 8) Широко используются игровые формы учебных занятий.
Многие находки Шаталова используются не только школьными учителями, но и
педагогами вузов и при обучении некоторым сложным профессиям.
96.
Огюсте́н Луи́ Коши́ (1789 - 1857) - великий французский математик, член Парижской, Петербургской и других академий.
К. написал свыше 800 работ. Много работал в области ком
плексного анализа, в частности, создал теорию интегральных
вычетов. В математической физике глубоко изучил краевую
задачу с начальными условиями, которая с тех пор называется
«задача Коши».
Заложил основы математической теории упругости : рас
сматривал тело как сплошную среду и вывел систему уравне
ний для напряжений и деформаций в каждой точке. В работах по оптике Коши
дал математическую разработку волновой теории света и теории дисперсии.
Вел исследования по геометрии, теории чисел, алгебре, астрономии.
Впервые дал строгое определение основным понятиям математического анализа
- пределу, непрерывности, производной, дифференциалу, интегралу, сходимости
ряда и т. д. Его определение непрерывности опиралось на понятие бесконечно
малого, которому он придал новый смысл: у К. бесконечно малое — переменная
величина, стремящаяся к нулю. Ввёл понятие радиуса сходимости ряда.
Курсы анализа К., основанные на систематическом использовании понятия
предела, послужили образцом для большинства курсов позднейшего времени.
97.
КРАТНЫЕ ИНТЕГРАЛЫЗадача 1 Вычислить массу неоднородной пластинки.
Задача 2 Задано потенциальное поле с потенциалом
U=U(x0,y0). Найти работу по перемещению материаль
ной точки массы m=1 вдоль кривой l D .
Задача 3 Имеется однородный шар радиуса R с плотно
стью . Найти потенциал гравитационного поля вне
этого шара.
Задача 4 Момент инерции гладкой материальной
оболочки L с непрерывной поверхностной плотностью
( M ) относительно прямой l .
Задача 5 Вычислить объем жидкости, протекающей
за единицу времени через заданную поверхность.
98.
Пусть множество D R 2 ограничено. x i h, y j h, i, j Z , h : 2 N , сеть прямых. DN - совокупность квадратных ячеек, содержащихсяв D , s N - площадь DN .
DN - совокупность квадратных
ячеек, пересекающихся с D ,
s N - площадь DN . ЛЕКЦИЯ 12 14.04.17
{DN } - последовательность вложенных друг в друга множеств {s N }
si ( D) = s : lim s N - нижняя мера
N
Жордана множества D .
Аналогично, {s N }
se ( D) = s : lim s N - верхняя мера
N
Жордана множества D .
N N s N si ( D) se ( D) s N
Множество D измеримо (по Жордану), если si ( D) se ( D) . s( D) s
: si ( D) se ( D) - двумерная мера Жордана (площадь) множества D
99.
Пусть множество D R 2 ограничено. x i h, y j h, i, j Z , h : 2 N , сеть прямых. DN - совокупность квадратных ячеек, содержащихсяв D , s N - площадь DN .
DN - совокупность квадратных
ячеек, пересекающихся с D ,
s N - площадь DN . ЛЕКЦИЯ 12 14.04.17
{DN } - последовательность вложенных друг в друга множеств {s N }
si ( D) = s : lim s N - нижняя мера
N
Жордана множества D .
Аналогично, {s N }
se ( D) = s : lim s N - верхняя мера
N
Жордана множества D .
N N s N si ( D) se ( D) s N
Множество D измеримо (по Жордану), если si ( D) se ( D) . s( D) s
: si ( D) se ( D) - двумерная мера Жордана (площадь) множества D
100.
Жордан(Jordan) Мари Эдмон Камиль(1838—1922, Париж), французский
математик, член-корреспондентом
Петербургской АН (1895).
Работы Ж. относятся к алгебре, теории
функций комплексного переменного и к
топологии и кристаллографии. С именем
Ж. связаны
нормальная (жорданова) форма матриц,
жорданова кривая,
мера Жордана множества,
понятие функции с ограниченным изменением.
Разобрал и опубликовал результаты Галуа о разрешимости
в квадратурах алгебраического уравнения.
ЛЕКЦИЯ 15.04.2016
101.
Кпр. Для гребешка Дирихле D нижняя мера Жордана si ( D) 0 , аверхняя мера se ( D) 1.
Граница ( D ) имеет нулевую жорданову меру, если
se ( ( D)) : lim s( DN \ DN ) lim ( s N s N ) 0 .
N
N
Пр . Граница окружности имеет меру Жордана s S ((0,0), R) 0 .
Кпр. Для гребешка Дирихле D ( D) {( x, y) R 2 : 0 x 1, 0 y 1}
s( ( D)) 1.
ЗАМЕЧАНИЕ 1 Множество D измеримо ( D) имеет нулевую
меру Жордана.
ЗАМЕЧАНИЕ 2 Если граница ( D) множества D R 22 является
кусочно-гладкой кривой, то это множество измеримо.
Пр. Для непрерывной функции f ( x) 0 криволинейная трапеция
D0, f (a, b) : ( x, y) R 2 : a x b, 0 y f ( x) измерима, так как график f
имеет нулевую жорданову меру. ЛЕКЦИЯ 14 21.04.21
102.
Диаметр множества D R 2 это числоd ( D) : sup ( M1 , M 2 ) : M1 , M 2 D .
Диаметр разбиения T : {D1 ,..., Dn } множества D R 2 на
подмножества D1 ,..., Dn это число d (T ) : max d ( D1 ),..., d ( Dn ) .
Пр. Диаметр прямоугольника равен длине диагонали, а диаметр
круга d ( D(M 0 , R)) 2R .
103.
Пусть на ограниченном измеримоммножестве D R 2 задана функция
f ( x, y ) . T : {D1 ,..., Dn } - разбиение D на
измеримые попарно непересекающиеся
подмножества. M k Dk , E : {M1 ,..., M n },
n
S f (T , E ) : f ( M k ) s ( Dk ) - интегральная
k 1
сумма, где s( Dk ) - площадь Dk .
Если s R 0 0 T : d (T ) , E | S f (T , E ) s | , то число
f ( x, y)dxdy f (M )ds : s - двойной интеграл (Римана) от
D
D
функции f ( x, y) на множестве D . (понятие, термин - Эйлер,1769)
f ( x, y ) интегрируема (по Риману) на множестве D .ЛЕКЦИЯ 17
Пр. Постоянная функция f ( x, y) C всегда интегрируема, причем
Cds C s( D) . УА-УИ ЛЕКЦИЯ 13 7.04.22
D
104.
Пусть на множестве D определены две функции g ( x, y) f ( x, y) .Gg , f ( D) : ( x, y, z ) : ( x, y) D, g ( x, y) z f ( x, y) цилиндрическое тело в R 3 .
ЛЕКЦИЯ 14 9.03.18
v(Gg , f ( D)) : ( f ( M ) g ( M ))ds - объем цилиндрического тела, если
D
существует интеграл.
ЗАМЕЧАНИЕ Начала теории кратных интегралов – в статье
Л.Эйлер О двойных интегралах. Novi Commentarii (С.-Петербург),1770.
105.
Леона́рд Э́йлер (1707-1783) - выдающийся математик, механик, физик,
астроном XVIII века. Автор более
чем 800 работ по теории чисел,
математическому анализу,
дифференциальной геометрии,
приближённым вычислениям,
небесной механике,
математической физике,
оптике, баллистике,
кораблестроению,
теории музыки и др.
Почти полжизни провёл в России (1726-1741, 1766-1783)
где внёс существенный вклад в становление россий
ской науки. Первые русские академики-математики
(С. К. Котельников) и астрономы (С. Я.Румовский)ученики Эйлера. Некоторые его потомки в России.
106.
СЛЕДСТВИЕ (геометрический смысл двойного интеграла)Функция f ( x, y) 0 интегрируема на ограниченном измеримом
множестве D цилиндрическое тело G0, f ( D) имеет объем.
29.04.2014
ЛЕКЦИЯ 16 2014
x, y Q [[0,1]
1,
Кпр. d ( x, y ) :
- двумерная функция Дирихле.
0,
x
или
y
I
[0,1]
Цилиндрическое тело G0, d : ( x, y, z ) : 0 x 1, 0 y 1, 0 z d ( x, y) -
щетка Дирихле. УТ-УЛ ЛЕКЦИЯ 16 8.04.2022
ЗАМЕЧАНИЕ Щетка Дирихле не имеет объем.
107.
ТЕОРЕМА 6.1 (свойства двойного интеграла)1) (теорема существования) Двойной интеграл f ( M )ds от
D
непрерывной функции f (M ) на ограниченном замкнутом
измеримом множестве D существует.
2) Если g ( x, y), f ( x, y) интегрируемы на множестве D , то
, R
( f (M ) g (M ))ds f (M ))ds g (M ))ds .
D
D
D
3) Если M D g (M ) f (M ) , то g ( M (ds) f ( M )ds .
D
D
4) Если f (M ) непрерывна на измеримом замкнутом ограниченном
f ( x, y ), M : max f ( x, y) , то m s( D) f ( x, y )dxdy M s( D)
множестве D и m : min
D
D
D
5) (теорема о среднем) В условиях предыдущего пункта
M 0 D f ( M )ds f ( M 0 ) s ( D) . ЛЕКЦИЯ 13 21.04.17
D
6) В условиях пункта 4) для любого разбиения D на измеримые
подмножества D1 ,..., Dn f (M )ds f ( M )ds ... f ( M )ds .
D
D1
Dn
108.
6) Пусть D D1 D2 , подмножества измеримы D1 , D2 и D1 D2 .Выберем по 0 такое 0 , что для разбиений
T1 D1,k , T2 D2,k с диаметрами d (T1 ) , d (T2 ) и
произвольных точек M1,k D1,k , M 2,k D2,k . По определению
n1
f ( M1,k ) s( D1,k ) ,
D f (M )ds
3
k 1
1
f ( M )ds f ( M 2,k ) s( D2,k ) ,
3
k 1
D2
n1
n2
k 1
k 1
3
f (M )ds f (M1,k )s( D1,k ) f (M 2,k )s( D2,k )
D
n2
f ( M )ds
D f (M )ds D f (M )ds
D
1
n1
2
n2
ê 1
ê 1
f ( M )ds f ( M1,k ) s( D1,k ) f ( M 2,k ) s( D2,k )
D
n1
n1
f ( M )ds f ( M 1,k ) s ( D1,k ) f ( M )ds f ( M 1,k ) s ( D1,k )
D
D
3 3 3
к 1
к 1
1
1
109.
Пусть функции ( x), ( x) непрерывны на [a, b] , ( x) ( x) , ифункция f ( x, y) непрерывна на криволинейной трапеции D , (a, b) .
( x)
Можно показать, что функция ( x) : f ( x, y)dy непрерывна на [a, b] .
( x)
b ( x)
b
a ( x)dx : a ( x ) f ( x, y)dydx - повторный интеграл.ЛЕКЦИЯ22.04.16
ТЕОРЕМА 6.2 1) (формула сведения двойного интеграла к
повторному) В условиях предыдущего определения имеет место
b ( x)
равенство f (M )ds f ( x, y)dydx , где D : D , (a, b) .
D
a ( x)
2) (формула замены переменных) Пусть непрерывно дифференцируемое отображение F : ( (u, v), (u, v)) : D D отображает взаимно
однозначно множество D с кусочно-гладкой границей на множество D с кусочно-гладкой границей. Пусть якобиан отображения
( , )
имеет постоянный знак на D и функция f ( x, y ) непрерывна
(u , v)
на D . f ( x, y )dxdy f ( (u, v), (u, v) | ( , ) | dudv .
D
D
(u , v)
110.
Ограничимся случаем, когда D : {( x, y) : a x b, c y d } естьпрямоугольник. Разобьем его на более мелкие прямоугольники
Di , j : {( x, y ) : xi 1 x xi , y j 1 y y j }, a : x0 ... xn : b, c : y0 ... ym : d
По теореме о среднем значении
xi
yj
ЛЕКЦИЯ 2015
yj
x y f ( x, y)dydx y f ( i , y)dy xi f ( i , j ) xi y j
i 1 j 1
j 1
по определению 0 0 T , d (T ) , E
n
m
xi
f ( M )ds
D
yj
bd
f ( x, y)dydx
D f (M )ds
a c
n
m
f ( x, y )dydx f ( M )ds f ( i , j ) xi y j .
i 1 j 1 x
i 1 j 1
y
D
i 1 j 1
bd
В силу произвольности f ( M )ds f ( x, y )dxdy .
D
ac
111.
ЗАМЕЧАНИЕ (алгоритм вычисления двойного интеграла)а) Область D разбить на последовательность криволинейных
трапеций D1 ,..., Ds .
б) Двойной интеграл представить в виде суммы интегралов функции
f ( x, y ) на этих трапециях по формуле f ( M )ds f ( M )ds ... f ( M )ds .
D
D1
Ds
в) Вычислить полученные интегралы с помощью перехода к повторн
Пр. Вычислить двойной интеграл. ЛЕКЦИЯ 14 26.04.17
112.
ПРИЛОЖЕНИЕ 1 Вычисление объема цилиндрического телаПр. Вычислить с помощью перехода к обобщенным полярным
x ar cos
x2 y 2 z 2
координатам
объем эллипсоида 2 2 2 1.
y
br
sin
a
b
c
ЛЕКЦИЯ 15 12.03.18
28.04.21
113.
114.
ПРИЛОЖЕНИЕ 2 Вычисление площади поверхности.Пусть функция f ( x, y ) имеет непрерывные частные
производные на ограниченном плоском множестве D с
кусочно-гладкой границей. L - поверхность с уравнени
ем z f ( x, y) . D1 ,..., Dn - разбиение D на подмножества с
кусочно-гладкими границами. Жордан «Курс анализа»
Выберем M k ( xk , yk ) Dk . Lk : f x (M k )( x xk ) f y (M k )( y yk ) ( z f (M k )) 0, k 1,..., n ,
- касательные плоскости к поверхности L в точках Nk : ( xk , yk , f (M k )) с
соответствующим вектором нормали n ( N k ) f x ( M k ), f y ( M k ), 1 .
Dk - часть касательной плоскости Lk , расположенная над Dk . s( Dk )
s ( Dk ) | cos(n ( N k ) OZ ) | , где n ( N k ) есть вектор нормали к поверхности в
точке N k . cos(n ( N k ) OZ ) (n ( N k ), k )
| n ( Nk ) | | k |
1
f x 2 ( M k ) f y 2 ( M k ) 1
n
n
k 1
k 1
площадь
поверхности L приближенно равна s(T , E ) : s( Dk ) f x 2 (M k ) f y 2 (M k ) 1 s( Dk )
S (L ) : lim S (T , E ) : f x 2 ( M ) f y 2 ( M ) 1ds - площадь поверхности.
d ( t ) 0
D
115.
ПРИЛОЖЕНИЕ 3 (масса неоднородной пластинки)На горизонтальной плоскости XOY расположена
материальная пластинка D с кусочно-гладкой
границей и непрерывной плотностью ( x, y) .
D1 ,..., Dn - разбиение ее на малые части с кусочно
гладкими границами. В пределах каждого куска
плотность считаем постоянной и равной (M k ) ,
где M k Dk . Плотность k -го куска (M k ) s( Dk ) ,
n
а плотность всей пластинки ( M k ) s( Dk ) .
k 1
n
m( D) : lim ( M k ) s( Dk )) : ( M )ds - масса неоднородной
d ( t ) 0
k 1
пластинки. ЛЕКЦИЯ 19.05.15
D
ВПМ ЛЕКЦИЯ 7 20.10.23
116.
ПРИЛОЖЕНИЕ 4 (координаты центра масс пластинки)В условиях предыдущего пункта координаты центра масс
1
x
(
D
)
x ( x, y )dxdy
ц
m( D ) D
пластинки вычисляются по формуле
.
y ( D) 1
y ( x, y )dxdy
ц
m( D ) D
◄ l1m1 l2 m2 0 xc x1 m1 x2 xc m2 xc
m1 x1 m2 x2
.
m1 m2
nk 1 mk xk
xc n m
k 1 k
M k ( xk , yk ), mk , k 1,..., n
. ЛЕКЦИЯ 19 16.05.19
nk 1 mk yk
yc n
k 1 mk
nk 1 xk ( xk , yk ) s ( Dk )
1
x
x
(
D
)
x ( x, y )dxdy
c
n
c
m
(
D
)
m
k 1 k
D
.
n
y ( x , y ) s ( Dk )
y ( D) 1
yc k 1 k n k k
y ( x, y )dxdy
c
m( D ) D
k 1 mk
117.
Пр. Найти координаты центра тяжести центр тяжестинеоднородной квадратной пластинки D ( x, y) : 0 x, y 1 с
плотностью ( x, y) 0, 2 y .
7.05.2014 ЛЕКЦИЯ 17 2014
УА-УИ ЛЕКЦИЯ 14 14.04.22
118.
Момент инерции материальной точки A( x, y) массы mотносительно оси l I l : m d 2 ( A, l ) .
Момент инерции системы материальных точек T : Ak ( xk , yk ) ,
k 1,2,..., n , соответствующих масс mk относительно оси l
n
I l : mk d 2 ( Ak , l ) .
k 1
I l (T , E ) : ( M k )d 2 ( M k , l )s( Dk ) I l ( D) : ( x, y)d 2 ( x, y ), l dxdy n
k 1
D
- момент инерции пластинки D относительно оси l.
119.
Пусть l R 2 - спрямляемая кривая ифункции f ( x, y), g ( x, y) определены l .
T : { A0 ,..., An } - разбиение l , Ak ( xk , yk ) .
Выберем M k Ak 1 Ak ; положим
E : {M k } ;
образуем интегральные
n
n
r 1
r 1
суммы Sx (T , E) : f ( M k ) xk , S y (T , E ) : g ( M k ) yk , где d (T ) : max k
k
- диаметр разбиения.
Если для некоторого sx 0 0 T : d (T ) , E | S x (T , E ) sx | ,
то f ( x, y)dx : sx - криволинейный интеграл второго рода
l
функции f ( x, y) по переменной x на дуге l . Аналогично,
g ( x, y)dy : s y - криволинейный интеграл второго рода функции
l
g ( x, y ) по переменной y на дуге l .
Если указанные интегралы,
существуют, то f ( x, y )dx g ( x, y )dy : f ( x, y )dx g ( x, y )dy
l
l
l
криволинейный интеграл второго рода (общего вида) (КИВР).
120.
F ( A1 )F ( A2 )
A1
r2
F ( A0 )
r1
An 1
A2
rk
Ak
F ( Ak )
F ( Ak 1 )
A0
Ak 1
rn
An
F ( An 1 )
121.
ЗАМЕЧАНИЕ 1 Если l кусочно-гладкая и функции f ( x, y), g ( x, y)непрерывны на ней, то формула вычисления КИВР
f ( x, y)dx g ( x, y)dy : f ( (t ), (t )) (t ) g ( (t ), (t )) (t ) dt .
l
ЗАМЕЧАНИЕ 2 Аналогично определяется и вычисляется КИВР
на пространственной кривой.
ЛЕКЦИЯ 16 19.03.18
x ( ( )t )
, t [0,1] порождает кривую
y ( ( )t )
1 x ( ( )t )
l :
, t [0,1]
y
(
(
)
t
)
с ориентацией, обратной ориентации кривой l .
Кривая l :
Из определения КИВР следует
f ( x, y)dx g ( x, y)dy f ( x, y)dx g ( x, y)dy .
l 1
l
122.
ПРИЛОЖЕНИЕ Пусть материальная точка единичной массыдвижется вдоль кусочно-гладкой кривой l под действием силы F ( M ) ,
приложенной в точках M кривой, и непрерывно зависящей от M .
Тогда работа силы F ( M ) по перемещению материальной точки по
этой дуге вычисляется по формуле ВПМ 2 ЛЕКЦИЯ 8 27.10.23
n
n
n
F ( A ) r f ( A ), g ( A ) x , y f ( A ) x g ( A ) y
k 1
k 1
k
k 1
k 1
k 1
k
k
k 1
k 1
k
k 1
k
f ( x, y )dx g ( x, y )dy : F ( M )dr .
l
l
работа по перемещению материальной точки вдоль кривой l под
действием силы F ( M ) (в силовом поле F ( M ) ).
123.
Пр. Вычислить работу силового поля F {3x 2 y 2 , 2 x3 y}по перемещению материальной точки вдоль кривой l : x, y( x) : x [ x1 , x2 ] източки M1 ( x1 , y1 ) в точку M 2 ( x2 , y2 ) . 29.04.16
x2
A F ( M )dr 3x y dx 2 x ydy 3x 2 y ( x ) 2 2 x 3 y ( x ) y x dx
2
l
2
3
M1M 2
x2
y ( x) 2 x3
x1
x1
УТС-УЛ ЛЕКЦИЯ 16 21.04.22
x
dx y ( x) 2 x 3
x2
x1
x23 y22 x13 y12 .
12.05.2014
ЛЕКЦИЯ 18 2014







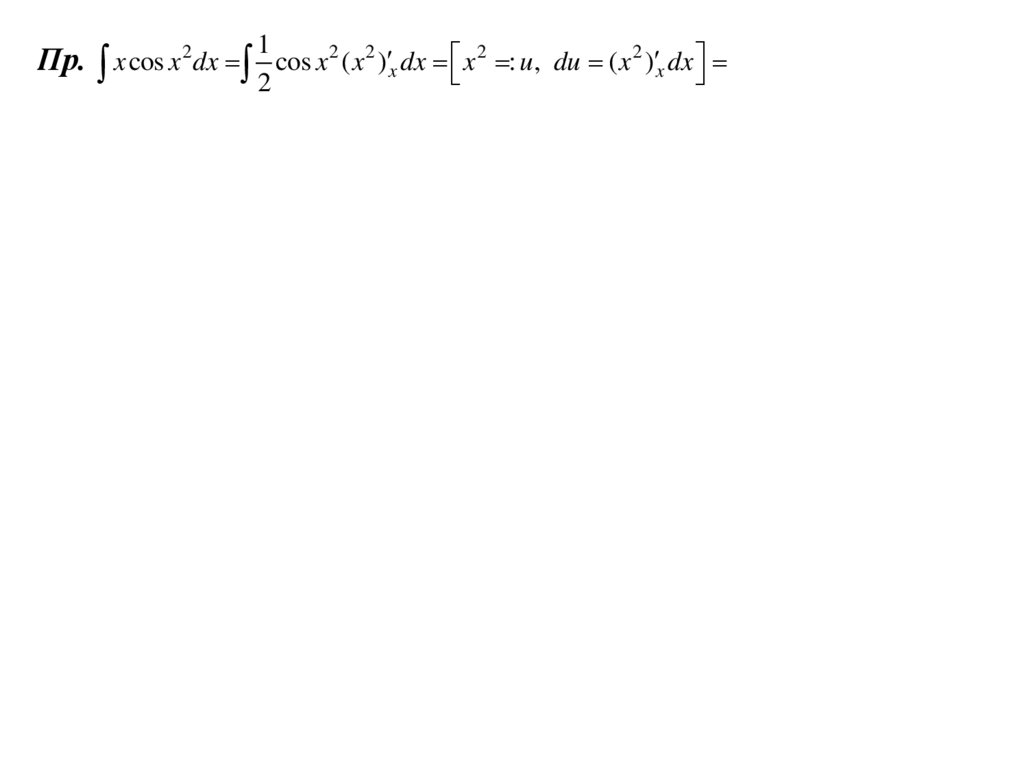















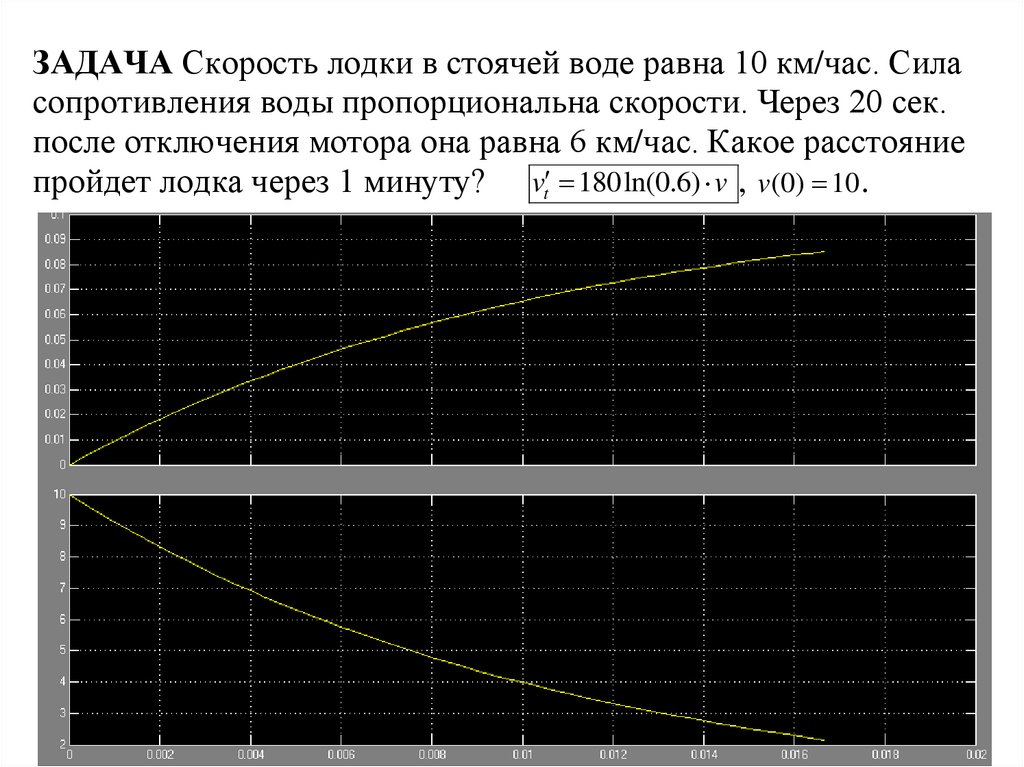




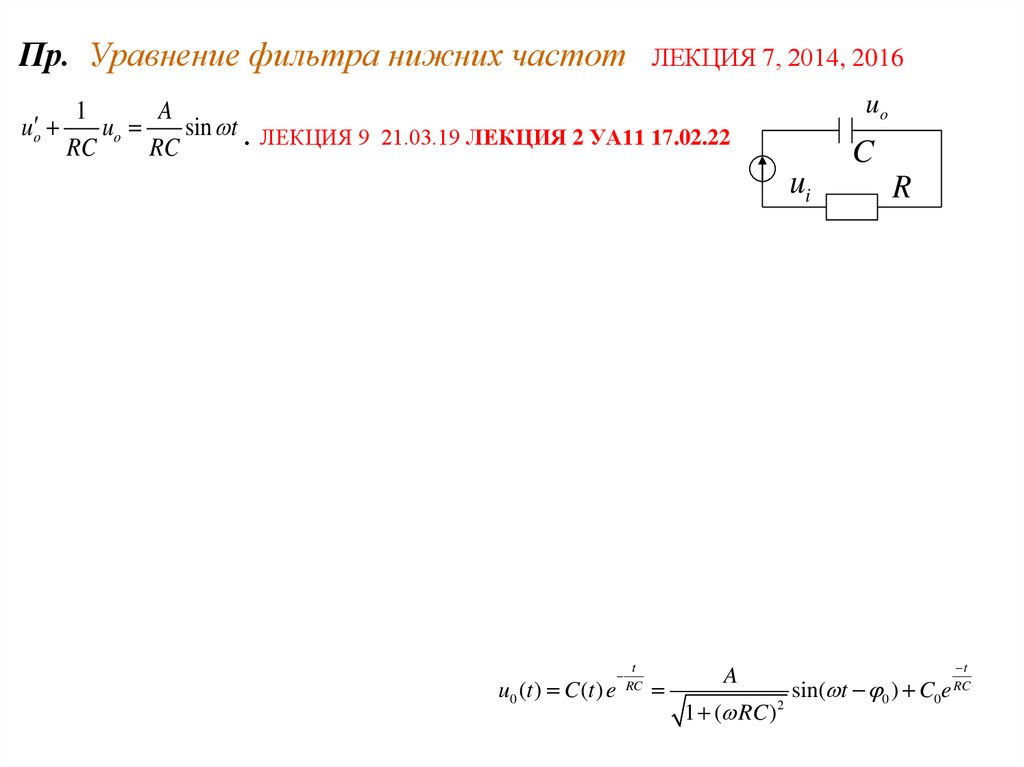
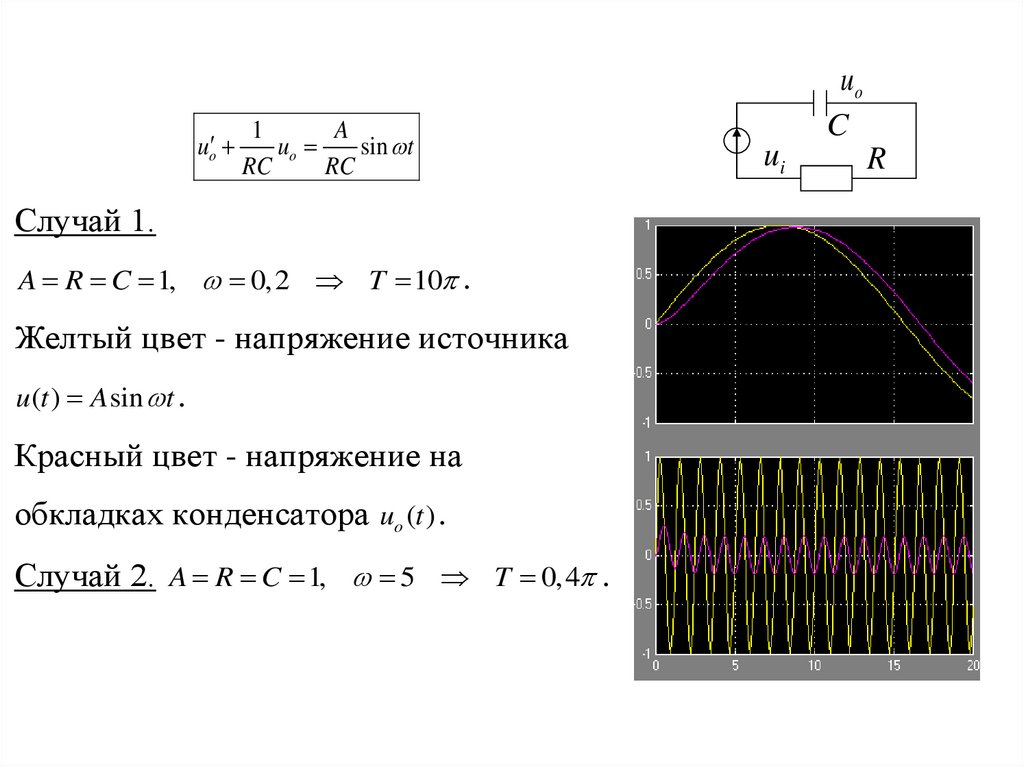










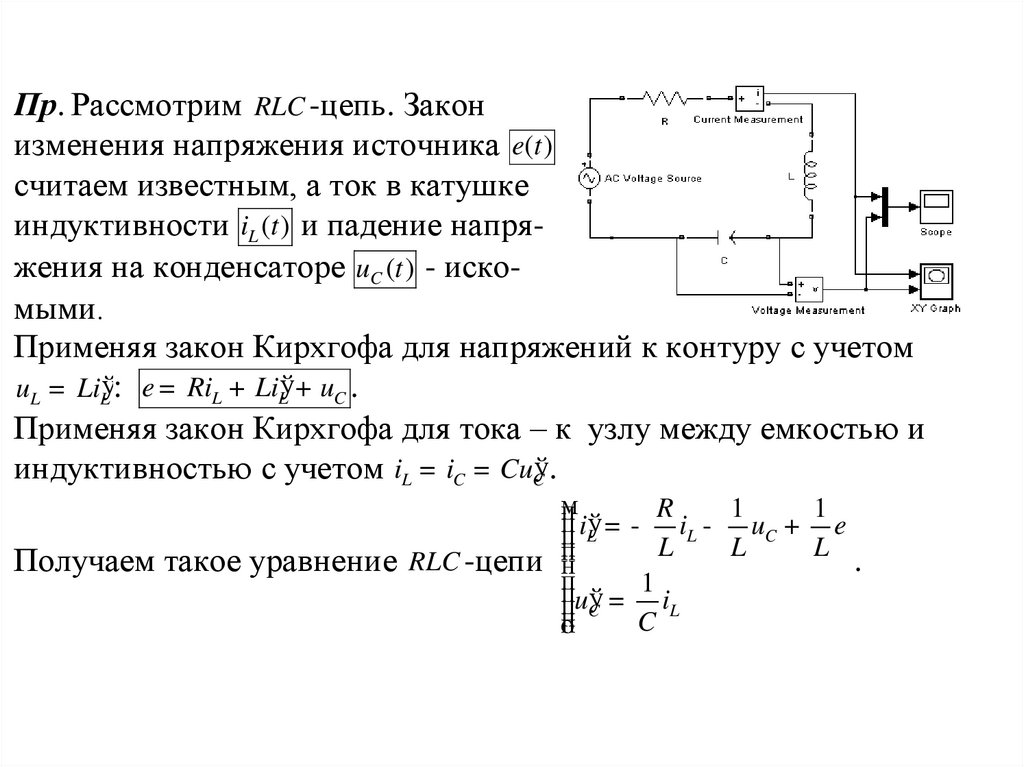














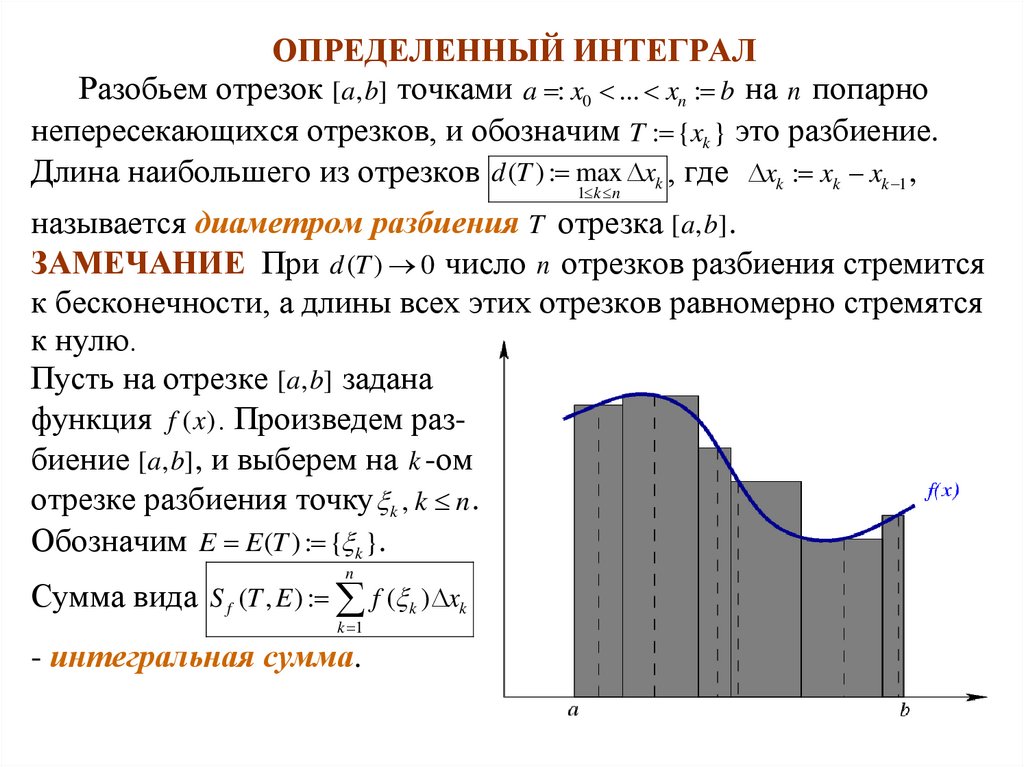
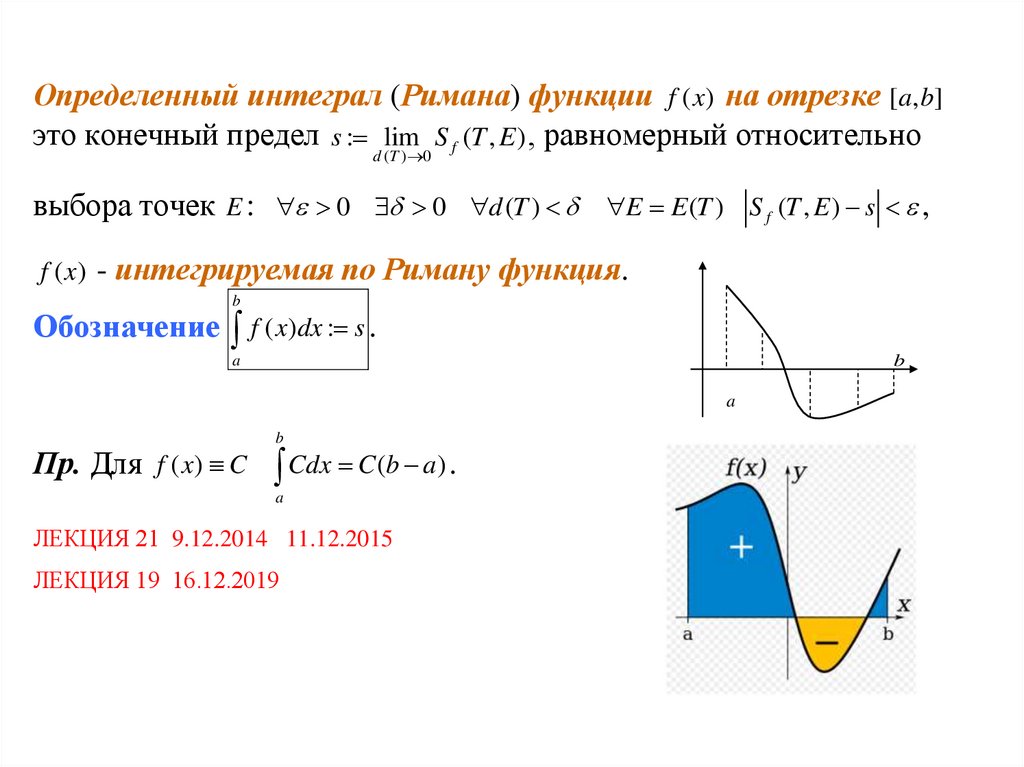




















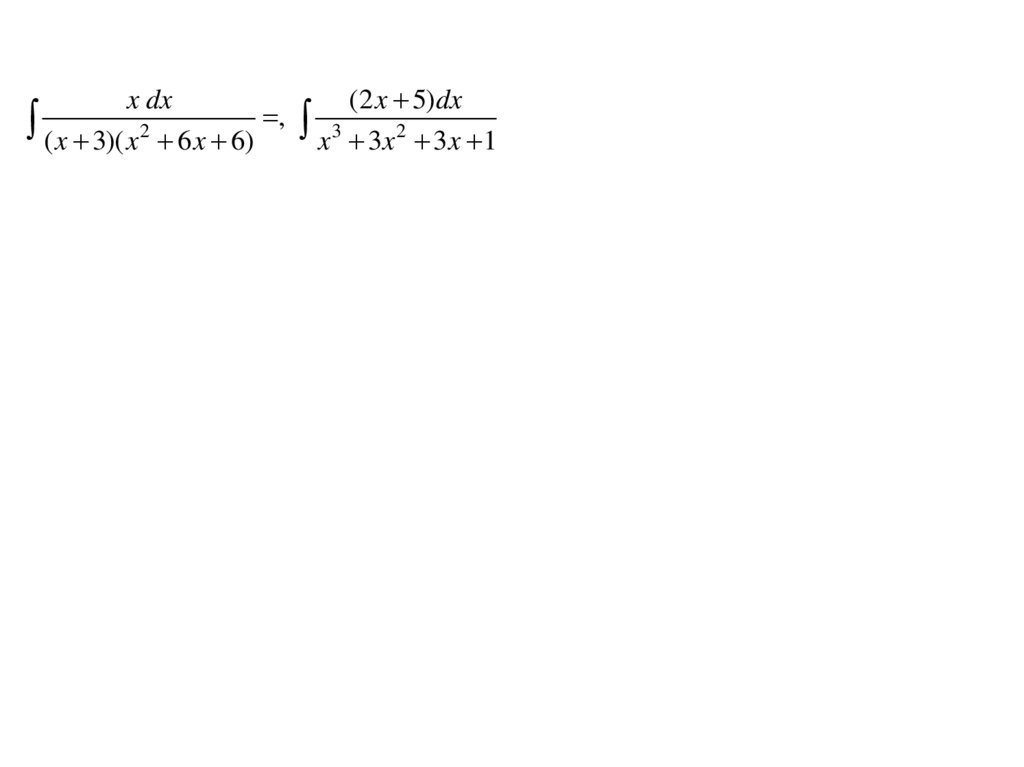



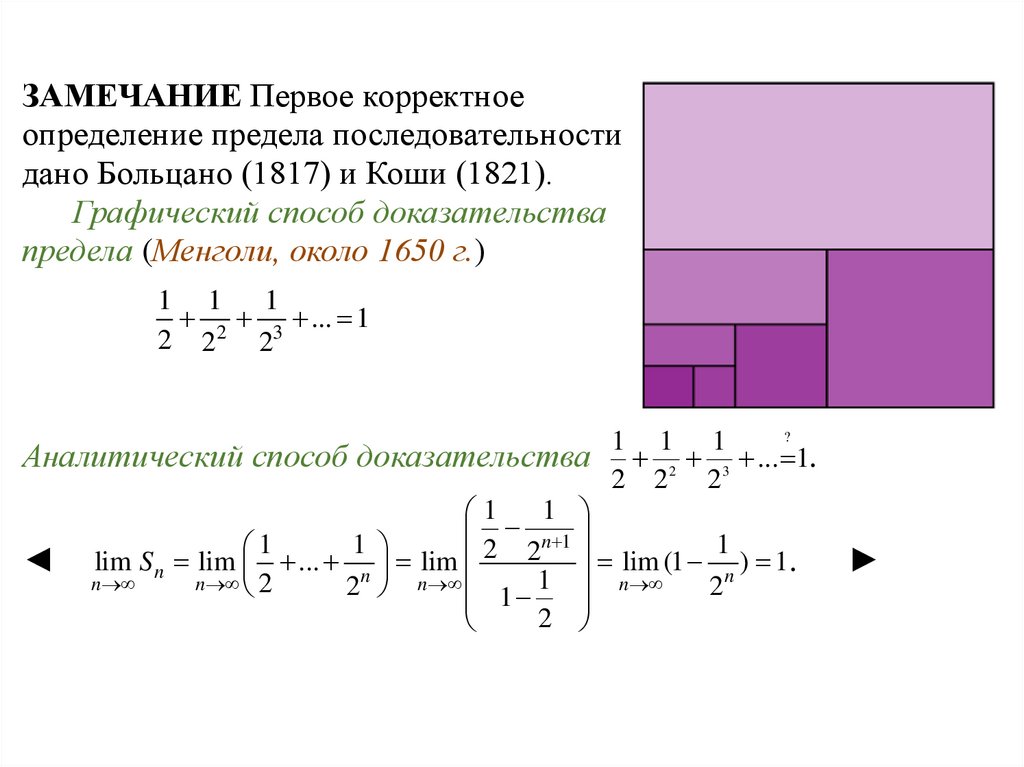





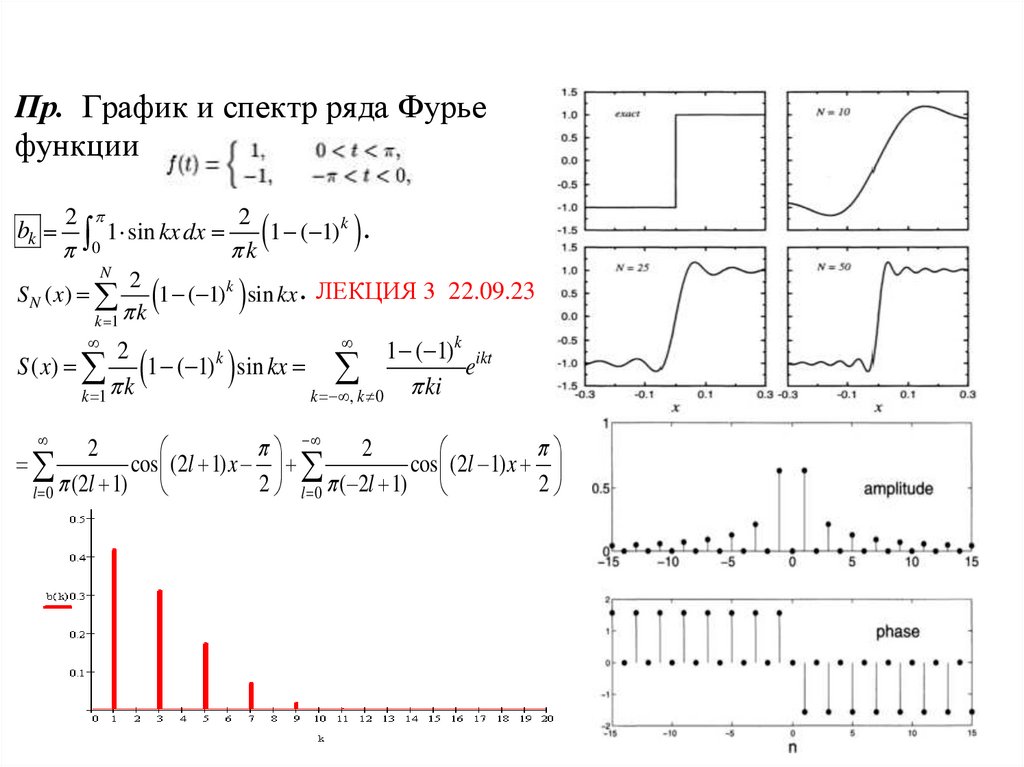
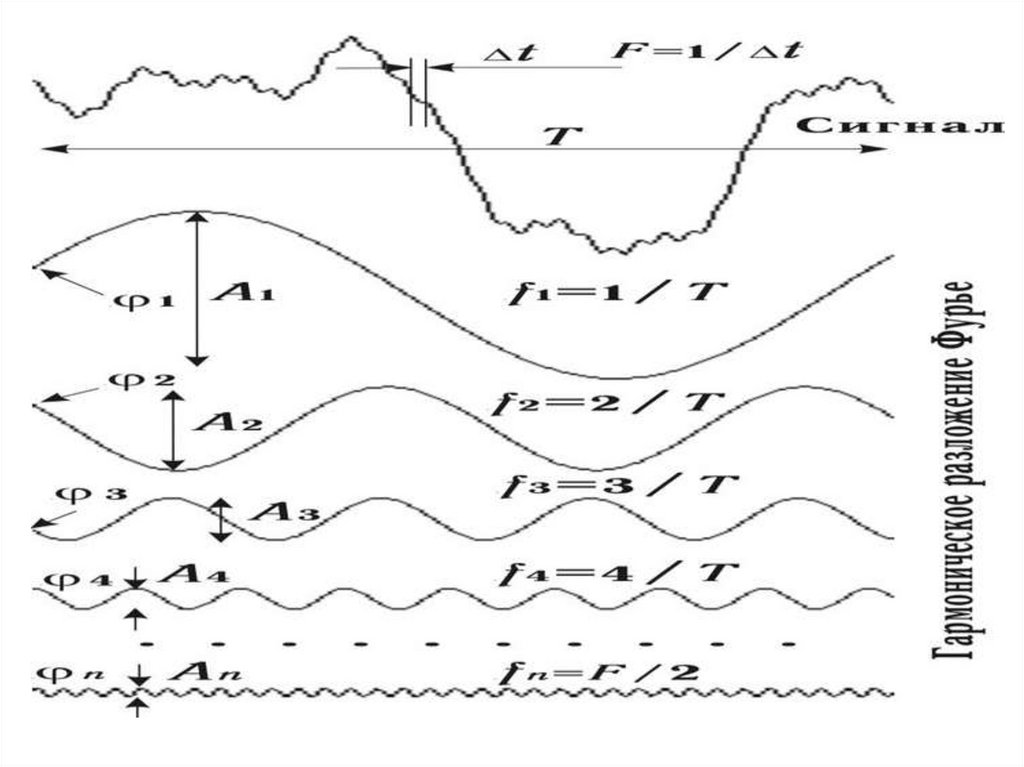
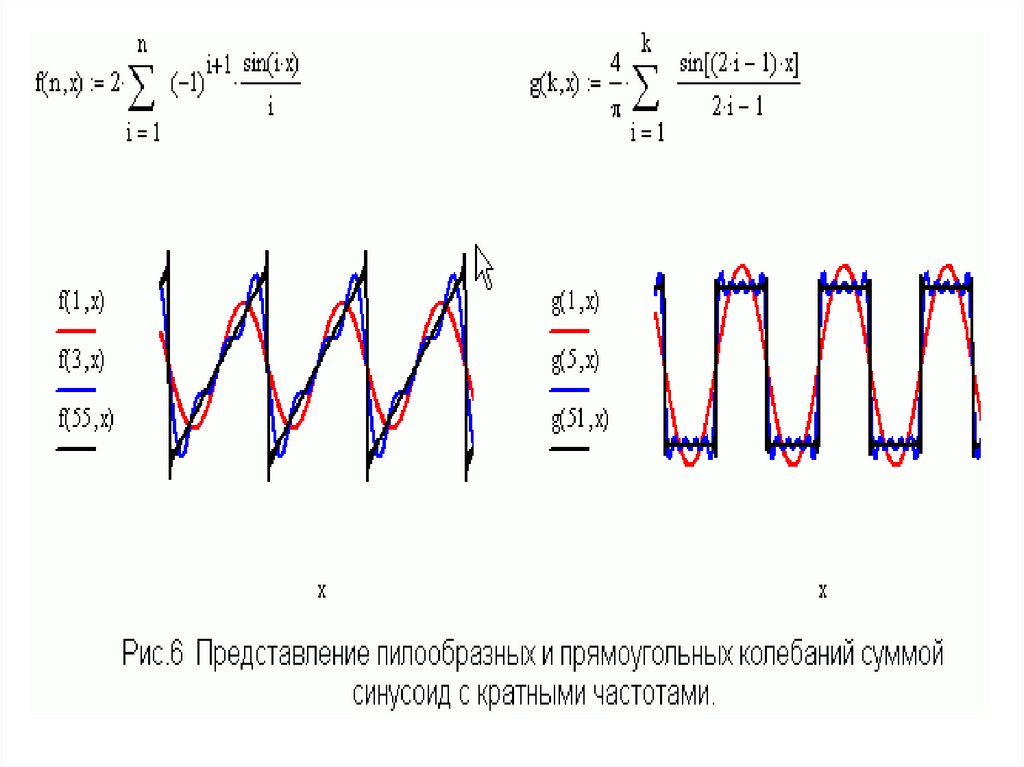








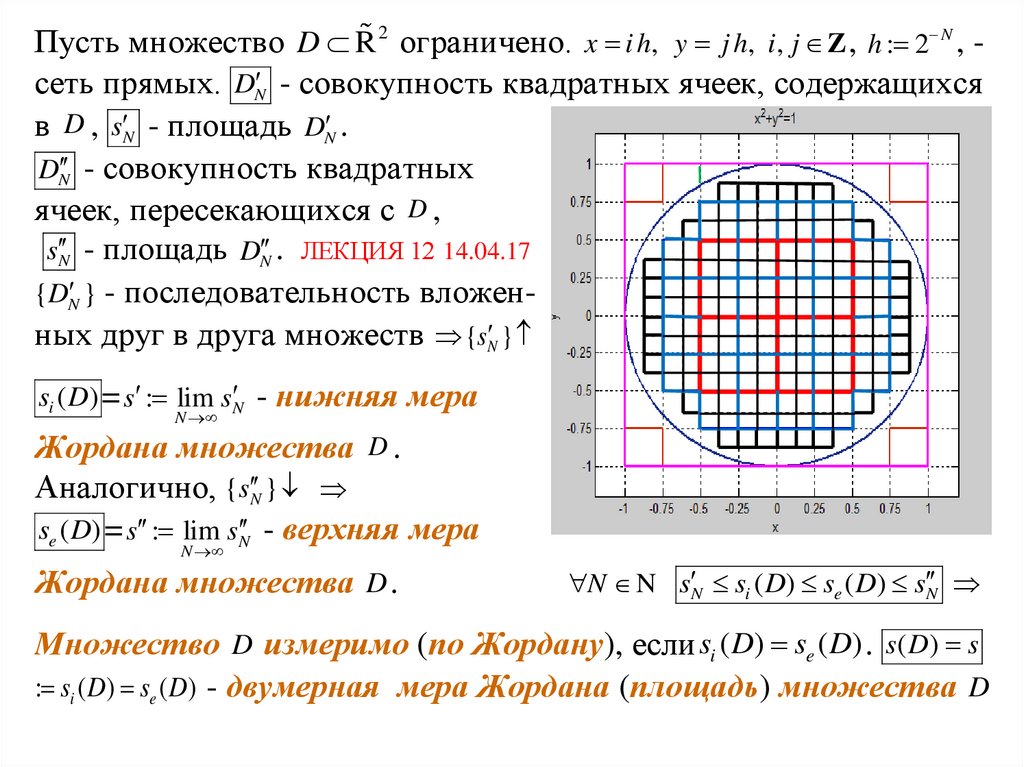


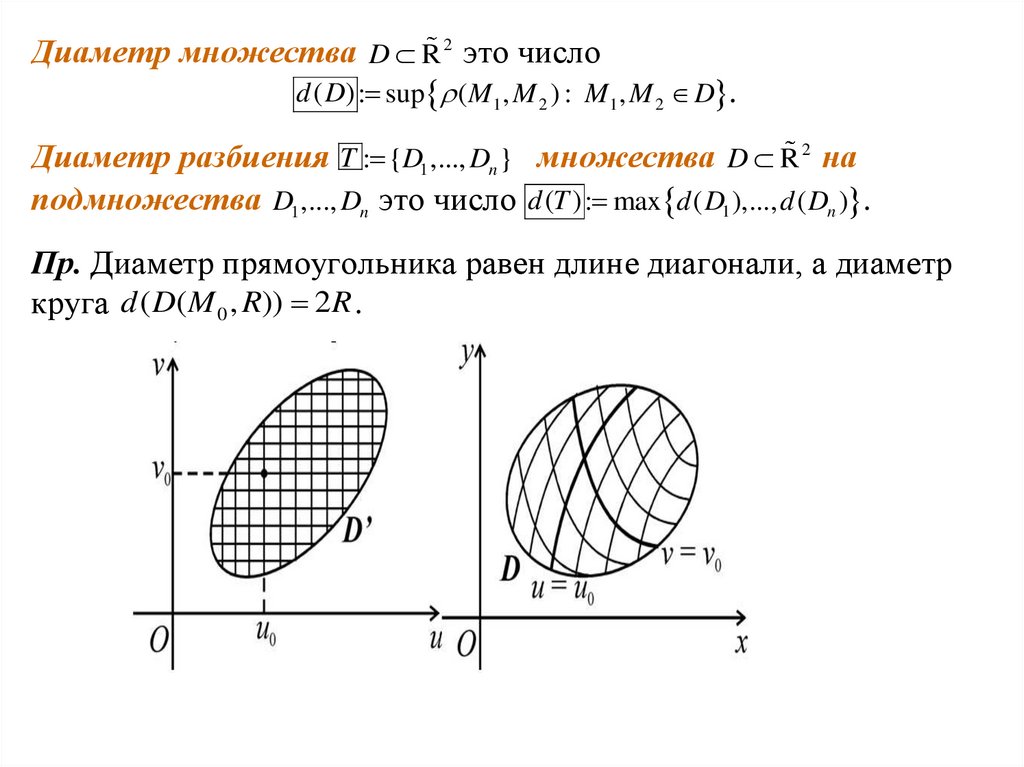

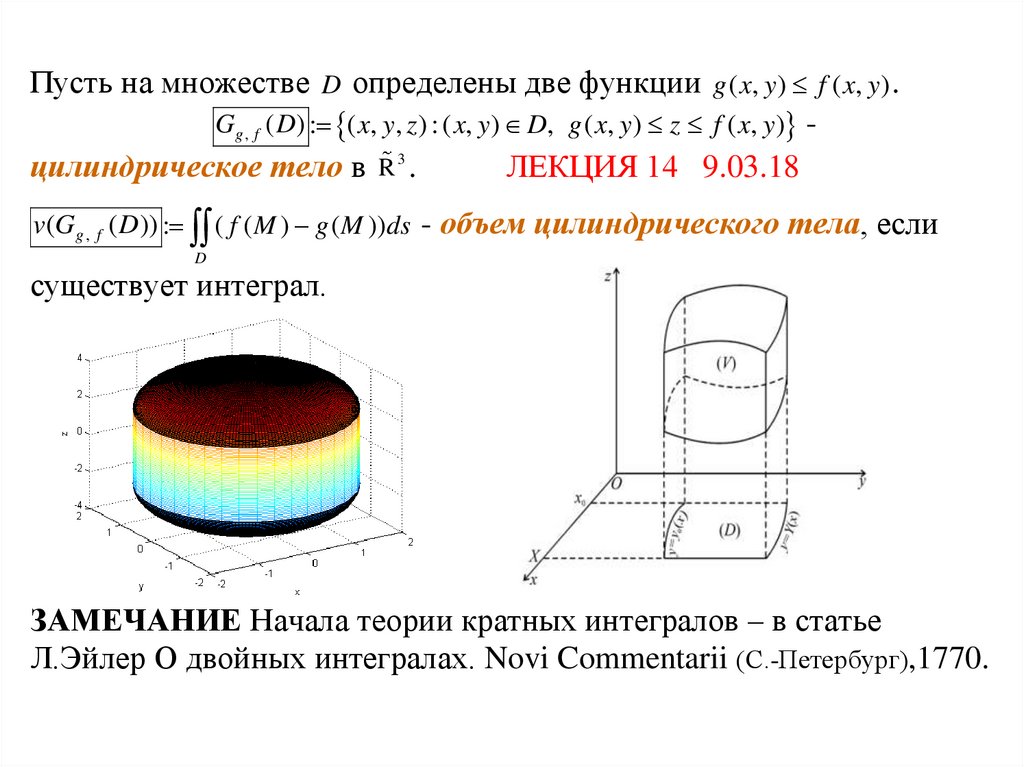

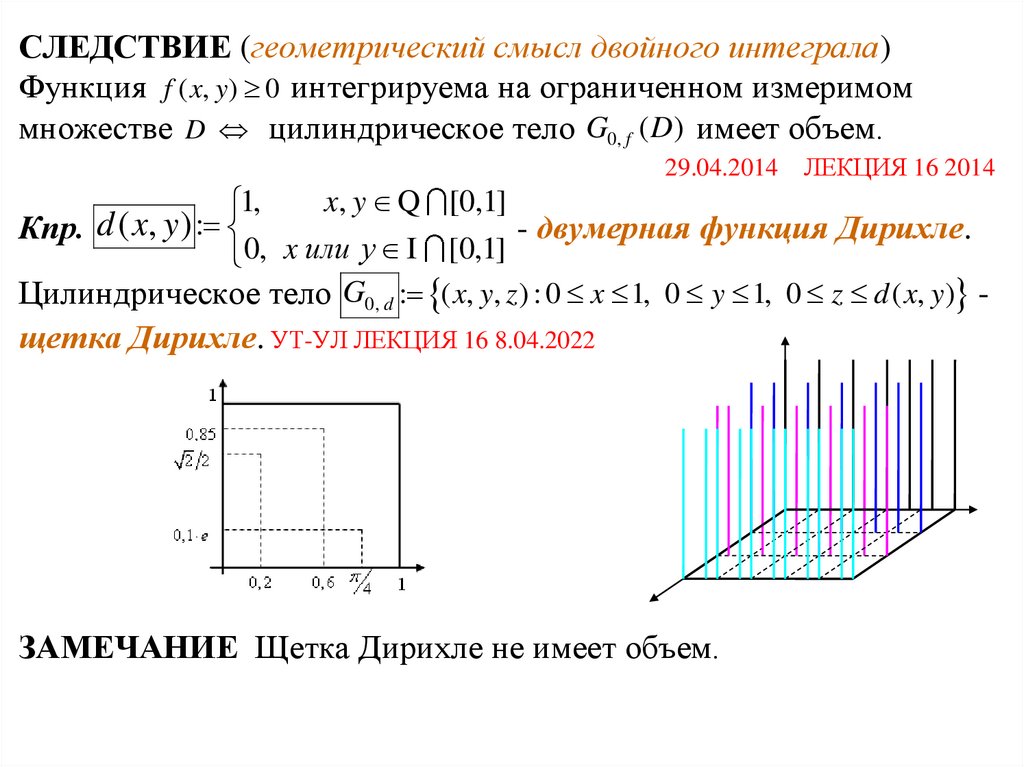






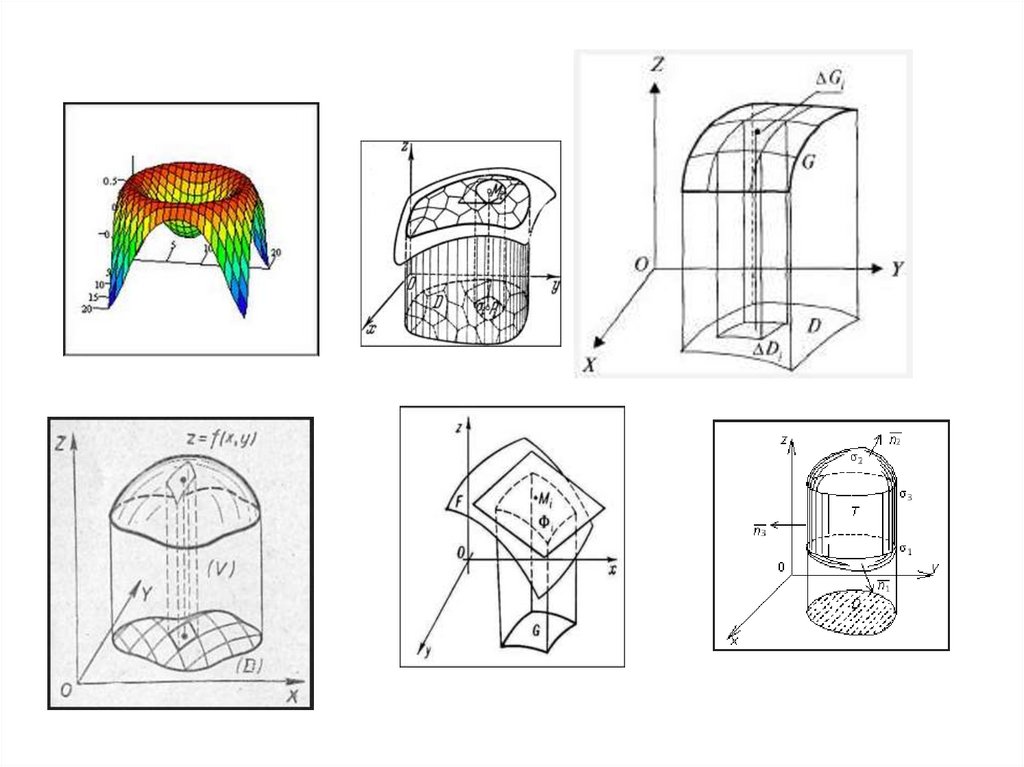






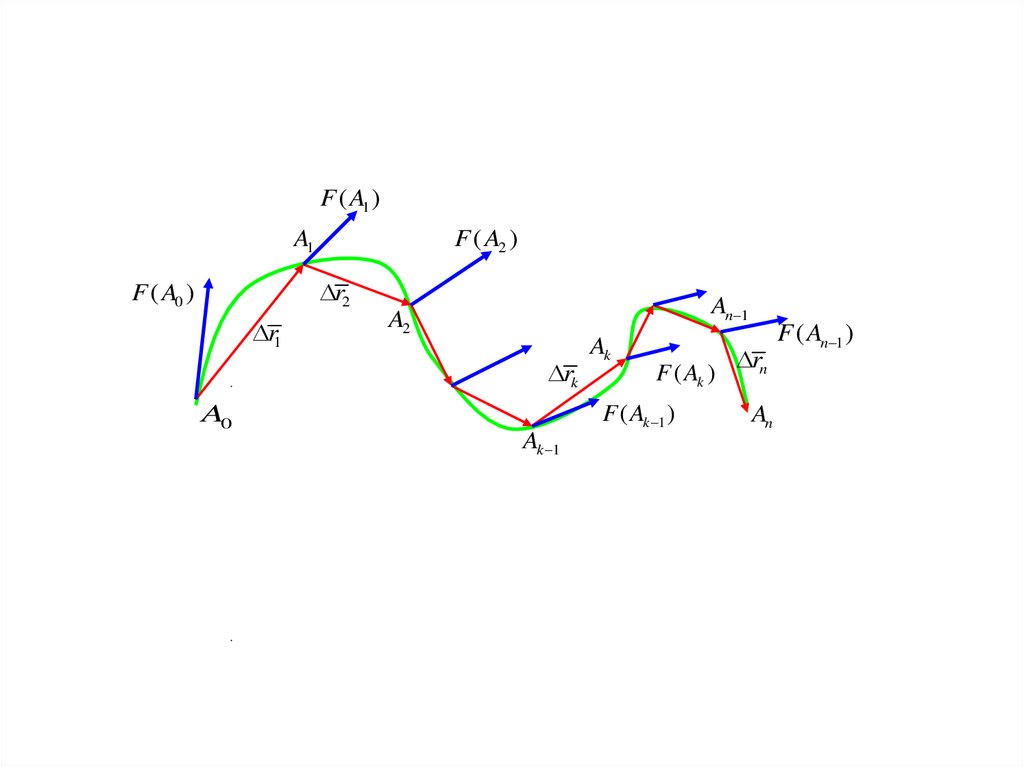



 Математика
Математика








