Похожие презентации:
Математический анализ. Определенный интеграл
1.
Математическийанализ
1 курс, 2-й семестр
1 курс, 2-й семестр
2.
2. Определенный интеграл2
3.
Постановка задачи• Рассмотрим движение физического тела. Для простоты полагаем,
что это материальная точка, которая движется вдоль числовой
оси.
• Перемещение точки описывается функцией s(t), которая
указывает координату точки в момент времени t. А скорость
точки описывается функцией v(t).
• Из курса дифференциального исчисления мы помним, что v(t) =
s’(t).
3
4.
Постановка задачи• Пусть в начальный момент времени t0 точка находится в
координате s(t0).
• Пусть далее мы получаем данные только о скорости движения
точки, то есть знаем функцию v(t).
• Как нам узнать, какое примерно расстояние прошла точка за
период времени с t0 по t1? Если бы скорость была постоянная, мы
воспользовались бы формулой: s(t1) – s(t0) = v(t1 – t0), умножив
скорость на время.
• Но что, если функция v(t) не константа? Ведь в реальности
скорость постоянно меняется.
4
5.
Постановка задачи• Чтобы в этом случае найти приближенное расстояние, логично
разбить промежуток времени на небольшие части и посчитать
расстояние в каждой части отдельно, приняв скорость за
постоянную внутри каждого кусочка. А затем сложить
полученные значения.
• Значения скорости внутри каждого отрезка можно выбирать
совершенно случайно.
5
6.
Постановка задачи• Например, s(0) = 0, мы можем получить значения v(t) и хотим
узнать, какое расстояние прошла точка за 60 секунд. Разобьём
участок [0, 60], например, на 3 интервала: [0, 20], [20, 40], [40, 60].
• Выберем произвольное значение скорости на каждом из этих
промежутков. Например, пусть v(10) = 23 м/с, v(30) = 63 м/с, v(50)
= 103 м/с.
• Тогда на первом участке времени расстояние примерно равно 20 ∙
23 = 460 м, на втором 20 ∙ 63 = 1260 м, на третьем 20 ∙ 103 = 2060
м. Общее расстояние примерно 3780 м.
6
7.
Постановка задачи• В данном примере мы разбили промежуток на равные
интервалы, но интервалы могут быть совершенно произвольные.
• Очевидно, что для того, чтобы уточнить значение, нужно разбить
промежуток на большее число меньших интервалов.
• Чем больше мы возьмём интервалов, тем точнее будет наше
примерное значение.
7
8.
Постановка задачи• Таким образом, используя значения скорости (т.е. производной)
на промежутке мы получили разность между значением
расстояния (т.е. первообразной) в конце и в начале промежутка:
n
s(t1 ) s(t 0 ) v(ξ i )Δt i .
i=1
• Здесь Δti – длина кусочков, на которые мы разбили интервал [t0,
t1], а ξi («кси») – произвольная точка внутри каждого такого
интервала.
• Это и есть понятие определенного интеграла.
8
9.
Интегральная сумма• Теперь введем понятие интеграла математически строго.
• Пусть функция f(x) определена на отрезке [a, b]. Разобьем отрезок
[a, b] на n кусочков точками a = x0 < x1 < … < xn = b. В каждом
кусочке выберем по точке ξi [xi–1, xi]. Обозначим через Δxi = xi –
xi–1 длину i-го кусочка. Составим интегральную сумму:
n
f(ξ ) x.
i 1
i
i
• Далее увеличиваем число кусочков, но так, чтобы длина
наибольшего кусочка при этом стремилась к 0.
9
10.
Интеграл Римана• Получаем предел:
n
lim
f(
ξ
x
i)
i.
n
1
max
x
0i
i
• Важно понимать, что только стремления n к бесконечности не
достаточно. Ведь мы можем, например, разбить интервал на 2
половины, а затем дробить до бесконечности только одну
половину. Тогда количество отрезков будет бесконечно
увеличиваться, но нужное нам точное значение предела мы не
получим, поскольку на оставшейся половине приближение будет
очень грубое.
10
11.
Интеграл Римана• Если построенный нами предел существует, то функция f(x)
называется интегрируемой по Риману на отрезке [a, b], а сам
предел называется интегралом Римана от функции f(x) на
отрезке [a, b] и обозначается
b
f(x)dx.
a
11
12.
Интегрируемые функции• Класс всех функций, интегрируемых по Риману на отрезке [a, b],
обозначается R[a, b].
• Таким образом, если функция f(x) интегрируема по Риману на
отрезке [a, b], то пишут f(x) R[a, b].
• Далее будем использовать термин «интегрируемость»,
подразумевая «интегрируемость по Риману».
12
13.
Необходимое условие интегрируемости• Утверждение (необходимое условие интегрируемости): Для того
чтобы функция f(x), определенная на отрезке [a, b], была
интегрируема на этом отрезке, необходимо, чтобы эта функция
была ограничена на этом отрезке.
• Таким образом, только ограниченная на отрезке функция может
быть интегрируема на этом отрезке, но не все ограниченные
функции интегрируемы.
13
14.
Достаточные условия интегрируемости• Утверждение (достаточное условие интегрируемости 1): Если
функция f(x), определенная на отрезке [a, b], непрерывна на этом
отрезке, то эта функция интегрируема на этом отрезке.
• Таким образом, имеет место вложение C[a, b] R[a, b].
• Утверждение (достаточное условие интегрируемости 2): Если
функция f(x), определенная и ограниченная на отрезке [a, b],
непрерывна на этом отрезке почти всюду (т.е. всюду, кроме, быть
может, конечного числа точек), то эта функция интегрируема на
этом отрезке.
14
15.
Достаточные условия интегрируемости• Утверждение (достаточное условие интегрируемости 3): Если
функция f(x), определенная на отрезке [a, b], монотонна на этом
отрезке, то эта функция интегрируема на этом отрезке.
• Теорема (критерий Лебега): Функция, определенная на отрезке,
интегрируема по Риману на этом отрезке тогда и только тогда,
когда она ограничена на этом отрезке и непрерывна почти во
всех его точках.
15
16.
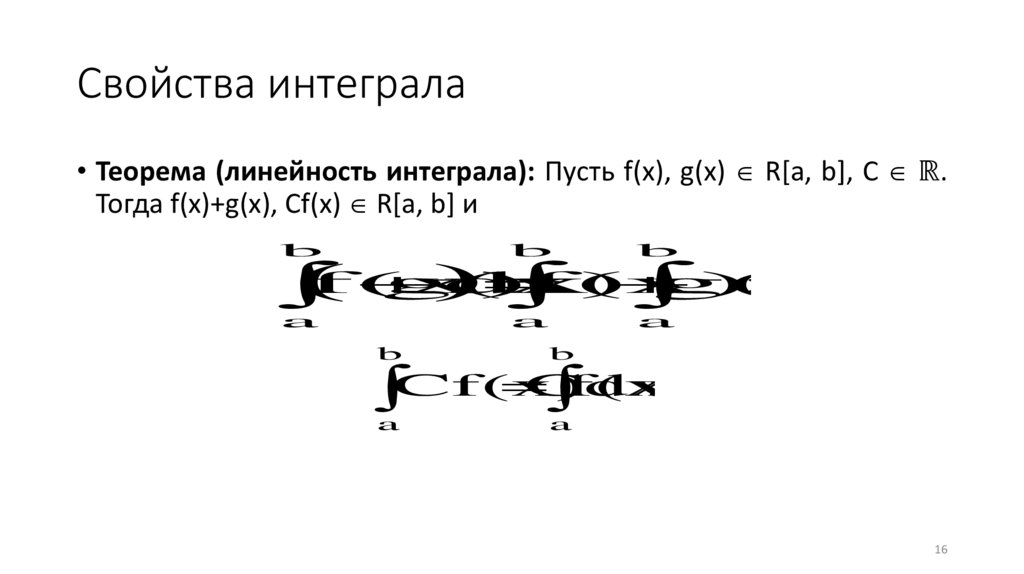
Свойства интеграла• Теорема (линейность интеграла): Пусть f(x), g(x) R[a, b], C ℝ.
Тогда f(x)+g(x), Cf(x) R[a, b] и
b
b
b
a
a
a
f(x)
g(x)
dx
f(x)dx
g(x)dx
;
b
b
a
a
C
.
Cf(x)dx
f(x)dx
16
17.
Свойства интеграла• Теорема (аддитивность интеграла): Пусть a < b < c и f(x) R[a, c].
Тогда f(x) R[a, b], f(x) R[b, c] и
с
b
c
a
a
b
f(x)dx
f(x)dx
f(x)dx
.
17
18.
Свойства интеграла• Также имеют место следующие свойства:
b
a
a
b
.
f(x)dx
f(x)dx
a
0.
f(x)dx
a
18
19.
Оценка интеграла• Теорема: Пусть f(x) R[a, b]. Тогда |f(x)| R[a, b] и справедливо
неравенство:
b
b
dx
.
f(x)dx
f(x)
a
a
• Если при этом |f(x)| ≤ С, то
b
dx
C(b
a)
.
f(x)
a
19
20.
Монотонность интеграла• Теорема: Пусть f(x), g(x) R[a, b] и f(x) ≤ g(x) на отрезке [a, b].
Тогда справедливо неравенство:
b
b
a
a
.
f(x)dx
g(x)dx
• Следствие 1: Если f(x) R[a, b] и m ≤ f(x) ≤ M на отрезке [a, b], то
b
m(b
a)
f(x)dx
M(b
a)
.
a
20
21.
Монотонность интеграла• Следствие 2: Если f(x) R[a, b], m = inf f(x), M = sup f(x) на отрезке
[a, b], то число μ [m, M]:
b
μ(b
a)
.
f(x)dx
a
• Следствие 3: Если f(x) C[a, b], то точка ξ [a, b]:
b
.
f
ξ
b
a
f(x)dx
a
21
22.
Первая теорема о среднем• Теорема (первая теорема о среднем): Если f(x), g(x) R[a, b], m =
inf f(x), M = sup f(x) на отрезке [a, b] и g(x) не меняет свой знак на
отрезке [a, b], то число μ [m, M]:
b
b
a
a
μ
.
f(x)g(x)dx
g(x)dx
• Следствие: Если в условиях теоремы f(x) C[a, b], то точка ξ
[a, b]:
b
b
a
a
f(x)g(x)dx
f
ξ
g(x)dx
.
22
23.
Вторая теорема о среднем• Теорема (вторая теорема о среднем): Если f(x), g(x) R[a, b] и
g(x) монотонная на отрезке [a, b] функция, то число ξ [a, b]:
b
ξ
b
a
a
ξ
f(x)g(x)dx
g(a)
f(x)dx
g(b)
f(x)dx
.
• Это равенство также называют формулой Бонне.
23
24.
Интеграл c переменным пределом• Пусть функция f(x) R[a, b]. Интегралом функции f(x) с
переменным верхним пределом называется функция
x
F(x)
f(t)dt
.
a
• Лемма: Если функция f(x) R[a, b] и непрерывна в точке x
[a, b], то функция F(x) дифференцируема в точке x и F’(x) = f(x).
24
25.
Формула Ньютона-Лейбница• Теорема (формула Ньютона-Лейбница): Пусть функция f(x)
R[a, b] и F(x) – любая из первообразных функции f(x). Тогда
b
F(b)
F(a).
f(x)dx
a
b
• Выражение F(b) – F(a) обозначается F(x) a .
25
26.
Интегрирование по частям• Формула интегрирования по частям в определенном интеграле:
b
b
uv
.
udv
vdu
b
a
a
a
26
27.
Замена переменной• Теорема: Пусть функция f(x) R[a, b], ϕ(t) – непрерывно
дифференцируемое, строго монотонное отображение отрезка [α,
β] в отрезок [a, b]: ϕ(α) = a, ϕ(β) = b. Тогда
b
β
a
α
f(x)dx
f
φ
(t)
φ'
(t)dt
.
27
28.
Приложения интеграла: площадь• Площадь криволинейной трапеции, ограниченной функцией f(x)
сверху, функцией g(x) снизу, прямой x = a и прямой x = b,
вычисляется по формуле:
b
dx
S
g(x)
.
f(x)
a
• Площадь криволинейного сектора, ограниченного в полярных
координатах кривой r = f(ϕ) и полярными радиусами ϕ = α, ϕ = β,
вычисляется по формуле:
β
1
2
S f(
φ
) d
φ
.
2α
28
29.
Длина дуги кривой• Пусть гладкая кривая задается уравнением y = f(x). Тогда длина
дуги кривой, заключенной между x = a и x = b, вычисляется по
b
формуле:
2
dx
s
.
1 f'(x)
a
• Если гладкая кривая задана в параметрической форме: x = ϕ(t),
y = ψ(t), то длина дуги кривой, заключенной между точками (ϕ(α),
ψ(α)) и (ϕ(β), ψ(β)), вычисляется по формуле:
β
dt
s
φ
'(t)
ψ
'(t)
.
2
2
α
29
30.
Объем тела вращения• Пусть дана криволинейная трапеция, ограниченная функцией f(x),
осью Ox и вертикалями x = a и x = b. Тогда объем тела,
образованного вращением этой криволинейной трапеции вокруг
оси Ox, вычисляется по формуле:
b
2
V
π
f
.
x
(x)dx
a
• Объем тела, образованного вращением этой криволинейной
трапеции вокруг оси Oy, вычисляется по формуле:
b
V
2
π
.
y
xf(x)dx
a
30
31.
Несобственный интеграл с бесконечными пределамиТогда определим несобственный интеграл как
Если предел существует и конечен то интеграл сходится.
Если предел бесконечен или не существует, то - расходится.
32.
Несобственный интеграл с бесконечными пределамиопределение не зависит от точки а.
33.
Несобственный интеграл с бесконечными пределамиКритерий Коши сходимости несобственного интеграла:
Для сходимости несобственного интеграла
необходимо и достаточно, чтобы
∀ ε > 0 ∃ b = b(ε) > a: ∀ b′ > b, ∀ b′′ > b ⇒
<ε
34.
Несобственный интеграл с бесконечными пределамиПусть функция f(x) интегрируема на полубесконечном интервале [A, ∞). Если наряду с
интегралом
сходится и интеграл
, то интеграл
называется абсолютно сходящимся, а функция – абсолютно интегрируемой на [A, ∞).
Если интеграл
сходится, а интеграл
называется условно сходящимся,
Из сходимости
Обратное не верно.
вытекает сходимость
расходится , то интеграл
35.
Несобственный интеграл с бесконечными пределами36.
Несобственный интеграл с бесконечными пределами37.
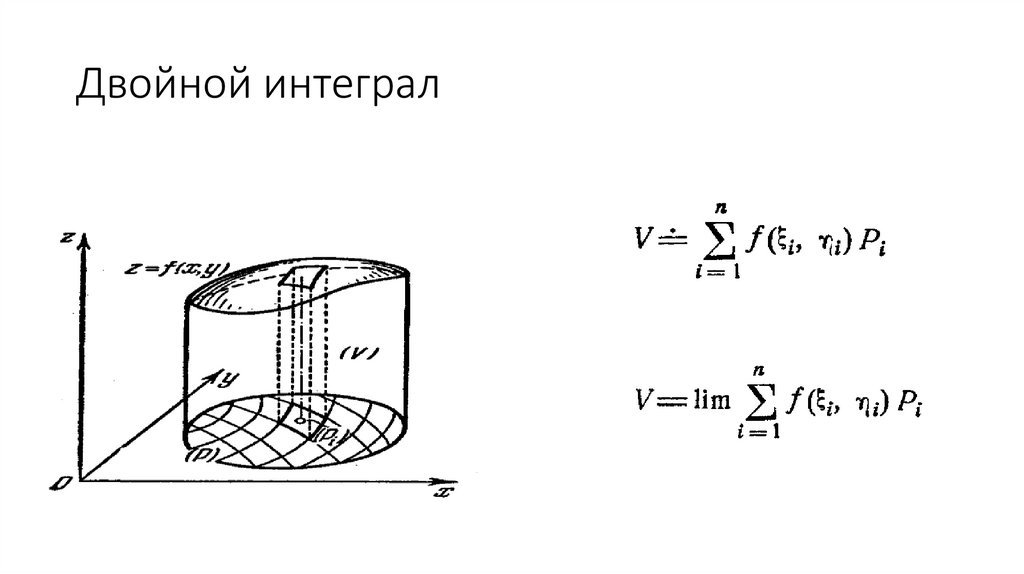
Несобственный интеграл от неограниченной функции38. Двойной интеграл
39. Двойной интеграл
40. Свойства двойного интеграла
Пусть функции f(x , y) и g(x , y) интегрируемы в области G R2, c –вещественная константа, область G можно разбить на
непересекающиеся области G1 и G2. Тогда:
1) f(x, y) g(x, y) dxdy f(x, y)dxdy g(x, y)dxdy .
G
G
G
2) cf(x, y)dxdy c f(x, y)dxdy .
G
G
3) f(x, y)dxdy f(x, y)dxdy f(x, y)dxdy .
G
G1
G2
40
41. Виды областей
Пусть область G ограничена слева и справа вертикалями x = a и x =b, а сверху и снизу кривыми y = y1(x) и y = y2(x). Такая область
называется y-трапециевидной.
Пусть область G ограничена сверху и снизу горизонталями y = a и y
= b, а слева и справа кривыми x = x1(y) и x = x2(y). Такая область
называется x-трапециевидной.
41
42. Сведение двойного к повторному
Теорема 1: Пусть G = {a ≤ x ≤ b, y1(x) ≤ y ≤ y2(x)} – y-трапециевиднаяобласть, функция f(x,y) интегрируема в области G и
фиксированного x интеграл
y 2 (x)
f(x, y)dy.
y1 (x)
Тогда повторный интеграл
b
y 2 (x)
a
y1 (x)
dx f(x, y)dy
42
43. Сведение двойного к повторному
и имеет место равенство:b
y 2 (x)
a
y1 (x)
f(x, y)dxdy dx f(x, y)dy
G
Теорема 2: Пусть G = {a ≤ y ≤ b, x1(y) ≤ x ≤ x2(y)} – x-трапециевидная
область, функция f(x,y) интегрируема в области G и
фиксированного y интеграл
x 2 (y)
f(x, y)dx .
x1 (y)
43
44. Сведение двойного к повторному
Тогда повторный интегралb
x 2 (y)
a
x1 (y)
dy f(x, y)dx
и имеет место равенство:
b
x 2 (y)
a
x1 (y)
f(x, y)dxdy dy f(x, y)dx
G
44
45. Замена переменных
Теорема: Пусть функции x = ϕ(u, v), y = ψ(u, v) отображают областьD плоскости (u, v) в область G плоскости (x, y) так, что:
1) это отображение взаимно однозначно;
2) ϕ, ψ С1(D);
'u ' v
3) якобиан отображения J ,ψ
0.
ψ'u
ψ'v
Пусть функция f(x, y) интегрируема в области G. Тогда
f(x, y)dxdy f( (u, v), ψ(u, v))J dudv.
,ψ
G
D
45
46. Замена переменных
Замечание: Если условия 1 или 3 нарушаются не более чем всчетном количестве точек, то формула остается верной.
Часто используемым примером замены является полярная замена:
x = r cosϕ, y = r sinϕ.
Якобиан полярной замены равен r.
46
47. Приложения двойного интеграла
Площадь области G равнаS dxdy .
G
Объем цилиндрического тела, имеющего в основании область G и
ограниченного сверху поверхностью z = f(x, y), равен
V f(x, y)dxdy .
G
47
48. Приложения двойного интеграла
Масса бесконечно тонкой пластинки G с плотностью ρ(x, y) равнаm ρ(x, y)dxdy .
G
Координаты центра тяжести этой пластинки равны
1
1
x 0 xρ(x, y)dxdy , y0 yρ(x, y)dxdy .
mG
mG
48
49. Тройной интеграл
Пусть T – кубируемое тело (т.е. имеет конечный объем). Пустьфункция f(x, y, z) определена на этом теле.
Разобьем тело T на n кусочков, в каждом кусочке выберем по точке
(ξi, ηi, ζi).
Пусть Δi – объем i-го кусочка тела T. Составим сумму
n
f(ξ , η , ζ )Δ .
i 1
i
i
i
i
Будем увеличивать количество кусочков в разбиении так, чтобы
объемы кусочков уменьшались.
49
50. Тройной интеграл
Если существует предел этой суммы, то он называется тройныминтегралом функции f(x, y, z) по телу T:
n
f(x, y, z)dxdydz lim f(ξ , η , ζ )Δ .
T
n
max Δ i 0 i 1
i
i
i
50
i
51. Необходимые условия интегрирования
Теорема 1: Функция, непрерывная в замкнутой кубируемойобласти, интегрируема в этой области.
Теорема 2: Функция, ограниченная в кубируемой области и
непрерывная почти всюду в этой области, интегрируема в этой
области.
51
52. Сведение тройного к повторному
Теорема 1: Пусть T = {a ≤ x ≤ b, y1(x) ≤ y ≤ y2(x), z1(x, y) ≤ z ≤ z2(x, y)},функция f(x,y,z) интегрируема на T и фиксированных x, y
интеграл
z 2 (x, y)
f(x, y, z)dz.
z1 (x, y)
Тогда повторный интеграл
b
y 2 (x)
z 2 (x, y)
a
y1 (x)
z1 (x, y)
dx dy f(x, y, z)dy
52
53. Сведение тройного к повторному
и имеет место равенство:b
y 2 (x)
z 2 (x, y)
a
y1 (x)
z1 (x, y)
f(x, y, z)dxdydz dx dy f(x, y, z)dy
T
Аналогично для других типов представления тела T.
53
54. Замена переменных
Теорема: Пусть функции x = ϕ(u,v,w), y = ψ(u,v,w), z = χ(u,v,w)отображают тело V пространства (u, v, w) в тело T пространства
(x, y, z) так, что:
1) это отображение взаимно однозначно;
2) ϕ, ψ, χ С1(V);
3) якобиан отображения J ,ψ,χ 0.
Пусть функция f(x, y, z) интегрируема на теле T. Тогда
f(x, y, z)dxdydz f( (u, v, w), ψ(u, v, w), χ(u, v, w))J
T
T
54
, ψ,χ
dudvdw .
55. Замена переменных
Замечание: Если условия 1 или 3 нарушаются не более чем всчетном количестве точек, то формула остается верной.
Часто используемыми примерами замены являются сферическая
замена: x = r sinθ cosϕ, y = r sinθ sinϕ, z = r cosθ, и
цилиндрическая замена: x = r cosϕ, y = r sinϕ, z = h.
55
56. Кривая
Пусть кривая L задана на плоскости параметризацией x = ϕ(t), y =ψ(t), t [a, b].
Кривая L называется простой, если функции ϕ(t) и ψ(t) непрерывны
на [a, b] и t1, t2 (a, b) (ϕ(t1), ψ(t1)) (ϕ(t2), ψ(t2)).
Если при этом (ϕ(a), ψ(a)) = (ϕ(b), ψ(b)), то кривая L называется
замкнутой, иначе – незамкнутой.
Кривая называется спрямляемой, если существует предел длин
ломанных, вписанных в эту кривую.
56
57. Криволинейный интеграл 1 рода
Пусть L – простая спрямляемая кривая. Пусть функция f(x, y)определена на этой кривой.
Разобьем кривую L на n кусочков, в каждом кусочке выберем по
точке (ξi, ηi).
Пусть Δi – длина дуги i-го кусочка кривой L. Составим сумму
n
f(ξ ,η )Δ .
i 1
i
i
i
Будем увеличивать количество кусочков в разбиении так, чтобы
длины дуг кусочков уменьшались.
57
58. Криволинейный интеграл 1 рода
Если существует предел этой суммы, то он называетсякриволинейным интегралом 1 рода функции f(x, y) по кривой L:
n
f(x,y)dl lim f(ξ ,η )Δ .
L
n
maxΔi 0 i 1
i
i
i
58
59. Вычисление криволинейного интеграла
Функция называется кусочно непрерывной, если она имеет неболее чем счетное число точек разрыва и эти точки только 1
рода.
Теорема: Пусть L – гладкая или кусочно гладкая кривая, заданная
уравнениями x = ϕ(t), y = ψ(t), t [a, b]. Пусть функция f(x, y)
кусочно непрерывная вдоль кривой L. Тогда существует
криволинейный интеграл 1 рода от функции f(x, y) по кривой L и
справедливо равенство:b
f(x,y)dl f(φ(t),ψ(t)) φ' (t)+ψ' (t)dt.
2
L
2
a
59
60. Следствия
Следствие 1: Пусть кривая L задана уравнением y = y(x), x [a, b].Тогда
b
2
f(x,y)dl
f(x,y(x))
1+y'
(x)dx.
L
a
Следствие 2: Пусть кривая L задана в полярных координатах r =
r(ϕ), ϕ [α, β]. Тогда
β
f(x,y)dl f(r(φ)cos φ,r(φ)sin φ)) r (φ)+r' (φ)dφ.
2
L
2
α
60
61. Трехмерный случай
Замечание: Все аналогичные понятия и формулы верны и длятрехмерного случая.
61
62. Приложения интеграла
Масса бесконечно тонкой кривой L с плотностью ρ(x, y) равнаm= ρ(x,y)dl
L
Координаты центра тяжести этой кривой равны
1
1
x 0 xρ(x,y)dl, y0 yρ(x,y)dl.
mL
mL
62
63. Криволинейный интеграл 2 рода
Пусть L – простая спрямляемая кривая, заданная уравнениями x =ϕ(t), y = ψ(t), t [a, b]. Пусть на этой кривой определены 2
функции P(x, y) и Q(x, y).
Разобьем кривую L на n кусочков точками a = t0 < t1 < … < tn = b. В
каждом кусочке выберем по точке (ξi, ηi).
Пусть Δxi = xi – xi–1, Δyi = yi – yi–1. Составим суммы
n
n
P(ξ ,η )Δx , Q(ξ ,η )Δy
i 1
i
i
i
i 1
i
i
i
Будем увеличивать количество кусочков в разбиении так, чтобы
длины дуг кусочков уменьшались.
63
64. Криволинейный интеграл 2 рода
Если существует предел этих сумм, то сумма этих пределовназывается криволинейным интегралом 2 рода функций P(x, y) и
Q(x, y) по кривой L:
n
n
P(x,y)dx+Q(x,y)dy lim P(ξ ,η )Δx + lim Q(ξ ,η )Δy .
L
n
maxΔx i 0 i 1
i
i
i
n
maxΔyi 0 i 1
64
i
i
i
65. Свойства
Для криволинейных интегралов выполняется большинствостандартных свойств интегралов – таких, как линейность и
аддитивность.
Основное отличие в свойствах: криволинейный интеграл 1 рода не
зависит от направления кривой, а 2 рода – зависит.
f(x,y)dl f(x,y)dl.
AB
BA
P(x,y)dx+Q(x,y)dy P(x,y)dx+Q(x,y)dy.
AB
BA
65
66. Вычисление криволинейного интеграла
Функция называется кусочно непрерывной, если она имеет неболее чем счетное число точек разрыва и эти точки только 1
рода.
Теорема: Пусть L – гладкая или кусочно гладкая кривая, заданная
уравнениями x = ϕ(t), y = ψ(t), t [a, b]. Пусть функции P(x, y) и
Q(x, y) кусочно непрерывны вдоль кривой L. Тогда существует
криволинейный интеграл 2 рода от функций P(x, y) и Q(x, y) по
кривой L и справедливо bравенство:
P(x,y)dx+Q(x,y)dy (P(φ(t),ψ(t))φ'(t)+Q(φ(t),ψ(t))ψ'(t))dt.
L
a
66
67. Замкнутая кривая
Если L – замкнутая кривая, то криволинейные интегралы по кривойL обозначаются значком ∫.
Положительным направлением обхода замкнутой кривой
считается такое направление, при котором область,
ограниченная этой кривой, остается слева.
67
68. Приложения интеграла
Пусть F(x, y) = (P(x, y), Q(x, y)) – вектор силы в точке с координатами(x, y). Тогда работа этой силы при перемещении материальной
точки массы 1 ед. из точки A в точку B вдоль кривой AB
вычисляется по формуле
P(x,y)dx+Q(x,y)dy
AB
68
69. Формула Грина
Теорема (формула Грина): Пусть функции P(x, y) и Q(x, y) и ихчастные производные P’y(x, y) и Q’x(x, y) непрерывны в области G,
ограниченной кривой L. Тогда
Q P
L P(x,y)dx+Q(x,y)dy G x y dxdy.
Направление обхода кривой L – положительное.
69



































































 Математика
Математика