почитайте

1.

Алгоритмы и сложность

2.

Алгоритмы и сложность
Алгоритм — это последовательность указаний, которые нужно исполнить, чтобы решить чётко
сформулированную задачу.
Быстрые и медленные алгоритмы
Суперкомпьютер может выполнить сложение за 10-10 секунды, а калькулятор — за 10-5
Вместо того, чтобы рассчитывать время выполнения на каждом компьютере, мы описываем время
выполнения через общее количество операций, необходимых алгоритму, — это характеристика
самого алгоритма, а не компьютера, который вы используете.

3.

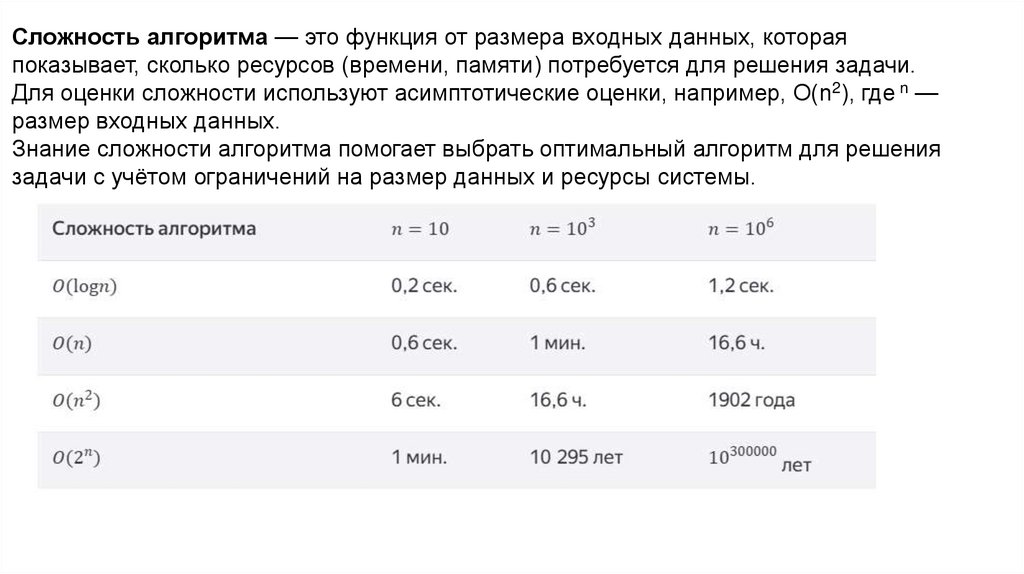
Сложность алгоритма — это функция от размера входных данных, которая
показывает, сколько ресурсов (времени, памяти) потребуется для решения задачи.
Для оценки сложности используют асимптотические оценки, например, О(n2), где n —
размер входных данных.
Знание сложности алгоритма помогает выбрать оптимальный алгоритм для решения
задачи с учётом ограничений на размер данных и ресурсы системы.

4.

Динамические структуры
данных

5.

Динамические структуры данных — конструкции, которые могут выделять память
под новые элементы или удалять выделенную память для ненужных элементов во
время работы программы.
Используют метод динамического распределения памяти: память под элементы
выделяется в момент их «существования» в процессе выполнения программы.

6.

Стек
упорядоченный набор элементов, в котором
добавление и удаление элементов происходит с
одного конца (вершины стека);
принцип работы — LIFO (Last In First Out, «последний
пришёл — первый ушёл»);
пример: детская пирамидка, где добавление и снятие
колец происходит согласно определению стека.

7.

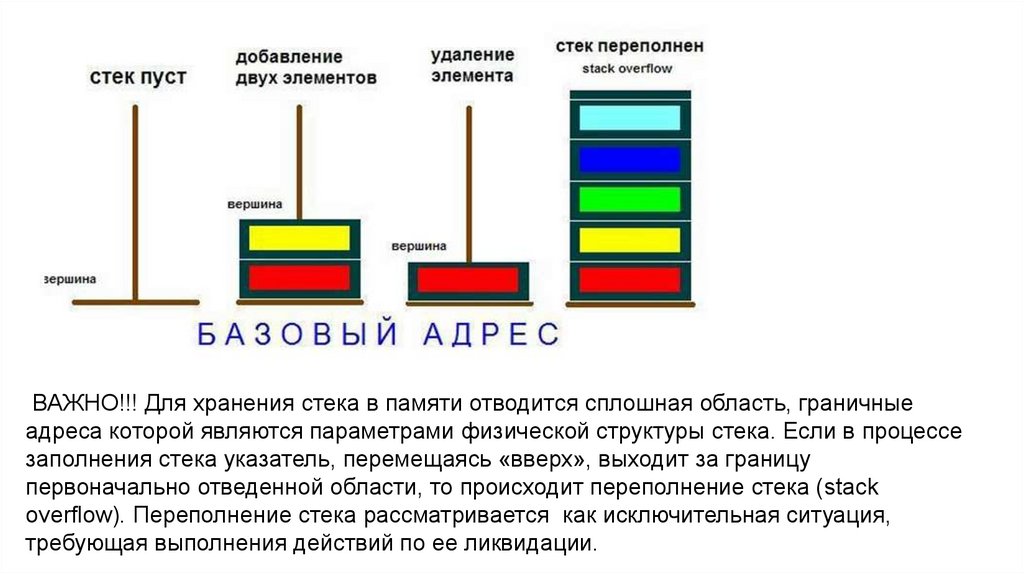
ВАЖНО!!! Для хранения стека в памяти отводится сплошная область, граничные
адреса которой являются параметрами физической структуры стека. Если в процессе
заполнения стека указатель, перемещаясь «вверх», выходит за границу
первоначально отведенной области, то происходит переполнение стека (stack
overflow). Переполнение стека рассматривается как исключительная ситуация,
требующая выполнения действий по ее ликвидации.

8.

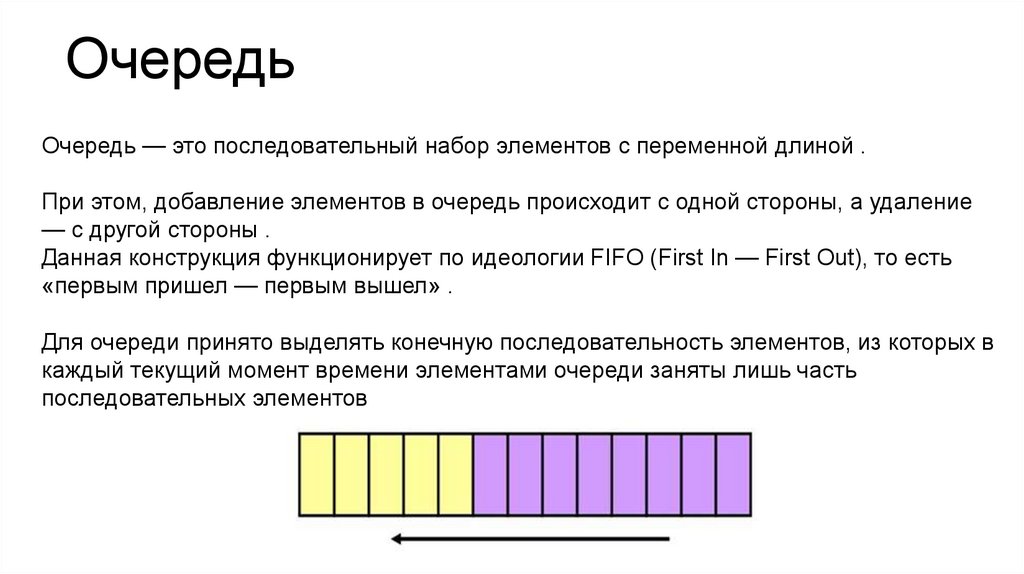
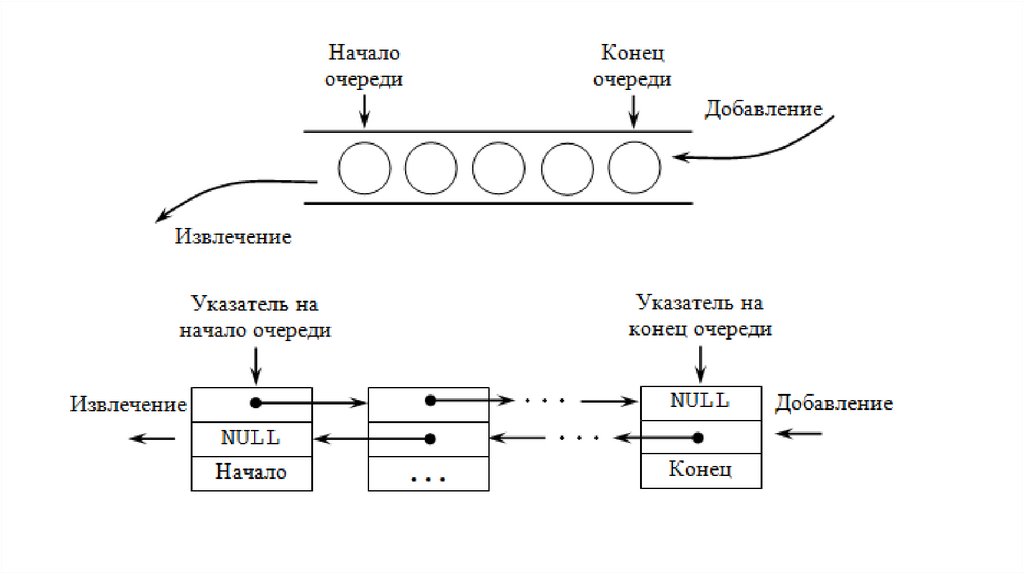
Очередь
Очередь — это последовательный набор элементов с переменной длиной .
При этом, добавление элементов в очередь происходит с одной стороны, а удаление
— с другой стороны .
Данная конструкция функционирует по идеологии FIFO (First In — First Out), то есть
«первым пришел — первым вышел» .
Для очереди принято выделять конечную последовательность элементов, из которых в
каждый текущий момент времени элементами очереди заняты лишь часть
последовательных элементов

9.

10.

Простая очередь (принцип FIFO) используется в задачах для упорядоченной обработки
данных, например, в операционных системах для планирования задач процессором,
печати, или в сетевых технологиях для управления потоками. Также она применяется в
системах обмена сообщениями для накопления и распределения задач между
исполнителями.

11.

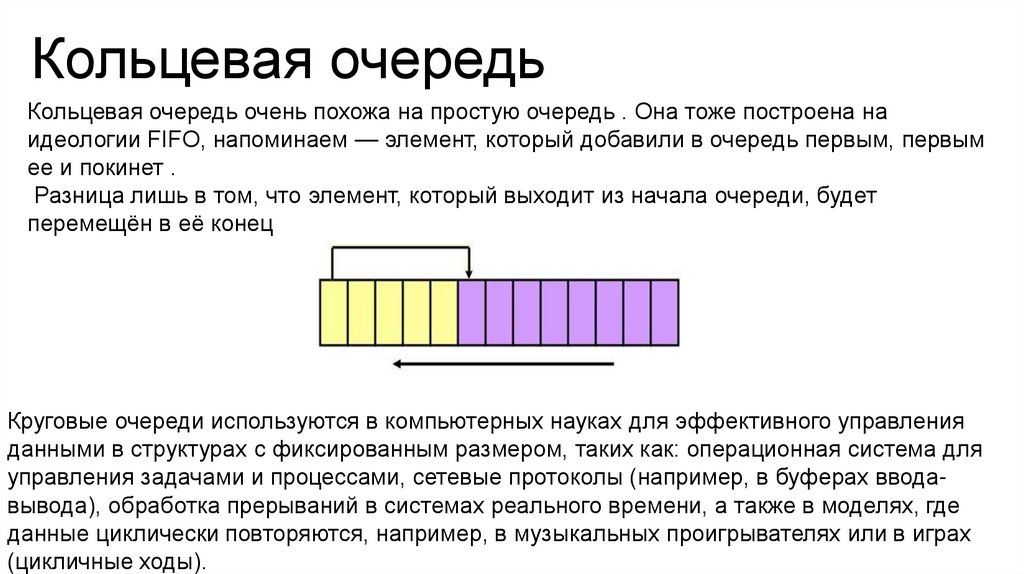
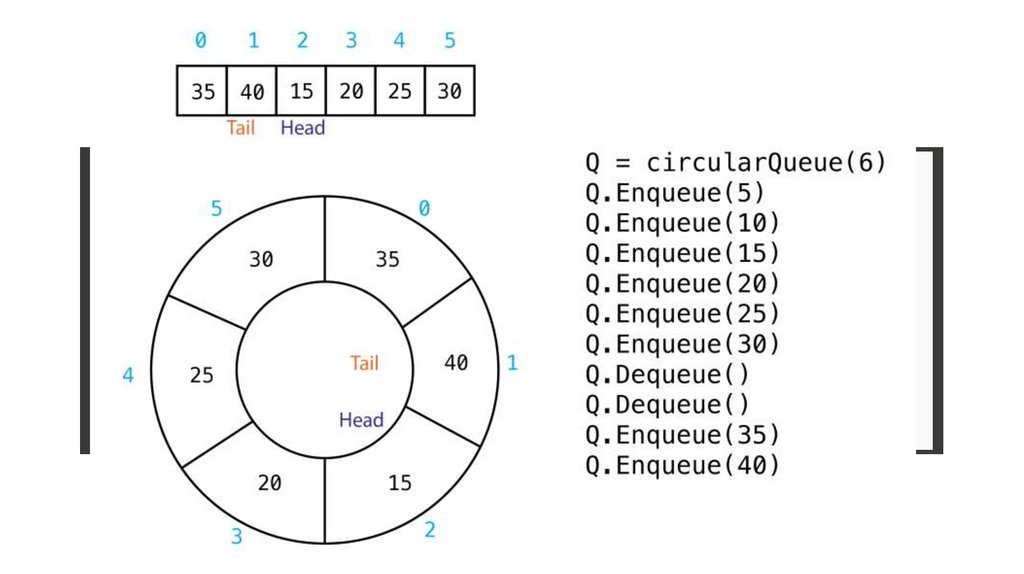
Кольцевая очередь
Кольцевая очередь очень похожа на простую очередь . Она тоже построена на
идеологии FIFO, напоминаем — элемент, который добавили в очередь первым, первым
ее и покинет .
Разница лишь в том, что элемент, который выходит из начала очереди, будет
перемещён в её конец
Круговые очереди используются в компьютерных науках для эффективного управления
данными в структурах с фиксированным размером, таких как: операционная система для
управления задачами и процессами, сетевые протоколы (например, в буферах вводавывода), обработка прерываний в системах реального времени, а также в моделях, где
данные циклически повторяются, например, в музыкальных проигрывателях или в играх
(цикличные ходы).

12.

13.

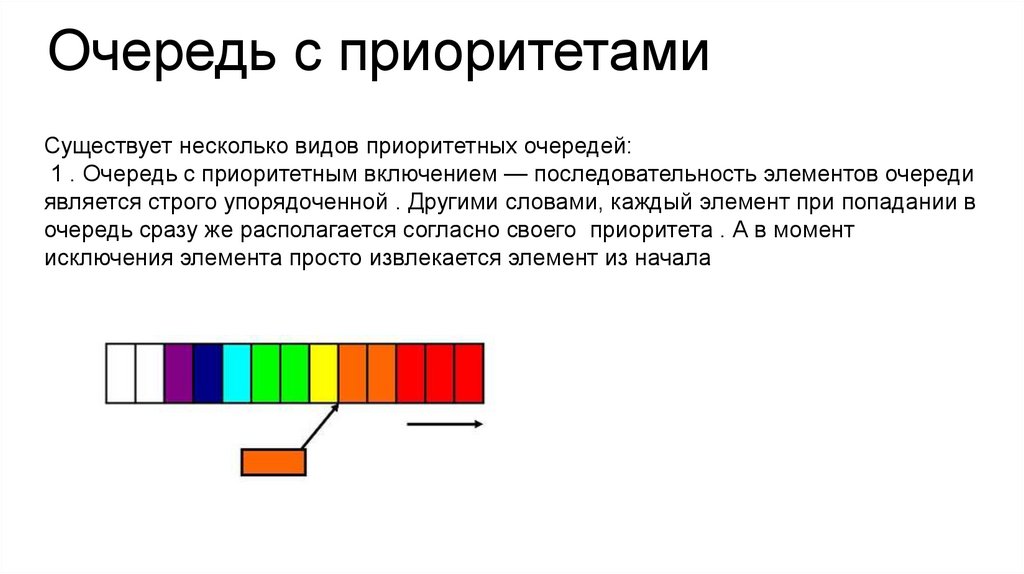
Очередь с приоритетами
Существует несколько видов приоритетных очередей:
1 . Очередь с приоритетным включением — последовательность элементов очереди
является строго упорядоченной . Другими словами, каждый элемент при попадании в
очередь сразу же располагается согласно своего приоритета . А в момент
исключения элемента просто извлекается элемент из начала

14.

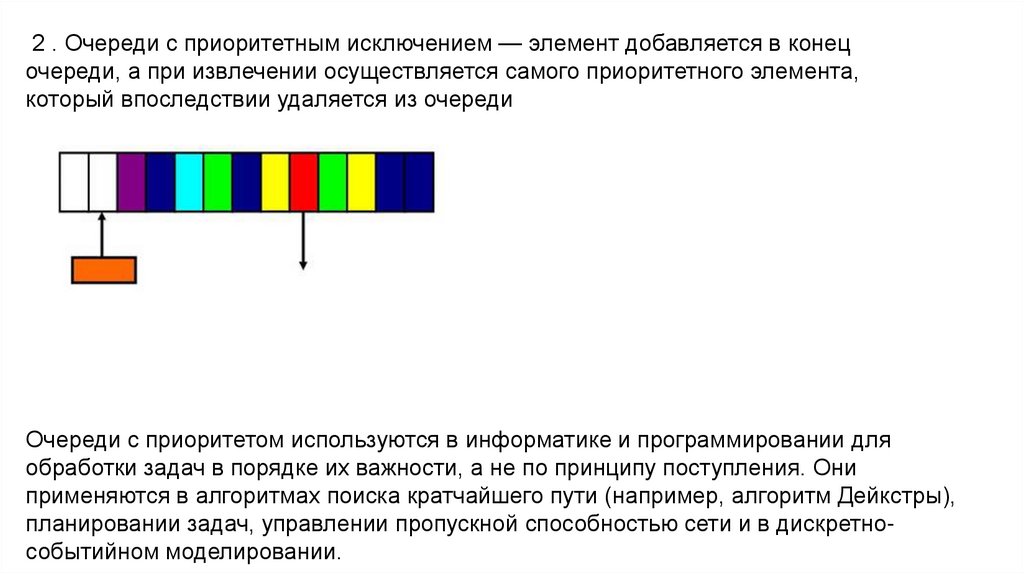
2 . Очереди с приоритетным исключением — элемент добавляется в конец
очереди, а при извлечении осуществляется самого приоритетного элемента,
который впоследствии удаляется из очереди
Очереди с приоритетом используются в информатике и программировании для
обработки задач в порядке их важности, а не по принципу поступления. Они
применяются в алгоритмах поиска кратчайшего пути (например, алгоритм Дейкстры),
планировании задач, управлении пропускной способностью сети и в дискретнособытийном моделировании.

15.

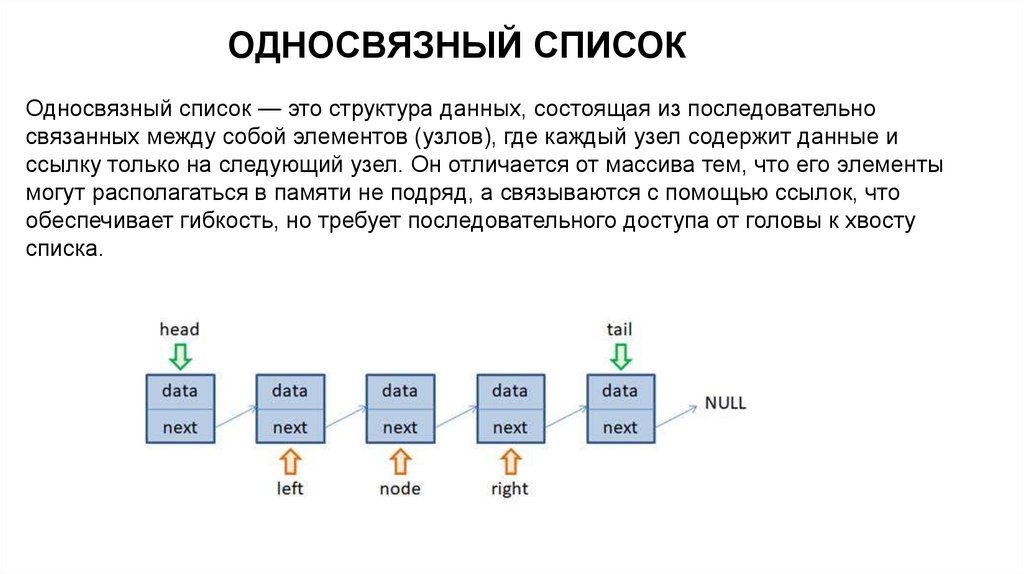
ОДНОСВЯЗНЫЙ СПИСОК
Односвязный список — это структура данных, состоящая из последовательно
связанных между собой элементов (узлов), где каждый узел содержит данные и
ссылку только на следующий узел. Он отличается от массива тем, что его элементы
могут располагаться в памяти не подряд, а связываются с помощью ссылок, что
обеспечивает гибкость, но требует последовательного доступа от головы к хвосту
списка.

16.

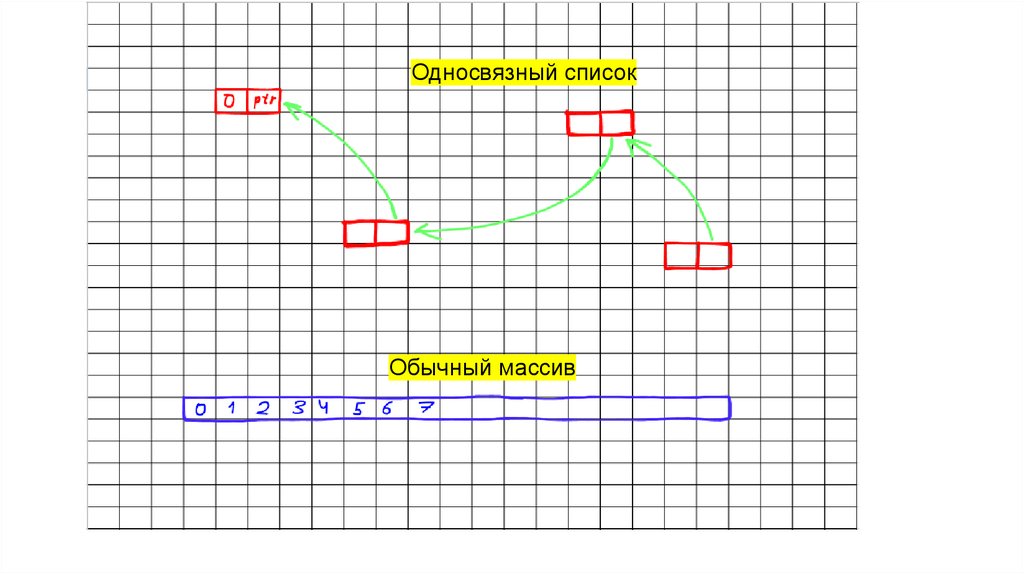
Односвязный список
Обычный массив

17.

Основные характеристики
Узлы: Каждый узел включает в себя поле для данных и поле для ссылки (указателя) на
следующий узел.
Связь: Каждый узел, кроме последнего, имеет ссылку на следующий элемент.
Голова: Первый элемент списка называется головой (head).
Хвост: Последний элемент списка ссылается на nullptr, указывая на конец списка.
Доступ: Доступ к элементам возможен только последовательно, начиная с головы
списка.
Гибкость: Позволяет легко добавлять и удалять элементы в любой части списка без
необходимости сдвигать другие элементы, как в массиве.

18.

Односвязные списки используются в задачах, где важны динамическое добавление и
удаление элементов, а также для реализации других структур данных, таких как стеки и
очереди. Они применяются в ситуациях, где хранятся упорядоченные наборы данных, и
требуется эффективное управление ими без необходимости частого доступа к элементам
по индексу.
Динамическое управление памятью: Они позволяют выделять и освобождать память
по мере необходимости, что было особенно важно на ранних компьютерах с
ограниченным объемом памяти.
Упорядоченное хранение данных: Используются для хранения последовательностей
однотипных элементов, где доступ к каждому элементу осуществляется по ссылке на
следующий.
Решение проблем производительности: При частых операциях добавления или
удаления данных, односвязный список часто более эффективен, чем массив, поскольку
не требует сдвигать большое количество элементов.
Реализация других структур: Могут использоваться для создания хеш-таблиц (как часть
решения коллизий), графов и других сложных структур данных.

19.

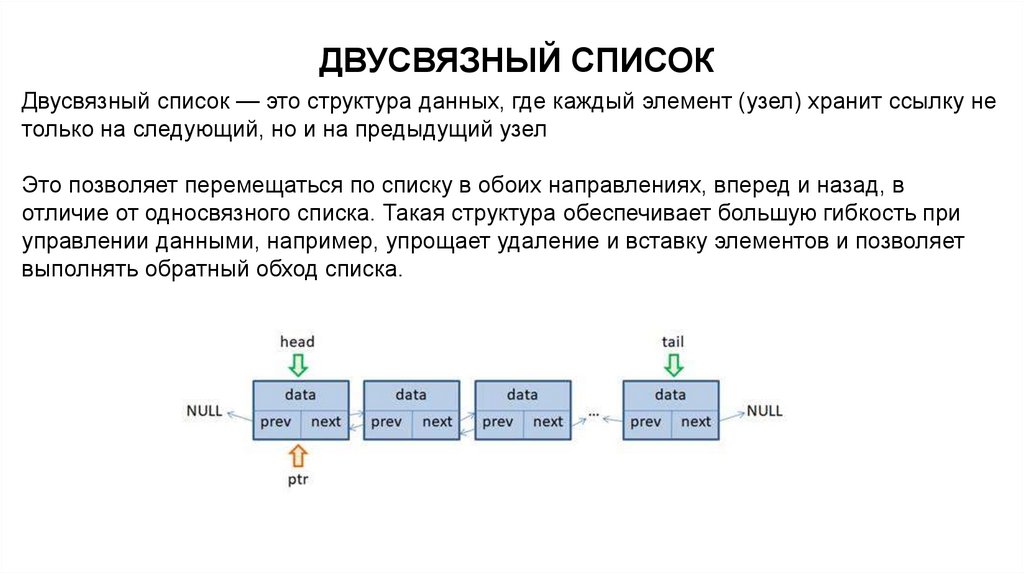
ДВУСВЯЗНЫЙ СПИСОК
Двусвязный список — это структура данных, где каждый элемент (узел) хранит ссылку не
только на следующий, но и на предыдущий узел
Это позволяет перемещаться по списку в обоих направлениях, вперед и назад, в
отличие от односвязного списка. Такая структура обеспечивает большую гибкость при
управлении данными, например, упрощает удаление и вставку элементов и позволяет
выполнять обратный обход списка.

20.

Каждый узел в двусвязном списке содержит:
-Данные (значение)
-Указатель на следующий узел (next)
-Указатель на предыдущий узел (prev)
Это отличает его от односвязного списка, где есть только указатель на следующий
элемент.
Преимущества перед односвязным списком
-Двунаправленный обход - можно идти как вперед, так и назад
-Более эффективное удаление - не нужно искать предыдущий элемент
-Удобные операции с концом списка
Недостатки
-Больше памяти - каждый узел хранит дополнительный указатель
-Сложнее реализация - нужно обновлять два указателя вместо одного

21.

22.

Применение на практике
-История браузера - переход вперед/назад
-Редакторы текста - undo/redo
-Музыкальные плееры - предыдущая/следующая песня
-Навигационные системы
-Кэширование (например, LRU Cache)

23.

Задание №1
Создайте шаблонный класс двусвязного списка для работы с целыми значениями.
Требуется создать реализации для типичных операций над элементами:
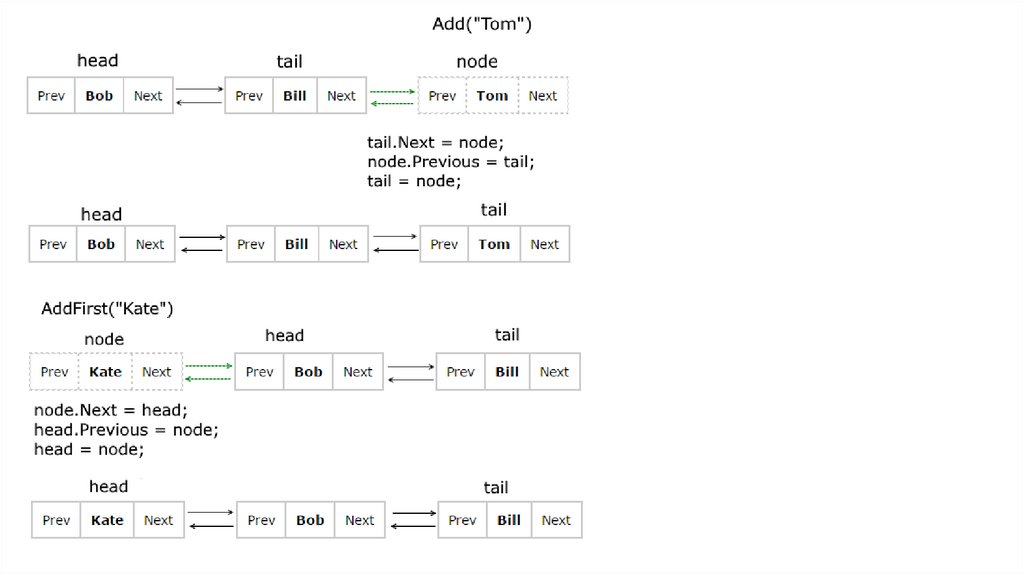
Prepend – добавление элемента в голову;
Append – добавление элемента в хвост;
RemoveFirst – удаление элемента из головы;
RemoveLast – удаление элемента из хвоста;
DeleteAll – удаление всех элементов;
Show – отображение всех элементов списка на экран.
Задание №2
Добавить в класс из задания 1 следующие функции: вставка элемента в заданную
позицию, удаление элемента по заданной позиции, поиск заданного элемента
(функция возвращает позицию найденного элемента в случае успеха или NULL в
случае неудачи), поиск и замена заданного элемента (функция возвращает true в
случае успеха или false в случае неудачи), переворот списка.

24.

Бинарное дерево

25.

Бинарное дерево — это структура данных, где каждый узел имеет не более двух
потомков: левого и правого. Для реализации используются указатели, которые связывают
узлы в иерархическую структуру.
Иначе, это конечное множество элементов, которое либо пусто, либо содержит элемент
(корень), связанный с двумя различными бинарными деревьями, называемыми левым и
правым поддеревьями. Каждый элемент бинарного дерева называется узлом. Связи
между узлами дерева называются его ветвями.

26.

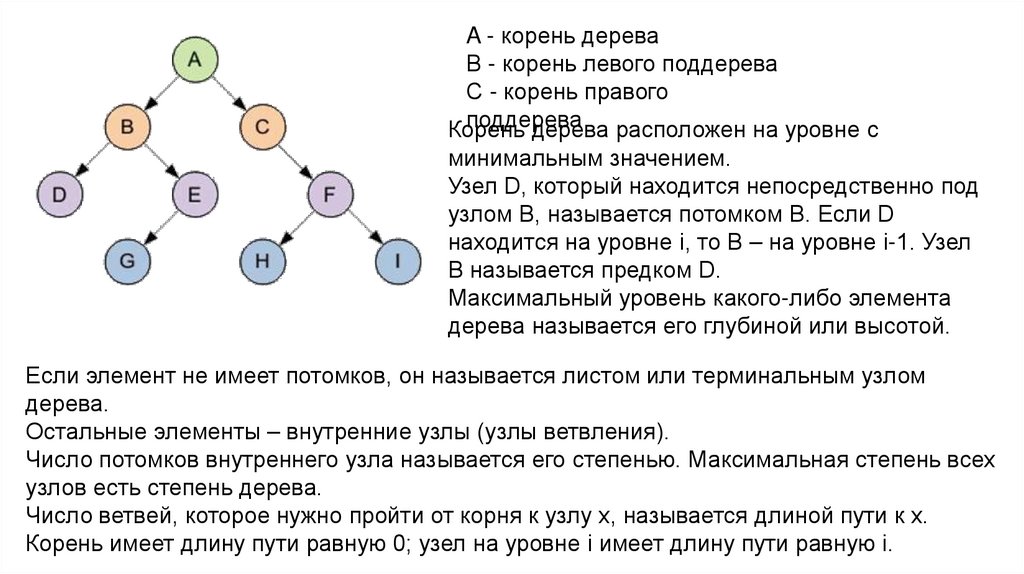
A - корень дерева
В - корень левого поддерева
С - корень правого
поддерева
Корень
дерева расположен на уровне с
минимальным значением.
Узел D, который находится непосредственно под
узлом B, называется потомком B. Если D
находится на уровне i, то B – на уровне i-1. Узел
B называется предком D.
Максимальный уровень какого-либо элемента
дерева называется его глубиной или высотой.
Если элемент не имеет потомков, он называется листом или терминальным узлом
дерева.
Остальные элементы – внутренние узлы (узлы ветвления).
Число потомков внутреннего узла называется его степенью. Максимальная степень всех
узлов есть степень дерева.
Число ветвей, которое нужно пройти от корня к узлу x, называется длиной пути к x.
Корень имеет длину пути равную 0; узел на уровне i имеет длину пути равную i.

27.

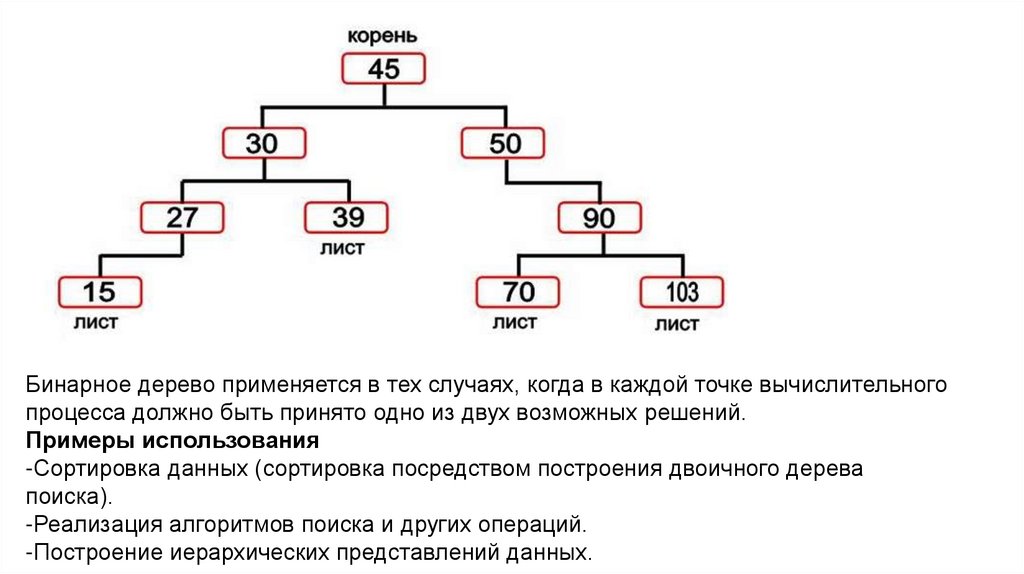
Бинарное дерево применяется в тех случаях, когда в каждой точке вычислительного
процесса должно быть принято одно из двух возможных решений.
Примеры использования
-Сортировка данных (сортировка посредством построения двоичного дерева
поиска).
-Реализация алгоритмов поиска и других операций.
-Построение иерархических представлений данных.

28.

1. Самый главный принцип бинарного дерева заключается в том, что для каждого узла
выполняется правило: в левой ветке содержатся только те ключи, которые имеют
значения, меньшие, чем значение данного узла. В правой же ветке содержатся ключи,
имеющие значения, большие, чем значение данного узла.
2. Каждый узел может иметь два, одного или ни одного потомка .
3. Лист — узел, не имеющий потомков .
4. Узел является родительским для своих потомков и дочерним для своего предка .
5. Левый потомок — дочерний узел слева от текущего
узла .
6. Правый потомок — дочерний узел справа от текущего узла .
7. Корень — основной узел, не имеющий родителей .
8. Каждый узел состоит из четырех частей:
■ Значение .
■ Указатель на родителя .
■ Указатель на левого потомка .
■ Указатель на правого потомка

29.

Способы обхода дерева
Существует три способа обхода дерева:
-Обход дерева сверху вниз (в прямом порядке): A, B, C - префиксная форма.
-Обход дерева в симметричном порядке (слева направо): B, A, C - инфиксная форма.
-Обход дерева в обратном порядке (снизу вверх): B, C, A - постфиксная форма.

30.

Задание
Написать программу, моделирующую работу автобусного парка. Сведения о каждом
автобусе содержат: номер автобуса, фамилию и имя водителя, номер маршрута,
количество мест в автобусе.
Сформировать информацию об автобусах в виде бинарного дерева.
Ключом для формирования дерева является номер автобуса.
Программа должна:
■ Предоставить интерфейс типа «меню»;
■ Выполнять поиск по указанному ключу;
■ Выводить информацию о найденном автобусе на экран;