Похожие презентации:
Материалы ОИИ 2025
1. Введение в искусственные нейронные сети
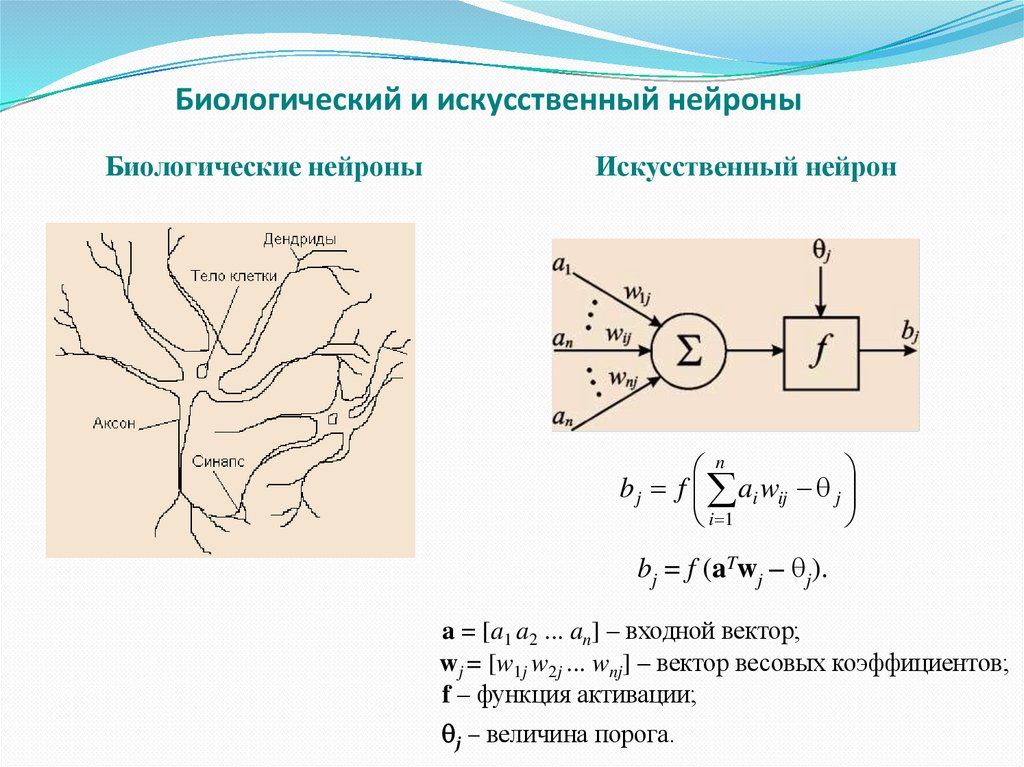
2. Биологический и искусственный нейроны
Биологические нейроныИскусственный нейрон
n
b j f ai wij j
i 1
bj = f (aTwj – j).
a = [a1 a2 ... an] – входной вектор;
wj = [w1j w2j ... wnj] – вектор весовых коэффициентов;
f – функция активации;
j – величина порога.
3. Виды функций активации
а) линейная функция f(x) = x,эквивалентная отсутствию порогового
элемента вообще;
б) кусочно-линейная функция, получаемая
из линейной ограничением диапазона ее
изменения в пределах диапазона [– , + ],
т.е.
, x ,
f ( x ) x, x ,
, x ;
в) ступенчатая пороговая функция
, x 0 ,
f ( x)
, x 0 ;
г) cигмоидная функция S(x)=1/(1+e–x);
д) гиперболический тангенс S(x)=tanh(x).
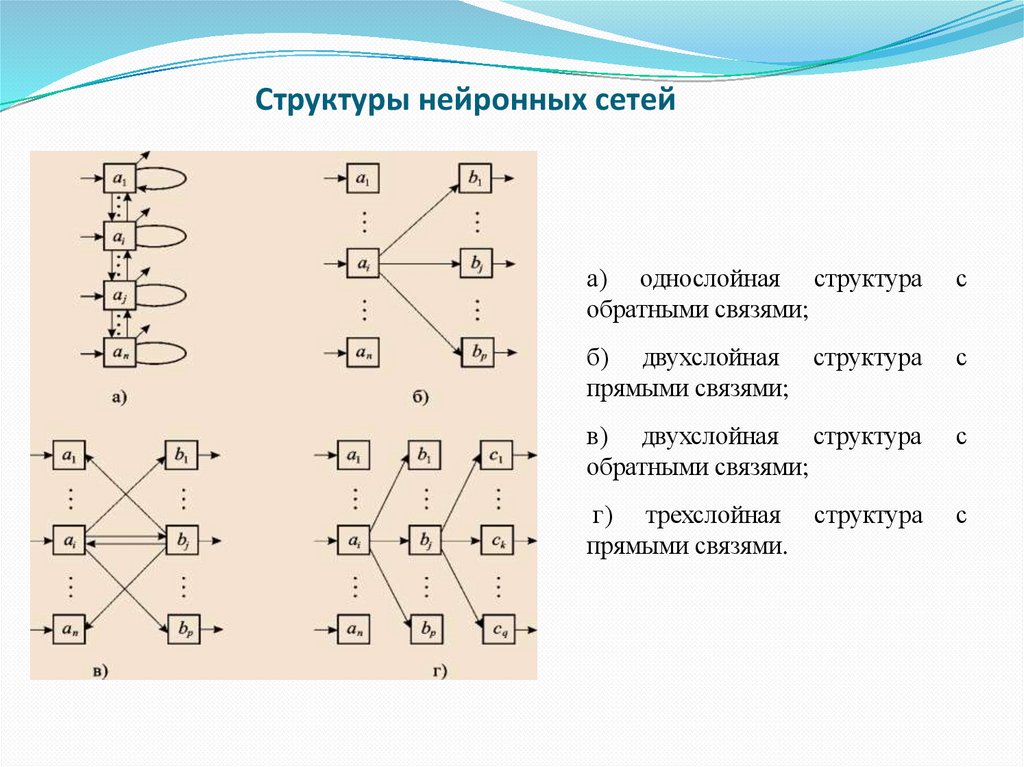
4. Структуры нейронных сетей
а) однослойная структураобратными связями;
с
б) двухслойная структура
прямыми связями;
с
в) двухслойная структура
обратными связями;
с
г) трехслойная
прямыми связями.
с
структура
5. Принципы обучения нейронных сетей
Обучение с учителем:предъявления сети последовательности обучающих пар (примеров) (Ai, Di),
i = 1, ..., m образов, называемой обучающей последовательностью.
обучающая последовательность состоит лишь из входных образов Ai
Алгоритм Хэбба:
wij(t+1) = wij(t) + ai(t) aj(t),
где wij(t) и wij(t+1) – значения веса связи нейрона i с нейроном j до настройки (на
шаге t) и после настройки (на шаге t +1), соответственно;
ai(t) – выход нейрона i на шаге t;
aj(t) – выход нейрона j на шаге t;
– параметр скорости обучения.
6.
Задачу обучения нейронной сети можно рассматривать как задачуминимизации некоторой целевой функции:
min F (W)
W
где W – синаптическая карта нейронной сети.
Итерационный алгоритм поиска
W(t+1)=W(t) + tpt,
где pt и t – направление поиска и величина шага на шаге t алгоритма.
Различные алгоритмы отличаются друг от друга лишь выбором
направления pt поиска. В частности, для градиентного алгоритма вектор
p противоположен вектору градиента, т.е. p = – F/ W.
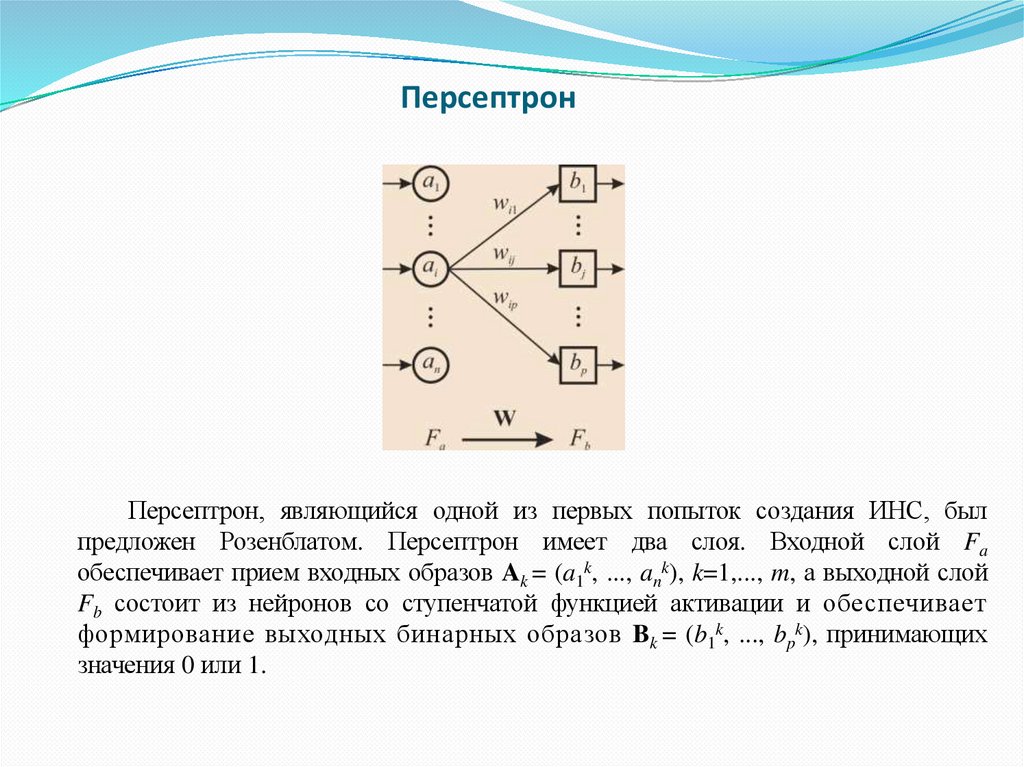
7. Персептрон
Персептрон, являющийся одной из первых попыток создания ИНС, былпредложен Розенблатом. Персептрон имеет два слоя. Входной слой Fa
обеспечивает прием входных образов Ak = (a1k, ..., ank), k=1,..., m, а выходной слой
Fb состоит из нейронов со ступенчатой функцией активации и обеспечивает
формирование выходных бинарных образов Bk = (b1k, ..., bpk), принимающих
значения 0 или 1.
8. Пример: задача дихотомии – 2 признака, 2 - класса
b=f (w1a1+w2a2 – ),где b – выход нейрона; f – ступенчатая функция активации; – значение порога.
Линейная разделяющая функция
Вывод:
возможности
персептрона
ограничены классом линейно разделимых
образов. В примере персептрон не способен
реализовать
функцию
«исключающее
ИЛИ», принимающую значение 0 при
равных значениях аргументов и 1 – для всех
остальных комбинаций.
9. Алгоритм обучения персептрона
1. Начальная инициализация весовых коэффициентов сети и пороговыхзначений всех нейронов случайными числами, принимающими значения в
интервале [–1,+1]:
wij(0) = r,
j = r, i = 1, 2, ..., n; j = 1, 2, ..., p.
2. Для каждого примера (Ak, Bk), k = 1, 2, ..., m из обучающей выборки
выполняются следующие действия.
2.1. Активация входного
i = 1, 2, ..., n.
слоя F a вектором A k , т.е. a i = a i k ,
2.2. Вычисление сигналов на выходе нейронов выходного слоя Fb согласно
выражению
n
b j f ( wij ai j )
j = 1, 2, ..., p,
i 1
где ступенчатая функция активации f(x)=1, если x > 0 и f(x) = 1 в противном
случае.
10.
2.3. Вычисление ошибки между вычисленными выходными величинами bjнейронов и компонентами желаемого выходного образа Bk обучающей выборки:
ej = (bjk –bj), j = 1, 2, ..., p.
2.4. Корректировка весовых коэффициентов согласно соотношению:
wij(t+1) = wij(t)+ аiej, i = 1, 2, ..., n, j = 1, 2, ..., p,
где параметр определяет скорость обучения.
3. Повторение шага 2 алгоритма до тех пор, пока ошибки ej,
j = 1, ..., n не станут достаточно малой величиной для всех обучающих примеров
(Ak, Bk), k = 1, 2, ..., m.
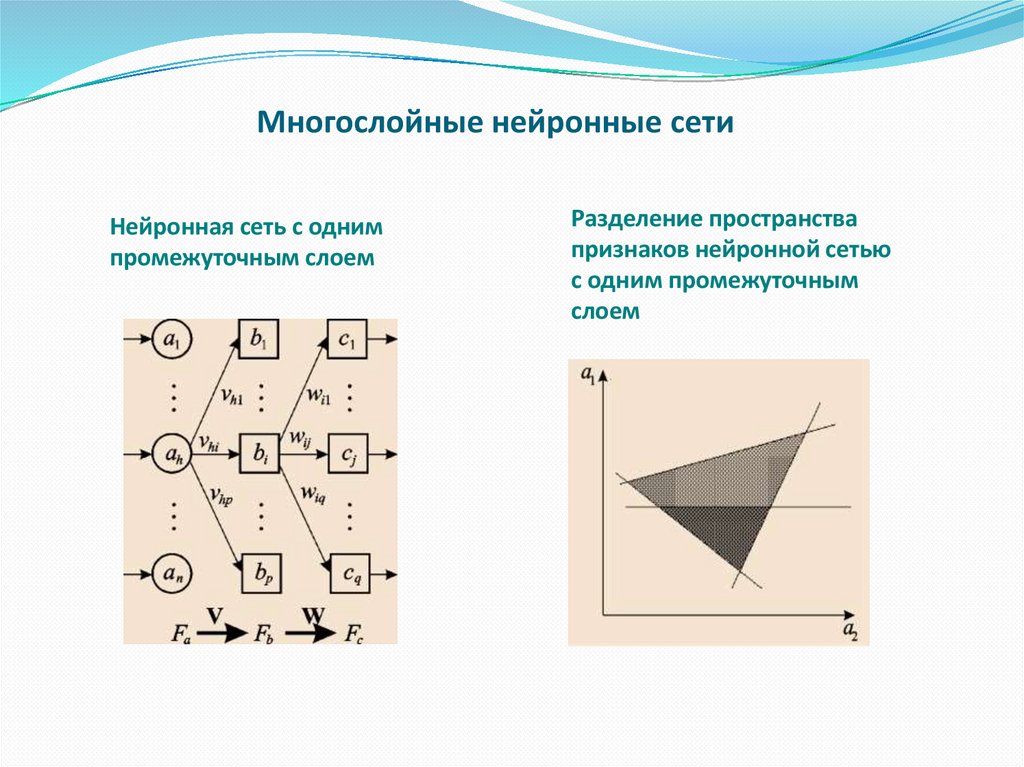
11. Многослойные нейронные сети
Нейронная сеть с однимпромежуточным слоем
Разделение пространства
признаков нейронной сетью
с одним промежуточным
слоем
12.
Требование к функции активации: дифференцируемость.Сигмоидная функция: y = 1/(1+e-x),
производная которой имеет простой вид
y y(1 y)
n
bi S ( ah vhi i )
i = 1, 2, ..., p;
h 1
p
c j S ( bi wij j )
i 1
j = 1, 2, ..., q.
13.
Обучение сети осуществляется с учителем, т.е. сети последовательнопредъявляются обучающие примеры (Ak, Dk), k=1, 2, ..., m, и производится
настройка синаптической карты таким образом, чтобы выходы Ck сети были
как можно ближе к заданным образам Dk для каждой обучающей пары.
Сформулируем
задачу
обучения
сети
как
оптимизационную
минимизировать квадрат нормы разности векторов
min D k C k
q
2
min Fk (d kj c j ) 2
j 1
задачу:
14. Алгоритм обратного распространения ошибки (backpropagation algorithm)
1. Начальная инициализация всех весовых коэффициентов и пороговых величинслучайными числами r:
vhi(0) = r,
i(0) = r, h = 1, 2, ..., n,
i = 1, 2, ..., p,
wij(0) = r,
j(0) = r, i = 1, 2, ..., p,
j = 1, 2, ..., q,
где wij – весовой коэффициент, соответствующий связи от i-го нейрона в слое
Fb к j-му нейрону в слое Fc;
i – пороговая величина i-го нейрона слоя Fb;
vhi – весовой коэффициент, соответствующий связи от h-го входа (слой Fa) к iму нейрону в слое Fb;
j – пороговая величина j-го нейрона в слое Fc;
r – случайные числа в диапазоне [–1,1].
15.
2. Для каждой пары (Ak, Dk), k=1, 2, ..., m из обучающей выборки выполняетсяследующая последовательность действий:
2.1. Активация входного слоя Fa входным вектором Ak, т.е.
ah = ahk , h = 1, 2, ..., n.
2.2. Вычисление выходных величин нейронов слоя Fb согласно выражению
n
bi S ( ah vhi i )
i=1, 2, ..., p,
h 1
где S(x) – функция активации вида 1/(1+e–x).
2.3. Вычисление выходных величин нейронов слоя Fс согласно выражению
p
c j S ( bi wij j )
i 1
j = 1, 2, ..., q.
16.
2.4. Вычисление ошибки между вычисленными выходными величинами cjнейронов и компонентами желаемого выходного вектора Dk обучающей выборки:
ej = cj(1 – cj)(djk – cj), j = 1, 2, ..., q.
2.5. Пересчет величины ошибки для всех нейронов слоя Fb:
q
i bi (1 bi ) wij e j
i = 1, 2, ..., p.
j 1
2.6. Корректировка весовых коэффициентов и пороговых величин
направлении, противоположном градиенту, согласно следующим соотношениям:
wij(t + 1) = wij(t) + biej ,
j(t + 1) = j(t) + ej, i = 1, 2, ..., p, j = 1, 2, ..., q,
vhi(t + 1) = vhi(t) + ah i,
i(t + 1) = i(t) + i, i = 1, 2, ..., p, h = 1, 2, ..., n,
где параметры и определяют скорость обучения.
в
17.
3. Повторение шага 2 алгоритма до тех пор, пока ошибки ej,j = 1, 2, ..., q не станут достаточно малыми величинами для всех обучающих
примеров (Ak, Dk), k = 1, 2, ..., m.
В данном алгоритме обучение сети примерам (Ak, Dk), k=1, 2, ..., m
осуществляется последовательно.
Эта стратегия не всегда приводит к успеху, т.к. при обучении очередному
примеру сеть может «забыть» предыдущие.
Можно обучать сеть сразу нескольким примерам (странице примеров). Для
этого необходимо несколько модифицировать исходную задачу оптимизации и
минимизировать суммарную целевую функцию вида
q
m
m
k 1
k 1 j 1
min Fk (d kj c j ) 2
В этом случае величины ошибок и градиентов в рассмотренном алгоритме
должны вычисляться путем их суммирования по всем примерам обучающей
выборки.
18. Механизмы хранения данных в ИНС
автоассоциативный - хранит образыA1, A2, ..., An .
гетероассоциативный - хранит пары образов
(A1, B1), (A2, B2), ..., (An, Bn).
Отображение: g(Ai, W) = Bi
Принцип ближайщего соседа: g(A Ai, W) = Bi
Выполнение интерполяции: g(A = Ai+ , W) = Bi+
по всем парам (Ai, Bi), i=1, ..., n.
19. Модель автоассоциативной памяти
Однонаправленная сетьХопфильда
Уравнение функционирования сети
n
a j (t 1) f ( ai (t ) wij )
i 1
где aj(t) – выход нейрона j на такте t;
f(x) – ступенчатая пороговая функция, принимающая
значения 1.
Матричная форма записи
A(t 1) f (A(t )W)
Формирование синаптической карты
Данную сеть можно
рассматривать как
ассоциативную память
m
W ATk A k
k 1
20. Алгоритм функционирования однонаправленной сети Хопфильда
1. Формирование синаптической карты сети W путем ее обучения по сериивходных образов Ak = [a1k, ..., ank], k = 1, ..., m:
m
W ATk A k I
k 1
2. Начальная активация сети входным образом C = [c1, ..., cn], т.е. приведение
нейронов сети в состояния: aj = cj, j = 1, ..., n.
3. Итерационное вычисление выходных сигналов сети до тех пор, пока сеть не
достигнет установившегося состояния
n
a j (t 1) f ( ai (t ) wij )
i 1
j = 1, ..., n
21. Пример
Имеются три входных образа:A1= [1 1 1 1 1], A2= [–1 –1 1 1 1], A3= [1 1 –1 –1 –1]
Вычисляется синаптическая карта
0 3 1 1 1
3 0 1 1 1
5
T
W ( A k A k I ) 1 1 0 3 3
k 1
1
1
3
0
3
1 1 3 3 0
Подадим на вход сети искаженный образ C = [1 1 1 1 –1 –1]
«Отпустим» сеть для того, чтобы она пришла в установившееся состояние.
результате получим
A(1) = f(A(0)W) = f([4 4 –8 –2 –2]) = [1 1 –1 –1 –1]
A(2)=f(A(1)W)=f([6 6 –8 –8 –8 ])= [1 1 –1 –1 –1]
Таким образом, сеть стабилизировалась уже после второго шага, скорректировав
искаженный образ в направлении ближайшего эталона A3.
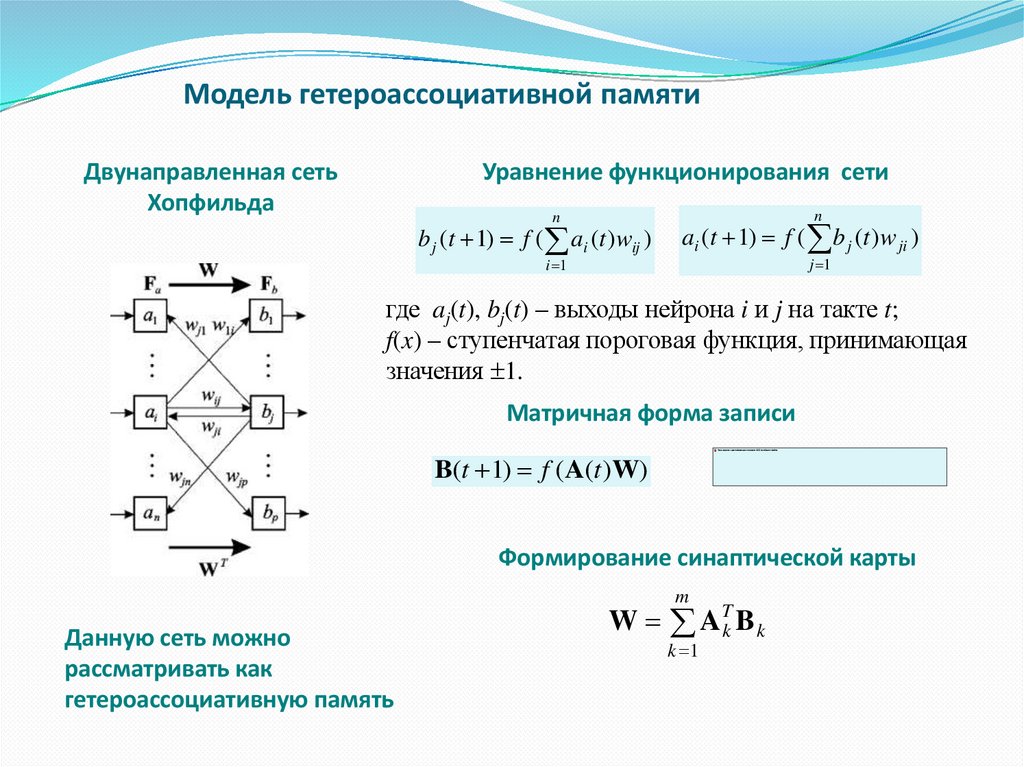
22. Модель гетероассоциативной памяти
Двунаправленная сетьХопфильда
Уравнение функционирования сети
n
b j (t 1) f ( ai (t ) wij )
i 1
n
ai (t 1) f ( b j (t ) w ji )
j 1
где aj(t), bj(t) – выходы нейрона i и j на такте t;
f(x) – ступенчатая пороговая функция, принимающая
значения 1.
Матричная форма записи
B(t 1) f (A(t )W)
Формирование синаптической карты
m
Данную сеть можно
рассматривать как
гетероассоциативную память
W ATk B k
k 1
23. Алгоритм функционирования двунаправленной сети Хопфильда
1. Активация слоя Fa сети входным образом C=[c1, ..., cn], т.е. приведениенейронов входного слоя в начальные состояния: ai(0)=ci.
2. Вычисление сигналов на выходе нейронов выходного слоя Fb согласно
выражению
n
b j (t ) f ( ai (t ) wij )
i 1
j = 1, ..., p
или в матричной форме B(t) = f(A(t)W). Затем внешнее возбуждение убирается.
3. Подача на входы нейронов слоя Fa с выходов нейронов слоя Fb (по
обратным связям) и вычисление новых состояний нейронов слоя Fa по формуле
p
ai t 1 f b j t w ji , i 1, ..., n
j 1
или в матричной форме А(t+1) = f(В(t)WT).
4. Повторение шагов 2–3 до тех пор, пока сеть не достигнет стабильного
состояния.
24. Пример
Обучающая выборка состоит из примеров:A1=[–1 –1 1 1],
A2=[1 1 –1 –1],
Вычисляется синаптическая карта:
B1=[1 –1 1];
B2=[–1 1 –1].
2 2
2
2
2
2 2
T
W A k Bk
2 2
2
k 1
2
2 2
Подавая на вход сети образ A1(0) = [–1 –1 1 1], получим:
B(0) = f(A(0)W) = f ([8 –8 8]) = [1 –1 1];
A(1) = f(B(0)WT) = f([–6 –6 6 6]) = [–1 –1 1 1].
Подадим на вход сети искаженный образ A(0) = C = [-1 1 1 1]
B(0) = f(A(0)W) = f([4 –4 4]) = [1 –1 1];
A(1) = f(B(0)W) = f([–6 –6 6 6]) = [–1 –1 1 1]
25. Оценка объема ассоциативной памяти
Автоассоциативная однонаправленная нейронная сеть:Количество запоминаемых классов m < 0,15 N.
Например, для m = 10 классов входных образов сеть должна содержать N = 70
нейронов и приблизительно 5000 связей между ними.
Гетероассоциативная двунаправленная нейронная сеть:
Количество запоминаемых ассоциаций m < N/(4log2N).
Например, для m = 25 ассоциаций сеть должна содержать N = 1024 нейронов.
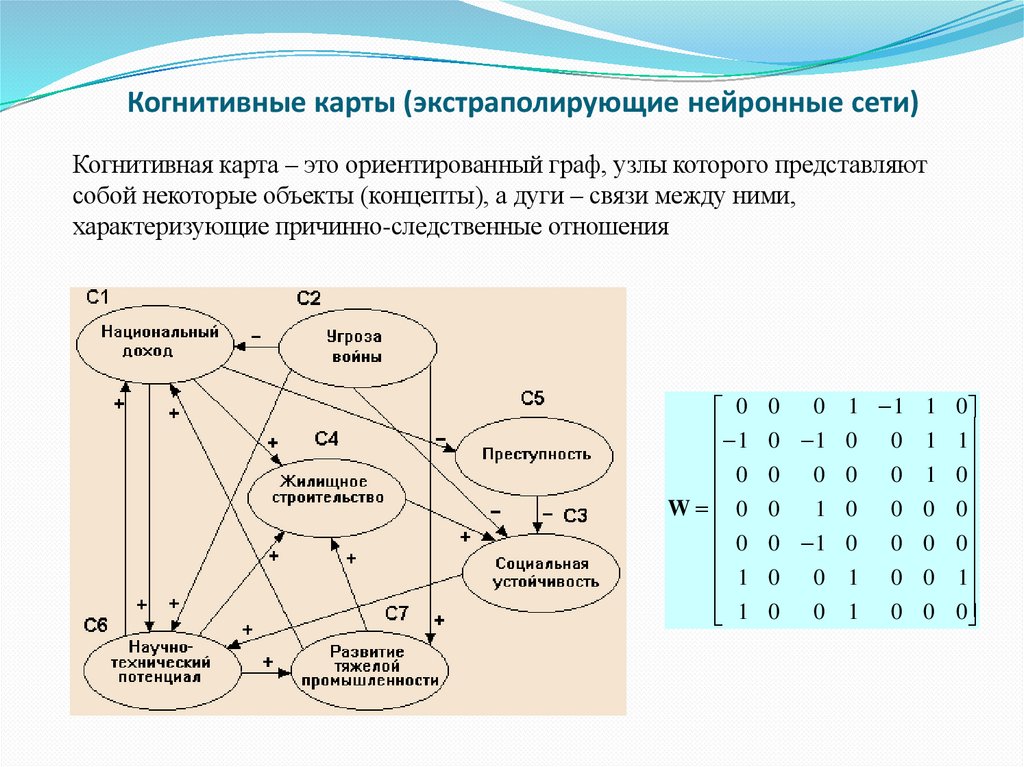
26. Когнитивные карты (экстраполирующие нейронные сети)
Когнитивная карта – это ориентированный граф, узлы которого представляютсобой некоторые объекты (концепты), а дуги – связи между ними,
характеризующие причинно-следственные отношения
0
1
0
W 0
0
1
1
0 0 1 1
0 1 0 0
0 0 0 0
0
1 0 0
0 1 0 0
0 0 1 0
0 0 1 0
1
1
1
0
0
0
0
0
1
0
0
0
1
0
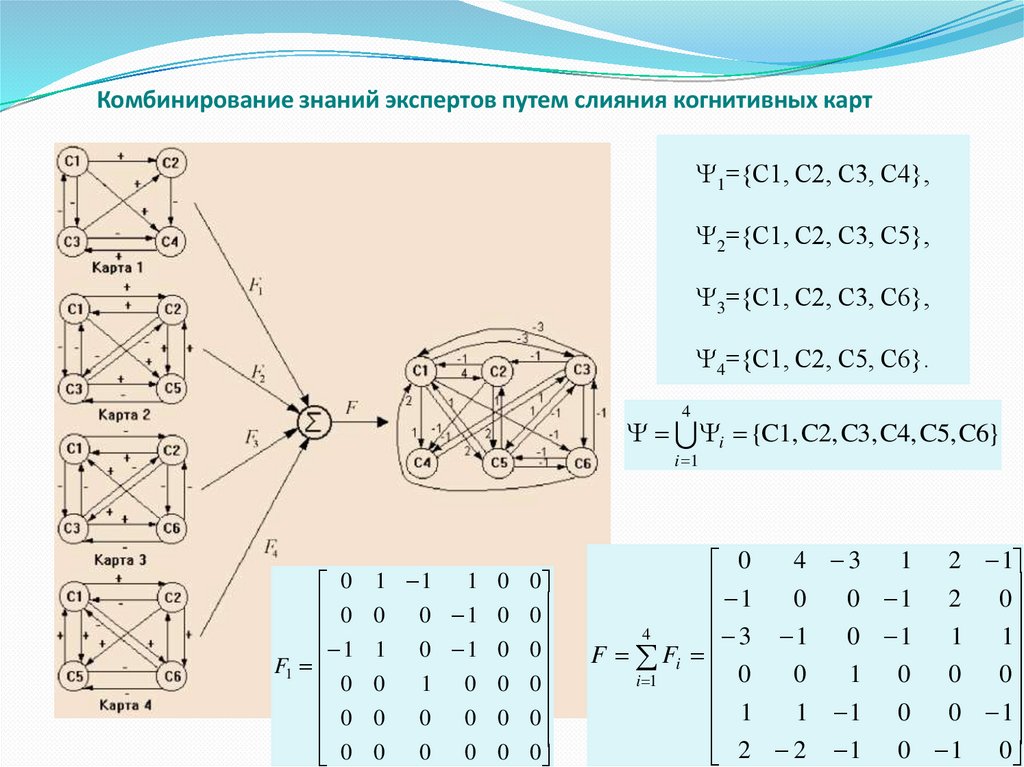
27.
Комбинирование знаний экспертов путем слияния когнитивных карт1={C1, C2, С3, С4},
2={C1, C2, С3, С5},
3={C1, C2, С3, С6},
4={C1, C2, С5, С6}.
4
i {C1, C2, C3, C4, C5, C6}
i 1
0
0
1
F1
0
0
0
1 1
1 0 0
0
0 1 0 0
1 0 1 0 0
0
1 0 0 0
0
0
0 0 0
0
0
0 0 0
4 3
1 2 1
0
1
0
0 1 2 0
4
3 1
0 1 1 1
F Fi
0
0
1
0
0
0
i 1
1
1 1 0 0 1
2
2
1
0
1
0
28.
Алгоритм функционирования экстраполирующей нейронной сетиПусть на вход сети поступает входной образ A=[a1 ... an], у которого k компонент,
составляющих множество k, известны точно, а остальные неопределенны.
1. Начальная инициализация нейронов сети при t = 0:
ai , i k ,
bi (0)
0, i k .
2. Вычисление новых состояний нейронов bi(t+1) сети для всех i k по формуле
n
bi (t 1) f bi (t )wij ,
j 1
3. Выполнение шага 2 до тех пор, пока сеть не достигнет устойчивого состояния.
29. Пример
Пусть нас интересует получение прогноза для случая угрозы войны(концепт 2). Тогда входной вектор А=[0 1 0 0 0 0 0]. Согласно алгоритму
выходной вектор В=[b1 ... b7] последовательно принимает следующие
состояния:
В(1)=f( [–1 1 –1 0 0 1 1] ) = [–1 1 –1 0 0 1 1],
B(2) = f( [1 1 –1 1 1 – 2] ) = [1 1 –1 1 1 –1 1],
B(3) = f( [1 1 –1 1 –1 1 0] ) = [1 1 –1 1 –1 1 0],
B(4) = f( [0 1 1 0 1 –1 2] ) = [0 1 1 0 1 –1 1],
B(5) = f( [–1 1 –2 0 0 2 0] ) = [–1 1 –1 0 0 1 0],
B(6) = f( [0 1 –1 0 1 –1 2] ) = [0 1 –1 0 1 –1 1],
B(7) = f( [–1 1 –2 0 0 0 0] ) = [–1 1 –1 0 0 0 0],
B(8) = f( [–1 1 –1 –1 1 –1 1] ) = [–1 1 –1 –1 1 –1 1],
B(9) = f( [–1 1 –3 –1 1 –1 0] ) = [–1 1 –1 –1 1 –1 0],
B(10) = f( [–2 1 –3 –2 1 –1 0] ) = [–1 1 –1 –1 1 –1 0],
B(11) = f( [–2 1 –3 –2 1 –1 0] ) = [–1 1 –1 –1 1 –1 0].
Прогноз характеризуется снижением С1 (национального дохода), С3
(социальной устойчивости), С4 (жилищного строительства) и увеличением С5
(преступности). Хотя между концептом С2 (угроза войны) и концептами С6
(научно-технический потенциал), С7 (развитие тяжелой промышленности)
существует непосредственная положительная связи, проявилась тенденция к их
снижению, что можно объяснить косвенным влиянием других концептов сети.






















 Информатика
Информатика








