Однополостный и двуполостный гиперболоиды
Введение
Однополостный гиперболоид
Однополостный гиперболоид
Однополостный гиперболоид
Двуполостный гиперболоид
Двуполостный гиперболоид
Двуполостный гиперболоид
Вывод канонических уравнений
Вывод канонического уравнения: однополостный гиперболоид
Вывод канонического уравнения: однополостный гиперболоид
Вывод канонического уравнения: однополостный гиперболоид
Вывод канонического уравнения: однополостный гиперболоид
Вывод канонического уравнения: двуполостный гиперболоид
Вывод канонического уравнения: двуполостный гиперболоид
Вывод канонического уравнения: двуполостный гиперболоид
Исследование методом сечений
Исследование методом сечений
Исследование методом сечений: однополостный гиперболоид. Сечения плоскостями z = h (горизонтальные сечения)
Исследование методом сечений: однополостный гиперболоид. Сечения плоскостями z = h (горизонтальные сечения)
Исследование методом сечений: однополостный гиперболоид. Сечения плоскостями z = h (горизонтальные сечения)
Исследование методом сечений: однополостный гиперболоид. Сечения плоскостями x = h и y = h (вертикальные сечения)
Исследование методом сечений: двуполостный гиперболоид. Сечения плоскостями z = h (горизонтальные сечения)
Исследование методом сечений: двуполостный гиперболоид. Сечения плоскостями z = h (горизонтальные сечения)
Исследование методом сечений: двуполостный гиперболоид. Сечения плоскостями z = h (горизонтальные сечения)
Исследование методом сечений: двуполостный гиперболоид. Сечения плоскостями x = h и y = h (вертикальные сечения)
Прямолинейные образующие
Прямолинейные образующие
Прямолинейные образующие
Применение в архитектуре и технике
Применение в архитектуре и технике. Шуховская башня
Применение в архитектуре и технике. Градирни ТЭЦ
Применение в архитектуре и технике. Оптика Кассегрена
1.82M
Похожие презентации:
Поверхности второго порядка
Поверхности второго порядка
Поверхности второго порядка
Поверхности второго порядка
Поверхности 2-го порядка
Поверхности 2-го порядка
Поверхности второго порядка
Поверхности второго порядка
Поверхности второго порядка
Поверхности второго порядка
Поверхности второго порядка. Однополостный и двуполостный гиперболоид
Поверхности второго порядка. Однополостный и двуполостный гиперболоид
Двуполостный гиперболоид
Двуполостный гиперболоид
Поверхности второго порядка
Поверхности второго порядка
Поверхности второго порядка
Поверхности второго порядка
Векторный анализ. Лекция 4
Векторный анализ. Лекция 4

Однополостный_и_двуполостный_гиперболоиды

1. Однополостный и двуполостный гиперболоиды

ОДНОПОЛОСТНЫЙ И
ДВУПОЛОСТНЫЙ ГИПЕРБОЛОИДЫ
КИ25-17/1Б
Сизинцев Дмитрий
Шувалов Иван
Панкеева Николь
Павлов Илья
Худаков Александар

2. Введение

Гиперболоидом называется поверхность,
которая в некоторой декартовой системе
координат описывается одним из
уравнений:
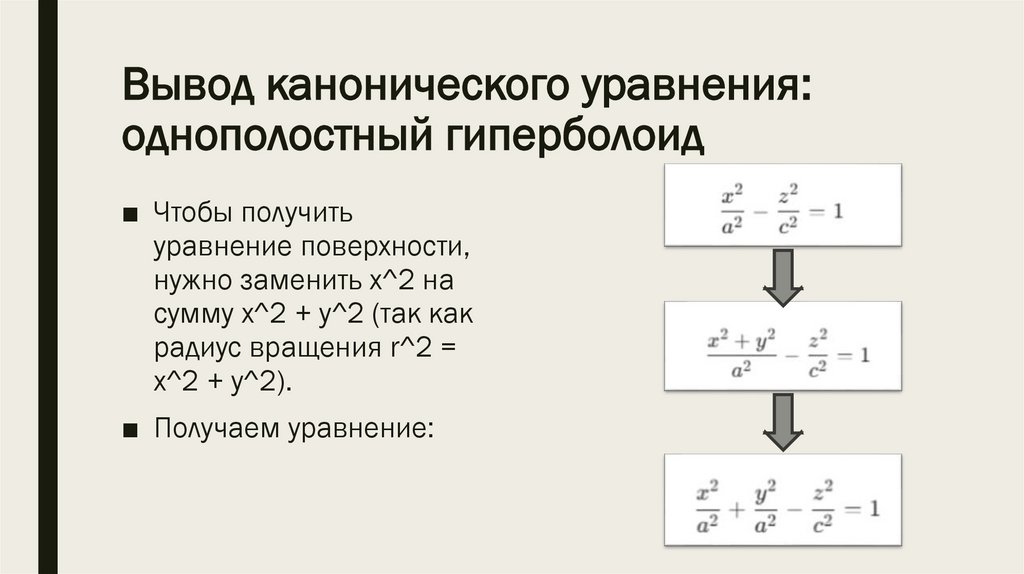
*1)
*2)
Величины a, b и c называются полуосями
гиперболоида.
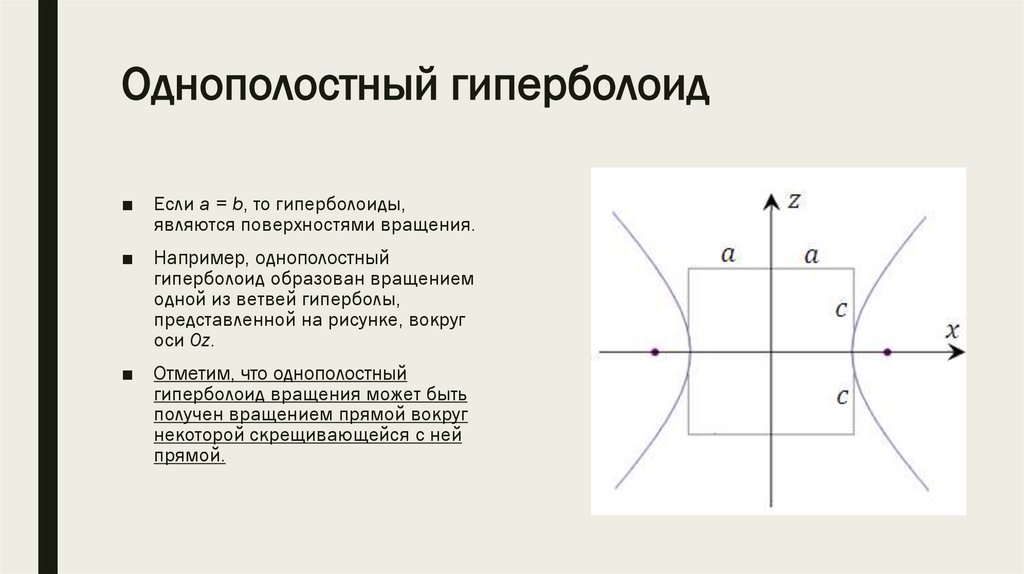
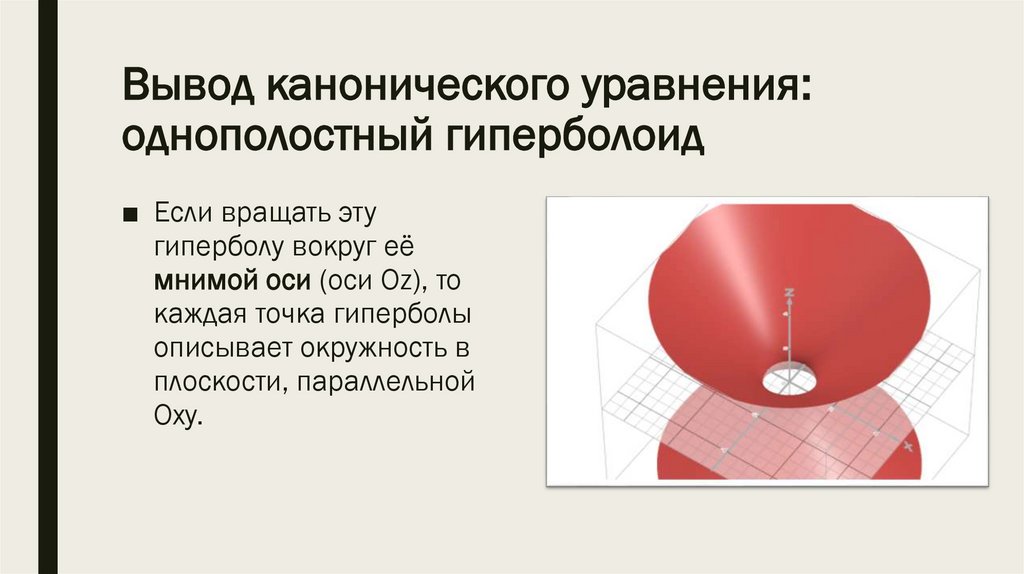
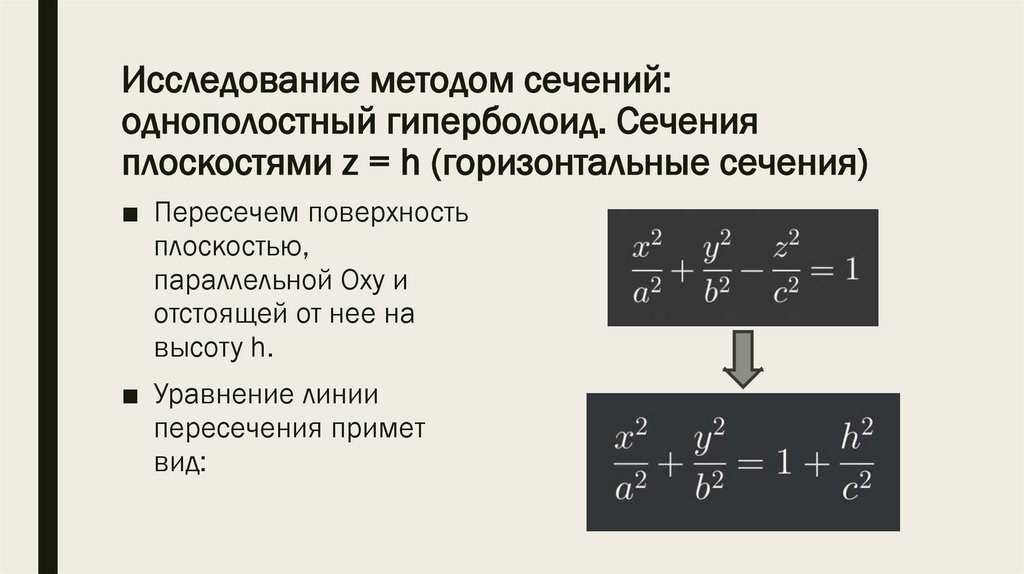
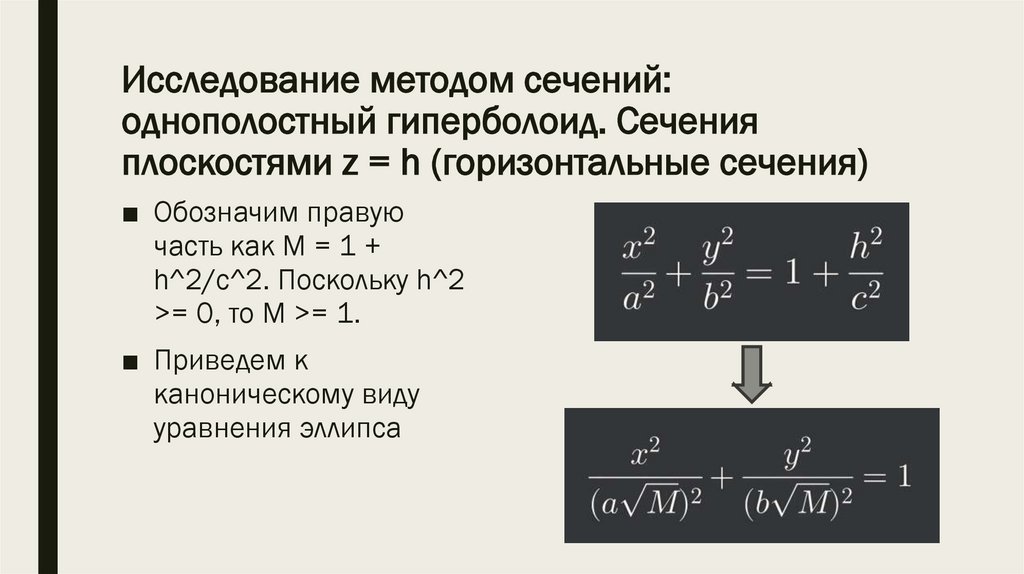
*1) Однополостный
гиперболоид
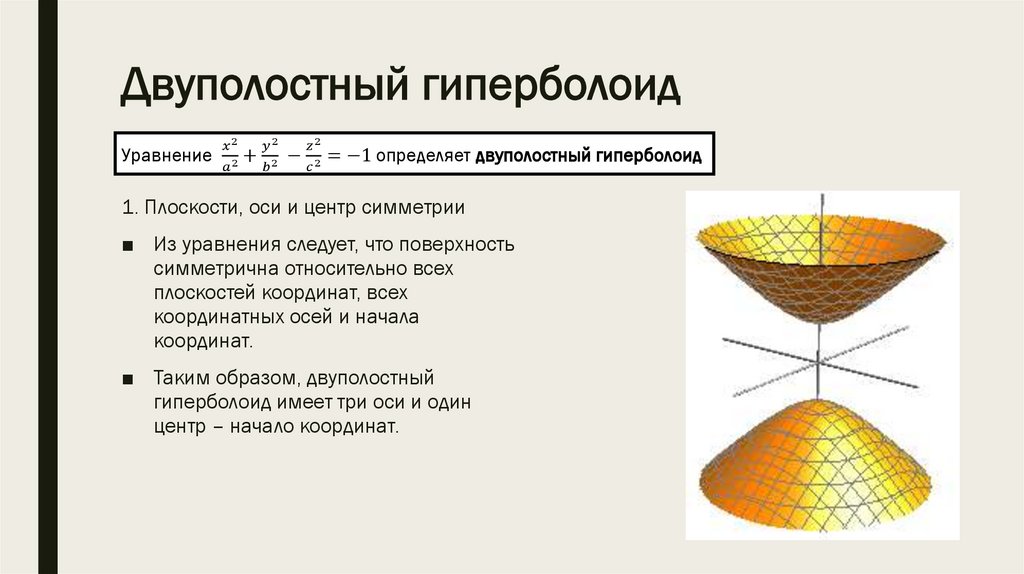
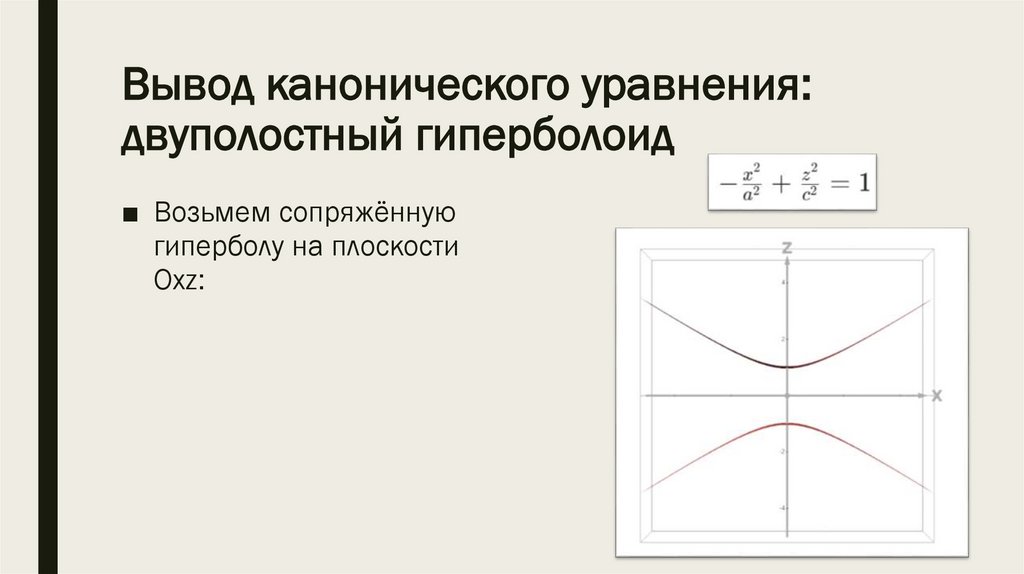
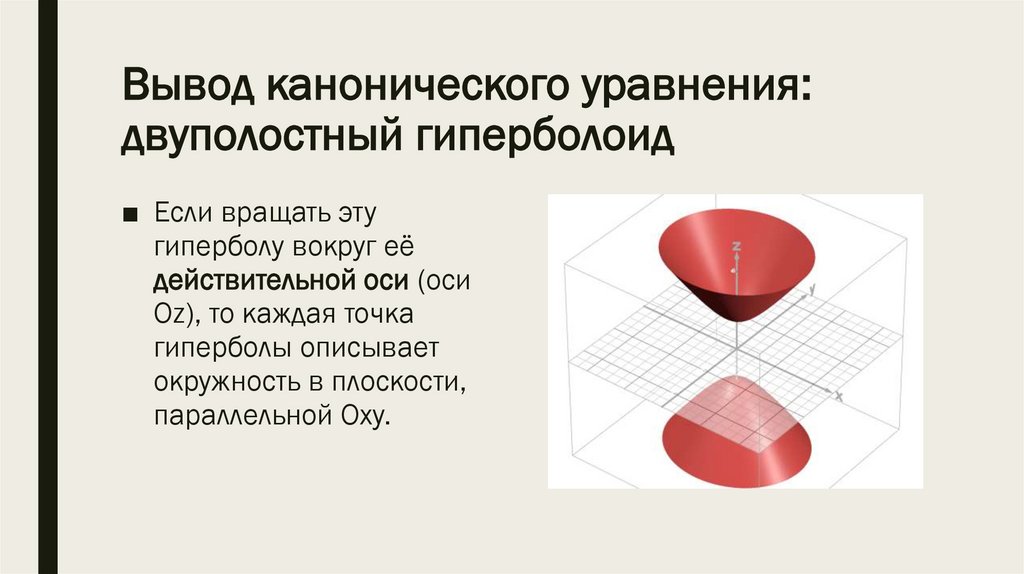
*2) Двуполостный
гиперболоид

3. Однополостный гиперболоид

English     Русский Правила