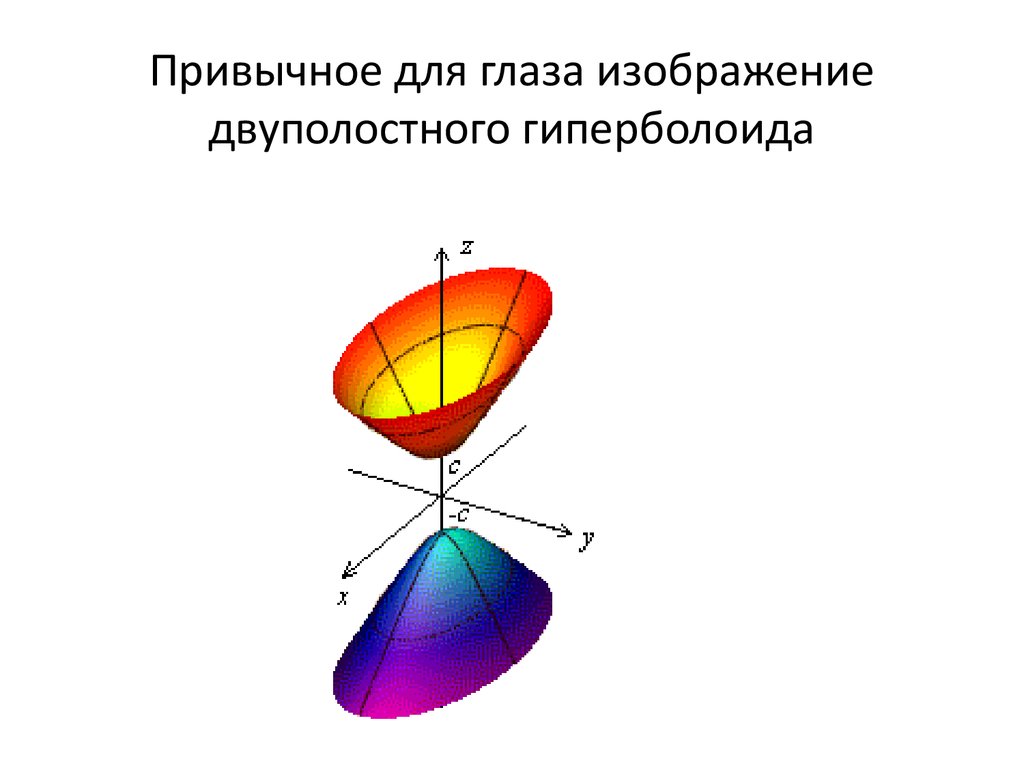
Двуполостный гиперболоид

1. Двуполостный гиперболоид

Двуполостным гиперболоидом называется поверхность,
каноническое уравнение которой имеет вид
или
где
- положительные числа.
Исследуем форму двуполостного гиперболоида. Так же, как эллипсоид и
однополостный гиперболоид, он имеет три плоскости симметрии, три оси
симметрии и центр симметрии. Ими являются соответственно
координатные плоскости, координатные оси и начало координат.

2.

Для построения гиперболоида найдем его сечения различными
плоскостями. Найдем линию пересечения с плоскостью
.
На этой плоскости
, поэтому
Координаты ни одной точки плоскости
не могут
удовлетворять данному уравнению. Следовательно, двуполостный
гиперболоид не пересекает эту плоскость.

3.

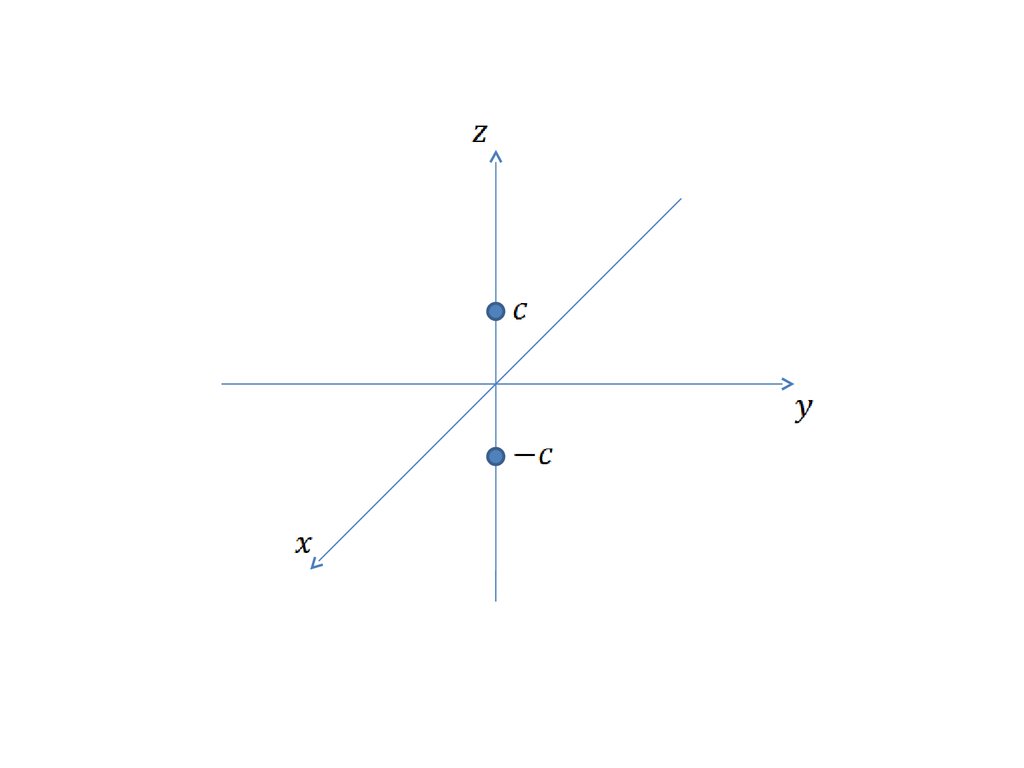
При
получаем
Плоскость имеет с исследуемой поверхностью точки
и
. Эти точки называются вершинами гиперболоида.

4.

5.

Найдем линии пересечения поверхности с плоскостями
Пусть
и
равны
и
соответственно

6.

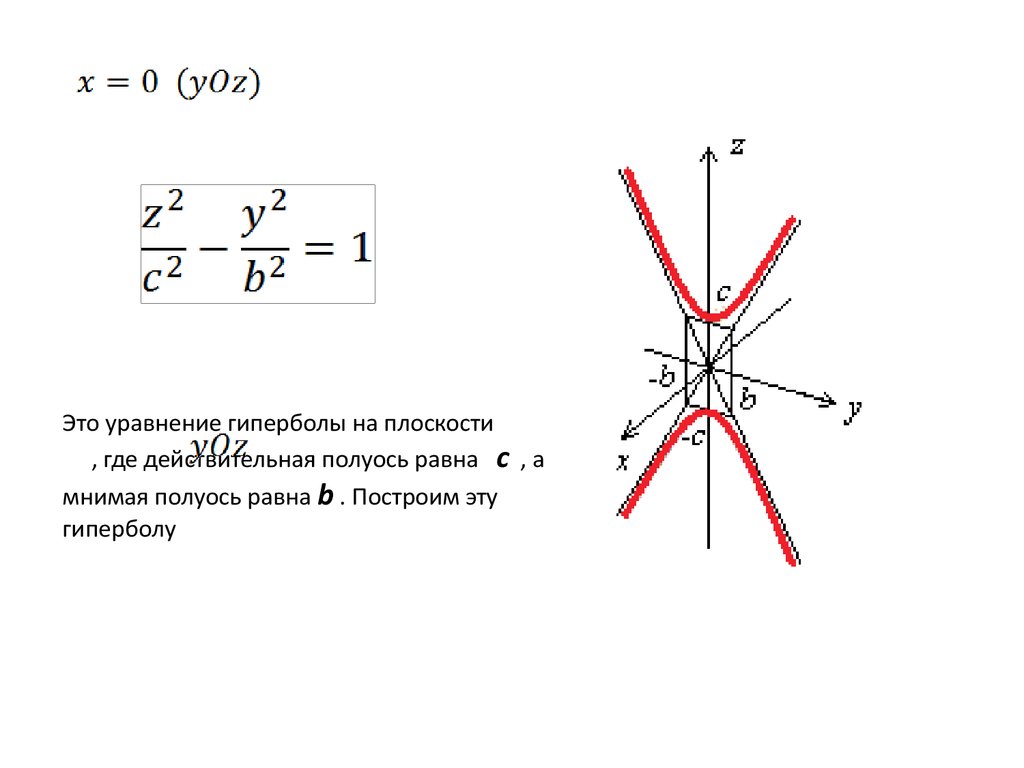
Это уравнение гиперболы на плоскости
, где действительная полуось равна с , а
мнимая полуось равна b . Построим эту
гиперболу

7.

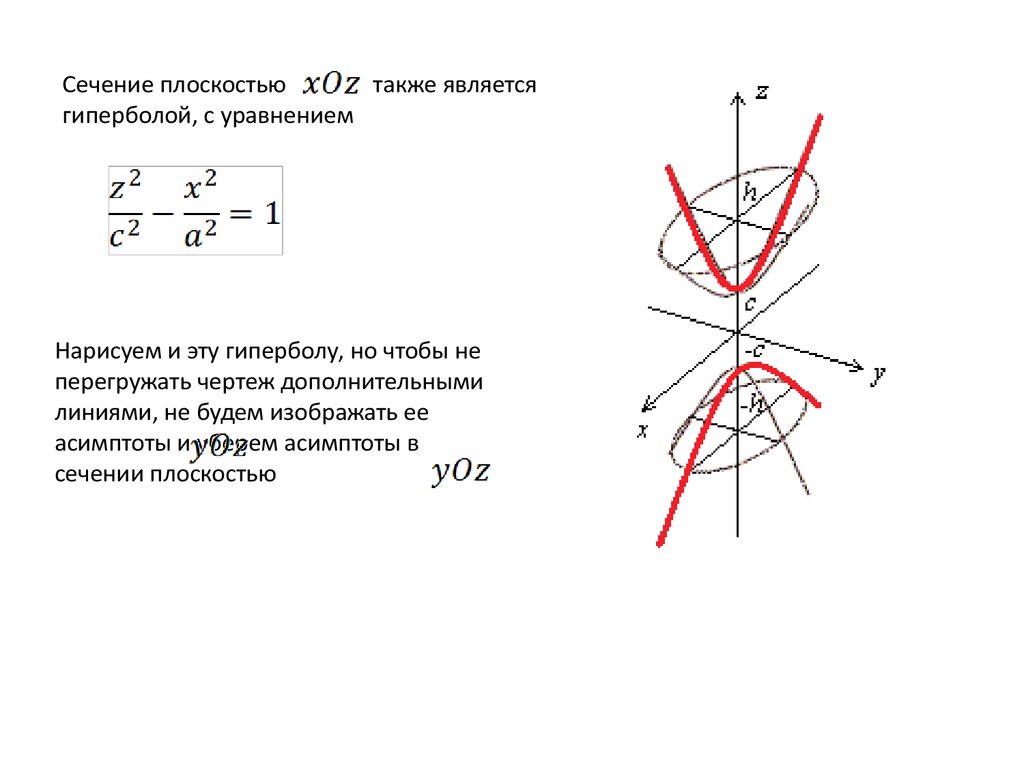
Сечение плоскостью
также является
гиперболой, с уравнением
Нарисуем и эту гиперболу, но чтобы не
перегружать чертеж дополнительными
линиями, не будем изображать ее
асимптоты и уберем асимптоты в
сечении плоскостью

8. Привычное для глаза изображение двуполостного гиперболоида