Похожие презентации:
Лекция №1 Механические колебания
1.
Лекция №1Колебательное движение
Механические колебания
2.
3.
4. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Механическими колебанияминазываются движения тел, точно
повторяющиеся через одинаковые
промежутки времени.
Закон движения тела, совершающего
колебания, задается с помощью
некоторой периодической функции
времени x = f(t)
х А sin( t )
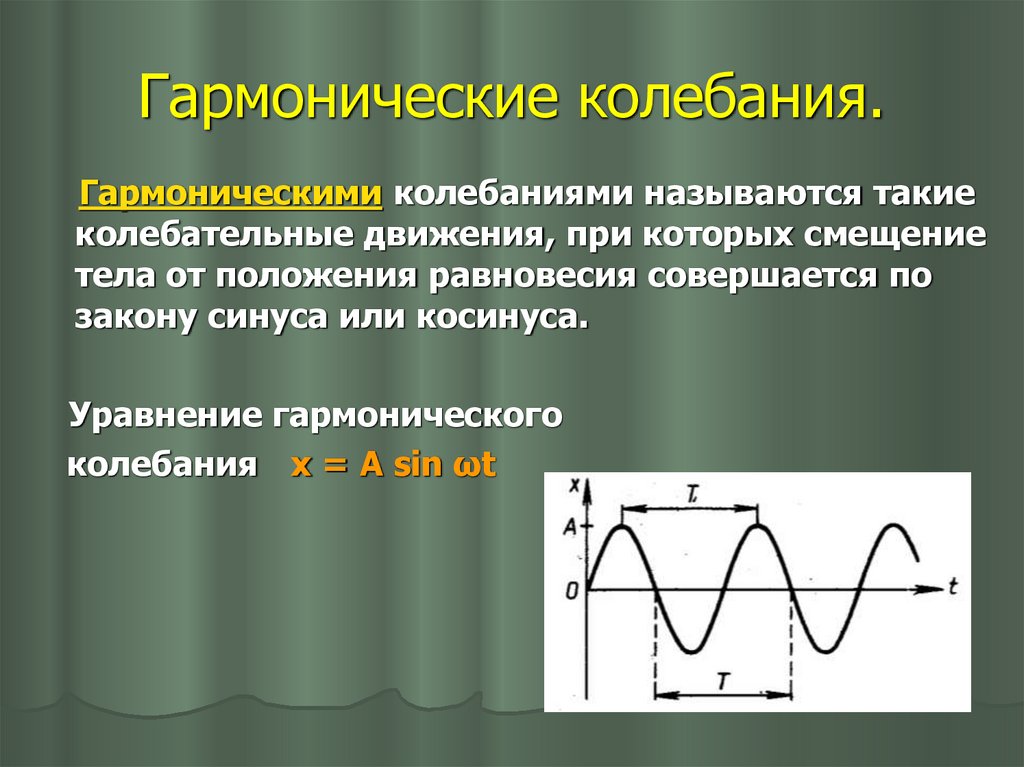
5. Гармонические колебания.
Гармоническими колебаниями называются такиеколебательные движения, при которых смещение
тела от положения равновесия совершается по
закону синуса или косинуса.
Уравнение гармонического
колебания х = А sin ωt
6. Гармонические колебания
Гармоническими колебаниями называются такиеколебательные движения, при которых смещение тела от
положения равновесия совершается по закону синуса или
косинуса
х А sin( t )
2
х X max sin(
t)
T
7. Характеристики колебаний.
Амплитуда ( А, хm) – наибольшеесмещение от положения равновесия. (м)
Период ( Т ) – время одного полного
колебания. (с)
Частота ( ۷ ) – число колебаний за 1с. (Гц)
Циклическая частота (ω ) – число
колебаний за время 2π с. (рад/с)
Фаза ( φ ) – величина, стоящая под знаком
синуса или косинуса. (рад)
8.
9.
10. Математический маятник Математический маятник – это материальная точка, подвешенная на нерастяжимой и невесомой (её масса мала
Математический маятникМатематический маятник – это материальная
точка, подвешенная на нерастяжимой и невесомой
(её масса мала по сравнению с весом тела) нити.
Математический маятник – это маятник, масса
груза которого намного больше нити, а нить
намного больше по размерам чем груз , при
этом груз является материальной точкой, а
нить невесомой
11. Математический маятник
Период математического маятникаl – длина нити маятника,
g- ускорение свободного падения
Запомни!
Период колебаний математического маятника зависит
только от длины нити. Не зависит от амплитуды
колебаний и массы груза
12. Характеристика математического маятника
Циклическая частота:13. Пружинный маятник.
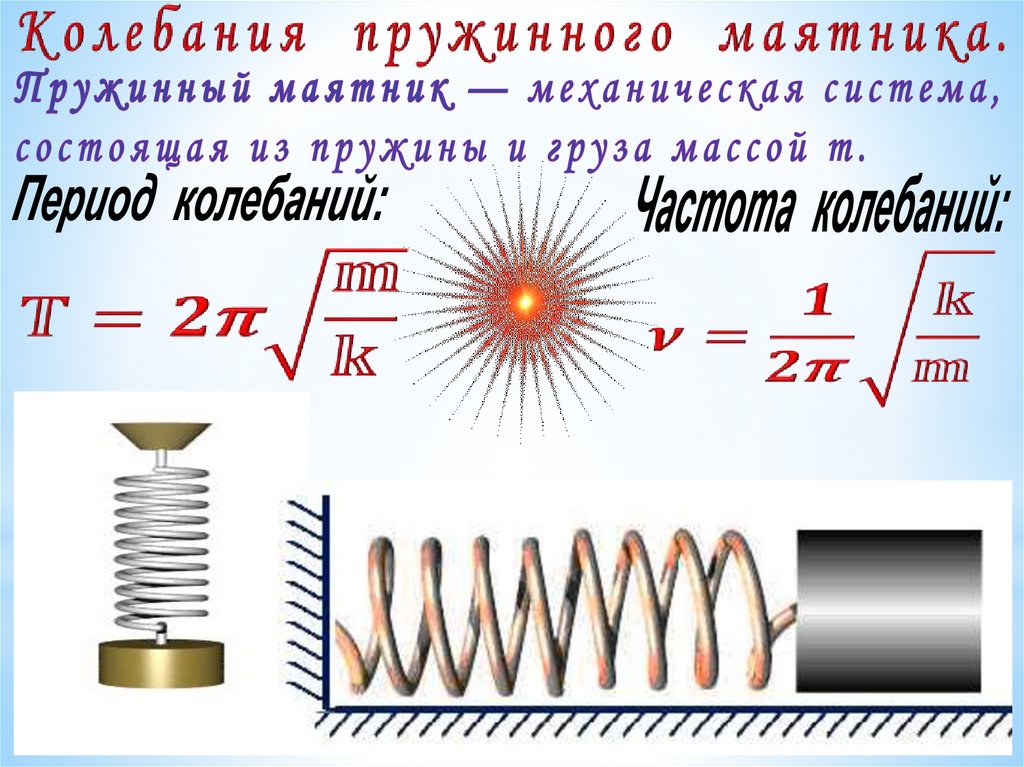
Маятник на пружине — механическая система, состоящаяиз пружины с коэффициентом упругости (жёсткостью) k ,
один конец которой жёстко закреплён, а на втором
находится груз массы m.
Пружинный маятник – это маятник, который
колеблется за счёт силы упругости
14. Пружинный маятник
Период пружинного маятникаF
m – масса груза,
k – жесткость пружины, (Н/м)
15. Характеристика пружинного маятника
Собственная частота ( ω0 )k – коэффициент жесткости пружины.
m – масса маятника.
Период (Т)
16. Виды колебаний
Свободные колебания –происходят только за счетпервоначального запаса энергии.
Условия существования колебаний:
• в колебательной системе должна действовать
внутреняя сила, возвращающая тело в
положение равновесия
• отсутствие силы трения
17. Виды колебаний
Затухающие колебания – амплитуда такихколебаний со временем уменьшается под
влиянием силы трения.
Чем больше силы сопротивления, тем быстрее колебания
прекращаются.
! Все свободные колебания – затухающие.
18. Виды колебаний
Вынужденные колебания – колебанияпроисходящие за счет внешней силы
периодически действующей на тело.
19. Превращения энергии при свободных механических колебаниях
При гармонических колебаниях происходит периодическоепревращение кинетической энергии в потенциальную и наоборот
• Для груза на пружине
• Для математического маятника


















 Физика
Физика








