Похожие презентации:
Математический и пружинный маятники. Урок 43
1. Урок 43. МАТЕМАТИЧЕСКИЙ И ПРУЖИННЫЙ МАЯТНИКИ
2. Механические колебания
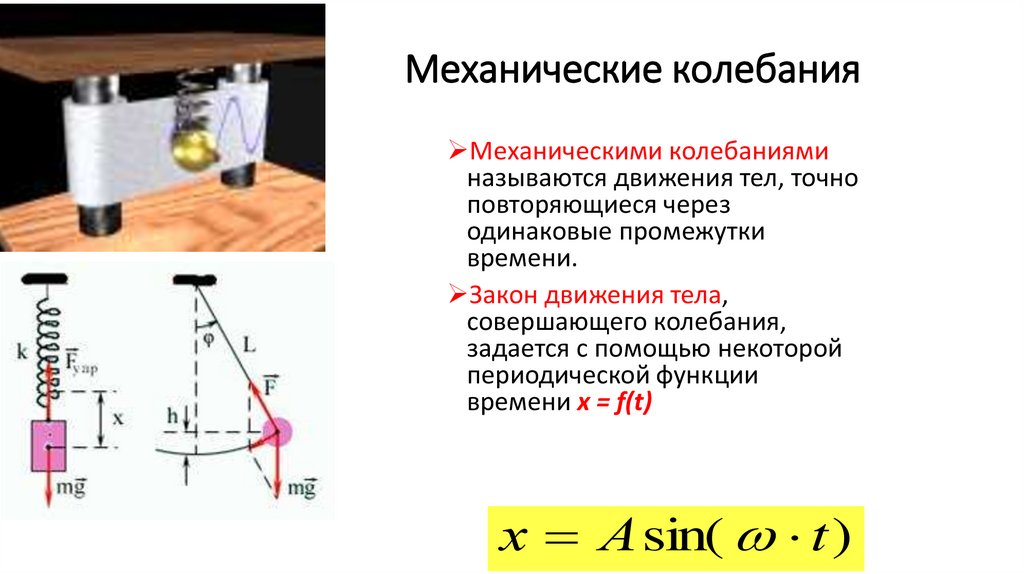
Механическими колебанияминазываются движения тел, точно
повторяющиеся через
одинаковые промежутки
времени.
Закон движения тела,
совершающего колебания,
задается с помощью некоторой
периодической функции
времени x = f(t)
х А sin( t )
3. Гармонические колебания
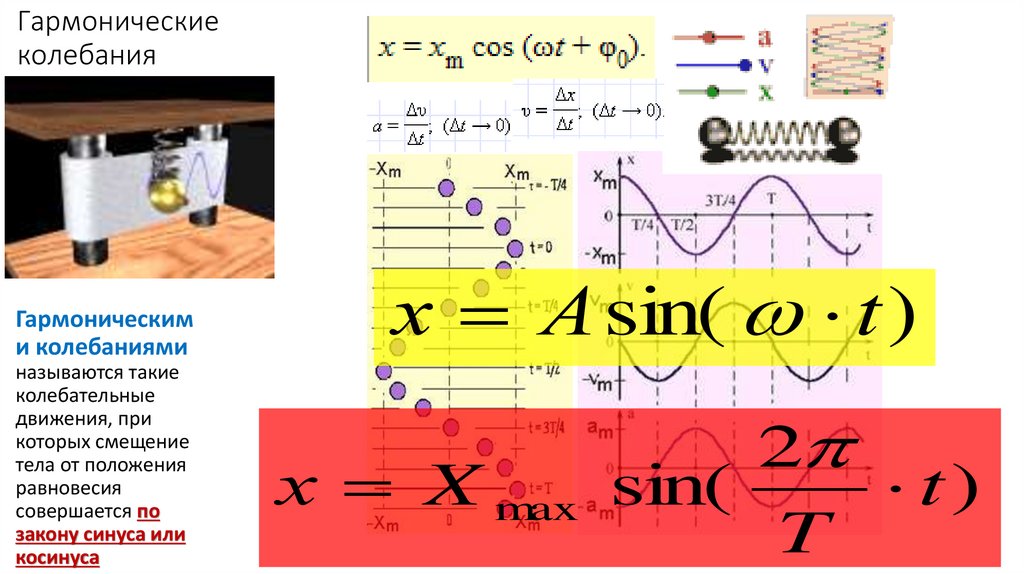
Гармоническими колебаниями
называются такие
колебательные
движения, при
которых смещение
тела от положения
равновесия
совершается по
закону синуса или
косинуса
х А sin( t )
2
х X max sin(
t)
T
4. Гармонические колебания
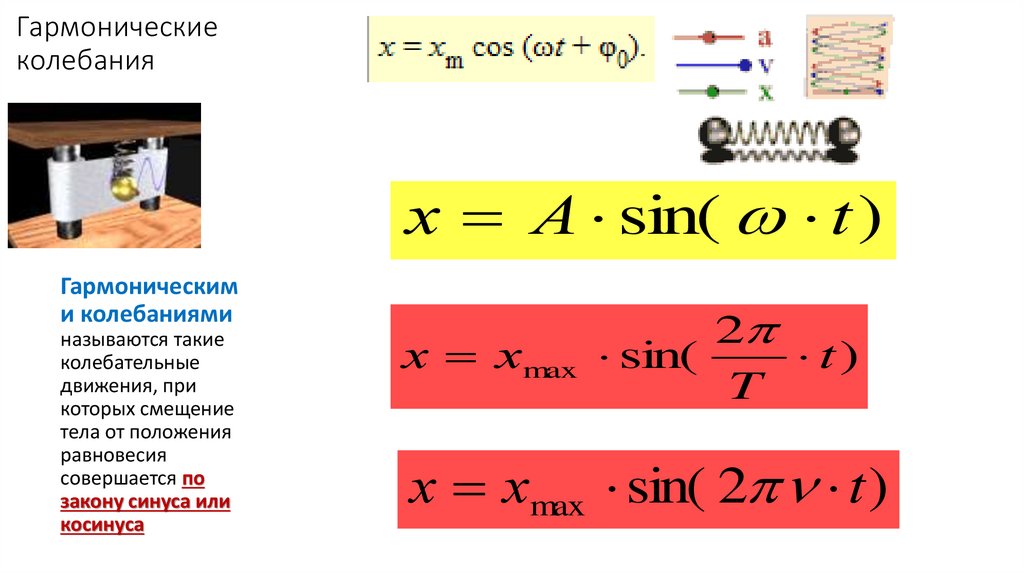
х А sin( t )Гармоническим
и колебаниями
называются такие
колебательные
движения, при
которых смещение
тела от положения
равновесия
совершается по
закону синуса или
косинуса
2
х хmax sin(
t)
T
х хmax sin( 2 t )
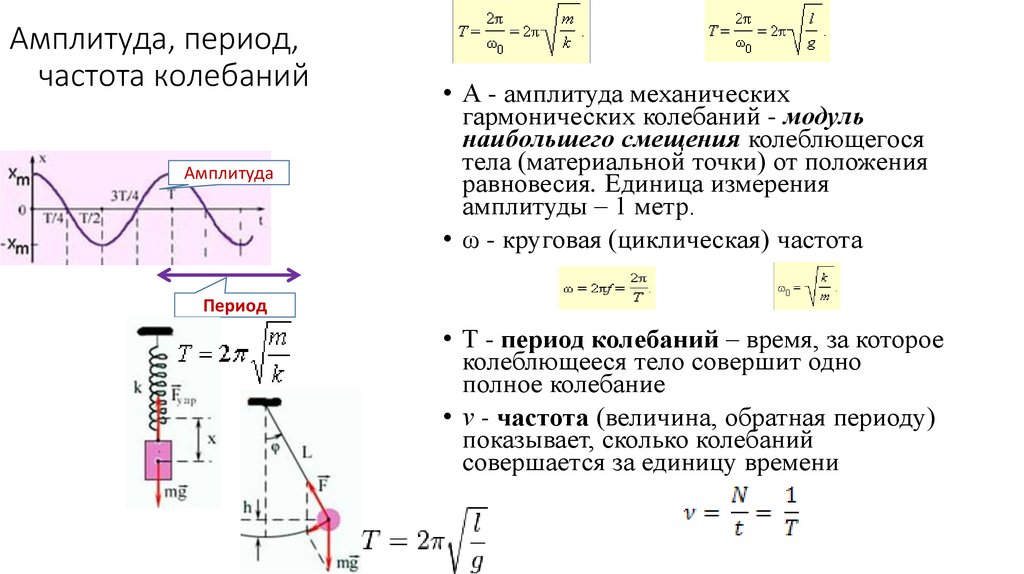
5. Амплитуда, период, частота колебаний
Амплитуда• А - амплитуда механических
гармонических колебаний - модуль
наибольшего смещения колеблющегося
тела (материальной точки) от положения
равновесия. Единица измерения
амплитуды – 1 метр.
• ω - круговая (циклическая) частота
Период
• Т - период колебаний – время, за которое
колеблющееся тело совершит одно
полное колебание
• ν - частота (величина, обратная периоду)
показывает, сколько колебаний
совершается за единицу времени
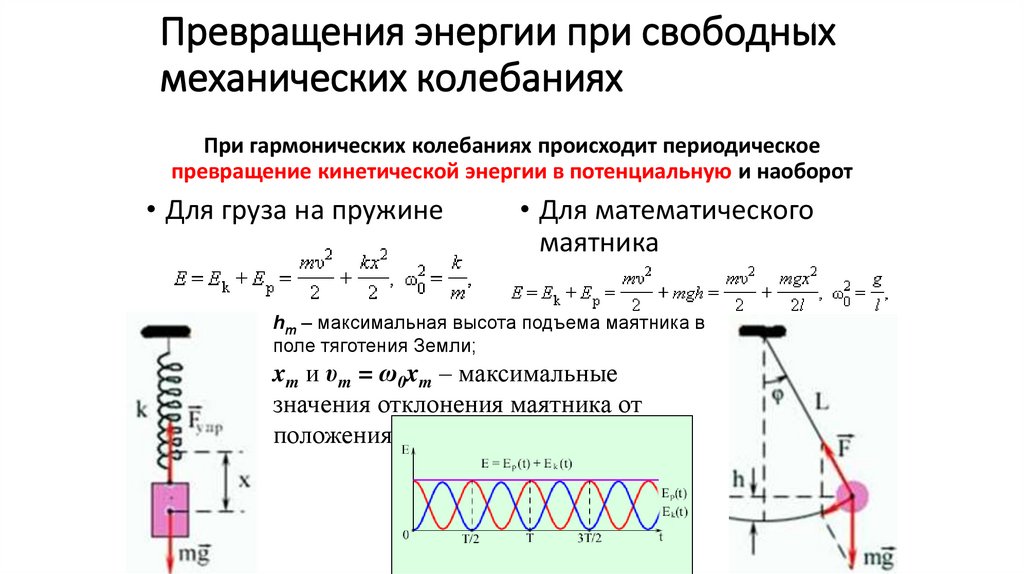
6. Превращения энергии при свободных механических колебаниях
При гармонических колебаниях происходит периодическоепревращение кинетической энергии в потенциальную и наоборот
• Для груза на пружине
• Для математического
маятника
hm – максимальная высота подъема маятника в
поле тяготения Земли;
xm и υm = ω0xm – максимальные
значения отклонения маятника от
положения равновесия и его скорости
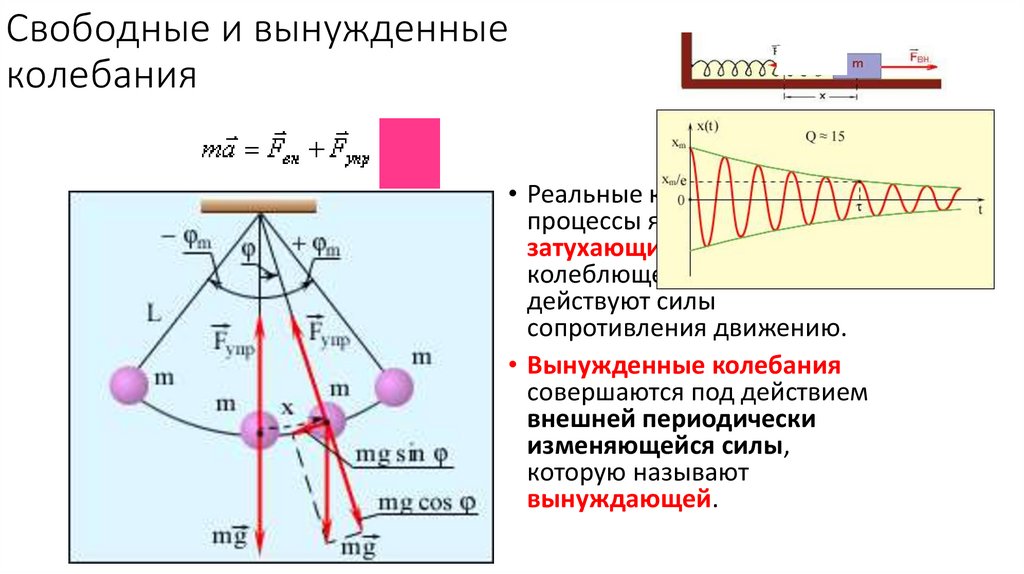
7. Свободные и вынужденные колебания
• Реальные колебательные• Свободные колебания имеют
процессы являются
место тогда, когда на колеблющееся затухающими, так как на
тело (материальную точку)
колеблющееся тело
действует только возвращающая
действуют силы
сила.
сопротивления движению.
• Свободные колебания являются
незатухающими, если не
• Вынужденные колебания
происходит рассеяния энергии в
совершаются под действием
окружающее пространство.
внешней периодически
• В этом случае полная механическая изменяющейся силы,
энергия колебательной системы
которую называют
остается постоянной
вынуждающей.
8.
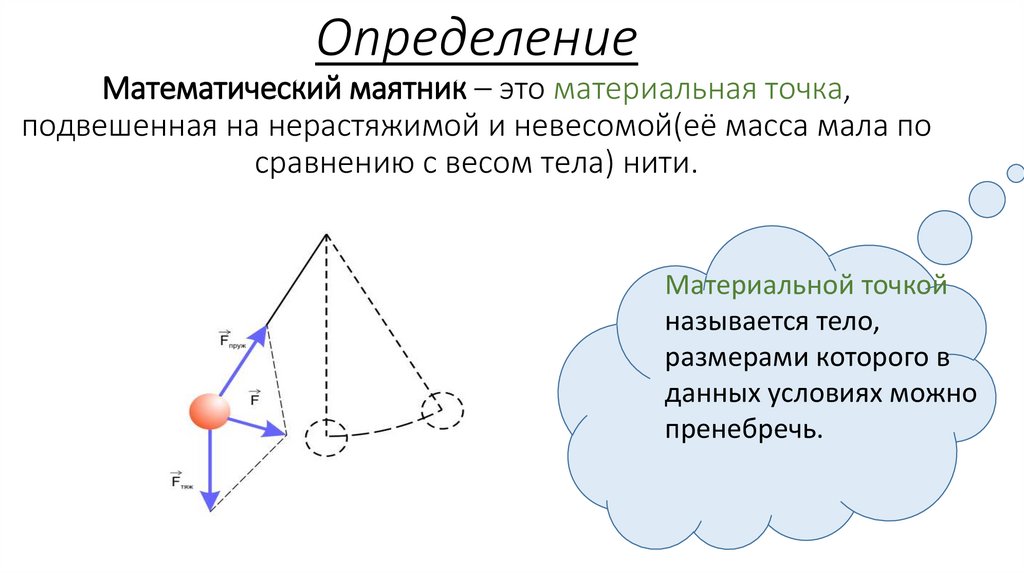
ОпределениеМатематический маятник – это материальная точка,
подвешенная на нерастяжимой и невесомой(её масса мала по
сравнению с весом тела) нити.
Материальной точкой
называется тело,
размерами которого в
данных условиях можно
пренебречь.
9. Определение Математический маятник – это материальная точка, подвешенная на нерастяжимой и невесомой(её масса мала по сравнению
Зависимость Математического маятникаГалилео Галилей
(1564-1642гг.)
Великий итальянский ученый –
один из создателей точного
естествознания.
Учился сначала в монастырской
школе, а затем в университете.
Уже в студенческие годы
Галилей увлекся изучением
колебаний. Он обнаружил, что
колебания маятника не зависят
от его массы, а определяются
длиной подвеса.
10. Зависимость Математического маятника
ХАРАКТЕРИСТИКА МАТЕМАТИЧЕСКОГО МАЯТНИКАПериод (T):
- длина маятника(м)
g - Ускорение свободного падения(м/с2)
Христиа́н Гю́йгенс
(1629-1695гг.)
11. ХАРАКТЕРИСТИКА МАТЕМАТИЧЕСКОГО МАЯТНИКА
Математический маятник– это маятник, масса
груза которого намного
больше нити, а нить
намного больше по размерам
чем груз , при
этом груз является
материальной точкой, а А
нить невесомой
Т 2
l
g
12.
ХАРАКТЕРИСТИКА МАТЕМАТИЧЕСКОГО МАЯТНИКА• Период (T):
- Длина маятника(м)
g - Ускорение свободного падения(м/с2)
Христиа́н Гю́йгенс
(1629-1695гг.)
13. ХАРАКТЕРИСТИКА МАТЕМАТИЧЕСКОГО МАЯТНИКА
ДА ЗДРАВСТВУЕТ ТОЧНОЕ ВРЕМЯ !14.
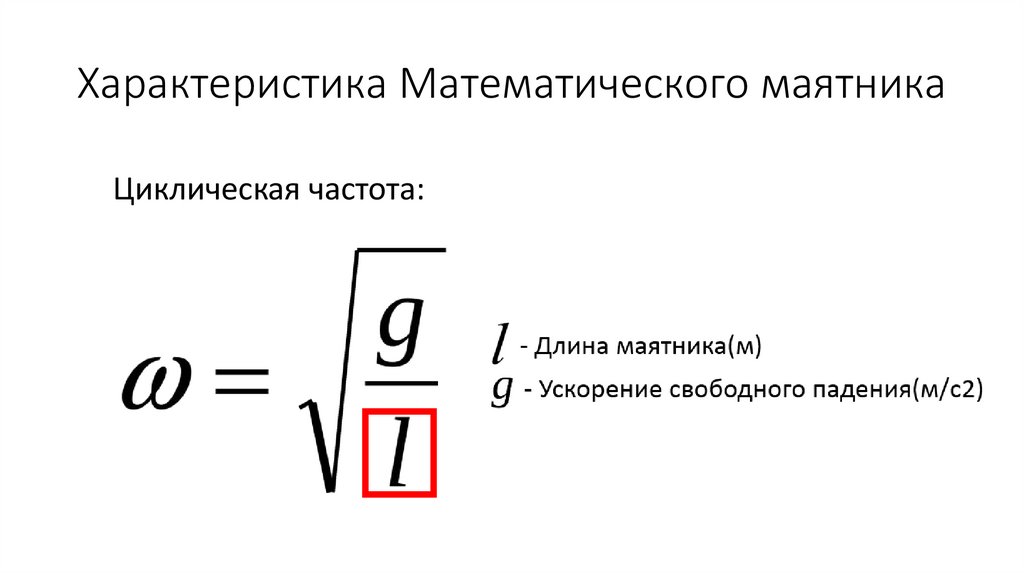
Характеристика Математического маятникаЦиклическая частота:
15. Характеристика Математического маятника
Циклическая частота:16. Характеристика Математического маятника
График устанавливает зависимость смещения тела со временем.17.
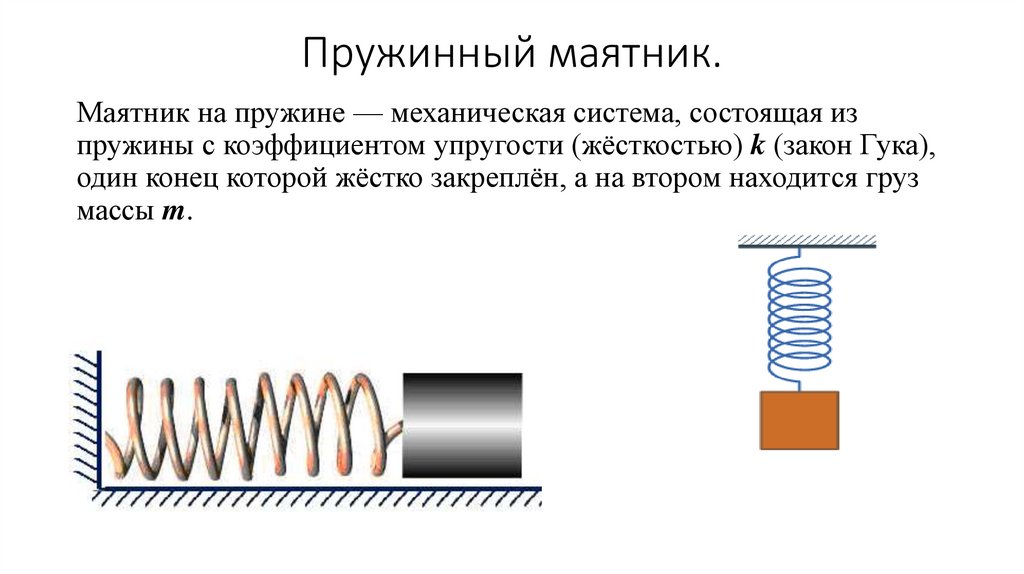
Пружинный маятник.Маятник на пружине — механическая система, состоящая из
пружины с коэффициентом упругости (жёсткостью) k (закон Гука),
один конец которой жёстко закреплён, а на втором находится груз
массы m.
18. Пружинный маятник.
Характеристика пружинных маятниковЗакон Гука:
Сила упругости пропорциональна смещению
тела (удлинению пружины):
Fупр = –kx.
k – коэффициент жесткости пружины.
x – отклонение груза от точки равновесия
19. Характеристика пружинных маятников
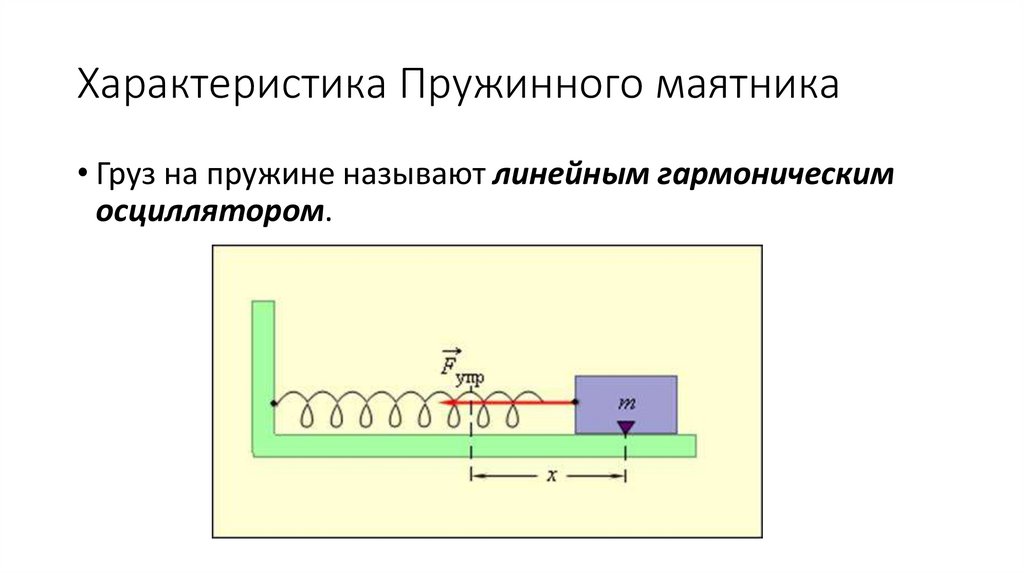
Характеристика Пружинного маятника• Груз на пружине называют линейным гармоническим
осциллятором.
20. Характеристика Пружинного маятника
Характеристика пружинного маятникаСобственная частота
( ω0 )
k – коэффициент жесткости пружины.
m – масса маятника.
Период
(Т)
k – коэффициент жесткости пружины.
m – масса маятника.
- математическая постоянная ≈ 3,14
21. Характеристика пружинного маятника
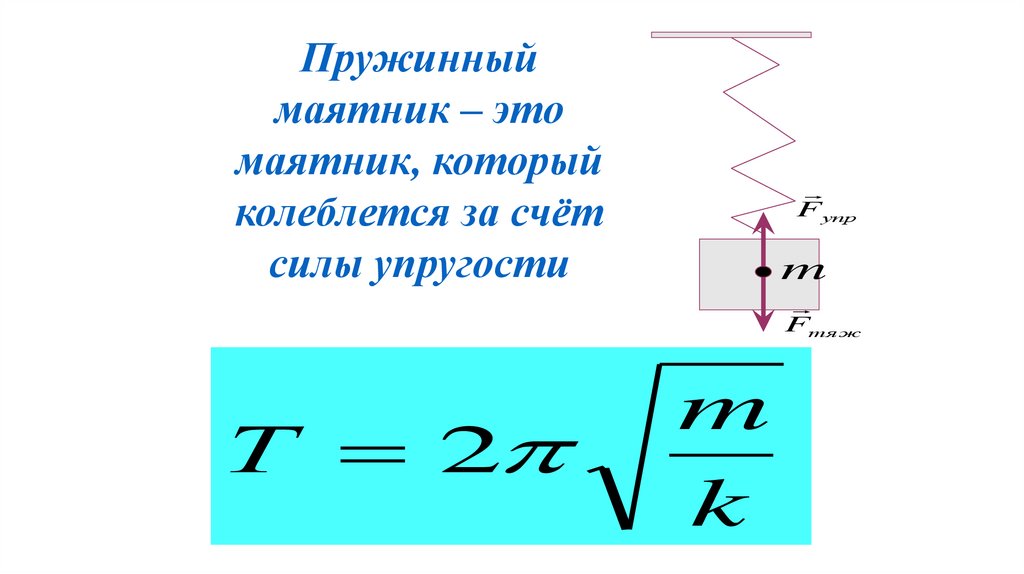
Пружинныймаятник – это
маятник, который
колеблется за счёт
силы упругости
Fупр
m
Fтя ж
Т 2
m
k
22.
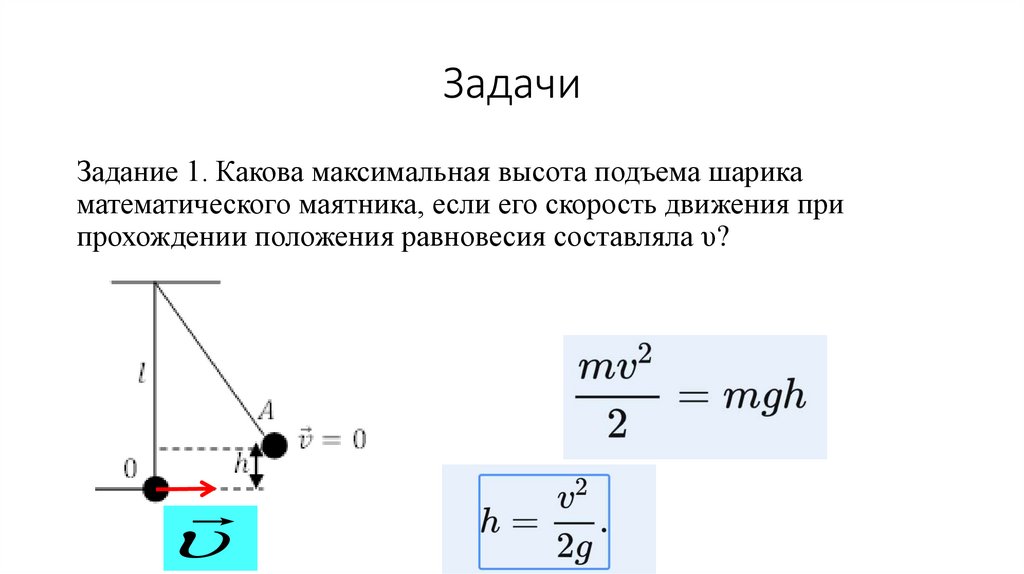
ЗадачиЗадание 1. Какова максимальная высота подъема шарика
математического маятника, если его скорость движения при
прохождении положения равновесия составляла υ?
23. Задачи
Задача №2.Тело массой m=2 кг подвешено к упругой пружине, совершает
гармонические колебания. Определите жёсткость k пружины, если
за время t=1,5мин число N полных колебаний равно 60.
Дано:
СИ
Решение
m=2кг;
t=1,5мин 90с
N=60
k -?
24. Задача №2.
Решение:Период гармонических колебаний тела, подвешенного на пружине
(пружинный маятник),
где m- масса тела; k- жёсткость пружины.
С другой стороны, период колебаний
где t – время, за которое совершается N полных колебаний.
Приравняв оба выражения
Найдём искомую жёсткость пружины
Ответ: k=35,1 Н/м.
25.
СПАСИБО ЗА ВНИМАНИЕ26. СПАСИБО ЗА ВНИМАНИЕ
Домашнее задание§31-33
Из нового учебника
1,2+ 3,4,5
3.
4. К пружине жесткостью 200 Н/м подвешен груз массой 2 кг. Определите период
этого маятника.
5. Координата колеблющегося тела изменяется по закону: x=5cos πt. Чему равны
амплитуда, период и частота колебаний, если в формуле все величины выражены в
единицах СИ?


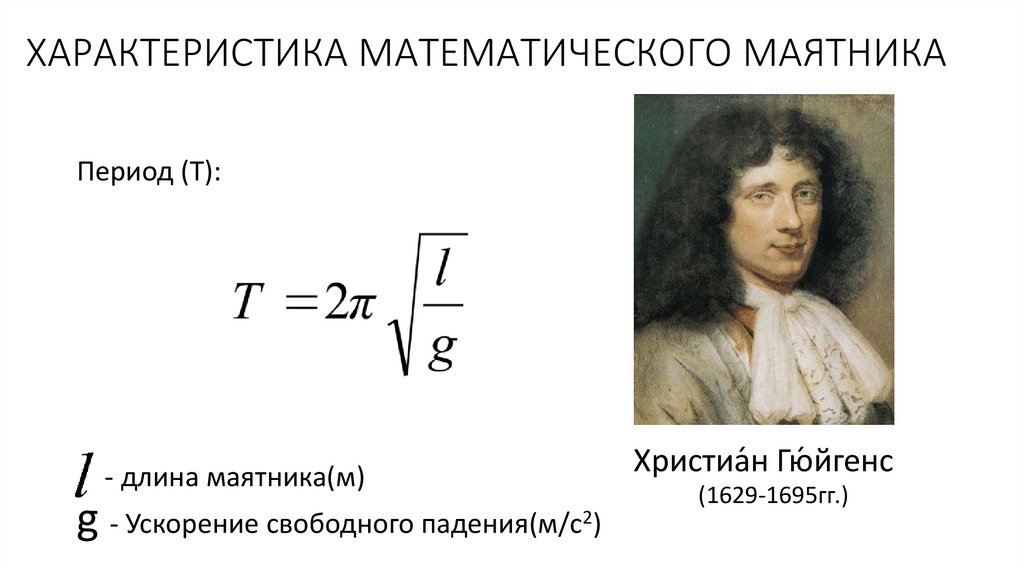










 Физика
Физика