Лекция_3_формулы_04.10.2023

1. Лекция №3 Вычислительная математика

Санкт-Петербургский политехнический университет Петра Великого
Лекция №3
Вычислительная математика
Воскобойников С.П.
Доцент ВШ ПИ ИКНТ, к.ф.-м.н.
Voskob_sp@spbstu.ru
04.10.2023

2. Содержание

• Метод Гаусса с выбором ведущего элемента
по столбцу.
• Связь метода Гаусса с LU-разложением.
• Единственность LU-разложения.
• Решение Ax=b, вычисление A-1 и
определителя

3. Метод Гаусса

a11x1
a x
21 1
.
ai1 x1
.
an1 x1
a12 x2
a22 x2
.
.
ai 2 x2
.
.
an 2 x2
.
.
.
.
.
.
.
.
a1i xi
a2i xi
.
.
aii xi
.
.
ani xi
.
.
.
.
.
.
.
.
a1n xn
a2 n xn
.
.
ain xn
.
.
ann xn
.
.
b1
b2
.
bi
.
bn
det A 0
a11
a
21
.
A
ai1
.
an1
a12
a22
.
ai 2
.
an 2
.
.
.
.
.
.
a1i
a2i
.
aii
.
ani
.
.
.
.
.
.
a1n
a2 n
.
ain
.
ann
x1
x
2
.
x
xi
.
xn
Ax b
b1
b
2
.
b
bi
.
bn

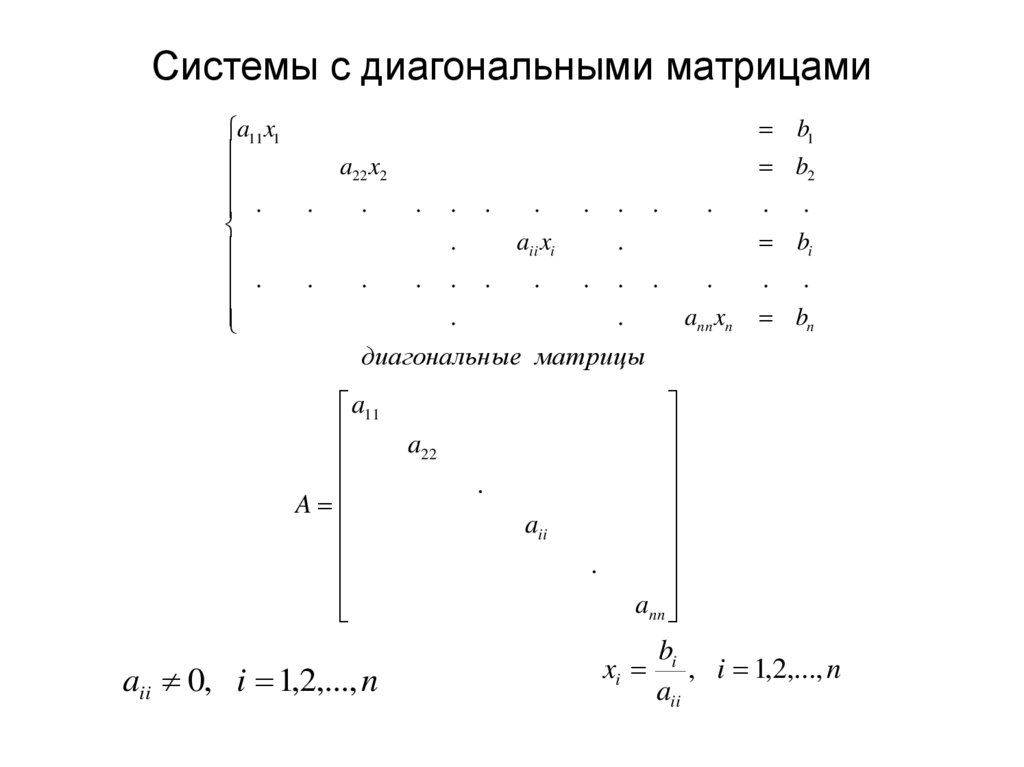
4. Системы с диагональными матрицами

a11x1
.
.
.
a22 x2
.
.
.
.
.
.
.
.
.
.
.
.
aii xi
.
.
.
.
.
.
.
.
.
.
.
ann xn
.
.
b1
b2
.
bi
.
bn
диагональные матрицы
a11
A
aii 0, i 1,2,..., n
a22
.
aii
.
ann
xi
bi
, i 1,2,..., n
aii

5. Системы с нижними треугольными матрицами

a11x1
a x a x
22 2
21 1
.
.
.
ai1 x1 ai 2 x2
.
.
.
an1 x1 an 2 x2
.
.
.
.
.
.
.
aii xi
.
.
ani xi
.
.
.
ann xn
.
.
b1
b2
.
bi
.
bn
нижние треугольные матрицы
a11
a
21
.
A
ai1
.
an1
a22
.
ai 2
.
an 2
aii 0, i 1,2,..., n
.
.
.
.
aii
.
ani
.
.
ann
xi
i 1
bi aij x j
j 1
aii
, i 1,2,..., n

6. Системы с верхними треугольными матрицами

a11x1 a12 x2
a22 x2
.
a1i xi
a2i xi
.
.
aii xi
.
.
.
.
.
a1n xn
a2 n xn
.
.
ain xn
.
.
ann xn
.
.
.
.
.
.
.
b1
b2
.
bi
.
bn
верхние треугольные матрицы
a11
A
a12
a22
.
.
.
a1i
a2i
.
aii
.
.
ain
a2 n
.
ain
.
ann
n
aii 0, i 1,2,..., n
xi
bi aij x j
j i 1
aii
n
, i n, n 1, ..,2,1
a 0, если m n
k m
k

7. Системы уравнений общего вида

a11x1
a x
21 1
.
ai1 x1
.
an1 x1
a12 x2
a22 x2
.
.
ai 2 x2
.
.
an 2 x2
aij(0) aij ,
.
.
a1i xi
a2i xi
.
.
aii xi
.
.
ani xi
.
.
.
.
.
.
bi(0) bi
a11( 0) x1 a12( 0) x2
(1)
a
x2
22
.
.
.
a1n xn
a2 n xn
.
.
ain xn
.
.
ann xn
.
.
.
.
.
.
.
.
b1
b2
.
bi
.
bn
A(0) A, b( 0) b
.
.
.
.
a1(i0) xi
a2(1i) xi
.
aii(i 1) xi
ведущие элементы aii( k ) , k 0,1,...n 1
.
.
.
.
.
.
.
.
.
a1(n0) xn
a2(1n) xn
.
ain(i 1) xn
.
( n 1)
ann
xn
aii( k ) 0
b1( 0)
b2(1)
.
.
bi(i 1)
.
.
bn( n 1)

8. Перестановка уравнений

,
a12 x2
a22 x2
.
.
ai 2 x2
.
.
an 2 x2
a11x1
a x
21 1
.
ai1 x1
.
an1 x1
.
.
a11 0
,
0
1
. .
P1i P1
1
.
1
.
0
.
.
.
.
.
.
a1i xi
a2i xi
.
.
aii xi
.
.
ani xi
.
.
.
.
.
.
.
.
a1n xn
a2 n xn
.
.
ain xn
.
.
ann xn
(0)
a11
max ai(10)
2 i n
. , i 1
.
1
P11 E
P1 Ax P1b
.
.
b1
b2
.
bi
.
bn

9. Исключение неизвестных

a11x1
a x
21 1
.
ai1 x1
.
an1 x1
( 0)
a21
( 0) ,
a11
( 0)
a31
( 0) ,
a11
a12 x2
a22 x2
.
.
ai 2 x2
.
.
an 2 x2
.
.
a1i xi
a2i xi
.
.
aii xi
.
.
ani xi
.
.
.
.
.
.
.
.
ai(10)
( 0) , i 2,3,...., n
a11
an( 10)
( 0)
a11
a11( 0) x1 a12( 0) x2
(1)
a
x2
22
.
ai(21) x2
.
an(12) x2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a1(i0) xi
a2(1i) xi
.
.
aii(1) xi
.
.
ani(1) x2
.
.
.
.
.
.
.
.
a1n xn
a2 n xn
.
.
ain xn
.
.
ann xn
.
.
b1
b2
.
bi
.
bn
ai(10)
1, i 2,3,...., n
( 0)
a11
a1(n0) xn
a2(1n) xn
.
.
ain(1) xn
.
.
(1)
ann
xn
.
.
b1( 0)
b2(1)
.
bi(1)
.
bn(1)

10. Исключение неизвестных. Первый шаг.

1
a (0)
21
(0)
a11
.
Э1 ai(10)
( 0 )
a11
.
a (0)
n( 10)
a11
1
.
.
1
1
a (0)
21
(0)
a11
.
. Э1P1 A( 0 ) ai(10)
( 0 )
a11
.
.
a (0)
1
n( 10)
a11
a11( 0)
0
.
(1)
(0)
A Э1P1 A
0
.
0
a12( 0)
(1)
a22
.
ai(21)
.
an(12)
1
.
.
1
.
.
.
.
.
.
a1(i0)
a2(1i)
.
aii(1)
.
ani(1)
a ( 0 )
11
(0)
a21
.
. ( 0 )
ai1
.
.
a ( 0 )
1 n1
.
.
.
.
.
.
a1(n0)
a2(1n)
.
(1)
ain
.
(1)
ann
a12( 0 )
(0)
a22
.
ai(20 )
.
an( 02)
.
.
.
.
.
.
a1(i0 )
a2( 0i )
.
aii( 0 )
.
ani( 0 )
.
.
.
.
.
.
Э1P1 Ax Э1P1b
a1(n0 )
a2( 0n)
.
ain( 0 )
.
(0)
ann

11. Исключение неизвестных. Второй шаг.

a11( 0)
0
.
(1)
A
0
.
0
a12( 0)
(1)
a22
.
ai(21)
.
an(12)
a1(i0)
a2(1i)
.
aii(1)
.
ani(1)
.
.
.
.
.
.
a1(n0)
a2(1n)
.
ain(1)
.
(1)
ann
.
.
.
.
.
.
(1)
a22
max ai(21)
P2
(1)
32
(1)
22
a
,
a
(1)
42
(1)
22
a
,
a
1
1
(1)
a31
(1)
a22
Э2
.
.
an(11)
(1)
a22
(1)
n2
(1)
22
a
,
a
.
1
b1( 0)
(1)
b2
.
(1)
b (1)
bi
.
(1)
bn
.
.
1
(1)
i2
(1)
22
a
,
a
3 i n
i 3,4,..., n
ai(21)
1,
(1)
a22
i 3,4,..., n
Э2 P2Э1P1 Ax Э2 P2Э1P1b

12. Исключение неизвестных. к-ый шаг

Pk Pki ,
Эk
i k
Pkk E, i k
akk( k 1) max aik( k 1) , k 1,2,..., n 1
k 1 i n
1
.
.
1
ak( k 1,1k)
akk
ak( k 21,)k
akk
.
.
an( k, k 1)
akk
1
1
.
.
1

13. Цепочка преобразований системы к системе с верхней треугольной матрицей

Эn 1Pn 1...Э2 P2 Э1P1 Ax Эn 1Pn 1...Э2 P2 Э1P1b
a11( 0)
Эn 1Pn 1...Э2 P2 Э1P1 A U
a12( 0)
(1)
a22
.
.
.
a1(i0)
a2(1i)
.
aii(i 1)
A( k ) Эk Pk A( k 1) , k 1,2,..., n 1
b ( k ) Эk Pk b ( k 1) ,
A( 0) A, b ( 0) b
A( n 1) U
.
.
a1(n0)
a2(1n)
.
ain(i 1)
.
( n 1)
ann

14. Цепочка преобразований системы к системе с верхней треугольной матрицей

Эn 1Pn 1...Э2 P2 Э1P1 Ax Эn 1Pn 1...Э2 P2 Э1P1b
~ P
~ ...Э P Э P A
Эn 1Pn 1Эn 2 Pn 2 ...Э2 P2Э1P1 A Эn 1 Pn 1Эn 2 Pn 1 Pn 1Pn 2 ...Э2 P2Э1P1 A Эn 1Э
n 2 n 2
2 2 1 1
~
~
Эn 2
Pn 2
~ P
~ ~
~ ~ ~
~
~ ~
Эn 1Э
n 2 n 2 Эn 3 Pn 3 ...Э2 P2 Э1P1 A Эn 1Эn 2 Pn 2 Эn 3 Pn 2 Pn 2 Pn 3 ...Э2 P2 Э1P1 A Эn 1Эn 2 Эn 3 Pn 3 ...Э2 P2 Э1P1 A
~
~
Эn 3
Pn 3
~ Э
~ P
~P
~ Э
~ P
~P
~ Э
~ ...Э
~Э
~P
~ ...Э
~Э PA Э Э
~ ...Э
~Э P
~P
~PA Э Э
~A
Эn 1Э
n 2 n 3 n 3
2 2 1 1
n 1 n 2 n 3 n 3
2 2 1 2
2 1
n 1 n 2 n 3
2 1 1
~
~
~
P P
1
~ ~
~~
Эn 1Эn 2Эn 3...Э2Э1PA U
Э1
P1
~ ~
~ ~
PA Э1 1Э2 1...Эn 13Эn 12 Эn 11U

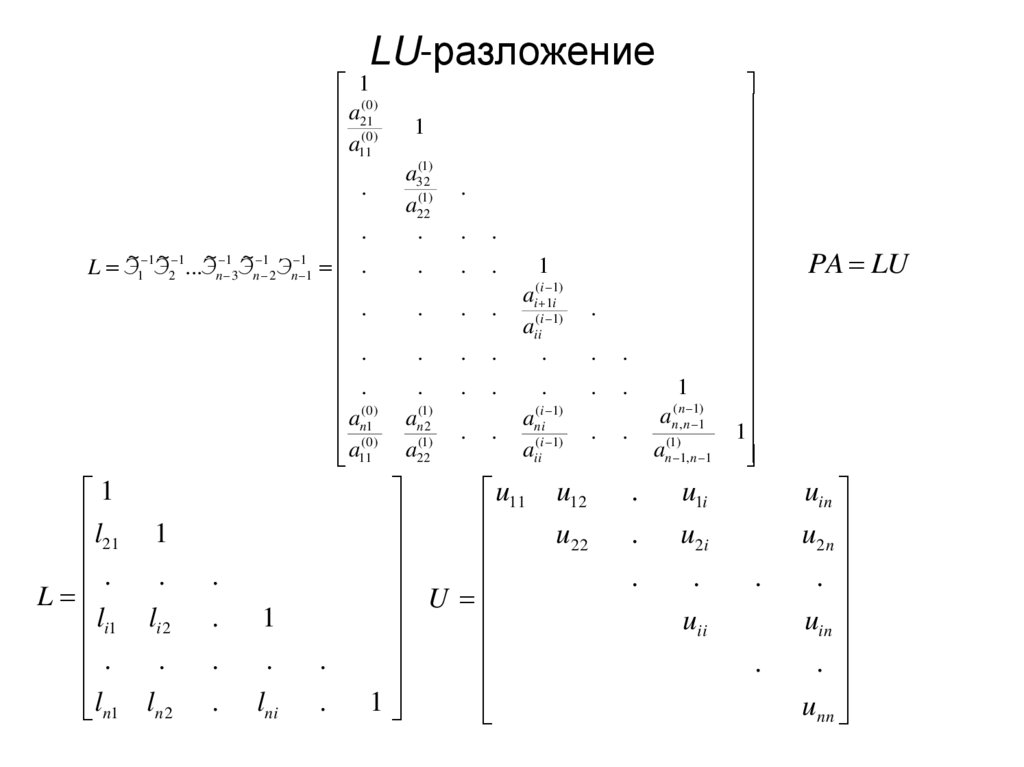
15. LU-разложение

1
a (0)
21
(0)
a11
.
.
~ 1Э
~ 1...Э
~ 1 Э
~ 1 1 .
L Э
1
2
n 3 n 2 Эn 1
.
.
.
a (0)
n( 10)
a11
1
l
21 1
.
.
L
li1 li 2
.
.
ln1 ln 2
.
.
.
.
1
.
lni
.
.
1
(1)
a32
(1)
a22
.
.
.
.
.
.
1
( i 1)
i 1i
( i 1)
ii
.
.
.
a
a
.
.
.
.
.
.
.
.
.
.
.
.
( i 1)
ni
( i 1)
ii
(1)
n2
(1)
22
a
a
.
.
a
a
u11
U
1
u12
u22
.
.
.
1
( n 1)
n , n 1
(1)
n 1, n 1
a
a
.
.
.
.
u1i
u2i
.
uii
1
.
.
PA LU
uin
u2 n
.
uin
.
unn

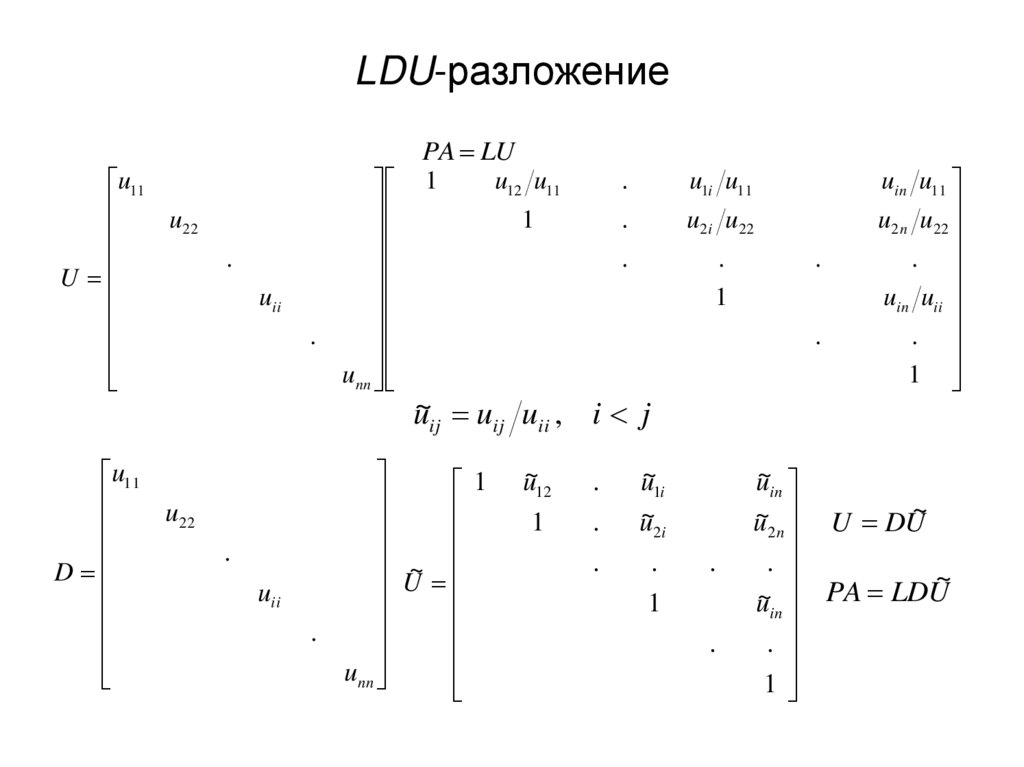
16. LDU-разложение

u11
u22
U
u11
u22
D
.
uii
.
.
uii
.
unn
PA LU
1
u12 u11
1
.
.
.
u1i u11
u2i u22
.
1
.
.
u~ij uij uii , i j
1
U~
unn
u~12
1
.
.
.
u~1i
u~2i
.
1
.
.
u~in
u~2 n
.
u~in
.
1
uin u11
u2 n u22
.
uin uii
.
1
U DU~
PA LDU~

17. Единственность LU-разложения

PA L2U 2
PA L1U1
L1U1 L2U 2
1
1
L
L
U
U
2 1
1
2
~
U~
L
~ U~
L
~
lij 0, i j
~
lij 1, i j
~
lij 1, i j
~ U~ E
L
L 21L1 E
u~ij 0,
L1 L2
i j
U1 U2

18. Применение LU-разложения.

Ax b
PA LU
вычисляется за число действий ~ n3
PAx Pb
LUx
Pb
Ly d
Ux y
y
d
вычисляется за число действий ~ n2
1
X A 1
AX E
A
Ax j e j ,
j 1,2,..., n
вычисляется за число действий ~ n3
PA LU
PAx j Pe j
j 1,2,..., n
Ly j d j
Ux j y j
LUx j Pe j
yj
dj
вычисляется за число действий ~ n3

19. Вычисление определителя. Схема хранения LU

det A det PLU
A PLU
det A 1 ukk
k 1
u11
l
21
.
li1
.
ln1
u12
u22
.
li 2
.
ln 2
.
.
.
.
.
.
u1i
u2 i
.
uii
.
lni
.
.
.
.
n
n
k 1
k 1
ln ukk ln ukk
n
t
det A det P det L det U
uin
u2 n
.
uin
.
unn
схема хранения матриц L и U
Матрица перестановки P не хранится.
Информация о перестановках хранится в векторе IPVT (n)
IPVT (i ) i,
IPVT (n) 1
i 1,2,..., n 1
i k
IPVT (k ) i
IPVT (i ) k
IPVT (n) IPVT (n)

20. Подпрограммы DECOMP и SOLVE

DECOMP (NDIM, N, A, COND, IPVT, WORK)
SOLVE(NDIM , N, A, B, IPVT)