9_Sistemy_koordinat

1. Системы координат

Прямоугольная система координат
Полярная система координат
Цилиндрическая система координат
Сферическая система координат
Преобразование систем координат

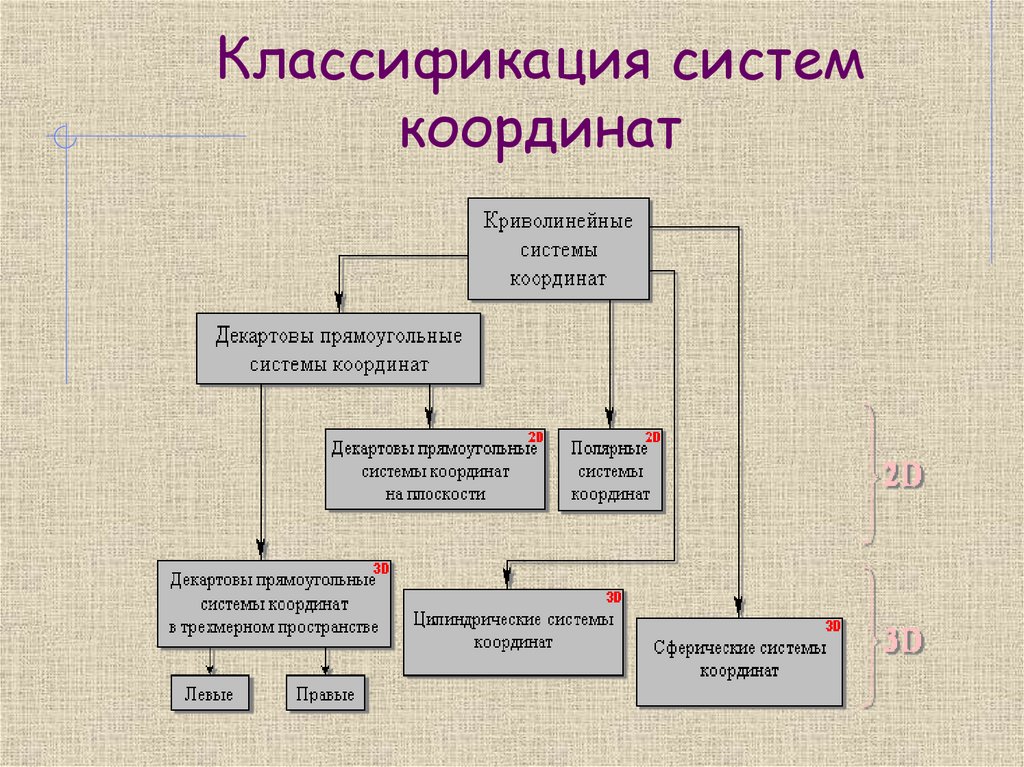
2. Классификация систем координат

3. Прямоугольная система координат

Косоугольная система координат называется прямоугольной, если
ее базис ортонормированный.
Выбирая стандартные базисы, получаем:
Oi- прямоугольная система
координат на прямой — это
точка О и единичный вектор i на
прямой. Точки A и О (рис.2.4) на
координатной оси Ox
обозначаются О (0) и A(1)

4. Прямоугольная система координат

O i j - прямоугольная система
координат на плоскости — это
точка О и два взаимно
перпендикулярных единичных
вектора i и j на плоскости (вектор
i - первый базисный вектор, a j —
второй; пара векторов i , j —
правая). Координатные оси Ox
(абсцисс) и Oy (ординат)
разбивают плоскость на 4 части,
называемые квадрантами
(четвертями). Точка А(1;1),
например, принадлежит I
четверти

5. Прямоугольная система координат

O i j k — прямоугольная система
координат в пространстве — это
точка О и три попарно
перпендикулярных единичных
вектора (вектор i - первый
базисный вектор, j- второй,а k третий; тройка векторов i , j , k
правая). Координатные оси
обозначаются: Ox — ось абсцисс,
Oy — ось ординат, Oz — ось
аппликат. Координатные плоскости ,
проходящие через пары
координатных осей, разбивают
пространство на 8 октантов
(рис.2.6). Точка А(1; 2;2), например,
принадлежит I октанту.

6. Прямоугольная система координат

Прямоугольные системы координат обозначают также
указанием начала координат и координатных осей,
например Ox, Oxy, Oxyz.
Координаты векторов и точек в прямоугольной системе
координат называются прямоугольными координатами.
Координатами вектора в прямоугольной системе
координат называются коэффициенты в разложении
вектора по стандартному базису.

7. Полярная система координат

Полярная система координат задается точкой О, называемой
полюсом и полярной осью р.
М
Положение точки М на плоскости
r
определяется двумя числами: ее
расстоянием r от полюса О,
φ
и углом φ, образованным отрезком ОМ
с полярной осью, отсчитываемый
против часовой стрелки.
0
Числа r и φ называют полярными координатами точки М ,
записывают: М(r ; φ).
; - полярный угол
r 0;
- полярный радиус
р

8. Полярная система координат

Установим связь между прямоугольными
и полярными координатами.
Для этого совместим полюс О с
началом координат системы координат
XOY, а полярную ось с положительным
направлением оси OX.
Y
М
y
r
φ
0
X
х
р
Прямоугольные координаты точки M выражаются через полярные
координаты следующим образом:
x r cos ,
y r sin .
Полярные координаты выражаются через декартовы по формулам:
r x 2 y 2 ,
y
tg x .
Определяя величину φ следует установить
четверть , в которой лежит угол и учитывать,
что .

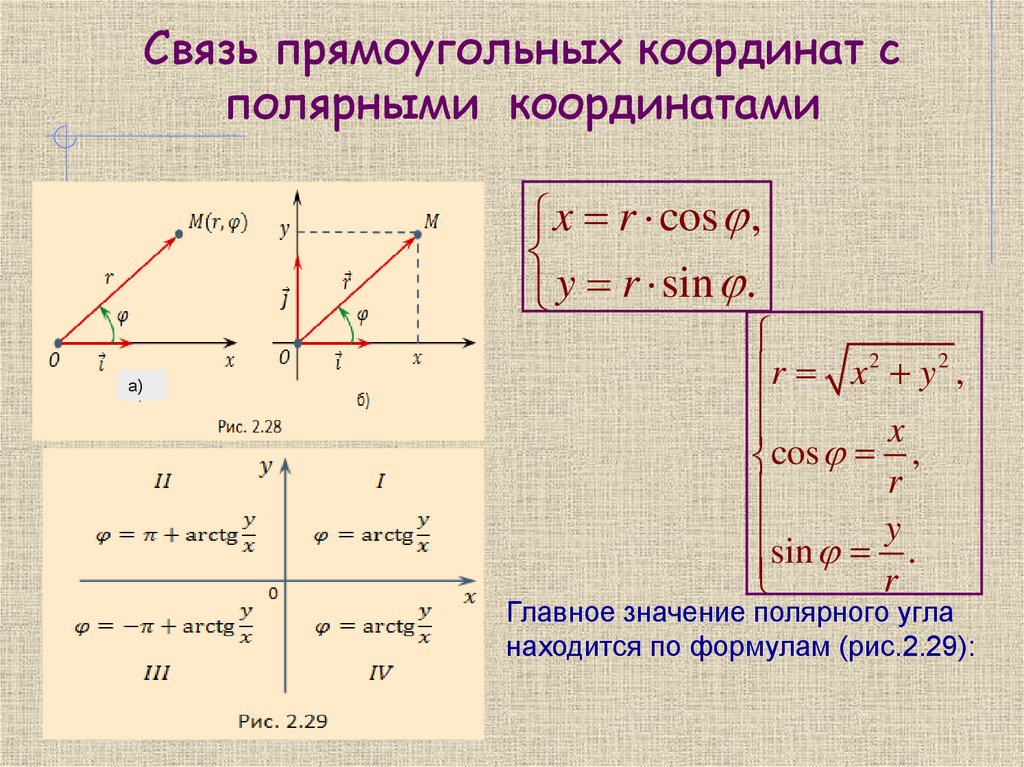
9. Связь прямоугольных координат с полярными координатами

x r cos ,
y r sin .
а)
r x 2 y 2 ,
x
cos ,
r
y
sin r .
Главное значение полярного угла
находится по формулам (рис.2.29):

10.

Примеры
Найти прямоугольные координаты точки М,если даны
2
её полярные координаты: M (2 ;
)
3 2
Решение:
Имеем: 2 ,
3
Находим:
2
2
1
x cos 2 cos
2 1
2 cos
3
3
2
2
3
2
y sin 2 sin
2
3
2 sin
3
2
3
Ответ. M ( 1; 3 )

11.

Найти полярные координаты точки М, если даны её
прямоугольные координаты: M ( 3 ; 1)
Решение:
Имеем: x 3 ,
y 1
Находим:
x 2 y 2 ( 3) 2 ( 1) 2 2
y
1
5
arctg
6
6
3
Ответ.
5
M (2; )
6
М
0
x
Р

12. Применение полярных систем координат

В военном деле:
Радиолокационные
станции (РЛС)
Координаты
цели
могут выдаваться в
полярной
системе
координат
(азимут,
дальность).

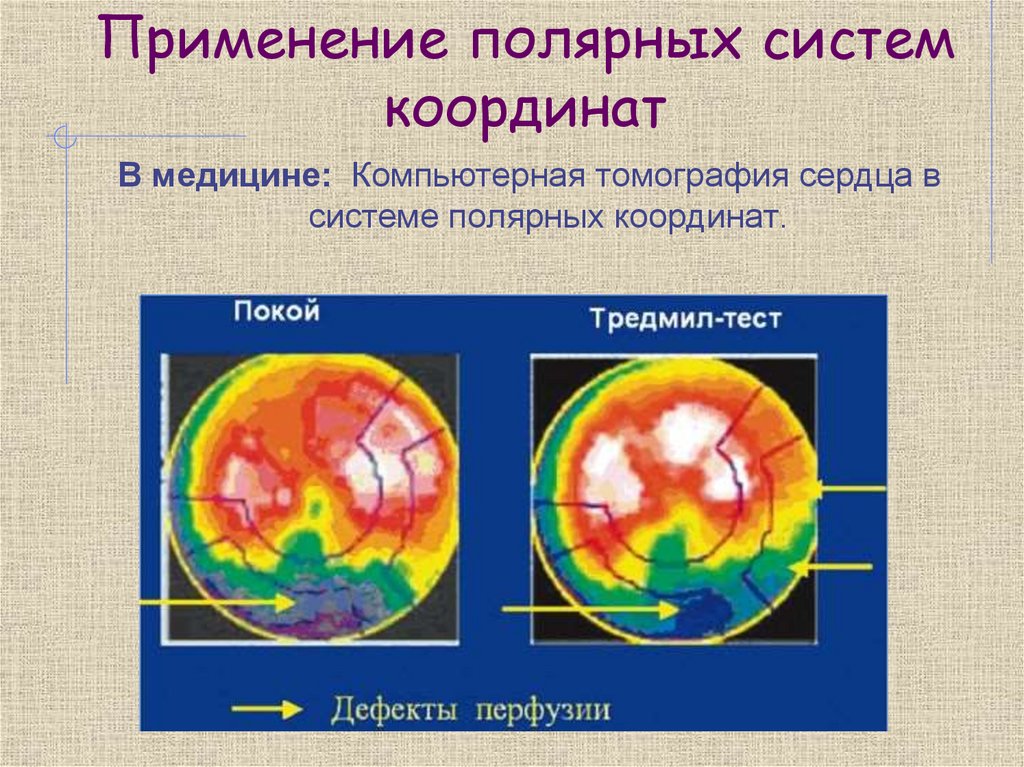
13. Применение полярных систем координат

В медицине: Компьютерная томография сердца в
системе полярных координат.

14. Применение полярных систем координат

В
геодезии:
получение
координат
точек объекта основано
на измерении полярных
углов и расстояний до
объекта.

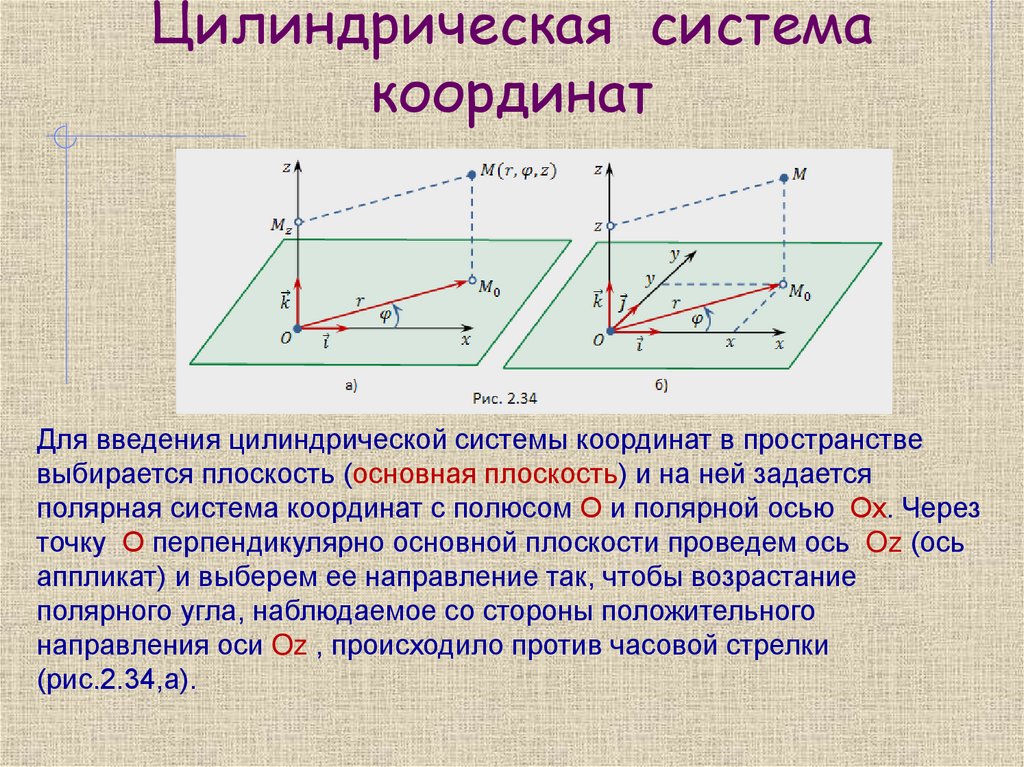
15. Цилиндрическая система координат

Для введения цилиндрической системы координат в пространстве
выбирается плоскость (основная плоскость) и на ней задается
полярная система координат с полюсом О и полярной осью Ох. Через
точку О перпендикулярно основной плоскости проведем ось Oz (ось
аппликат) и выберем ее направление так, чтобы возрастание
полярного угла, наблюдаемое со стороны положительного
направления оси Oz , происходило против часовой стрелки
(рис.2.34,а).

16. Цилиндрическая система координат

В цилиндрической системе координат положение точки М, не
принадлежащей оси аппликат, характеризуется полярными
координатами r , точки M 0 — ортогональной проекции точки М
на основную плоскость, и аппликатой z — координатой точки M z —
ортогональной проекции точки M на ось аппликат. Таким образом,
цилиндрические координаты точки M — это упорядоченная тройка r , , z
чисел
— полярный радиус r, полярный угол и аппликата z . У
точек, принадлежащих оси аппликат, не определен полярный угол,
они задаются указанием нулевого полярного радиуса и аппликатой.

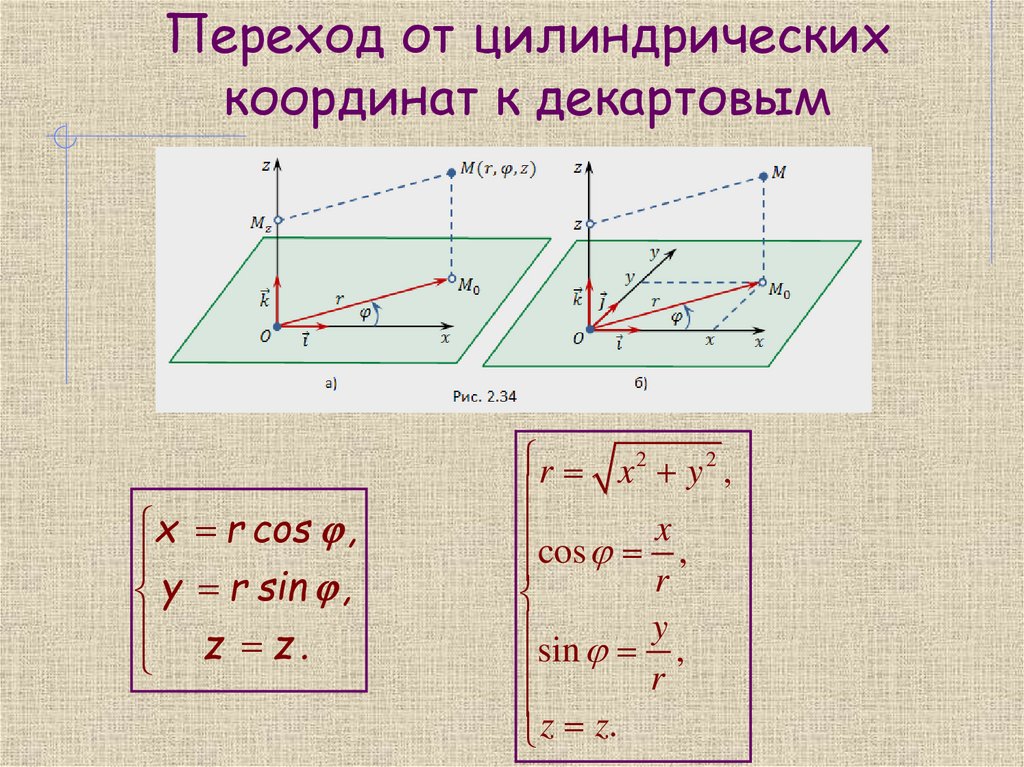
17. Переход от цилиндрических координат к декартовым

С цилиндрической системой координат Or z можно связать ДСК
(рис.2.34,б), у которой начало и базисные векторы i , k совпадают с
началом цилиндрической системы координат и единичными
векторами на полярной оси и оси аппликат соответственно, а
базисный вектор j выбирается так, чтобы тройка была правой (при
этом базис оказывается стандартным) и наоборот.

18. Переход от цилиндрических координат к декартовым

x r cos ,
y r sin ,
z z.
r x 2 y 2 ,
x
cos r ,
sin y ,
r
z z.

19. Примеры

1) найти цилиндрические координаты точки А, если
известны ее прямоугольные координаты А(4;-3;2);
2) найти прямоугольные координаты точки В , если
2
известны ее цилиндрические координаты B (2; ;1).
3

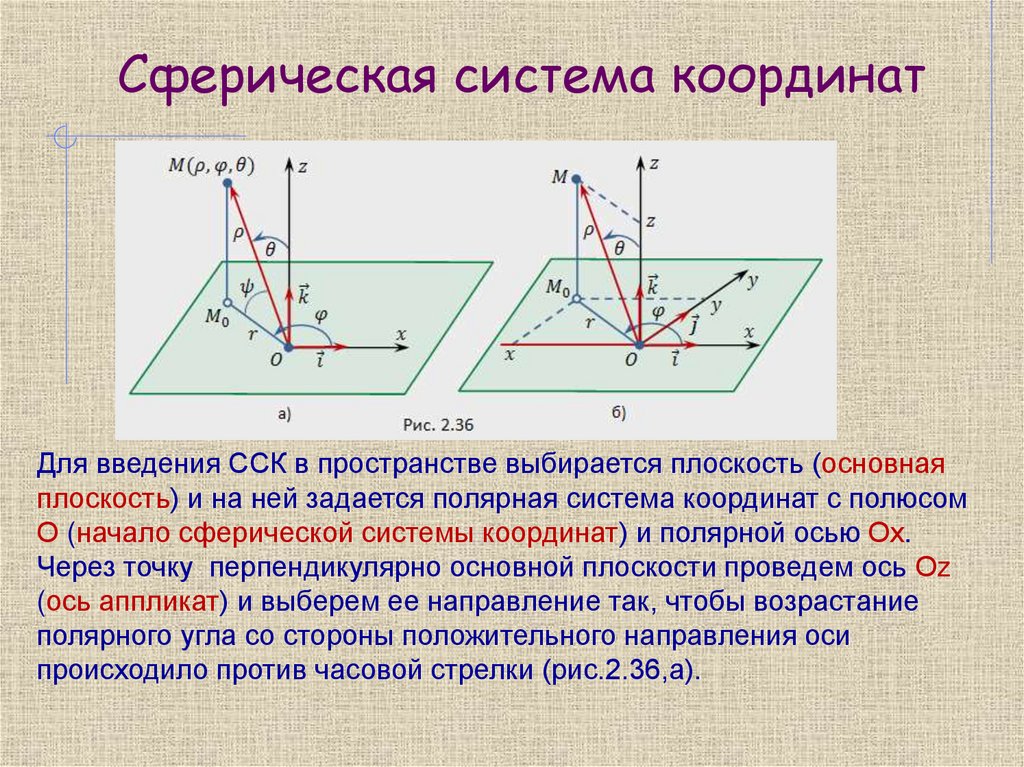
20. Сферическая система координат

Для введения ССК в пространстве выбирается плоскость (основная
плоскость) и на ней задается полярная система координат с полюсом
О (начало сферической системы координат) и полярной осью Ох.
Через точку перпендикулярно основной плоскости проведем ось Оz
(ось аппликат) и выберем ее направление так, чтобы возрастание
полярного угла со стороны положительного направления оси
происходило против часовой стрелки (рис.2.36,а).

21.

Сферическая система координат
В сферической системе координат положение точки
М, не
принадлежащей оси аппликат, характеризуется , точки M 0
—
ортогональной проекции точки М на основную плоскость и углом θ
между вектором OM и положительным направлением оси аппликат.
Таким образом, сферические координаты точки M - это упорядоченная
тройка чисел ρ,φ,θ ρ– радиус(ρ⩾0) φ - долгота (−π<φ⩽π)
θ - широта (0⩽θ⩽π)
У точек, принадлежащих оси аппликат, не определена долгота, их
положение задается радиусом ρ и широтой θ=0 для положительной
части оси Oz и θ=π для отрицательной ее части. Начало координат
задается нулевым значением радиуса ρ. Иногда вместо угла θ
широтой называют угол ψ=π/2−θ, принимающий значения −π/2⩽ψ⩽π/2

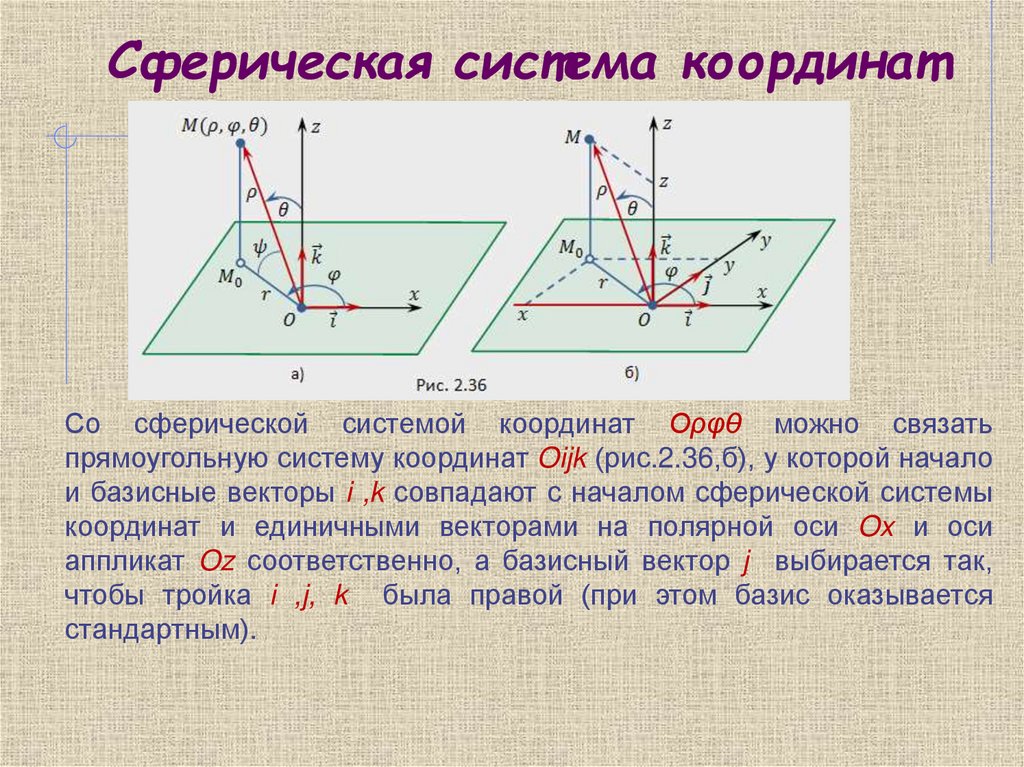
22.

Сферическая система координат
Со сферической системой координат Oρφθ можно связать
прямоугольную систему координат Oijk (рис.2.36,б), у которой начало
и базисные векторы i ,k совпадают с началом сферической системы
координат и единичными векторами на полярной оси Ox и оси
аппликат Oz соответственно, а базисный вектор j выбирается так,
чтобы тройка i ,j, k была правой (при этом базис оказывается
стандартным).

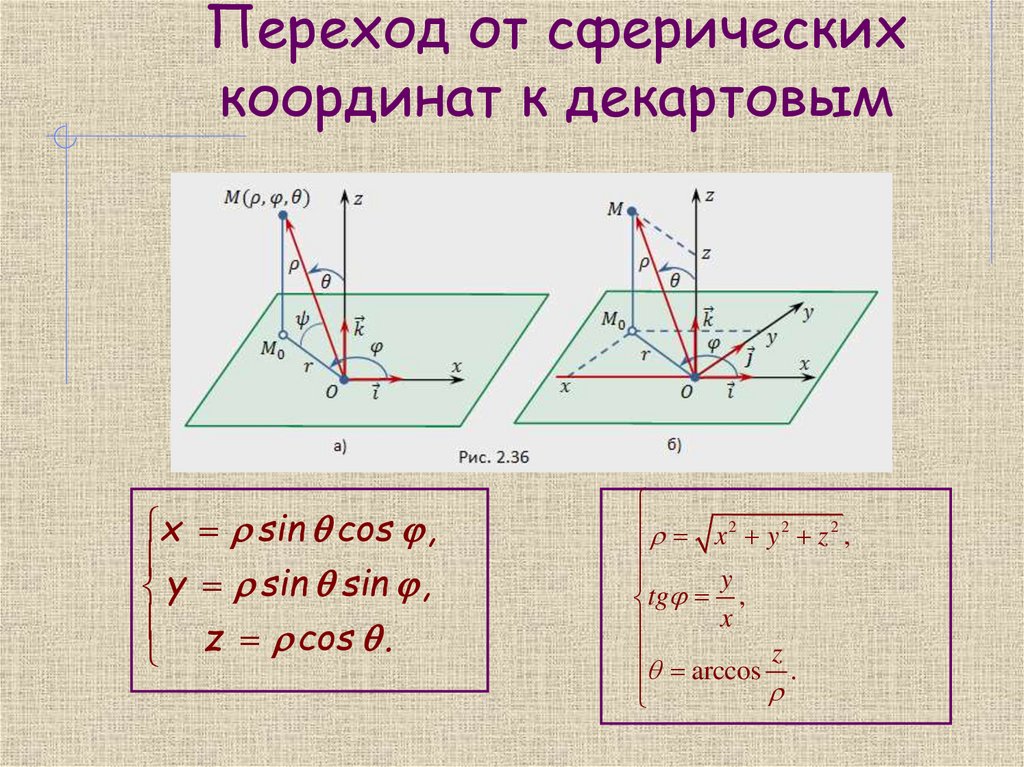
23. Переход от сферических координат к декартовым

x sin cos ,
y sin sin ,
z cos .
x2 y 2 z 2 ,
y
tg
,
x
z
arccos
.

24. Примеры

1) найти сферические координаты точки А, если
известны ее прямоугольные координаты А(4;-3;12);
2) найти прямоугольные координаты точки В , если
известны ее сферические координаты B(4;
2 3
; )
3 4

25.

Параллельный перенос (пп) осей
координат.
Под пп осей координат понимают переход от системы
координат OXY к новой системе O’X’Y’ , при котором
меняется положение начала координат, а направление
осей и масштаб остаются прежними.
Y
Y’
X’
0’
0
X

26.

Y
Y’
y
M
Пусть O’(x0;y0)- начало
новой системы координат
O’X’Y’
y’
y0
j
0’
0
x0
i
x’ X’
x X
M(x;y) – координаты точки в системе OXY
M(x’;y’) – координаты точки в системе O’X’Y’

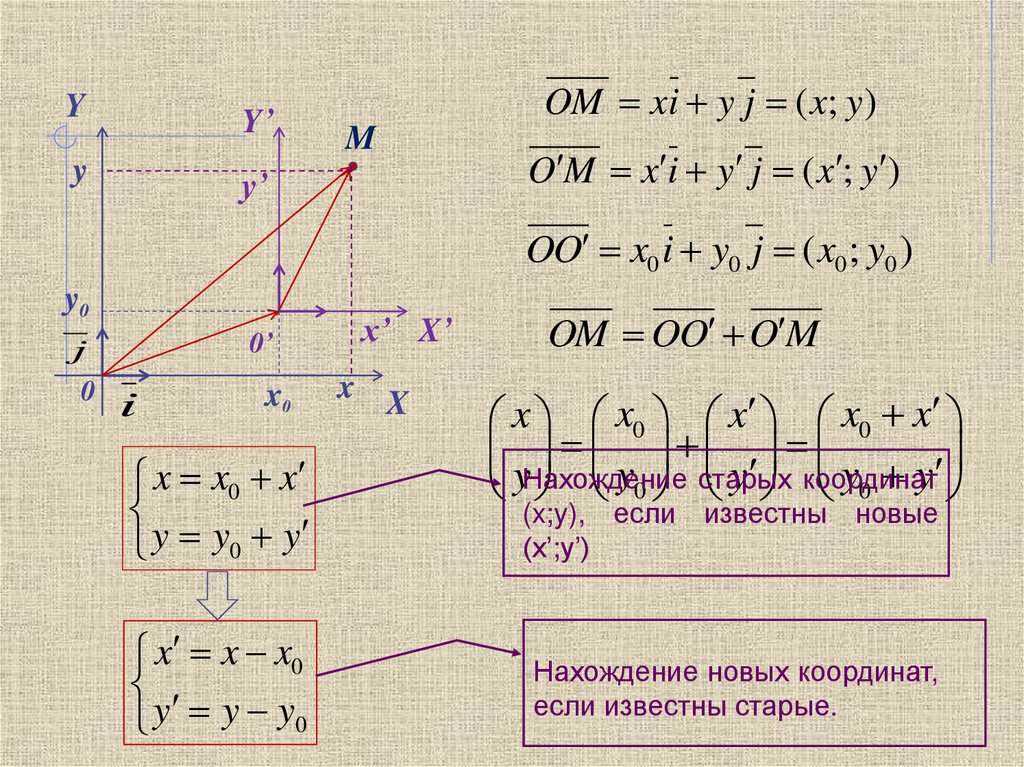
27.

Y
Y’
y
OM xi y j ( x; y )
M
y’
O M x i y j ( x ; y )
OO x0 i y0 j ( x0 ; y0 )
y0
j
0’
0
x0
i
x x0 x
y y0 y
x x x0
y y y0
x’ X’
x X
OM OO O M
x x0 x x0 x
y y y
yНахождение
0 старых
y координат
0
(x;y), если известны новые
(x’;y’)
Нахождение новых координат,
если известны старые.

28.

Примеры
Путем пп осей за новое начало координат взята
точка O’(2;-5). Найти координаты точки P в новой
системе, если её координаты в старой системе (-3;4)
Решение:
Имеем:
O (2; 5) x0 2 ,
P( 3;4)
y0 5
x 3 , y 4 (OXY )
P( x ; y ) в (O X Y )
Находим:
x x x0 3 2 5
y y y0 4 ( 5) 9
Ответ.
P ( 5 ; 9)

29.

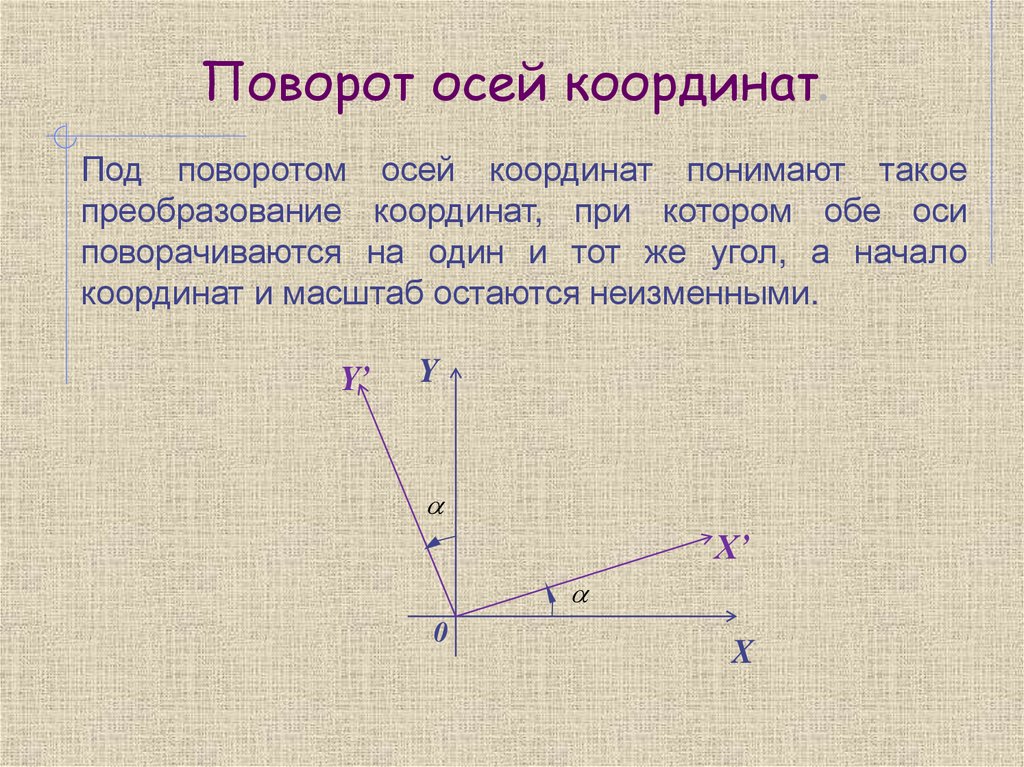
Поворот осей координат.
Под поворотом осей координат понимают такое
преобразование координат, при котором обе оси
поворачиваются на один и тот же угол, а начало
координат и масштаб остаются неизменными.
Y’
Y
X’
0
X

30.

Y’
Y
y
M
Пусть O(x’; y’)- начало новой
системы координат OX’Y’
y’
x’
0
x
X’
X
M(x;y) – координаты точки в системе OXY
M(x’;y’) – координаты точки в системе OX’Y’

31.

Y’
y’
Y
y
M
0
x’ X’
x
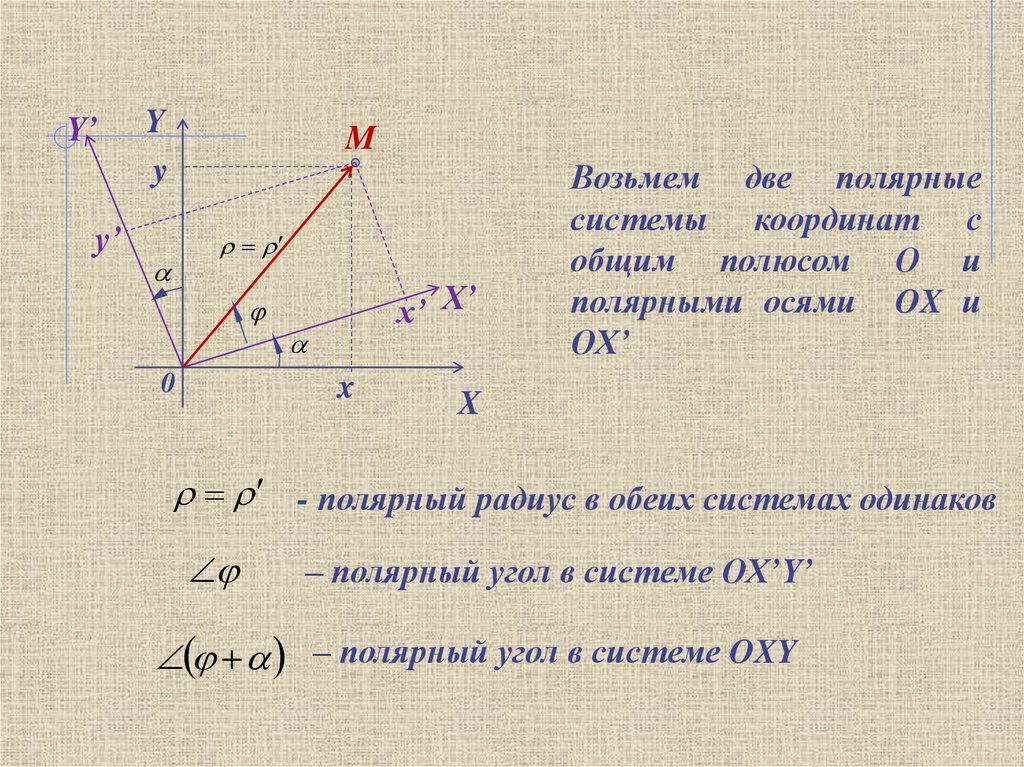
Возьмем две полярные
системы координат с
общим полюсом О и
полярными осями OX и
OX’
X
- полярный радиус в обеих системах одинаков
– полярный угол в системе OX’Y’
– полярный угол в системе OXY

32.

По формулам перехода от полярных координат к
прямоугольным:
x cos
y sin
⇒
Так как
то
x cos cos sin sin
y sin cos cos sin
x cos
y sin
x x cos y sin
y x sin y cos
определяет
старые
координаты (x;y) через новые
(x’;y’)

33.

Выведем формулу, которая позволяет выразить новые координаты
через старые:
x x cos y sin
y x sin y cos
cos
sin
sin
cos
x
y
x sin
y
cos
cos
x
sin
y
Найдем x’ и y’
cos 2 sin 2 1
x cos y sin x
y cos x sin y
так
как
так как
x
x
y
y

34.

Итак:
x x cos y sin
y y cos x sin
(1) определяет
координаты
(x’;y’)
старые (x;y)
новые
через

35. Поворот системы координат

Преобразование (1) в матричных обозначениях имеет
вид
X R2 X
x
X
y
x
X
y
cos
R2
sin
sin
cos
Преобразование (2) в матричных
обозначениях имеет вид
X R2 X
Матрица вращения
плоскости

36.

Новые оси повернуты относительно старых на угол α=π/4
Найти выражения старых координат произвольной точки
плоскости (х;у) через её новые координаты (x’;y’)
cos
4
sin
4
2
2
x x cos y sin
y x sin y cos
⇒
2
2
2
x y
x
y
x
2
2
2
y 2 x 2 y 2 x y
2
2
2

37.

Найти координаты точки Р в новой системе,
повернутой относительно старой на угол α=π/6 , если
её координаты в старой системе равны (-2;3).
Имеем:
P( 2;3)
cos
6
3
2
sin
6
1
2
x 2 , y 3 (OXY )
P( x ; y ) в (O X Y )
3
1 1
3 3 2 3
x x cos y sin 2
2
2 2
y y cos x sin 3 3 2 1 1 2 3 3
2
2 2

38.

Y’
~
Y
Y
~y
y
M
y’
x
x x0 ~
~
y
y
y
0
X’
x’
y0
j
0
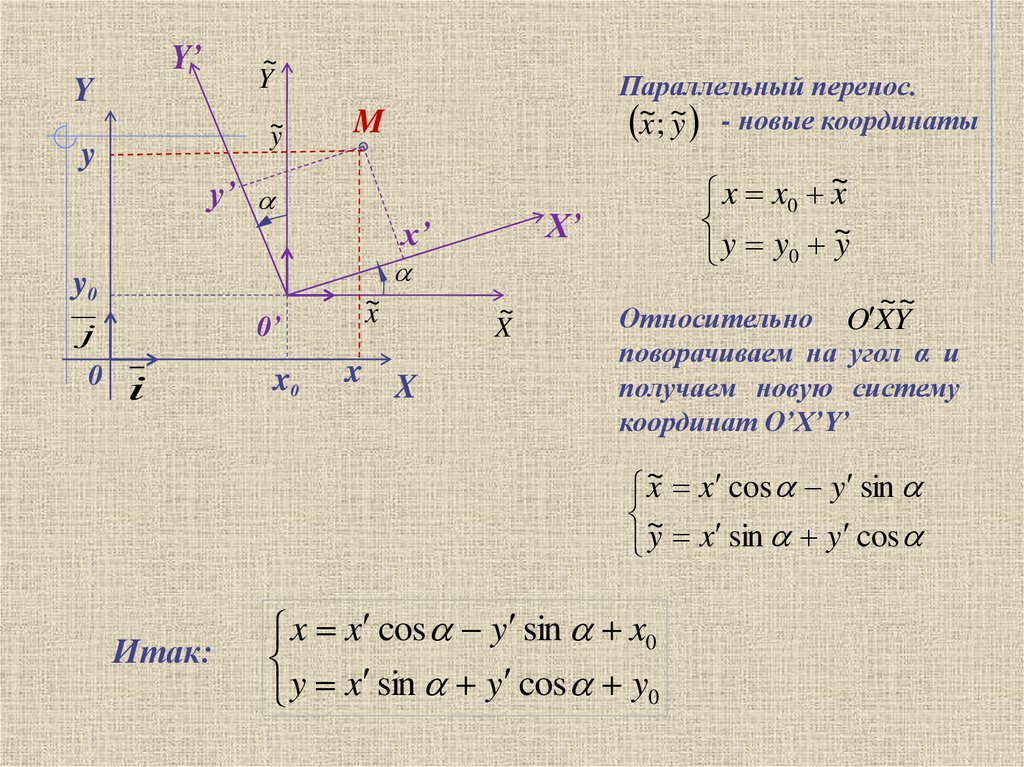
Параллельный перенос.
~x ; ~y - новые координаты
i
0’
~
x
x0
x X
~
X
~~
Относительно O XY
поворачиваем на угол α и
получаем новую систему
координат O’X’Y’
x x cos y sin
~
~
y x sin y cos
Итак:
x x cos y sin x0
y x sin y cos y0

39.

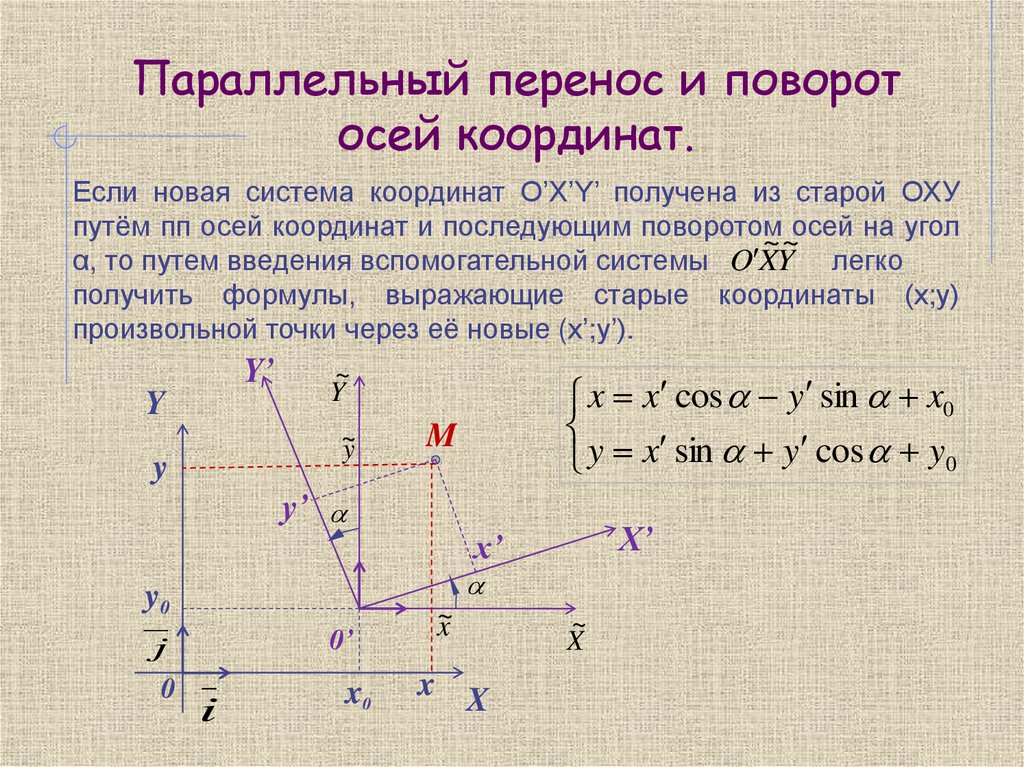
Параллельный перенос и поворот
осей координат.
Если новая система координат O’X’Y’ получена из старой ОХУ
путём пп осей координат и последующим поворотом осей на угол
~~
α, то путем введения вспомогательной системы O XY легко
получить формулы, выражающие старые координаты (х;у)
произвольной точки через её новые (x’;y’).
Y’
Y
~
Y
~y
y
x x cos y sin x0
y x sin y cos y0
M
y’
X’
x’
y0
j
0’
~
x
0
x0
x X
i
~
X