Преобразование координатного базиса

1.

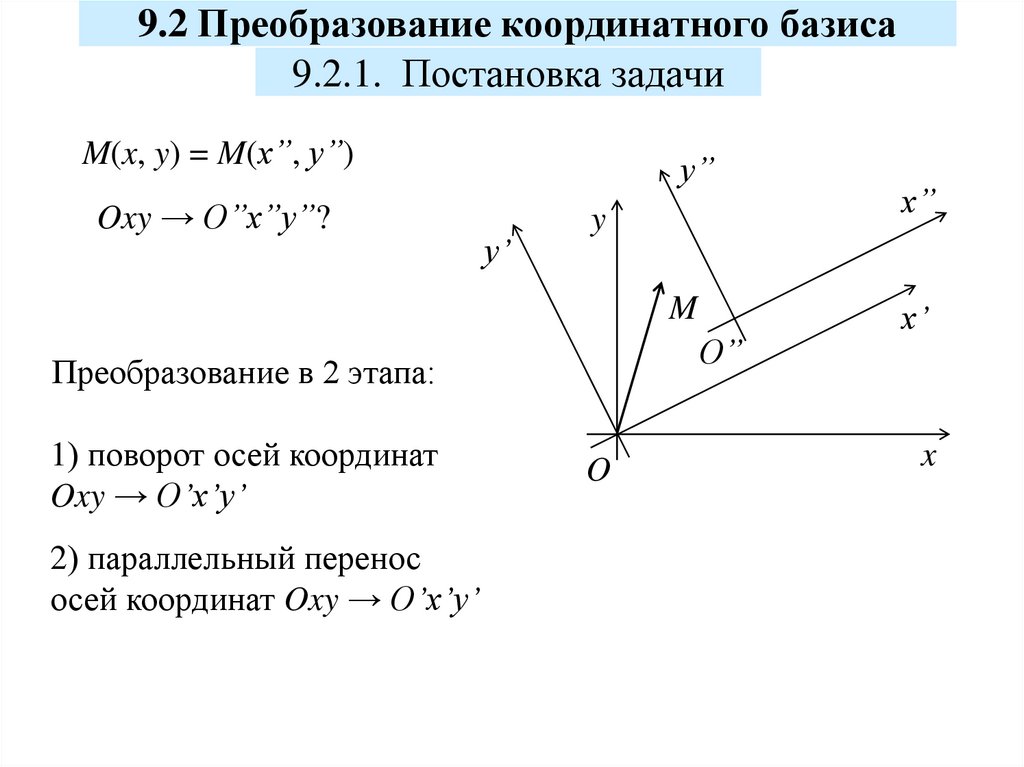
9.2 Преобразование координатного базиса
9.2.1. Постановка задачи
M(x, y) = M(x”, y”)
Oxy → O”x”y”?
y”
y’
y
M
O”
Преобразование в 2 этапа:
1) поворот осей координат
Oxy → O’x’y’
2) параллельный перенос
осей координат Oxy → O’x’y’
O
x”
x’
x

2.

9.2.2. Поворот осей координат
Радиус-вектор точки не меняется:
OM = r = r’
y’
но координаты различны:
r = xi + yj
r’ = x’i’ + y’j’
xi + yj = x’i’ + y’j’
∙i:
∙j:
y
M
φ
r
j
i’ φ
j’
i
O
x’
x
xii + yji = x’i’i + y’j’i
xij + yjj = x’i’j + y’j’j
x = x’cosφ + y’cos(900+φ)
y = x’cos(900-φ) + y’cosφ
x = x’cosφ +
+ y’(cos900 cosφ - sin900 sinφ)
y = x’(cos900 cosφ + sin900 sinφ)
+ y’cosφ
y = x’sinφ + y’cosφ
x = x’cosφ - y’sinφ

3.

Получаем систему уравнений:
или, в матричном виде:
или, ещё короче:
r T r ',
Свойства матрицы поворота:
1. det(Tφ) = 1 при любом φ.
cos
2. T
sin
3. Tα∙Tβ = Tβ∙Tα
1
4. Tα+β = Tα∙Tβ
sin
T
cos
x x 'cos y 'sin
y x 'sin y 'cos
x cos
y sin
sin x '
cos y '
где Tφ - матрица поворота

4.

9.2.3. Параллельный перенос осей координат
O’x’y’ → O”x”y”?
y”
y’
M
Пусть:
r’
x'
r ' - радиус-вектор точки М
y0
y
'
в исходной системе коор-т
x"
r " - радиус-вектор точки М
O’
y " в новой системе коор-т
r0
r”
O”
x0
x0
r0 - радиус-вектор начала новой
y0 системы координат в старой
r ' r " r0
или
x ' x " x0
y ' y " y
0
или
x ' x " x0
y ' y " y0
x”
x’

5.

9.3 Квадратичная форма
9.3.1. Понятие квадратичной формы
Форма - однородный многочлен, все члены которого имеют
одинаковую степень.
Квадратичная форма - однородный многочлен второй степени:
F(x, y) = a11x2 + 2a12xy + a22y2.
Матрица квадратичной формы:
x
Пусть r .
y
F ( x, y ) r Ar x
T
a11
A
a12
a12
a22
Тогда:
a11
y
a12
a12 x
2
2
a
x
2
a
xy
a
y
.
11
12
22
a22 y

6.

Пример:
1 2
1 2 x
x
A
F ( x, y ) x y
x 3y 2x 4 y
3 4
3 4 y
y
x 3 y x 2 x 4 y y x 2 3xy 2 xy 4 y 2 x 2 5 xy 4 y 2
9.3.2. Геометрический смысл квадратичной формы
Пусть x, y - координаты точки на плоскости. Тогда
F(x, y) = c или
a11x2 + a12xy + a22y2 = c или
a11x2 + a12xy + a22y2 + c’ = 0 - уравнение кривой 2-го порядка.

7.

9.3.3. Собственный вектор и собственное число
Пусть
a11
A
a12
a12
a22
x
r .
y
A∙r = R - некоторый вектор. Пусть существует такой вектор r,
что R = λr, т.е. A∙r = λr. Такой r называется собственным.
Для собственного вектора: A∙r || r.
Очевидно, если A∙r = λr, то A∙(αr) = λ(αr), где α - число ≠ 0.
Т.е. вектор (αr) будет также собственным. Т.е. собственный
вектор задаётся с точностью до константы и определяет
некоторое направление.

8.

9.3.4. Геометрический смысл собственного вектора
Пусть F(x, y) = a11x2 + a12xy + a22y2 – квадратичная форма.
Тогда a11x2 + a12xy + a22y2 = c – уравнение кривой 2-го порядка.
F
F
dx
dy.
Полный дифференциал: dF ( x, y )
x
y
=> 2(a11x + a12y)dx + 2(a12x + a22y)dy
y
n
dr
a11 a12 x
dx dy
0
a12 a22 y
или dr·A·r = 0
Обозначим A·r = n
x
dr
n
n || r на осях симметрии => в этих точках n = λr или A∙r = λr

9.

9.3.5. Вычисление собственных векторов и
собственных чисел
Итак, пусть A∙r = λr => A∙r – λr = 0 или
a11
a12
a12
1 0 x 0
a22
0 1 y 0
(a11 ) x a12 y 0
a12 x (a22 ) y 0
Система имеет ненулевое решение, если
a11
a12
a12
1 0
0
a22
0 1
a11
a12
a12
a22
0
или, в матричном виде:
A E 0 - характеристическое уравнение на нахождение λ.
Полученные λi подставляем в исходную систему и находим
собственные вектора ri. Проверяем результат: r1∙r2 = 0.

10.

Пример:
Найти: Собственные числа и собственные векторы для
квадратичной формы F(x, y) = 5x2 + 4xy + 2y2.
Составляем матрицу и
характеристическое уравнение:
Решаем харак-ое уравнение:
5 2
A
,
2 2
4 x 2 y 0
2 1:
2x y 0
2
2
2
0
2 7 6 0 1 6, 2 1.
(5 ) x 2 y 0
2 x (2 ) y 0
Выбираем y1 = 1, r 2 Проверяем:
1
1
находим x1 = 2
r1∙r2 =
= 2∙1+1∙(-2) =
1
Выбираем x2 = 1, r
2
2 = 0
находим y2 = -2
Составляем систему для
нахождения собственных векторов:
x 2 y 0
1 6 :
2x 4 y 0
5

11.

9.3.6. Теоремы о собственных векторах
Теорема 1. Для симметричной матрицы существуют
собственные числа и собственные векторы.
Теорема 2. Собственные векторы симметричной матрицы,
соответствующие различным собственным числам, ортогональны.
Замечание. Для матрицы второго порядка достаточно найти один
собственный вектор. Второй можно найти из условия: r1∙r2 = 0.
x1
Пусть r1 .
y1
Тогда
y1
r2
.
x1

12.

9.3.7. Матрица поворота
Главное направление квадратичной формы - это направление
осей симметрии соответствующей кривой 2-го порядка.
x1
x2
Пусть λ1 ≠ λ2. Им соответствуют векторы: r1 , r2
y1
y2
x1
x2
r1
r2
1
1
, e2
Нормируем их: e1
2
2
2
2 y
y
r1
r
x1 y1 1
x2 y2 2
2
x1
e1x
x y
2
1
y
y’
φ e1y
e2
e1
O
x’
φ
e1x
x
2
1
cos , e1 y
y1
x y
2
1
2
1
sin .
cos
sin
e1
, e2
.
sin
cos
(e1|e2) образуют матрицу поворота
к главным направлениям кв.формы:
cos
T
sin
sin
cos

13.

9.3.8. Приведение квадратичной формы к
каноническому виду
Дана квадратичная форма F(x, y) = a11x2 + a12xy + a22y2 .
Нужно привести её к каноническому виду: F(x, y) = λ1x2 + λ2y2.
1 0
.
Матрица квадратичной формы: A
0 2
Теорема 1. Каждая квадратичная форма имеет единственный
канонический вид.
Теорема 2. При повороте координатных осей до главных
направлений квадратичная форма принимает канонический вид
с коэффициентами, равными собственным числам.

14.

Как привести квадратичную форму к каноническому виду:
1. Составить матрицу A.
2. Найти собственные числа λ1 и λ2.
3. Записать квадратичную форму в каноническом виде:
F(x, y) = λ1x2 + λ2y2.
Для нахождения угла поворота к главным направлениям
вычисляем нормированный собственный вектор e1.
9.3.9. Геометрический смысл приведения
Приведение к каноническому виду геометрически означает
поворот осей координат до главных направлений кв. формы.
При этом:
1. λ1 и λ2 - одного знака: кв. форма эллиптического типа.
2. λ1 и λ2 - разного знака: кв. форма гиперболического типа.
3. λ1 = 0 или λ2 = 0: кв. форма параболического типа.