Похожие презентации:
Линейная алгебра. Курс лекций
1.
Министерство образования и науки Республики КазахстанКарагандинский государственный университет им. Е.А. Букетова
Факультет математики и информационных технологий
Кафедра алгебры, математической логики и геометрии
имени профессора Т.Г.Мустафина
Математика-I
Авторы: Макажанова Т.Х., к.ф.-м.н., доцент
Ульбрихт О.И., старший преподаватель
Вид занятий: лекция
Караганда 2016
2.
Тематика курсаТема
1. Матрицы и операции над ними.
Тема 2. Определители. Миноры и
алгебраические дополнения. Обратная матрица.
Тема 3. Системы линейных уравнений и методы
их решения.
Тема 4. Комплексные числа.
Тема 5. Многочлены степени п.
3.
Тематика курсаТема
6. Векторы и операции над ними.
Координаты точек и векторов.
Тема 7. Скалярное, векторное и смешанное
произведение векторов.
Тема 8. Прямая на плоскости.
Тема 9. Прямая в пространстве.
Тема 10. Плоскость в пространстве.
Тема 11. Смешанные задачи на прямую и
плоскость в пространстве.
Тема 12. Кривые второго порядка, заданные
канонически.
4.
Матрицы и операции над нимиТема 1
5.
ПЛАН1.
2.
3.
4.
5.
Определение матрицы. Виды матриц.
Операции над матрицами.
Свойства матричных операций.
Транспонирование матрицы.
Свойства операции транспонирования.
ЛИТЕРАТУРА
6.
7.
8.
9.
Курош А.Г. Курс высшей алгебры. - М.: Наука,
1975.
Кострикин А.И. Введение в алгебру. Физматлит, 2001.
Окунев Л.Я. Высшая алгебра. - М., 1966.
Ильин В.А., Поздняк Э.Г. Линейная алгебра. Уч.
пос., 3-изд. доп. М., Наука, 1999.
6.
Определение матрицы. Видыматриц
Матрицей размера m×n называется таблица чисел,
содержащая m строк и n столбцов. Числа, составляющие
матрицу, называются элементами матрицы. Место
каждого элемента однозначно определяется номером
строки и столбца, на пересечении которых он находится.
Элементы матрицы обозначаются aij, где i - номер
строки, а j - номер столбца.
a11
a 21
Обозначение: A
...
a m1
a12
a 22
...
am 2
... a1n
... a 2 n
или A aij m n .
... ...
... a mn
7.
Матрица может состоять как из одной строки, так ииз одного столбца. Вообще говоря, матрица может
состоять даже из одного элемента.
Матрицу, имеющую только одну строку, называют
матрицей-строкой.
( a11 a12 ... a1n ) - матрица-строка.
Матрицу, имеющую только один столбец, называют
матрицей-столбцом.
a11
a12
... - матрица-столбец.
an1
Будем считать две матрицы равными, если эти
матрицы имеют одинаковые порядки и все их
соответствующие элементы совпадают.
8.
Если число столбцов матрицы равно числу строк (m =n), то матрица называется квадратной, а число n
называется порядком квадратной матрицы.
a11 a12 a1n
a21 a22 a2 n
(1)
- квадратная матрица.
an1 an 2 a nn
В случае квадратной матрицы вводятся понятия
главной и побочной диагоналей.
Главной диагональю матрицы (1) называется
диагональ а11 а12 … ann идущая из левого верхнего угла
этой матрицы в правый нижний ее угол.
Побочной диагональю матрицы (1) называется
диагональ аn1 а(n-1)2 … a1n , идущая из левого нижнего
угла в правый верхний угол.
9.
Если все недиагональные элементыматрицы равны нулю, то матрица
диагональной:
0 ... 0
a11
0 a 22 ... 0
... ... ... 0 .
0 ... a nn
0
квадратной
называется
Квадратная матрица называется скалярной, если на
главной диагонали стоит одно и то же число k, а все
элементы вне этой диагонали равны нулю:
k 0 ... 0
0 k ... 0
... ... ... 0
0 0 ... k
10.
Если у диагональнойдиагональные элементы
называется единичной
обозначается буквой Е:
1
0
Е=
...
0
матрицы n-го порядка все
равны единице, то матрица
матрицей n-го порядка и
0
1
...
0
... 0
... 0
.
... ...
... 1
Матрица любого размера называется нулевой, или
нуль-матрицей, если все её элементы равны нулю:
0 0 ... 0
0 0 ... 0
O
.
... ... ... ...
0 0 ... 0
11.
Операции над матрицамиСложение и вычитание матриц определены только для
матриц одинакового размера.
Пусть A aij m n и B bij m n .
Суммой (разностью) матриц А и В является матрица
C cij m n (С = А ± В), элементами которой являются
соответственно сумма (разность) элементов исходных
матриц, т.е. cij aij bij , i 1, m, j 1, n.
1 2
2 3
Пример 1. Найти А+В, если A
и B
.
4 3
4 5
1 2 2 3 1 2 2 3 3 5
A B
.
4 3 4 5 4 4 3 5 8 8
12.
Операция умножения (деления) матрицы любогоразмера на произвольное число сводится к умножению
(делению) каждого элемента матрицы на это число:
a11
a 21
A
...
a m1
a12
a 22
...
a m 2
... a1n
... a 2 n
.
...
...
... a mn
1 2
Пример 2. Найти 5А, если A
.
3 4
1 2 5 1 5 2 5 10
5 A 5
.
3 4 5 3 5 4 15 20
13.
Произведение двух матриц определено, когда числостолбцов первой матрицы равно числу строк второй.
Пусть A aij m k и B bij k n . Произведением матриц
А и В называется матрица C cij m n (С=АВ), элементы
которой cij ai1b1 j ai 2 b2 j ... aik bkj , i 1, m, j 1, n.
2
Пример 3. Найти АВ, если A
3
4
3 1
и B 5
2 1
6
4 6
2 3 1
A B
5 4
3 2 1
6 5
2 4 3 5 1 6 2 6 3 4 1 5 29 29
.
3 4 2 5 1 6 3 6 2 4 1 5 28 31
6
4 .
5
14.
Свойства матричных1)операций
А+В=В+А
2) (А+В)+С=А+(В+С)
3) А+О=О+А=А
4) 1А=А1=А
5) 0А=А0=О; λО=Оλ=О
6) λ(μА)=(λμ)А
7) (λ+μ)А=λА+μА
8) λ(А+В)=λА+λВ
9) λ(АВ)=(λА)В
15.
Свойства матричныхопераций
10)
(А+В)С=АС+ВС
11) А(В+С)=АВ+АС
12) А(ВС)=(АВ)С
13) АЕ=ЕА=А
14) Если произведение АВ существует, то ВА может и
не существовать.
15) Если даже АВ и ВА существуют, то они могут быть
матрицами разных размеров.
16) В случае, когда АВ и ВА существуют и оба –
матрицы одинакового размера, вообще говоря, АВ ВА.
17) Из того, что АВ=0, не следует, что А=0, или В=0.
16.
Транспонирование матрицыa11 a12 ... a1n
a21 a22 ... a2 n
Рассмотрим матрицу A
.
... ... ... ...
as1 as 2 ... asn
Транспонированной матрицей к матрице А
T
называется матрица A , получающаяся из А заменой
строк столбцами:
a11 a 21 ... a s1
a12 a 22 ... a s 2
T
A
... ... ... ...
.
a
1n a 2 n ... a sn
17.
Пример4. Найти транспонированную матрицу
2 3 1
относительно матрицы A
.
3 2 1
2 3
T
A 3 2 .
1 1
18.
Свойства операциитранспонирования
1)
(АТ)Т = А
2)
(λА)Т = λАТ
3)
(А+В)Т = АТ+ВТ
4)
(АВ)Т = ВТАТ
19.
РезюмеПредставлены
основные
определения
и
операции
над
матрицами
и
их
свойства,
являющиеся базовыми в теории
матриц.
20.
Определители. Миноры иалгебраические дополнения.
Обратная матрица
Тема 2
21.
ПЛАН1.
2.
3.
4.
5.
6.
Определитель квадратной матрицы.
Свойства определителей.
Миноры и алгебраические дополнения.
Теорема о разложении определителя по строке (столбцу).
Обратная матрица и её свойства.
Матричные уравнения.
ЛИТЕРАТУРА
Курош А.Г. Курс высшей алгебры. - М.: Наука, 1975.
8. Кострикин А.И. Введение в алгебру. - Физматлит,
2001.
9. Окунев Л.Я. Высшая алгебра. - М., 1966.
10.Воеводин В.В. Линейная алгебра. Уч. пос. - М.,
Наука, 1980.
7.
22.
Определитель квадратной матрицыПусть А – квадратная матрица порядка п с числовыми
элементами:
a11
a21
A
...
an1
a12
a22
...
an 2
... a1n
... a2 n
.
... ...
... ann
Определитель (детерминант) квадратной матрицы А
– это число, которое ставится в соответствие матрице и
вычисляется по ее элементам согласно определённому
правилу.
Определитель матрицы А обозначается как:
det(A), |А| или Δ(A).
23.
Определителем матрицы A (a11 ) порядка n 1называется единственный элемент этой матрицы:
det A | a11 | a11 .
Определитель 2-го порядка можно вычислить по
формуле:
a11
a12
| A |
a11a22 a12a21.
a21 a22
1 2
Пример 1. Пусть A
, тогда
3 4
1 2
det A A
1 4 2 3 4 6 2 .
3 4
24.
Определитель 3 –го порядка:a11 a12 a13
| A | a21 a22 a23 a11 a22 a33 a12 a23a31 a13a21a32
a31 a32 a33
a13a22 a31 a12 a21a33 a11 a23 a32 .
Для запоминания приведённой формулы используется
правило
треугольников.
Схематически
правило
вычисления положительных и отрицательных членов
выглядит следующим образом:
25.
Можно также воспользоваться правилом Саррюса:к матрице приписать справа первый и второй
столбцы, вычислить произведения элементов, стоящих
на каждой из указанных шести прямых, а затем найти
алгебраическую сумму этих произведений, при этом
произведение элементов на прямых, параллельных
главной диагонали, берутся со знаком плюс, а
произведение элементов на прямых, параллельных
побочной диагонали – со знаком минус:
26.
Пример 2.2 3 1
Найти A , если A 2 4 3 .
1 2 3
2 3 1
det A A 2 4 3 2 4 3 3 3 1 1 2 2 1 4 1 2 3 2 3 2 3
1 2 3
24 9 4 4 12 18 3.
27.
Свойства определителейСвойство 1. Определитель
транспонировании.
не
меняется
при
Замечание. Из свойства 1 вытекает, что всякое
утверждение о строках определителя справедливо и для его
столбцов и обратно, т.е. что в определителе строки и
столбцы равноправны.
Свойство 2. Если одна из строк определителя состоит
из нулей, то определитель равен нулю.
Свойство 3. Если в определителе поменять две какиелибо строки местами, то определитель лишь изменит знак
на противоположный.
28.
Свойство 4. Определитель,одинаковые стоки, равен нулю.
содержащий
две
Свойство 5. Если все элементы некоторой строки
определителя умножить на некоторое число k, сам
определитель умножится на k. Отсюда следует, что если
все элементы какой-нибудь строки определителя имеют
общий множитель, то его можно вынести за знак
определителя.
Свойство 6. Определитель,
содержащий
пропорциональные строки, равен нулю.
две
29.
Свойство 7. Если все элементы i-ой строкиопределителя n-го порядка представлены в виде суммы
двух слагаемых aij b j c j , j 1,..., n , то определитель
равен сумме двух определителей, у которых все строки,
кроме i-ой – такие же, как и в заданном определителе, а
i-ая строка в одном из слагаемых состоит из элементов
b j , а в другом – из элементов c j .
Свойство 8. Если одна из строк определителя есть
линейная комбинация его других строк, то
определитель равен нулю.
Свойство 9. Определитель не меняется, если к
элементам одной из его строк прибавляются
соответственные элементы другой строки, умноженные
на одно и то же число.
30.
Миноры и алгебраические дополненияa11
a 21
A
...
Пусть
a
n1
a12
a 22
...
an2
... a1n
... a 2 n
... ...
квадратная матрица n-го
... a nn
порядка.
Минором Mij элемента aij определителя n-го порядка
называется
определитель
(n-1)-го
порядка,
получающийся после вычеркивания из определителя nго порядка i-ой строки и j-го столбца.
Алгебраическим дополнением Aij
элемента aij
определителя n-го порядка называется минор Mij
элемента aij , взятый со знаком (-1)i+j:
Aij ( 1) i j M ij .
31.
Пример 3.2 3 1
Пусть A 2 4 3 .
1 2 3
Тогда минор M 23 элемента a23:
2 3
M 23
4 3 1.
1 2
Алгебраическое дополнение элемента a23 :
3
2 3
52
A23 ( 1) M 23 ( 1)
(4 3) 1.
1 2
32.
Теорема о разложении определителяпо строке (столбцу)
Определитель n-го порядка d равен сумме
произведений всех элементов произвольной его строки
(столбца) на их алгебраические дополнения.
Т. е. имеет место следующее разложение определителя
d по i-ой строке:
d a i1 Ai1 a i 2 Ai 2 ... a in Ain .
Аналогичное
разложение
определителя
получить по любому его столбцу.
можно
33.
Пример 4. Вычислить определитель1 2 0 1
1 3 0 2
0 1 2 3
.
1 1 1 0
Разложим определитель по первой строке:
a11 A11 a12 A12 a13 A13 a14 A14 =
3 0 2
1 0 2
1 3 2
1 ( 1)1 1 1 2 3 2 ( 1)1 2 0 2 3 0 ( 1)1 3 0 1 3
1 1 0
1 1 0
1 1 0
1 3 0
1 ( 1)1 4 0 1 2 (0 0 2 4 0 9) 2 (0 0 0 4 0 3)
1 1 1
0 (1 6 0 0 0 2) 11 2 ( 7) 5 11 14 5 2.
34.
Определитель, у которого все элементы, находящиесявыше или ниже главной диагонали, равны нулю,
называется определителем треугольного вида.
Используя
свойства
определителей
всякий
определитель п-го порядка можно привести к
треугольному виду.
Теорема. Если
все
элементы
определителя,
расположенные по одну сторону от главной диагонали
равны нулю, то этот определитель равен произведению
элементов, стоящих на главной диагонали.
35.
Обратная матрица и еёсвойства
Квадратная матрица называется вырожденной (или
особенной), если её определитель равен нулю, и
невырожденной
(или
неособенной)
–
в
противоположном случае.
Обратной матрицей к квадратной матрице
называется такая матрица А-1 , что А-1А=АА-1 = Е.
А
36.
Теорема. Квадратная матрица А n-го порядкаимеет обратную матрицу А-1 , причем единственную,
тогда и только тогда, когда матрица А
невырожденная.
В этом случае обратная матрица вычисляется по
следующей формуле:
A11
1 A12
1
A
det A ...
A1n
A21
A22
...
A2 n
... An1
... An 2
,
... ...
... Ann
где Аij – алгебраическое дополнение элемента aij
матрицы А.
37.
Дляневырожденных
следующие свойства:
1.
(А-1)-1 = А
2.
(АВ)-1 = В-1А-1
3.
(А-1)Т = (АТ)-1
4.
det(A-1) = (detA)-1.
матриц
выполняются
38.
Матричные уравнения1) Рассмотрим матричное уравнение
A X B ,
(1)
где A – квадратная невырожденная (det A ≠ 0) матрица
порядка n, B – матрица размера n × m и X – неизвестная
матрица.
Умножим обе части уравнения слева на матрицу A−1:
A 1 ( A X ) A 1 B .
Ввиду ассоциативности умножения матриц, имеем:
( A 1 A) X A 1 B E X A 1 B X A 1 B
Таким образом, искомое решение матричного уравнения
(1) определяется формулой
X A 1 B .
39.
2) Рассмотрим матричное уравнениеY A B ,
(2)
где A – квадратная невырожденная (det A ≠ 0) матрица
порядка n, B – матрица размера m × n и Y – неизвестная
матрица.
Умножим обе части уравнения справа на матрицу A−1 .
По определению обратной матрицы и используя
свойство ассоциативности умножения матриц, получим:
(Y A) A 1 B Y 1 Y ( A A 1 ) B Y 1
Y E B Y 1 Y B Y 1
Таким образом,
уравнения (2):
искомое
решение
Y B Y 1 .
матричного
40.
3) Рассмотрим ещё один вид матричного уравнения:A X B C ,
(3)
где А, В и С – квадратные матрицы п-го порядка, А и В
– невырожденные, а С – произвольная. Умножим
сначала обе части уравнения слева на A 1 , получим:
A 1 ( A X B ) A 1 C ( A 1 A) X B A 1 C
E X B A 1 C X B A 1 C
Теперь умножим обе части полученного равенства
справа на B 1 :
X B B 1 A 1 C B 1 X E A 1 C B 1 X A 1 C B 1
Таким образом,
уравнения (3):
искомое
решение
X A 1 C B 1 .
матричного
41.
РезюмеВведены
понятия
определителя,
минора, алгебраического дополнения
и их свойства, играющие важную
роль
при
решении
систем
алгебраических
уравнений
и
использующиеся
при
изучении
аналитической геометрии.
42.
Системы линейных уравнений иметоды их решения
Тема 3
43.
ПЛАН1.
2.
3.
4.
5.
6.
7.
8.
Системы линейных алгебраических уравнений (СЛАУ) и их
решения.
Однородная система линейных уравнений.
Метод Крамера для решения СЛАУ.
Матричный метод решения СЛАУ.
Эквивалентные системы.
Элементарные преобразования систем.
Ступенчатая система.
Метод Гаусса для решения СЛАУ.
ЛИТЕРАТУРА
Курош А.Г. Курс высшей алгебры. - М.: Наука, 1975.
10.Кострикин А.И. Введение в алгебру. - Физматлит,
2001.
11.Окунев Л.Я. Высшая алгебра. - М., 1966.
12.Воеводин В.В. Линейная алгебра. Уч. пос. - М.,
Наука, 1980.
9.
44.
Системы линейныхалгебраических уравнений
Пусть данаи система
из т линейных уравнений
(СЛАУ)
их решения
с n
неизвестными:
a11 x1 a12 x2 .. a1n xn b1
a x a x .. a x b
21 1
22 2
2n n
2
(*)
..........................................
a m1 x1 a m 2 x2 .. a mn xn bm
a11 , a12 , ...,a mn
Здесь x1 , x 2 , ..., x n
– неизвестные,
–
коэффициенты системы и b1 , b2 , ...,bm – свободные
члены (предполагаются
известными).
Индексы
коэффициентов a ij
системы обозначают номера
уравнения i и неизвестного j, при котором стоит этот
коэффициент, соответственно.
45.
Решением системы (*) называется упорядоченнаясистема ( 1 , 2 ,..., n ) из n чисел, удовлетворяющих
этой системе. Эти числа при подстановке на место
соответствующих
переменных
обращают
все
уравнения системы в числовые равенства.
Если система имеет хотя бы одно решение, то она
называется совместной. Если не имеет ни одного
решения, то она называется несовместной.
Совместная система называется определенной, если
система имеет одно решение. Если совместная система
имеет больше одного решения, то она называется
неопределенной.
46.
Однородная системалинейных уравнений
Система линейных алгебраических уравнений, у
которой все свободные члены равны нулю, называется
однородной системой:
a11 x1 a12 x2 .. a1n xn 0
a x a x .. a x 0
21 1
22 2
2n n
.
..........................................
a s1 x1 a s 2 x2 .. a sn xn 0
Эта
система
всегда
совместна,
т.к.
x1 x2 ... xn 0 является (нулевым) решением.
47.
Метод Крамера для решенияСЛАУ
При определенных условиях решить систему можно с
помощью правила Крамера.
Теорема.
Пусть дана система
a11 x1 a12 x2 .. a1n xn b1
a x a x .. a x b
21 1
22 2
2n n
2
.
..........................................
an1 x1 an 2 x2 .. ann xn bn
48.
Еслиопределитель
матрицы
системы
a11 a12 ... a1n
a21 a22 ... a2 n
0 , то система имеет одно
... ... ... ...
an1 an 2 ... a nn
единственное решение, определяемое следующими
формулами (формулами Крамера):
xj
x j
, j 1,..., n , где - определитель матрицы
системы, а x j - определитель матрицы, полученной
из заменой j-го столбца столбцом свободных
членов.
49.
Пример 1. Решить систему с помощью формулКрамера:
x1 x2 x3 1
x1 2 x2 x3 2 .
3x x x 3
1 2 3
Выпишем определитель матрицы коэффициентов
системы:
1 1 1
1 2 1 2 1 3 6 1 1 2 0 , следовательно,
3 1 1
система имеет одно единственное решение, которое
можно найти по формулам Крамера.
50.
Имеем:1
x1 2
3
1
x2 1
3
1
x3 1
3
Тогда,
1
2
1
1
2
3
1
2
1
1
1 2 2 3 6 2 1 2 ;
1
1
1 2 3 3 6 3 1 2 ;
1
1
2 6 6 1 6 2 3 2 .
3
x1 2
x2 2
,
x1
1
x2
1,
2
2
x3
2
x3
1.
2
51.
Если, при решении системы линейных уравнений спомощью правила Крамера, мы приходим к тому, что
определитель системы равен нулю, буквально правило
Крамера применить нельзя. Однако можно точно сказать
о совместности системы.
При выводе правила Крамера мы переходим от
данных уравнений к уравнениям:
x1 x1 , x2 x2 , ……...., xn xn ,
являющимся их следствиями.
Отсюда видно, что если ∆ = 0, а хотя бы один из
определителей x1 , x 2 ,…, x n не равен нулю, то данная
система уравнений несовместна (противоречива) и если
все определители x1 , x 2 ,…, x n равны нулю, то
система неопределенна, т.е. имеет множество решений.
52.
Пример 2.Решить систему уравнений:
2 x y 3 z 9
3 x 5 y z 4 .
4 x 7 y z 5
Здесь мы имеем тот особый
определитель системы равен нулю:
случай,
когда
2 1 3
∆ = 3 5 1 = 2∙(–5)∙1 + (–7)∙3∙3 + 1∙(–1) ∙4 –
4 7 1
– 4∙(–5)∙3 – 3∙(–1) ∙1 – (–7)∙1∙2 = –10 – 63 – 4 + 60 + 3 + 14
= 0.
53.
Поэтому правило Крамера применить нельзя. Однако,подсчитав определитель x1:
9 1 3
x1 = 4 5 1 = 9∙(–5) ∙1 + (–7) ∙(–4) ∙3 + (–1) ∙1∙5 –
5 7 1
– 3∙(–5) ∙5 – (–4) ∙(–1) ∙1 – (–7) ∙1∙9 = –45 + 84 – 5+75–4+63
= –168,
видим, что он отличен от нуля. Откуда сразу можно
заключить, что система несовместна.
54.
Матричный метод решенияСЛАУ
Матричный метод также применим к решению
систем уравнений, где число уравнений равно числу
неизвестных.
Пусть дана система уравнений:
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1
22 2
2n n
2
...............................................
a n1 x1 a n 2 x2 ... a nn xn bn
55.
Составим матрицы:a11
a21
A=
...
an1
a12
a22
...
an 2
... a1n
... a2 n
;
... ...
... a nn
x1
x2
X = ;
...
xn
b1
b2
B = .
...
bn
Систему уравнений можно записать в виде
матричного уравнения:
A X = B.
Решая его, получим: A-1 A X = A-1 B, т.к. А-1 А = Е,
то Е Х = А-1 В и
Х = А-1 В.
56.
Пример 3.Решить систему матричным способом:
x1 x2 2 x3 5,
2 x1 x2 2 x3 3,
4 x x 4 x 9.
1
2
3
Выпишем матрицы:
1 1 2
x1
5
A 2 1 2 , X x2 , B 3 .
4 1 4
x
9
3
Решение системы запишется в виде X A 1 B .
57.
Имеем, A 16 2 4
1
0 4 2 , тогда
6
3 3
6
6 2 4 5
30 6 36
1
1
1
X A B 0 4 2 3 12 18
6
9 6 30 9 27
6
3
3
0 0
1
6 1 , откуда x1 0 , x2 1, x3 2 .
6
12 2
58.
Эквивалентные системыПусть даны системы:
a11 x1 a12 x 2 .. a1n x n b1
a x a x .. a x b
21 1
22 2
2n n
2
..........................................
a s1 x1 a s 2 x 2 .. a sn x n bs
a'11 x1 a '12 x 2 .. a '1n x n b'1
a' x a' x .. a' x b'
21 1
22 2
2n n
2
..........................................
и
a' s1 x1 a' s 2 x 2 .. a ' sn x n b' s
(1)
(2)
Две системы (1) и (2) с одинаковым количеством
переменных
называются
эквивалентными
(равносильными), если обе системы несовместны или обе
совместны и обладают одними и теми же решениями.
59.
Элементарныепреобразования систем
1. Перемена мест двух уравнений в системе;
2. Умножение обеих частей уравнения на число, отличное
от 0;
3. Прибавление к частям какого-нибудь уравнения
соответствующих
частей
другого
уравнения,
предварительно умноженных на какое-нибудь число;
4. Выбрасывание уравнения вида 0=0;
5. Перемена мест двух слагаемых во всех уравнениях
системы.
Теорема. При элементарных преобразованиях
система приводится к эквивалентной системе.
60.
Ступенчатая системаСистема называется ступенчатой, если каждое
уравнение имеет хотя бы 1 отличный от 0 коэффициент
или свободный член и, начиная со 2-го уравнения, 1-ое
отличное от 0 слагаемое расположено правее 1-го
отличного от 0 слагаемого предыдущего уравнения:
a11 x1 a12 x2 ............ a1n xn b1 ,
a22 x2 ........... a2 n xn b2 ,
..................................
a ss x s ... a sn xn bs
Теорема. Всякая система линейных уравнений при
помощи элементарных преобразований приводится к
равносильной ступенчатой системе.
61.
Метод Гаусса для решенияСЛАУ
Метод Гаусса может быть применен к системам
линейных уравнений с произвольным числом
уравнений и неизвестных.
Суть метода заключается в последовательном
исключении
неизвестных,
когда
с
помощью
элементарных преобразований система уравнений
приводится к равносильной системе ступенчатого (или
треугольного) вида, из которой последовательно,
начиная с последних (по номеру) переменных,
находятся все остальные переменные.
62.
Рассмотрим систему линейных уравнений:a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1
22 2
2n n
2
...............................................
am1 x1 am 2 x2 ... amn xn bm
(*)
Разделим обе части 1–го уравнения на a11 0,
затем: 1) умножим на а21 и вычтем из второго
уравнения; 2) умножим на а31 и вычтем из третьего
уравнения и т.д.
63.
Получим:x1 d12 x2 ... d1n xn d1
d x d x ... d x d
22 2
23 3
2n n
2
,
..............................................
d m 2 x2 d m 3 ... d mn xn d m
где d1j = a1j /a11, j = 2, 3, …,n+1;
dij = aij – ai1d1j , i = 2, 3, … , n;
j = 2, 3, … , n+1.
Далее повторяем эти же действия для второго
уравнения системы, потом – для третьего и т.д., пока
не получим равносильную систему ступенчатого (или
треугольного) вида.
64.
При этом система будет несовместной, если впроцессе преобразований мы получим уравнение, в
котором коэффициенты при всех неизвестных равны
нулю, а свободный член отличен от нуля, в противном
случае система будет совместной.
Совместная система уравнений будет
определённой, если она приводится к треугольному
виду, и неопределённой, если приводится к
трапецоидальному виду, в котором число уравнений
меньше числа неизвестных.
65.
Пример. Решить систему линейных уравненийметодом Гаусса:
2 x1 x2 x3 5
x1 2 x2 3 x3 3
7 x x x 10 .
1
2
3
Решение. Составим расширенную матрицу системы:
2 1 1 5
A = 1 2 3 3
7 1 1 10
и приведём её к ступенчатому виду.
66.
Для этого поменяем местами первую и вторуюстроки, затем от второй строки вычтем первую,
умноженную на 2, а от третьей строки вычтем первую,
умноженную на 7. В полученной матрице от третьей
строки отнимем вторую, умноженную на 3. Получим:
2 1 1 5 1 2 3 3
A = 1 2 3 3 ~ 2 1 1 5 ~
7 1 1 10 7 1 1 10
3
3 1 2 3 3
1 2
~ 0 5
7 11 ~ 0 5 7 11
0 15 22 31 0 0 1 2 .
67.
Таким образом, исходная система может бытьпредставлена в виде:
x1 2 x2 3 x3 3
,
5 x2 7 x3 11
x 2
3
откуда получаем: x3 = 2, x2 = 5, x1 = 1.
68.
РезюмеРассмотрены
основные
методы
решения
системы
линейных
алгебраических
уравнений,
использующиеся
в
линейной
алгебре и некоторых вопросах
аналитической геометрии.
69.
Комплексные числаТема 4
70.
ПЛАН1.
2.
3.
4.
5.
Алгебраическая форма комплексного числа.
Геометрическое изображение и тригонометрическая форма
комплексного числа.
Действия над комплексными числами, записанными в
тригонометрической форме. Формула Муавра.
Извлечение корня п-ой степени из комплексного числа. Корни из
единицы. Первообразные корни.
Показательная форма комплексного числа.
ЛИТЕРАТУРА
6.
7.
8.
9.
Курош А.Г. Курс высшей алгебры. - М.: Наука, 1975.
Кострикин А.И. Введение в алгебру. - Физматлит,
2001.
Окунев Л.Я. Высшая алгебра. - М., 1966.
Ван дер Варден Б.Л. Алгебра. -М.: Наука, 1976.
71.
Алгебраическая формакомплексного числа
Комплексным числом z называется выражение вида
z a bi , где a и b – действительные числа, i – мнимая
единица, которая определяется соотношением i 2 1.
При этом число a называется действительной частью
комплексного числа z (a = Re z), а b - мнимой частью
числа z (b = Im z).
Если a =Re z =0, то число z=bi будет чисто мнимым,
если b = Im z = 0, то число z=a будет действительным.
Множество
символом C.
комплексных
чисел
обозначается
72.
Каждое действительное число a можно представить ввиде a = a+0 i. В частности, 0=0+0 i, 1=1+0 i. Таким
образом, всякое действительное число является
комплексным, т.е. множество комплексных чисел
расширяет множество действительных чисел: R C.
Числа z a bi и z a bi называются комплексно –
сопряженными.
Два комплексных числа z1 a1 b1i и z 2 a2 b2i
называются равными, если соответственно равны их
действительные и мнимые части: a1 a2 ; b1 b2 ;
Комплексное число равно нулю, если соответственно
равны нулю действительная и мнимая части: a b 0.
73.
Сложение, умножение, вычитание и делениекомплексных чисел, записанных в виде a bi ,
производятся следующим образом:
(a bi ) (c di ) (a c) (b d )i ;
(a bi ) (c di ) (a c) (b d )i ;
(a bi ) (c di ) (ac bd ) (ad bc)i ;
a bi ac bd bc ad
2
2
i.
2
2
c di c d
c d
74.
Примеры.1)
(2 5i ) (1 7i ) (2 1) (5 7)i 3 2i ;
2)
(3 9i ) (7 i ) (3 7) ( 9 1)i 4 10i ;
3)
(1 2i )(3 i ) 3 i 6i 2i 2 3 5i 2 5 5i ;
23 i (23 i )(3 i ) 69 23i 3i i 2
2
i
1
4)
2
2
3 i
(3 i )(3 i )
3 i
69 20i 1 70 20i
7 2i .
9 1
10
75.
Геометрическое изображение итригонометрическая форма
комплексного числа
Понятие комплексного числа имеет геометрическое
истолкование.
Если любое действительное число может быть
геометрически представлено в виде точки на числовой
прямой, то комплексное число a bi представляется
точкой на плоскости A(a, b) , координатами которой
являются соответственно действительная и мнимая
части комплексного числа. При этом горизонтальная
ось Ox , на которой расположены действительные
числа a a 0 i называется действительной осью, а
вертикальная Oy, на которой расположены чисто
мнимые числа bi 0 bi – мнимой осью.
76.
yA(a,b)
r
0
b
a
x
С каждой точкой A(a, b) комплексной плоскости
связан радиус-вектор этой точки OA , длина которого r
называется модулем комплексного числа z и
обозначается | z |. Угол , образованный радиусвектором OA с осью Ox, называется аргументом
комплексного числа z и обозначается Arg z. Из значений
= Arg z выделяется главное значение Аrg z,
удовлетворяющее условию - Аrg z .
77.
Из геометрических соображений видно, чтоa r cos ; b r sin . Тогда комплексное число
можно
представить
в
виде:
z a bi
z r cos ir sin или
z r (cos i sin ) .
Такая
форма
записи
называется
тригонометрической формой комплексного числа.
При этом
a
cos r ,
2
2
r | z | a b 0 ,
или
b
sin .
r
b
Arg z arctg .
a
78.
Пример 1. Пример. Найти модуль и аргументкомплексного числа 1 i 3 . Записать это число в
тригонометрической форме.
В нашей задаче a = –1, b 3 , тогда
3
1
2
2
sin
. Отсюда
r ( 1) 3 2; cos ,
2
2
2
.
3
Решение.
Теперь
запишем
тригонометрическую форму
2
2
комплексного числа: 1 i 3 2 cos i sin .
3
3
79.
Действия над комплекснымичислами, записанными в
тригонометрической форме.
Формула
Муавра
Пусть z1 r1 (cos
1 i sin 1 ) , z 2 r2 (cos 2 i sin 2 ).
Тогда
z z1 z2 r1r2 ((cos 1 cos 2 sin 1 sin 2 )
i (sin 1 cos 2 cos 1 sin 2 ))
r1r2 (cos( 1 2 ) i sin( 1 2 ))
z1 r1 cos 1 i sin 1
z
z 2 r2 cos 2 i sin 2
r1 (cos 1 i sin 1 )(cos( 2 ) i sin( 2 ))
r2
(cos 2 i sin 2 )(cos 2 i sin 2 )
r1
(cos( 1 2 ) i sin( 1 2 )) ( r2 0) .
r2
80.
Из операцииследует, что
умножения
комплексных
z 2 zz r 2 (cos 2 i sin 2 )
В общем случае получим формулу Муавра:
z n r n (cos n i sin n ) ,
где n – целое положительное число.
чисел
81.
Пример 2.1 i 3 cos i sin
Вычислить
.
2(1 i )
Решение. Представив числа 1 i 3 и 1 i в
тригонометрической форме и используя правила
умножения и деления комплексных чисел, записанных
в тригонометрической форме, получим:
82.
55
2 cos
i sin cos i sin
1 i 3 cos i sin 3
3
7
7
2(1 i )
2 2 cos
i sin
4
4
5
5
2 cos
i sin
3
3
7
7
2 2 cos
i sin
4
4
1
7
7
5
5
cos
i
sin
2
4
4
3
3
2
cos
i sin
.
2
12
12
83.
Извлечение корня п-ой степенииз комплексного числа. Корни из
единицы. Первообразные корни
Пусть z r (cos i sin ) .
n
z n r (cos i sin ) (cos i sin )
Возводя обе части равенства в степень п, получим:
n (cos n i sin n ) r (cos i sin )
Отсюда: n r ;
n
z n r (cos
n 2 k ; k Z . Тогда
2 k
2 k
i sin
), k 0, 1, 2, ..., n 1. (*)
n
n
При k = n, n+1, … значения корня уже будут повторяться.
84.
Таким образом, корень n – ой степени изкомплексного числа (не равного нулю) имеет n
различных значений.
Все значения корня n-ой степени расположены на
окружности радиуса n z с центром в нуле и делят эту
окружность на n равных частей.
85.
Пример 3. Найти корни уравнения z6+1=0.Решение. Данное уравнение можно переписать так:
z6 = –1 или z = 6 1. Число –1 в тригонометрической
форме имеет вид:
–1 = 1 (cos i sin ) , тогда корни исходного
уравнения
2 k
2 k
z k 1 cos
i sin
, где
6
6
k 0, 1, 2, 3, 4, 5 .
Придавая k последовательно знания 0, 1, …,5,
находим все шесть возможных корней данного
уравнения z6+1=0:
86.
3z 0 cos i sin i ,
6
6
2
z1 cos i sin i ,
2
2
5
5
3 1
z 2 cos
i sin
i,
6
6
2
2
7
7
3 1
z3 cos
i sin
i,
6
6
2 2
3
3
z 4 cos i sin
i ,
2
2
11
11
3 1
z5 cos
i sin
i.
6
6
2 2
87.
Особенно важен случай извлечения корня n-ой степенииз числа 1. Ввиду равенства 1 cos 0 i sin 0 и формулы
(*) все корни п-ой степени из единицы, даются
формулой:
n
1 cos
2 k
2 k
i sin
,
n
n
k 0, 1, 2, ..., n 1.
(**)
Этот корень имеет п различных значений, которые
обозначаются ε0, ε1, …, εn-1.
Все корни из 1 имеют модуль, равный 1, так что их
изображения находятся на окружности радиуса 1 с
центром в точке 0. Один из них при k 0 есть просто
число 1 и изображается точкой пересечения
положительной полуоси вещественной оси с единичной
окружностью.
88.
Теорема 1. Все значения корня n-ой степени изкомплексного числа z можно получить умножением
одного из этих значений на все корни n-ой степени
из единицы.
Теорема 2. Произведение двух корней п-ой
степени из единицы само есть корень п-ой степени из
единицы.
89.
Пример 4. Написать корни из единицы степени 4.Решение. Корень 4 1 имеет 4 различных значения.
Согласно формуле (**) имеем:
0 cos 0 i sin 0 1,
1 cos i sin i ,
2
2
2 cos i sin 1,
3
3
3 cos
i sin
i .
2
2
Итак, 4 1 1; i .
90.
Корень n-ой степени из единицы, который неявляется корнем из единицы никакой меньшей
степени, называется первообразным корнем n-ой
степени из единицы.
Теорема 3. Корень n-ой степени из единицы ε тогда
и только тогда будет первообразным, если его степени
εk, k = 0,1,…, n-1, различны, т.е. если ими
исчерпываются все корни n-ой степени из единицы.
91.
2 k2 k
i sin
есть
n
n
первообразный корень n-ой степени из 1 в том и только
том случае, если k и п взаимно просты.
Теорема
4.
Число
k cos
Теорема 5. Если p – простое число, то
первообразными корнями p-ой степени из 1 будут все
эти корни, кроме самой единицы.
92.
Примерстепени 6.
5.
Выписать
первообразные
корни
Решение. Целыми положительными числами,
меньшими 6 и взаимно простыми с ним являются 1 и
5, поэтому первообразными корнями степени 6
являются:
2
2
1
3
;
1 cos
i sin
cos i sin i
6
6
3
3 2
2
2 5
2 5
5
5 1
3
5 cos
i sin
cos
i sin
i
6
6
3
3 2
2
93.
Показательная формакомплексного числа
Показательная и тригонометрические функции в
области комплексных чисел связаны между собой
формулой
e i cos i sin ,
которая
носит
название формулы Эйлера.
Пусть комплексное число z в тригонометрической
форме имеет вид z r (cos i sin ) . На основании
формулы Эйлера выражение в скобках можно заменить
на показательное выражение. В результате получим
z re i .
Эта
запись
называется
показательной
формой комплексного числа. Здесь r | z |, arg z .
94.
При умножении и делении показательных функцийдействуют известные правила:
a
e
e a e b e a b , b e a b .
e
Поэтому
для
комплексных
z 2 r2 e i 2 умножение
следующим образом:
z1 z 2 r1r2 e
и
i ( 1 2 )
чисел
деление
,
(В последнем случае r2 0 ).
z1 r1e i 1 и
выполняются
z1 r1 i ( 1 2 )
e
.
z 2 r2
95.
Пример 6. Представить числопоказательной форме.
z (1 i ) 3 в
Решение. Вычислим модуль и аргумент числа
~z 1 i :
r | ~z | 12 12 2 ;
~
arg z arctg( 1) .
4
В показательной форме ~
z 2e
z ~z 3 2 2e
3
4
i
.
4
i
, следовательно,
96.
РезюмеПриведены основные результаты,
касающиеся комплексных чисел,
дана
их
алгебраическая
и
геометрическая интерпретация.
97.
Многочлены степени пТема 5
98.
ПЛАН1.
2.
3.
4.
5.
6.
Основные определения.
Деление многочленов с остатком.
Делимость многочленов. Свойства делимости.
НОД. Алгоритм Евклида.
Корни многочленов. Теорема Безу. Схема Горнера.
Кратные корни. Основная теорема алгебры.
ЛИТЕРАТУРА
Курош А.Г. Курс высшей алгебры. - М.: Наука,
1975.
8. Кострикин А.И. Введение в алгебру. Физматлит, 2001.
9. Окунев Л.Я. Высшая алгебра. - М., 1966.
10.Ван дер Варден Б.Л. Алгебра. -М.: Наука, 1976.
7.
99.
Основные определенияМногочленом (или полиномом) п-ой степени от
неизвестного х, называется выражение вида
a 0 x n a1 x n 1 ... a n 1 x a n ,
где a 0 , a1 , ... a n 1 , a n произвольные комплексные числа,
называемые коэффициентами многочлена, причём
a 0 0 ; п целое неотрицательное число, называемое
степенью многочлена.
Это выражение может состоять и из одного
слагаемого такой многочлен называется, естественно,
одночленом.
100.
nn 1
f
(
x
)
a
x
a
x
... an 1 x an
Пусть
0
1
произвольный многочлен. При a 0 0 коэффициент
a0 называют старшим коэффициентом многочлена
f (x ) , а сам одночлен a0 x n его старшим членом.
Коэффициент an называется свободным членом.
Степень многочлена f (x ) часто обозначается через
deg f ( x ) (от английского слова degree степень).
2
5
4
3
Например, deg( 2 x 3x ) 2 , deg(0 x 0 x x ) 3 .
101.
Если все коэффициенты многочлена f (x ) равны 0, мыбудем называть многочлен нулевым и обозначать его
символом 0.
Нулевой
многочлен
является
единственным
многочленом, степень которого не определена.
Если же f ( x ) a0 0 , многочлен f (x ) имеет степень
0, т.е. отличные от нуля комплексные числа являются
многочленами нулевой степени.
Многочлены
f ( x ) a0 x n a1 x n 1 ... an 1 x an ,
g ( x ) b0 x n b1 x n 1 ... bn 1 x bn
если коэффициенты при
совпадают: a0 b0 , …, an bn .
называются равными,
одинаковых степенях х
102.
Операции сложения и умножения многочленовn
n 1
f
(
x
)
a
x
a
x
... an 1 x an , a 0 0 ;
Пусть
0
1
g ( x ) b0 x k b1 x k 1 ... bk 1 x bk , b0 0 , n k .
1) Чтобы
выражении
сложить
два
многочлена,
нужно
f ( x ) g ( x ) a0 x n a1 x n 1 ... an b0 x k b1 x k 1 ... bk
в
привести подобные члены, представив его как некоторый
новый многочлен.
Cтепень суммы многочленов
наибольшей из степеней слагаемых.
не
превосходит
103.
2) Чтобы вычислить произведение многочленовf (x ) и g (x ) , нужно раскрыть скобки по обычным
правилам и в полученном выражении привести
подобные:
f ( x ) g ( x ) a0 x n a1 x n 1 ... an b0 x k b1 x k 1 ... bk
a0b0 x n k ( a0b1 a1b0 ) x n k 1 ... an bk .
Степень произведения двух ненулевых многочленов
равна сумме степеней сомножителей:
deg( f ( x ) g ( x )) deg f ( x ) deg g ( x ) .
104.
Деление многочленов состатком
Теорема (о делении многочленов с остатком).
Для любых двух многочленов f(x) и g(x) можно найти
такие многочлены q(x) и r(x), что f(x)=g(x)q(x)+r(x),
причем степень r(x) меньше степени g(x) или же
r(x)=0. Многочлены q(x) и r(x), удовлетворяющие
этому условию, определяются однозначно.
При этом q(x) называется (неполным) частным от
деления f(x) на g(x), r(x) – остатком от этого
деления.
Для нахождения частного и остатка так же, как при
делении целых чисел, применяют способ «деления
углом».
105.
Делимость многочленов.Свойства делимости
Пусть f(x) и g(x) ненулевые многочлены с
комплексными коэффициентами. Если остаток от
деления f(x) на g(x) равен нулю, то говорят, что f(x)
делится (или нацело делится) на g(x), при этом
многочлен g(x) называется делителем многочлена f(x).
Теорема. Многочлен g(x) тогда и только тогда будет
делителем многочлена f(x), если существует многочлен
q(x), удовлетворяющий равенству:
f(x) = g(x)q(x).
106.
Основные свойства делимости многочленовЕсли f (x ) делится на g (x ) , а g (x ) делится на
h(x ) , то f (x ) будет делиться на h(x ) .
1)
2) Если f (x ) и g (x ) делятся на h(x ) , то их сумма
и разность также делятся на h(x ) .
Если f (x ) делится на h(x ) , то произведение
f (x ) на любой многочлен g (x ) также будет делиться
на h(x ) .
3)
107.
4) Всякий многочлен f (x )многочлен нулевой степени.
делится на любой
Если f (x ) делится на h(x ) , то f (x ) делится и на
ch(x ), где с – произвольное число, отличное от нуля.
5)
6) Тогда и только тогда многочлены f (x ) и g (x )
одновременно делятся друг на друга, если g ( x ) cf ( x ) ,
c 0 .
7)
Всякий делитель одного из двух многочленов
f (x ) , cf (x ) , где c 0 , будет делителем и для другого
многочлена.
108.
НОД. Алгоритм ЕвклидаПусть f(x) и g(x) произвольные многочлены. Многочлен
h(x) называется общим делителем для f(x) и g(x), если он
служит делителем для каждого из этих многочленов.
Свойство 4) показывает, что к числу общих делителей
многочленов f(x) и g(x) принадлежат все многочлены
нулевой степени. Если других общих делителей эти два
многочлена не имеют, то они называются взаимно
простыми.
Наибольшим общим делителем отличных от нуля
многочленов f(x) и g(x) называется такой многочлен d(x),
который является их общим делителем и, вместе с тем,
сам делится на любой другой общий делитель этих
многочленов. Обозначается: d(x) = НОД (f(x), g(x)).
109.
Теорема. Любыедва
многочлена
наибольшим общим делителем.
обладают
Для нахождения НОД двух многочленов применим
алгоритм Евклида или алгоритм последовательного
деления.
Пусть даны многочлены f (x) и g (x) . Делим f (x) на
g (x) и получаем, вообще говоря, некоторый остаток
r1 ( x) . Делим затем g (x) на r1 ( x) и получаем остаток
r2 ( x ) , делим r1 ( x) на r2 ( x ) и т. д. Наибольшим общим
делителем многочленов f (x) и g (x) будет последний
отличный от нуля остаток rk (x ) , на который нацело
делится предыдущий остаток rk 1 ( x ) .
110.
Если d (x ) есть наибольший общий делительмногочленов f (x) и g (x) , то, как показывают свойства
6) и 7), в качестве наибольшего общего делителя этих
многочленов можно было бы выбрать также многочлен
сd (x ) , где с произвольное число, отличное от нуля.
Наибольший общий делитель двух многочленов
определён лишь с точностью до множителя нулевой
степени.
Теорема. Два многочлена тогда и только тогда
взаимно просты, если их наибольший общий делитель
равен единице.
111.
Корни многочленов. ТеоремаБезу. Схема Горнера
n
n 1
Если f ( x ) a 0 x a1 x ... a n 1 x a n есть некоторый
многочлен, а c некоторое число, то число
f ( c ) a 0 c n a1c n 1 ... a n 1c a n , полученное заменой в
выражении для f(x) неизвестного x числом с и
последующим выполнением всех указанных операций,
называется значением многочлена f(x) при x = c.
Если f(с) = 0, то с называется корнем многочлена f(x)
(или уравнения f(x)=0).
112.
Если мы будем делить многочлен f (x) напроизвольный многочлен первой степени (линейный
двучлен), то остаток будет некоторым числом r.
Теорема Безу. Остаток от деления многочлена f(x)
на линейный двучлен x–c равен значению f(с)
многочлена f(x) при x=c, т.е. f(x)=(x–c)q(x)+f(с).
Следствие. Число с является корнем f(x) тогда и
только тогда, когда f(x) делится на x–c (нацело).
113.
Деление многочлена f (x) на линейный двучлен( x c ) особенно удобно проводить при помощи метода
Горнера.
n
n 1
f
(
x
)
a
x
a
x
... a n 1 x a n и пусть
Пусть
0
1
f ( x ) ( x c ) q( x ) r ,
(*)
n 1
n 2
n 3
q
(
x
)
b
x
b
x
b
x
... bn 1 .
где
0
1
2
Сравнивая коэффициенты при одинаковых степенях х в
(*), получим:
a 0 b0 ,
a1 b1 cb0 ,
a 2 b2 cb1 ,
...................
a n 1 bn 1 cbn 2 ,
a n r cbn 1
b0 a 0 ,
bk cbk 1 a k ,
r cbn 1 a n ,
k 1, 2, ..., n 1.
114.
Таким образом, коэффициенты частного и остатокможно последовательно получать при помощи
однотипных вычислений, которые располагаются в
схему, называемую схемой Горнера:
с
a 0 a1 a 2 … a n 1 a n
b0 b1 b2 … bn 1
r
В
первой
строке
таблицы
расположены
коэффициенты многочлена f (x ) , а во второй –
соответствующие коэффициенты частного и остаток,
последовательно вычисляемые, а слева сбоку –
значение с.
115.
Пример.5
4
3
f
(
x
)
2
x
x
3
x
x 3 на x 3 .
Разделить
Решение. Деление проведём методом
Составим таблицу:
2 –1 –3 0
1
–3
3
2 5 12 36 109 324
Таким образом, искомое частное будет:
q x 2 x 4 5 x 3 12x 2 36x 109 ,
а остаток r f (3) 324 .
Горнера.
116.
Кратные корни.Основная теорема алгебры
Если с корень многочлена f (x ) , то f (x ) делится
на x c . Может оказаться, что многочлен f (x )
делится не только на первую степень линейного
двучлена x c , но и на более высокие его степени.
Если
f(x) = (x–c)k φ(x),
где φ(x) на x–c уже не делится, то с называется kкратным корнем f(x), а число k – кратностью корня
с.
Если k=1, то говорят, что корень с – простой.
117.
Основная теорема алгебры. Всякий многочленстепени n 1 с комплексными коэффициентами имеет
хотя бы один корень, в общем случае комплексный.
Следствие 1. Всякий многочлен f (x ) степени n≥1 с
комплексными коэффициентами раскладывается в
произведение п линейных множителей:
f ( x ) a0 ( x 1 )( x 2 )...(x n ) .
Это разложение единственно с точностью до порядка
сомножителей. Ясно при этом, что 1 , ..., n это корни
многочлена f (x ) .
Следствие 2. Всякий многочлен степени n≥1 с
комплексными коэффициентами имеет n корней, если
считать каждый корень столько раз, какова его
кратность.
118.
РезюмеПриведены
основные
свойства,
касающиеся
делимости
многочленов,
даны
основные
результаты,
связанные
с
нахождением корней многочленов.
119.
Векторы и операции над ними.Координаты точек и
векторов
Тема 6
120.
ПЛАН1.
2.
3.
4.
Линейные операции над векторами.
Базисы. Прямоугольные системы координат.
Свойства координат точек и векторов.
Полярная система координат.
ЛИТЕРАТУРА
5.
6.
7.
8.
Александров П.С. Лекции по аналитической
геометрии. – М., 1968.
Макажанова Т.Х., Муканов А.А., Медеубаев Н.К.
Практикум по аналитической геометрии. –
Караганда, КарГУ, 2003.
Погорелов А.В. Геометрия. – М., 1984.
Макажанова Т.Х., Муканов А.А., Ульбрихт О.И.
Аналитическая геометрия. Электронный учебник.
(2,5 Мб). –Караганда, 2011.
121.
Линейные операции надвекторами
Вектор – это направленный отрезок, т.е. отрезок прямой, у
которого указано, какой конец отрезка является началом, а
какой конец отрезка – концом вектора.
Для обозначения вектора используются символы
– это
вектор, у которого точка А – начало, точка В – конец вектора.
Могут обозначаться векторы и малыми буквами или а.
122.
Длинойвектора
называется длина отрезка,
изображающего этот вектор, направление определяется
указанием начала и конца вектора.
Параллельным переносом вектора
называется такое его
преобразование, когда в любой момент вектор
занимает
положение , при этом
.
Приложить вектор к точке О – это значит произвести такой
параллельный перенос этого вектора, чтобы его начало
попало в точку О.
123.
Два вектора а и b называются сонаправленными (илиодинаково направленными), если при приложении к одной
точке они лежат на одной прямой, а их концы находятся по
одну сторону от точки приложения. Обозначают
сонаправленность знаком
.
Векторы а и b называются противоположно направленными,
если при приложении к одной точке они лежат на одной
прямой, а их концы находятся по разные стороны от точки
приложения; обозначают противоположную направленность
знаком
.
124.
Сонаправленные и противоположно направленные векторыобразуют совокупность коллинеарных векторов; таким
образом, векторы коллинеарны, если при приложении к одной
точке они лежат на одной прямой. Обозначают коллинеарные
векторы знаком ||.
В общем случае коллинеарные векторы лежат на
параллельных прямых.
Вектор а называется параллельным прямой l (
), если
при приложении к какой-либо точке прямой l вектор а
целиком лежит на l.
Векторы называются компланарными, если при приложении
к одной точке они лежат в одной плоскости. В общем случае
они лежат на параллельных плоскостях.
125.
Вектор а компланарен плоскости (), если при
приложении к какой-либо точке плоскости вектор а лежит
на плоскости .
Два вектора называются равными, если у них равны длины и
совпадают направления.
Таким образом, векторы будут равны, если при приложении к
одной точке они совпадут.
Нулевым вектором 0 называют вектор нулевой длины, т.е.
вектор, у которого начало и конец совпадают. Направление
нулевого вектора не определено.
126.
Отношением двух коллинеарных векторов а и b,называется число, определяемое так:
,
Осью называется прямая, на которой задан ненулевой вектор
е, длина которого принята за единицу, а направление
считается положительным направлением на прямой. Вектор
е называется единичным вектором оси.
е
127.
Пусть вектор а лежит на оси (или на прямой, параллельнойоси), т.е.
. Координатой вектора а на оси, называется
число
, т.е.
Для векторов вводятся две линейные операции.
Пусть даны два вектора а и b.
128.
Приложим вектор к точке О, получим вектор,
приложим вектор b к точке А, получим вектор
тогда вектор
назовём суммой векторов
а и b:
.
Пусть задан вектор а и число . Произведением
вектора а на число называется вектор а,
определяемый следующим образом:
длина | а| = | | |a|;
а а, если 0 и
а а, если < 0.
,
129.
Замечания. 1) Всегда а || а, если, то
.
2) Пусть a|| b
), тогда
, где
.
3) Если имеется ось, то
, где
– координата
вектор на данной оси.
Свойства линейных операций.
1.
(коммутативность сложения):
2.
(ассоциативность сложения);
3. а + 0 = 0 + а;
4. ( а) = ( )а (ассоциативность умножения на число);
дистрибутивность;
5. ( + )а = а + а 6. (а + b) = а + b
7. 0 а = 0;
8. 0 = 0.
130.
Противоположным к вектору а называется вектор (– а),имеющий такую же, как и вектор а длину, но
противоположное вектору а направление. Нетрудно видеть,
что (– а) = (–1) а.
Разностью векторов а и b назовём сумму векторов а и (– b):
а – b = a + (– b).
131.
Базисы. Прямоугольные системыкоординат
Рассмотрим системы координат. На плоскости
прямоугольную систему координат (СК) ОХY образует
упорядоченная пара взаимно перпендикулярных осей.
Первая ось с единичным вектором
называется осью абсцисс ОХ, вторая ось
с единичным вектором
– осью ординат ОY, точка пересечения осей О называется
началом системы координат, векторы
и
имеют
одинаковую единичную длину. Векторы
и
образуют
базис, а их направления определяют положительные полуоси
ОХ и ОY соответственно.
132.
Возьмём произвольную точку А и построим её проекцию наось ОХ, для чего проведём через
точку А прямую,
параллельную оси ОY, точка пересечения этой прямой и оси
ОХ и будет проекцией
точки А на ось ОХ. Аналогично
строится проекция точки А на ось ОY. Очевидно
,
, поэтому можно говорить о координатах этих
векторов на осях ОХ и ОY соответственно:
,
,
полученные числа х и у называются координатами точки А;
х – абсцисса А, у – ордината А.
133.
При этом, если проекциялежит на положительной
(отрицательной) полуоси ОХ, то
(
).
Аналогично для ординаты у.
Справедливы равенства
,
и
.
Для того чтобы построить проекцию на оси вектора
нужно построить проекции его начала и конца.
,
134.
Проекциейна ось ОХ будет вектор
, на ось ОY –
вектор
. Координатами вектора
назовём
,
и обозначим
. Легко проверяется равенство
, т.е. координаты вектора – это коэффициенты в
разложении вектора по базису
. Если заданы
координаты точек А и В, т.е.
,
, то координаты
вектора получим, если от координат конца отнимем
соответствующие координаты начала:
.
135.
Свойства координат точек иОсновные свойства координат.
векторов
1) Пусть
2)Пусть
,
.
.
.
Замечание. Если мы приложим вектор
к началу координат
О, то координаты вектора
совпадут с координатами
конца вектора В.
В пространстве прямоугольную СК образует упорядоченная
тройка взаимно перпендикулярных осей, пересекающихся в
общей точке О, называемой началом СК. К осям абсцисс ОХ
с единичным вектором
и ОY с единичным вектором
,
прибавляется ось аппликат OZ с единичным вектором
.
136.
Возьмём точку А. Для того чтобы построить проекцию Ахточки А на ось ОХ, мы через точку А проведём плоскость,
параллельную плоскости OYZ, которая пересечёт ось ОХ в
точке Ах. Аналогично строим проекции Аy и Аz
на оси ОY и OZ и определяем координаты
,
,
,
.
137.
Для того чтобы построить проекции вектора, строим
проекции его начала и конца и получаем на осях векторы ,
и
соответственно, получаем
,
,
и тогда вектор
будет иметь координаты
и
будет справедливо разложение:
.
Если
,
, то
.
Используя метод координат, легко получить критерий
коллинеарности векторов.
138.
Предложение 1. Пусть,
, тогда
.
Рассмотрим задачу о делении отрезка в данном отношении.
Пусть задан ненулевой отрезок АВ, требуется на прямой АВ
найти точку М так, чтобы для заданного числа
выполнялось условие
или
.
Замечание.
.
139.
Введём СК OXYZ (на плоскости ОХY).Предложение 2. Пусть
,
точка М имеет координаты
искомая
.
Замечание. Особый интерес представляет случай, когда
точка М является серединой отрезка АВ, т.е.
. В этом
случае мы получаем формулы
, т.е.
координаты середины отрезка являются полусуммами
координат концов отрезка.
140.
Введём определение: за уголмежду
двумя
векторами а и b принимается угол такой,
что
(т.е. меньший из двух возможных).
Пусть задана СК OXYZ и вектор
.
Пусть
,
,
. Нетрудно получить
формулы
, возводя правые и левые части этих
равенств в квадрат и складывая, получим
равенство
, называемое теоремой о
направляющих косинусах.
141.
Замечание. На плоскости с системой координат ОХY, гдеи
, мы получим формулы
.
Полезным для дальнейшего будет отметить следующие
свойства векторов.
На плоскости вектор
.
В пространстве вектор
.
(соответственно
,
);
вектор
плоскости
(соответственно
,
).
Используя прямоугольные координаты, легко получить
формулу вычисления длины вектора.
142.
Пусть,
, приложив его к началу координат О, имеем
,
– проекции вектора а на оси ОХ и ОY, при этом
,
и
,
треугольника
, из прямоугольного
имеем
Замечание 1. Очевидно в пространстве, если
.
, то
143.
Замечание 2. Легко получить и формулу длины отрезка сконцами
и
. Очевидно, что
,
учитывая, что
, получаем формулу
.
Наряду с прямоугольными системами координат
рассматриваются и другие системы координат.
Наиболее важная из них – полярная СК на плоскости.
Полярная СК на плоскости включает в себя ось с выделенной
на ней точкой О – полюсом и определяет положительное
направление вращения (обычно это вращение против
часовой стрелки).
144.
Полярная система координатНаряду с прямоугольными системами координат
рассматриваются и другие системы координат.
Наиболее важная из них – полярная СК на плоскости.
Полярная СК на плоскости включает в себя ось с
выделенной на ней точкой О – полюсом и определяет
положительное направление вращения (обычно это
вращение против часовой стрелки).
145.
Положение каждой точки А определяется полярнымрадиусом
и полярным углом – положительного
поворота вокруг полюса единичного вектора е до того, как он
ляжет на прямую ОА; записывают
.
Существует тесная связь прямоугольных и полярных СК.
Для каждой полярной СК строится прямоугольная СК: полюс
считаем началом, полярная ось берётся за ось ОХ, вектор
, произведя положительный поворот на угол
полярной оси вокруг полюса мы получим ось ОY, при этом
повороте вектор е займёт положение вектора
.
146.
И наоборот: для прямоугольной СК ОХY определяемполярную СК, где ось ОХ совпадает с полярной осью, а
положительное вращение определяет направление в котором
нужно повернуть на угол
вектор
для того, чтобы он
совместился с
.
При таком соответствии легко получить формулы,
связывающие прямоугольные и полярные координаты точки
,
,
.
147.
РезюмеИзучаются векторы и основные операции над
ними.
Определяются прямоугольные системы
координат, вводятся координаты точек и
векторов, рассматриваются их свойства. Тем
самым, создаётся база для использования в
геометрии современного алгебраического
аппарата.
148.
Скалярное, векторное и смешанноепроизведение векторов
Тема 7
149.
ПЛАН1.
2.
3.
4.
5.
Скалярное произведение векторов.
Ориентация плоскости, пространства.
Векторное произведение векторов.
Смешанное произведение векторов.
Объём ориентированного параллелепипеда.
ЛИТЕРАТУРА
6.
7.
8.
9.
Александров П.С. Лекции по аналитической
геометрии. – М., 1968.
Макажанова Т.Х., Муканов А.А., Медеубаев Н.К.
Практикум по аналитической геометрии. –
Караганда, КарГУ, 2003.
Погорелов А.В. Геометрия. – М., 1984.
Макажанова Т.Х., Муканов А.А., Ульбрихт О.И.
Аналитическая геометрия. Электронный учебник.
(2,5 Мб). –Караганда, 2011.
150.
Скалярное произведение векторовВведём операцию скалярного произведения векторов.
Скалярным произведением любых двух векторов а и b
называется число
, где
.
Свойства скалярного произведения.
1)
коммутативность;
2)
(а и b перпендикулярны),
острый,
– тупой.
2
2
1)
(
a
,
a
)
a
|
a
|
0 , (a, a) 0 a = 0;
3)
4)
однородность;
5)
аддитивность.
Введём теперь СК OXYZ и пусть
–
.
151.
Введём теперь СК OXYZ и пусть a {x1 , y1 , z1 } , b {x2 , y2 , z2 } .Предложение 1.
.
Доказательство.
Представим
тогда
a x1e1 y1e2 z1 e3 , b x 2 e1 y 2 e2 z 2 e3 ,
и с учётом свойств
скалярного произведения, получим:
Так как векторы взаимно перпендикулярны, то
(e1 , e 2 ) (e1 , e3 ) (e 2 , e3 ) 0 и (e1 , e1 ) (e 2 , e 2 ) (e3 , e3 ) 1
, откуда
получаем формулу
.
152.
153.
Рассматриваемыйнами
базисявляется
ортонормированным, т.е. удовлетворяет условию
Для координат x,y,z вектора справедливы формулы ,y,z.
Действительно,,
, тогда , что с учётом
ортонормированности
базиса,
даёт
равенство.
154.
Ориентация плоскости, пространстваБудем вводить понятие ориентации плоскости и
пространства.
Рассмотрим на плоскости упорядоченную пару
неколлинеарных векторов а и b. Будем говорить, что эта
пара векторов имеет правую (левую) ориентацию, если
ближайший поворот от первого вектора а ко второму
вектору b происходит против (по) часовой стрелке.
На рисунке изображена правая пара векторов.
155.
В пространстве рассмотрим упорядоченную тройкунекомпланарных векторов а, b, с. тройка векторов а, b,
с будет правой (левой) пря выполнении условия: если
смотреть из конца третьего вектора с, то ближайший
поворот от первого вектора а ко второму вектору b
происходит
против
(по)
часовой
стрелке.
На рисунке изображена левая тройка векторов а, b, с.
Плоскость
или
пространство
считаются
ориентированными, если указано какая ориентация
считается положительной (обычно это правая
ориентация).
На
ориентированной
плоскости
(или
в
ориентированном
пространстве)
рассматриваются
положительные
(правые)
базисы.
156.
Векторное произведение векторовОпределим операцию векторного произведения
векторов.
Пусть имеется упорядоченная пара векторов а и b.
Векторным произведением [a, b] векторов а и b
называется вектор n, длина и направление которого
задаются условиями:
1) | n | | a | | b | sin , a, b .
2) n a, n b .
1) a, b, n – правая тройка.
3)
157.
1)2)
3)
4)
[ a, b] [b, a] антикоммутативность.
[ a, b] 0 a || b .
[ a1 a 2 , b] [a1 , b] [ a 2 , b] аддитивность.
[ a, b] [a, b] .
158.
Проверим, например, свойство 2). Вектор . Обращениев 0 последнего произведения возможно, если (или )
или .
Но 0, и нулевой вектор может иметь любое
направление, в частности быть коллинеарным вектору
b.
Если же , то или ,, что приводит к коллинеарности
векторов а и b.
159.
Если векторы а и b заданы координатами: a {x1 , y1 , z1} , b {x2 , y2 , z2 }то вектор
, где x y1 z1 , y z1 x1 , z x1 y1 ,
n [a, b] {x, y, z} ,
y 2 zможно
z 2 x2
x2 y 2
2
для вычисления которых
использовать разложение по третьей строке
определителя матрицы, составленной из координат
векторов а и b и базиса
:
.
160.
Зная координаты векторного произведения, можнополучить формулу для вычисления площади
параллелограмма, построенного на векторах а и b:
S▱= | [a, b] | y1 z1
y2 z2
2
z x
1 1
z 2 x2
2
x y
1 1
x2 y 2
2
.
Если векторы
и
рассматривать
лежащими на плоскости ОХY, т.е. можно считать что
координаты
, то для площади параллелограмма получим
формулу: S▱=
,
соответственно площадь треугольника, построенного
на векторах а и b можно вычислить по формуле
161.
Смешанное произведение векторовРассмотрим упорядоченную тройку векторов .
Смешанным произведением векторов называется
число, определяемое следующим образом:
, т.е. векторно перемножаем а и b и полученный вектор
скалярно умножаем на вектор с.
Введём определение. Пусть имеются три вектора .
Приложим их к одной точке и построим
параллелепипед, образующими рёбрами которого будут
векторы .
162.
Еслиориентированноготройка векторов – правая (левая),
то и
Объём
параллелепипеда
параллелепипед будем называть
правоориентированным (левоориентированным).
Объёмом ориентированного параллелепипеда,
построенного на векторах , называется число,
обозначаемое <>и равное объёму этого
параллелепипеда, если тройка – правая; если тройка
векторов левая, то объём ориентированного
параллелепипеда равен объёму параллелепипеда,
взятому со знаком минус.
Замечание. Если векторы компланарны, то естественно
считать, что объём ориентированного параллелепипеда
<>= 0.
163.
Предложение 2.()=<>, т.е. смешанное произведение– это объём ориентированного параллелепипеда,
построенного
на
заданных
векторах.
Наряду с параллелепипедом с помощью векторов ()
можно строить ориентированный тетраэдр и тогда для
объёма ориентированного тетраэдра будет справедлива
формула .
164.
Свойствасмешанного
произведения.
1) Смешанное произведение не меняется при круговой
перестановке векторов:
, т.к. при этом не
меняется ориентация тройки, а значит не меняется
объём
.
2) Перестановка любых двух векторов меняет знак
смешанного произведения:
,
т.к. при такой перестановке меняется ориентация
тройки.
3) Смешанное произведение линейно по каждому
аргументу:
например,
по
второму
.
С учётом предыдущих свойств легко получить
линейность, например, по третьему аргументу:
165.
4)(a, b, c) = 0 векторы a,b,c компланарны – только вэтом случае мы получим параллелепипед нулевого
объёма. В частности, (a, b, c) = 0 , если среди векторов
есть два коллинеарных вектора.
5) С учётом свойства 1 имеем равенство
,
расписав которое
получим, что скобку векторного произведения можно
сдвигать на одно место, т.е. смешанное произведение
ассоциативно относительно операции векторного
произведения.
166.
Введём прямоугольную СК ОXYZ. Получимформулы, выражающие смешанное произведение
векторов через их прямоугольные координаты. Пусть
a {x1 , y1 , z1 } , b {x 2 , y 2 , z 2 } , c {x3 , y 3 , z 3 } ,
по определению
Как известно
.
, тогда
x1 y1 z1
y1 z1
z1 x1
x1 y1
([a, b], c)
x
y
z x 2 y 2 z 2 ,
y 2 z 2 3 z 2 x2 3 x2 y 2 3
x3 y 3 z 3
т.е. смешанное произведение равно определителю
матрицы, строками (или столбцами) которой являются
координаты векторов a,b,c. Знак определителя
определяет ориентацию тройки: "+" – правая, "–" –
левая ориентация.
Равенство 0 определителя является критерием того,
что векторы a,b,c являются компланарными.
167.
РезюмеСкалярное, векторное и смешанное
произведения векторов, их свойства,
представление в прямоугольных
координатах представляют собой основной
современный аппарат геометрических
исследований.
168.
Прямая на плоскостиТема 8
169.
ПЛАН1.
2.
3.
4.
5.
6.
Линии первого порядка.
Теорема о линиях первого порядка.
Различные уравнения прямой.
Параллельность вектора и прямой нормали прямой.
Расположение двух прямых и углы между ними.
Пучок прямых.
ЛИТЕРАТУРА
Александров П.С. Лекции по аналитической
геометрии. – М., 1968.
8. Макажанова Т.Х., Муканов А.А., Медеубаев Н.К.
Практикум по аналитической геометрии. –
Караганда, КарГУ, 2003.
9. Погорелов А.В. Геометрия. – М., 1984.
10.Макажанова Т.Х., Муканов А.А., Ульбрихт О.И.
Аналитическая геометрия. Электронный учебник.
(2,5 Мб). –Караганда, 2011.
7.
170.
Линии первого порядкаНапомним определение. Пусть на плоскости (или в
пространстве) задана CK OXY (соответственно OXYZ).
Будем говорить, что уравнение F(x, y) = 0 (F(x, y, z) = 0)
является уравнением линии L (поверхности P), если этому
уравнению удовлетворяют координаты любой точки
линии L (поверхности P) и не удовлетворяют координаты
никакой другой точки плоскости (пространства).
171.
Уравнение вида Ax+By+C=0 (Ax+By+Cz+D=0), называютсяуравнениями 1-го порядка, если
(соответственно
), а линии (поверхности), которые они определяют,
называются линиями (поверхностями) первого порядка.
Пусть на плоскости задана прямая d. Вектор a будем называть
параллельным прямой d, если при приложении к какой-либо
точке на d вектор a целиком будет лежать на d.
Всякий ненулевой вектор, параллельный прямой d,
будем называть направляющим вектором прямой.
Очевидно, что у прямой имеется бесчисленное
множество направляющих векторов, состоящее из всех
ненулевых векторов, коллинеарных какому либо
направляющему вектору прямой.
172.
1)а
d
M0
2)
M1
M2
3)
п
M0
173.
Теорема о линиях первого порядкаТеорема 1.Линии 1-го порядка на плоскости – прямые и
только они.
Доказательство теоремы основано на том, что если у
нас есть уравнение 1-го порядка Ах+Ву+С=0 ( ), то взяв
вектор 0, точку , где
и построив прямую d, проходящую через точку и
имеющую направляющим вектором вектор а, мы
построим линию уравнением которой будет уравнение
Ах+Ву+С=0.
174.
Наоборот, если имеется прямая d, проходящая черезточку
и имеющая направляющий вектор
, то для любой точки
вектор
,
но
, откуда получаем уравнение
или
. С учётом того, что вектор
0, т.е.
0, полученное уравнение прямой
d
будет уравнением первого порядка.
Замечание 1. Как было отмечено, за направляющий
вектор прямой d, определяемой уравнением
Ах+Ву+С=0 всегда можно взять вектор
или
любой ненулевой вектор ему коллинеарный.
175.
Замечание 2. Отметим характеристики прямой d в зависимостиот значений коэффициентов А, В, С в её уравнении:
1. C O O(0, 0) d ;
2. A O, B O a { B, O} d || OX ;
3. B O, A O a {O, A} d || OY ;
4. A C O d OX ;
5. B C O d OY .
Уравнение
называется общим уравнением
прямой.
176.
Различные уравнения прямойРассмотрим различные уравнения прямой.
Пусть прямая задана точкой
и направляющим
вектором
, для любой
точки
на прямой
.
Записав последнее условие через отношение координат, мы
получим каноническое уравнение прямой
Если мы условие
запишем в виде
пробегает всё множество вещественных чисел
параметрическое уравнение прямой
, где t
, то получим
177.
M 1 ( x1 , y1 ) , M 2 ( x 2 , y 2 )Если прямая задана неравными точками , то за
направляющий вектор можно взять
вектор . Подставив в каноническое уравнение эти
данные, получим уравнение прямой, проходящей через
заданные точки .
Если прямая задана точкой и вектором ,
перпендикулярным прямой, то для любой точки на
прямой вектор , т.е. , откуда получаем уравнение
178.
Для любого вектора∦OY, т.е. если , вводится понятиеуглового коэффициента . Очевидно, что угловой
коэффициент одинаков у всех коллинеарных векторов и
k = tg , где – угол поворота против часовой стрелки
от базисного вектора до вектора а.
Если задана прямая, то угловым коэффициентом
прямой назовём угловой коэффициент её
направляющих векторов. Геометрически угловой
коэффициент прямой – это тангенс угла поворота оси
ОХ (вектора ) против часовой стрелки до первого
пересечения с прямой.
179.
Если прямая задана общим уравнением, то
взяв за направляющий вектор
, получим, что
угловой коэффициент
.
Если задана точка
на прямой и угловой
коэффициент
, где
– направляющий
вектор прямой, то подставляя в
каноническое уравнение эти данные, мы придём к
уравнению
учтём, что
, и получим
уравнение прямой
.
180.
Если задана точка А на оси ОХ (В на оси OY), товеличиной отрезка ОА (ОВ) будем называть длину
отрезка ОА (ОВ), если А лежит на положительной
полуоси ОХ (В на положительной полуоси OY), и длину
ОА (ОВ) со знаком минус, если А лежит на
отрицательной полуоси ОХ (В – на отрицательной
полуоси OY).
Если в качестве точки на прямой возьмём точку В
пересечения прямой с осью OY,
т.е. B(,b) (где b – величина отрезка,
отсекаемого прямой на оси OY),
получим так называемое
уравнение прямой с угловым
коэффициентом
.
181.
Пусть теперь A (a, 0) , B (0, b) – точки пересеченияпрямой с осями ОХ и ОY соответственно, подставляя
координаты точек А и В в уравнение прямой, заданной
двумя точками, получим уравнение
называемое уравнением прямой в отрезках (здесь а, b –
величины отрезков, отсекаемых прямой на осях ОХ и
OY). Пусть прямая d задана общим уравнением .
182.
Параллельность вектора и прямой,нормали прямой
Пусть прямая d задана общим уравнением .
Предложение 1. Вектор .
Доказательство легко следует из того, что вектор является
направляющим вектором d, а из условия
следует соотношение, что говорит о коллинеарности векторов
аи.
Предложение 2. Вектор n = {А, В} перпендикулярен прямой d.
183.
Действительно, вектор будет перпендикулярен прямойтогда, когда он перпендикулярен какому-либо
направляющему вектору этой прямой. Возьмём
направляющий вектор
и рассмотрим
откуда n a .
184.
Пусть прямая задана общим уравнением,
вектор
называется нормалью прямой. Прямая
делит плоскость на две полуплоскости. Возьмём какуюлибо точку на прямой и приложим к ней вектор
нормали
. Та полуплоскость, в которой будет
находиться конец вектора нормали, будет называться
положительной полуплоскостью, оставшаяся
полуплоскость – отрицательной.
185.
Для каждой точкиплоскости введём число
.
Предложение 3. Если
, то точка М лежит в
положительной полуплоскости;
– точка М
лежит в отрицательной полуплоскости;
–
точка М лежит на прямой.
186.
Расположение двух прямых и углы между нимиУглом между двумя прямыми (не только на плоскости,
но и в пространстве) называется угол между двумя
любыми направляющими векторами этих прямых.
Таким образом определяются два смежных угла и ,+ .
Если прямые заданы общими уравнениями:
d 1 A1 x B1 y C1 0 , d 2 A2 x B2 y C 2 0 ,
то, взяв за направляющие
векторы и , получим
формулу
.
187.
Следствие. 1) Прямые d1 и d 2 перпендикулярныA1 A2 B1 B2 0 .
2) Если прямые d1 и d 2 заданы угловыми
коэффициентами k1 и k 2 , то они будут перпендикулярны
k1 k 2 1.
Рассмотрим расположение прямых d1 и d 2 . Они могут
быть параллельными (т.е. не иметь общих точек),
пересекаться (т.е. иметь одну общую точку), совпадать.
Предложение 4.
A1 B1 C1
1) Прямые d1 и d 2 параллельны
.
A2 B2 C 2
A B
2) d1 и d 2 пересекаются 1 1 .
A2 B2
A1 B1 C1
3) d1 и d 2 совпадают
.
A2 B2 C 2
188.
Следствие. Для двух параллельных прямых всегдаможно довести их общие уравнения до вида,
отличающегося только свободными членами
C1 и C 2 : d 1 Ax By C1 0 , d 2 Ax By C 2 0 .
Рассмотрим прямую d. Расстоянием
от точки М
до прямой d называется длина перпендикуляра
,
проведённого из точки М на прямую d.
Предложение 5. Пусть прямая d задана уравнением
, точка
| Ax 0 By 0 C |
.
M 0 ( x 0 , y 0 ) ( M 0 , d )
A2 B 2
189.
Следствие. Пусть заданы две параллельные прямыеd1 Ax By C1 0 ,
d 2 Ax By C 2 0 ,
расстоянием между ними может служить расстояние
от любой точки одной прямой до другой прямой.
Возьмём точку M 0 ( x 0 , y 0 ) на прямой d1, т.е.
Ax0 By 0 C1 0 , тогда
(d 1 , d 2 ) ( M 0 , d 2 )
| Ax 0 By 0 C 2 C1 C1 |
2
A B
2
| C 2 C1 |
A2 B 2
190.
РезюмеДоказывается теорема о том, что линии
первого порядка - прямые и только они.
Рассматриваются различные уравнения
прямой, исследуется поведение прямых в
зависимости от коэффициентов общего
уравнения Ах+Ву+С=0.
Рассматривается расположение двух
прямых и углы между ними.
191.
Прямая в пространствеТема 9
192.
ПЛАН1.
2.
3.
4.
Основные уравнения прямой в пространстве.
Расстояние от точки до прямой.
Расположение двух прямых в пространстве.
Расстояние между двумя прямыми в пространстве.
ЛИТЕРАТУРА
5.
6.
7.
8.
Александров П.С. Лекции по аналитической
геометрии. – М., 1968.
Макажанова Т.Х., Муканов А.А., Медеубаев Н.К.
Практикум по аналитической геометрии. –
Караганда, КарГУ, 2003.
Погорелов А.В. Геометрия. – М., 1984.
Макажанова Т.Х., Муканов А.А., Ульбрихт О.И.
Аналитическая геометрия. Электронный
учебник. (2,5 Мб). –Караганда, 2011.
193.
Основные уравнения прямой впространстве
Вводим в пространстве СК OXYZ. Если прямая
задана точкой M 0 x0 , y 0 , z 0 и направляющим вектором
a a1 , a 2 , a3 , то также, как и в случае прямой на
плоскости, получаем каноническое уравнение прямой
x x0 y y 0 z z 0
и параметрическое уравнение
a1
a2
a3
x x0 ta1
1
y y 0 ta 2 , t R .
z z ta
0
3
Если прямая задана неравными точками M 1 x1 , y1 , z1
и M 2 x 2 , y 2 , z 2 , то получаем уравнение
x x1
y y1
z z1
.
x 2 x1 y 2 y1 z 2 z1
194.
Расстояние от точки до прямойПусть прямая d определена точкой M 0 x 0 , y 0 , z 0 и
направляющим вектором a a1 , a 2 , a3 . Получим
формулу для вычисления расстояния от точки
M x, y, z до прямой d.
| [M 0 M , a] |
Предложение 1. M , d
.
|a|
Замечание. В прямоугольных координатах формула
расстояния будет иметь вид
M , d
y y0
z z0
a2
a3
2
z z0
x x0
a3
a1
a12 a 22 a 32
2
x x0
y y0
a1
a2
2
195.
Расположение двух прямых впространстве
Напомним,
что,
две
прямые
называются
скрещивающимися, если они не лежат в одной
плоскости.
Если прямые нескрещивающиеся, т.е. лежат в одной
плоскости, то они могут быть параллельными,
пересекающимися и совпадающими.
196.
Пусть прямая d1 задана точкой M 1 ( x1 , y1 , z1 ) инаправляющим вектором a {a 1 , a 2 , a3 }, прямая d 2 –
точкой M 2 ( x 2 , y 2 , z 2 ) и направляющим вектором
b b1 , b2 , b 3 .
Составим матрицы
a2
a3
a1
a1 a 2 a 3
Q1
b2
b3 ,
и Q2 b1
b1 b2 b3
x x y y z z
2
1
2
1
2
1
пусть r1 – ранг Q1, r2 – ранг Q2 , r1 r2 .
197.
Предложение 2.1) d1 и d 2 скрещиваются r2 3 ;
2) d1 и d 2 пересекаются r1 r2 2 ;
3) d1 || d 2 r1 1, r2 2 ;
4) d1 d 2 r1 r2 1.
198.
Расстояние между двумя прямыми впространстве
Введём определение. Расстоянием ( d1 , d 2 ) между
прямыми d1 и d 2 называется длина общего
перпендикуляра к обеим прямым.
Можно показать, что общий перпендикуляр к прямым d1
и d 2 существует. Он является высотой параллелепипеда,
построенного на векторах а, b,
M 1 M 2 , проведённой к
основанию, построенному
векторами а и b.
199.
Если V – объём параллелепипеда, S – площадьпараллелограмма, со сторонами а и b, то
V
(d1 , d 2 ) h .
С
учётом
того,
что
S
получаем
V mod(a, b, M 1 M 2 ) ,
S | [ a, b] |,
формулу
mod(a, b, M 1 M 2 )
.
( d 1 , d 2 )
| [ a, b ] |
200.
РезюмеИзучаются различные уравнения прямой в
пространстве.
Получены формулы расстояния от точки до
прямой, между двумя прямыми.
Расположение прямых в пространстве.
201.
Плоскость в пространствеТема 10
202.
ПЛАН1.
2.
3.
4.
Теорема о поверхностях первого порядка.
Уравнения плоскости при различных её заданиях.
Параллельность вектора и плоскости, нормали плоскости.
Взаимное расположение двух плоскостей и углы между ними.
ЛИТЕРАТУРА
5.
6.
7.
8.
Александров П.С. Лекции по аналитической
геометрии. – М., 1968.
Макажанова Т.Х., Муканов А.А., Медеубаев Н.К.
Практикум по аналитической геометрии. –
Караганда, КарГУ, 2003.
Погорелов А.В. Геометрия. – М., 1984.
Макажанова Т.Х., Муканов А.А., Ульбрихт О.И.
Аналитическая геометрия. Электронный
учебник. (2,5 Мб). –Караганда, 2011.
203.
Теорема о поверхностях первогопорядка
Напомним, что уравнение Ax+By+Cz+D, где ,
называется уравнением первого порядка, а
поверхность, определяемая этим уравнением –
поверхностью первого порядка.
Напомним, что вектор акомпланарен плоскости , если
при приложении к какой-либо точке плоскости он будет
лежать на этой плоскости, обозначаем .
204.
Теорема 1. Поверхности первого порядка – плоскости итолько они.
Плоскость в пространстве можно задавать различными
способами:
1) точкой плоскости и двумя неколлинеарными векторами,
компланарными плоскости;
2) тремя точками плоскости, не лежащими на одной
прямой;
3) точкой плоскости и ненулевым вектором,
перпендикулярным плоскости
205.
Уравнения плоскости приразличных её заданиях
Если
имеется
плоскость,
заданная
точкой
и
неколлинеарными
векторами
M 0 ( x0 , y 0 , z 0 )
а a1 , a 2 , a3 и b {b1 , b2 , b3 }. Проведенная через них
плоскость будет иметь уравнение
х х0 у у 0 z z 0
a1
a2
a 3 0 .
b1
b2
b2
Подсчитав определитель, получим уравнение
Ax By Cz D 0 ,
которое называется общим уравнением плоскости.
206.
Можно записать и параметрическое уравнениеэтой плоскости:
x x 0 sa1 tb1
1
,
где
.
y
y
sa
tb
s
,
t
R
0
2
2
z z sa tb
0
3
3
207.
Если плоскость задана тремя не лежащими наодной прямой точками M 1 ( x1 , y1 , z1 ) , M 2 ( x 2 , y 2 , z 2 ) ,
M 3 ( x3 , y 3 , z 3 ) , то, взяв точку M 0 M 1 и векторы
a M 1 M 2 , b M 1 M 3 , мы получим уравнение этой
плоскости:
x x1
x 2 x1
x3 x1
y y1
y 2 y1
y 3 y1
z z1
z 2 z1 0 .
z 3 z1
208.
Если плоскость заданавектором
и
точкой
n
M 0 ( x0 , y 0 , z 0 ) , то для любой
точки M ( x, y, z ) , лежащей на
плоскости вектор n M 0 M , т.е.
(n, M 0 M ) 0 . Получаем уравнение плоскости:
A( x x 0 ) B ( y y 0 ) ) C ( z z 0 ) 0 .
209.
Параллельность вектора иплоскости, нормали плоскости
Предложение 1. Пусть плоскость задана
уравнением Ax By Cz D 0 , a {a1 , a 2 , a3 }
a || Aa1 Ba2 Ca 3 0 .
Предложение 2. Пусть Ax By Cz D 0 ,
n { A, B, C} n .
Вектор
плоскости.
n { A, B, C}
называется
нормалью
210.
Пусть заданы две плоскости и.Рассмотрим возможные случаи расположения
плоскостей и в пространстве:
1) и параллельны (, т.е. не имеют общих точек;
2) и пересекаются, т.е. имеют общие точки, но не
совпадают;
3)
211.
Предложение 3.1) =;
2) и пересекаются нарушено одно из равенств в
соотношениях =;
3) =.
Доказательство.
1) их нормали иколлинеарны, т.е. = . Если
предположить, что =, то уравнение будет иметь вид , а
тогда плоскости и и будут иметь общие точки.
212.
2) и будут пересекаться нормали этих плоскостей ине будут коллинеарными координаты и не будут
пропорциональны.
3) , т.е. =, и плоскости и имеют общие точки. Если
предположить, что =, то мы получаем случай 1)
параллельности плоскостей.
213.
Как известно, углом между плоскостями и называетсядвугранный угол между ними, измеряемый линейным
углом.
Такое определение дает два смежных угла и :. Один из
этих углов совпадает с углом между нормалями и ,
поэтому справедлива формула , т.е.
214.
Условием перпендикулярности плоскостей будетравенство
Каждая плоскость делит пространство на два
полупространства: положительное – то, куда направлен
вектор нормали плоскости п, и отрицательное –
оставшееся полупространство ( то, куда направлен
вектор (–п)).
215.
Если плоскость задана общим уравнением:, M(x,y,z)–точка пространства, , то также, как при рассмотрении
полуплоскостей, имеем:
1) М лежит в положительном полупространстве;
2) М лежит в отрицательномполупространстве;
3) М лежит на плоскости.
216.
Расстояниемот точки М до плоскости называетсядлина перпендикуляра, проведённого из точки М на
плоскость .
По аналогии с выводом формулы расстояния от точки
до прямой на плоскости получим формулу расстояния
от точки до плоскости.
Пусть Ax By Cz D 0 , M 0 ( x 0 , y 0 , z 0 )
| Ax0 By 0 Cz 0 D |
.
( M 0 , )
2
2
2
A B C
217.
Замечание. Две параллельные плоскости, как ужеотмечалось, мы можем задать уравнениями,
отличающимися только свободным членом: , . За
расстояние между параллельными плоскостями можно
принять расстояние от какой-либо точки одной
плоскости до другой плоскости. Используя только что
полученную формулу, можно доказать, что
Как известно, углом между прямой и плоскостью
называется угол между прямой и её прямоугольной
проекцией на плоскость. По определению имеем два
смежных угла.
218.
РезюмеДоказывается теорема о том, что
поверхности первого порядка – плоскости и
только они.
Рассмотрены различные способы задания
плоскостей и получающиеся при этом
уравнения плоскостей.
Исследуя общие уравнения плоскостей,
делается вывод о расположении плоскостей
и углах между ними.
219.
Смешанные задачи на прямую иплоскость в пространстве
Тема 11
220.
ПЛАН1.
2.
Углы между прямой и плоскостью.
Расположение прямой и плоскости в пространстве.
ЛИТЕРАТУРА
3.
4.
5.
6.
Александров П.С. Лекции по аналитической
геометрии. – М., 1968.
Макажанова Т.Х., Муканов А.А., Медеубаев
Н.К. Практикум по аналитической
геометрии. – Караганда, КарГУ, 2003.
Погорелов А.В. Геометрия. – М., 1984.
Макажанова Т.Х., Муканов А.А., Ульбрихт
О.И. Аналитическая геометрия.
Электронный учебник. (2,5 Мб). –Караганда,
2011.
221.
Углы между прямой и плоскостьюУглом между прямой d и плоскостью называется угол
между прямой и её прямоугольной проекцией d1 на
плоскость. По определению имеем два смежных угла.
222.
Пусть имеется плоскостьи прямая, где точка на d, – направляющий вектор
d.
Предложение 1. Пусть
223.
Доказательство.Построим ортогональную проекцию прямой d на
плоскость , к точке пересечения прямой d и плоскости
приложим вектор нормалиплоскости . Если – углы
между прямой d и её проекцией ,
– угол между вектором n и направляющим вектором
прямой d, то , откуда
.
Но =
формула для .
,откуда и получается нужная
Замечание. Плоскость и прямая d
будут взаимно перпендикулярны
d)
n || a A B C
a1 a2 a3
224.
Расположение прямой и плоскостив пространстве
Рассмотрим вопрос о расположении прямой d и
плоскости .
Предложение 2. 1) d лежит в плоскости
Aa1 Ba2 Ca3 0 , Ax0 By0 Cz 0 D 0 ;
2) d || (т.е. не имеют общих точек)
Aa1 Ba2 Ca3 0 , Ax0 By0 Cz 0 D 0 ;
3) d пересекает (т.е. имеет с одну общую
точку) Aa1 Ba2 Ca3 0.
225.
Доказательство.1)
d направляющий вектор a || (т.е.
Aa1 Ba2 Ca3 0 ),
M 0 ( x0 , y0 , z0 )
(т.е.
Ax0 By0 Cz 0 D 0 ).
2) d || a || (т.е. Aa1 Ba2 Ca3 0 ), M 0
(т.е. Ax0 By0 Cz 0 D 0 ).
3)
d пересекает а∦ (т.е. Aa1 Ba2 Ca3 0).
226.
РезюмеПолучены формулы, позволяющие судить о
расположении прямой и плоскости,
вычислять углы между прямой и
плоскостью.
227.
Кривые второго порядка,заданные канонически
Тема 12
228.
ПЛАН1.
2.
3.
4.
Каноническое уравнение эллипса и его свойства.
Каноническое уравнение гиперболы и её свойства.
Каноническое уравнение параболы и её свойства.
Касательные к эллипсу, гиперболе, параболе.
ЛИТЕРАТУРА
5.
6.
7.
8.
Александров П.С. Лекции по аналитической
геометрии. – М., 1968.
Макажанова Т.Х., Муканов А.А., Медеубаев Н.К.
Практикум по аналитической геометрии. –
Караганда, КарГУ, 2003.
Погорелов А.В. Геометрия. – М., 1984.
Макажанова Т.Х., Муканов А.А., Ульбрихт О.И.
Аналитическая геометрия. Электронный
учебник. (2,5 Мб). –Караганда, 2011.
229.
Каноническое уравнение эллипсаи его свойства
Напомним, что если на плоскости задана система
координат OXY, то уравнение F(x, y)=0 является
уравнением линии (или кривой) второго порядка, если
F(x, y) представляет из себя алгебраический
многочлен второго порядка. Общий вид такого
многочлена может быть записан в виде:
F(x, y)= A11 x 2 2 A12 xy A22 y 2 2 A13 x 2 A23 y A33 ,
где коэффициенты A11 , A12 и A22 одновременно в 0 не
обращаются.
230.
Эллипсом называется множество точек плоскости,сумма расстоянии которых до двух заданных точек
плоскости F1 и F2 , называемых фокусами, есть
постоянная величина 2а, большая расстояния между
фокусами 2с.
у
d1
d2
B2
A1
F1
O
M
F2
A2
х
B1
Построим систему координат OXY: ось OX будет
проходить через фокусы F1 и F2 , начало координат
поместим в середину отрезка F1 F2 .
231.
Имеем F1 ( c, 0) , F2 (c, 0) и для точек M ( x, y ) наэллипсе выполняется уравнение | F1 M | | F2 M | 2a .
Распишем
его
в
координатах: ( x c) 2 y 2 ( x c) 2 y 2 2a .
Полагая b 2 a 2 c 2 0 ,
уравнение эллипса:
получим
x2 y2
(Э ) 2 2 1.
a
b
каноническое
232.
В построенной нами системе координат осисимметрии эллипса совпадают с осями OX и OY, а центр
симметрии – с началом координат. Для точек эллипса
M ( x, y ) имеем | x | a , | y | b . Точки пересечения
эллипса с осями симметрии называются вершинами
эллипса: это A1 ( a, 0) , A2 (a, 0) , B1 (0 b) , B2 (b, 0) .
Отрезок
A1 A2 2a называют большой осью,
B1 B2 2b – малой осью эллипса. Соответственно
OA1 OA2 a большая полуось, OB1 OB2 b – малая
полуось эллипса.
233.
cОтношение называется эксцентриситетом
a
эллипса. Очевидно для эллипса <1.
Для каждой точки M ( x, y ) на эллипсе r1 | F1 M | и
r2 | F2 M | называются фокальными радиусами точки
M. Для фокальных радиусов справедливы равенства
r1 a x , r2 a x .
Учитывая отмеченную симметрию, легко построить
часть эллипса в первом квадранте ( x 0 , y 0 ), а
затем симметрично отобразить её.
234.
Прямые d1 и d 2 , перпендикулярные большой осиa
эллипса и отстоящие от центра эллипса на расстояние ,
называются директрисами эллипса.
a
Уравнениями директрис будут: x .
Фокус и ближайшая к нему директриса будут
называться односторонними.
Предложение 1. Пусть r – фокальный радиус точки
эллипса М, – расстояние от точки М до односторонней
r
с этим фокусом директрисы .
235.
Каноническое уравнение гиперболы и её свойстваГиперболой называется множество точек плоскости,
абсолютное значение разности расстояний которых до
заданных точек F1 и F2 , называемых фокусами, есть
постоянная величина 2а, меньшая, чем расстояние 2с
между фокусами.
Систему координат OXY строим также как и для
эллипса.
d1
F1
у
A1
d2
A2 F2
O
х
236.
Тогдаимеем
F1 ( c, 0) ,
F2 (c, o) ,
и
уравнение
гиперболы будет F1 M – F2 M = 2a .
Распишем
его
в
координатах
После
( x c) 2 y 2 ( x c) 2 y 2 2a .
двукратного возведения в квадрат, получим:
полагая
x 2 (c 2 a 2 ) a 2 y 2 a 2 ( c 2 a 2 ) ,
b 2 c 2 a 2 0,
2
2
,
поделим
на
и получим
a
b
2 2
2 2
2 2
b x a y a b
каноническое уравнение гиперболы
x2 y2
(Г) 2 2 1.
a
b
237.
Гипербола имеет две оси симметрии. Первая осьсимметрии проходит через фокусы и называется
действительной осью гиперболы; вторая ось
симметрии проходит через середину отрезка F1 F2 ,
перпендикулярно действительной оси, и называется
мнимой осью гиперболы. Здесь это оси OX и OY.
Точка пересечения осей гиперболы являются
центром симметрии.
Для точек M ( x, y ) на гиперболе, как это следует из
уравнения (Г), абсциссы точек удовлетворяют
x a
условиям
, т. е. гипербола состоит из двух
x a
различных ветвей: правой ( x a ) и ( x a ) .
238.
Точки пересечения гиперболы A1 ( a, 0) и A2 (a, 0) с еедействительной осью называются вершинами гиперболы,
с мнимой осью точек пересечения у гиперболы нет.
Расстояние а называется действительной полуосью, b –
мнимой полуосью.
c
Эксцентриситет гиперболы задаётся формулой и
a
1.
Фокальные радиусы r1 | F1 M |, r2 | F2 M | для точек
гиперболы M ( x, y ) определяются по формуле r1 | a x |,
r2 | a x |.
Асимптоты гиперболы задаются уравнениями:
b
y x .
a
239.
Прямые d1 и d 2 , перпендикулярные действительнойоси, и находящиеся от центра симметрии на расстоянии
a
, называются директрисами гиперболы.
В построенной СК уравнениями директрис будут
a
x .
Так же как и для эллипса справедливо
Предложение 2. Отношение расстояния точек
гиперболы до фокуса к расстоянию до односторонней
с фокусом директрисы равно эксцентриситету.
240.
x2 y2Гиперболы с уравнениями 2 2 1 и
a
b
x2 y2
2 1
2
a
b
называются сопряженными, у них совпадают оси
симметрии и асимптоты.
Гипербола,
у
равносторонней.
которой
a b ,
называется
Критерием равносторонней гиперболы является
взаимная перпендикулярность её асимптот.
241.
Каноническое уравнение параболы и её свойстваПараболой называется множество точек плоскости,
расстояния которых до заданной точки F, называемой
фокусом, и до заданной прямой d, называемой
директрисой, равны.
Расстояние ( F , d ) от фокуса F до директрисы d
обозначается
через
р
и
d у
называется
параметром
M ( x, y )
параболы.
Q O
F
Строим систему координат.
х
Ось ОХ проводим через фокус,
перпендикулярно директрисе.
Если через Q обозначим
точку пересечения оси ОХ и директрисы, то начало
координат будет находиться в середине отрезка FQ,
положительная полуось ОХ направлена в сторону фокуса.
242.
pВ построенной СК F , 0 , директриса d будет иметь
2
p
уравнение x .
2
Для
точек
2
M ( x, y )
параболы
имеем
2
p
p
2
| FM | x y ,
( M , d ) x ,
2
2
приравнивая эти расстояния, получаем уравнение
2
2
p
p
2
параболы
x
y
x
, возводя в
2
2
квадрат, получаем каноническое уравнение параболы
( П ) y 2 2 px .
243.
Парабола симметрична относительно оси ОХ, т.е.прямой, проходящей через фокус перпендикулярно
директрисе. Эта ось симметрии называется осью
параболы.
Парабола пересекает ось в единственной точке,
делящей пополам перпендикуляр от фокуса до
директрисы и называемой вершиной параболы.
y2
Из уравнения y 2 px имеем, что x
0 ,
2p
поэтому построим часть параболы в первом
квадранте ( x 0, y 0 ), а затем симметрично
отобразим ее относительно оси ОХ.
2
Очевидно, что с увеличением y возрастает и х,
( x 0, y 0 ), поэтому парабола будет иметь
указанный на рисунке вид.
244.
Касательной к кривой в точке M называетсяпредельное положение секущей MP, когда точка P,
находясь на кривой, стремится к точке
у
M.
Р
М
Пусть кривая задана уравнением y =
ƒ(x), M x0 , y 0 , P x 0 x, y 0 y .
х
Напишем уравнение секущей MP:
y
y
– угловой коэффициент
y y 0 x x0 , где
x
x
прямой.
y
Если P M , т.е. x 0 , то
x 0 f x0 и мы
x
получаем уравнение касательной в точке M 0
y y0 f ( x0 )( x x0 ) .
245.
Напишем уравнения касательных для изученных намикривых второго порядка в точке M 0 x0 , y 0 .
x2 y2
Рассмотрим
уравнение
эллипса
2 1,
2
a
b
x2
y b 1 2 , причем квадратный корень берем с тем же
a
знаком, что и y0 .
Уравнение касательной (*) будет иметь вид
х0 b
х0 b
y y 0
( x x0 ) или y y 0
( x x0 ) .
2
2
y0 a
x0
2
a 1 2
a
y0
Умножая его на 2 и перенося все члены в левую часть,
b
x x0 y y 0
x x0 y y 0
получим 2 2 1 0 или 2 2 1.
a
b
a
b
246.
x2 y2Для гиперболы 2 2 1, производя аналогичные
a
b
выкладки,
получим
уравнение
касательной
x x0 y y 0
1.
2
2
a
b
Рассмотрим уравнение параболы y 2 2 px , откуда
y2
и уравнение касательной будет иметь вид
x
2p
y0
x x 0 ( y y 0 ) или y y 0 y 02 px 0 px 0 , но
p
y 02 2 px0 , откуда получаем уравнение y y 0 p ( x x0 ) .
247.
РезюмеПостроены канонические системы
координат и получены канонические
уравнения эллипса, гиперболы и параболы.
Изучены основные свойства, рассмотрены
для канонического случая уравнения
касательных.























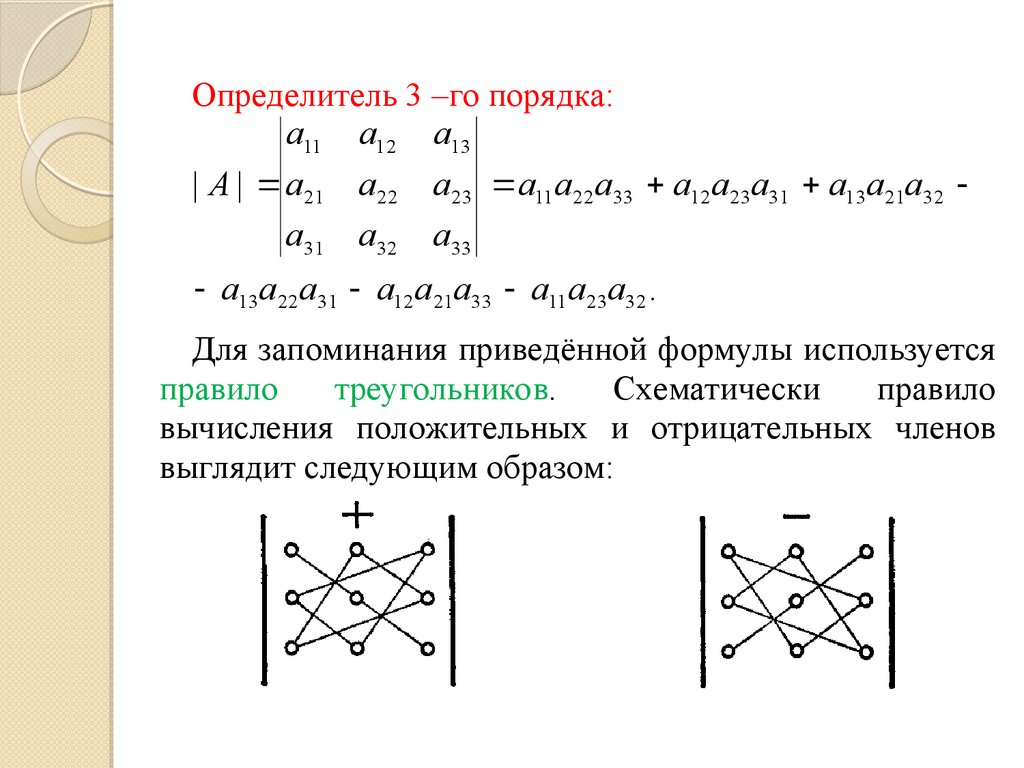
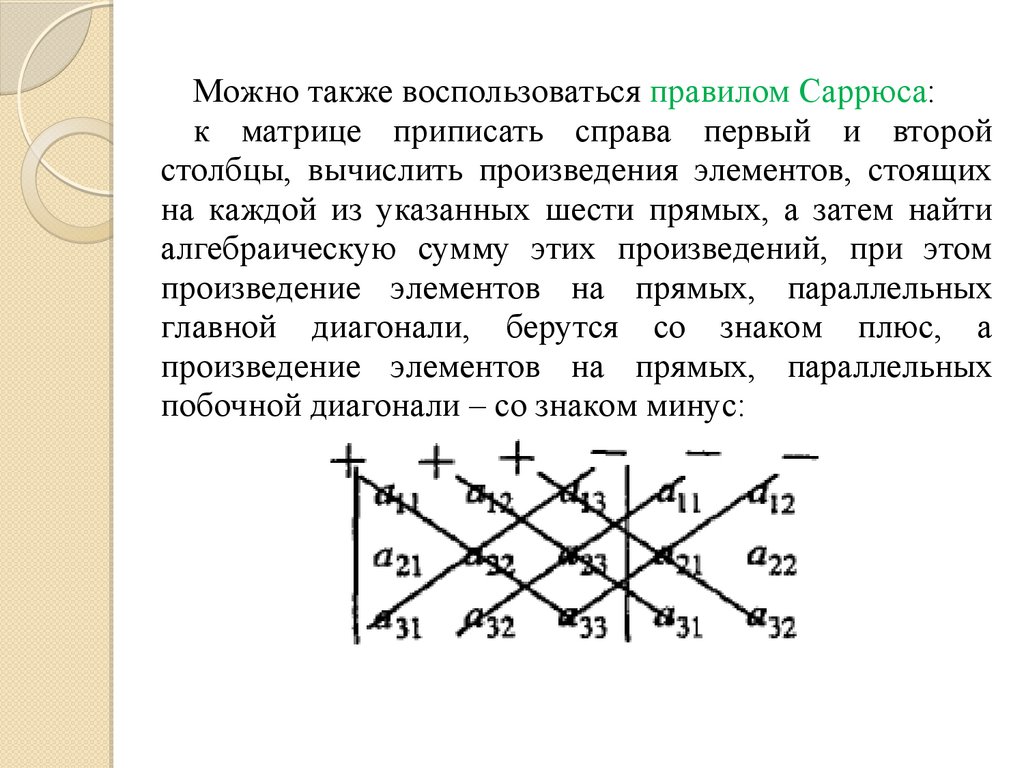
























































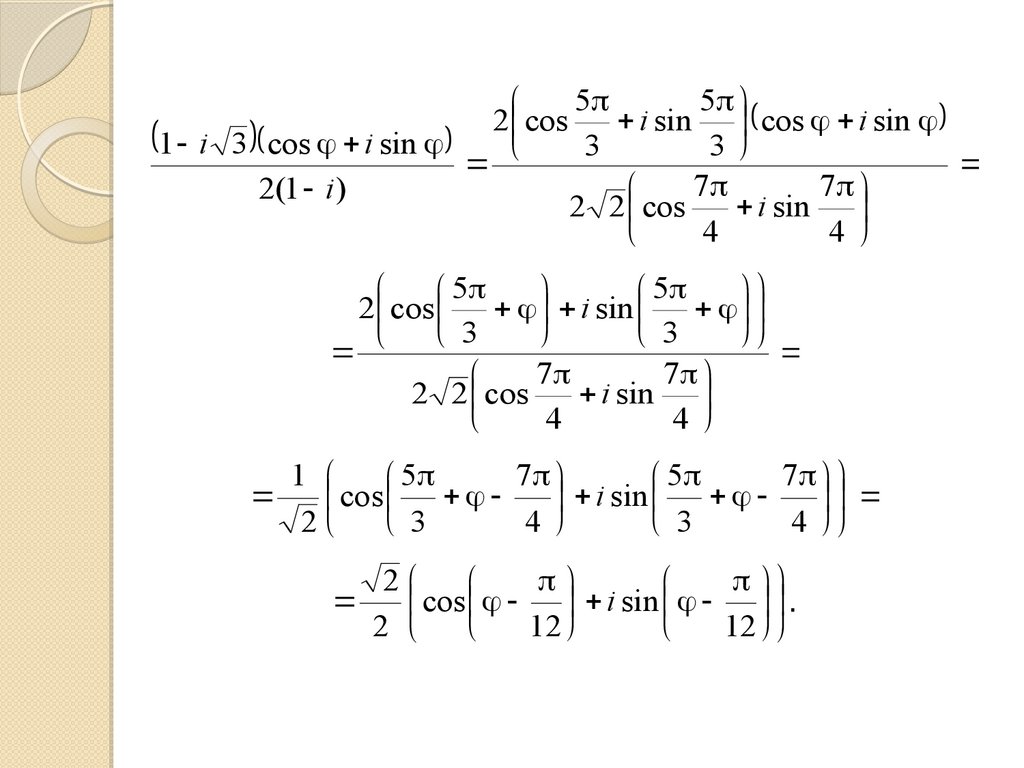



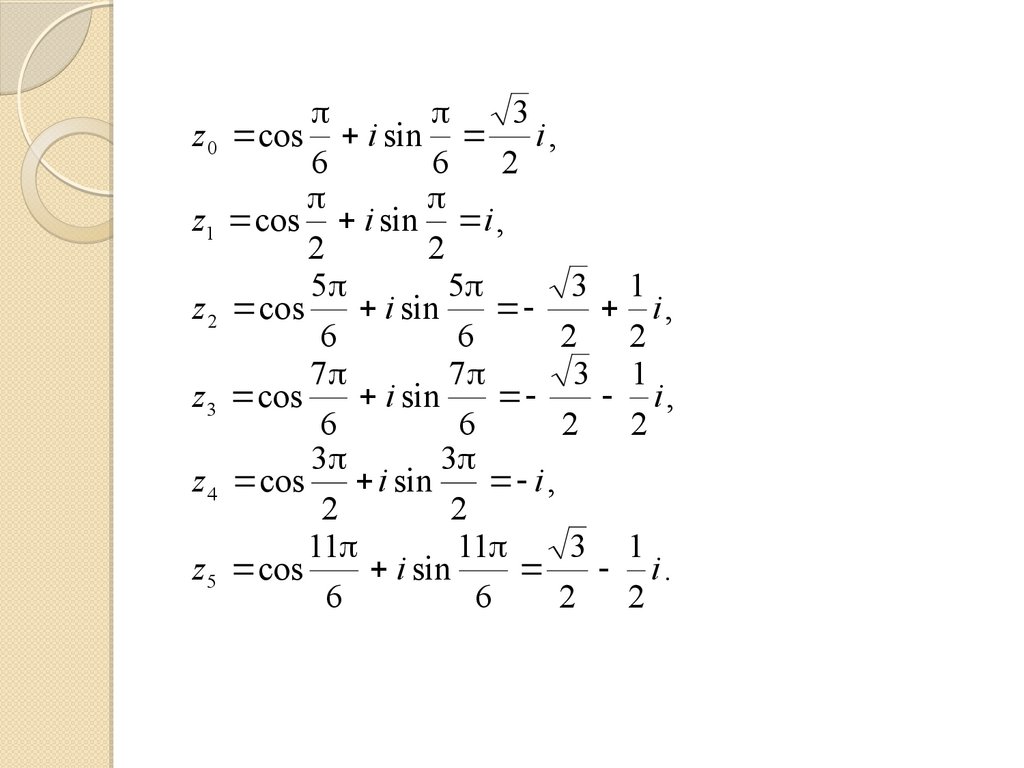

















































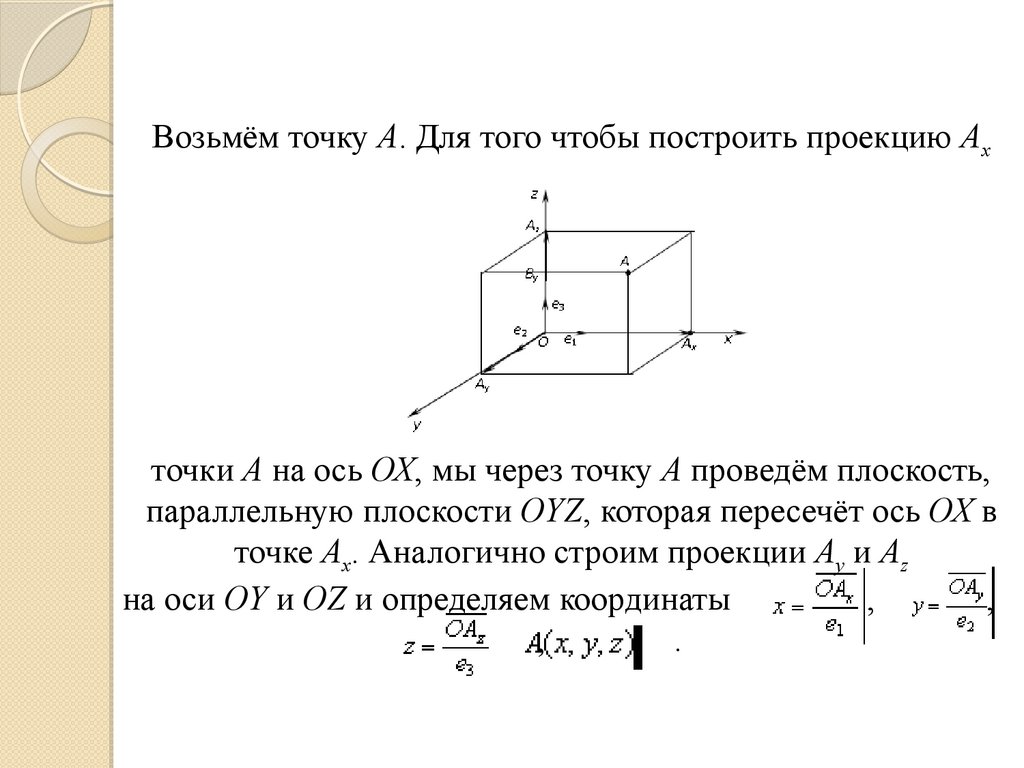



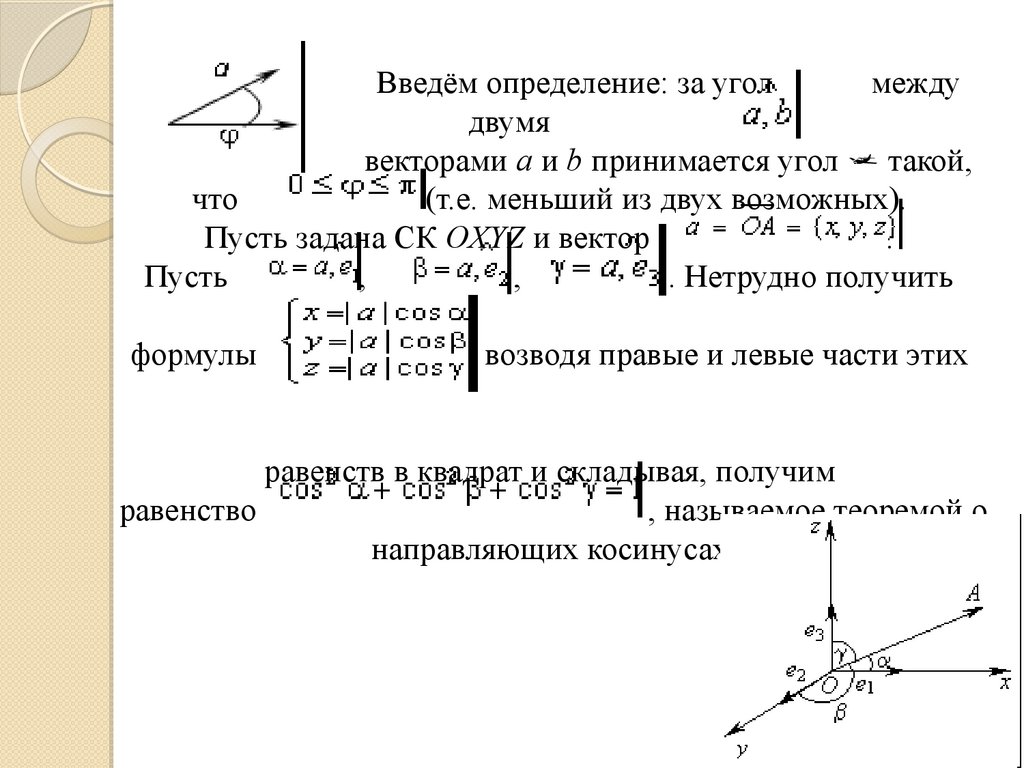

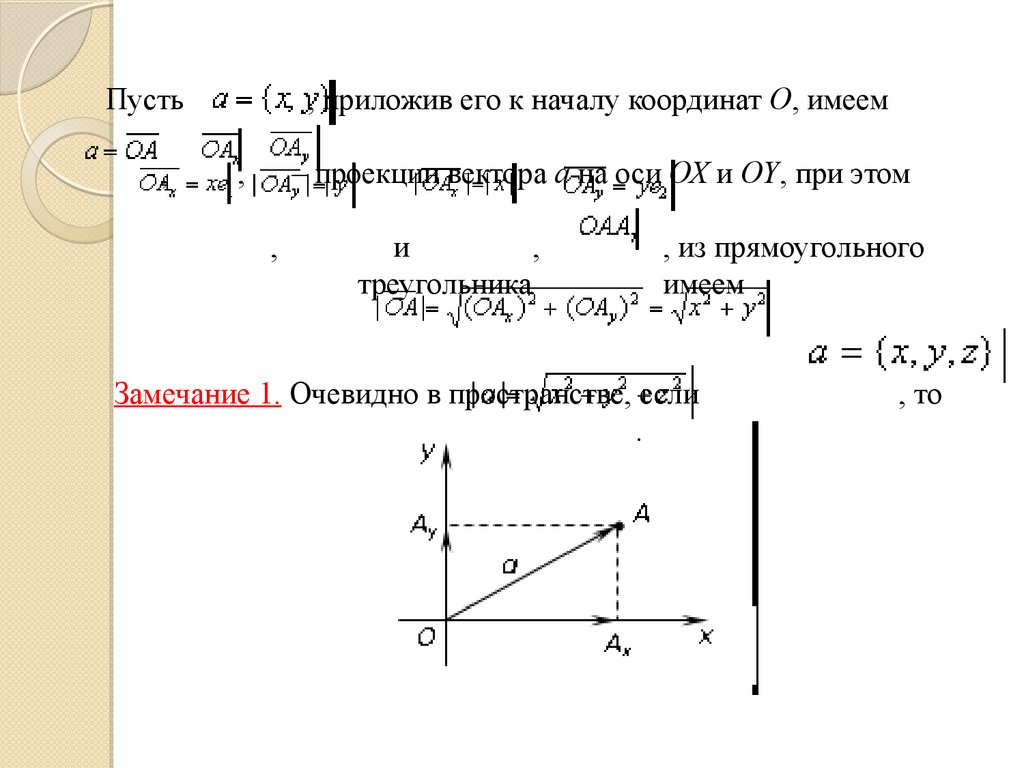














































































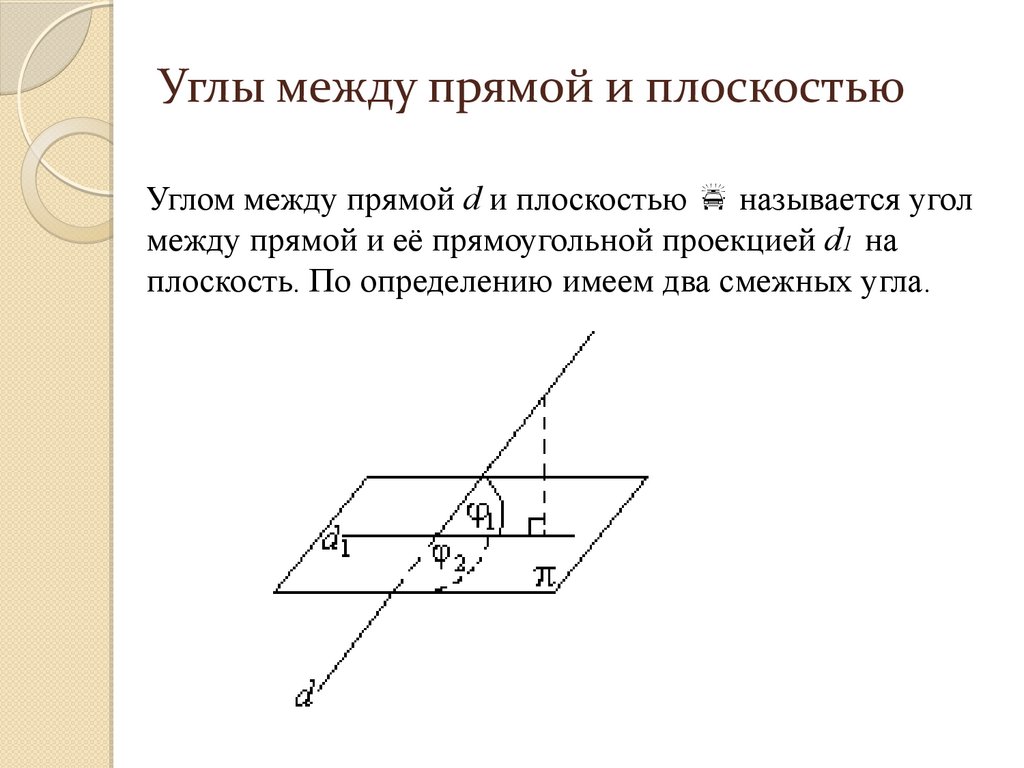

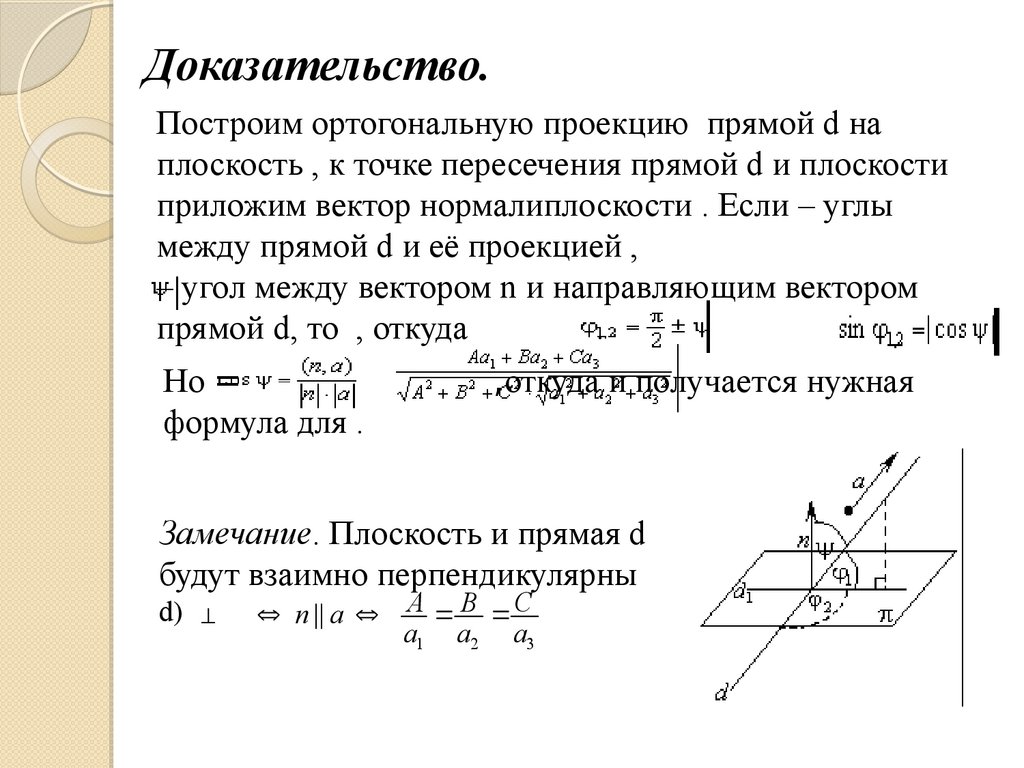











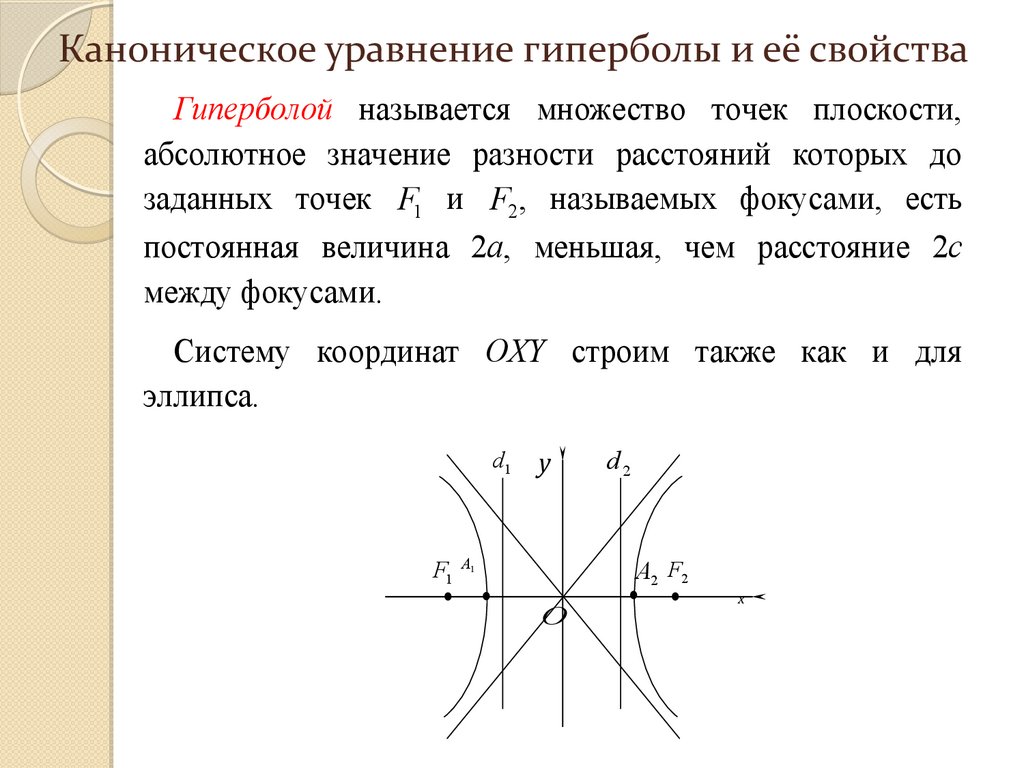












 Математика
Математика








