Лекция_4_формулы_18.10.2023

1. Лекция №4 Вычислительная математика

Санкт-Петербургский политехнический университет Петра Великого
Лекция №4
Вычислительная математика
Воскобойников С.П.
Доцент ВШ ПИ ИКНТ, к.ф.-м.н.
voskob_sp@spbstu.ru
18.10.2023

2. Содержание

• QR-разложение. Связь с ортогонализацией
векторов Грамма-Шмидта
• UDVT –разложение
• Решение систем с матрицей Хессенберга
• Подобные матрицы и их свойства
• Приведение матрицы к форме Хессенберга
подобными преобразованиями
• Пример использования подобных
преобразований при решении систем
уравнений.

3. QR -разложение

Ax b
a12 x2
a22 x2
.
.
ai 2 x2
.
.
an 2 x2
.
.
.
.
.
.
.
.
a1i xi
a2i xi
.
.
aii xi
.
.
ani xi
a11(1) x1 a12(1) x2
( 2)
a
x2
22
.
.
.
.
.
a11x1
a x
21 1
.
ai1 x1
.
an1 x1
.
.
.
.
.
.
.
.
a1n xn
a2 n xn
.
.
ain xn
.
.
ann xn
.
.
a1(i1) xi
a2( 2i ) xi
.
aii(i 1) xi
.
.
.
.
.
.
.
.
.
a1(1n) xn
a2( 2n) xn
.
ain(i 1) xn
.
( n 1)
ann
xn
b1
b2
.
bi
.
bn
b1(1)
b2( 2)
.
.
bi(i 1)
.
.
bn( n 1)

4. QR -разложение

( 0)
ij
a
aij ,
( 0)
i
b
bi
A(0) A, b( 0) b
H1 E
2
T
u
u
2 1 1
u1 2
a11(1) x1 a12(1) x2
(1)
a
22 x2
.
ai(21) x2
.
an(12) x2
.
.
. a1(i1) xi
. a2(1i) xi
. .
.
. . aii(1) xi
. .
.
. ani(1) xi
a11 0
0
a21
.
.
u1 ai 10
0
ai 1,1
.
.
0
an1
.
.
. a1(1n) xn
. a2(1n) xn
. .
.
. ain(1) xn
. .
.
(1)
. . ann
xn
1
0
.
.
n
0 2
a
0
i1
i 1
0.
.
.
0
.
.
b1(1)
b2(1)
.
bi(1)
.
bn(1)
H1 Ax H1b
A(1) H1 A( 0) , b(1) H1b( 0) ,

5. QR -разложение

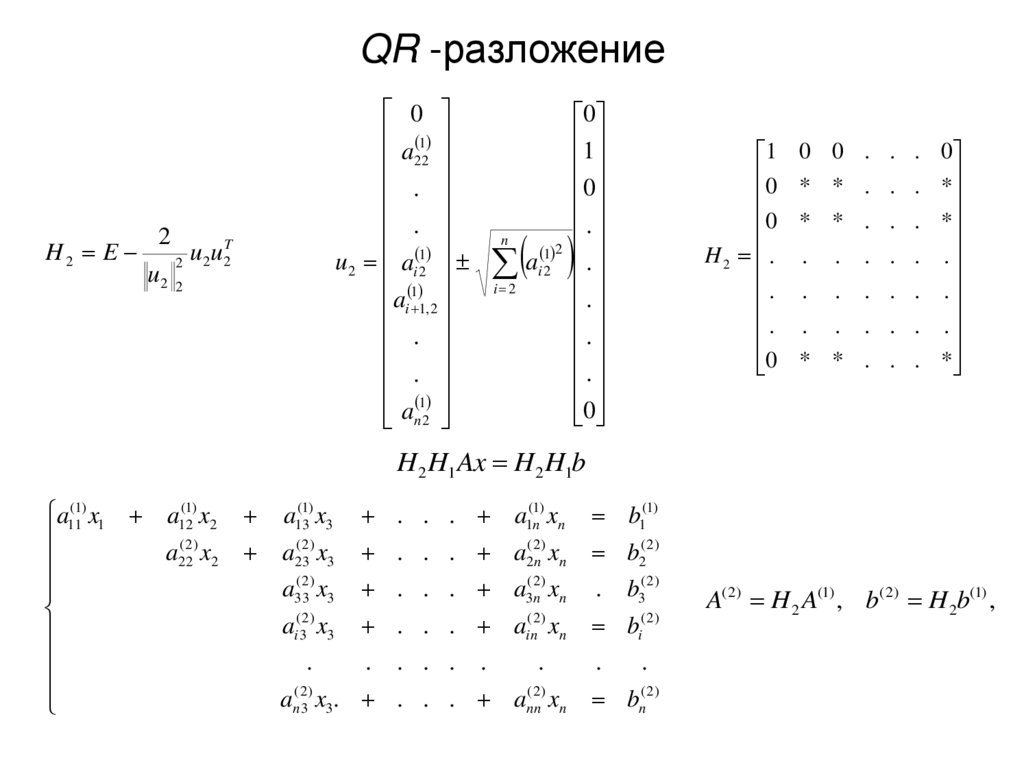
H2 E
2
0
1
a22
.
.
1
u2 ai 2
1
ai 1, 2
.
.
1
an 2
T
u
u
2
2
2
u2 2
0
1
0
.
n
2
ai 12 .
i 2
.
.
.
0
1
0
0
H2 .
.
.
0
0 0 . . . 0
* * . . . *
* * . . . *
. . . . . .
. . . . . .
. . . . . .
* * . . . *
H 2 H1 Ax H 2 H1b
a11(1) x1 a12(1) x2
( 2)
a22
x2
a13(1) x3
( 2)
a23
x3
( 2)
a33
x3
ai(32) x3
.
an( 23) x3 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a1(1n) xn
a2( 2n) xn
a3( 2n) xn
ain( 2) xn
.
( 2)
ann
xn
.
.
b1(1)
b2( 2)
b3( 2)
bi( 2)
.
bn( 2)
A( 2) H 2 A(1) , b( 2) H 2b(1) ,

6. QR -разложение

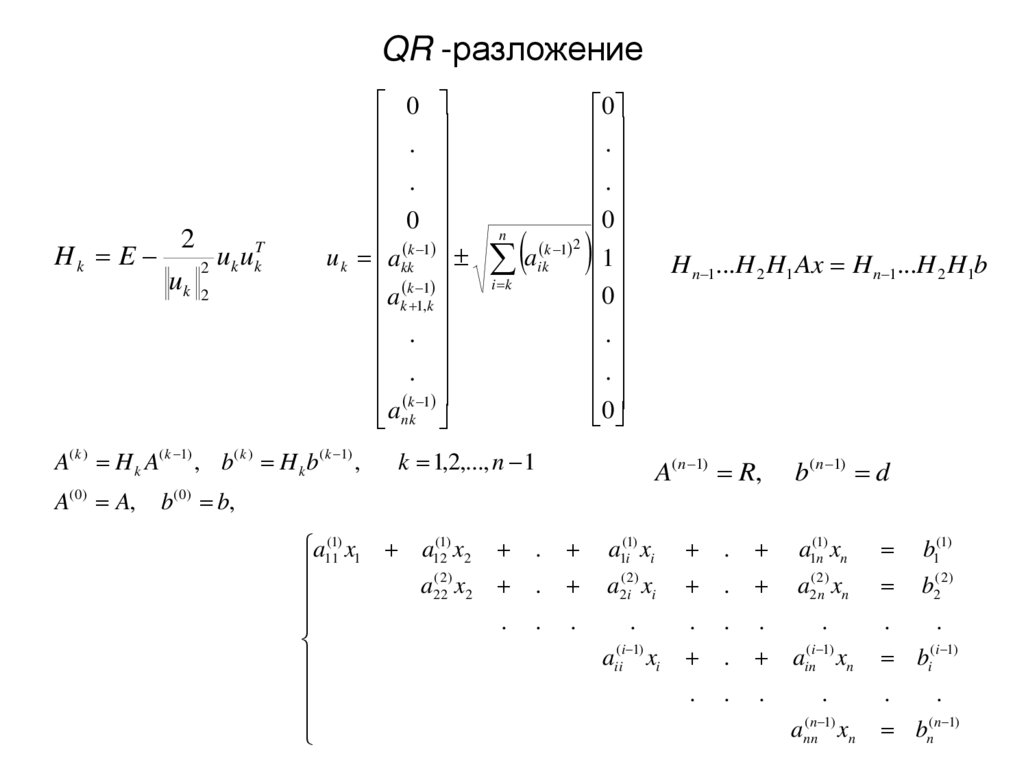
Hk E
2
T
u
u
k
k
2
uk 2
0
.
.
0
k
1
u k akk
k 1
ak 1,k
.
.
k 1
ank
A( k ) H k A( k 1) , b( k ) H k b( k 1) ,
A( 0) A,
0
.
.
0
n
2
aik k 1 1
i k
0
.
.
0
k 1,2,..., n 1
A( n 1) R,
b( 0) b,
a11(1) x1 a12(1) x2
( 2)
a22
x2
.
.
.
.
H n 1...H 2 H1 Ax H n 1...H 2 H1b
.
a1(i1) xi
a2( 2i ) xi
.
aii(i 1) xi
.
.
.
.
.
.
.
.
.
b( n 1) d
a1(1n) xn
a2( 2n) xn
.
ain(i 1) xn
.
( n 1)
ann
xn
b1(1)
b2( 2)
.
.
bi(i 1)
.
.
bn( n 1)

7. QR -разложение

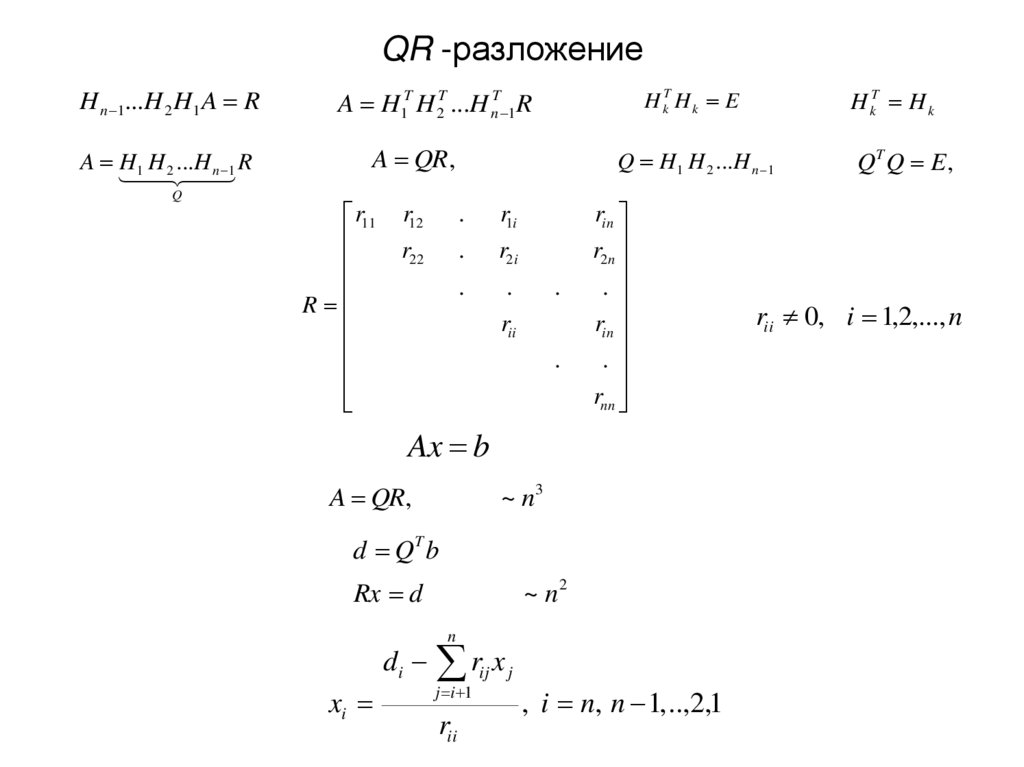
H n 1...H 2 H1 A R
A H1 H 2 ...H n 1 R
Q
H kT H k E
H kT H k
Q H1 H 2 ...H n 1
QT Q E ,
A H1T H 2T ...H nT 1R
A QR ,
r11
R
r12
r22
.
.
.
r1i
r2i
.
rii
.
.
rin
r2 n
.
rin
.
rnn
Ax b
A QR,
~ n3
d QT b
Rx d
~ n2
n
xi
d i rij x j
j i 1
rii
, i n, n 1, ..,2,1
rii 0, i 1,2,..., n

8. Ортогонализация векторов Грамма-Шмидта

a1 , a2 ,..., an R ( n )
q , q 10,,
q1 , q2 ,..., qn R ( n )
i
j
i j
qi 2
i j
qi , qi
q~1
q1
,
~
q1 2
q~1 a1,
q~2 a2 r12q1,
q~2 , q1 0
r12 a2 ,q1
k 3,4,..., n
k 1
q~k ak rjk q j ,
j 1
q~ , q 0,
k
j
q~2
q2
,
~
q2 2
j 1,2,..., k 1 rjk ak , q j
k 1
ak q~k rjk q j ,
q~k qk q~k 2 qk rkk ,
j 1
k 1
k
j 1
j 1
ak rkk qk rjk q j rjk q j , k 1,2,..., n
q~k
qk
,
~
qk 2

9. Связь ортогонализации векторов Грамма-Шмидта с QR -разложением

a1 , a2 ,..., an R ( n )
q1 , q2 ,..., qn R ( n )
k
q , q 10,,
i
j
ak rjk q j , k 1,2,..., n
i j
qi 2
i j
qi , qi
j 1
a1
A QR ,
a2 . ak
. an q1 q2 . qk
~R
~,
A QOOR Q
1
1
.
O
r11 r12
r22
. qn
.
.
1
.
.
.
r1k
r2 k
.
rkk
.
.
.
.
.
~ ~
QT Q E
r1n
r2 n
.
rkn
.
rnn

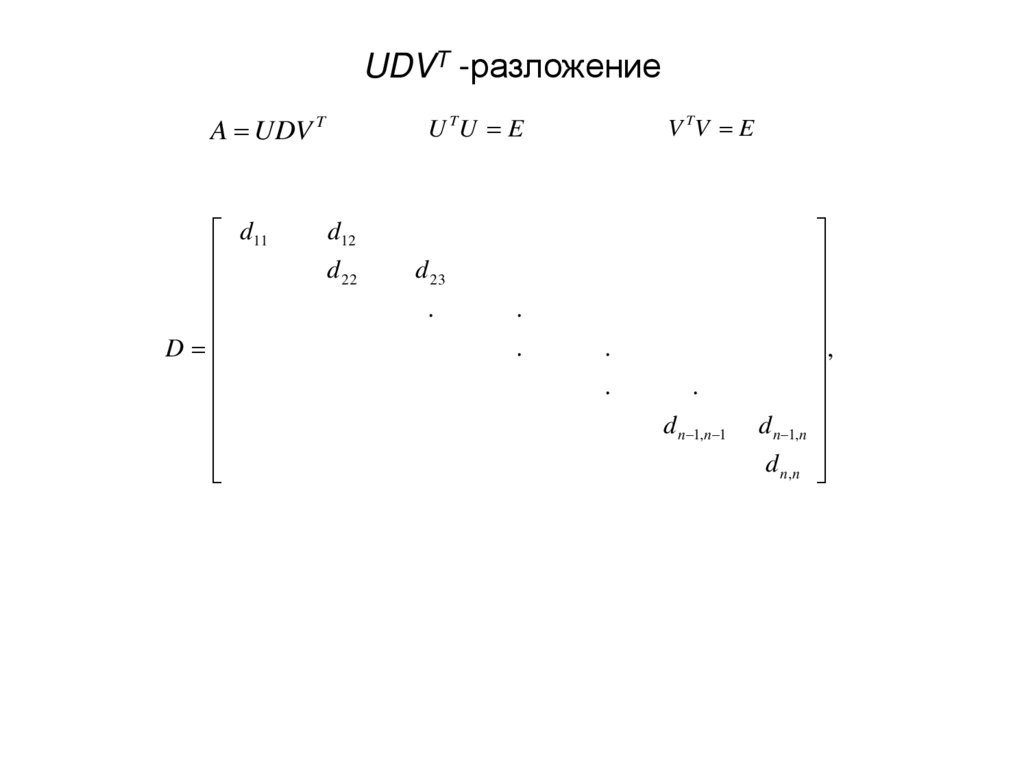
10. UDVT -разложение

d11
D
V TV E
U TU E
A UDV T
d12
d 22
d 23
.
.
.
.
.
.
d n 1,n 1
,
d n 1,n
d n ,n

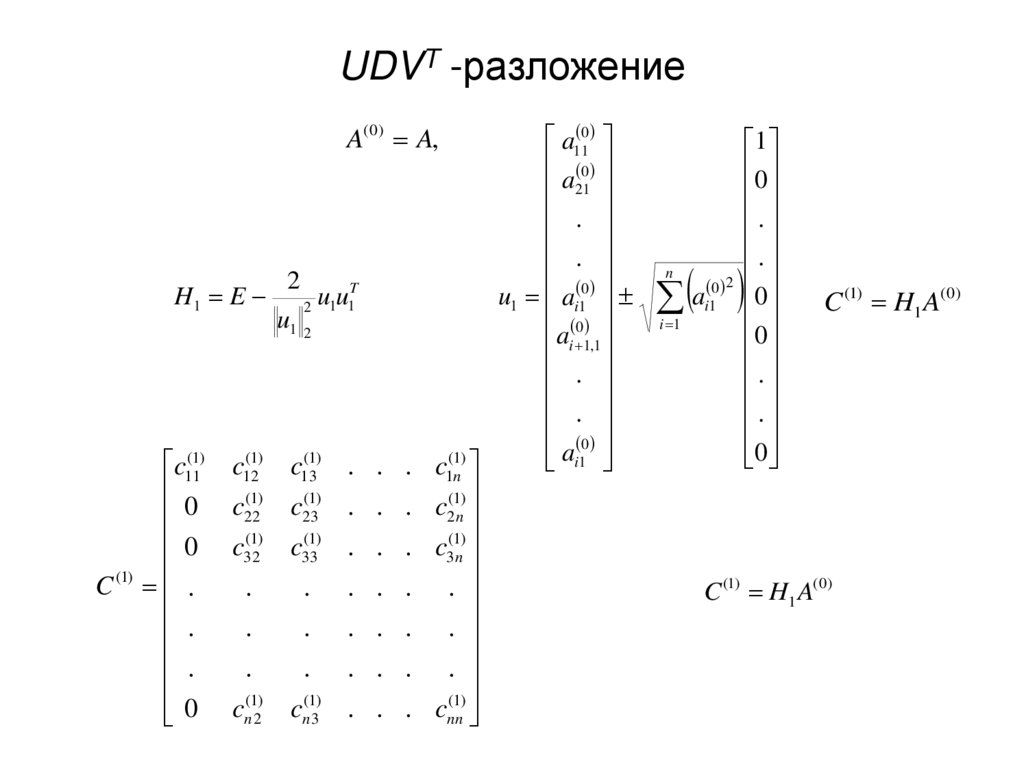
11. UDVT -разложение

a11 0
0
a21
.
.
u1 ai 10
0
ai 1,1
.
.
0
(1)
ai1
c1n
c2(1n)
c3(1n)
.
.
.
(1)
cnn
A(0) A,
H1 E
c11(1)
0
0
C (1) .
.
.
0
2
2
u1 2
u1u1T
c12(1)
(1)
c22
c13(1) . . .
(1)
c23
. . .
(1)
c32
.
(1)
c33
. . .
. . . .
.
.
.
.
. . .
. . .
cn(12)
cn(13) . . .
1
0
.
.
n
0 2
a
0
i1
i 1
0
.
.
0
C (1) H1 A( 0)
C (1) H1 A( 0)

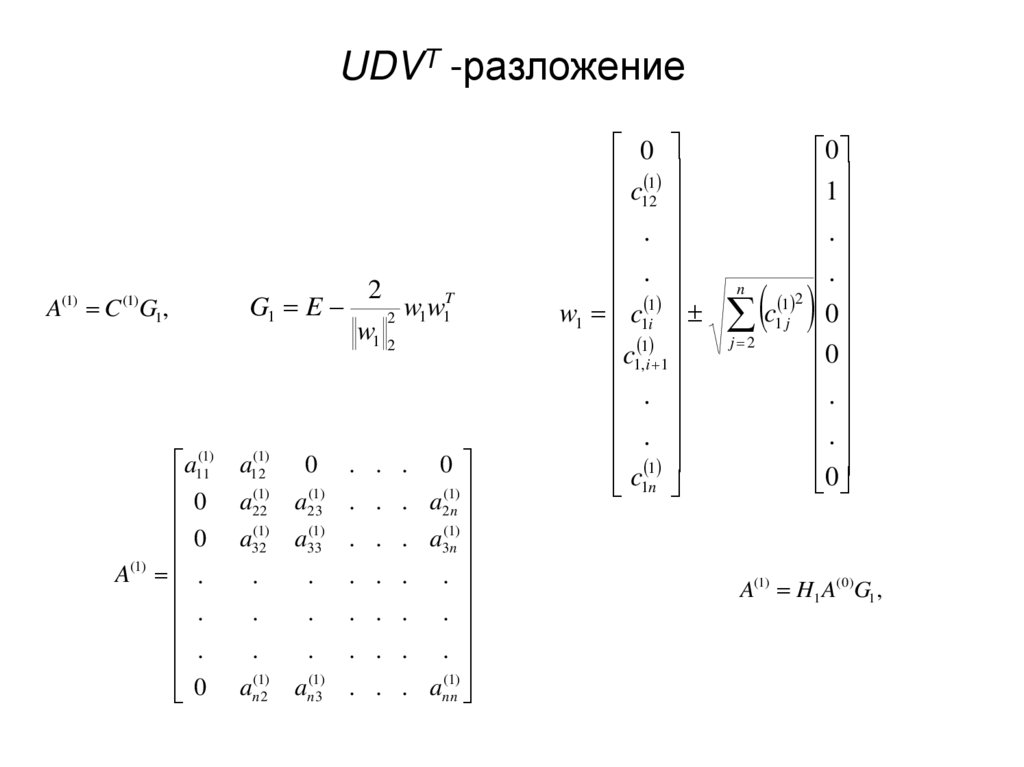
12. UDVT -разложение

A(1) C (1)G1 ,
a11(1)
0
0
A(1) .
.
.
0
G1 E
a12(1)
(1)
a22
(1)
a32
.
.
.
an(12)
2
2
w1 2
w1w1T
0 . . . 0
(1)
a23
. . . a2(1n)
(1)
a33
. . . a3(1n)
. . . . .
. . . . .
. . . . .
(1)
an(13) . . . ann
0
1
c12
.
.
w1 c1 1i
1
c1,i 1
.
.
1
c1n
0
1
.
.
n
1 2
c
0
1j
j 2
0
.
.
0
A(1) H1 A( 0)G1 ,

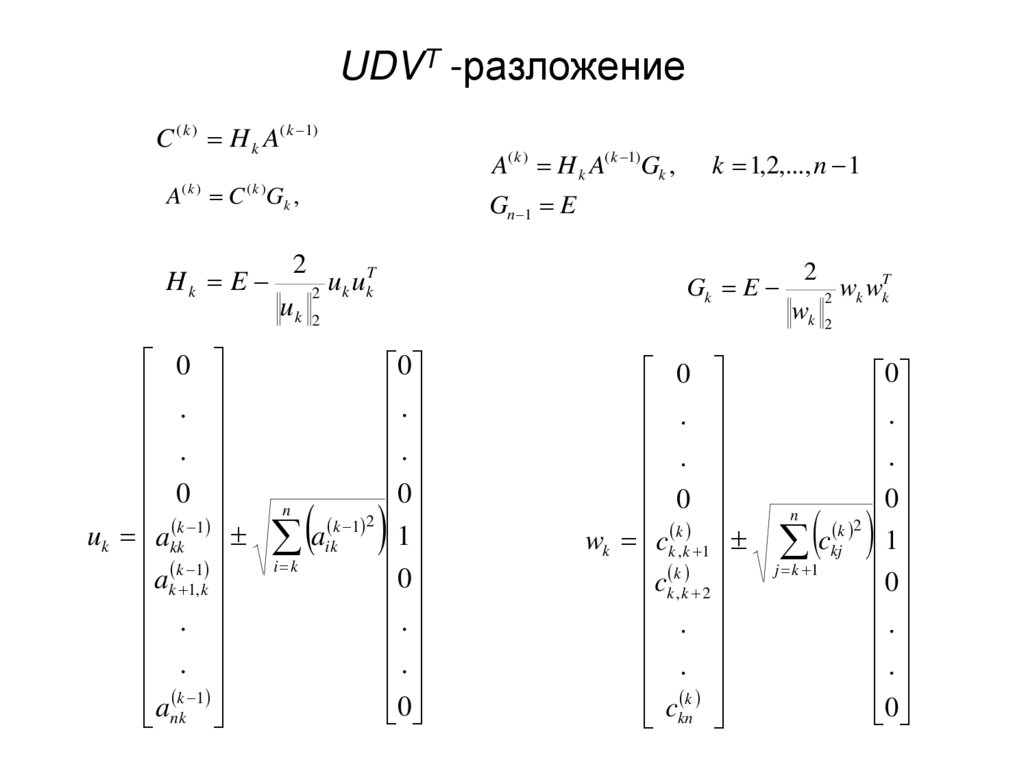
13. UDVT -разложение

C ( k ) H k A( k 1)
A( k ) H k A( k 1)Gk ,
A( k ) C ( k )Gk ,
Hk E
0
.
.
0
uk akk k 1
k 1
ak 1, k
.
.
k 1
ank
k 1,2,..., n 1
Gn 1 E
2
T
u
u
2 k k
Gk E
uk 2
0
.
.
0
n
k 1 2
a
1
ik
i k
0
.
.
0
0
.
.
0
wk ck k, k 1
k
ck , k 2
.
.
k
ckn
2
2
wk 2
wk wkT
0
.
.
0
n
k 2
c
1
kj
j k 1
0
.
.
0

14. UDVT -разложение

H n 1...H 2 H1 AG1G2 ...Gn 1 D
A H nT 1...H 2T H1T DGnT 1...G2T G1T
A H nT 1...H 2T H1T DGnT 1...G2T G1T
U H nT 1...H 2T H1T H n 1...H 2 H1
U H n 1...H 2 H1
V T GnT 1...G2T G1T G1G2 ...Gn 1
T
V G1G2 ...Gn 1
U H n 1...H 2 H1
Ax b
f U b
Dy f
T
A UDV ,
T
~n
3
x Vy
yn
fn
,
d nn
f i d i ,i 1 yi 1
yi
, i n 1, ..,2,1
d ii

15. Решение систем с матрицей Хессенберга

Ax b
a11x1 a12 x2
a x a x
22 2
21 1
a32 x2
a13 x3 ... a1, n 2 xn 2
a23 x3 ... a2, n 2 xn 2
a33 x3 ... a3, n 2 xn 3
.
.
.
an 1, n 2 xn 2
a11 a12
a
21 a22
a32
A
a13 . . .
a23 . . .
a33 . . .
.
a1, n 1 xn 1
a2, n 1 xn 1
a3, n 1 xn 1
.
.
an 1, n 1 xn 1
an, n 1 xn 1
a1, n 2
a2, n 2
a3, n 2
.
an 1, n 2
a1n xn
a2 n xn
a3, n xn
.
.
an 1, n xn
ann xn
a1, n 1
a1n
a2, n 1
a2 n
a3, n 1
a3, n
.
.
an 1, n 1 an 1, n
an , n 1
ann
b1
b2
b3
.
.
bn 1
bn

16. Решение систем с матрицей Хессенберга

A(0) A, aij(0) aij ,
Для k 1,2,..., n 2
1
Gk
A( k ) Gk A( k 1) ,
.
.
.
1
gk ,k
g k , k 1
g k 1, k
g k 1, k 1
1
.
.
,
.
1
gk ,k
g k , k 1
ak( k, k 1)
a a
( k 1) 2
k ,k
( k 1) 2
k 1, k
ak( k 1,1k)
a a
( k 1) 2
k ,k
g k 1, k 1 g k , k ,
g k 1, k g k , k 1 ,
( k 1) 2
k 1, k
,
,

17. Решение систем с матрицей Хессенберга

R A( N 2) Gn 2 G2G1 A,
r11
R
A QR
r12
r22
.
.
.
r1i
r2i
.
rii
.
.
r1n
r2 n
.
,
rin
.
rnn
~ n2
Q G1T G2T GnT 2 ,
QT Q E
Ax b
d Gn 2 G2G1b
Rx d
n
xi
d i rij x j
j i 1
rii
, i n, n 1, ..,2,1
~ n2

18. Подобные матрицы и их свойства

B S 1 AS ,
A SBS 1 ,
A AT ,
B BT ,
Ax x
By y
A SBS T ,
S T S E,
B S T AS ,
X x1
x2 . . . xn ,
Y y1
y2 . . . yn ,
1. i i
2. xi Syi , i 1,2,...n
Ax x,
A SBS 1 ,
SBS 1 x x,
BS 1x S 1x,
y S 1 x,
By y,
X SY

19. Приведение матрицы к форме Хессенберга подобными преобразованиями

A(0) A, aij(0) aij ,
Hk E
A( k ) H k A( k 1) H kT ,
k 1,2,..., n 2
2
2
uk 2
0
.
.
0
uk ak k 11,k
k 1
ak 2 , k
.
.
k 1
ank
A( k ) , aij( k ) ,
uk ukT ,
a~11
a~
21
~
( n 2)
A
A
a~12
a~22
a~32
a~13 . . .
a~23 . . .
a~33 . . .
.
0
.
.
0
n
k 1 2
a
1 ,
ik
i k 1
0
.
.
0
a~1, n 2
a~2, n 2
a~3, n 2
.
a~n 1, n 2
a~1, n 1
a~1n
a~2, n 1
a~2 n
a~3, n 1
a~3, n
,
.
.
a~n 1, n 1 an 1, n
~
~
an, n 1
ann

20. Приведение матрицы к форме Хессенберга подобными преобразованиями

~ H ...H H AH T H T ...H T ,
A
n 2
2 1
1
2
n 2
Q H n 2 ...H 2 H1
QT H1T H 2T ...H nT 2
QT Q E
~ QAQT ,
A
~
A QT AQ,
~ n3 ,
~ ,
A A
~ A
~T ,
A AT , A
a~11
a~
21
~
( n 2)
A
A
a~21
a~22 a~32
a~32 a~33 a~43
.
.
.
a~n 1, n 2
a~n 1, n 1
a~n , n 1
,
a~n , n 1
~
ann

21. Пример использования подобных преобразований и формы Хессенберга при решении систем уравнений

A i E x b,
i 1,2,..., m
Q A~ Q Q Q x b,
~
A QT AQ,
T
A~ E y d ,
y Qx ,
d Qb,
i
~ QAQT ,
A
~ n3
A~ E y d ,
i 1,2,..., m
i
a~11 i
a~
21
~
A i E
~ E Qx b,
QT A
i
T
i
a~12
a~22 i
a~32
x QT y ,
a~13
...
a~23
...
a~33 i . . .
.
a~1, n 2
a~2, n 2
a~3, n 2
.
a~n 1, n 2
~ mn 2
a~1, n 1
a~2, n 1
a~3, n 1
.
a~n 1, n 1 i
a~n , n 1
a~1n
a~2 n
a~3, n
,
.
an 1, n
a~nn i
~ n3 mn2

22. Пример использования подобных преобразований и формы Хессенберга при решении систем уравнений

~ A
~T ,
A
~
A QT AQ,
A AT ,
A i E x b,
A~ E y d ,
i 1,2,..., m
y Qx ,
d Qb,
i
~ QAQT ,
A
~ n3
A~ E y d ,
i 1,2,..., m
i
a~11 i
a~
21
~
A i E
x QT y ,
a~21
a~22 i
a~32
a~32
a~33 i
.
a~43
.
.
a~n 1, n 2
~ mn
a~n 1, n 1 i
a~n , n 1
~ n 3 mn
,
a~n, n 1
~
ann i