Похожие презентации:
Лекция_8
1.
§ 11. Интеграл уравнения и его свойстваy f ( x; y )
(1)
y( x0 ) y0
(2)
y ( x; C )
(3)
( x; y ) C
(4)
2.
xy ; x 0; y 0
y
Пример.
x2 y2 C
С>0
( x; y) x y const
2
2
Рассмотрим некоторое решение уравнения, например, проходящее через точку
(0;1).
y 1 x
2
2
( x; y) x 1 x 1
2
2
3.
( x; y) С1 ( D)d (1)
dx
dy (1)
dx
f ( x; y)dx 0
x
y
x
y
d
f ( x; y ) 0
dx (1) x
y
x
f ( x; y )
y
0
y 0 x 0 f ( x; y )
0
(5)
(6)
(7)
4.
d (1) 0;2
0.
x y
2
5.
2 ( x; y) ( 1 ( x; y))(8)
( z ) 0
2 d
1
;
x
dz z 1 x
2 d
1
.
y
dz z 1 y
2 2
1 1
d
d
d 2 (1)
f ( x; y ) dx
f ( x; y ) dx
d 1 (1) 0
y
dz z 1 x
y
dz z 1
x
6.
22
d
2 2
1
1
0.
y
x
y
dz
x
z 1
2
2
1 ( x; y) C
⇒
1 ( x; y ) C
Это свойство означает, что уравнение (1) имеет бесконечно много интегралов на
множестве D и позволяет записать общий интеграл в наиболее удобной форме.
7.
Любые два интеграла уравнения (1) на одном и том же множестве зависимы,т.е. связаны соотношением вида (8) при некотором выборе функции Φ(


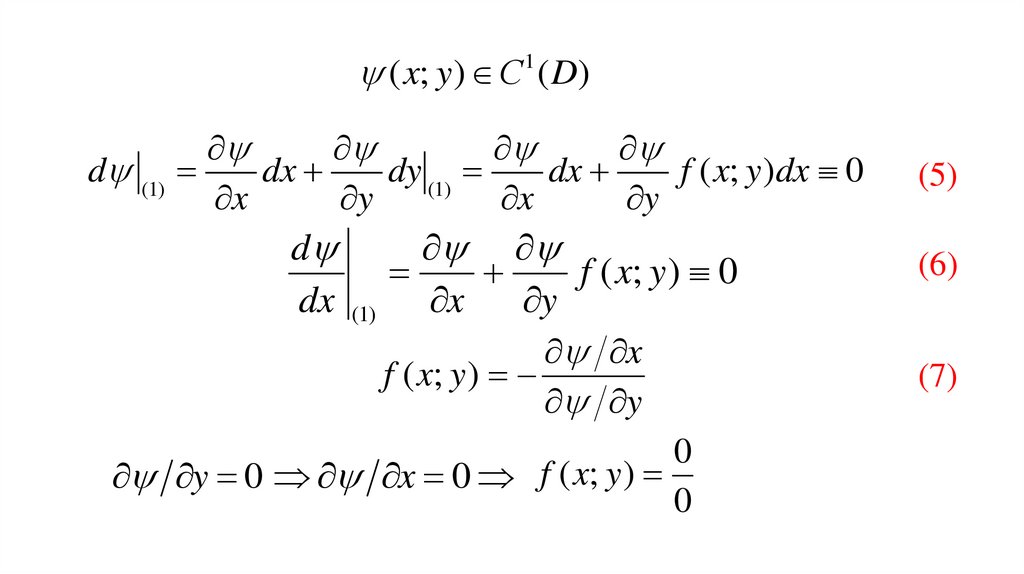

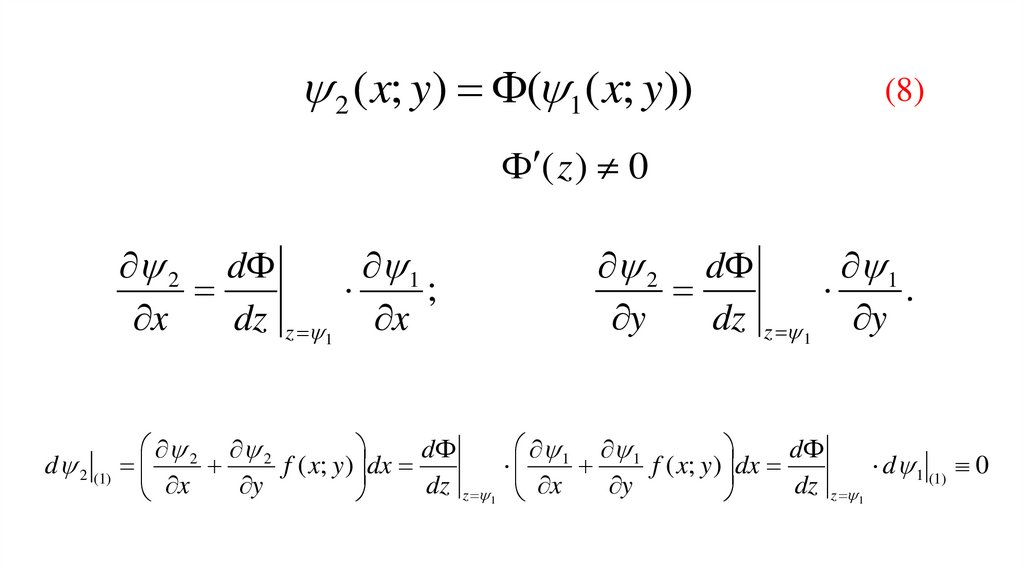


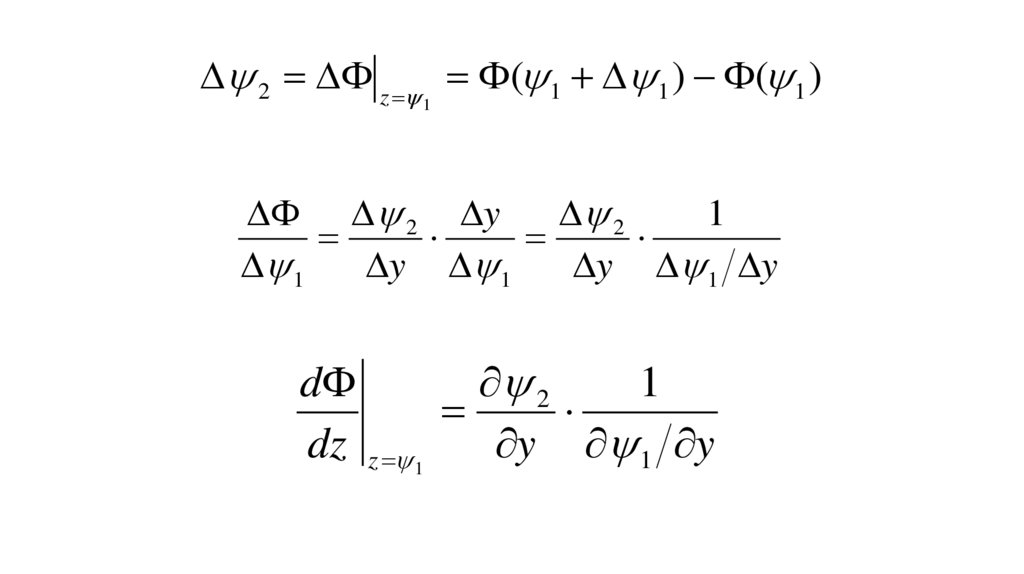





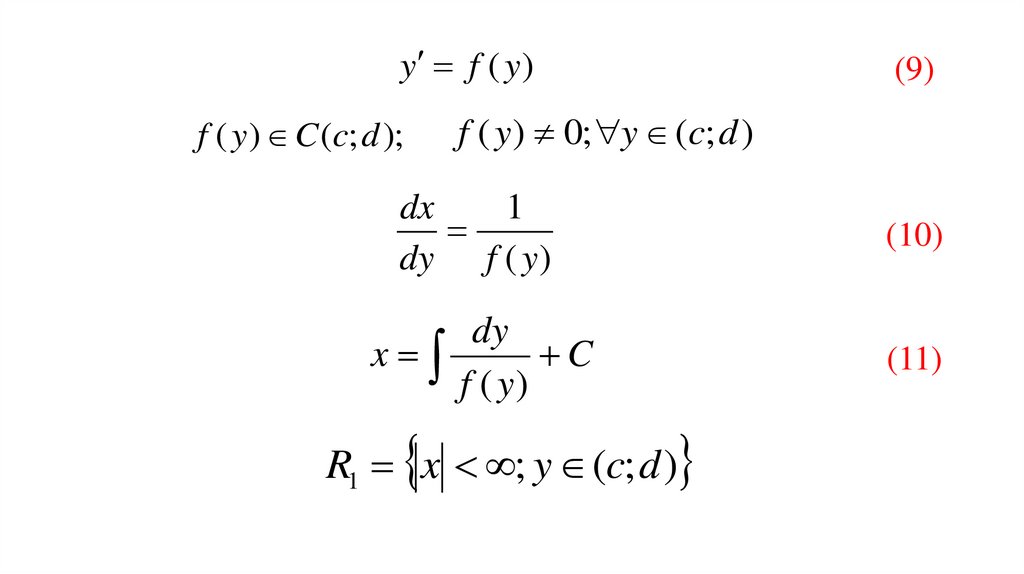

















 Математика
Математика








