Лекция_1_формулы_06.09.2023 (4)

1. Лекция №1 Вычислительная математика

Санкт-Петербургский политехнический университет Петра Великого
Лекция №1
Вычислительная математика
Воскобойников С.П.
Доцент ВШ ПИ ИКНТ, к.ф.-м.н.
voskob_sp@spbstu.ru
06.09.2023

2. Содержание

Нормы векторов и матриц. Аксиомы норм.
Оценка |λ|max и |λ|min матрицы
Теорема Гершгорина. Круги Гершгорина.
Диагональное преобладание в матрице по строкам и
столбцам. Следствие Адамара.
Лемма о матрице E+C.
Решение систем Ax=b. Невязка, ошибка и их связь.
Число обусловленности и его свойства.
Неравенства для оценки погрешности решения Ax=b.
Обусловленность ортогональных матриц

3. Нормы векторов. Аксиомы норм.

вещественные векторы размерности N
x1
x
2
x
xN
y1
y
2
y
y N
x
1. x 0, x 0, x 0
2. x x
3. x y x y

4. Нормы векторов и матриц. Аксиомы норм.

x y x y
x x y y x y y
x y x y
y y x x y x x
y x y x
x y y x
x y x y

5. Примеры векторных норм

N
x p p xi ,
p
p 1,2,3,...
i 1
N
x 1 xi
i 1
x2
N
2
x
i
i 1
x max xi
i
2
x 1
3
x1 6
x 2 14
x 3

6. Нормы матриц. Аксиомы норм.

вещественные квадратные матрицы размерности N
a11 a12 ... a1 j ... a1N
a
a
...
a
...
a
21
22
2j
2N
A
...
aN 1 aN 2 ... aNj ... aNN
b11 b12 ... b1 j ... b1N
b
b
...
b
...
b
21
22
2j
2N
B
...
bN 1 bN 2 ...bNj ...bNN
A
1. A 0, A 0, A 0
2. A A
3. A B A B
4. AB A B
каноническая норма
5. A ai , j
6. ai , j bi , j
A B

7. Нормы матриц. Аксиомы норм.

согласованная матричная норма
Ax A x
подчинённая векторной норме матричная норма
Ax
A sup
x
x 0
,
N
A 1 max aij
j
i 1
A 2 max
i i AT A
N
A max aij
i
5 2 1
A 1 4 2
3 2 7
A 1 10
j 1
A 2 8.80326192114174
A 12

8. Оценка |λ|max матрицы

Ax x
x Ax
,
x Ax
x Ax
A
max A

9. Оценка |λ|min матрицы

Ax x
A 1 x 1 x
1 x A 1 x
1 x A 1 x
1 x A 1 x
1 A 1
1 max A 1
1
min
A 1
1
min 1
A

10. Теорема Гершгорина

Ax x
N
a x x
N
a x a x
j 1
j i
ij
j
ii
ij
j 1
j
i
xi максимальн ый по модулю элемент
i
xj
N
a x a
j 1
j i
N
xj
j 1
j i
xi
aii aij
ij
ii
i
N
xj
j 1
j i
xi
aij
N
xj
j 1
j i
xi
aij
N
Ri aij
j 1
j i
aii Ri , i 1,2,..., N
N
aij
j 1
j i

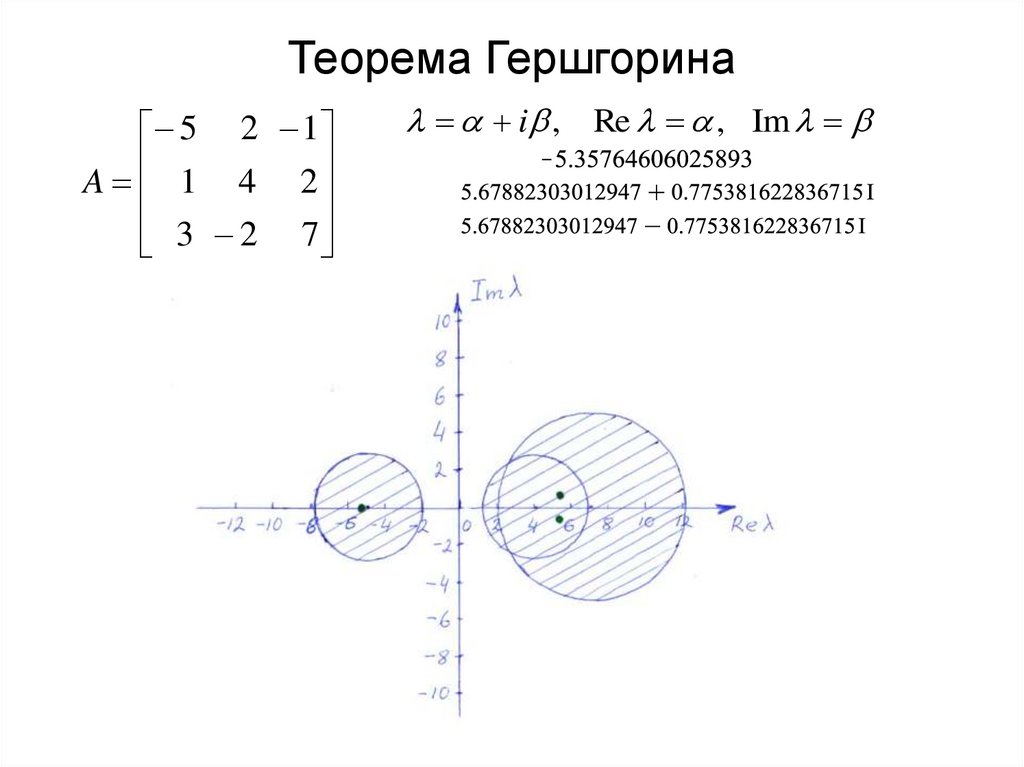
11. Теорема Гершгорина

5 2 1
A 1 4 2
3 2 7
i , Re , Im

12. Диагональное преобладание

N
aii Ri aij , i 1,2,..., N диагональн ое преобладание по строкам
j 1
j i
N
a jj R j aij , j 1,2,..., N диагональное преобладание по столбцам
i 1
i j
N
aii Ri aij , i 1,2,..., N строгое диагональное преобладание по строкам
j 1
j i
N
a jj R j aij , j 1,2,..., N строгое диагональное преобладание по столбцам
i 1
i j
Матрица со строгим диагональным преобладанием
по строкам (или столбцам) невырожденна.

13. Лемма о матрице Е+С

C N N матрица
1.
C 1
det E C 0 и E C
1
E C 1
2.
E C x
1
1 C
E C x x Cx x Cx x C x 1 C x 0
E C x 0
x 0
E C x 1 C x
x
1
E C x 1 C
w E C x
E C 1 w
1
w
E C
1
sup
w 0
E C 1 w
w
x E C w
1
1 C
E C
1
1
1 C

14. Системы линейных алгебраических уравнений

a11x1 a12 x2 ... a1 j x j ... a1N xN b1
a21x1 a22 x2 ... a2 j x j ... a2 N xN b2
...
aN 1 x1 aN 2 x2 ... aNj x j ... aNN xN bN
det A 0
a11 a12 ... a1 j ... a1N
a
a
...
a
...
a
21
22
2j
2N
A
...
aN 1 aN 2 ... aNj ... aNN
Ax b
b1
b
b 2
...
bN

15. Невязка и ошибка

Ax b
~
x
невязка r b A~
x
ошибка (погрешность) решения z x ~
x
r b A~
x A A 1b ~
x A x ~
x Az
r Az
z A 1r
Az r

16. Оценка невязки и ошибки. Число обусловленности.

Ax b
z A 1 r
z
1 r
A
x
x
b
x
A
z
1 r
A A
x
b
z
r
A
x
b
A cond A A A 1
r
~ M
b
A ~
1
M
почти вырожденные или
алгоритмически вырожденные
плохообусловленные системы
r
A ~ 1
b

17. Свойства числа обусловленности

Ax b
A cond A A A 1
max
1. A
min
2. 1 A ,
0 rcond ( A)
3. AB A B
1
1
A
1
max A
min
A 1
max
A A 1
min
AB AB AB 1 AB B 1 A 1 A B B 1 A 1 A B

18. Оценка погрешности решения для возмущённой системы

Ax b
det A 0
A F ~x b f
x ~
x
F
1
A 1
1. det A F 0
A
F
f
, где A cond A A A 1
2.
F A
x
b
1 A
A

19. Оценка погрешности решения для возмущённой системы

A F A E A 1F
A 1F A 1 F A 1
1
1
1
A
det E A 1F 0
E A F
1
1
1
1
1
1
1 A F 1 A F
1
1 A A
1
F
A
1
F
1 A
A

20. Оценка погрешности решения для возмущённой системы

1
1
~
x A F b A F f
1
1
~
x x A F Ax x A F f
1
1
~
x x A F A E A 1 A F x A F f
1
1
~
x x A F F x A F f
1
1
~
x x A F F x A F f
~
x x
1
1 f
A F F A F
x
x

21. Оценка погрешности решения для возмущённой системы

A F A E A 1F
A F 1 E A 1F 1 A 1
A F
1
1
E A F
A
1
1
~
x x
1
1
1
1
1
1 f
E A F
A F E A F
A
x
x
~
x x
F
f
1
1
E A 1F
A A 1
E A 1F
A A 1
x
A
b
~
F
x x
f
1
1
1
E A F
A A
x
b
A
~
x x
x
A
F
f
F A
b
1 A
A
~
x x
f
A ,
x
b
F 0
b
x
A

22. Пример влияния возмущения системы на решение

1,000 x1 0,999 x2 1,999
0,999 x1 1,000 x2 1,999
1,000 0,999
A
0,999 1,000
x1 0,999~
x2 2,000
1,000 ~
~
~
0,999 x1 1,000 x2 1,998
0,001
f
0,001
x
A
f
b
1,999
b
1,999
~
x1 2
x1 1
~
x2 0
x2 1
1
1
A cond A A A 1
0,999
103 1
A
1
1,999 0,999
1
A 1 1,999
A 1 1000
1
f1
0,002
A 1
1999
1
b1
3,998
1 0,001
A 1 1999
f 1 0,002
1 x ~
x 1 2
2 1,999
x 1 2
A 2 1999
b 1 3,998
1
x1
1

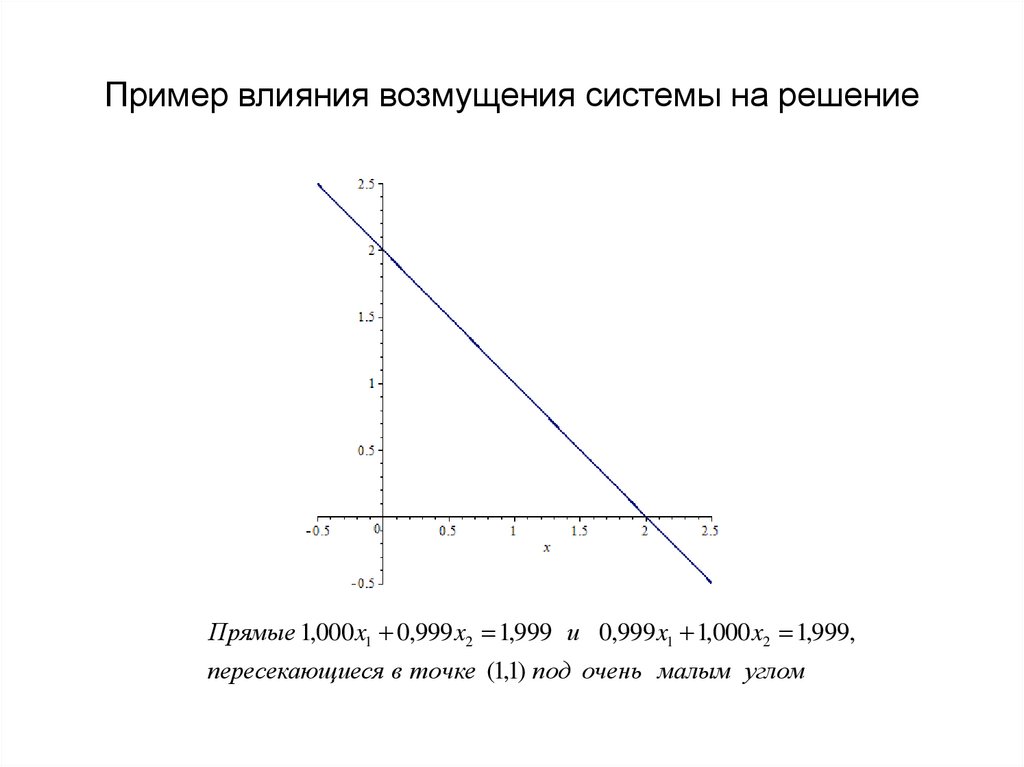
23. Пример влияния возмущения системы на решение

Прямые 1,000 x1 0,999 x2 1,999 и 0,999 x1 1,000 x2 1,999,
пересекающиеся в точке (1,1) под очень малым углом

24. Обусловленность ортогональных матриц

оптимально обусловленные матрицы A 1
Ортогональные матрицы
QT Q 1
Q Q E
T
y, x y T x
x, y xT y
x, x xT x x 22
y Qx
y 2 Qx 2 Qx Qx xT QT Qx xT x x 2
2
Qx
Q sup
x
x 0
2
2
T
Q 2 sup
x 0
Qx 2
x2
1
2 Q Q 2 Q 1 2 1
Q 1 QT sup
2
2
x 0
QT x
x2
2
1

25. Литература по курсу

• 1.Зимницкий В.А., Устинов С.М.
"Вычислительная математика"
Дополнительная
• 2.Самарский А.А., Гулин А.Б. "Численные
методы".
• 3.Бахвалов Н.С.,Жидков, Кобельков
"Численные методы".
• 4.Калиткин Н.Н. "Численные методы".
• 5.Голуб Дж., Ван Лоун Ч. Матричные
вычисления.