Презентация Прямоугольная система координат в пространстве

1.

Вспомним, как определяется координатная(числовая) прямая.
1) Изображаем произвольную прямую;
2) Придаем ей положительное направление и обозначаем её;
3) Выбираем произвольную точку за начало отсчета;
4) Определяем длину единичного отрезка (масштаб).
М
0
1
х
а
Тогда любой точке этой координатной прямой соответствует
единственное действительной число a. И наоборот, любое
действительное число может быть изображено единственной
соответствующей точкой, для которой это число является
координатой. Записывают: M(a).

2.

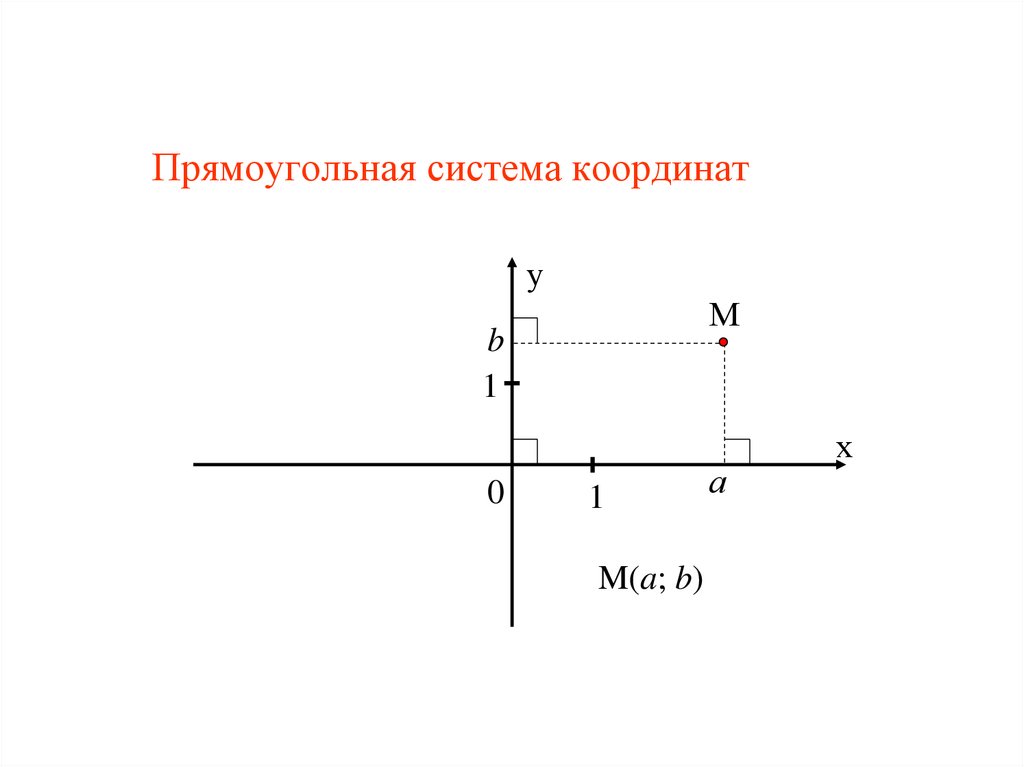
Прямоугольная система координат
у
М
b
1
0
1
M(a; b)
а
х

3. Прямоугольная система координат

Прямоугольной системой координат в пространстве называется
тройка взаимно перпендикулярных координатных прямых с общим
началом координат. Общее начало координат обозначается буквой
O, а координатные прямые обозначаются Ox, Oy, Oz и называются
соответственно осью абсцисс, осью ординат и осью аппликат .
Плоскости, проходящие через пары координатных прямых,
называются координатными плоскостями и обозначаются Oxy, Oxz и
Oyz соответственно.

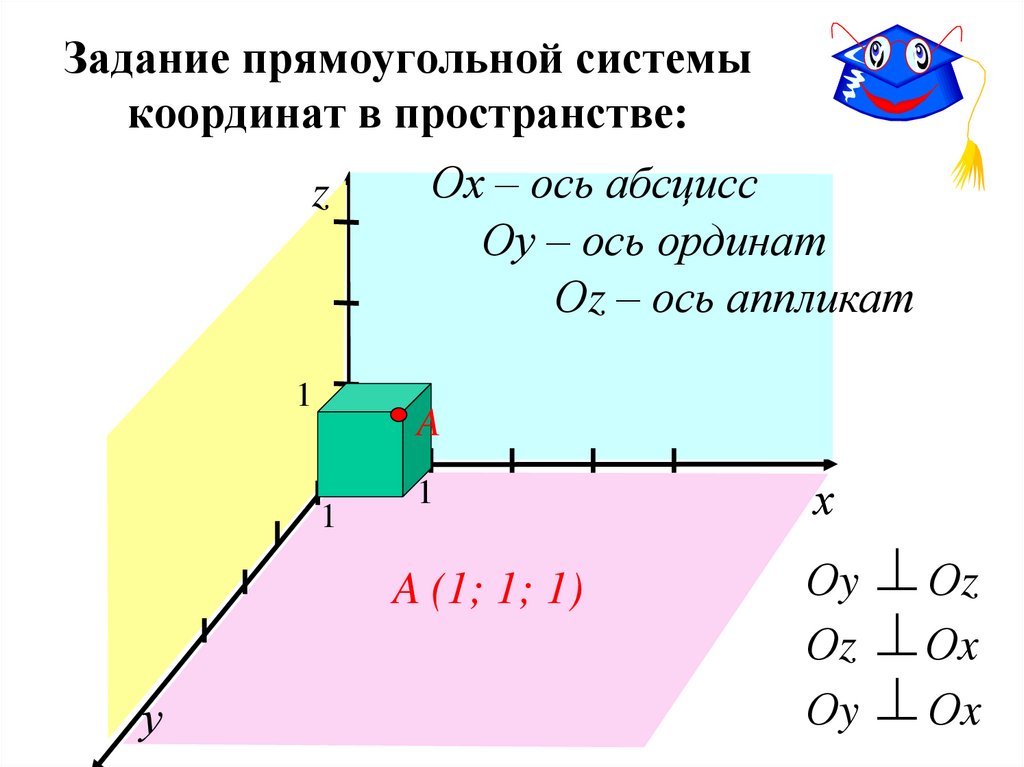
4. Задание прямоугольной системы координат в пространстве:

z
1
Ох – ось абсцисс
Оу – ось ординат
Оz – ось аппликат
A
1
О
1
A (1; 1; 1)
у
х
Оy Оz
Оz Оx
Оy Оx

5.

z
1
0
1
1
х
у
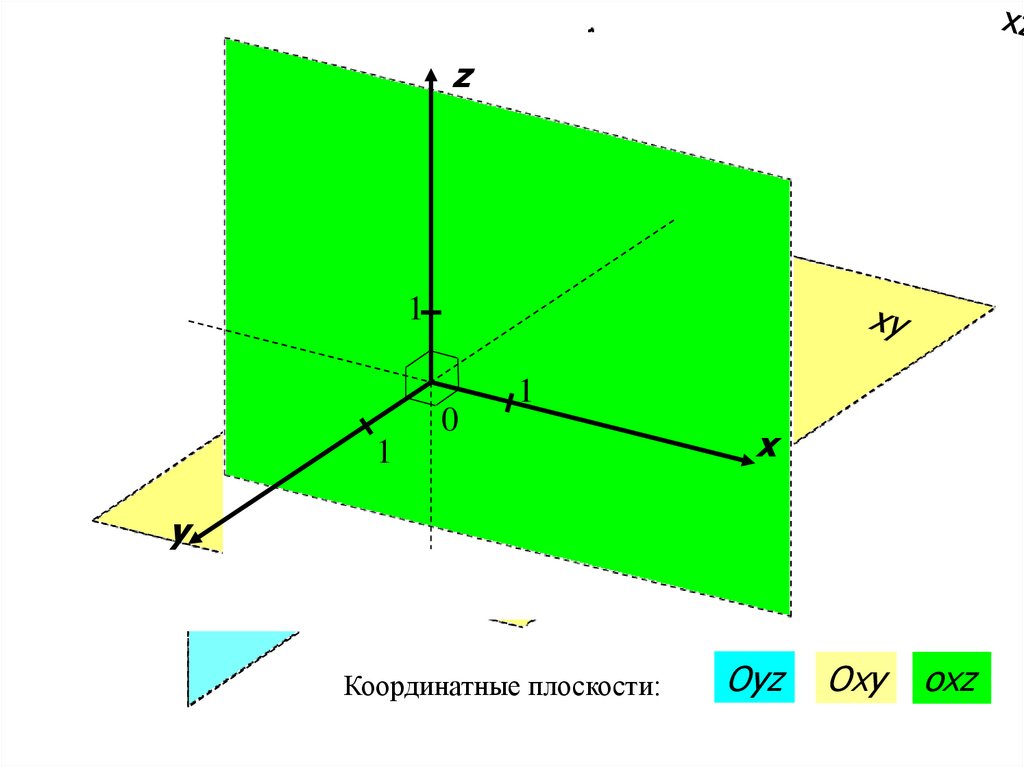
Координатные плоскости:
Oуz
Oxy
охz

6. Координаты точки

Пусть A - произвольная точка пространства, в котором выбрана
прямоугольная система координат. Через точку A проведем
плоскость, перпендикулярную оси Ox, и точку ее пересечения с
осью Ox обозначим Ax. Координата этой точки на оси Ox называется
абсциссой точки A и обозначается x. Аналогично на осях Oy и Oz
определяются точки Ay и Az, координаты которых называются
соответственно ординатой и аппликатой точки A и обозначаются y и
z соответственно. Тройка чисел (x, y, z) называется координатами
точки A в пространстве.

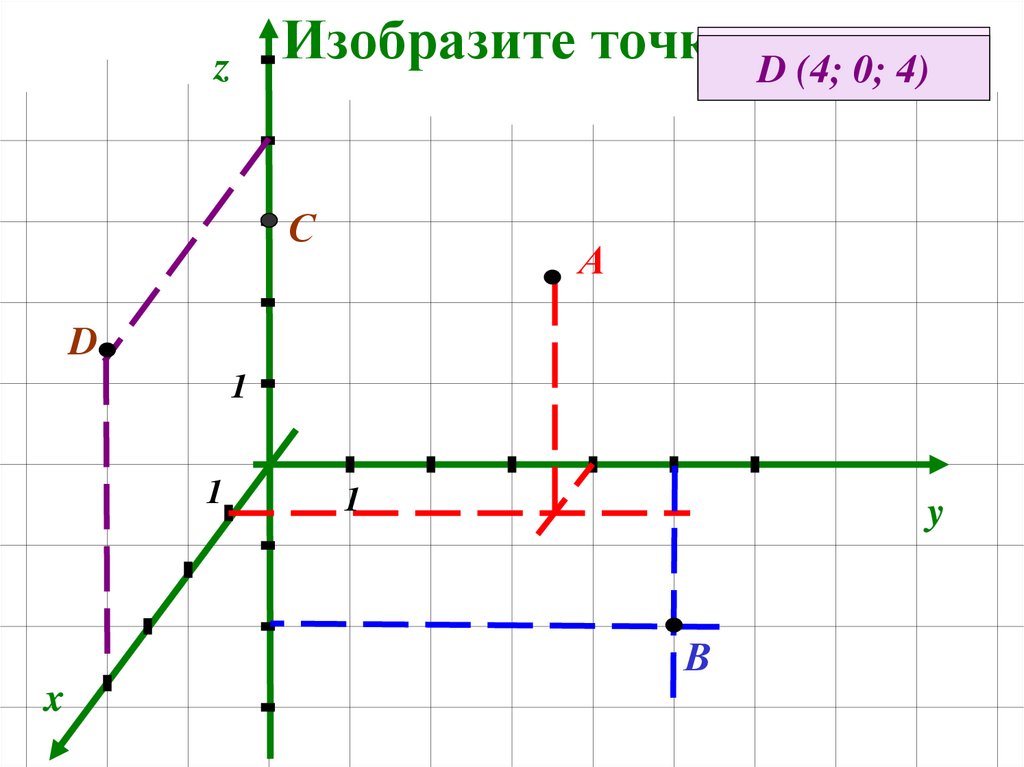
7. Изобразите точки

ВDАС (0;
(1;
4;
3)
(0;
(4; 5;
0;
0; -3)
3)
4)
z
С
А
D
1
1
1
y
В
x

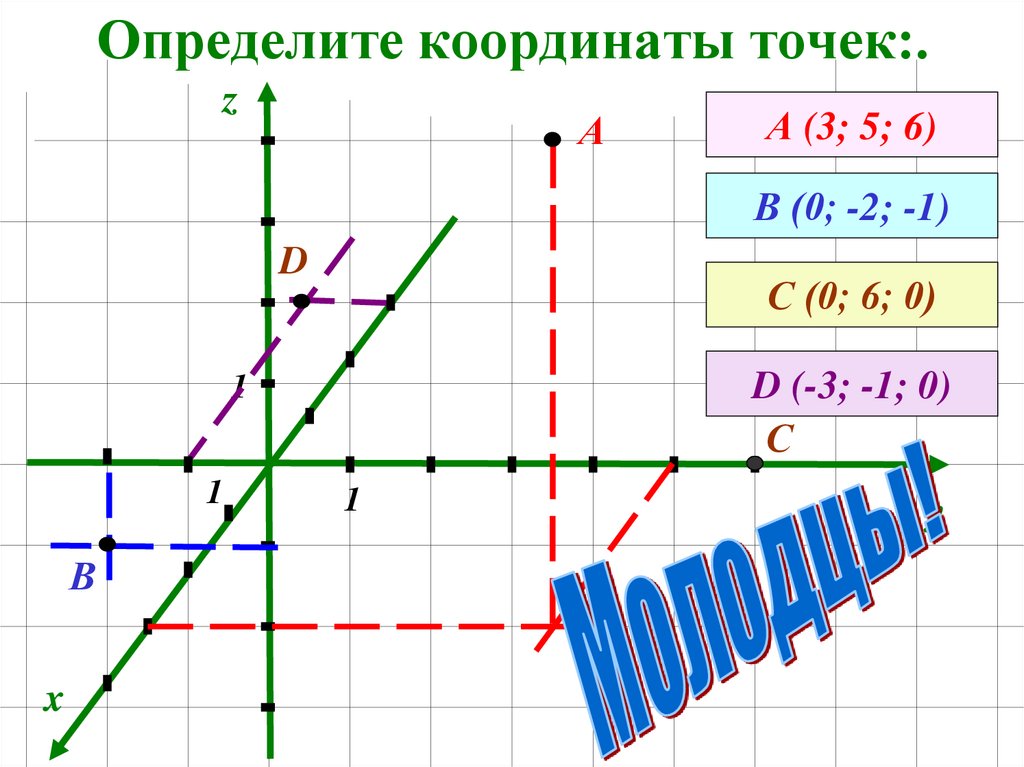
8. Определите координаты точек:.

z
А
А (3; 5; 6)
В (0; -2; -1)
D
С (0; 6; 0)
D (-3; -1; 0)
С
1
1
В
x
1
y

9.

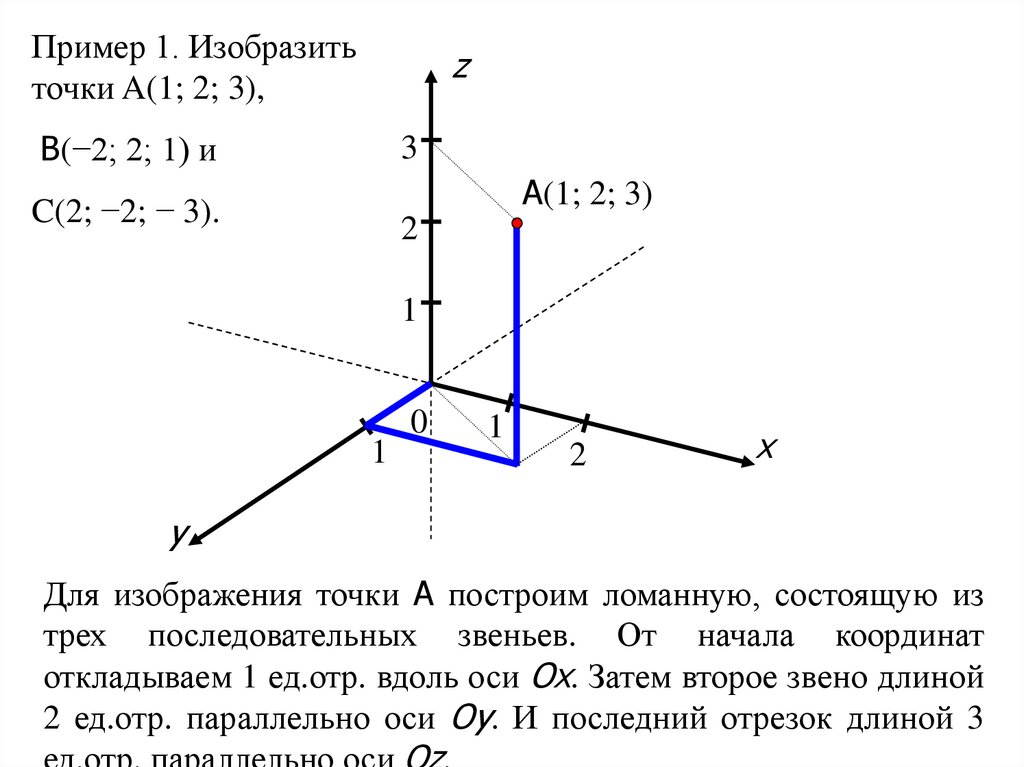
Пример 1. Изобразить
точки A(1; 2; 3),
z
B(−2; 2; 1) и
3
A(1; 2; 3)
C(2; −2; − 3).
2
1
1
0
1
2
х
у
Для изображения точки A построим ломанную, состоящую из
трех последовательных звеньев. От начала координат
откладываем 1 ед.отр. вдоль оси Ox. Затем второе звено длиной
2 ед.отр. параллельно оси Oy. И последний отрезок длиной 3

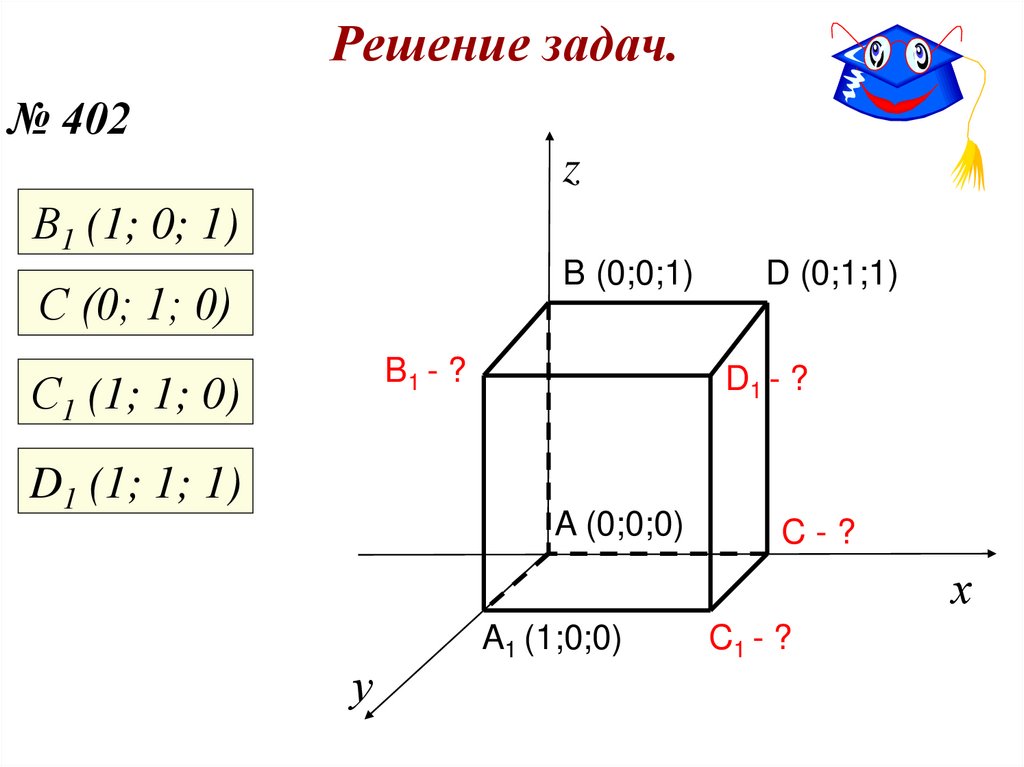
10. Решение задач.

№ 402
z
В1 (1; 0; 1)
B (0;0;1)
С (0; 1; 0)
B1 - ?
С1 (1; 1; 0)
D1 (1; 1; 1)
D (0;1;1)
D1 - ?
A (0;0;0)
C-?
х
у
A1 (1;0;0)
C1 - ?

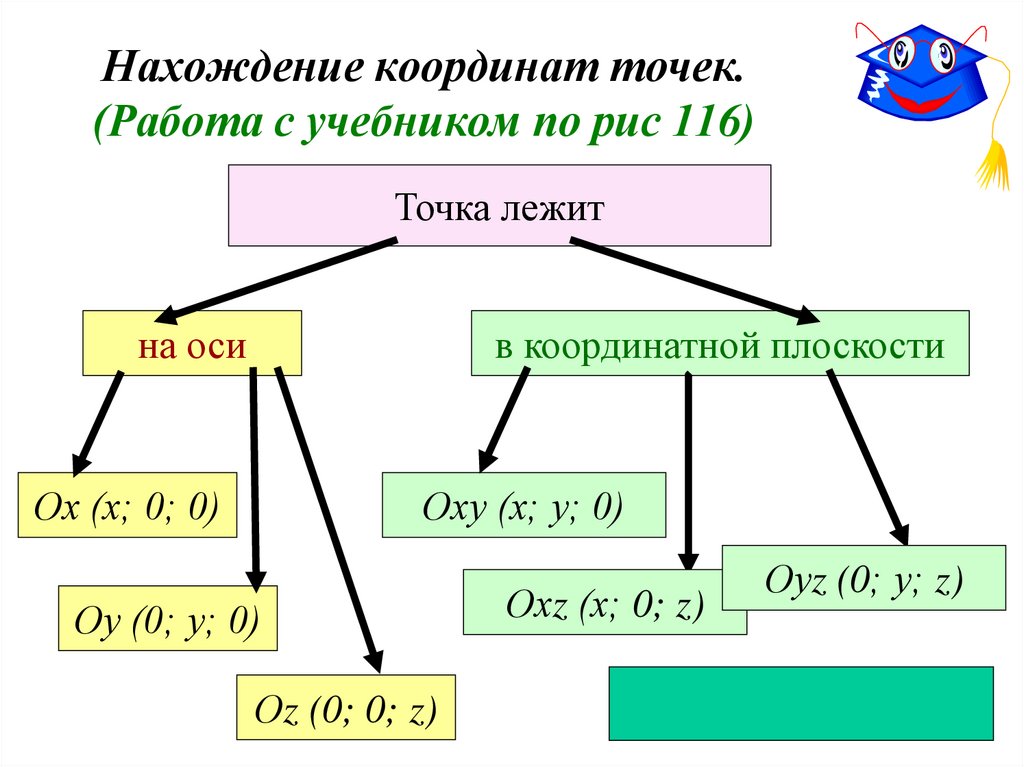
11. Нахождение координат точек. (Работа с учебником по рис 116)

Точка лежит
на оси
в координатной плоскости
Ох (х; 0; 0)
Оху (х; у; 0)
Оу (0; у; 0)
Оz (0; 0; z)
Охz (х; 0; z)
Оуz (0; у; z)

12. Повторение.

Даны точки:
А (2; -1; 0)
В (0; 0; -7)
С (2; 0; 0)
D (-4; -1; 0)
Е (0; -3; 0)
F (1; 2; 3)
Р (0; 5; -7)
К (2; 0; -4)
Назовите точки, лежащие
в плоскости Оуz.
Назовите точки, лежащие
в плоскости Охz.
В (0; 0; -7)
Назовите точки, лежащие
в плоскости Оху.
С (2; 0; 0)
Е (0; -3; 0)

13. Расстояние между точками

Теорема. Расстояние между точками A1(x1, y1, z1), A2(x2, y2, z2) в
пространстве выражается формулой
A1 A2 ( x2 x1 ) ( y2 y1 ) ( z2 z1 ) .
2
2
2

14.

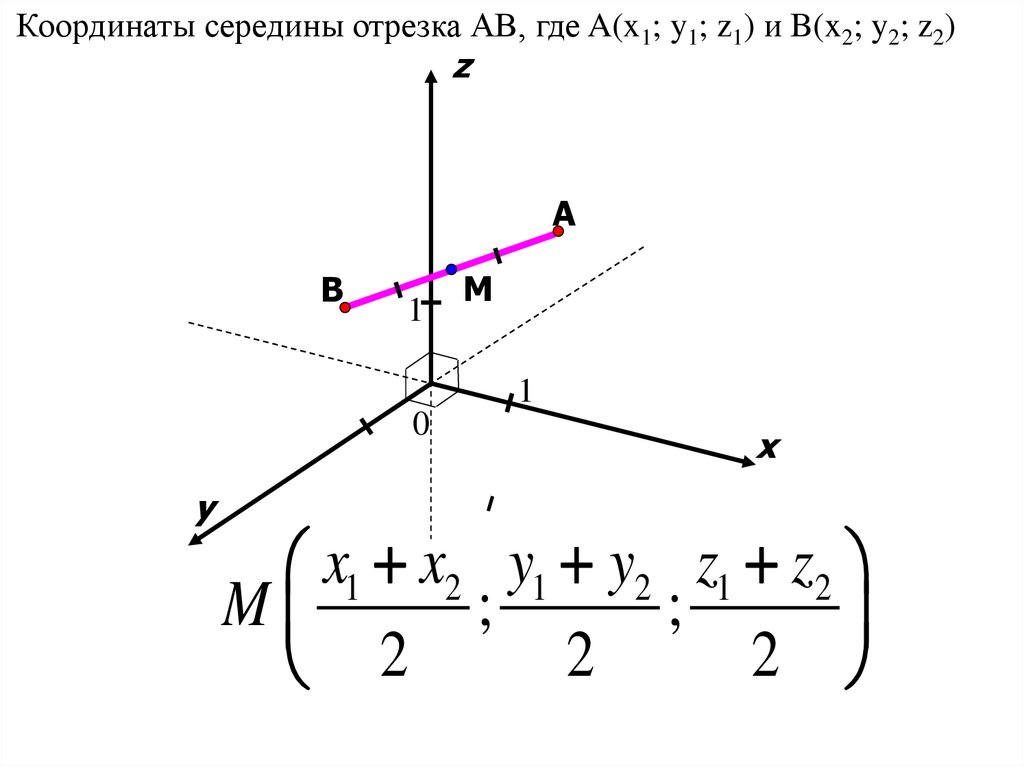
Координаты середины отрезка АВ, где A(x1; y1; z1) и B(x2; y2; z2)
z
A
B
1
M
1
0
у
х
x1 x2 y1 y2 z1 z2
M
;
;
2
2
2

15. Деление отрезка в данном отношении.

Пи
Если отрезок АВ разделен точкой С в отношении
АС:СВ= , то координаты точки С находятся по
формулам
х А x B
y A y B
z A y B
хС 1 ; yC 1 ; zC 1

16. Уравнение сферы.

Пусть центр сферы находится в точке A (a; b; c), а
радиус сферы равен R. Точками сферы являются те и
только те точки пространства, расстояние от которых
до точки A равно R. Квадрат расстояния от любой
точки B (x; y; z) сферы до точки A равен (x – a)2 + (y –
b)2 + (z – c)2. Поэтому уравнение сферы с
центром A (a; b; c) и радиусом R имеет вид
(x – a)2 + (y – b)2 + (z – c)2 = R2

17. Упражнение 1

Найдите расстояние между точками A1(1, 2, 3) и A2(-1, 1, 1),
B1(3, 4, 0) и B2(3, -1, 2).
Ответ: 3,
29.

18. Упражнение 2

Какая из точек A (2, 1, 5) или B (-2, 1, 6) лежит ближе к началу
координат?
Ответ: Точка A.

19. Упражнение 3

Найдите координаты ортогональных проекций точек A(1, 3, 4) и
B(5, -6, 2) на: а) плоскость Oxy; б) плоскость Oyz; в) ось Ox; г)
ось Oz.
Ответ: а) (1, 3, 0), (5, -6, 0); б) (0, 3, 4), (0, -6, 2); в) (1, 0, 0), (5, 0, 0);
г) (0, 0, 4), (0, 0, 2).

20. Упражнение 4

Определите вид треугольника, если его вершины имеют
координаты: A(0, 0, 2), B(0, 2, 0), C(2, 0, 0).
Ответ: Равносторонний.

21. Упражнение 5

Даны точки M (1, -2, -3), N (-2, 3, 1) и K (3, 1, -2). Найдите
периметр треугольника MNK.
Ответ:
2(5 7 19).

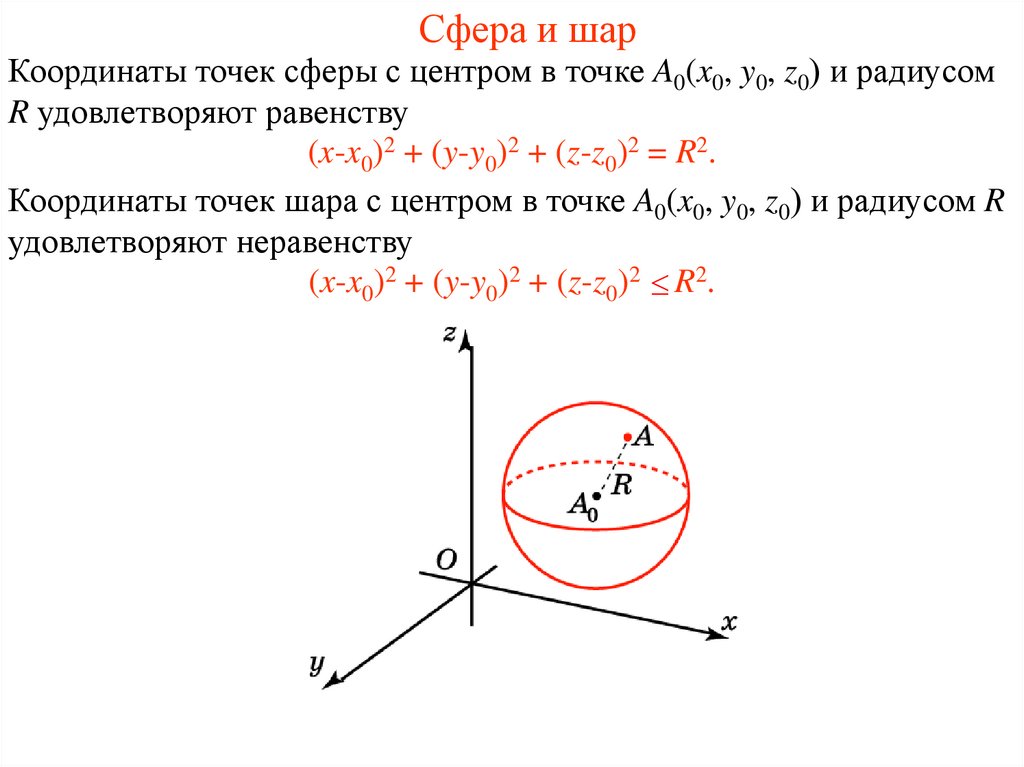
22. Сфера и шар

Координаты точек сферы с центром в точке A0(x0, y0, z0) и радиусом
R удовлетворяют равенству
(x-x0)2 + (y-y0)2 + (z-z0)2 = R2.
Координаты точек шара с центром в точке A0(x0, y0, z0) и радиусом R
удовлетворяют неравенству
(x-x0)2 + (y-y0)2 + (z-z0)2 R2.

23. Упражнение 5

Найдите координаты центра C и радиус R сферы, заданной
уравнением:
а) (x - 2)2 + (y + 5)2 + z2 = 9;
б) x2 + (y - 6)2 + (z + 1)2 = 11.
Ответ: а) C(2, -5, 0), R = 3;
б) C(0,6,-1), R = 11.

24. Упражнение 6

Напишите уравнение сферы:
а) с центром в точке O(0, 0, 0) и радиусом 1;
б) с центром в точке C (1, -2, 3) и радиусом 4.
Ответ: а) x2 + y2 +z2 = 1;
б) (x-1)2 + (y+2)2 + (z-3)2 = 16.

25. Упражнение 7

Что представляет собой геометрическое место точек
пространства, для которых: а) первая координата равна нулю; б)
вторая координата равна нулю; в) третья координата равна нулю;
г) первая и вторая координаты равны нулю; д) первая и третья
координаты равны нулю; е) вторая и третья координаты равны
нулю; ж) все координаты равны нулю?
Ответ: а) Плоскость Oyz; б) плоскость Oxz; в) плоскость Oxy;
г) ось Oz; д) ось Oy; е) ось Ox; ж) начало координат.

26. Упражнение 8

На каком расстоянии находится точка A(1, -2, 3) от координатной
плоскости: а) Oxy; б) Oxz; в) Oyz?
Ответ: а) 3;
б) 2;
в) 1.

27. Упражнение 9

На каком расстоянии находится точка A(1, -2, 3) от координатной
прямой: а) Ox; б) Oy; в) Oz?
Ответ: а) 13;
б) 10;
в)
5.

28. Упражнение 10

Каким является геометрическое место точек пространства, для
которых: а) первая координата равна единице; б) первая и вторая
координаты равны единице?
Ответ: а) Плоскость, параллельная плоскости Oyz и проходящая
через точку (1, 0, 0);
б) прямая, параллельная оси Oz и и проходящая через точку (1,
1, 0).

29. Упражнение 11

Какому условию удовлетворяют координаты точек пространства,
одинаково удаленные от: а) двух координатных плоскостей Oxy,
Oyz; б) всех трех координатных плоскостей?
Ответ: а) z=x;
б) x=y=z.

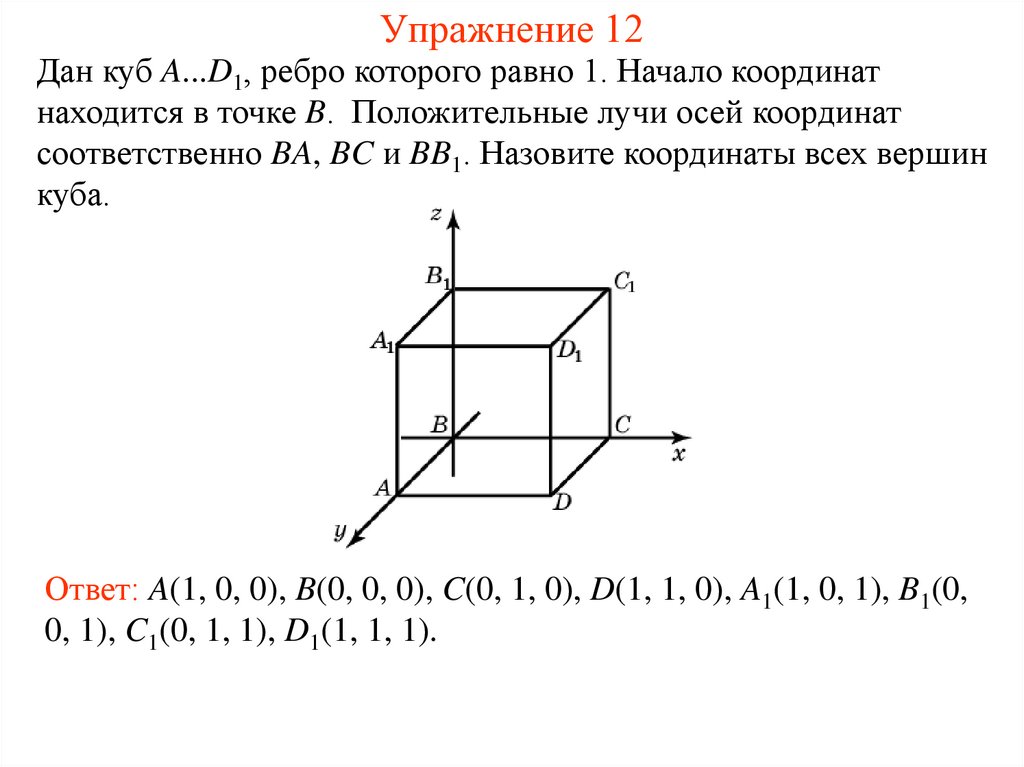
30. Упражнение 12

Дан куб A...D1, ребро которого равно 1. Начало координат
находится в точке B. Положительные лучи осей координат
соответственно BA, BC и BB1. Назовите координаты всех вершин
куба.
Ответ: A(1, 0, 0), B(0, 0, 0), C(0, 1, 0), D(1, 1, 0), A1(1, 0, 1), B1(0,
0, 1), C1(0, 1, 1), D1(1, 1, 1).

31. Упражнение 13

Куб A...D1 помещен в прямоугольную систему координат так,
что началом координат является центр нижнего основания куба,
ребра куба параллельны соответствующим осям координат,
вершина A имеет координаты (-2, 2, 0). Найдите координаты всех
остальных вершин куба.
Ответ: B(-2, -2, 0), C(2, -2, 0), D(2, 2, 0), A1(-2, 2, 4), B1(-2, -2, 4),
C1(2, -2, 4), D1(2, 2, 4).

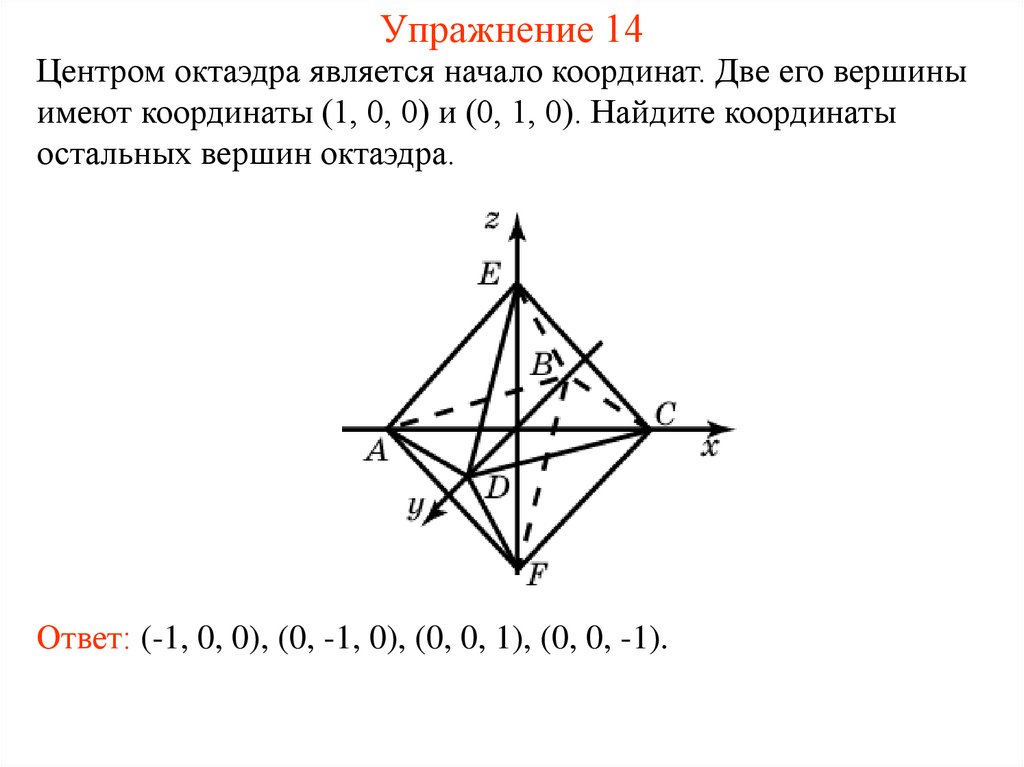
32. Упражнение 14

Центром октаэдра является начало координат. Две его вершины
имеют координаты (1, 0, 0) и (0, 1, 0). Найдите координаты
остальных вершин октаэдра.
Ответ: (-1, 0, 0), (0, -1, 0), (0, 0, 1), (0, 0, -1).

33. Упражнение 15

Как расположена сфера радиуса 2 с центром в точке с
координатами (1, 2, 3) относительно координатных плоскостей?
Ответ: Не имеет общих точек с координатной плоскостью Oxz;
касается координатной плоскости Oxz; пересекает
координатную плоскость Oyz.

34. Упражнение 16

Точка A имеет координаты (x, y, z). Найдите координаты
симметричной точки относительно: а) координатных
плоскостей; б) координатных прямых; в) начала координат.
Ответ: а) (-x, y, z), (x, -y, z), (x, y, -z);
б) (-x, -y, z), (-x, y, -z), (x, -y, -z);
в) (-x, -y, -z).

35. Упражнение 17

Найдите координаты середины отрезка: а) AB, если A(1, 2, 3) и
B(-1, 0, 1); б) CD, если C(3, 3, 0) и D(3, -1, 2).
Ответ: а) (1, 1, 2);
б) (3, 1, 1).