ДС_Л 8_3-м Хаос

1. ДИНАМИЧЕСКИЕ СИСТЕМЫ В ПРОСТРАНСТВЕ. ЭЛЕМЕНТЫ ХАОСА

2. Понятие детерминированного хаоса

3. Понятие детерминированного хаоса

4. Понятие детерминированного хаоса

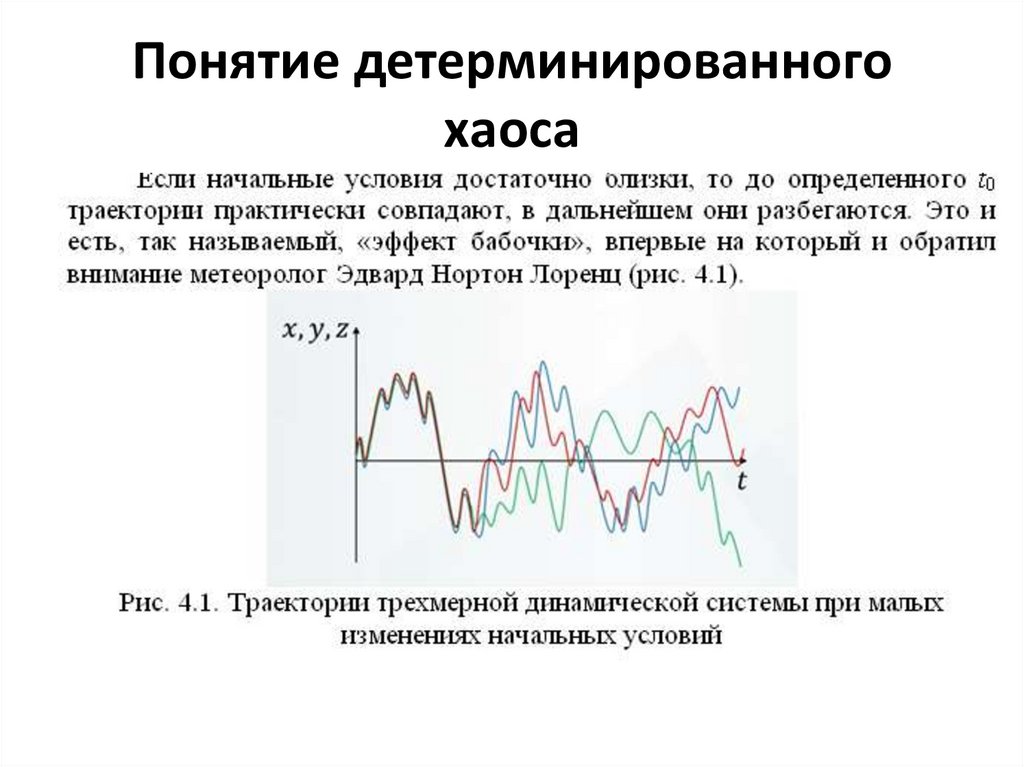
5. Понятие детерминированного хаоса

6. Понятие детерминированного хаоса

• Хаотические, странные аттракторы
соответствуют непредсказуемому поведению
систем, не имеющих строго периодической
динамики, это математический образ
детерминированных непериодических
процессов.
• Странные аттракторы могут иметь весьма
сложные и необычные конфигурации в
трехмерном пространстве.

7. Понятие детерминированного хаоса

8. Понятие детерминированного хаоса

9. Понятие детерминированного хаоса

• Таким образом, системы, поведение которых детерминируется
правилами, не включающим случайность, с течением времени
проявляют непредсказуемость за счет нарастания, усиления,
амплификации малых неопределенностей, флуктуаций.
• Наглядный образ системы с нарастанием неопределенности - так
называемый биллиард Я. Г. Синая: достаточно большая
последовательность соударений шаров неизбежно ведет к
нарастанию малых отклонений от исчисляемых траекторий (за счет не
идеально сферической поверхности реальных шаров, не идеально
однородной поверхности сукна) и непредсказуемости поведения
системы.
• В таких системах «случайность создается подобно тому, как
перемешивается тесто или тасуется колода карт». Так называемое
«преобразование пекаря» с последовательным растягиванием и
складыванием, бесконечным образованием складок - одна из
моделей возникновения перехода от порядка к хаосу; при этом число
преобразований может служить мерой хаоса.

10. Критерий Рауса – Гурвица

• Для определения типа и характера устойчивости точек при
использовании линейного приближения вычисляют якобиан и
составляя характеристическое уравнение находят собственные
значения на основании значения которых делают выводы.
• В критерии Рауса – Гурвица нет необходимости решать
характеристичекое уравнение, что упрощает математические
вычисления.
• Если система на плоскости, то не возникает проблем в решении
квадратичного уравнения. Для трехмерных систем и выше
решать такие уравнения становится затруднительно.
• Абелем была доказана теорема: при размерности уравнения
N >= 5 порядка невозможно получить алгебраическое выражение
для корней этого полинома.

11. Критерий Рауса – Гурвица

12. Критерий Рауса – Гурвица

13. Критерий устойчивости Рауса – Гурвица

14. Критерий устойчивости Рауса – Гурвица