Основы электропривода технологических установок. Лекция 8

1.

Самарский государственный университет путей сообщения
«ОСНОВЫ
ЭЛЕКТРОПРИВОДА
ТЕХНОЛОГИЧЕСКИХ
УСТАНОВОК»
Автор: БУШТРУК Т. Н.
г. Самара 2020

2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЭП

UП
RP
Uзд
R1
ГЕНЕРАТОР- ДВИГАТЕЛЬ
+
R2
Р
Uy
УМ
Uя
Uв
G
O
B
M
M
OBG
Uос
-
BR
ТИРИСТОРНЫЙ ПРЕОБРАЗОВАТЕЛЬДВИГАТЕЛЬ
UП
RP
+
R2
Uзд
Р
Uy
Uя
ТП
O
B
Д
Д
R1
Uос
BR
ФУНКЦИОНАЛЬНАЯ СХЕМА ЭП
-

3. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЭП

ПРИНЦИПИАЛЬНАЯ СХЕМА ЭП

4. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЭП

В структурной схеме каждый элемент электропривода представлен передаточной функцией
(ПФ) Wi(s), где s – аргумент преобразования Лапласа.
СТРУКТУРНАЯ СХЕМА ЭП

5. ПРИНЦИПЫ ФОРМИРОВАНИЯ АЭП

ЭЛЕКТРОПРИВОД ПЕРЕМЕННОГО ТОКА
ЭЛЕКТРОПРИВОД ПОСТОЯННОГО ТОКА
Принципы формирования АЭП
1. По отклонению.
. 2. По возмущению.
3. Комбинированный.

6. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ.

Состояние САУ называется устойчивым, если отклонение от него
остаётся сколь угодно малым при любых достаточно малых
изменениях входных сигналов.
Устойчивость САУ оценивается прямым (экспериментальным)и
косвенным методами.
Прямой метод реализуется получением переходного процесса при
специальных входных воздействиях.
Косвенные методы - на основе критериев.
Критерии подразделяются на алгебраические и частотные.
Алгебраические – Рауса, Гурвица, Рауса-Гурвица
Частотные - Михайлова, Найквиста

7. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ. ТИПОВЫЕ ВХОДНЫЕ ВОЗДЕЙСТВИЯ

Переходная и импульсная характеристики.
Для целей сравнительного анализа динамических характеристик
звеньев и систем используют типовые входные воздействия в качестве
которых выбирают либо наиболее вероятные, либо наиболее
неблагоприятные
входные
воздействия.
Наибольшее
распространение среди них получили:
1)единичное ступенчатое входное воздействие
x(t)=1(t)={0,t<01,t>0 , x(t)- входной сигнал.
В реальных процессах этому соответствует
изменение нагрузки.
2) единичное импульсное входное воздействие
x(t)=δ(t)={0,t≠0∞,t=0
скачкообразное
С математической точки зрения эта функция представляет собой
описание ударов в системе и является идеальным импульсом с
бесконечно
малой
длительностью
с
бесконечно
большой
амплитудой площадь которого = 1. ∫δ(t)dt=1, d1(t)/dt= δ(t).
3) синусоидальный гармонический сигнал x(t)=sinωt
Кроме них используют более сложные сигналы.

8. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЭП

Необходимым условием работоспособности системы АЭП
(автоматический электропривод) , является её устойчивость.
Под устойчивостью принято понимать свойство системы
восстанавливать состояние равновесия, из которого она была
выведена под влиянием возмущающих факторов, после
прекращения их воздействия.
Устойчивость системы автоматического управления, способность
системы АЭП нормально функционировать и противостоять различным
неизбежным возмущениям (воздействиям). Состояние САУ называется
устойчивым, если отклонение от него остаётся сколь угодно малым при
любых достаточно малых изменениях входных сигналов. У. САУ разного
типа определяется различными методами. Точная и строгая теория У.
систем,
описываемых
обыкновенными
дифференциальными
уравнениями, создана А. М. Ляпуновым в 1892.
В структурной схеме каждый элемент электропривода представлен передаточной функцией
(ПФ) Wi(s), где s – аргумент преобразования Лапласа.

9. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЭП

Для анализа системы управления ЭП используют аппарат
теории управления. Систему автоматического управления ЭП
исследуют на устойчивость и определяют показатели качества.
Устойчивость и качественные показатели работы системы АЭП
определяют
по
переходному
процессу.
Построение
переходного процесса является достаточно трудоемкой
процедурой. Однако существуют косвенные методы или
критерии для определения устойчивости и качественных
показателей.
Для исследования системы ЭП
использовать критерий Гурвица.
на
устойчивость
можно
Для применения критерия Гурвица нужно получить ПФ замкнутой
системы. Прежде получим ПФ разомкнутой системы, для этого
нужно разомкнуть контур регулирования по обратной связи, при
этом элементы системы электропривода будут соединены
последовательно.

10.

8.2. Алгебраические критерии устойчивости
8.2.1. Необходимое условие устойчивости
Характеристическое уравнение системы с помощью теоремы
Виета может быть записано в виде
D(p) = aopn + a1pn-1 + a2pn-2 + ... + an = ao(p-p1)(p-p2)...(p-pn) = 0,
где p1, p2, ..., pn - корни этого уравнения. Если система устойчива,
значит все корни левые, то есть вещественные части всех корней
отрицательны, что можно записать как ai = -|ai| < 0. Подставим их в
уравнение: a0(p + |a1|)(p + |a2| - j2)(p + |a2| + j2)... = 0.
Перемножая комплексно сопряженные выражения, получим:
a0(p + |a1|)((p + |a2|)2 + (2)2)... = 0.
После раскрытия скобок должно получиться выражение
a0pn + a1pn-1 + a2pn-2 + ... + an = 0.
Так как в скобках нет ни одного отрицательного числа, то ни один
из коэффициентов a0,a1,...,an не будет отрицательным.
Поэтому необходимым условием устойчивости САУ является
положительность всех коэффициентов характеристического
уравнения: a0 > 0, a1 > 0, ... , an > 0. В дальнейшем будем
рассматривать только уравнения, где a0 > 0. В противном случае
уравнение домножается на -1.
Рассмотренное условие является необходиным, но не
достаточным условием. Необходимые и достаточные условия дают

11. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЭП

Эквивалентную ПФ разомкнутой системы определяют
произведением ПФ элементов системы АЭП
r
,
Wэкв s Wi s
i 1
bm 1s bm
а0 s п а1s п 1 а2 s п 2 ... ап 1s ап
где а и b – коэффициенты, r – число элементов (звеньев)
разомкнутой системы ЭП, n = 1, 2, 3…, m = 1, s=j , – круговая
частота. где Wп.ц(s) = Wр(s)Wум(s)Wг(s)Wд(s) – ПФ прямой цепи.
Знаменатель ПФ Wзс(s)является характеристическим уравнением.
Критерий Гурвица формулируется следующим образом. Для того
чтобы система автоматического регулирования была устойчива,
необходимо и достаточно, чтобы при >0 все диагональные
определители матрицы, составленной по определенному правилу
из коэффициентов знаменателя (характеристического уравнения)
ПФ замкнутой системы , были больше нуля. Из критерия Гурвица
вытекает, что все коэффициенты характеристического уравнения
устойчивой системы положительны.

12. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЭП

Правило составления определителя Гурвица сводится к
следующему. Выписывают по главной диагонали все
коэффициенты от a1 до an в порядке возрастания индексов.
Дополняют столбцы вверх от коэффициентов диагонали,
вписывая в столбец коэффициенты с последовательно
возрастающими
индексами.
Вниз
от
коэффициентов
диагонали
дополняют
столбцы
коэффициентами
с
последовательно
убывающими
индексами.
Вместо
коэффициентов, индексы у которых могли бы быть больше n и
меньше нуля, проставляют нули:
а1
а0
п 0
...
0
а3
а2
а1
...
0
а5
а4
а3
...
0
...
...
...
...
...
0
0
0
...
ап
Для устойчивости системы третьего и четвертого порядков
необходимо и достаточно, чтобы: а) все коэффициенты
характеристического уравнения были положительны; б) все
определители матрицы Гурвица были больше нуля.

13. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЭП

Оценить устойчивость системы, структурная схема которой имеет
вид: (критерий Михайлова)
Определим передаточную функцию системы
запишем ее характеристический полином
Заменой p на j перейдем к выражению для годографа
Михайлова которое представим в форме
Построим годограф Михайлова. Он проходит последовательно
три квадранта, не обращаясь в ноль
и стремясь к бесконечности в
третьем квадранте. Следовательно,
исследуемая система устойчива.

14. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЭП

Оценить устойчивость системы, структурная схема которой имеет
вид: критерий Михайлова
Определим передаточную функцию системы
запишем ее характеристический полином
Заменой p на j перейдем к выражению для годографа
Михайлова которое представим в форме
Построим годограф Михайлова. Он проходит последовательно
три квадранта, не обращаясь в ноль
и стремясь к бесконечности в
третьем квадранте. Следовательно,
исследуемая система устойчива.

15. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ АЭП

Критерий устойчивости Найквиста. Критерий Найквиста позволяет
определить устойчивость системы с обратной связью (замкнутой
системы) по экспериментально снятой или полученной на основе
передаточной функции амплитудно - фазовой частотной
характеристике разомкнутой системы.
Формулировка критерия Найквиста:
для устойчивости замкнутой системы
необходимо и достаточно чтобы амплитудно
- фазовая характеристика устойчивой
- разомкнутой системы при изменении
- от 0 до не охватывала точку с
- координатами {-1, j0}.

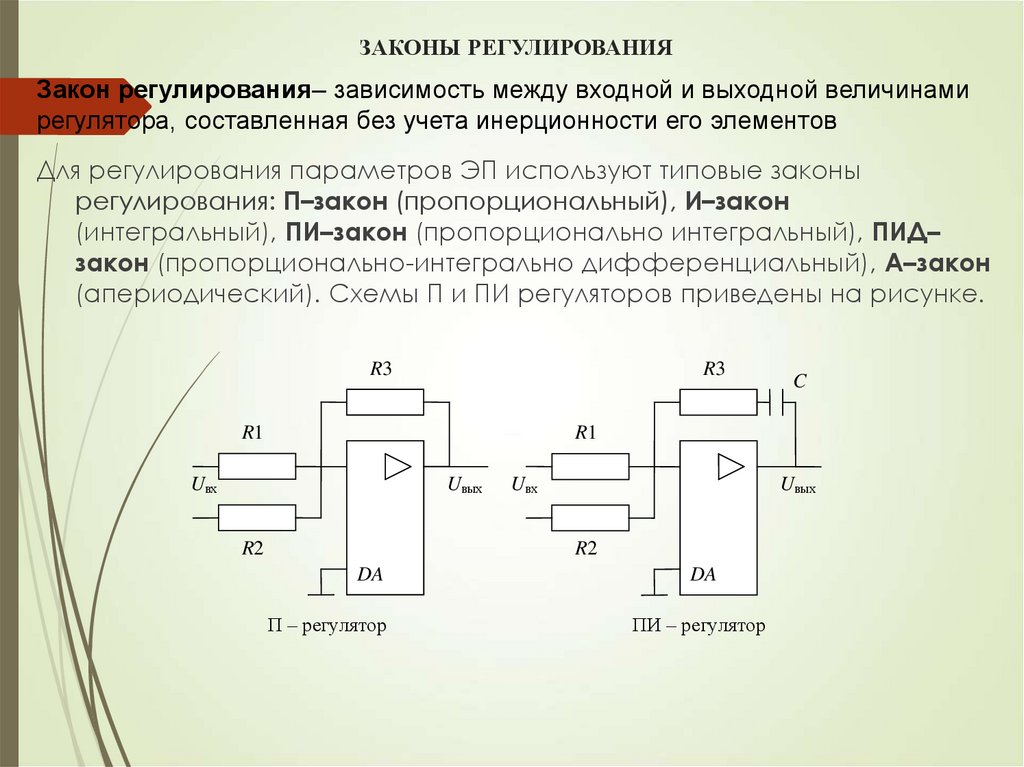
16. ЗАКОНЫ РЕГУЛИРОВАНИЯ

Закон регулирования– зависимость между входной и выходной величинами
регулятора, составленная без учета инерционности его элементов
Для регулирования параметров ЭП используют типовые законы
регулирования: П–закон (пропорциональный), И–закон
(интегральный), ПИ–закон (пропорционально интегральный), ПИД–
закон (пропорционально-интегрально дифференциальный), А–закон
(апериодический). Схемы П и ПИ регуляторов приведены на рисунке.
R3
R3
R1
C
R1
Uвх
Uвых
R2
Uвх
Uвых
R2
DA
П – регулятор
DA
ПИ – регулятор

17.

ЗАКОНЫ РЕГУЛИРОВАНИЯ
Пропорциональные регуляторы (П-регуляторы)
Осуществляют регулирование по закону:
Передаточная функция такого элемента имеет вид:
+
Его достоинство – быстродействие, недостаток – наличие статической ошибки регулирования.
гдеTu– постоянная времени такого регулятора (ее, кстати, может и не быть).
И-регуляторы воздействуют на ОУ до полного исключения установившейся ошибки.

18. ПЕРЕХОДНЫЕ ПРОЦЕССЫ

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЭП
ПЕРЕХОДНЫЕ ПРОЦЕССЫ

19. Устойчивость САУ ЭП

Все состояния линейной САУ либо устойчивы, либо неустойчивы, поэтому можно говорить об
устойчивости системы в целом. Для устойчивой стационарной линейной (СЛУ), описываемой
обыкновенными дифференциальными уравнениями, необходимо и достаточно, чтобы все корни
соответствующего характеристического уравнения имели отрицательные действительные части
(тогда САУ асимптотически устойчива). Существуют различные критерии (условия), позволяющие
судить о знаках корней характеристического уравнения, не решая это уравнение – непосредственно
по его коэффициентам. При исследовании устойчивости САУ, описываемых дифференциальными
уравнениями невысокого порядка (до 4-го), пользуются критериями Раусса - Гурвица (Э. Раусс,
английский. механик; А. Гурвиц, немецкий. математик). Однако этими критериями пользоваться во
многих случаях (например, в случае САУ, описываемых уравнениями высокого порядка) практически
невозможно из-за необходимости проведения громоздких расчётов; кроме того, само нахождение
характеристических уравнений сложных САУ сопряжено с трудоёмкими математическими
выкладками. Между тем частотные характеристики любых сколь угодно сложных СЛУ легко
находятся посредством простых графических и алгебраических операций. Поэтому при
исследовании и проектировании линейных стационарных САУ обычно применяют частотные
критерии Найквиста и Михайлова (Х. Найквист, амер. физик; А. В. Михайлов, сов. учёный в
области автоматического управления). Особенно прост и удобен в практическом применении
критерий Найквиста. Совокупность значений параметров САУ, при которых система устойчива,
называется областью устойчивости Близость САУ к границе области У. оценивается запасами У. по
фазе и по амплитуде, которые определяют по амплитудно-фазовым характеристикам разомкнутой
САУ.

20. Устойчивость САУ ЭП

Современная теория линейных САУ даёт методы исследования устойчивости систем с
сосредоточенными и с распределёнными параметрами, непрерывных и дискретных
(импульсных), стационарных и нестационарных.
Проблема устойчивости нелинейных САУ имеет ряд существенных особенностей в
сравнении с линейными. В зависимости от характера нелинейности в системе одни
состояния могут быть устойчивыми, другие – неустойчивыми. В теории устойчивости
нелинейных систем говорят об устойчивости данного состояния, а не системы как
таковой. устойчивости какого-либо состояния нелинейной САУ может сохраняться, если
действующие возмущения достаточно малы, и нарушаться при больших возмущениях.
Поэтому вводятся понятия устойчивости в малом, большом и целом.

21. Устойчивость САУ ЭП

Важное значение имеет понятие абсолютной У., т. е. У. САУ при произвольном
ограниченном начальном возмущении и любой нелинейности системы (из
определённого класса нелинейностей). Исследование У. нелинейных САУ
оказывается довольно сложным даже при использовании ЭВМ. Для
нахождения достаточных условий У. часто применяют метод функций
Ляпунова. Достаточные частотные критерии абсолютной У. предложены рум.
математиком В. М. Поповым и др. Наряду с точными методами исследования
У. применяются приближённые методы, основанные на использовании
описывающих
функций,
например
методы
гармонической
или
статистической линеаризации.
Устойчивость САУ при воздействии на неё случайных возмущений и помех
изучается теорией У. стохастических систем.
Современная вычислительная техника позволяет решать многие проблемы
У. линейных и нелинейных САУ различных классов как путём использования
известных алгоритмов, так и на основе новых специфических алгоритмов,
рассчитанных на возможности современных ЭВМ и вычислительных систем.