b06e310ae2924af8b33b9377015ff560

1.

Ортогональная проекция
многоугольника и ее
площадь.

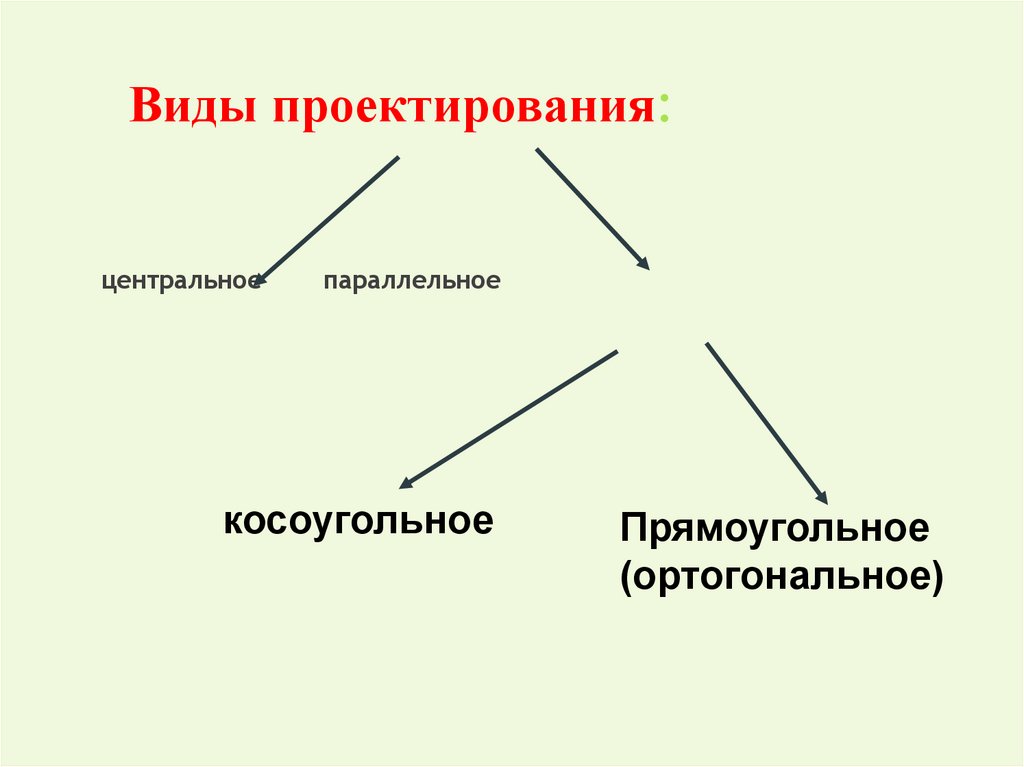
2. Виды проектирования:

центральное
параллельное
косоугольное
Прямоугольное
(ортогональное)

3. Свойства ортогонального проектирования

Проекцией прямой является
прямая.
Проекцией параллельных прямых
являются параллельные прямые.
Сохраняется отношение отрезков,
лежащих на параллельных прямых.

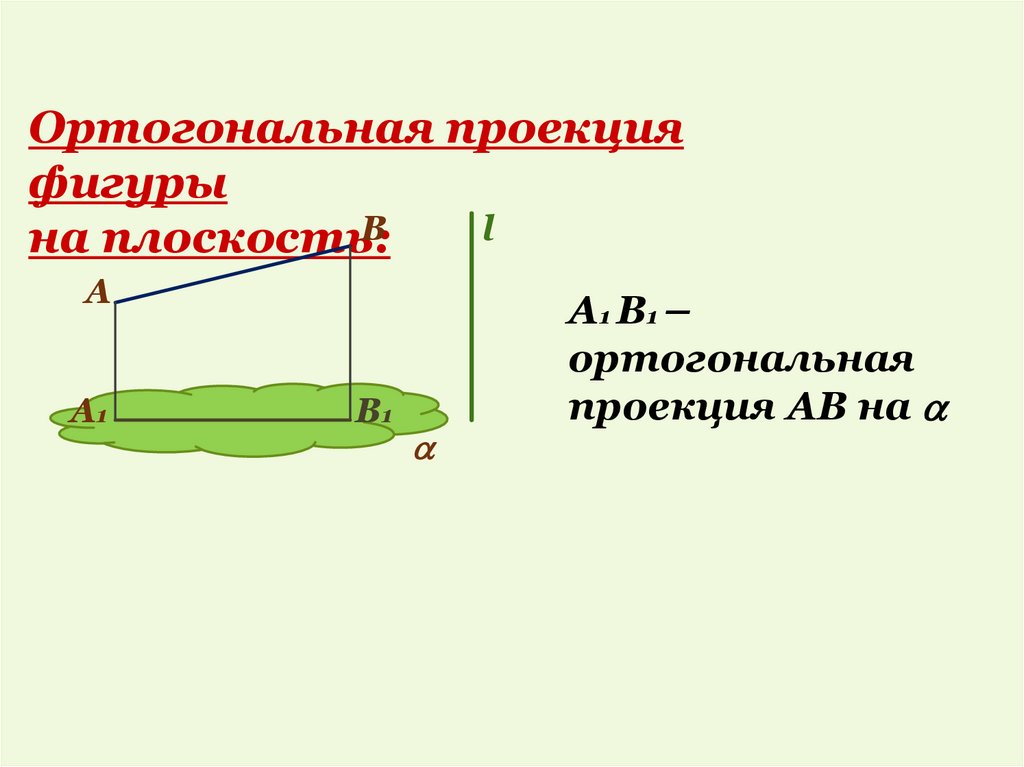
4.

Ортогональная проекция
фигуры
B
l
на плоскость:
A
A1
B1
A 1 B1 –
ортогональная
проекция АВ на

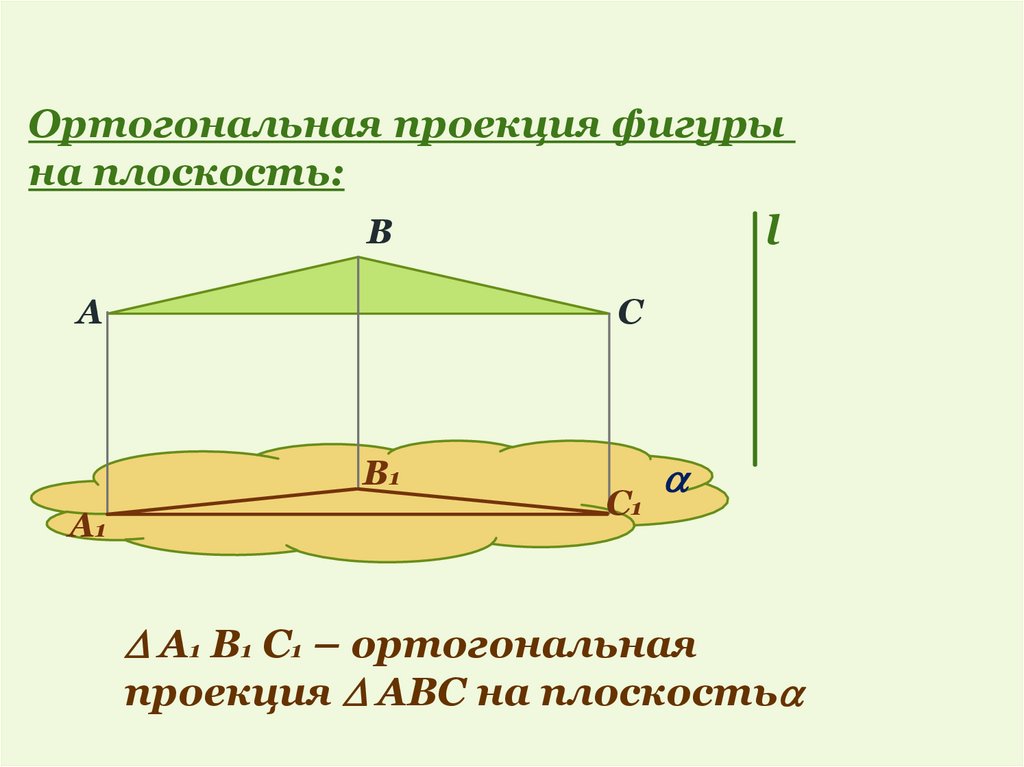
5.

Ортогональная проекция фигуры
на плоскость:
B
l
A
C
B1
A1
C1
А1 В1 С1 – ортогональная
проекция АВС на плоскость

6.

Ортогональная проекция фигуры
на плоскость:
АВС и А1 В1 С1 могут быть равны,
а могут быть и не равны.
РАВНЫ: если (АВС) .
НЕ РАВНЫ: если угол между их
плоскостями 0 90 .

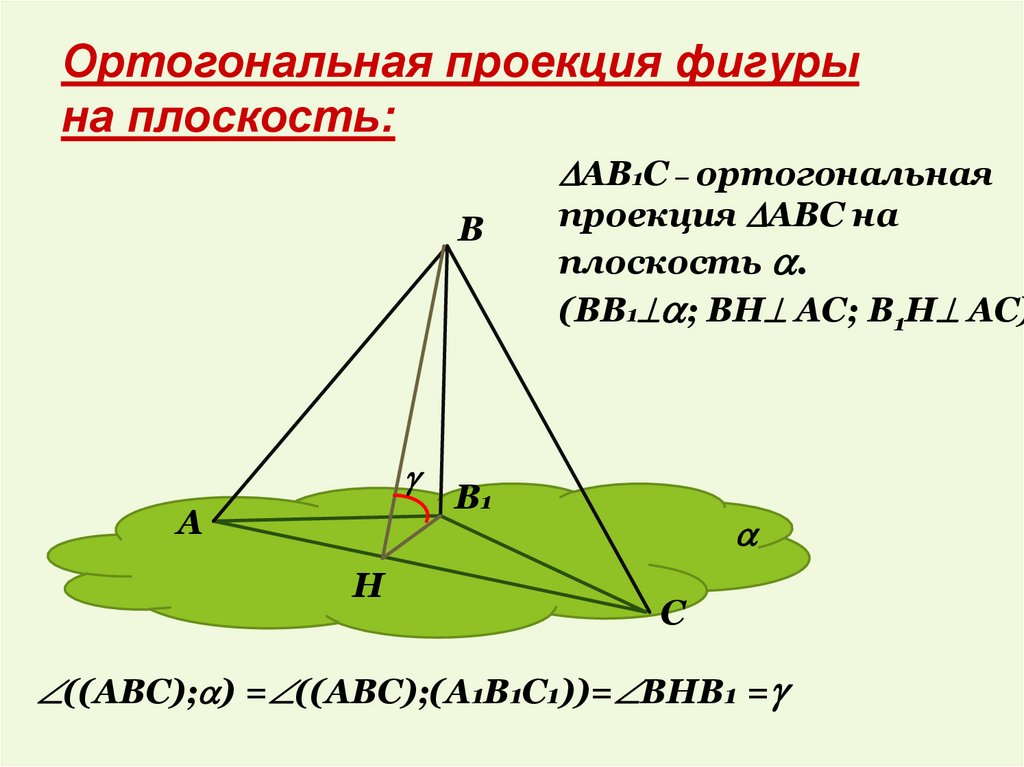
7.

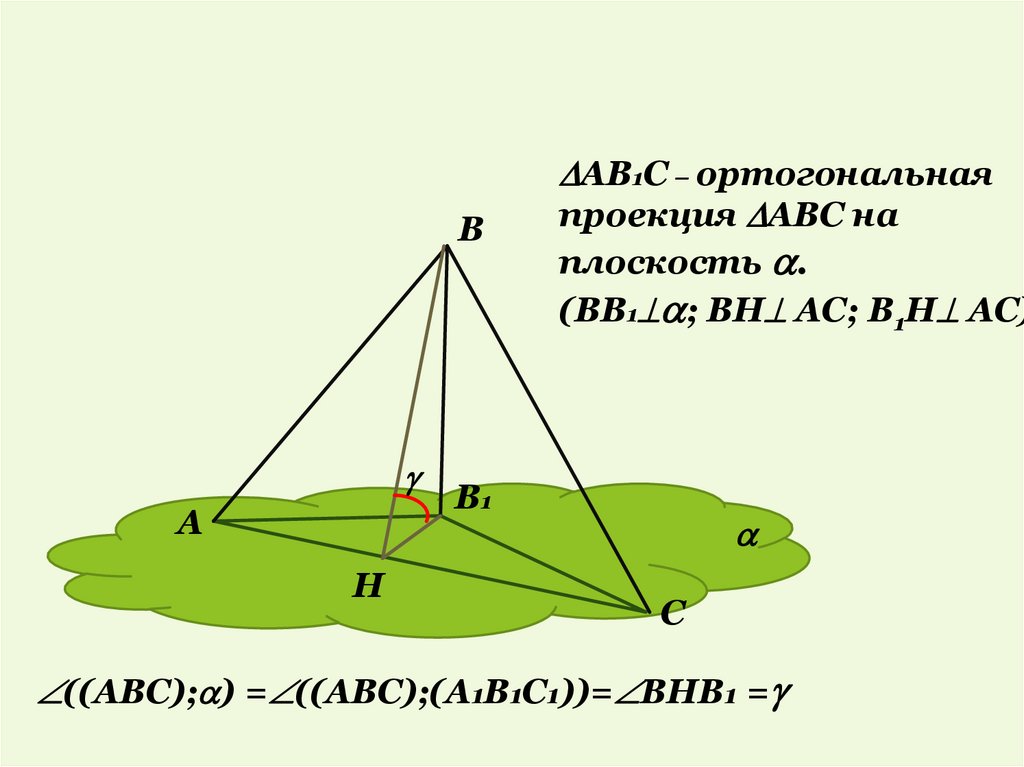
Ортогональная проекция фигуры
на плоскость:
В
А
Н
АВ1С – ортогональная
проекция АВС на
плоскость .
(ВВ1 ; ВН АС; В1Н АС)
В1
С
((АВС); ) = ((АВС);(А1В1С1))= ВНВ1 =

8.

S AB1C =S ABC cos
Площадь ортогональной проекции
треугольника равна произведению площади
треугольника на косинус угла между их
плоскостями.

9.

В
А
Н
АВ1С – ортогональная
проекция АВС на
плоскость .
(ВВ1 ; ВН АС; В1Н АС)
В1
С
((АВС); ) = ((АВС);(А1В1С1))= ВНВ1 =

10. Задача № 1

Большее основание равнобедренной трапеции, принадлежит
плоскости α, которая с плоскостью трапеции образует угол 60°.
Зная, что основания трапеции 15 см и 5 см, а боковая сторона 5 см,
найти расстояние между меньшим основанием и плоскостью α и угол
между диагональю трапеции и плоскостью α.

11.

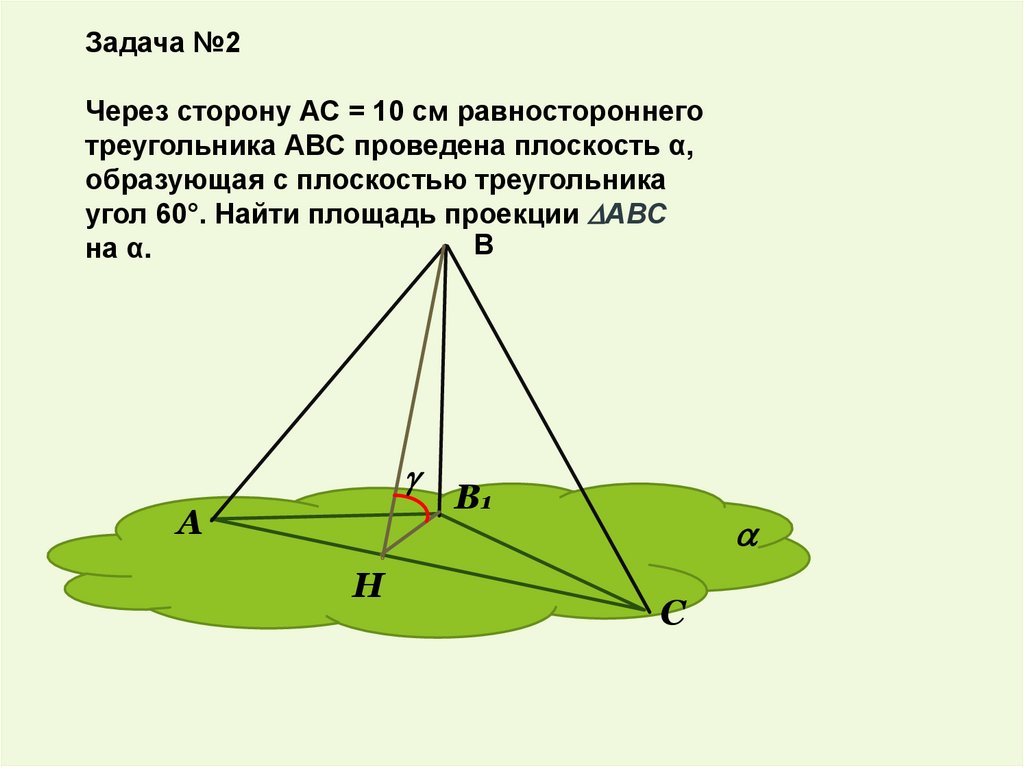
Задача №2
Через сторону АС = 10 см равностороннего
треугольника АВС проведена плоскость α,
образующая с плоскостью треугольника
угол 60°. Найти площадь проекции АВС
В
на α.
А
Н
В1
С

12.

Задача №3
Ортогональной проекцией треугольника,
площадь которого 420 является
треугольник со сторонами 39; 17; 28 см.
Найдите угол между плоскостями.

13.

Задание на дом:
В правильной пирамиде боковое ребро
6 см наклонено к плоскости основания
под углом 60°. Найти периметр
основания, площадь основания.